Existence Results for Nonlinear Fractional Problems with Non-Homogeneous Integral Boundary Conditions
Abstract
1. Introduction
2. Preliminary Results
3. Linear Problem
- 1.
- G is a continuous function on.
- 2.
- If then for all
- 3.
- Consider the functionand the positive content M, introduced in Lemma 2. Then the following inequality holds:withand
- It is obvious from the continuity of , and .
- From Lemma 2 and for and , since , we haveNow, using again Lemma 2, from equation (8) we obtainWhich completes the proof. ☐
4. Nonlinear Problem
4.1. Existence of Solutions
- (1)
- If there exists such that for all and all , then .
- (2)
- If for all and all , then .
- (3)
- Let be open in X such that . Then
- (4)
- If then there exists such that .
- (H1)
- is a continuous function.
4.2. Non-Existence Results
- (i)
- for and , where .
- (ii)
- for and , with ( given in Lemma 6).
- (i)
- Suppose, on the contrary, that there exists , on I, u not identically zero on I, that solves (1). As we have seen, this property is equivalent to the fact that . As a consequence, since , for , we haveTherefore, we get , which is a contradiction.
- (ii)
- In this case, it the result is false, we have that there exists , on I, with , such that .Then, for , we haveUsing that for all and, since is a continuous, non-negative and non-trivial function on , we have thatIn particular, previous inequalities show us thatMoreoverwhich is a contradiction. ☐
5. A Particular Example
Author Contributions
Funding
Conflicts of Interest
References
- Butzer, P.L.; Westphal, U. An introduction to fractional calculus. In Applications of Fractional Calculus in Physics; Hilfer, R., Ed.; World Scientific: Hackensack, NJ, USA, 2000. [Google Scholar]
- Gorenflo, R.; Mainardi, F. Fractional calculus: Integral and differential equations of fractional order. In Fractals and Fractional Calculus in Continuum Mechanics; Carpinteri, A., Mainardi, F., Eds.; Springer: New York, NY, USA, 1997; pp. 223–276. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists, 2nd ed.; World Scientific: Singapore, 2014. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Povstenko, Y. Linear. In Fractional Diffusion-Wave Equation for Scientists and Engineers; Birkhäuser: New York, NY, USA, 2015. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: Yverdon, Switzerland, 1993. [Google Scholar]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin, Germany, 2013. [Google Scholar]
- Ahmad, B.; Alsaedi, A.; Alghamdi, B.S. Analytic approximation of solutions of the forced Duffing equation with integral boundary conditions. Nonlinear Anal. Real World Appl. 2008, 9, 1727–1740. [Google Scholar] [CrossRef]
- Cabada, A.; Aleksić, S.; Tomović, T.V.; Dimitrijević, S. Existence of Solutions of Nonlinear and Non-local Fractional Boundary Value Problems. Mediterr. J. Math. 2019, 16, 119. [Google Scholar] [CrossRef]
- Chen, P.; Gao, Y. Positive solutions for a class of nonlinear fractional differential equations with nonlocal boundary value conditions. Positivity 2018, 22, 761–772. [Google Scholar] [CrossRef]
- Graef, J.R.; Kong, L.Q.; Wang, M. Uniqueness of positive solutions of fractional boundary value problems with non-homogeneous integral boundary conditions. Fract. Calc. Appl. Anal. 2012, 15, 509–528. [Google Scholar] [CrossRef]
- Jiang, J.; Liu, W.; Wang, H. Positive solutions to singular Dirichlet-type boundary value problems of nonlinear fractional differential equations. Adv. Differ. Equ. 2018. [Google Scholar] [CrossRef]
- Tellab, B.; Haouam, K. Solvability of semilinear fractional differential equations with nonlocal and integral boundary conditions. Math. Eng. Sci. Aerosp. 2019, 10, 341–356. [Google Scholar]
- Zhang, X.; Wang, L.; Sun, Q. Existence of positive solutions for a class of nonlinear fractional differential equations with integral boundary conditions and a parameter. Appl. Math. Comput. 2014, 226, 708–718. [Google Scholar] [CrossRef]
- Ahmad, B.; Nieto, J.J. Existence results for nonlinear boundary value problems of fractional integro differential equations with integral boundary conditions. Bound. Value Probl. 2009. [Google Scholar] [CrossRef]
- Benchohra, M.; Cabada, A.; Seba, D. An existence result for nonlinear fractional differential equations on Banach spaces. Bound. Value Probl. 2009. [Google Scholar] [CrossRef]
- Feng, M.; Liu, X.; Feng, H. The existence of positive solution to a nonlinear fractional differential equation with integral boundary conditions. Adv. Differ. Equ. 2011. [Google Scholar] [CrossRef]
- Guo, D.; Lakshmikantham, V. Nonlinear Problems in Abstract Cones; Academic Press: New York, NY, USA, 1988. [Google Scholar]
- Zeidler, E. Nonlinear Functional Analysis and Its Applications. I. Fixed-Point Theorems; Translated from the German by Peter R. Wadsack; Springer: New York, NY, USA, 1986. [Google Scholar]
- Amann, H. Fixed point equations and nonlinear eigenvalue problems in ordered Banach spaces. SIAM Rev. 1976, 18, 620–709. [Google Scholar] [CrossRef]
- Cabada, A.; Infante, G.; Tojo, F.A.F. Nonzero solutions of perturbed Hammerstein integral equations with deviated arguments and applications. Topol. Methods Nonlinear Anal. 2016, 47, 265–287. [Google Scholar] [CrossRef]
- Frigon, M.; Infante, G.; Jebelean, P. Fixed Point Theory and Variational Methods for Nonlinear Differential and Integral Equations; Lecture Notes in Nonlinear Analysis, 16. Juliusz Schauder Center for Nonlinear Studies, Toruń; Nicholas Copernicus University: Toruń, Poland, 2017; p. 192. [Google Scholar]
- Infante, G.; Webb, J.R.L. Nonlinear nonlocal boundary value problems and perturbed Hammerstein integral equations. Proc. Edinb. Math. Soc. 2006, 49, 637–656. [Google Scholar] [CrossRef]
- Lan, K.Q.; Webb, J.R.L. Positive solutions of semilinear differential equations with singularities. J. Differ. Equ. 1998, 148, 407–421. [Google Scholar] [CrossRef]
- Webb, J.R.L. Remarks on positive solutions of three point boundary value problems. Discret. Contin. Dyn. Syst. 2003, 905–915. [Google Scholar] [CrossRef]
- Cabada, A.; Wanassi, O.K. Existence and uniqueness of positive solutions for nonlinear fractional mixed problems. arXiv 2019, arXiv:1903.09042. [Google Scholar]
- Kong, Y.; Chen, P. Positive solutions for periodic boundary value problem of fractional differential equation in Banach spaces. Adv. Differ. Equ. 2018. [Google Scholar] [CrossRef]
- Lan, K.Q. Multiple positive solutions of semilinear differential equations with singularities. J. Lond. Math. Soc. 2001, 63, 690–704. [Google Scholar] [CrossRef]
- Liang, S.; Zhang, J. Existence of multiple positive solutions for m-point fractional boundary value problems on an infinite interval. Math. Comput. Model. 2011, 54, 1334–1346. [Google Scholar] [CrossRef]
- Cabada, A.; Hamdi, Z. Existence results for nonlinear fractional Dirichlet problems on the right side of the first eigenvalue. Georgian Math. J. 2017, 24, 41–53. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations. In North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherland, 2006; Volume 204. [Google Scholar]
- Lloyd, N.G. Degree Theory; Cambridge University Press: Cambridge, UK; New York, NY, USA; Melbourne, Australia, 1978; Volume 73. [Google Scholar]
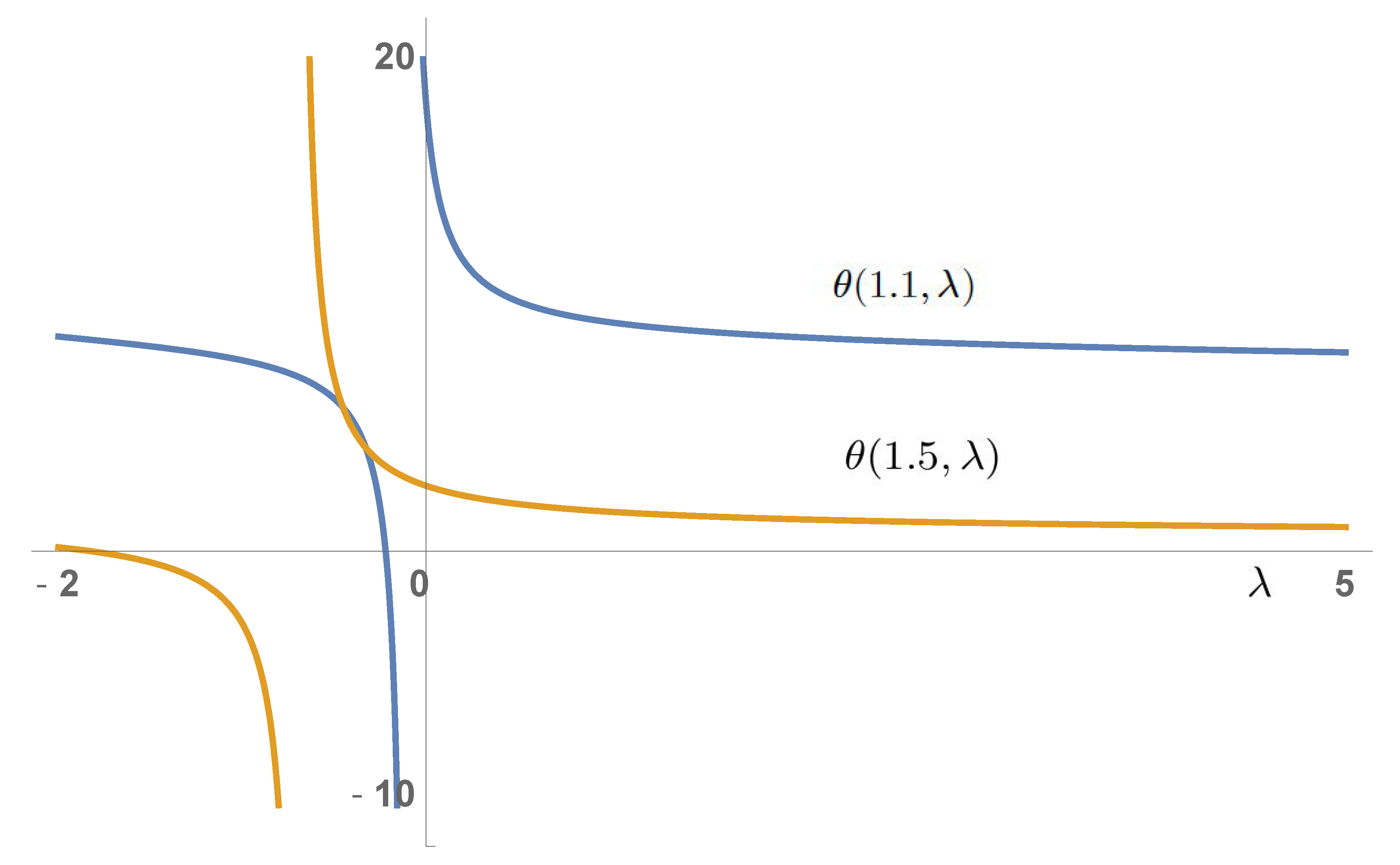
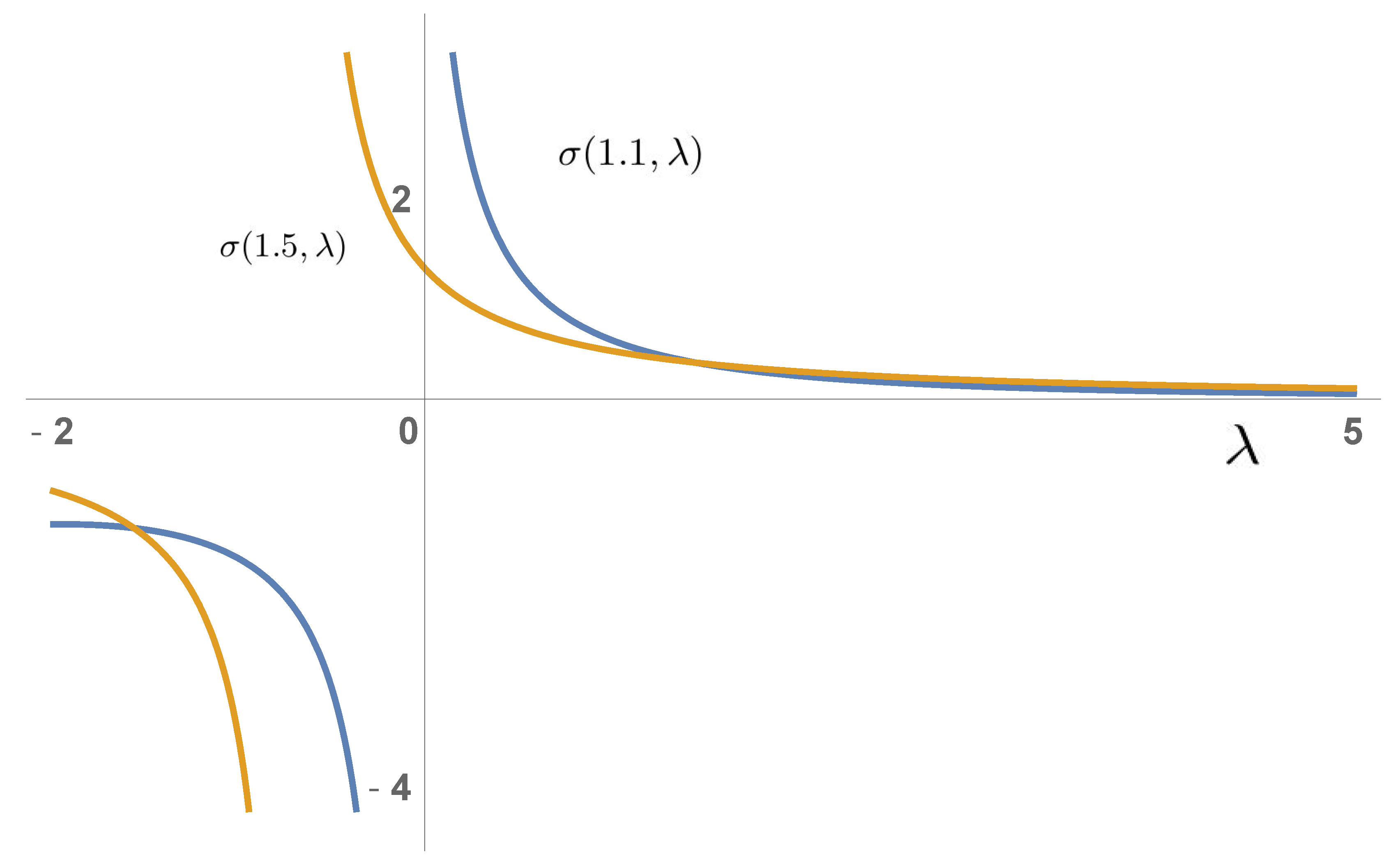
| 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | 2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| −5 | −4.5 | −4 | −3.5 | −3 | −2.5 | −2 | −1.5 | −1 | −0.5 | |
| 12.647 | 5.62054 | 2.83501 | 1.47577 | 0.657725 | −0.0336574 | −1.21724 | 54.6033 | 2.13745 | 1.20846 | |
| −4.52049 | −1.94567 | −0.99204 | −0.688973 | −0.638201 | −0.777128 | −1.40827 | 38.7227 | 1.22996 | 0.630732 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabada, A.; Wanassi, O.K. Existence Results for Nonlinear Fractional Problems with Non-Homogeneous Integral Boundary Conditions. Mathematics 2020, 8, 255. https://doi.org/10.3390/math8020255
Cabada A, Wanassi OK. Existence Results for Nonlinear Fractional Problems with Non-Homogeneous Integral Boundary Conditions. Mathematics. 2020; 8(2):255. https://doi.org/10.3390/math8020255
Chicago/Turabian StyleCabada, Alberto, and Om Kalthoum Wanassi. 2020. "Existence Results for Nonlinear Fractional Problems with Non-Homogeneous Integral Boundary Conditions" Mathematics 8, no. 2: 255. https://doi.org/10.3390/math8020255
APA StyleCabada, A., & Wanassi, O. K. (2020). Existence Results for Nonlinear Fractional Problems with Non-Homogeneous Integral Boundary Conditions. Mathematics, 8(2), 255. https://doi.org/10.3390/math8020255