Differential Equations Associated with Two Variable Degenerate Hermite Polynomials

Abstract

In this paper, we introduce the two variable degenerate Hermite polynomials and obtain some new symmetric identities for two variable degenerate Hermite polynomials. In order to give explicit identities for two variable degenerate Hermite polynomials, differential equations arising from the generating functions of degenerate Hermite polynomials are studied. Finally, we investigate the structure and symmetry of the zeros of the two variable degenerate Hermite equations.

1. Introduction

The classical Hermite numbers $H_n$ and Hermite polynomials $H_n\left(x\right)$ are usually defined by the generating functions:

$$e^{2xt-t^2}=\sum _{n=0}^{\infty }{H}_n\left(x\right){\displaystyle \frac{t^n}{n!}}$$

and

$$e^{-t^2}=\sum _{n=0}^{\infty }{H}_n{\displaystyle \frac{t^n}{n!}}.$$

Clearly, $H_n=H_n\left(0\right)$.

It can be seen that these numbers and polynomials play an important role in various areas of mathematics and physics, including numerical theory, combinations, special functions, and differential equations. Many interesting properties about them have been explored (see [1,2,3,4,5,6]). For example, in mathematics and physics, the Hermite polynomials are a classical orthogonal polynomial sequence. In probability, they appears as the Edgeworth series; in combinatorics, they arise in the umbral calculus as an example of an Appell sequence; in numerical analysis, they play a role in Gaussian quadrature; and in physics, they give rise to the eigenstates of the quantum harmonic oscillator. The polynomials $H_n\left(x\right)$ satisfy the Hermite differential equation:

$${\displaystyle \frac{d^{2}H\left(x\right)}{d{x}^2}}-2x{\displaystyle \frac{dH\left(x\right)}{dx}}+2nH\left(x\right)=0,n=0,1,2,\dots .$$

Thus, the Hermite polynomials $H_n\left(x\right)$ satisfy the second-order linear differential equation:

$$v^{″}-2x{v}^{\prime }+2nv=0.$$

The special polynomials of two variables provided a new means of analysis for the solution of large classes of partial differential equations often encountered in physical problems. Most of the special polynomials of mathematical physics and their generalization have been proposed by physical problems. As another application of the Hermite differential equation for $H_n(x,y)$, we recall that the two variable Hermite polynomials $H_n(x,y)$ defined by the generating function (see [2]):

$$\sum _{n=0}^{\infty }{H}_n(x,y){\displaystyle \frac{t^n}{n!}}=e^{xt+y{t}^2}$$

(1)

are the solution of heat equation:

$${\displaystyle \frac{\partial }{\partial y}}{H}_n(x,y)={\displaystyle \frac{{\partial }^2}{\partial x^2}}{H}_n(x,y),H_n(x,0)=x^n.$$

(2)

Observe that

$$H_n(2x,-1)=H_n\left(x\right).$$

Motivated by their potential and importance for applications in certain problems in probability, combinatorics, number theory, differential equations, numerical analysis, and other fields of mathematics and physics, several kinds of some special polynomials and numbers were recently studied by many authors (see [1,2,3,4,5,6,7]). Many mathematicians have studied the area of the degenerate Bernoulli polynomials, degenerate Euler polynomials, and degenerate tangent polynomials (see [8,9,10,11]). One of the important aspect of the study of any degenerate polynomials is to find their definition. Recently, Haroon and Khan [12] proposed the degenerate Hermite-Bernoulli polynomials, which are formulated in terms of p-adic invariant integral on ${\mathbb{Z}}_p$:

$$\sum _{n=0}^{\infty }{}_H{B}_n(x,y|\lambda ){\displaystyle \frac{t^n}{n!}}={\displaystyle \frac{log{(1+\lambda t)}^{{\displaystyle \frac{1}{\lambda }}}}{{(1+\lambda t)}^{{\displaystyle \frac{1}{\lambda }}}-1}}{(1+\lambda t)}^{{\displaystyle \frac{x}{\lambda }}}{(1+\lambda t^2)}^{{\displaystyle \frac{y}{\lambda }}}.$$

Mathematicians have studied the differential equations arising from the generating functions of special polynomials (see [13,14,15,16,17,18]). Based on the results so far, in the present work, a new class of degenerate Hermite polynomials is constructed. We can derive the differential equations generated from the generating function of two variable degenerate Hermite polynomials. By using the coefficients of this differential equation, we have explicit identities for the two variable degenerate Hermite polynomials.

We remember that the classical Stirling numbers of the first kind $S_1(n,k)$ and the second kind $S_2(n,k)$ are defined by the relations (see [8,9,10,11,12]):

$${\left(x\right)}_n=\sum _{k=0}^n{S}_1(n,k)x^k\mathrm{and}{x}^n=\sum _{k=0}^n{S}_2(n,k){\left(x\right)}_k,$$

respectively. Here, ${\left(x\right)}_n=x(x-1)\cdots (x-n+1)$ denotes the falling factorial polynomial of order n. We also have:

$$\sum _{n=m}^{\infty }{S}_2(n,m){\displaystyle \frac{t^n}{n!}}={\displaystyle \frac{{(e^t-1)}^m}{m!}}\mathrm{and}\sum _{n=m}^{\infty }{S}_1(n,m){\displaystyle \frac{t^n}{n!}}={\displaystyle \frac{{(log(1+t))}^m}{m!}}.$$

(3)

The rest of the paper is organized as follows. In Section 2, we introduce the two variable degenerate Hermite polynomials and obtain the basic properties of these polynomials. In Section 3, we give some symmetric identities for two variable degenerate Hermite polynomials. In Section 4, we derive the differential equations generated from the generating function of two variable degenerate Hermite polynomials. Using the coefficients of this differential equation, we have explicit identities for the two variable degenerate Hermite polynomials. In Section 5, we investigate the zeros of the two variable degenerate Hermite equations by using a computer. Further, we observe the pattern of scattering phenomenon for the zeros of two variable degenerate Hermite equations. Our paper ends with Section 6, where the conclusions and future directions of this work are presented.

2. Basic Properties for the Two Variable Degenerate Hermite Polynomials

In this section, a new class of the two variable degenerate Hermite polynomials is considered. Further, some properties of these polynomials are also obtained.

We define the two variable degenerate Hermite polynomials ${\mathcal{H}}_n(x,y,\lambda )$ by means of the generating function:

$$\sum _{n=0}^{\infty }{\mathcal{H}}_n(x,y,\lambda ){\displaystyle \frac{t^n}{n!}}={(1+\lambda )}^{{\displaystyle \frac{xt}{\lambda }}}{(1+\lambda )}^{{\displaystyle \frac{y{t}^2}{\lambda }}}.$$

(4)

Since ${(1+\lambda )}^{\frac{t}{\lambda }}\to e^t$ as $\lambda \to 0$, it is evident that Equation (4) reduces to Equation (1). Observe that Khan’s degenerate Hermite-Bernoulli polynomials ${}_H{B}_n(x,y|\lambda )$ vary from the two variable degenerate Hermite polynomials ${\mathcal{H}}_n(x,y,\lambda )$. Another application of the differential equation for ${\mathcal{H}}_n(x,y,\lambda )$ is as follows: Note that:

$$F(t,x,y,\lambda )={(1+\lambda )}^{{\displaystyle \frac{xt}{\lambda }}}{(1+\lambda )}^{{\displaystyle \frac{y{t}^2}{\lambda }}}$$

satisfies

$${\displaystyle \frac{log(1+\lambda )}{\lambda }}{\displaystyle \frac{\partial F(t,x,y,\lambda )}{\partial y}}-{\displaystyle \frac{{\partial }^{2}F(t,x,y,\lambda )}{\partial x^2}}=0.$$

Substitute the series in Equation (4) for $F(t,x,y,\lambda )$ to get:

$${\displaystyle \frac{\partial }{\partial y}}{\mathcal{H}}_n(x,y,\lambda )-{\displaystyle \frac{\lambda }{log(1+\lambda )}}{\displaystyle \frac{{\partial }^2}{\partial x^2}}{\mathcal{H}}_n(x,y,\lambda )=0.$$

Thus, the two variable degenerate Hermite polynomials ${\mathcal{H}}_n(x,y,\lambda )$ in the generating function (4) are the solution of equation:

$${\displaystyle \frac{\partial }{\partial y}}{\mathcal{H}}_n(x,y,\lambda )={\displaystyle \frac{\lambda }{log(1+\lambda )}}{\displaystyle \frac{{\partial }^2}{\partial x^2}}{\mathcal{H}}_n(x,y,\lambda ),{\mathcal{H}}_n(x,0,\lambda )={\left({\displaystyle \frac{\lambda }{log(1+\lambda )}}\right)}^n{x}^n.$$

(5)

Since ${\displaystyle \frac{\lambda }{log(1+\lambda )}}\to 1$ as $\lambda$ approaches zero, it is apparent that Equation (5) descends to Equation (2).

By Equation (3), we also need the binomial theorem: for a variable x,

$$\begin{array}{cc}\hfill {(1+\lambda )}^{xt/\lambda }& ={\displaystyle \sum _{m=0}^{\infty }}{\left({\displaystyle \frac{tx}{\lambda }}\right)}_m{\displaystyle \frac{{\lambda }^m}{m!}}\hfill \\ & ={\displaystyle \sum _{m=0}^{\infty }}\left({\displaystyle \sum _{l=0}^m}{S}_1(m,l){\left({\displaystyle \frac{tx}{\lambda }}\right)}^l{\displaystyle \frac{{\lambda }^m}{m!}}\right)\hfill \\ & ={\displaystyle \sum _{l=0}^{\infty }}\left({\displaystyle \sum _{m=l}^{\infty }}{S}_1(m,l)x^l{\lambda }^{m-l}{\displaystyle \frac{l!}{m!}}\right){\displaystyle \frac{t^l}{l!}}.\hfill \end{array}$$

(6)

The generating function (4) is useful for deriving several properties of the two variable degenerate Hermite polynomials ${\mathcal{H}}_n(x,y,\lambda )$. For example, we have the following expression for these polynomials:

Theorem 1.

For any positive integer n, we have:

$$H_n(x,y)=n!\sum _{k=0}^{\left[\frac{n}{2}\right]}{\displaystyle \frac{y^k{x}^{n-2k}}{k!(n-2k)!}},$$

where $\left[\right]$ denotes taking the integer part.

Proof. 

By Equations (4) and (6), we have:

$$\begin{array}{cc}\hfill {\displaystyle \sum _{n=0}^{\infty }}{\mathcal{H}}_n(x,y,\lambda ){\displaystyle \frac{t^n}{n!}}& ={(1+\lambda )}^{{\displaystyle \frac{xt}{\lambda }}}{(1+\lambda )}^{{\displaystyle \frac{y{t}^2}{\lambda }}}\hfill \\ & ={\displaystyle \sum _{k=0}^{\infty }}{\left({\displaystyle \frac{ylog(1+\lambda )}{\lambda }}\right)}^k{\displaystyle \frac{t^{2k}}{k!}}{\displaystyle \sum _{l=0}^{\infty }}{\left({\displaystyle \frac{xlog(1+\lambda )}{\lambda }}\right)}^l{\displaystyle \frac{t^l}{l!}}\hfill \\ & ={\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^{\left[\frac{n}{2}\right]}}{\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^{n-k}{y}^k{x}^{n-2k}{\displaystyle \frac{n!}{k!(n-2k)!}}\right){\displaystyle \frac{t^n}{n!}}.\hfill \end{array}$$

On comparing the coefficients of $\frac{t^n}{n!}$, the expected result of Theorem 1 is achieved. □

When $\lambda \to 0$, then we have:

$$H_n(x,y)=n!\sum _{k=0}^{\left[\frac{n}{2}\right]}{\displaystyle \frac{y^k{x}^{n-2k}}{k!(n-2k)!}}.$$

The following basic properties of the two variable degenerate Hermite polynomials ${\mathcal{H}}_n(x,y,\lambda )$ are derived from (4). We, therefore, chose to omit the details involved.

Theorem 2.

For any positive integer n, we have:

$$\begin{array}{l}\left(1\right){\mathcal{H}}_n(x,0,\lambda )={\displaystyle \sum _{m=n}^{\infty }}{S}_1(m,n)x^n{\lambda }^{m-n}{\displaystyle \frac{n!}{m!}}.\\ \left(2\right){\mathcal{H}}_n(x,y,\lambda )=n!{\displaystyle \sum _{k=0}^{\left[\frac{n}{2}\right]}}\left({\displaystyle \sum _{m=k}^{\infty }}{\displaystyle \frac{S_1(m,k)y^k{\lambda }^{m-k}}{m!}}{\displaystyle \sum _{m=n-2k}^{\infty }}{\displaystyle \frac{S_1(m,n-2k)x^{n-2k}{\lambda }^{m-n+2k}}{m!}}\right).\\ \left(3\right){\mathcal{H}}_n(x_1+x_2,y,\lambda )={\displaystyle \sum _{l=0}^n}\left(\genfrac{}{}{0pt}{}{n}{l}\right){\mathcal{H}}_l(x_1,y,\lambda ){\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^{n-l}{x}_2^{n-l}.\\ \left(4\right){\mathcal{H}}_n(x_1+x_2,y,\lambda )={\displaystyle \sum _{l=0}^n}\left(\genfrac{}{}{0pt}{}{n}{l}\right){\mathcal{H}}_{n-l}(x_1,y,\lambda ){\displaystyle \sum _{m=l}^{\infty }}{S}_1(m,l)x_2^l{\lambda }^{m-l}{\displaystyle \frac{l!}{m!}}.\\ \left(5\right){\mathcal{H}}_n(x,y_1+y_2,\lambda )={\displaystyle \sum _{k=0}^{\left[\frac{n}{2}\right]}}{\mathcal{H}}_k(x,y_1,\lambda ){\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^{n-2k}{y}_2^{n-2k}{\displaystyle \frac{n!}{k!(n-2k)!}}.\\ \left(6\right){\mathcal{H}}_n(x,y_1+y_2,\lambda )=n!{\displaystyle \sum _{k=0}^{\left[\frac{n}{2}\right]}}{\displaystyle \sum _{m=k}^{\infty }}{\displaystyle \frac{S_1(m,k)y_2^k{\lambda }^{m-k}}{m!(n-2k)!}}{\mathcal{H}}_{n-2k}(x,y_1,\lambda ).\\ \left(7\right){\mathcal{H}}_n(x_1+x_2,y_1+y_2,\lambda )={\displaystyle \sum _{l=0}^n}\left(\genfrac{}{}{0pt}{}{n}{l}\right){\mathcal{H}}_l(x_1,y_1,\lambda ){\mathcal{H}}_{n-l}(x_2,y_2,\lambda ).\end{array}$$

3. Symmetric Identities for the Two Variable Degenerate Hermite Polynomials

In this section, we give some new symmetric identities for the two variable degenerate Hermite polynomials. We also get some explicit formulas and properties for the two variable degenerate Hermite polynomials.

Let $a,b>0$ and $a\ne b.$ We start with:

$$\mathcal{F}(t,\lambda )={(1+\lambda )}^{{\displaystyle \frac{abxt}{\lambda }}}{(1+\lambda )}^{{\displaystyle \frac{a^2{b}^{2}y{t}^2}{\lambda }}}.$$

Then, the expression for $\mathcal{F}(t,\lambda )$ is symmetric in a and b:

$$\mathcal{F}(t,\lambda )=\sum _{m=0}^{\infty }{\mathcal{H}}_m(ax,a^{2}y,\lambda ){\displaystyle \frac{{\left(bt\right)}^m}{m!}}=\sum _{m=0}^{\infty }{b}^m{\mathcal{H}}_m(ax,a^{2}y,\lambda ){\displaystyle \frac{t^m}{m!}}.$$

On similar lines, we can obtain that:

$$\mathcal{F}(t,\lambda )=\sum _{m=0}^{\infty }{\mathcal{H}}_m(bx,b^{2}y,\lambda ){\displaystyle \frac{{\left(at\right)}^m}{m!}}=\sum _{m=0}^{\infty }{a}^m{\mathcal{H}}_m(bx,b^{2}y,\lambda ){\displaystyle \frac{t^m}{m!}}.$$

Comparing the coefficients of ${\displaystyle \frac{t^m}{m!}}$ in the last two equations, we have the following theorem.

Theorem 3.

Let $a,b>0$ and $a\ne b.$ The following identity holds true:

$$a^m{\mathcal{H}}_m(bx,b^{2}y,\lambda )=b^m{\mathcal{H}}_m(ax,a^{2}y,\lambda ).$$

Again, we now use:

$$\mathcal{G}(t,\lambda )={\displaystyle \frac{abt{(1+\lambda )}^{{\displaystyle \frac{abxt}{\lambda }}}{(1+\lambda )}^{{\displaystyle \frac{a^2{b}^{2}y{t}^2}{\lambda }}}\left({(1+\lambda )}^{{\displaystyle \frac{abt}{\lambda }}}-1\right)}{\left({(1+\lambda )}^{{\displaystyle \frac{at}{\lambda }}}-1\right)\left({(1+\lambda )}^{{\displaystyle \frac{bt}{\lambda }}}-1\right)}}.$$

For $\lambda \in \mathbb{C}$, we define the degenerate Bernoulli polynomials given by the generating function:

$$\sum _{n=0}^{\infty }{\mathcal{B}}_n(x,\lambda ){\displaystyle \frac{t^n}{n!}}={\displaystyle \frac{t}{{(1+\lambda )}^{{\displaystyle \frac{t}{\lambda }}}-1}}{(1+\lambda )}^{{\displaystyle \frac{xt}{\lambda }}}.$$

When $x=0$ and ${\mathcal{B}}_n\left(\lambda \right)={\mathcal{B}}_n(0,\lambda )$ are called the degenerate Bernoulli numbers. The first few follow immediately from this generating function,

$$\begin{array}{l}{\mathcal{B}}_0\left(\lambda \right)={\displaystyle \frac{\lambda }{log(1+\lambda )}},\\ {\mathcal{B}}_1\left(\lambda \right)=-{\displaystyle \frac{1}{2}}+x,\\ {\mathcal{B}}_2\left(\lambda \right)={\displaystyle \frac{log(1+\lambda )}{6\lambda }}-{\displaystyle \frac{xlog(1+\lambda )}{\lambda }}+{\displaystyle \frac{x^{2}log(1+\lambda )}{\lambda }},\\ {\mathcal{B}}_3\left(\lambda \right)={\displaystyle \frac{xlog{(1+\lambda )}^2}{2{\lambda }^2}}-{\displaystyle \frac{3x^{2}log{(1+\lambda )}^2}{2{\lambda }^2}}+{\displaystyle \frac{x^{3}log{(1+\lambda )}^2}{{\lambda }^2}},\\ {\mathcal{B}}_4\left(\lambda \right)=-{\displaystyle \frac{log{(1+\lambda )}^3}{30{\lambda }^3}}+{\displaystyle \frac{x^{2}log{(1+\lambda )}^3}{{\lambda }^3}}-{\displaystyle \frac{2x^{3}log{(1+\lambda )}^3}{{\lambda }^3}}+{\displaystyle \frac{x^{4}log{(1+\lambda )}^3}{{\lambda }^3}}.\end{array}$$

For each integer $k\ge 0$, ${\mathcal{T}}_k\left(n\right)=0^k+1^k+2^k+\cdots +{(n-1)}^k$ is called the sum of integers.

A generalized falling factorial sum ${\sigma }_k(n,\lambda )$ can be defined by the generation function:

$$\sum _{k=0}^{\infty }{\sigma }_k(n,\lambda ){\displaystyle \frac{t^k}{k!}}={\displaystyle \frac{{(1+\lambda )}^{{\displaystyle \frac{(n+1)t}{\lambda }}}-1}{{(1+\lambda )}^{{\displaystyle \frac{t}{\lambda }}}-1}}.$$

Note that ${lim}_{\lambda \to 0}{\sigma }_k(n,\lambda )={\mathcal{T}}_k\left(n\right).$ From $\mathcal{G}(t,\lambda )$, we get the following result:

$$\begin{array}{cc}\hfill \mathcal{G}(t,\lambda )& ={\displaystyle \frac{abt{(1+\lambda )}^{{\displaystyle \frac{abxt}{\lambda }}}{(1+\lambda )}^{{\displaystyle \frac{a^2{b}^{2}y{t}^2}{\lambda }}}\left({(1+\lambda )}^{{\displaystyle \frac{abt}{\lambda }}}-1\right)}{\left({(1+\lambda )}^{{\displaystyle \frac{at}{\lambda }}}-1\right)\left({(1+\lambda )}^{{\displaystyle \frac{bt}{\lambda }}}-1\right)}}\hfill \\ & ={\displaystyle \frac{abt}{\left({(1+\lambda )}^{{\displaystyle \frac{at}{\lambda }}}-1\right)}}{(1+\lambda )}^{{\displaystyle \frac{abxt}{\lambda }}}{(1+\lambda )}^{{\displaystyle \frac{a^2{b}^{2}y{t}^2}{\lambda }}}{\displaystyle \frac{\left({(1+\lambda )}^{{\displaystyle \frac{abt}{\lambda }}}-1\right)}{\left({(1+\lambda )}^{{\displaystyle \frac{bt}{\lambda }}}-1\right)}}\hfill \\ & =b{\displaystyle \sum _{n=0}^{\infty }}{\mathcal{B}}_n\left(\lambda \right){\displaystyle \frac{{\left(at\right)}^n}{n!}}{\displaystyle \sum _{n=0}^{\infty }}{\mathcal{H}}_n(bx,b^{2}y,\lambda ){\displaystyle \frac{{\left(at\right)}^n}{n!}}{\displaystyle \sum _{n=0}^{\infty }}{\sigma }_k(a-1,\lambda ){\displaystyle \frac{{\left(bt\right)}^n}{n!}}\hfill \\ & ={\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{i=0}^n}{\displaystyle \sum _{m=0}^i}\left(\genfrac{}{}{0pt}{}{n}{i}\right)\left(\genfrac{}{}{0pt}{}{i}{m}\right)a^i{b}^{n+1-i}{\mathcal{B}}_m\left(\lambda \right){\mathcal{H}}_{i-m}(bx,b^{2}y,\lambda ){\sigma }_{n-i}(a-1,\lambda )\right){\displaystyle \frac{t^n}{n!}}.\hfill \end{array}$$

In a similar fashion, we have:

$$\begin{array}{cc}\hfill \mathcal{G}(t,\lambda )& ={\displaystyle \frac{abt}{\left({(1+\lambda )}^{{\displaystyle \frac{bt}{\lambda }}}-1\right)}}{(1+\lambda )}^{{\displaystyle \frac{abxt}{\lambda }}}{(1+\lambda )}^{{\displaystyle \frac{a^2{b}^{2}y{t}^2}{\lambda }}}{\displaystyle \frac{\left({(1+\lambda )}^{{\displaystyle \frac{abt}{\lambda }}}-1\right)}{\left({(1+\lambda )}^{{\displaystyle \frac{at}{\lambda }}}-1\right)}}\hfill \\ & =a{\displaystyle \sum _{n=0}^{\infty }}{\mathcal{B}}_n\left(\lambda \right){\displaystyle \frac{{\left(bt\right)}^n}{n!}}{\displaystyle \sum _{n=0}^{\infty }}{\mathcal{H}}_n(bx,b^{2}y,\lambda ){\displaystyle \frac{{\left(bt\right)}^n}{n!}}{\displaystyle \sum _{n=0}^{\infty }}{\sigma }_k(a-1,\lambda ){\displaystyle \frac{{\left(at\right)}^n}{n!}}\hfill \\ & ={\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{i=0}^n}{\displaystyle \sum _{m=0}^i}\left(\genfrac{}{}{0pt}{}{n}{i}\right)\left(\genfrac{}{}{0pt}{}{i}{m}\right)b^i{a}^{n+1-i}{\mathcal{B}}_m\left(\lambda \right){\mathcal{H}}_{i-m}(ax,a^{2}y,\lambda ){\sigma }_{n-i}(b-1,\lambda )\right){\displaystyle \frac{t^n}{n!}}.\hfill \end{array}$$

By comparing the coefficients of ${\displaystyle \frac{t^m}{m!}}$ on the right-hand sides of the last two equations, we have the theorem below.

Theorem 4.

Let $a,b>0$ and $a\ne b.$ The the following identity holds true:

$$\begin{array}{l}{\displaystyle \sum _{i=0}^n}{\displaystyle \sum _{m=0}^i}\left(\genfrac{}{}{0pt}{}{n}{i}\right)\left(\genfrac{}{}{0pt}{}{i}{m}\right)a^i{b}^{n+1-i}{\mathcal{B}}_m\left(\lambda \right){\mathcal{H}}_{i-m}(bx,b^{2}y,\lambda ){\sigma }_{n-i}(a-1,\lambda )\\ ={\displaystyle \sum _{i=0}^n}{\displaystyle \sum _{m=0}^i}\left(\genfrac{}{}{0pt}{}{n}{i}\right)\left(\genfrac{}{}{0pt}{}{i}{m}\right)b^i{a}^{n+1-i}{\mathcal{B}}_m\left(\lambda \right){\mathcal{H}}_{i-m}(ax,a^{2}y,\lambda ){\sigma }_{n-i}(b-1,\lambda ).\end{array}$$

Making the N-times derivative for Equation (4) with respect to t, we have:

$${\left({\displaystyle \frac{\partial }{\partial t}}\right)}^{N}F(t,x,y,\lambda )={\left({\displaystyle \frac{\partial }{\partial t}}\right)}^N{(1+\lambda )}^{{\displaystyle \frac{xt}{\lambda }}}{(1+\lambda )}^{{\displaystyle \frac{y{t}^2}{\lambda }}}=\sum _{m=0}^{\infty }{\mathcal{H}}_{m+N}(x,y,\lambda ){\displaystyle \frac{t^m}{m!}}.$$

(7)

By multiplying the exponential series $e^{xt}={\sum }_{m=0}^{\infty }{x}^m{\displaystyle \frac{t^m}{m!}}$ in both sides of Equation (7) and the Cauchy product, we get:

$$\begin{array}{l}{e}^{-n\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)t}{\left({\displaystyle \frac{\partial }{\partial t}}\right)}^{N}F(t,x,y,\lambda )\\ =\left({\displaystyle \sum _{m=0}^{\infty }}{(-n)}^m{\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^m{\displaystyle \frac{t^m}{m!}}\right)\left({\displaystyle \sum _{m=0}^{\infty }}{\mathcal{H}}_{m+N}(x,y,\lambda ){\displaystyle \frac{t^m}{m!}}\right)\\ ={\displaystyle \sum _{m=0}^{\infty }}\left({\displaystyle \sum _{k=0}^m}\left(\genfrac{}{}{0pt}{}{m}{k}\right){(-n)}^{m-k}{\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^{m-k}{\mathcal{H}}_{N+k}(x,y,\lambda )\right){\displaystyle \frac{t^m}{m!}}.\end{array}$$

(8)

By Equation (8) and the Leibniz rule, we have:

$$\begin{array}{l}{e}^{-n\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)t}{\left({\displaystyle \frac{\partial }{\partial t}}\right)}^{N}F(t,x,y,\lambda )\\ ={\displaystyle \sum _{k=0}^N}\left(\genfrac{}{}{0pt}{}{N}{k}\right)n^{N-k}{\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^{N-k}{\left({\displaystyle \frac{\partial }{\partial t}}\right)}^k\left(e^{-n\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)t}F(t,x,y,\lambda )\right)\\ ={\displaystyle \sum _{m=0}^{\infty }}\left({\displaystyle \sum _{k=0}^N}\left(\genfrac{}{}{0pt}{}{N}{k}\right)n^{N-k}{\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^{N-k}{\mathcal{H}}_{m+k}(x-n,y,\lambda )\right){\displaystyle \frac{t^m}{m!}}.\end{array}$$

(9)

Hence, by Equations (8) and (9), comparing the coefficients of ${\displaystyle \frac{t^m}{m!}}$ gives the below theorem.

Theorem 5.

Let $m,n,N$ be nonnegative integers. Then,

$$\begin{array}{l}{\displaystyle \sum _{k=0}^m}\left(\genfrac{}{}{0pt}{}{m}{k}\right){(-n)}^{m-k}{\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^{m-k}{\mathcal{H}}_{N+k}(x,y,\lambda )\\ ={\displaystyle \sum _{k=0}^N}\left(\genfrac{}{}{0pt}{}{N}{k}\right)n^{N-k}{\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^{N-k}{\mathcal{H}}_{m+k}(x-n,y,\lambda ).\end{array}$$

(10)

If we take $m=0$ in (10), then we have the following:

Theorem 6.

For $N=0,1,2,\dots ,$ we have:

$${\mathcal{H}}_N(x,y,\lambda )=\sum _{k=0}^N\left(\genfrac{}{}{0pt}{}{N}{k}\right)n^{N-k}{\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^{N-k}{\mathcal{H}}_k(x-n,y,\lambda ).$$

4. Differential Equations Associated with Two Variable Degenerate Hermite Polynomials

In this section, we study the differential equations with coefficients $a_i(N,x,y,\lambda )$ arising from the generating functions of the two variable degenerate Hermite polynomials:

$${\left({\displaystyle \frac{\partial }{\partial t}}\right)}^{N}F(t,x,y,\lambda )-a_0(N,x,y,\lambda )F(t,x,y,\lambda )-\cdots -a_N(N,x,y,\lambda )t^{N}F(t,x,y,\lambda )=0.$$

By using the coefficients of this differential equation, we can derive explicit identities for the two variable degenerate Hermite polynomials ${\mathcal{H}}_n(x,y,\lambda )$. Recall that:

$$F=F(t,x,y,\lambda )={(1+\lambda )}^{{\displaystyle \frac{xt}{\lambda }}}{(1+\lambda )}^{{\displaystyle \frac{y{t}^2}{\lambda }}}=\sum _{n=0}^{\infty }{\mathcal{H}}_n(x,y,\lambda ){\displaystyle \frac{t^n}{n!}},\lambda ,x,t\in \mathbb{C}.$$

(11)

Then, by Equation (11), we have:

$$\begin{array}{cc}\hfill F^{\left(1\right)}& ={\displaystyle \frac{\partial }{\partial t}}F(t,x,y,\lambda )\hfill \\ & ={\displaystyle \frac{\partial }{\partial t}}\left({(1+\lambda )}^{{\displaystyle \frac{xt}{\lambda }}}{(1+\lambda )}^{{\displaystyle \frac{y{t}^2}{\lambda }}}\right)\hfill \\ & =\left({\displaystyle \frac{(x+2yt)log(1+\lambda )}{\lambda }}\right){(1+\lambda )}^{{\displaystyle \frac{xt}{\lambda }}}{(1+\lambda )}^{{\displaystyle \frac{y{t}^2}{\lambda }}}\hfill \\ & =\left({\displaystyle \frac{(x+2yt)log(1+\lambda )}{\lambda }}\right)F(t,x,y,\lambda ),\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill F^{\left(2\right)}& ={\displaystyle \frac{\partial }{\partial t}}{F}^{\left(1\right)}(t,x,y,\lambda )\hfill \\ & =\left({\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}\right)F(t,x,y,\lambda )+\left({\displaystyle \frac{(x+2yt)log(1+\lambda )}{\lambda }}\right)F^{\left(1\right)}(t,x,y,\lambda )\hfill \\ & =\left(\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)2y+{\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^2{x}^2\right)F(t,x,y,\lambda )\hfill \\ & +\left({\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^{2}4xy\right)tF(t,x,y,\lambda )\hfill \\ & +\left({\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^2{\left(2y\right)}^2\right)t^{2}F(t,x,y,\lambda ).\hfill \end{array}$$

(13)

Continuing this process as shown in Equation (13), we can guess that:

$$F^{\left(N\right)}={\left({\displaystyle \frac{\partial }{\partial t}}\right)}^{N}F(t,x,y,\lambda )=\sum _{i=0}^N{a}_i(N,x,y,\lambda )t^{i}F(t,x,y,\lambda ),(N=0,1,2,\dots ).$$

(14)

Differentiating Equation (14) with respect to t, we have:

$$\begin{array}{ccc}\hfill F^{(N+1)}& ={\displaystyle \frac{\partial F^{\left(N\right)}}{\partial t}}\hfill & ={\displaystyle \sum _{i=0}^N}{a}_i(N,x,y,\lambda )i{t}^{i-1}F(t,x,y,\lambda )\hfill \\ & & +{\displaystyle \sum _{i=0}^N}{a}_i(N,x,y,\lambda )t^i{F}^{\left(1\right)}(t,x,y,\lambda )\hfill \\ & ={\displaystyle \sum _{i=0}^N}i{a}_i\hfill & (N,x,y,\lambda )t^{i-1}F(t,x,y,\lambda )\hfill \\ & +& {\displaystyle \sum _{i=0}^N}{\displaystyle \frac{xlog(1+\lambda )}{\lambda }}{a}_i(N,x,y,\lambda )t^{i}F(t,x,y,\lambda )\hfill \\ & +& {\displaystyle \sum _{i=0}^N}{\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}{a}_i(N,x,y,\lambda )t^{i+1}F(t,x,y,\lambda )\hfill \\ & ={\displaystyle \sum _{i=0}^{N-1}}& (i+1)a_{i+1}(N,x,y,\lambda )t^{i}F(t,x,y,\lambda )\hfill \\ & +& {\displaystyle \sum _{i=0}^N}{\displaystyle \frac{xlog(1+\lambda )}{\lambda }}{a}_i(N,x,y,\lambda )t^{i}F(t,x,y,\lambda )\hfill \\ & +& {\displaystyle \sum _{i=1}^{N+1}}{\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}{a}_{i-1}(N,x,y,\lambda )t^{i}F(t,x,y,\lambda ).\hfill \end{array}$$

(15)

Now, replacing N by $N+1$ in Equation (14), we find:

$$F^{(N+1)}=\sum _{i=0}^{N+1}{a}_i(N+1,x,y,\lambda )t^{i}F(t,x,y,\lambda ).$$

(16)

Comparing the coefficients on both sides of Equations (15) and (16), we obtain:

$$\begin{array}{l}{a}_0(N+1,x,y,\lambda )=a_1(N,x,y,\lambda )+{\displaystyle \frac{xlog(1+\lambda )}{\lambda }}{a}_0(N,x,y,\lambda ),\\ a_N(N+1,x,y,\lambda )={\displaystyle \frac{xlog(1+\lambda )}{\lambda }}{a}_N(N,x,y,\lambda )+{\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}{a}_{N-1}(N,x,y,\lambda ),\\ a_{N+1}(N+1,x,y,\lambda )={\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}{a}_N(N,x,y,\lambda ),\end{array}$$

(17)

and:

$$\begin{array}{cc}\hfill a_i(N+1,x,y,\lambda )& =(i+1)a_{i+1}(N,x,y,\lambda )+{\displaystyle \frac{xlog(1+\lambda )}{\lambda }}{a}_i(N,x,y,\lambda )\hfill \\ & +{\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}{a}_{i-1}(N,x,y,\lambda ),(1\le i\le N-1).\hfill \end{array}$$

(18)

In addition, by Equation (14), we have:

$$F(t,x,y,\lambda )=F^{\left(0\right)}(t,x,y,\lambda )=a_0(0,x,y,\lambda )F(t,x,y,\lambda ).$$

(19)

By Equation (19), we get:

$$a_0(0,x,y,\lambda )=1.$$

(20)

It is not difficult to show that:

$$\begin{array}{l}{\displaystyle \frac{xlog(1+\lambda )}{\lambda }}F(t,x,y,\lambda )+{\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}tF(t,x,y,\lambda )\\ =F^{\left(1\right)}(t,x,y,\lambda )\\ ={\displaystyle \sum _{i=0}^1}{a}_i(1,x,y,\lambda )t^{i}F(t,x,y,\lambda )\\ =a_0(1,x,y,\lambda )F(t,x,y,\lambda )+a_1(1,x,y,\lambda )tF(t,x,y,\lambda ).\end{array}$$

(21)

Thus, by Equations (12) and (21), we also get:

$$a_0(1,x,y,\lambda )={\displaystyle \frac{xlog(1+\lambda )}{\lambda }},a_1(1,x,y,\lambda )={\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}.$$

(22)

From Equation (17), we note that:

$$\begin{gathered} \begin{array}{l}{a}_0(N+1,x,y,\lambda )=a_1(N,x,y,\lambda )+{\displaystyle \frac{xlog(1+\lambda )}{\lambda }}{a}_0(N,x,y,\lambda ),\\ a_0(N,x,y,\lambda )=a_1(N-1,x,y,\lambda )+{\displaystyle \frac{xlog(1+\lambda )}{\lambda }}{a}_0(N-1,x,y,\lambda ),\\ \dots \\ a_0(N+1,x,y,\lambda )={\displaystyle \sum _{i=0}^N}{\left({\displaystyle \frac{xlog(1+\lambda )}{\lambda }}\right)}^i{a}_1(N-i,x,y,\lambda ) \\ +{\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^{N+1}{x}^{N+1},\end{array} \end{gathered}$$

(23)

$$\begin{array}{cc}\hfill a_N(N+1,x,y,\lambda )& ={\displaystyle \frac{xlog(1+\lambda )}{\lambda }}{a}_N(N,x,y,\lambda )+{\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}{a}_{N-1}(N,x,y,\lambda ),\hfill \\ \hfill a_{N-1}(N,x,y,\lambda )& ={\displaystyle \frac{xlog(1+\lambda )}{\lambda }}{a}_{N-1}(N-1,x,y,\lambda )\hfill \\ & +{\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}{a}_{N-2}(N-1,x,y,\lambda ),\dots \hfill \\ \hfill a_N(N+1,x,y,\lambda )& =(N+1)x{\left(2y\right)}^N{\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^{N+1},\hfill \end{array}$$

(24)

and:

$$\begin{array}{l}{a}_{N+1}(N+1,x,y,\lambda )={\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}{a}_N(N,x,y,\lambda ),\\ a_N(N,x,y,\lambda )={\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}{a}_{N-1}(N-1,x,y,\lambda ),\dots \\ a_{N+1}(N+1,x,y,\lambda )={\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^{N+1}{\left(2y\right)}^{N+1}.\end{array}$$

(25)

For $i=1$ in Equation (18), we have:

$$\begin{array}{cc}\hfill a_1(N+1,x,y,\lambda )=& 2{\displaystyle \sum _{k=0}^N}{\left({\displaystyle \frac{xlog(1+\lambda )}{\lambda }}\right)}^k{a}_2(N-k,x,y,\lambda )\hfill \\ & +{\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}{\displaystyle \sum _{k=0}^N}{\left({\displaystyle \frac{xlog(1+\lambda )}{\lambda }}\right)}^k{a}_0(N-k,x,y,\lambda ),\hfill \end{array}$$

(26)

Continuing this process, we can deduce that, for $1\le i\le N-1,$

$$\begin{array}{cc}\hfill a_i(N+1,x,y,\lambda )=& (i+1){\displaystyle \sum _{k=0}^N}{\left({\displaystyle \frac{xlog(1+\lambda )}{\lambda }}\right)}^k{a}_{i+1}(N-k,x,y,\lambda )\hfill \\ & +{\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}{\displaystyle \sum _{k=0}^N}{\left({\displaystyle \frac{xlog(1+\lambda )}{\lambda }}\right)}^k{a}_{i-1}(N-k,x,y,\lambda ).\hfill \end{array}$$

(27)

Note that, here, the matrix $a_i{(j,x,y,\lambda )}_{0\le i,j\le N+1}$ is given by:

$$\left(\begin{array}{ccccc}1& {\displaystyle \frac{xlog(1+\lambda )}{\lambda }}& {\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}+{\left({\displaystyle \frac{xlog(1+\lambda )}{\lambda }}\right)}^2& \cdots & ·\\ 0& {\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}& {\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^{2}4xy& \cdots & ·\\ 0& 0& {\left({\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}\right)}^2& \cdots & ·\\ ⋮& ⋮& ⋮& \ddots & ·\\ 0& 0& 0& \cdots & {\left({\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}\right)}^{N+1}\end{array}\right)$$

Therefore, by Equations (20)–(27), we obtain the following theorem.

Theorem 7.

For $N=0,1,2,\dots ,$ the differential equation:

$${\left({\displaystyle \frac{\partial }{\partial t}}\right)}^{N}F(t,x,y,\lambda )-\left(\sum _{i=0}^N{a}_i(N,x,y)t^i\right)F(t,x,y,\lambda )=0$$

has a solution

$$F=F(t,x,y,\lambda )={(1+\lambda )}^{{\displaystyle \frac{xt}{\lambda }}}{(1+\lambda )}^{{\displaystyle \frac{y{t}^2}{\lambda }}},$$

where:

$$\begin{array}{l}{a}_0(N+1,x,y,\lambda )={\displaystyle \sum _{i=0}^N}{\left({\displaystyle \frac{xlog(1+\lambda )}{\lambda }}\right)}^i{a}_1(N-i,x,y,\lambda )\hfill \\ +{\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^{N+1}{x}^{N+1},\hfill \\ a_N(N+1,x,y,\lambda )=(N+1)x{\left(2y\right)}^N{\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^{N+1},\hfill \\ a_{N+1}(N+1,x,y,\lambda )={\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^{N+1}{\left(2y\right)}^{N+1},\hfill \\ a_i(N+1,x,y,\lambda )=(i+1){\displaystyle \sum _{k=0}^N}{\left({\displaystyle \frac{xlog(1+\lambda )}{\lambda }}\right)}^k{a}_{i+1}(N-k,x,y,\lambda )\hfill \\ +{\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}{\displaystyle \sum _{k=0}^N}{\left({\displaystyle \frac{xlog(1+\lambda )}{\lambda }}\right)}^k{a}_{i-1}(N-k,x,y,\lambda ),(1\le i\le N-2).\end{array}$$

Here is a plot of the surface for this solution.

In Figure 1a, we chose $-2\le x\le 2,-2\le t\le 2,\lambda =1/2,$ and $y=0.1$. In Figure 1b, we chose $-2\le y\le 2,-1\le t\le 1,\lambda =1/2,$ and $x=0.1$.

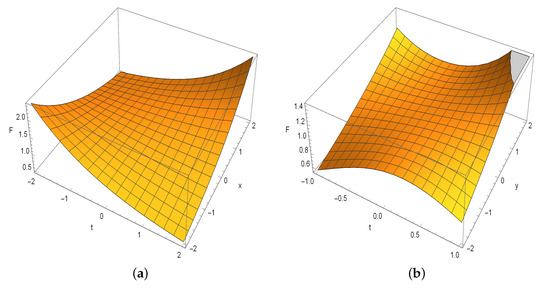
Figure 1. The surface for the solution of $F(t,x,y,\lambda )=0$. (a) $-2\le x\le 2,-2\le t\le 2,\lambda =1/2,$ and $y=0.1$; (b) $-2\le y\le 2,-1\le t\le 1,\lambda =1/2,$ and $x=0.1$

Making the N-times derivative for Equation (4) with respect to t, we have:

$${\left({\displaystyle \frac{\partial }{\partial t}}\right)}^{N}F(t,x,y,\lambda )={\displaystyle \sum _{m=0}^{\infty }}{\mathcal{H}}_{m+N}(x,y,\lambda ){\displaystyle \frac{t^m}{m!}}.$$

(28)

By Equation (28) and Theorem 7, we have:

$$\begin{array}{l}{a}_0(N,x,y,\lambda )F(t,x,y,\lambda )+a_1(N,x,y,\lambda )tF(t,x,y,\lambda )+\cdots +a_N(N,x,y,\lambda )t^{N}F(t,x,y,\lambda )\\ ={\displaystyle \sum _{m=0}^{\infty }}{\mathcal{H}}_{m+N}(x,y,\lambda ){\displaystyle \frac{t^m}{m!}}.\end{array}$$

Hence, we have the following theorem.

Theorem 8.

For $N=0,1,2,\dots ,$ we get:

$${\mathcal{H}}_{m+N}(x,y,\lambda )=\sum _{i=0}^m{\displaystyle \frac{{\mathcal{H}}_{m-i}\left(x\right)a_i(N,x,y,\lambda )m!}{(m-i)!}}.$$

(29)

If we take $m=0$ in Equation (29), then we have the corollary below.

Corollary 1.

For $N=0,1,2,\dots ,$ we have:

$${\mathcal{H}}_N(x,y,\lambda )=a_0(N,x,y,\lambda ),$$

where:

$$\begin{array}{ccc}\hfill a_0(0,x,y,\lambda )=1,& & \\ \hfill a_0(N+1,x,y,\lambda )& ={\displaystyle \sum _{i=0}^N}\hfill & {\left({\displaystyle \frac{xlog(1+\lambda )}{\lambda }}\right)}^i{a}_1(N-i,x,y,\lambda )\hfill \\ & & +{\left({\displaystyle \frac{log(1+\lambda )}{\lambda }}\right)}^{N+1}{x}^{N+1}.\hfill \end{array}$$

The first few of them are:

$$\begin{array}{l}{\mathcal{H}}_0(x,y,\lambda )=1,\\ {\mathcal{H}}_1(x,y,\lambda )={\displaystyle \frac{xlog(1+\lambda )}{\lambda }},\\ {\mathcal{H}}_2(x,y,\lambda )={\displaystyle \frac{2ylog(1+\lambda )}{\lambda }}+{\displaystyle \frac{x^2{(log(1+\lambda ))}^2}{{\lambda }^2}},\\ {\mathcal{H}}_3(x,y,\lambda )={\displaystyle \frac{6xy{(log(1+\lambda ))}^2}{{\lambda }^2}}+{\displaystyle \frac{x^3{(log(1+\lambda ))}^3}{{\lambda }^3}},\\ {\mathcal{H}}_4(x,y,\lambda )={\displaystyle \frac{12y^2{(log(1+\lambda ))}^2}{{\lambda }^2}}+{\displaystyle \frac{12x^{2}y{(log(1+\lambda ))}^3}{{\lambda }^3}}+{\displaystyle \frac{x^4{(log(1+\lambda ))}^4}{{\lambda }^4}},\\ {\mathcal{H}}_5(x,y,\lambda )={\displaystyle \frac{60x{y}^2{(log(1+\lambda ))}^3}{{\lambda }^3}}+{\displaystyle \frac{20x^{3}y{(log(1+\lambda ))}^4}{{\lambda }^4}}+{\displaystyle \frac{x^5{(log(1+\lambda ))}^5}{{\lambda }^5}}.\end{array}$$

5. Zeros of the Two Variable Degenerate Hermite Polynomials

This section shows the benefits of supporting theoretical prediction through numerical experiments and finding a new interesting pattern of the zeros of the two variable degenerate Hermite equations ${\mathcal{H}}_n(x,y,\lambda )=0$. By using a computer, the two variable degenerate Hermite polynomials ${\mathcal{H}}_n(x,y,\lambda )$ can be determined explicitly. We investigated the zeros of the two variable degenerate Hermite equations ${\mathcal{H}}_n(x,y,\lambda )=0$. The zeros of the ${\mathcal{H}}_n(x,y,\lambda )=0$ for $n=30,y=2,-2,2+i,-2-i,\lambda =1/2,$ and $x\in \mathbb{C}$ are displayed in Figure 2.

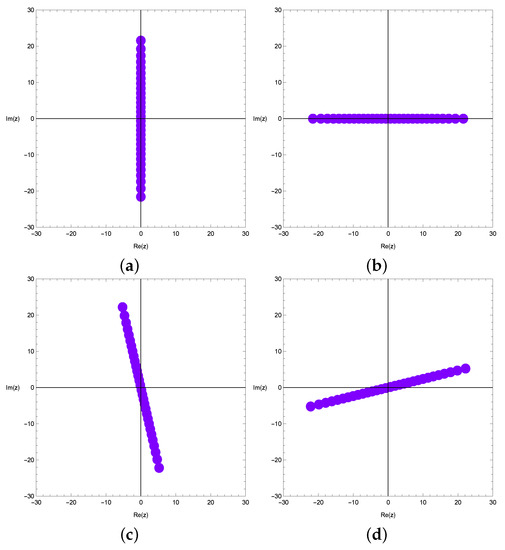
Figure 2. Zeros of ${\mathcal{H}}_n(x,y,\lambda )=0$. (a) $n=30$ and $y=2$; (b) $n=30$ and $y=-2$; (c) $n=30$ and $y=2+i$; (d) $n=30$ and $y=-2-i$.

In Figure 2a, we chose $n=30$ and $y=2$. In Figure 2b, we chose $n=30$ and $y=-2$. In Figure 2c, we chose $n=30$ and $y=2+i$. In Figure 2d, we chose $n=30$ and $y=-2-i$.

Stacks of zeros of the two variable degenerate Hermite equations ${\mathcal{H}}_n(x,y,\lambda )=0$ for $1\le n\le 30,\lambda =1/2$ from a 3D structure are presented in Figure 3.

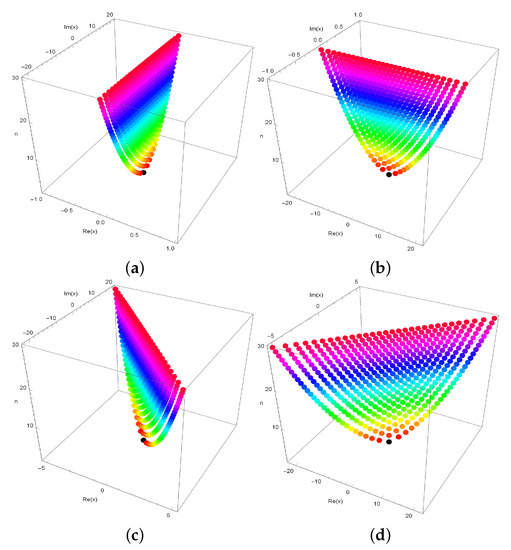
Figure 3. Stacks of zeros of ${\mathcal{H}}_n(x,y,\lambda )=0,1\le n\le 30$. (a) $y=2$; (b) $y=-2$; (c) $y=2+i$; (d) $y=-2-i$.

In Figure 3a, we chose $y=2$. In Figure 3b, we chose $y=-2$. In Figure 3c, we chose $y=2+i$. In Figure 3d, we chose $y=-2-i$.

Our numerical results for approximate solutions of real zeros of the two variable degenerate Hermite equations ${\mathcal{H}}_n(x,y,\lambda )=0$ are displayed (Table 1 and Table 2).

Table 1. Numbers of real and complex zeros of ${\mathcal{H}}_n(x,y,\lambda )=0$.

	$\mathit{y}=2,\mathit{\lambda }=1/2$		$\mathit{y}=-2,\mathit{\lambda }=1/2$.
Degree n	Real Zeros	Complex Zeros	Real Zeros	Complex Zeros
1	1	0	1	0
2	0	2	2	0
3	1	2	3	0
4	0	4	4	0
5	1	4	5	0
6	0	6	6	0
7	1	6	7	0
8	0	8	8	0
9	1	8	9	0
10	0	10	10	0

Table 2. Approximate solutions of ${\mathcal{H}}_n(x,y,\lambda )=0,x\in \mathbb{R}$.

Degree n	x
1	0
2	−2.2209,    2.2209
3	−3.8468,    0,    3.8468
4	−5.1846,    −1.6479,    1.6479,    5.1846
5	−6.3452,    −3.0108,    0,    3.0108,    6.3452
6	−7.3830,    −4.1958,    −1.3697,    1.3697,    4.1958,    7.3830
7	−8.3295,    −5.2564,    −2.5639,    0,    2.5639,    5.2564,    8.3295

We observed a remarkable regular structure of the complex roots of the two variable degenerate Hermite equations ${\mathcal{H}}_n(x,y,\lambda )=0$ and also hoped to verify the same kind of regular structure of the complex roots of the two variable degenerate Hermite equations ${\mathcal{H}}_n(x,y,\lambda )=0$ (Table 1).

The plot of the real zeros of the two variable degenerate Hermite equations ${\mathcal{H}}_n(x,y,\lambda )=0$ for the $1\le n\le 30,\lambda =1/2$ structure is presented in Figure 4.

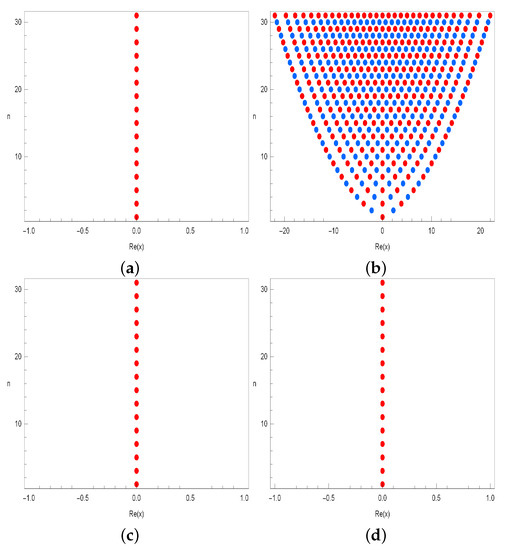
Figure 4. Real zeros of ${\mathcal{H}}_n(x,y,\lambda )=0for1\le n\le 40$. (a)$y=2$; (b) $y=-2$; (c) $y=2+i$; (d) $y=-2-i$.

In Figure 4a, we chose $y=2$. In Figure 4b, we chose $y=-2$. In Figure 4c, we chose $y=2+i$. In Figure 4d, we chose $y=-2-i$.

Next, we calculated an approximate solution satisfying ${\mathcal{H}}_n(x,y,\lambda )=0,x\in \mathbb{C}$. The results are given in Table 2. In Table 2, we chose $y=-2$ and $\lambda =1/2$.

6. Conclusions and Future Directions

In this article, we defined the two variable degenerate Hermite polynomials and obtained some new symmetric identities for two variable degenerate Hermite polynomials. We constructed differential equations arising from the generating function of the two variable degenerate Hermite polynomials ${\mathcal{H}}_n(x,y,\lambda )$. We also investigated the symmetry of the zeros of the two variable degenerate Hermite equations ${\mathcal{H}}_n(x,y,\lambda )=0$ for various variables x and y. As a result, we found that the distribution of the zeros of two variable degenerate Hermite equations ${\mathcal{H}}_n(x,y,\lambda )=0$ is a very regular pattern. Therefore, we made the following series of conjectures with numerical experiments:

Let us use the following notations. $R_{{\mathcal{H}}_n(x,y,\lambda )}$ denotes the number of real zeros of ${\mathcal{H}}_n(x,y,\lambda )=0$ lying on the real plane $Im\left(x\right)=0$, and $C_{{\mathcal{H}}_n(x,y,\lambda )}$ denotes the number of complex zeros of ${\mathcal{H}}_n(x,y,\lambda )=0$. Since n is the degree of the polynomial ${\mathcal{H}}_n(x,y,\lambda )$, we have $R_{{\mathcal{H}}_n(x,y,\lambda )}=n-C_{{\mathcal{H}}_n(x,y,\lambda )}$.

We can see a good regular pattern of the complex roots of the two variable degenerate Hermite equations ${\mathcal{H}}_n(x,y,\lambda )=0$ for y and $\lambda$. Therefore, the following conjecture is possible.

Conjecture 1.

Let n be an odd positive integer. For$y>0$or$y\in \mathbb{C}\setminus \left\{y\right|y<0\}$, prove or disprove that:

$$R_{{\mathcal{H}}_n(x,y,\lambda )}=1,C_{{\mathcal{H}}_n(x,y,\lambda )}=2\left[{\displaystyle \frac{n}{2}}\right],{\mathcal{H}}_n(0,y,\lambda )=0,$$

where$\mathbb{C}$is the set of complex numbers.

Conjecture 2.

For$y<0$, prove or disprove that:

$$R_{{\mathcal{H}}_n(x,y,\lambda )}=n,C_{{\mathcal{H}}_n(x,y,\lambda )}=0.$$

As a result of investigating more y and $\lambda$ variables, it is still unknown whether the Conjectures 1 and 2 are true or false for all variables y and $\lambda$.

We observed that solutions of the two variable degenerate Hermite equations ${\mathcal{H}}_n(x,y,\lambda )=0$ have no $Re\left(x\right)=a$ reflection symmetry for $a\in \mathbb{R}$. It is expected that solutions of the two variable degenerate Hermite equations ${\mathcal{H}}_n(x,y,\lambda )=0$ have $Re\left(x\right)=0$ reflection symmetry (see Figure 2, Figure 3 and Figure 4).

Conjecture 3.

Prove that${\mathcal{H}}_n(x,y,\lambda ),x\in \mathbb{C},y>0$, has$Im\left(x\right)=0$reflection symmetry analytic complex functions. Prove that${\mathcal{H}}_n(x,y,\lambda ),x\in \mathbb{C},y<0$, has$Re\left(x\right)=0$reflection symmetry analytic complex functions.

Finally, we considered the more general problems. How many zeros does ${\mathcal{H}}_n(x,y,\lambda )$ have? We were not able to decide if ${\mathcal{H}}_n(x,y,\lambda )=0$ had n distinct solutions. We would like to know the number of complex zeros $C_{{\mathcal{H}}_n(x,y,\lambda )}$ of ${\mathcal{H}}_n(x,y,\lambda )=0.$

Conjecture 4.

Prove or disprove that${\mathcal{H}}_n(x,y,\lambda )=0$has n distinct solutions.

As a result of investigating more n variables, it is still unknown whether the conjecture is true or false for all variables n (see Table 1 and Table 2).

We expect that research in these directions will make a new approach using the numerical method related to the research of the two variable degenerate Hermite equations ${\mathcal{H}}_n(x,y,\lambda )=0$, which appear in applied mathematics and mathematical physics.