1. Introduction
The construction of state observers for nonlinear systems is difficult in general when it is required to ensure the property of global stability for the estimation error. Such a proof is obtained by means of the Lyapunov method. Here we address the stability analysis of the error dynamics by using input-to-state stability (ISS) [
1,
2], where the disturbances are regarded as input, and the role of the state is played by the estimation error incurred by the observer. Moreover, we will address the design of state observers for polynomial nonlinear systems by using the SOS (sum-of-squares) approach [
3,
4].
The Lyapunov method has been applied in many research areas to analyze the stability of dynamic systems [
5,
6]. To prove that a system is stable in the sense of Lyapunov, a positive definite function of the state variables is shown to decrease along system trajectories. Recently, extensions of the Lyapunov approach to deal with fractional and impulsive systems have been proposed [
2,
7,
8]. Indeed, the stability of the estimation error of observers for noise-free systems can be addressed by using Lyapunov functions. However, the so-called ISS Lyapunov functions turn out to be more appropriate, as the effects of both system and measurement noises are treated, while simultaneously dealing with stability in a noise-free setting. An observer with input-to-state stable error dynamics (ISS observer, for short) is prevented to suffer from the occurrence of phenomena of finite escape and hence the use of ISS analysis is considered in various works on estimation for nonlinear systems. First results are reported in [
9,
10]. The connection between ISS and passivity w.r.t measurement disturbances is dealt with in [
11]. ISS sampled-data observers are analyzed in [
12]. The design of ISS estimators is addressed in [
13,
14,
15,
16].
Generally speaking, the first results on the construction of observers for nonlinear continuous-time systems are reported in [
17,
18,
19]. Next, state-space transformations have been studied to obtain a linear dynamics of the estimation in the new coordinates [
20,
21,
22,
23]. This entails the solution of partial differential equations (see, e.g., [
24]) to find the required transformation but makes the stability analysis straightforward. Later, quadratic Lyapuonv functions have been massively adopted to prove global stability [
25,
26,
27]. The literature on nonlinear observers reports various attempts of improvement by relaxing system assumptions and devising less conservative design conditions (see, e.g., [
28,
29]). Among others, the so-called high-gain observer has become quite popular [
30], especially for the purpose of output feedback control [
31]. More recently, Lyapunov functionals have been proposed in [
32] to prove stability for time-varying high-gain observers in line with the idea of reducing the peaking during the transient [
33,
34].
The contribution of this paper lies in highlighting the motivations to rely on ISS to both analyze the stability and construct observers for nonlinear systems. Toward this end, we deal with the problem in quite a general nonlinear setting, where the design of observers is reduced to the satisfaction of a Hamilton–Jacobi inequality [
35,
36]. Specifically, ISS is regarded in terms of
-gain to measure the attenuation of the estimation error w.r.t. the disturbances. Based on the aforesaid, we focus on the construction of observers for a class of polynomial nonlinear systems by relying on the practical
-gain proposed in [
37] and using the sum-of-squares (SOS) approach, which has become widely used in a number of applications involving polynomials [
3,
4] and is based on semidefinite programming (SDP) [
38,
39]. Following this approach, we can design observers for such polynomial systems under feasible conditions that can be easily treated.
The paper is organized as follows. The use of ISS to analyze the stability of the estimation error provided by state observers is considered in
Section 2. The special case of observers for polynomial systems is discussed in
Section 3. Numerical results concerning a case study are presented in
Section 4. The conclusions are drawn in
Section 5.
The following notation and definitions will be used throughout the paper. denotes the set of the nonnegative real numbers. stands for the set of the real matrices with n rows and m columns. Given a symmetric , () means that P is positive (negative) definite. Given a continuously differentiable function , let us define the gradients and as column vectors. The Euclidean norm in is denoted by . Let us denote by the closed ball centered in with radius . A continuous function is positive definite if it is null only in zero and is said to belong to class if it is strictly increasing. Moreover, it is said to belong to class if it is of class and also . A continuous function is said to belong to class if, for each fixed s, the mapping belongs to class w.r.t. to and, for each fixed r, the mapping is decreasing with respect to and . denotes the ring of real polynomials of ; denotes the set of the SOS polynomials of x, i.e., of the polynomials written as with . Let us denote by and the ring of real matrix polynomials of size and the set of the SOS polynomials of degree equal or less than m, respectively.
2. Input-to-State Stability for State Observers
Estimation for nonlinear noise-free continuous-time systems is usually accomplished by using observers, which are dynamic systems that aim at tracking the state variables by using only incomplete information on the state. Let the dynamic equations be given by
where
and
are smooth functions;
,
, and
are the state, input, and measurement vectors, respectively. A full-order state observer is in general described by the dynamic equation
where
is the estimate of
at time
and
is a smooth function to be chosen in such a way as to ensure that the estimation error
with dynamics given by
is asymptotically stable to zero. Moreover, usually
, i.e., roughly speaking, not all of the state variables are accessible. Notice that the dynamics of the estimation error (
3) depends in general on the system trajectory and it would always be preferable to ensure the global asymptotic stability to zero for the estimation error. In line with [
11], the interest concerns observers for systems described by (
1) with globally asymptotically stable estimation error by finding a suitable mapping
and a smooth Lyapunov function
such that
for all
,
, and
, where
,
of class
and
is continuous positive definite.
If the system is affected by disturbances, the performances deteriorate in such a way as to make the estimation error increase with the growth of the uncertainty. Anyway, it is expected to keep the estimation error asymptotically stable to zero without noise. This combination can be given with mathematical rigor by using the notion of ISS. Thus, we focus on
where
is the disturbance;
and
are smooth. Therefore, the dynamics of the estimation error is given by
where
is used instead of
as in Equation (
3) with a little abuse of notation. Based on the aforesaid, we say that the observer (
2) is ISS if there exists a function
of class
and a function
of class
such that
where
. The above ISS statement can be equivalently expressed by means of an ISS Lyapunov function [
1]: inequality (
8) holds if and only if there exist functions
,
of class
and
,
of class
such that
for all
,
,
,
, and
. The observer problem needs to be more reliably formulated in an ISS framework since a system may admit a Lyapuonv function in a noise-free case, while being not input-to-state stable. By contrast, an input-to-state stable system is asymptotically stable to zero if the external input is null. As pointed out in [
11], small noises can cause the instability of the estimation error and thus an observer with a globally asymptotically stable error may exist in the absence of disturbances, whereas the error dynamics turns out to be not input-to-state stable, as shown the following example presented in [
15].
Example 1. Considering for the system (Example 3, p. 50, [15])with , the observerprovides an estimation error that is asymptotically stable to zero if for all . If, instead, we chose , , and for all , it follows thatand the state is bounded, but the dynamics of the observer turns out to be with for all andand hence the second and third observer state variables are divergent, thus showing that ISS for the estimation error does not hold since the estimation error is unbounded with a bounded disturbance. The above example suggests constructing observers together with an ISS Lyapunov function for the dynamics of the associated estimation error. Toward this end, instead of the condition (10), let us consider the equivalent inequality
where
,
are of class
. Once the ISS Lyapunov functions are chosen, one may analyze the effect of attenuation and the disturbances on the estimation error. Thus, using (
13), let us consider
for all
, which provides an upper bound on
based on the initial conditions and a measure of the “energy” of the noises. If
V is a continuously differentiable function, (
14) holds if (
13) is satisfied. The function
V is thus a storage function, while
and
have to be regarded as dissipation and supply rates, respectively. If
and
belong to the
space of functions of time, the link between ISS and the
approach is easily found [
40]. Let us now focus on the case with the dynamics of the estimation error affine in the noises.
Theorem 1. Consider observer (2) for systems described by (6) such thatwhere and . If there exists a continuously differentiable function such that the inequalities (4) are satisfied for some functions , of class and the Hamilton–Jacobi inequalityholds for some and all , , , and . Then, is an ISS Lyapunov function and the –to– dissipative inequality (14) is satisfied with , , i.e.,for all and thus observer (2) is input-to-state stable. Proof. From Equations (
7) and (
15), we obtain
Using the assumption (
16), the previous inequality yields
and hence we can conclude about ISS with inequality (
17) as a final result. □
We say that the observer admits an
-gain
w.r.t.
if (
17) holds. Clearly, a small gain is preferable since it entails a stronger noise attenuation. In the following, we will analyze how to take care of the Hamilton–Jacobi inequality (
16), starting with the following example.
Example 2. Let us considerand letbe a candidate observer for system (19). It is straightforward to obtainwhereLet us consider as a candidate ISS Lyapunov function. We have Since , , and , , Equation (21) yieldsfor if . Thus, observer (20) is ISS with an -gain larger than 1. The next section regards the application of what has been presented so far to observers for a class of polynomial systems.
3. State Observers for Polynomial Systems
After choosing a given observer structure, the problem reduces to find an ISS Lyapunov function that the condition (
16) holds. Unfortunately, conditions like (
16) are not easy to be satisfied, which has motivated the investigation on the weaker notion of practical
-gain proposed in [
37]. We will address the problem of constructing observers with practical
-gain for a class of polynomial systems.
Let us focus on
where
,
,
,
,
, and the pair
is detectable. To estimate the state, we rely on observers given by
with the gain
chosen such that
has eigenvalues with a strictly negative real part. This condition can be satisfied owing to the detectability assumption and ensures that the estimation error dynamics
is locally asymptotically stable to zero in the absence of noise, i.e., with
for all
. More specifically, in such a case we have
In the noisy setting, for the sake of brevity, let us rewrite Equation (
24) as
with
Though a polynomial system may be asymptotically stable without admitting a polynomial Lyapunov function [
41], it is convenient to search for polynomial ISS Lyapunov functions
and especially such that inequality (
17) holds for some
. Given a candidate Lyapunov function, we may apply the SOS decomposition of such a function and of the opposite of its time derivative by using a positivity certification, which does not depend on the characteristics of the chosen polynomial since the following holds [
39,
42].
Theorem 2. A polynomial in has sum-of-squares decomposition (or is said to be SOS) if and only if there exists a real symmetric and positive semidefinite matrix such that , where is the vector of all the monomials in the components of of degree equal to or less than , i.e.,of dimension Proof. See (Proposition 2.1, p. 17, [
43]). □
Thus, from now on, we will refer to well-established definitions as follows [
44]. A polynomial
is
-SOS polynomial if
with
,
is SOS for some “small” tolerance
. In addition, a polynomial, square matrix
with
for
is said to be an
-SOS matrix if the bipartite polynomial
is
-SOS for all
. In this respect,
is said to be a bipartite
-SOS polynomial.
Theorem 3. Consider observer (23) for system (22). If there exist a bipartite ε-SOS and such thatfor all and , where is the column vector of all the monomials in e and x appearing in and with such thatThen, observer (23) is ISS with -gain equal to μ. Proof. The proof is line with [
14]. The time derivative of
is given by
and, using (
27), we obtain
Using (Lemma 4.2, p. 861 in [
14]), from (26), it follows that
and, after replacing this upper bound in Equation (
28), it follows that (
18) (see the proof of Theorem 1) holds if (
25) is satisfied, which allows for concluding. □
Based on the aforesaid, one can proceed with the observer design. Let be with and , and the problem to solve is the following.
Problem 1. Find a bipartite ε-SOS , , and such that the conditions (25) and (26) hold and μ is minimized. Indeed, the available SOS tools do not allow for solving Problem 1. Thus, we will address the observer design by relying on the so-called practical
-gain proposed in [
37]. However, first of all consider the pure linear case by dealing with a system like in (
22) without
and with
and
being real matrices, as follows:
where the pair
is detectable,
, and
. The observer equation is as follows:
Since the dynamics of the estimation error is
and, after a little algebra and using the Schur complement (p. 39, [
45]), inequality (
16) becomes
with
and
. Since the pair
is detectable, the above linear matrix inequality (LMI) admits a solution in
P and
Y, and it follows
. Moreover, using popular LMI-based tools [
45], it is straightforward to minimize
exactly since the problem is convex. Thus, one may search for approximate solutions to Problem 1 for Equations (
22) and (
23) by relying on the solution obtained after neglecting the nonlinearities. Thus, instead of Problem 1, let us consider the much simpler LMI problem
After finding the solution denoted by
, the gain is given by
, which provides a local
-gain
with the Lyapunov function
for Equations (
22) and (
23). Since it is difficult to ensure a constant
-gain over all the operating points, we will rely on the notion of practical
-gain proposed in [
37]. Based on the practical
-gain, one can overcome the problem of finding a globally fixed
-gain. More specifically, assume that there exists a bipartite
-SOS function
such that
for
, then
holds if
is chosen such that
and thus
is referred to as practical
-gain. Based on the aforesaid, the problem to solve reduces to the following.
Problem 2. Given as a solution of (29), find a bipartite ε-SOS such that inequality (30) holds. The solution of Problem 2 allows for adopting a more flexible notion of attenuation w.r.t. the noises by using an
-gain that may depend on both
e and
x. Following the same reasoning of the proof of Theorem 1, instead of inequality (
18), we obtain
from (
31) if inequality (
30) holds with
subject to (
32). Thus, the condition (
33) may be used whenever the
-gain cannot be bounded from above in the usual sense such as in Example 2, for which the lower bound (given by 1) holds globally, i.e., for all
e,
. In practice, the attenuation w.r.t. the disturbances are left to vary in the state space. Moreover, the condition (
31) is easier to be satisfied as compared with (
30). Indeed, additional constraints can be introduced by constraining the estimation error to belong to suitable compact sets and/or taking into account the boundedness of the state trajectories [
14]. This allows for facilitating feasibility when solving Problem 2.
In the next section, we will show numerical results obtained in a simulation case study.
4. Numerical Results
In this section, we will show how to apply the proposed approach by exploiting the polynomial structure of the system and observer equations. Thanks to the use of SOS toolbox [
44], we will find an ISS polynomial Lyapunov function, which guarantees stability, as illustrated so far. The numerical results are obtained by dealing with the Van der Pol oscillator, which is an interesting example of a polynomial system with a stable limit cycle (p. 57, [
5]) and is thus well-suited for the purpose of testing.
Let us consider a system with two coupled Van der Pol oscillators with the first and third state variable as outputs, i.e.,
where
,
,
,
The observer is thus given by
with the gain
obtained by solving problem (29) with Yalmip [
46]. The solution provides a value of
equal to 4.6575. Using the SOS toolbox [
44], we solved Problem 2 with
and additional constraints
and
, thus obtaining the Lyapunov function
which certifies that this observer is ISS.
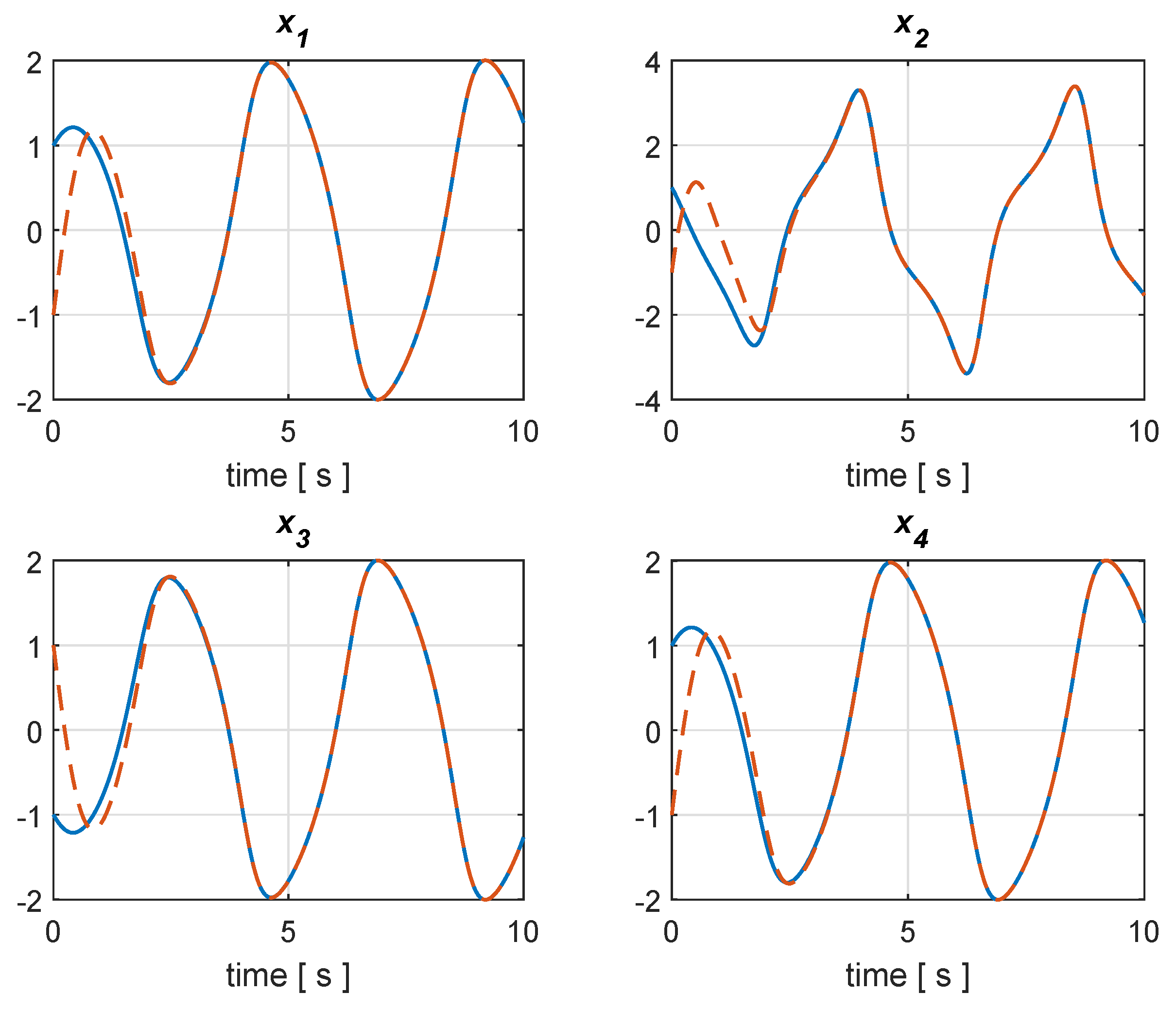
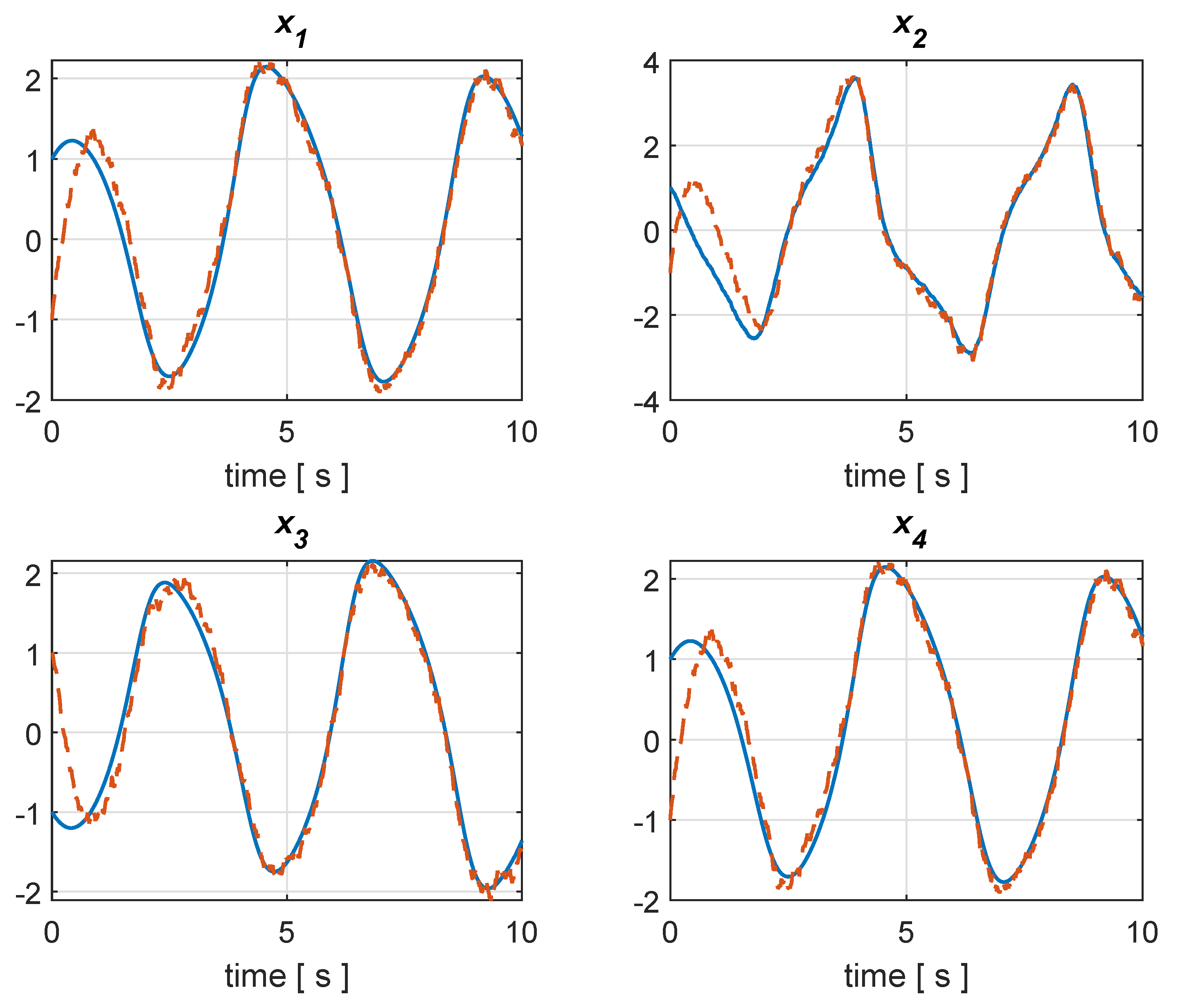
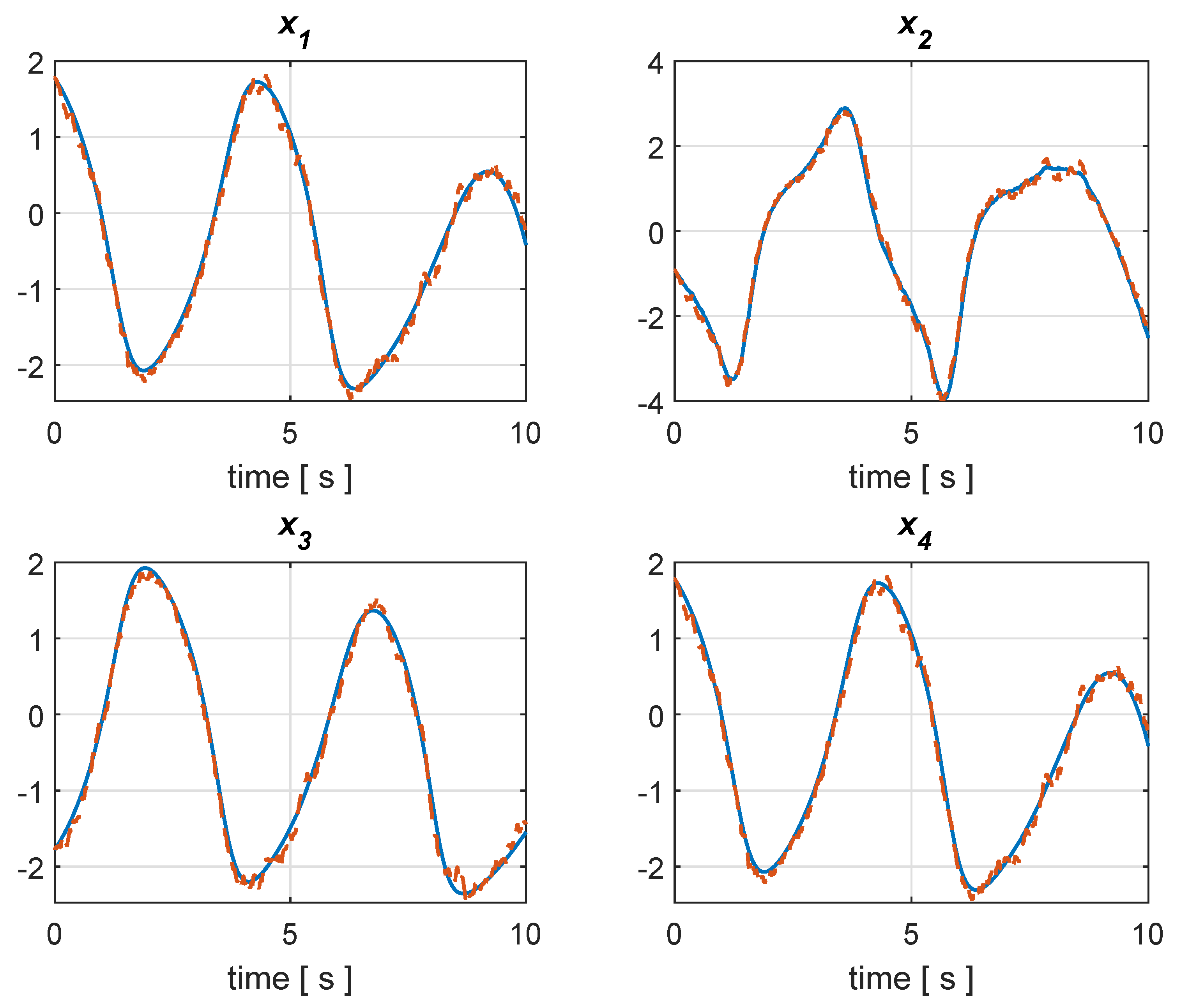
Figure 1,
Figure 2,
Figure 3 and
Figure 4 illustrate the simulation results.
Figure 1 and
Figure 2 showcase the transient behavior of the state variables and corresponding estimates in two different simulation runs, i.e., in a noise-free case and under the presence of random noises. Such simulation runs show that the time response of the observer is less than the oscillation period of the oscillators, namely it converges quite quickly in such a way as to feed the possible close-loop controllers with the estimates for the purpose of syncronization (see [
47] and the references therein). The behaviors at the regime can be analyzed by looking at
Figure 3 and
Figure 4. In
Figure 3, it is shown that the estimation error is kept to zero when the initial state and estimated state coincide and neither system nor measurement disturbances affect the plant. In the presence of noises, the estimation error stays bounded since the estimated state is close to the true state over time, as depicted in
Figure 4.