Truth-Teller–Liar Puzzles with Self-Reference

Abstract

In this paper, we use commonsense reasoning and graph representation to study logical puzzles with three types of people. Strong Truth-Tellers say only true atomic statements, Strong Liars say only false atomic statements, and Strong Crazy people say only self-contradicting statements. Self-contradicting statements are connected to the Liar paradox, i.e., no Truth-Teller or a Liar could say “I am a Liar”. A puzzle is clear if it only contains its given statements to solve it, and a puzzle is good if it has exactly one solution. It is known that there is no clear and good Strong Truth-Teller–Strong Liar (also called SS) puzzle. However, as we prove here, there are good and clear Strong Truth-Teller, Strong Liar and Strong Crazy puzzles (SSS-puzzles). The newly investigated type ‘Crazy’ drastically changes the scenario. Some properties of the new types of puzzles are analyzed, and some statistics are also given.

1. Introduction

Logical puzzles have various roles in our life. They are helpful for training our brains, to learn logical thinking, and also for recreation. In terms of problem solving processes without human intervention, some techniques and methods have been proposed in order to solve logical puzzles (see, e.g., [1] for recent results). The formal study of various types of puzzles can be done by commonsense reasoning or by formal logic. Knight and Knave puzzles are logical puzzles that were introduced by Smullyan [2]. Formal solution methods for solving these puzzles by using classical propositional calculus were discussed in [3]. Similarly, in [4], based on logical representations, automated reasoning was used to solve puzzles. In a nutshell, Knights are Truth-Tellers and Knaves are Liars. Various types of Truth-Teller–Liar puzzles have been further popularized by various books and papers [5,6,7,8,9,10] under various names. In the simplest type of them, the participants say only statements about their types. Strong and Weak Truth-Tellers and Liars were introduced in [11,12]. Strong Truth-Tellers can say only true atomic statements, whilst Strong Liars can tell only false atomic statements. (In contrast, Weak Liars must say at least one false atomic statement, whilst Weak Truth-Tellers must say at least one true atomic statement, if they say anything.) In [11,13], it was proven that there is no SS-puzzle, i.e., a puzzle with Strong Truth-Tellers and Strong Liars such that it has a unique solution without any additional information, e.g., without knowing the number of Truth-Tellers. In various puzzles, there are not only Truth-Tellers and Liars; to complete the picture, one needs Normals, who are persons who can say false and true atomic statements, see, e.g., [6]. In [14], people who cannot say true and cannot say false statements were defined as Mutes (see

Table 1. Type of people and their possible statements by their truth value in the literature.

	Can Say False Statements	Cannot Say False Statements
Can say true statements	Normal	Knight/Truth-Teller
Cannot say true statements	Knave/Liar	Mute

). In the puzzles studied in [14], Mutes were stated as not being able to say anything, as their name infers. In puzzles where the allowed statements are of the form “X can/cannot say the truth”, “X can/cannot say false statement”, in the solution, it could be that some people neither can say true nor false statements; thus, they are Mutes. We also note that puzzles have various connections to graphs, to Boolean programming [15], and to other scientific disciplines. In [6,16], diagrammatical logic was used to represent various Knight–Knave and Knight–Normal–Knave puzzles, as well as their solutions. Various degrees of truthfulness of people in the puzzle and some paradoxical statements were also presented in [17]. Neutrals (a type somehow between Knights and Knaves) were used in [9].

As was proven in [11,13], there are no SS-puzzles with one solution, so our central aim was to reconsider these simplest puzzles by extending the possible types of people. On the other hand, there could be such a scenario in some puzzles in which some statements cannot be true and cannot be false; thus, people who cannot say true and cannot say false can still say some (paradoxical) statement. In this paper, we present a new type of puzzle. We investigate a new type of persons, the (Strong) Crazy people, and we use them along with Strong Truth-Tellers and Strong Liars in our SSS-puzzles. We show that, in contrast to SS-puzzles, there are SSS-puzzles with a unique solution without any additional information. In our puzzles, we use atomic statements of the form “X is a Liar” or “X is a Truth-Teller.” However, we are still able to show an interesting extension of the binary world and see how to manage if there are more types of people in the puzzles, especially if the set of allowed truth-values of the statements is extended. Now, we use a novel approach to deal with paradoxical statements. We investigate the new type, the Crazy persons, instead of Mutes (see

Table 2. Type of people and their possible statements by their truth value in our approach.

	Can Say False Statements	Cannot Say False Statements
Can say true statements	Normal	Truth-Teller
Cannot say true statements	Liar	Crazy

). This is a new approach in puzzles to deal with sentences that have a third truth-value; Crazy people can say self-contradictory statements that are not true and not false if a Truth-Teller or a Liar, respectively, would say them. We prove that these statements contain self-reference. In the present paper, we work with three types of people in puzzles.

In the next sections, we recall SS-puzzles and define our SSS-puzzles. We also show that many but not all unsolvable SS-puzzles become solvable if we shift the type of the puzzle to the SSS-puzzle.

2. Strong Truth-Teller and Strong Liar Puzzles (SS-Puzzles)

In this section, we recall Truth-Teller–Liar puzzles, which of one of the simplest types. Let us start with an example, then show the formal definition (based, e.g., on [13]).

Example 1.

Assume that we have a puzzle with three people: Mark, Sara, and Antony. Mark said that Antony is a Liar. Sara said that Mark is a Liar. Decide which of the three persons is Liar or Truth-Teller.

We solve this puzzle later on. Now, let us recall some definitions about puzzles.

Definition 1.

Let A be a person. Atomic statements are the sentences which are not divisible into smaller sentences, and they are in the following two forms: “A is a Liar” or “A is a Truth-Teller.”

Definition 2.

Let us have a set of persons and atomic statements about them, so the puzzle is a function which assigns to each person a set of atomic statements that he/she said about other persons or about himself/herself.

In Example 1, we have two atomic statements.

As already mentioned, there are various ways to define or understand the concept of Truth-Tellers and Liars, e.g., putting conjunction or disjunction between the atomic statements of a person and evaluating the obtained sentence. Depending on these concepts, various puzzles have been investigated in, e.g., [11,12]. In this paper, we use one of the simplest and yet very usual approaches that leads to the concepts of Strong Truth-Tellers and Strong Liars.

Definition 3.

A person is a Strong Liar if all his/her atomic statements are false (if he/she says any statement in the puzzle), whilst a person is Strong Truth-Teller if all his/her atomic statements are true (if he/she says any statement).

Definition 4.

A puzzle with set N of persons is an SS-puzzle if each person in the puzzle can be either Strong Liar or Strong Truth-Teller. (In the name “SS-puzzle”, the double S is for showing that both types of people, the Truth-Tellers and the Liars, are of the Strong type.)

The concept of puzzles is connected to the concept of solutions in a somewhat similar manner to how models are connected to logics. The next definition gives a detailed picture about Strong Truth-Tellers and Strong Liars in SS-puzzles.

Definition 5.

Let an SS-puzzle with set N of persons be given. A function N → {Truth-Teller, Liar} is a solution of the puzzle if the following holds for each person $A_k$ who said anything in the puzzle:

• Person $A_k$ is Truth-Teller if the following condition satisfies for every $A_i\in N$:
  if $A_k$ said atomic statement about $A_i$, and this atomic statement is in the form:

  ➢

  “$A_i$ is a Liar”, then $A_i$ is a Liar (the atomic statement is true).

  ➢

  “$A_i$ is a Truth-Teller”, then $A_i$ is a Truth-Teller (the atomic statement is true).

• Person $A_k$ is Liar if the following condition satisfies for every $A_i\in N$:
  if $A_k$ said atomic statement about $A_i$, and this atomic statement is in the form:

  ➢

  “$A_i$ is a Liar”, then $A_i$ is a Truth-Teller (the atomic statement is false).

  ➢

  “$A_i$ is a Truth-Teller," then $A_i$ is a Liar (the atomic statement is false).

Definition 6.

A puzzle is solvable if it has at least one solution.

Though, by Definition 5, each person can tell statements about herself/himself, for puzzles having solution(s), the following fact holds.

Remark 1.

In a solvable SS-puzzle, there is no atomic statement in the form “I am a Liar.”

Example 1 (continued).

There are two solutions. The first solution is if we assume that Mark is a Liar, and then Sara and Antony are Truth-Tellers. Another solution is if Mark is Truth-Teller, and then Sara and Antony are Liars. Thus, we do not have a unique solution.

One can also see the solutions from another point of view.

Lemma 1.

A solution of an SS-puzzle with set N of persons can also be seen such that the following holds for each person $A_k$about whom anybody said something in the puzzle:

• If person$A_k$is Truth-Teller, then for all$A_i$who said atomic statement about$A_k$, the atomic statement is in the form:

  ➢

  “$A_k$is a Liar”, then$A_i$is a Liar.

  ➢

  “$A_k$is a Truth-Teller”, then$A_i$is a Truth-Teller.

• If person$A_k$is Liar, then for all$A_i$who said atomic statement about$A_k$, the atomic statement is in the form:

  ➢

  “$A_k$is a Liar”, then$A_i$is a Truth-Teller.

  ➢

  “$A_k$is a Truth-Teller”, then$A_i$is a Liar.

Proof. 

It is obvious by Definition 5. □

We continue with another example.

Example 2.

Let us have an SS-puzzle with three people: Mark, Sara, and Antony. Mark said that Antony is a Liar. Sara said that Mark is a Liar. Antony said that “I am a Liar.” Who is the Liar, and who is the Truth-Teller?

In a solution of the SS-puzzle of Example 2, if we assume that Mark is a Liar, then Sara is a Truth-Teller, but Antony is neither Liar nor Truth-Teller. On the other hand, if we assume that Mark is a Truth-Teller, then Sara is Liar, but again Antony is neither a Liar nor a Truth-Teller. Thus, this SS-puzzle does not have any solution.

Example 3.

Let us have another SS-puzzle with three people: Anne, Bale and Suzan. Anne said that Bale is a Truth-Teller and Suzan is a Liar, Bale said that Suzan is a Truth-Teller, and Suzan did not say any statement. Decide who is a Truth-Teller and who is a Liar?

In the solution of the puzzle in the previous example, if we assume that Anne is a Truth-Teller, then Bale is a Truth-Teller and Suzan is a Liar; however, Bale (who has the same type as Anne) said that Suzan is a Truth-Teller, which is a contradiction. On the other hand, if we assume that Anne is a Liar, then Bale is a Liar and Suzan is a Truth-Teller; however, Bale said that Suzan is a Truth-Teller, which is a contradiction, since Bale is a Liar and said a true statement. Consequently, the puzzle is unsolvable.

3. Strong Truth-Teller, Strong Liar and Strong Crazy Puzzles (SSS-Puzzles)

In this section, we introduce a new type of puzzle. As Table 2 shows, we distinguish the four types of people not in the previously shown (Table 1) usual way. In binary logic, every statement is either true or false, which led to the previous Mute type of people in the lower right corner of Table 1. However, there is another option if we allow statements that are not true and not false (e.g., typical paradoxical self-reference statements), because people who cannot say true and cannot say false may still say some statements. In our newly investigated puzzles, these people are called Crazy people. In this section, puzzles in which three types of people may appear are considered. Let us see the formal definitions.

Definition 7.

A self-contradictory statement is an atomic statement that has the following property independently of other statements: It is neither false nor true independently if a Truth-Teller or a Liar says it.

Definition 8.

An SSS-puzzle is a puzzle with a set of persons N = {$A_1$, $A_2$, …, $A_n$} and their atomic statements in which $A_i$ (where 0 < i ≤ n) can be Strong Liar, Strong Truth-Teller, or a Strong Crazy such that:

• Strong Truth-Teller (T) and Strong Liar (L) previously have been defined (see Definition 3).
• A person is a Strong Crazy person (C) if all of his/her statements are self-contradictory statements (if he/she says any statement).

Definition 9.

Let an SSS-puzzle with set N of persons be given. A function N → {Truth-Teller, Liar, Crazy} is a solution of the puzzle if the following holds for each person $A_k$ who said anything in the puzzle:

• $A_k$is Truth-Teller exactly as in Definition 5.
• Person$A_k$is Liar if the following holds for every$A_i\in N$:
  if$A_k$said atomic statement about$A_i$, then this atomic statement is in the form:

  ➢

  “$A_i$is a Liar”, then$A_i$is a Truth-Teller or a Crazy (not a Liar).

  ➢

  “$A_i$is a Truth-Teller”, then$A_i$is a Liar or a Crazy (not a Truth-Teller).

• Person$A_k$is a Crazy person if$A_k$said only self-contradictory statements.

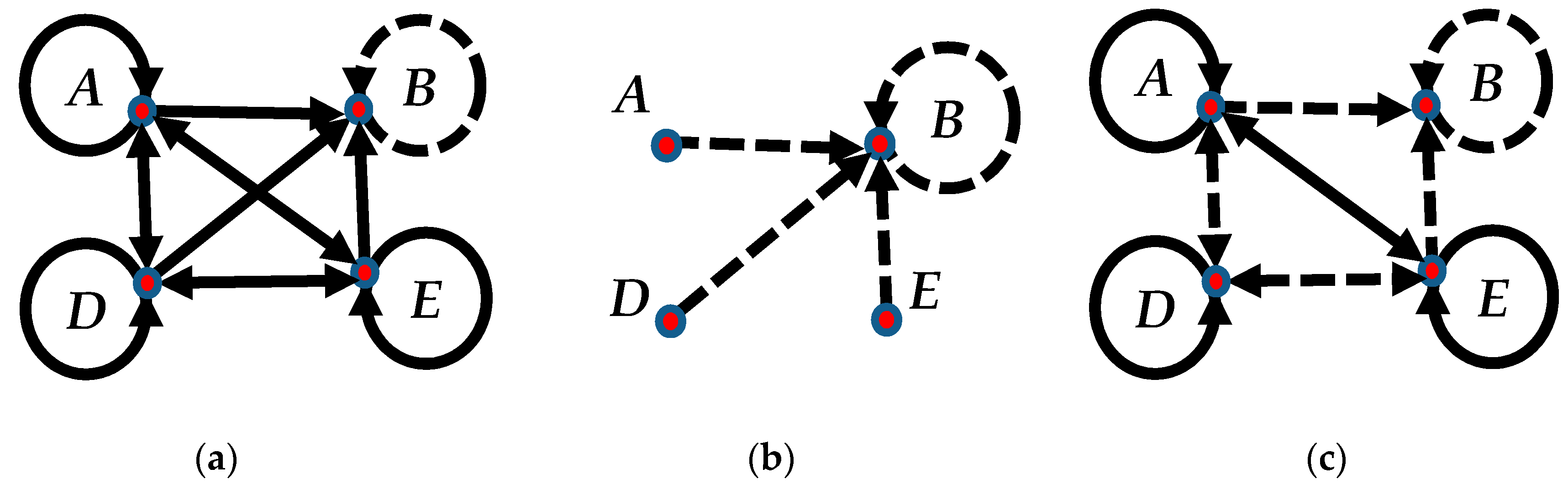
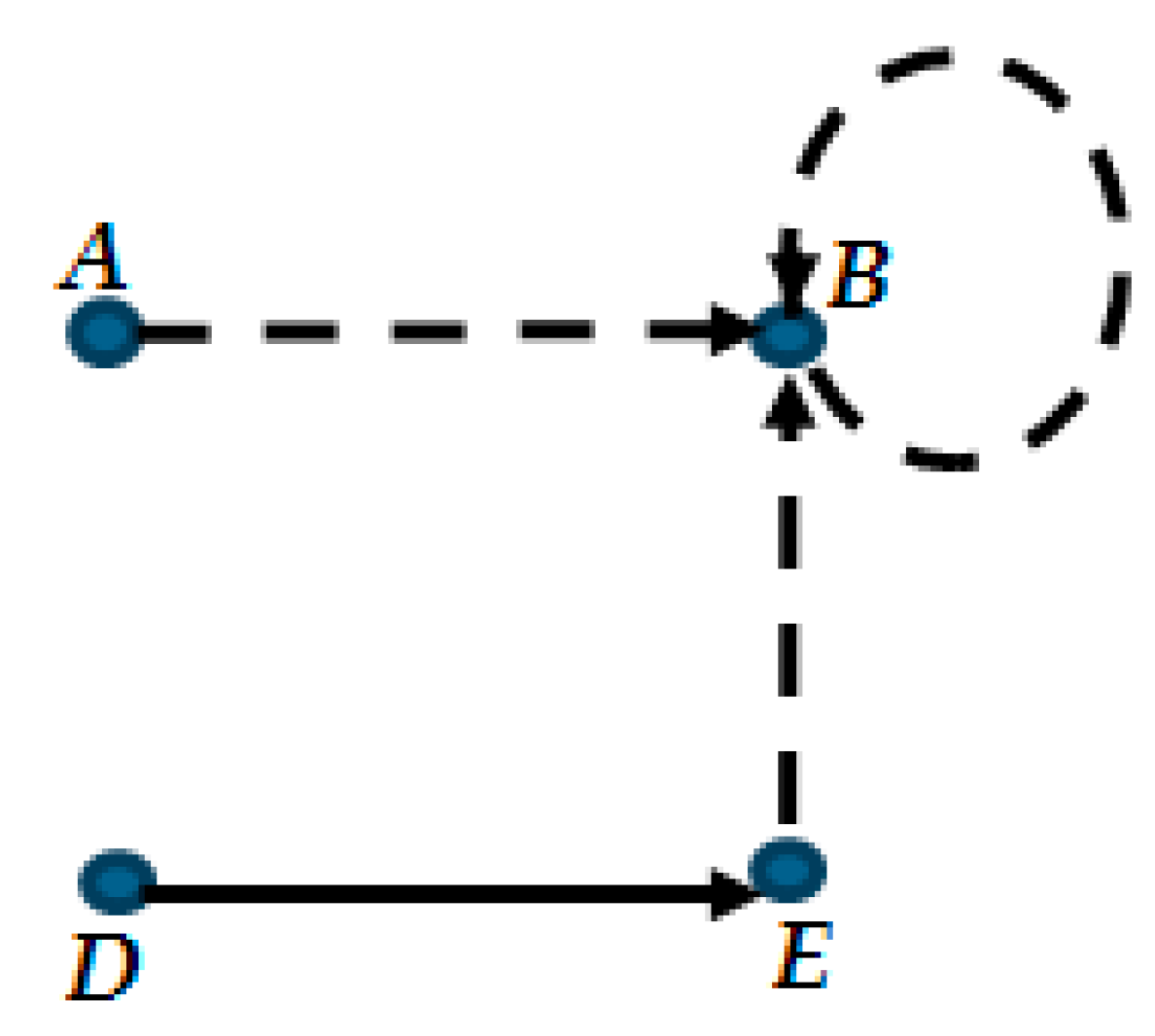
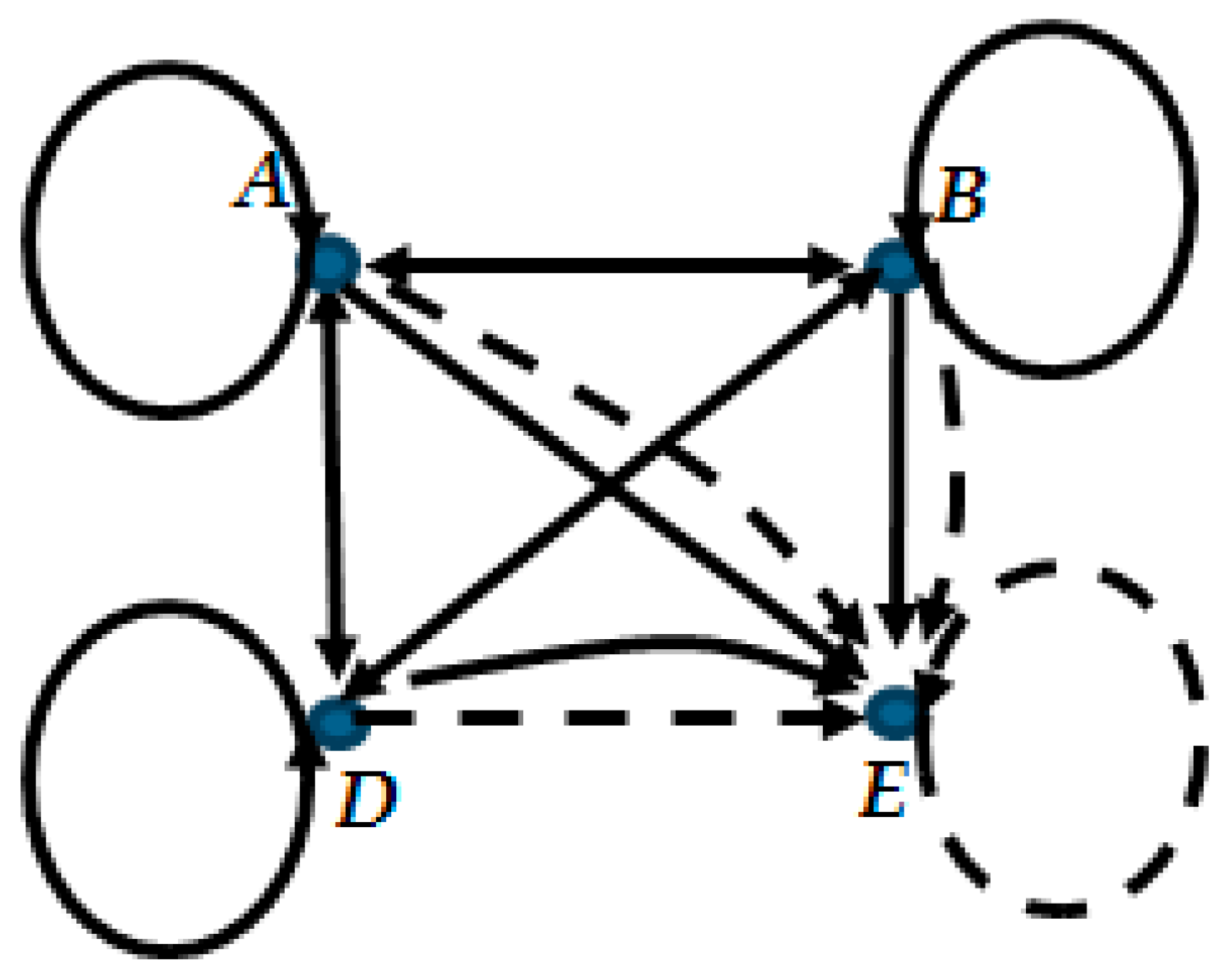
3.1. Graph Representation of the Puzzle

• Nodes represent the persons.
• Directed edges represent the atomic statements:

  ■

  Solid edge from A to B: A said that B is a Truth-Teller ($\overline{AB}$).

  ■

  Broken edge from A to B: A said that B is a Liar ($\stackrel{⃛}{AB}$).

• In graph G, if two persons say the same type of statements about each other, then the representation of these statements, the two edges pointing in opposite directions, can be substituted by a bidirectional same type (i.e., broken or solid) edge between the two nodes.

3.2. Notations and Definitions

• N: The set of all people in the puzzle.
• G is the graph representation of the puzzle.

Let N be a set of people in the puzzle. If $A_i\in N$, then ${\mathrm{\Gamma }}_{i,0}$ is a set of persons named by $A_i$ as Liars, and ${\mathrm{\Gamma }}_{i,1}$ is a set of persons named by $A_i$ as Truth-Tellers. Further in this paper, we refer to a statement as $A_j\in {\mathrm{\Gamma }}_{i,m}$, where $A_j$, $A_i\in N$ and m $\in$ {0,1}.

Let us fix a/the solution of a solvable puzzle.

• T is the set of Strong Truth-Tellers, L is the set of Strong Liars, and C is the set of Strong Crazy people in the puzzle. T, L and C are disjoint sets; moreover, N = T $\cup$ L $\cup$ C.
• True atomic statements $\left(\mathsf{\alpha }\right)$: The set of all statements that are logically true.
• False atomic statements ($\beta$): The set of all statements that are logically false.
• Paradoxical statements ($\gamma$): The set of all self-contradictory statements in the puzzle.

3.3. Preliminary Results

The first result about our new type of puzzle is already connected to the new type of people.

Proposition 1.

Let an SSS-puzzle be given with set N of persons, and let $A_k,A_i\in N$ with i ≠ k. Let a/the solution be given such that $A_i\in C$. If $A_k\in T$ or $A_k\in C$ in the solution, then $A_k$ cannot say any statement about $A_i$. Therefore, if i ≠ k, then $A_k$ can say a statement about $A_i$ only if $A_k\in L$.

Proof. 

In contrast, let us assume first that person $A_k\in T$ says a statement about $A_i\in C$. If $A_i\in {\mathrm{\Gamma }}_{k,0}$, then it is a false statement said by a Truth-Teller. Analogously, $A_i\in {\mathrm{\Gamma }}_{k,1}$ also leads to a contradiction. Second, a Crazy person cannot say any statement about another Crazy person, since this statement would be a false statement and it contradicts to the definition of Crazy person. Thus, based on these arguments, only Liars (e.g., $A_k\in L$) can say statements about a Crazy person $A_i$ (with the condition i ≠ k). □

Now we recall some additional definitions about puzzles.

Definition 10.

A puzzle is clear when there is no additional information given to solve it (only the statements of its persons).

The number of Liars or Truth-Tellers is an example of additional information in the puzzle.

Definition 11.

A puzzle is a good puzzle if it has a unique solution.

One of the most important results known about SS-puzzles is the following:

Theorem 1.

There is no clear and good SS-puzzle.

Proof. 

See [11]. □

3.4. Analyzing SSS-Puzzles

In contrast to Theorem 1, if we consider the puzzle of Example 2 as an SSS-puzzle, then this puzzle has exactly one solution (see also Example 4 below). This fact is not only an important property of SSS-puzzles, as it also highlights the different nature of SS- and SSS-puzzles. On the other hand, Theorem 1 has a straightforward implication for our SSS-puzzles.

Corollary 1.

In the solution of good and clear SSS-puzzle, $C\ne \left\{\right\}$.

Example 4.

Let an SSS-puzzle with three persons be given: Mark said that Antony is a Liar. Sara said that Mark is a Liar, and Antony said “I am a Liar.” Who is the Liar, who is the Truth-Teller, and who is the Crazy?

This puzzle has one solution such that Antony is a Crazy, Mark is a Liar and Sara is a Truth-Teller. This is because Antony said a self-contradictory statement, and Mark said a false statement about Antony, so Mark is a Liar and Sara is a Truth-Teller because she said a true atomic statement about Mark.

As Crazy people play an important role in solutions, let us identify them. The first step is about Crazy people who are not silent in the puzzle.

Lemma 2.

In a solvable SSS-puzzle with set N of persons and their atomic statements, if $A_i\in {\Gamma }_{i,0}$, then $A_i\in C.$

Proof. 

Let us fix a solution. If ($A_i\in {\mathrm{\Gamma }}_{i,0}$) $\in \alpha$, then $A_i\in$ T, since he/she said a true atomic statement, but, in fact, $A_i$ said about himself/herself that he/she is a Liar which implies that $A_i\in L$. That implies that ($A_i\in {\mathrm{\Gamma }}_{i,0}$) $\in \beta$, which contradicts our assumption ($A_i\in {\mathrm{\Gamma }}_{i,0}$) $\in \alpha$. If we assume ($A_i\in {\mathrm{\Gamma }}_{i,0}$) $\in \beta$, then $A_i\in$ L since he/she said a false atomic statement, but, since $A_i$ said about himself/herself that he/she is a Liar, $A_i\in T$, which implies that ($A_i\in {\mathrm{\Gamma }}_{i,0}$) $\in \alpha$, which contradicts to our assumption ($A_i\in {\mathrm{\Gamma }}_{i,0}$) $\in \beta$. Consequently, the only possibility is ($A_i\in {\mathrm{\Gamma }}_{i,0}$) $\in \gamma ,$ which means that $A_i\in C$. □

By Lemma 2, in the solution of Example 4, Antony is a Crazy person, since he said the statement “I am a Liar.”

Lemma 3.

Let a solvable SSS-puzzle be given with a/the solution. If the type of $A_j$ is the same as the type of $A_k$ ($A_j,A_k\in N$, j ≠ k) in the solution, then $A_j\notin {\Gamma }_{k,0}$ and $A_k\notin {\Gamma }_{j,0}$.

Proof. 

Let us fix a solution. Let $A_j$, $A_k\in N$ (j ≠ k) such that at least one of $A_j$ and $A_k$ says some statement. Let us assume that $A_j$ $\in {\mathrm{\Gamma }}_{k,0}$ (or $A_k\in {\mathrm{\Gamma }}_{j,0})$. Then, if $A_j$, $A_k\in C$, this means that $A_j$, $A_k$ said only self-contradictory statements, but $A_j\in {\mathrm{\Gamma }}_{k,0}$ (or $A_k\in {\mathrm{\Gamma }}_{j,0})$ is a false atomic statement, which means that this statement is not self-contradictory, which contradicts the assumption that $A_j$, $A_k\in C$. If we assume that $A_j$, $A_k\in T$, then $A_j\in {\mathrm{\Gamma }}_{k,0}$ (or $A_k\in {\mathrm{\Gamma }}_{j,0}$) means that $A_j\in {\mathrm{\Gamma }}_{k,0}$ (or $A_k\in {\mathrm{\Gamma }}_{j,0}$) is a false atomic statement said by a Truth-Teller that is also a contradiction. Finally, if $A_j$, $A_k\in L$, then $A_j\in {\mathrm{\Gamma }}_{k,0}$ (or $A_k\in {\mathrm{\Gamma }}_{j,0}$) implies that ($A_j\in {\mathrm{\Gamma }}_{k,0}$) $\in \alpha$ (or ($A_k\in {\mathrm{\Gamma }}_{j,0}$) $\in \alpha$), which means that $A_j\in {\mathrm{\Gamma }}_{k,0}$ (or $A_k\in {\mathrm{\Gamma }}_{j,0}$) is a true atomic statement said by a Liar that contradicts Definition 9. Finally, if neither $A_j$ and $A_k$ says any statement in the puzzle, then, clearly, both $A_j\notin {\mathrm{\Gamma }}_{k,0}$ and $A_k\notin {\mathrm{\Gamma }}_{j,0}$ are satisfied. Therefore, there is no solution for an SSS-puzzle in which two persons, $A_j$, $A_k$, have the same type and $A_j\in {\mathrm{\Gamma }}_{k,0}$ (or $A_k\in {\mathrm{\Gamma }}_{j,0}).$ □

Consequently, by Lemma 3, if the puzzle is solvable, then in the graph representation G, there is no broken edge between any two persons who have the same type (i.e., both of them are Truth-Tellers, both of them are Liars, or both of them are Crazy) in the solution of the puzzle.

Corollary 2.

In an SSS-puzzle, if there are two persons $A_{i}and{A}_j$ such that $A_i\in {\Gamma }_{j,0}$ (or $A_j\in {\Gamma }_{i,0}$), and both $A_{i}and{A}_j$ said the same statement about a third person $A_k$, then the puzzle is unsolvable.

As the corollary states, there are SSS-puzzles without a solution. We have seen already that some of the SS-puzzles that have no solutions become solvable if we think about them as SSS-puzzles, i.e., if we allow not only Truth-Tellers and Liars but also Crazy people in the target of the solution function. Now, it turns out that not every puzzle becomes solvable in this way.

We continue to find out who are the Crazy people in the solutions.

Lemma 4.

In the solution of an SSS-puzzle with set N of persons, for a person $A_i\in N$ if

• ${\Gamma }_{i,0}=\varnothing ,{\Gamma }_{i,1}=\varnothing$and
• $\exists A_j,A_k\in N$/$\left\{A_i\right\}$such that the type of$A_j$is the same as the type of$A_k$, and$A_i\in {\Gamma }_{j,0},$$A_i\in {\Gamma }_{k,1}$(or$A_i\in {\Gamma }_{k,0}and{A}_i\in {\Gamma }_{j,1}$),
  then$A_i\in C$and$A_j,A_k\in L$.

Proof. 

In case $j\ne k$ and the type of $A_j$ is the same as the type of $A_k$ but they say two different statements about $A_i$ (“$A_i$ is a Liar” and “$A_i$ is a Truth-Teller”), then in order to have a solution, $A_j,A_k\in L$ and $A_i\in C$; otherwise, the puzzle is unsolvable.

If $j=k$, then this means that there is one person $A_j$ who said two different statements about $A_i$. Therefore, in order to have a solution, $A_j\in L$ and $A_i\in C$; otherwise the puzzle is unsolvable. □

Now, we are ready to give a characterization of the Crazy people.

Theorem 2.

In a solvable SSS-puzzle with set N of person, if $A_i$ $\in C$, then $A_i$ can say at most one atomic statement, which is $A_i$ $\in {\Gamma }_{i,0}$.

Proof. 

In an SSS-puzzle, any person $A_i$ can say only two forms of atomic statements: either $A_j$ $\in {\mathrm{\Gamma }}_{i,0}$ or $A_j\in {\mathrm{\Gamma }}_{i,1}$, where $A_j\in N$. Suppose that $A_i$ $\in C$ and $A_j\in {\mathrm{\Gamma }}_{i,0}$, where i ≠ j. If $A_j\in L$, then ($A_j\in {\mathrm{\Gamma }}_{i,0}$) $\in \alpha$, which contradicts to $A_i\in C$. If $A_j\in T$, then ($A_j\in {\mathrm{\Gamma }}_{i,0}$) $\in \beta$ which contradicts to $A_i\in C$. If $A_j\in C$, then ($A_j\in {\mathrm{\Gamma }}_{i,0}$) $\in \beta$; thus, ($A_j\in {\mathrm{\Gamma }}_{i,0}$) $\notin \gamma$ and $A_i\notin C$.

Assume now that $A_i\in C$ and $A_j\in {\mathrm{\Gamma }}_{i,1}$ with i ≠ j. If $A_j\in L$, then ($A_j\in {\mathrm{\Gamma }}_{i,1}$) $\in \beta$, which contradicts $A_i\in C$. If $A_j\in T$, then ($A_j\in {\mathrm{\Gamma }}_{i,1}$) $\in \alpha$; thus $A_i\notin C$. If $A_j\in C$, then ($A_j\in {\mathrm{\Gamma }}_{i,1}$) $\in \beta$; thus ($A_j\in {\mathrm{\Gamma }}_{i,1}$) $\notin \gamma$ and $A_i\notin C$. If $A_i$ $\in C$, then ($A_i\in {\mathrm{\Gamma }}_{i,1}$) $\in \beta$, which also contradicts $A_i$ $\in C$.

Consequently, the only statement Crazy person $A_i$ can tell is $A_i$ $\in {\mathrm{\Gamma }}_{i,0}$, which is a self-contradictory statement. □

Based on Theorem 2 and Lemma 2, if $A_i\in C$, $A_i$ can say only $A_i\in {\mathrm{\Gamma }}_{i,0}$; or, based on Lemma 4, $A_i$ does not say any atomic statement about other persons.

For further analysis, we use the graph representations of the puzzles.

Definition 12.

A solution of the graph G is a function that assigns either C, L or T to each node, such that all statements that are represented by the edges of the graph are satisfied.

Proposition 2.

The solutions of the puzzle are the same as the solutions of the graph representation G of the puzzle.

Proof. 

In graph G, the nodes and the edges of G represent the persons and the statements in the puzzle that are represented by G, respectively. Therefore, based on Definitions 9 and 12, the solution set of the puzzle is the same as the solution set of G. □

Let us recall the notion of complete graphs from graph theory. $K_n$ is a graph of n nodes such that each pair of nodes is connected by an edge. In particular, $K_3$, the triangle graph, is a graph that contains three nodes such that there is an edge between any two vertices. In the next result, we show how triangle graphs are connected to solvable puzzles.

Proposition 3.

If the graph representation G of an SSS-puzzle P contains a subgraph whose underlying undirected graph is $K_3$ with broken edges, then P has no solution.

Proof. 

Let us assume that the graph representation G of the puzzle contains a subgraph with broken edges, such that the underlying undirected graph of this subgraph is exactly $K_3$ Considering this subgraph, there are two possible forms of non-isomorphic subgraphs in G with broken edges. Figure 1 shows these two subgraphs. Let us start with the graph shown in Figure 1a. In the solution of the puzzle, $A$ and $D$ have same type, since they say the same statement about $B$. However, according to Lemma 3, in order to have a solution $A\notin {\mathrm{\Gamma }}_{D,0}$ and $D\notin {\mathrm{\Gamma }}_{A,0}$, there must be a contradiction in the formation of puzzle that has edges that are represented by subgraph shown in Figure 1a. Considering Figure 1b in the solution of the puzzle, $A\notin C$, $B\notin C$ and $D\notin C$, because by Theorem 2, a Crazy person cannot say any statement about other persons. Let us assume that $A\in T$; therefore, $D\in L$ and $B\in L$, but $B\in {\mathrm{\Gamma }}_{D,0}$, which contradicts Lemma 3. On the other hand, if we assume that $A\in L$, then $D\in T$ and $B\in T$ but $B\in {\mathrm{\Gamma }}_{D,0}$, which also contradicts Lemma 3. □

The last proposition is helpful if one wants to provide an unsolvable puzzle by using its graph representation.

4. Comparing SS-Puzzles and SSS-Puzzles

One may ask what the chance for a “random” puzzle to be solvable or to be good is. Some statistics about puzzles that are generated by computers were presented in [5]. In this section, we also present some statistics about the puzzles studied here, e.g., about the number of puzzles depending on the number of persons. Then, we give some details on the number of edges in the puzzle graphs.

In the following statistical data, we considered puzzles in which each person can say only one statement about any person in the puzzle. Because an SS-puzzle becomes unsolvable if any person says both types of statements about a person, this restriction is used in the comparison.

Table 3. The number of good, solvable (including good ones), and unsolvable Strong Truth-Teller–Strong Liar (SS)- and Strong Truth-Teller–Strong Liar–Strong Crazy (SSS)-puzzles with two, three and four persons.

Puzzle Type	Two-Person Puzzle		Three-Person Puzzle		Four-Person Puzzle
	SSS-Puzzle	SS-Puzzle	SSS-Puzzle	SS-Puzzle	SSS-Puzzle	SS-Puzzle
Good puzzles	9	0	553	0	136,017	0
Solvable puzzles	41	28	2619	1880	668,849	506,896
Unsolvable puzzles	40	53	17,064	17,803	42,377,872	42,539,825
Total	81	81	19,683	19,683	43,046,721	43,046,721

shows the number of good puzzles, solvable puzzles with more than one solution, and unsolvable puzzles with two, three, and four persons of SS- and SSS-puzzles.

Table 4. The number of SS- and SSS-puzzles with one, two, three, four, five, or more solutions for puzzles with two, three or four persons.

Puzzle Type	Two-Person Puzzle		Three-Person Puzzle		Four-Person Puzzle
	SSS-Puzzle	SS-Puzzle	SSS-Puzzle	SS-Puzzle	SSS-Puzzle	SS-Puzzle
Good puzzles	9	0	553	0	136017	0
Two-solution puzzles	18	24	1467	1728	443876	490752
Three-solution puzzles	10	0	411	0	66836	0
Four-solution puzzles	1	4	51	144	7350	15552
Five-solution puzzles	0	0	24	0	3963	0
Puzzles with more than five solutions	3	0	113	8	10807	592

presents the number of solvable SS- and SSS-puzzles with two, three and four persons. In fact, the SS- and SSS-puzzles correspond to each other by the statements, but their solvability differs, as is shown.

Table 5. The number of good SSS-puzzles with one, two, three or four Crazy persons in the solution.

Number of Crazy Persons in the Solution	Two-Person Puzzle	Three-Person Puzzle	Four-Person Puzzle
One	8	504	124480
Two	1	48	11328
Three	-	1	208
Four	-	-	1

shows the number of good SSS-puzzles with one, two, three or four Crazy persons in their solutions if there are two, three or four persons in the puzzle. The number of four-person good puzzles with one Crazy person in the solution is 124,480, the number of four-person good puzzles with two Crazy persons is 11,328, the number of four-person good puzzles with three Crazy persons 208, and the number of four-person good puzzles with four Crazy persons is 1.

Now, we turn to analyze the number of edges in the puzzles. In the case of SS puzzles, there are no good puzzles, and the maximal number of edges in a solvable puzzle with n persons is exactly n² because each person can say exactly one of the statements about any person (including himself/herself).

The maximum number of edges in good SSS-puzzles with four persons is 13 (see, e.g., Figure 2a and observe that some of the edges are bidirectional), the maximum number of edges in good SSS-puzzles with three persons is 7, and the maximum number of edges in good SSS-puzzles with two persons is 3. The minimum number of edges in good SSS-puzzles with four persons is 4 (as it is shown, e.g., in Figure 2b), the minimum number of edges in good SSS-puzzles with three persons is 3, and the minimum number of edges in good SSS-puzzles with two persons is 2. Meanwhile, the maximum number of broken edges in good SSS-puzzles with four persons is 7 (see Figure 2c), the maximum number of broken edges in good SSS-puzzles with three persons is 4, and the maximum number of broken edges in good SSS-puzzles with two persons is 2. Additionally, the minimum number of broken edges is in good SSS-puzzles with four persons is 1 (see Figure 2a for a graph with this property), and the maximum number of solid edges is 12 (Figure 2a has also this feature), and the minimum number of solid edges is 0 (see Figure 2b for an example).

The number of unsolvable puzzles increases dramatically as the number of persons in the puzzle increases (see Table 3). In SS-puzzles, there are no puzzles with an odd number of solutions, since a solution and its dual (assigning Truth-Teller to the former Liars and Liar to the former Truth-Tellers) are both solutions for the SS-puzzle. In contrast, as Table 4 shows, there are various SSS-puzzles with an odd number of solutions. Table 5 shows that the majority of the good SSS-puzzles have exactly one Crazy in their solution.

From here, we consider SSS-puzzles, where it is allowed for each person to say both type of statements about any other person in the puzzle, and we show some facts about the possible number of edges in the graphs of the puzzles.

Lemma 5.

For any good SSS-puzzle with n persons, the graph representation G of the puzzle has at least n edges.

Proof. 

Let us consider minimal puzzles in terms of the number of edges in their graph representation G. We may have $m$ different connected components, where $m\le n$. From Corollary 1, each one of these components must have a Crazy person; otherwise, the puzzle is not a good puzzle. Let us assume that in each component (let $k_i$ denote the nodes of the i-th component) of these m components, the number of the nodes equals to $n_i$, such that ${\sum }_{i=1}^m{n}_i=n$ and $\exists A_{k_i}\in C,A_{k_i}\in k_i$. Therefore, in any connected component in graph G, there are at least $n_i-1$ edges that make that component connected and one more edge that makes $A_{k_i}$ Crazy person. Thus, the total number of edges in each component is at least $n_i$. Consequently, the total number of edges in the graph representation G is equal to:

$${\displaystyle \sum }_{i=1}^m{n}_i=n$$

 □

Example 5.

Figure 3 shows the graph representation of a minimal four-person good SSS-puzzle, which has four edges. The solution of this puzzle is: $A\in L,B\in C,D\in LandE\in L.$

Because one person may say two different statements about another in good SSS-puzzles, it is interesting to count the maximal number of edges in such puzzles. Though the case of SSS-puzzles and SS-puzzles are completely different from this point view, the result is very similar to the maximal number of edges in solvable SS-puzzles and good SSS-puzzles. Formally, we have:

Lemma 6.

For any good SSS-puzzle with n persons, the graph representation G of the puzzle has at most $n^2$ edges.

Proof. 

Let us consider maximal puzzles in terms of the number of edges in their graph representation G. First, we show that between any two nodes A and B, there are, at most, two edges. If in the solution of the puzzle $A\notin C\mathrm{and}B\notin C$, then between A and B, there will be, at most, two same type edges in opposite directions. If A or B have two different types of outgoing edges toward the other, then the puzzle will be unsolvable. If $A\in C\mathrm{and}B\in C$, then by Theorem 2, both of them can have a self-broken edge and there are no edges between them. Finally, if $A\in C$ and $B\notin C$ ($B\in L$ or $B\in T$), then in the maximal graph G, $\stackrel{⃛}{BA}\in G$ and $\overline{BA}\in G$ (in case of $B\in L$).

In the solution of the puzzle with maximal graph G, let us assume that there are m Crazy persons and $n-m$ Non-Crazy persons. Thus, the maximum number of edges between Non-Crazy persons equals ${\left(n-m\right)}^2$, since each one of these Non-Crazy persons has $n-m-1$ outgoing edges toward others and one self-solid edge, and the maximum number of edges between Non-Crazy and Crazy persons is $2\left(n-m\right)m$, since each Non-Crazy person can have two types of outgoing edges toward every Crazy person (if the Non-Crazy persons are Liars). By Theorem 2, graph G has m self-broken edges, since each Crazy person can have one self-broken edge. Therefore, the total maximum number of edges is given by:

$${\left(n-m\right)}^2+2\left(n-m\right)m+m=n^2-2nm+m^2+2nm-2m^2+m=n^2-m^2+m$$

That is maximal when $m=1$, since m = 0 is not possible (the puzzle cannot be good if there is no Crazy person in the solution). Hence, in the maximal graph G, the maximum number of edges equals to $n^2$ and the number of Crazy persons equals 1. □

Example 6.

Figure 4 shows the graph representation of a maximal four-person good SSS-puzzle, which has 16 edges, where the solution for such puzzle is: $A\in L,B\in L,D\in LandE\in C.$

5. Conclusions

Truth-Tellers and Liars appear in various puzzles. In this paper, a new type of people was investigated: Crazy people, who can say only statements that are self-contradictory, i.e., no Truth-Teller or Liars could say them. Thus, SSS-puzzles are similar to SS-puzzles, but there can be three types of people in the solution instead of the original two. By investigating Crazy people, several unsolvable puzzles were found to become solvable, and it was shown that there are clear and good SSS-puzzles (which was not the case with SS-puzzles), just to recall our main results. It was also shown that there are unsolvable SSS-puzzles (based on Proposition 3, one can easily create such puzzles). A statistical comparison between SS-puzzles and SSS-puzzles was been presented for puzzles of up to four persons. Some features and characteristics of the graph representation of the good SSS-puzzles, e.g., the minimum and maximum number of edges in any good SSS-puzzle, were also discussed.

By considering the newly introduced Crazy type, message service systems, where neighboring units rely on each other, might benefit from such improved models. As a specific application of SSS-puzzles, we can generalize the scenario of [10], where satellites could send messages to mechanics about the status of neighborhood satellites regarding whether they are working properly.

As this is the first paper on SSS-puzzles, some questions are left open. In the future, we would like to find some easily checkable properties that characterize the good, solvable, and unsolvable SSS-puzzles. Another type of puzzles can also be considered in the future, where the person can say a new type of atomic statement which is “$A_i$ is a Crazy person”.