Some Second-Order σ Schemes Combined with an H1-Galerkin MFE Method for a Nonlinear Distributed-Order Sub-Diffusion Equation
Abstract
1. Introduction
2. Some Lemmas
3. Numerical Approximation and Analysis of Stability
4. A Priori Error Analysis
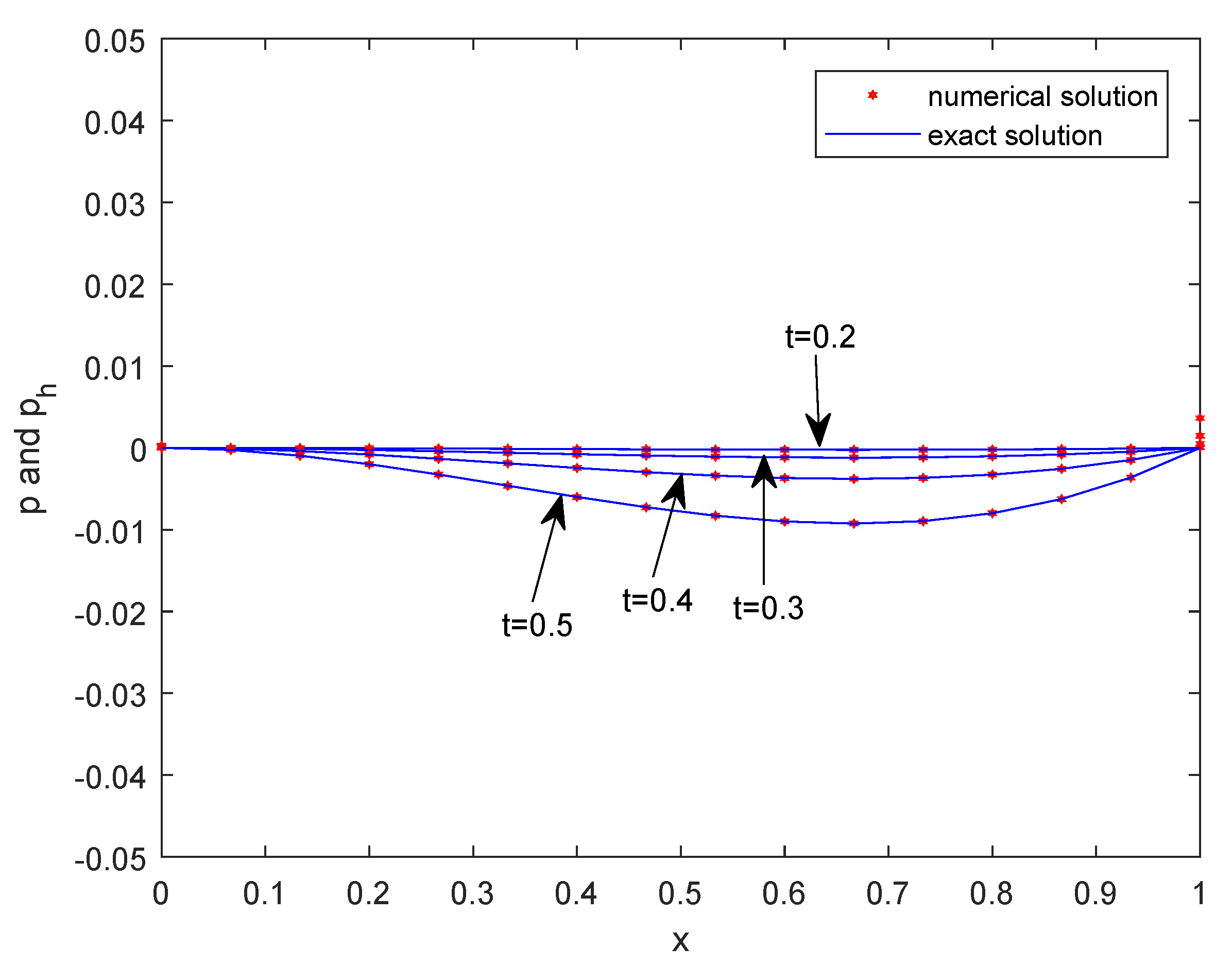
5. Numerical Example
Author Contributions
Funding
Conflicts of Interest
References
- Feng, L.B.; Zhuang, P.; Liu, F.; Turner, I.; Gu, Y.T. Finite element method for space-time fractional diffusion equation. Numer. Algor. 2016, 72, 749–767. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, A.J.; Wang, H. A preconditioned fast Hermite finite element method for space-fractional diffusion equations. Discrete Contin. Dyn. Syst.-Ser. B 2017, 22, 3529–3545. [Google Scholar] [CrossRef][Green Version]
- Zayernouri, M.; Karniadakis, G.E. Discontinuous spectral element methods for time-and space-fractional advection equations. SIAM J. Sci. Comput. 2014, 36, B684–B707. [Google Scholar] [CrossRef]
- Yuste, S.B.; Quintana-Murillo, J. A finite difference method with non-uniform time steps for fractional diffusion equations. Comput. Phys. Commun. 2012, 183, 2594–2600. [Google Scholar] [CrossRef]
- Yin, B.L.; Liu, Y.; Li, H. A class of shifted high-order numerical methods for the fractional mobile/immobile transport equations. Appl. Math. Comput. 2020, 368, 124799. [Google Scholar] [CrossRef]
- Zeng, F.; Li, C.; Liu, F.; Turner, I. The use of finite difference/element approaches for solving the time-fractional subdiffusion equation. SIAM J. Sci. Comput. 2013, 35, A2976–A3000. [Google Scholar] [CrossRef]
- Liu, Y.; Du, Y.W.; Li, H.; He, S.; Gao, W. Finite difference/finite element method for a nonlinear time-fractional fourth-order reaction-diffusion problem. Comput. Math. Appl. 2015, 70, 573–591. [Google Scholar] [CrossRef]
- Liu, Y.; Du, Y.W.; Li, H.; Liu, J.C.; He, S. A two-grid mixed finite element method for a nonlinear fourth-order reaction-diffusion problem with time-fractional derivative. Comput. Math. Appl. 2015, 70, 2474–2492. [Google Scholar] [CrossRef]
- Li, C.P.; Ding, H.F. Higher order finite difference method for the reaction and anomalous-diffusion equation. Appl. Math. Model. 2014, 38, 3802–3821. [Google Scholar] [CrossRef]
- Lin, Y.M.; Xu, C.J. Finite difference/spectral approximations for the time fractional diffusion equation. J. Comput. Phys. 2007, 225, 1533–1552. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, M.; Li, H.; Li, J.C. High-order local discontinuous Galerkin method combined with WSGD-approximation for a fractional subdiffusion equation. Comput. Math. Appl. 2017, 73, 1298–1314. [Google Scholar] [CrossRef]
- Donatelli, M.; Mazza, M.; Serra-Capizzano, S. Spectral analysis and structure preserving preconditioners for fractional diffusion equation. J. Comput. Phys. 2016, 307, 262–279. [Google Scholar] [CrossRef]
- Lin, X.L.; Ng, M.K.; Sun, H.W. A multigrid method for linear systems arising from time-dependent two-dimensional space-fractional diffusion equations. J. Comput. Phys. 2017, 336, 69–86. [Google Scholar] [CrossRef]
- Bu, W.; Liu, X.; Tang, Y.; Jiang, Y. Finite element multigrid method for multi-term time fractional advection-diffusion equations. Int. J. Model. Simulat. Sci. Comput. 2015, 6, 1540001. [Google Scholar] [CrossRef]
- Bu, W.P.; Tang, Y.F.; Yang, J.Y. Galerkin finite element method for two-dimensional Riesz space fractional diffusion equations. J. Comput. Phys. 2014, 276, 26–38. [Google Scholar] [CrossRef]
- Jin, B.; Lazarov, R.; Liu, Y.K.; Zhou, Z. The Galerkin finite element method for a multi-term time-fractional diffusion equation. J. Comput. Phys. 2015, 281, 825–843. [Google Scholar] [CrossRef]
- Yang, X.H.; Zhang, H.X.; Xu, D. Orthogonal spline collocation method for the two-dimensional fractional sub-diffusion equation. J. Comput. Phys. 2014, 256, 824–837. [Google Scholar] [CrossRef]
- Wang, J.F.; Zhang, M.; Li, H.; Liu, Y. Finite difference/H1-Galerkin MFE procedure for a fractional water wave model. J. App. Anal. Comput. 2016, 6, 409–428. [Google Scholar]
- Liu, Y.; Yu, Z.D.; Li, H.; Liu, F.W.; Wang, J.F. Time two-mesh algorithm combined with finite element method for time fractional water wave model. Int. J. Heat Mass Transfer 2018, 120, 1132–1145. [Google Scholar] [CrossRef]
- Atangana, A. On the stability and convergence of the time-fractional variable order telegraph equation. J. Comput. Phys. 2015, 293, 104–114. [Google Scholar] [CrossRef]
- Liu, Y.; Du, Y.W.; Li, H.; Liu, F.W.; Wang, Y.J. Some second-order θ schemes combined with finite element method for nonlinear fractional Cable equation. Numer. Algor. 2019, 80, 533–555. [Google Scholar] [CrossRef]
- Wang, Y.J.; Liu, Y.; Li, H.; Wang, J.F. Finite element method combined with second-order time discrete scheme for nonlinear fractional Cable equation. Eur. Phys. J. Plus. 2016, 131, 61. [Google Scholar] [CrossRef]
- Rebenda, J.; Smarda, Z. Numerical solution of fractional control problems via fractional differential transformation. In Proceedings of the European Conference on Electrical Engineering and Computer Science (EECS), Bern, Switzerland, 17–19 November 2017. [Google Scholar] [CrossRef]
- Mainardi, F.; Pagnini, G.; Gorenflo, R. Some aspects of fractional diffusion equations of single and distributed order. Appl. Math. Comput. 2007, 187, 295–305. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Numerical analysis for distributed-order differential equations. J. Comput. Appl. Math. 2009, 225, 96–104. [Google Scholar] [CrossRef]
- Ford, N.J.; Morgado, M.L.; Rebelo, M. An implicit finite difference approximation for the solution of the diffusion equation with distributed order in time. Electron. Trans. Numer. Anal. 2015, 44, 289–305. [Google Scholar]
- Ye, H.; Liu, F.; Anh, V. Compact difference scheme for distributed-order time-fractional diffusion-wave equation on bounded domains. J. Comput. Phys. 2015, 298, 652–660. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Nane, E.; Vellaisamy, P. Distributed-order fractional diffusions on bounded domains. J. Math. Anal. Appl. 2011, 379, 216–228. [Google Scholar] [CrossRef]
- Luchko, Y. Boundary value problems for the generalized time-fractional diffusion equation of distributed order. Fract. Calc. Appl. Anal. 2009, 12, 409–422. [Google Scholar]
- Gao, G.H.; Alikhanov, A.A.; Sun, Z.Z. The temporal second order difference schemes based on the interpolation approximation for solving the time multi-term and distributed-order fractional sub-diffusion equations. J. Sci. Comput. 2017, 73, 93–121. [Google Scholar] [CrossRef]
- Lorenzo, C.F.; Hartley, T.T. Variable order and distributed order fractional operators. Nonlinear Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
- Li, J.; Liu, F.; Feng, L.; Turner, I. A novel finite volume method for the Riesz space distributed-order diffusion equation. Comput. Math. Appl. 2017, 74, 772–783. [Google Scholar] [CrossRef]
- Alikhanov, A.A. A new difference scheme for the time fractional diffusion equation. J. Comput. Phys. 2015, 280, 424–438. [Google Scholar] [CrossRef]
- Li, X.L.; Rui, H.X. Two temporal second-order H1-Galerkin mixed finite element schemes for distributed-order fractional sub-diffusion equations. Numer. Algor. 2018, 79, 1107–1130. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Dehghan, M. An improved meshless method for solving two-dimensional distributed order time-fractional diffusion-wave equation with error estimate. Numer. Algor. 2017, 75, 173–211. [Google Scholar] [CrossRef]
- Liu, Y.; Du, Y.W.; Li, H.; Wang, J.F. An H1-Galerkin mixed finite element method for time fractional reaction-diffusion equation. J. Appl. Math. Comput. 2015, 47, 103–117. [Google Scholar] [CrossRef]
- Pani, A.K. An H1-Galerkin mixed finite element methods for parabolic partial differential equations. SIAM J. Numer. Anal. 1998, 35, 712–727. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H. H1-Galerkin mixed finite element methods for pseudo-hyperbolic equations. Appl. Math. Comput. 2009, 212, 446–457. [Google Scholar]
- Guo, L.; Chen, H. H1-Galerkin mixed finite element method for the regularized long wave equation. Computing 2006, 77, 205–221. [Google Scholar] [CrossRef]
- Wang, J.F.; Liu, T.Q.; Li, H.; Liu, Y.; He, S. Second-order approximation scheme combined with H1-Galerkin MFE method for nonlinear time fractional convection-diffusion equation. Comput. Math. Appl. 2017, 73, 1182–1196. [Google Scholar] [CrossRef]
- Shi, Z.G.; Zhao, Y.M.; Liu, F.; Tang, Y.F.; Wang, F.L.; Shi, Y.H. High accuary analysis of an H1-Galerkin mixed finite element method for two-dimensional time fractional diffusion equations. Comput. Math. Appl. 2017, 74, 1903–1914. [Google Scholar] [CrossRef]
- Shi, D.Y.; Wang, J.J.; Yan, F.N. Unconditional superconvergence analysis of an H1-Galerkin mixed finite element method for nonlinear Sobolev equations. Numer. Meth. Part. Differ. Equ. 2018, 34, 145–166. [Google Scholar] [CrossRef]
- Sun, H.; Sun, Z.Z.; Gao, G.H. Some temporal second order difference schemes for fractional wave equations. Numer. Meth. Part Differ. Equ. 2016, 32, 970–1001. [Google Scholar] [CrossRef]

| Rate | Rate | Time (s) | ||||
|---|---|---|---|---|---|---|
| 1/10 | 0.6720 | 1.59 × 10 | - | 1.35 × 10 | - | 146.4 |
| 1/20 | 0.6487 | 4.04 × 10 | 1.9491 | 3.41 × 10 | 1.9848 | 325.5 |
| 1/40 | 0.6290 | 1.03 × 10 | 1.9717 | 8.39 × 10 | 2.0230 | 685.9 |
| Rate | Rate | Time (s) | ||||
|---|---|---|---|---|---|---|
| 1/2 | 0.6856 | 3.21 × 10 | - | 1.08 × 10 | - | 0.4 |
| 1/4 | 0.6431 | 2.22 × 10 | 3.8494 | 5.67 × 10 | 4.2515 | 7.5 |
| 1/8 | 0.6125 | 1.48 × 10 | 3.9069 | 2.90 × 10 | 4.2892 | 132.0 |
| h | Rate | Rate | Time (s) | |||
|---|---|---|---|---|---|---|
| 1/10 | 0.5820 | 5.06 × 10 | - | 3.11 × 10 | - | 171.2 |
| 1/20 | 0.5820 | 1.41 × 10 | 1.8435 | 7.79 × 10 | 1.9972 | 337.0 |
| 1/40 | 0.5820 | 3.71 × 10 | 1.9249 | 1.95 × 10 | 1.9982 | 673.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, Y.; Wen, C.; Li, H.; Liu, Y.; Fang, Z.; Yang, Y. Some Second-Order σ Schemes Combined with an H1-Galerkin MFE Method for a Nonlinear Distributed-Order Sub-Diffusion Equation. Mathematics 2020, 8, 187. https://doi.org/10.3390/math8020187
Hou Y, Wen C, Li H, Liu Y, Fang Z, Yang Y. Some Second-Order σ Schemes Combined with an H1-Galerkin MFE Method for a Nonlinear Distributed-Order Sub-Diffusion Equation. Mathematics. 2020; 8(2):187. https://doi.org/10.3390/math8020187
Chicago/Turabian StyleHou, Yaxin, Cao Wen, Hong Li, Yang Liu, Zhichao Fang, and Yining Yang. 2020. "Some Second-Order σ Schemes Combined with an H1-Galerkin MFE Method for a Nonlinear Distributed-Order Sub-Diffusion Equation" Mathematics 8, no. 2: 187. https://doi.org/10.3390/math8020187
APA StyleHou, Y., Wen, C., Li, H., Liu, Y., Fang, Z., & Yang, Y. (2020). Some Second-Order σ Schemes Combined with an H1-Galerkin MFE Method for a Nonlinear Distributed-Order Sub-Diffusion Equation. Mathematics, 8(2), 187. https://doi.org/10.3390/math8020187






