The Extinction of a Non-Autonomous Allelopathic Phytoplankton Model with Nonlinear Inter-Inhibition Terms and Feedback Controls

Abstract

A non-autonomous allelopathic phytoplankton model with nonlinear inter-inhibition terms and feedback controls is studied in this paper. Based on the comparison theorem of differential equation, some sufficient conditions for the permanence of the system are obtained. We study the extinction of one of the species by using some suitable Lyapunov type extinction function. Our analyses extend those of Xie et al. (Extinction of a two species competitive system with nonlinear inter-inhibition terms and one toxin producing phytoplankton. Advances in Difference Equations, 2016, 2016, 258) and show that the feedback controls and toxic substances have no effect on the permanence of the system but play a crucial role on the extinction of the system. Some known results are extended.

1. Introduction

Recently, competition models with nonlinear inter-inhibition terms have been considered by many scholars [1,2,3,4,5,6,7]. Wang, Liu and Li [1] considered the following competition system:

$$\begin{array}{c}{x}_1^{\prime }(t)=x_1(t)(r_1(t)-a_1(t)x_1(t)-\frac{b_1(t)x_2(t)}{1+x_2(t)}),\hfill \\ x_2^{\prime }(t)=x_2(t)\left(r_2(t)-\frac{b_2(t)x_1(t)}{1+x_1(t)}-a_2(t)x_2(t)\right),\hfill \end{array}$$

(1)

where $x_1(t),x_2(t)$ indicate the species $x_1$ and $x_2$ densities at time t, respectively; $r_i(t),i=1,2$ denote the net rates of production of two species; $a_i(t),i=1,2$ are the rates of intraspecific competition of the species $x_1$ and $x_2$, respectively; $b_i(t),i=1,2$ represent the interspecific competing rates. The nonlinear inter-inhibition terms $\frac{b_1(t)x_2(t)}{1+x_2(t)}$ and $\frac{b_2(t)x_1(t)}{1+x_1(t)}$ implie that for large phytoplankton density, the interspecific competing rate tends to a certain value. In other words, the interspecific competing rate will not increase infinitely with the increase of phytoplankton density, which could make us understand the real ecosystems deeper. For more information about the nonlinear inter-inhibition terms, see [8]. Based on differential inequality, the module containment theorem and constructing the Lyapunov function, Wang et al. [1] gave the sufficient conditions for the global asymptotic stability of system.

As we all know, phytoplankton is the primary producer in ocean and plays an important role in energy flow and nutrient cycling of marine ecosystems. In addition, phytoplankton can absorb carbon dioxide for photosynthesis, which has a significant impact on the climate regulation. The importance of phytoplankton to marine ecosystem has been widely recognized. Besides, many authors attempted to explain the bloom phenomenon by different approaches, and find that toxic phytoplankton certainly play an important role in the bloom phenomenon. Therefore, in recent years, many scholars have stuied the allelopathic toxic phytoplankton model [4,5,7,9,10,11,12,13,14,15,16,17,18,19,20]. Rashi Gupta [9] considered Holling type-II and Holling type-IV functional responses in a model of non-toxic phytoplankton-toxic phytoplankton-zooplankton. He gave the the condition for diffusive instability of a locally stable equilibrium of spatial and non-spatial model for one dimensional system. Based on the work of Yue [4], recently, Xie et al. [5] further considered the effect of toxin on a non-autonomous competitive phytoplankton system, written in the form as

$$\begin{array}{c}{x}_1^{\prime }(t)=x_1(t)(r_1(t)-a_1(t)x_1(t)-\frac{b_1(t)x_2(t)}{1+x_2(t)}-c_1(t)x_1(t)x_2(t)),\hfill \\ x_2^{\prime }(t)=x_2(t)(r_2(t)-\frac{b_2(t)x_1(t)}{1+x_1(t)}-a_2(t)x_2(t)),\hfill \end{array}$$

(2)

where $c_1(t)$ denotes the rate of toxic inhibition for the species $x_1$ released by the second species. The authors obtained the sufficient conditions for the extinction of a species and the global attractivity of the other one. On the other hand, through experimental data of a experimental study on two phytoplankton species, namely C. polylepis and H. triquetra, Sole et al. [10] found that the allelopathic interaction using $r{x_1(t)}^2{x_2}^2(t)$ is more suitable. M. Bandyopadhyay [11] proposed and studied the following mathematical model of two competing phytoplankton species with allelopathic interaction term:

$$\begin{array}{c}{x}_1^{\prime }(t)=x_1(t)(r_1-a_1{x}_1(t)-b_1{x}_2(t))-\gamma x_1^2(t){x_2}^2(t),\hfill \\ x_2^{\prime }(t)=x_2(t)(r_2-a_2{x}_2(t)-b_2{x}_1(t)).\hfill \end{array}$$

(3)

Since the influence of human behavior on the ecosystems is more and more great, a large number of precious species are facing extinction. It is important to know how to protect endangered species and maintain the diversity of ecosystems. In ecology, we want to know that whether or not an ecosystem can withstand those unpredictable disturbances. In the language of control variables, we use feedback control variables to represent these unpredictable disturbances. In order to describe the effect of people’s behavior, many researchers focused on the research of the systems with feedback control variables [7,15,21,22,23,24,25,26]. Muroya Y. [21] studied a Lotka-Volterra systems with infinite delays and feedback controls, the authors applied a Lyapunov functional and established that the feedback controls have no effect on the attractivity of a saturated equilibrium. Recently, Liu et al. [22] proposed the following system with feedback controls:

$$\begin{array}{c}{\displaystyle x_1(n+1)=x_1(n)\exp \{r_1(n)-a_1(n)x_1(t)-\frac{b_1(n)x_2(n)}{1+x_2(n)}-e_1(n)u_1(n)\},}\hfill \\ {\displaystyle x_2(n+1)=x_2(n)\exp \{r_2(n)-\frac{b_2(n)x_1(n)}{1+x_1(n)}-a_2(n)x_2(n)-e_2(n)u_2(n)\},}\hfill \\ \Delta u_1(n)=-b_1(n)u_1(n)+d_1(n)x_1(n),\hfill \\ \Delta u_2(n)=-b_2(n)u_2(n)+d_2(n)x_2(n),\hfill \end{array}$$

(4)

where $\Delta u_i(n)=u_i(n+1)-u_i(n),i=1,2$ are the forward difference operators; $u_i(n),i=1,2$ denote the feedback control variables. $b_i(n),d_i(n)$ and $e_i(n),i=1,2$ are bounded positive almost periodic sequences. Liu et al. [22] studied the existence and uniformly asymptotic stability of unique positive almost periodic solution of system (4). Furthermore, based on a suitable Lyapunov function, Yu [7] obtained the sufficient conditions for the extinction of one species.

As is well known, if the amount of the species is enough large, the continuous model is more appropriate. But, to this day, still no scholar propose and study the continuous form of system (4) with toxin and feedback controls. Motivated by the above work, in this paper, we consider the following nonautonomous allelopathic phytoplankton model with nonlinear-inhibition terms and feedback control variables:

$$\begin{array}{c}{\displaystyle x_1^{\prime }(t)=x_1(t)(r_1(t)-a_1(t)x_1(t)-\frac{b_1(t)x_2(t)}{1+x_2(t)}-\gamma (t)x_1(t)x_2^2(t)-c_1(t)u_1(t)),}\hfill \\ {\displaystyle x_2^{\prime }(t)=x_2(t)(r_2(t)-\frac{b_2(t)x_1(t)}{1+x_1(t)}-a_2(t)x_2(t)-c_2(t)u_2(t)),}\hfill \\ u_1^{\prime }(t)=-e_1(t)u_1(t)+d_1(t)x_1(t),\hfill \\ u_2^{\prime }(t)=-e_2(t)u_2(t)+d_2(t)x_2(t).\hfill \end{array}$$

(5)

Recently, a few studies about the effect of feedback controls on allelopathic phytoplankton model have been carried out, it is worth noting that in this paper. Besides, the allelopathic interaction term is replaced by $\gamma {x_1(t)}^2{x_2}^2(t)$ instead of $\gamma {x_1(t)}^2{x}_2(t)$. Our main objective is to study the effects of toxicity and feedback controls on the dynamics of the system.

The paper is organized as follows. In Section 2, we will state some necessary Lemmas and prove the permanence of the system (5). In Section 3, we will discuss the extinction of one species. Four examples together with their numeric simulations are present in Section 4, as we will show the feasibility of the main results. We give a a briefly discussion in the end of this paper.

2. Permanence

Given a continuous and bounded function $f(t)$, let $f^u$ and $f^l$ denote ${sup}_{t\in R}f(t)$ and ${\inf }_{t\in R}f(t)$, respectively. From the point of view of biology, we assume that $x_i(0)>0,u_i(0)>0,i=1,2$. We can easily obtain the solution $(x_1(t),x_2(t),u_1(t),u_2(t))$ passing through $(x_1(0),x_2(0),u_1(0),u_2(0))$ is positive.

Definition 1

([27]).

(1) 

Population x(t) is said to be permanent if there exist two constant M and m such that $m\le {\displaystyle \underset{t\to +\infty }{\lim \inf }}x(t)\le {\displaystyle \underset{t\to +\infty }{\lim \sup }}x(t)\le M$.

(2) 

Population x(t) is said to be extinct if ${\displaystyle \underset{t\to +\infty }{\lim }}x(t)=0$ almost surely.

Lemma 1.

(1) 

If $a>0,b>0$ and $\dot{x}\ge b-ax$, when $t\ge 0$ and $x(0)>0$, we have ${\displaystyle \underset{t\to +\infty }{\lim \inf }}x(t)\ge \frac{b}{a}.$

(2) 

If $a>0,b>0$ and $\dot{x}\le b-ax$, when $t\ge 0$ and $x(0)>0$, we have ${\displaystyle \underset{t\to +\infty }{\lim \sup }}x(t)\le \frac{b}{a}.$

Lemma 2.

(1) 

If $a>0,b>0$ and $\dot{x}\ge x(b-ax)$, when $t\ge 0$ and $x(0)>0$, we have ${\displaystyle \underset{t\to +\infty }{\lim \inf }}x(t)\ge \frac{b}{a}.$

(2) 

If $a>0,b>0$ and $\dot{x}\le x(b-ax)$, when $t\ge 0$ and $x(0)>0$, we have ${\displaystyle \underset{t\to +\infty }{\lim \sup }}x(t)\le \frac{b}{a}.$

Lemma 3.

Every positive solution ${(x_1(t),x_2(t),u_1(t),u_2(t))}^T$ of system (5) satisfies

$$\underset{t\to +\infty }{\lim \sup }{x}_i(t)\le \frac{r_i^u}{a_i^l}\stackrel{\mathrm{def}}{=}{M}_i,\underset{t\to +\infty }{\lim \sup }{u}_i(t)\le \frac{d_i^u{r}_i^u}{e_i^l{a}_i^l}\stackrel{\mathrm{def}}{=}{N}_i,i=1,2.$$

(6)

Proof. 

It follows from the first and second equation of system (5) yields

$$x_i^{\prime }(t)\le x_i(t)(r_i(t)-a_i(t)x_i(t))\le x_i(t)\left(r_i^u-a_i^l{x}_i(t)\right),i=1,2.$$

(7)

According to Lemma 2 and differential inequality (7), we have

$$\underset{t\to +\infty }{\lim \sup }{x}_i(t)\le \frac{r_i^u}{a_i^l}\stackrel{\mathrm{def}}{=}{M}_i,i=1,2.$$

(8)

From (8), there exists a $T_1>0$, such that for $t>T_1$ and any small positive constant $\epsilon >0$,

$$x_i(t)\le M_i+\epsilon .$$

(9)

From the third and fourth equation of system (5) it follows that

$$u_i^{\prime }(t)=-e_i^l{u}_i(t)+d_i^u(M_i+\epsilon ).$$

(10)

By applying Lemma 1 to differential inequality (10), we have

$$\underset{t\to +\infty }{\lim \sup }{u}_i(t)\le \frac{d_i^u}{e_i^l}(M_i+\epsilon ),i=1,2.$$

Setting $\epsilon \to 0$ in above inequalities leads to

$$\underset{t\to +\infty }{\lim \sup }{u}_i(t)\le \frac{d_i^u}{e_i^l}{M}_i=\frac{d_i^u{r}_i^u}{e_i^l{a}_i^l}\stackrel{\mathrm{def}}{=}{N}_i,i=1,2.$$

 □

Theorem 1.

Assume that

$$r_1^l>b_1^u\frac{r_2^u}{a_2^l},r_2^l>b_2^u\frac{r_1^u}{a_1^l}$$

(11)

holds. Then, for any positive solution ${\left(x_1(t),x_2(t),u_1(t),u_2(t)\right)}^T$ of the system (5), we have

$$\begin{array}{c}{m}_i\le {\displaystyle \underset{t\to +\infty }{\lim \inf }}{x}_i(t)\le {\displaystyle \underset{t\to +\infty }{\lim \sup }}{x}_i(t)\le M_i,\hfill \\ n_i\le {\displaystyle \underset{t\to +\infty }{\lim \inf }}{u}_i(t)\le {\displaystyle \underset{t\to +\infty }{\lim \sup }}{u}_i(t)\le N_i,\hfill \end{array}i=1,2.$$

i.e., system (5) is permanent.

Remark 1.

Theorem 1 shows that two kinds of phytoplankton can coexist under certain conditions. Besides, the conditions of Theorem 1 show that the feedback control variables and toxic substances do not effect on the permanence of the system.

Proof. 

From (5), for any small positive constant $\epsilon >0$, we may choose $\epsilon$ small enough such that

$$r_1^l>b_1^u\left(\frac{r_2^u}{a_2^l}+\epsilon \right)=b_1^u(M_2+\epsilon ),r_2^l>b_2^u\left(\frac{r_1^u}{a_1^l}+\epsilon \right)=b_2^u(M_1+\epsilon ).$$

(12)

For $\epsilon >0$ above, from Lemma 3 it follows that there exists $T_2>0$ such that for $t>T_2$,

$$x_i(t)\le M_i+\epsilon ,u_i(t)\le N_i+\epsilon ,i=1,2.$$

(13)

From the first equation of system (5), we have

$$\begin{array}{c}{x}_1^{\prime }(t)=x_1(t)(r_1(t)-a_1(t)x_1(t)-\frac{b_1(t)x_2(t)}{1+x_2(t)}-\gamma (t)x_1(t)x_2^2(t)-c_1(t)u_1(t))\hfill \\ \ge x_1(t)\left(r_1(t)-a_1(t)x_1(t)-b_1(t)x_2(t)-\gamma (t)x_1(t)x_2^2(t)-c_1(t)u_1(t)\right)\hfill \\ \ge x_1(t)(r_1^l-a_1^u(M_1+\epsilon )-b_1^u(M_2+\epsilon )-{\gamma }^u(M_1+\epsilon ){(M_2+\epsilon )}^2-c_1^u(N_1+\epsilon ))\hfill \\ \stackrel{\mathrm{def}}{=}{I}_1^{\epsilon }{x}_1(t).\hfill \end{array}$$

(14)

Integrating the above differential inequality from s to t, we have

$$x_1(s)\le x_1(t)\exp \left[-I_1^{\epsilon }(t-s)\right].$$

(15)

By the third equation of system (5), it follows

$${u_1}^{\prime }(t)\le -{e_1}^l{u}_1(t)+{d_1}^u{x}_1(t).$$

According to Lemma 2.3 of [24] and inequality (15), integrateing the above differential inequality from $t_1$ ($t_1>T_2$) to t, we have

$$\begin{array}{ccc}\hfill u_1(t)& \le & u_1(t_1)\exp \left[-e_1^l(t-t_1)\right]+{\int }_{t_1}^t{d_1}^u{x}_1(s)\exp \left[e_1^l(s-t)\right]ds,\hfill \\ & \le & u_1(t_1)\exp \left[-e_1^l(t-t_1)\right]+{\int }_{t_1}^t{d}_1^u{x}_1(t)\exp \left[-I_1^{\epsilon }(t-s)\right]ds,\hfill \\ & =& u_1(t_1)\exp \left[-e_1^l(t-t_1)\right]+d_1^u{x}_1(t)\frac{1}{I_1^{\epsilon }}\left(1-\exp \left\{-{I_1}^{\epsilon }(t-t_1)\right\}\right),\hfill \\ & \le & (N_1+\epsilon )\exp \left[-e_1^l(t-t_1)\right]+d_1^u{x}_1(t)\frac{1}{I_1^{\epsilon }}\left(1-\exp \left\{-{I_1}^{\epsilon }(t-t_1)\right\}\right).\hfill \end{array}$$

(16)

There exists a $T_1^{*}$ such that $t-t_1={T_1}^{\prime }\ge {T_1}^{*}$, we have

$${c_1}^u(N_1+\epsilon )\exp (-e_1^l{T_1}^{*})<\frac{1}{2}(r_1^l-b_1^u(M_2+\epsilon )),$$

(17)

$$\begin{array}{ccc}\hfill u_1(t)& \le & (N_1+\epsilon )\exp (-e_1^1{T_1}^{*})+d_1^u{x}_1(t)\frac{1}{A_1^{\epsilon }}(1-\exp (-I_1^{\epsilon }{T_1}^{*}))\hfill \\ & =& (N_1+\epsilon )\exp (-e_1^1{T_1}^{*})+D_1^{\epsilon }{x}_1(t).\hfill \end{array}$$

(18)

where $D_1^{\epsilon }=d_1^u\frac{1}{I_1^{\epsilon }}(1-\exp (-I_1^{\epsilon }{T_1}^{*})).$

By the first equation of system (5), we have

$$\begin{array}{ccc}\hfill x_1^{\prime }(t)& \ge & x_1(t)[r_1^l-a_1^u{x}_1(t)-b_1^u(M_2+\epsilon )-{\gamma }^u{x}_1(t){(M_2+\epsilon )}^2\hfill \\ & & -c_1^u(N_1+\epsilon )\exp (-{e_1}^l{T_1}^{*})-c_1^u{D}_1^{\epsilon }{x}_1(t)]\hfill \\ & =& x_1(t)[r_1^l-b_1^u(M_2+\epsilon )-c_1^u(N_1+\epsilon )\exp (-{e_1}^l{T_1}^{*})\hfill \\ & & -(a_1^u+{\gamma }^u{(M_2+\epsilon )}^2+c_1^u{D}_1^{\epsilon })x_1(t)].\hfill \end{array}$$

(19)

By applying Lemma 2 to the above differential inequality, it follows that

$$\underset{t\to +\infty }{\lim \inf }{x}_1(t)\ge \frac{r_1^l-b_1^u(M_2+\epsilon )-c_1^u(N_1+\epsilon )\exp (-{e_1}^l{T_1}^{*})}{a_1^u+{\gamma }^u{(M_2+\epsilon )}^2+c_1^u{D}_1^{\epsilon }}.$$

Setting $\epsilon \to 0$ in this inequality leads to

$$\underset{t\to +\infty }{\lim \inf }{x}_1(t)\ge \frac{r_1^l-b_1^u{M}_2-c_1^u{N}_1\exp (-{e_1}^l{T_1}^{*})}{a_1^u+{\gamma }^u{M}_2^2+c_1^u{D}_1}\stackrel{\mathrm{def}}{=}{m}_1,$$

(20)

where

$$D_1=d_1^u\frac{1}{I_1}(1-\exp (-I_1{T_1}^{*})),$$

$$I_1=r_1^l-a_1^u{M}_1-b_1^u{M}_2-{\gamma }^u{M}_1{M}_2^2-c_1^u{N}_1.$$

From the second equation of system (5) it follows that

$$x_2^{\prime }(t)\ge x_2(t)\left(r_2^l-b_2^u(M_1+\epsilon )-a_2^u(M_2+\epsilon )-c_2^u(N_2+\epsilon )\right)\stackrel{\mathrm{def}}{=}{I}_2^{\epsilon }{x}_2(t).$$

(21)

Integrating this inequality from s to t, we get

$$x_2(s)\le x_2(t)\exp \left\{-I_2^{\epsilon }(t-s)\right\}.$$

(22)

By the fourth equation of system (5), we have

$${u_2}^{\prime }(t)\le -{e_2}^l{u}_2(t)+{d_2}^u{x}_2(t).$$

(23)

Integrating this inequality from $t_2$ to t, it follows

$$\begin{array}{ccc}\hfill u_2(t)& \le & u_2(t_2)\exp \left[-e_2^l(t-t_2)\right]+{\int }_{t_2}^t{d_2}^u{x}_2(s)\exp \left[e_2^l(s-t)\right]ds,\hfill \\ & \le & u_2(t_2)\exp \left[-e_2^l(t-t_2)\right]+d_2^u{x}_2(t)\frac{1}{I_2^{\epsilon }}\left(1-\exp \left\{-{I_2}^{\epsilon }(t-t_2)\right\}\right).\hfill \end{array}$$

(24)

From Lemma 3, we have

$$u_2(t_2)\le N_2+\epsilon ,t_2>T_2.$$

There exists a $T_2^{*}$ such that $t-t_2={T_2}^{\prime }\ge {T_2}^{*}$, we have

$${c_2}^u(N_2+\epsilon )\exp (-e_2^l{T_2}^{*})<\frac{1}{2}(r_2^l-b_2^u(M_1+\epsilon )),$$

$$\begin{array}{c}\hfill u_2(t)\le (N_2+\epsilon )\exp (-e_2^1{T_2}^{*})+D_2^{\epsilon }{x}_2(t),\end{array}$$

(25)

where $D_2^{\epsilon }=d_2^u\frac{1}{I_2^{\epsilon }}\left(1-\exp (-I_2^{\epsilon }{T_2}^{*})\right).$

From the second equation of system (5), we have

$$\begin{array}{ccc}\hfill x_2^{\prime }(t)& \ge & x_2(t)[r_2^l-b_2^u(M_1+\epsilon )-c_2^u(N_2+\epsilon )\exp (-{e_2}^l{T_2}^{*})\hfill \\ & & -(a_2^u+c_2^u{D}_2^{\epsilon })x_2(t)].\hfill \end{array}$$

Similarly to the analysis of (19), we can obtain

$$\underset{t\to +\infty }{\lim \inf }{x}_2(t)\ge \frac{r_2^l-b_2^u{M}_1-c_2^u{N}_2\exp (-{e_2}^l{T_2}^{*})}{a_2^u+c_2^u{D}_2}\stackrel{\mathrm{def}}{=}{m}_2,$$

(26)

where

$$D_2=d_2^u\frac{1}{I_2}(1-\exp (-I_2{T_2}^{*})),$$

$$I_2=r_2^l-b_2^u{M}_1-a_2^u{M}_2-c_2^u{N}_2.$$

For any small positive constant $\epsilon <\frac{1}{2}min\{m_1,m_2\}$, from (20) and (26) it follows that there exists a $T_3>T_i^{\prime },i=1,2$. such that for $t>T_3$, we have

$$x_i(t)\ge m_i-\epsilon ,i=1,2.$$

(27)

From the third and fourth equation of system (5) it follows that

$$u_i^{\prime }(t)\ge -e_i^u{u}_i(t)+d_i^l(m_i-\epsilon ),i=1,2.$$

(28)

From Lemma 1, we obtain

$$\underset{t\to +\infty }{\lim \inf }{u}_i(t)\ge \frac{d_i^l(m_i-\epsilon )}{e_i^u}.$$

(29)

Setting $\epsilon \to 0$ in this inequality leads to

$$\underset{t\to +\infty }{\lim \inf }{u}_i(t)\ge \frac{d_i^l{m}_i}{e_i^u}\stackrel{\mathrm{def}}{=}{n}_i,i=1,2.$$

(30)

 □

3. Extinction

Theorem 2.

Assume that

$$r_1^l>(1+M_1)r_2^u\frac{a_1^u{e}_1^l+c_1^u{d}_1^u}{b_2^l{e}_1^l},r_1^l>r_2^u\frac{b_1^u{e}_2^u}{a_2^l{e}_2^u+c_2^l{d}_2^l}$$

(31)

and

$${\gamma }^u<\min \frac{1}{M_1{M}_2^2}\left\{\begin{array}{c}{\displaystyle r_1^l-(1+M_1)r_2^u\frac{a_1^u{e}_1^l+c_1^u{d}_1^u}{b_2^l{e}_1^l},r_1^l-r_2^u\frac{b_1^u{e}_2^u}{a_2^l{e}_2^u+c_2^l{d}_2^l}}\hfill \end{array}\right\}$$

(32)

hold, then the species $x_1$ is permanent and the species $x_2$ will be extinct, that is, for any positve solution ${(x_1(t),x_2(t),u_1(t),u_2(t))}^T$ of system (5),

$$\underset{t\to +\infty }{\lim }{x}_2(t)=0,\underset{t\to +\infty }{\lim }{u}_2(t)=0.$$

Remark 2.

Theorem 2 gives the conditions for the permanence of nontoxic phytoplankton and the extionction of toxic phytoplankton. From Theorem 2, we known that lower rate of toxic production could not avoid the extinction of the second species.

Proof. 

Condition (31) is equivalent to

$$\begin{array}{c}\hfill {\displaystyle \frac{c_1^u}{e_1^l}<\frac{r_1^l{b}_2^l}{(1+M_1)r_2^u{d}_1^u}-\frac{a_1^u}{d_1^u},\frac{c_2^l}{e_2^u}>\frac{r_2^u}{r_1^l}\frac{b_1^u}{d_2^l}-\frac{a_2^l}{d_2^l}.}\end{array}$$

(33)

From (32) and (33), there exist positive constants $\alpha ,\beta ,{\delta }_1,{\delta }_2$ and enough small positive $\epsilon$ such that

$$\begin{array}{c}{\displaystyle \frac{r_1^l}{r_2^u}>\frac{\beta }{\alpha },\frac{c_1^u}{e_1^l}<\frac{{\delta }_1}{\alpha }<\frac{\beta b_2^l-(1+M_1+\epsilon )\alpha a_1^u}{(1+M_1+\epsilon )\alpha d_1^u}<\frac{r_1^l{b}_2^l}{(1+M_1+\epsilon )r_2^u{d}_1^u}-\frac{a_1^u}{d_1^u},}\hfill \\ {\displaystyle \frac{c_2^l}{e_2^u}>\frac{{\delta }_2}{\beta }>\frac{\alpha b_1^u-\beta a_2^l}{\beta d_2^l}>\frac{b_2^u}{b_1^l}\frac{b_1^u}{d_2^l}-\frac{a_2^l}{d_2^l},}\hfill \\ {\displaystyle \frac{(1+M_1+\epsilon )(a_1^u{e}_1^l+c_1^u{d}_1^u)}{b_2^l{e}_1^l}<\frac{\beta }{\alpha }<\frac{r_1^l-{\gamma }^u(M_1+\epsilon ){(M_2+\epsilon )}^2}{r_2^u},}\hfill \\ {\displaystyle \frac{b_1^u{e}_2^u}{a_2^l{e}_2^u+c_2^l{d}_2^l}<\frac{\beta }{\alpha }<\frac{r_1^l-{\gamma }^u(M_1+\epsilon ){(M_2+\epsilon )}^2}{r_2^u}.}\hfill \end{array}$$

That is

$$\begin{array}{c}\alpha c_1^u-{\delta }_1{e}_1^l<0,{\delta }_2{e}_2^u-\beta c_2^l<0,\hfill \\ {\displaystyle \alpha a_1^u-\frac{\beta b_2^l}{1+M_1+\epsilon }+{\delta }_1{d}_1^u<0,\alpha b_1^u-\beta a_2^l-{\delta }_2{d}_2^l<0,}\hfill \\ -\alpha r_1^l+\beta r_2^u+\alpha {\gamma }^u(M_1+\epsilon )(M_2+\epsilon {)}^2=-{\xi }_1<0.\hfill \end{array}$$

(34)

Let ${(x_1(t),x_2(t),u_1(t),u_2(t))}^T$ be a positive solution of system (5). For above $\epsilon$, from Lemma 2, there exists a enough large $T_4$, such that

$$x_i(t)<M_i+\epsilon ,u_i(t)<N_i+\epsilon ,t\ge T_4,i=1,2.$$

(35)

Let

$$V_1(t)=x_1^{-\alpha }(t)x_2^{\beta }(t)\exp ({\delta }_1{u}_1(t)-{\delta }_2{u}_2(t)).$$

(36)

Calculating the derivative of $V_1(t)$, from (35), for $t\ge T_4$, we can otain

$$\begin{array}{ccc}\hfill D^{+}{V}_1(t)& =& V_1(t)[(-\alpha r_1(t)+\beta r_2(t))+\left(\alpha a_1(t)-\frac{\beta b_2(t)}{1+x_1(t)}+{\delta }_1{d}_1(t)\right)x_1(t)\hfill \\ & & +\left(\frac{\alpha b_1(t)}{1+x_2(t)}-\beta a_2(t)-{\delta }_2{d}_2(t)\right)x_2(t)+(\alpha c_1(t)-{\delta }_1{e}_1(t))u_1(t)\hfill \\ & & +(-\beta c_2(t)+{\delta }_2{e}_2(t))u_2(t)+\alpha \gamma (t)x_1(t)x_2^2(t)]\hfill \\ & \le & V_1(t)[(-\alpha r_1^l+\beta r_2^u)+(\alpha a_1^u-\frac{\beta b_2^l}{1+(M_1+\epsilon )}+{\delta }_1{d}_1^u)x_1(t)\hfill \\ & & +(\alpha b_1^u-\beta a_2^l-{\delta }_2{d}_2^l)x_2(t)+(\alpha c_1^u-{\delta }_1{e}_1^l)u_1(t)\hfill \\ & & +(-\beta c_2^l+{\delta }_2{e}_2^u)u_2(t)+\alpha {\gamma }^u(M_1+\epsilon ){(M_1+\epsilon )}^2].\hfill \end{array}$$

From inequalities (34), we obtain

$$V_1^{\prime }(t)\le -{\xi }_1{V}_1(t).$$

(37)

Integrating the above inequality from $T_4$ to $t(\ge T_4)$, we have

$$V_1(t)\le V_1(T_4)\exp (-{\xi }_1(t-T_4)).$$

(38)

It follows from (35) that

$$\begin{array}{c}{V}_1(T_1)=x_1^{-\alpha }(T_4)x_2^{\beta }(T_4)\exp ({\delta }_1{u}_1(T_4)-{\delta }_2{u}_2(T_4))<+\infty .\hfill \\ V_1(t)=x_1^{-\alpha }(t)x_2^{\beta }(t)\exp ({\delta }_1{u}_1(t)-{\delta }_2{u}_2(t))\hfill \\ >{(M_1+\epsilon )}^{-\alpha }{x}_2^{\beta }(t)\exp (-{\delta }_2(N_2+\epsilon )).\hfill \end{array}$$

(39)

Combining inequalities (38) and (39), we have

$$x_2(t)\le C\exp \left(-\frac{{\xi }_1}{\beta }(t-T_4)\right),$$

where

$$C={(M_1+\epsilon )}^{\frac{\alpha }{\beta }}\exp \left(\frac{{\delta }_2}{\beta }(N_2+\epsilon )\right)V_1{(T_4)}^{\frac{1}{\beta }}.$$

Hence we obtain that

$$\underset{t\to +\infty }{\lim }{x}_2(t)=0.$$

(40)

And so, $\forall \epsilon >0$, $\exists T_5>T_4$, such that $x_2(t)<\epsilon$ for all $t>T_5$. From the fourth equation of system (5), we have

$$u_2^{\prime }(t)\le -e_2^l{u}_2(t)+d_2^u\epsilon .$$

(41)

From Lemma 1, we obtain

$$\underset{t\to +\infty }{\lim }{u}_2(t)\le \underset{t\to +\infty }{\lim \sup }{u}_2(t)\le \frac{d_2^u\epsilon }{e_2^l}.$$

Setting $\epsilon \to 0$ leads to

$$\underset{t\to +\infty }{\lim }{u}_2(t)\le \underset{t\to +\infty }{\lim \sup }{u}_2(t)\le 0,$$

thus

$$\underset{t\to +\infty }{\lim }{u}_2(t)=0.$$

(42)

By using the analysis technique of [24], one could show that under the conditions of Theorem 2, the first species of system (5) is permanent. We omit the detail here. This ends the proof of Theorem 2. □

Theorem 3.

Assumes that

$$r_1^u<r_2^l\frac{a_1^l{e}_1^u+c_1^l{d}_1^l}{b_2^u{e}_1^u},r_1^u<\frac{1}{1+M_2}{r}_2^l\frac{b_1^l{e}_2^l}{a_2^u{e}_2^l+c_2^u{d}_2^u}$$

(43)

hold, then the species $x_1$ will be extinct and the species $x_2$ is permanent, that is, for any positve solution ${(x_1(t),x_2(t),u_1(t),u_2(t))}^T$ of system (5),

$$\underset{t\to +\infty }{\lim }{x}_1(t)=0,\underset{t\to +\infty }{\lim }{u}_1(t)=0.$$

Proof. 

The proof of Theorem 3 is similar to Theorem 2, which we omit here. □

Remark 3.

Theorem 3 gives the conditions for the permanence of toxic phytoplanktonand the extionction of nontoxic phytoplankton. Besides, when $c_i=0,i=1,2$, Theorem 1 obtained by Xie and Xue et al. [5] are the corollary of Theorem 3, which extends the results of Xie and Xue et al. [5] and reveal that by choosing suitable feedback control variables, the extinction property of system still contains.

4. Example

Example 1.

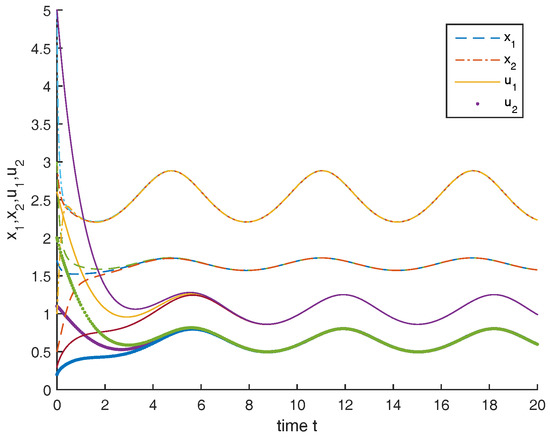
Consider the following equations

$$\begin{array}{c}{x}_1^{\prime }(t)=x_1\left(6-(3.2+0.2\sin t)x_1-\frac{0.5x_2}{1+x_2}-0.005x_1{x_2}^2-0.3u_1\right),\hfill \\ x_2^{\prime }(t)=x_2\left(12.05-0.05\cos t-\frac{5x_1}{1+x_1}-(3.5+0.5\sin t)x_2-0.3u_2\right),\hfill \\ u_1^{\prime }(t)=-(0.8+0.2\sin t)u_1+0.5x_1,\hfill \\ u_2^{\prime }(t)=-(0.8+0.2\sin t)u_2+0.2x_2.\hfill \end{array}$$

(44)

Corresponding to system (44), one has

$$r_1^l=6>b_1^u\frac{r_2^u}{a_2^l}\approx 2.02,r_2^l=12>b_2^u\frac{r_1^u}{a_1^l}=10.$$

Clearly, condition (11) are satisfied, from Theorem 1, we know that the system (44) is permanent. Figure 1 shows the dynamic behaviors of system (44) which is consistent with the conclusion obtained above.

Figure 1. Dynamic behaviors of the solution ${(x_1(t),x_2(t),u_1(t),u_2(t))}^T$ of system (44) with the initial conditions $(x_1(0),x_2(0),u_1(0),u_2(0))$ = ${(0.5,1,5,2)}^T$, ${(3,5,0.3,0.2)}^T$ and ${(1.7,3,2.6,1.1)}^T$, respectively.

Example 2.

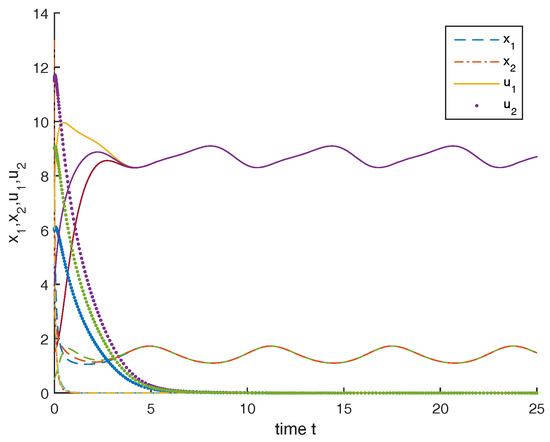
Consider the following equations

$$\begin{array}{c}{x}_1^{\prime }(t)=x_1\left(6-(2.5+0.5\sin t)x_1-\frac{0.5x_2}{1+x_2}-0.00005x_1{x_2}^2-0.3u_1\right),\hfill \\ x_2^{\prime }(t)=x_2\left(0.95-0.05\cos t-\frac{5x_1}{1+x_1}-3x_2-0.3u_2\right),\hfill \\ u_1^{\prime }(t)=-(0.8-0.2\sin t)u_1+5x_1,\hfill \\ u_2^{\prime }(t)=-(0.8-0.2\sin t)u_2+2x_2.\hfill \end{array}$$

(45)

By calculation, one has

$$M_1=\frac{r_1^u}{a_1^u}=3,M_2=\frac{r_2^u}{a_2^u}=\frac{1}{3},$$

$$(1+M_1)r_2^u\frac{a_1^u{e}_1^l+c_1^u{d}_1^u}{b_2^l{e}_1^l}=4.4,r_2^u\frac{b_1^u{e}_2^u}{a_2^l{e}_2^u+c_2^l{d}_2^l}=\frac{5}{36},$$

$$\frac{1}{M_1{M}_2^2}\left(r_1^l-(1+M_1)r_2^u\frac{a_1^u{e}_1^l+c_1^u{d}_1^u}{b_2^l{e}_1^l}\right)=4.8,$$

$$\frac{1}{M_1{M}_2^2}\left(r_1^l-r_2^u\frac{b_1^u{e}_2^u}{a_2^l{e}_2^u+c_2^l{d}_2^l}\right)=\frac{211}{12}.$$

We assume that ${\gamma }^u=0.00005$, clearly, conditions (31) and (32) are satisfied, from Theorem 2, we know that the first species is permanent and the rest of species is driven to extinction. Figure 2 shows the dynamic behaviors of system (45) which is consistent with the conclusion obtained above.

Figure 2. Dynamic behaviors of the solution ${(x_1(t),x_2(t),u_1(t),u_2(t))}^T$ of system (45) with the initial conditions $(x_1(0),x_2(0),u_1(0),u_2(0))$ = ${(9,13,7,11.5)}^T$, ${(0.5,5,1.5,6)}^T$ and ${(3,7,4,9)}^T$, respectively.

Example 3.

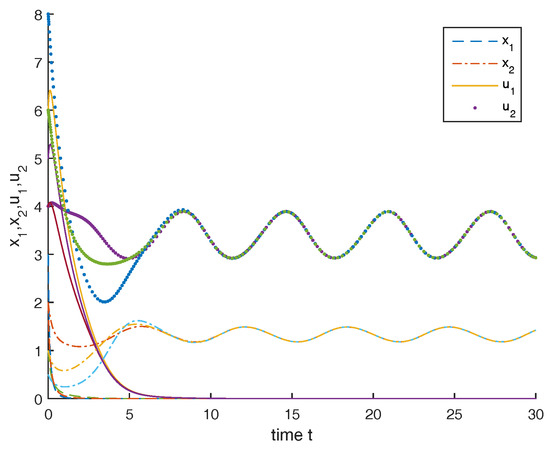
Consider the following equations

$$\begin{array}{l}{x}_1^{\prime }(t)=x_1\left(1-(3.2+0.2\sin t)x_1-\frac{5x_2}{1+x_2}-0.00005x_1{x_2}^2-0.3u_1\right),\\ x_2^{\prime }(t)=x_2\left(1.55-0.05\cos t-\frac{1.5x_1}{1+x_1}-0.4x_2-0.3u_2\right),\\ u_1^{\prime }(t)=-(0.8-0.2\sin t)u_1+5x_1,\\ u_2^{\prime }(t)=-(0.8-0.2\sin t)u_2+2x_2.\end{array}$$

(46)

By calculation, one has

$$r_2^l\frac{a_1^l{e}_1^u+c_1^l{d}_1^l}{b_2^u{e}_1^u}=4.5,\frac{1}{1+M_2}{r}_2^l\frac{b_1^l{e}_2^l}{a_2^u{e}_2^l+c_2^u{d}_2^u}\approx 1.071.$$

Clearly, $r_1^u<4.5,r_1^u<1.071$, condition (43) are satisfied, from Theorem 3, we know that the second species is permanent and the rest of species is driven to extinction.

Figure 3 shows the dynamic behaviors of system (46) is consistent with the conclusion obtained above.

Figure 3. Dynamic behaviors of the solution ${(x_1(t),x_2(t),u_1(t),u_2(t))}^T$ of system (4.3) with the initial conditions $(x_1(0),x_2(0),u_1(0),u_2(0))$ = ${(3,2,6,4)}^T$, ${(1,0.5,4,8)}^T$ and ${(2,1,5,6)}^T$, respectively.

5. Conclusions

(1) In this paper, we consider a non-autonomous allelopathic phytoplankton model with nonlinear inter-inhibition terms and feedback controls, i.e., Equation (5), The difference from the model in [5] is that we consider two feedback control variables $u_i(t),i=1,2$ and the allelopathic interaction term is replaced by $\gamma {x_1(t)}^2{x_2}^2(t)$ instead of $\gamma {x_1(t)}^2{x}_2(t)$. We further investigate the influence of feedback control variables and toxic substances on the dynamic behaviors of system (5).

(2) Theorem 2 and 3 show that the feedback control variables and toxic substances play an important role on the extinction of system (5). Despite the second species could produce toxic, but lower rate of toxic production could not avoid the extinction of the second species. The conditions of Theorem 1 show that the feedback control variables and toxic substances do not effect on the permanence of the system.

(3) Moreover, when $c_i=0,i=1,2$, moldel (5) becomes (2), we can easily find that Theorems 2.1 and 2.5 obtained by Xie and Xue et al. [5] are the corollary of Theorem 2 and 3, which extends the results of Xie and Xue et al. [5]. When $c_i=0,i=1,2,\gamma =0$, moldel (5) becomes (1), we can easily find that Theorem 1 and 2 obtained by Yu [18] are the corollary of Theorem 2 and 3, which extends the results of Yu [18].