Robust Finite-Time Tracking Control for Robotic Manipulators with Time Delay Estimation

Abstract

In this study, a robust H_∞ finite-time tracking controller is proposed for robotic manipulators based on time delay estimation. In this controller, there is no need to know the dynamics of robots, so it is quite simple. The high-gain observer is employed to estimate the joint velocities, which makes it much lower in cost. The theorem proof shows that the closed-loop system is finite-time stable and has a L₂ gain that is less than or equal to γ, which shows high accuracy and strong robustness to estimation errors and external disturbances. Simulations on a two-link robot illustrate the effectiveness and advantages of the proposed controllers.

1. Introduction

The control performances of robotic manipulators are becoming more and more important in industrial fields, especially fast response, high precision, and strong robustness. However, it is quite difficult to obtain the satisfied performances due to highly coupled nonlinear dynamics, time-varying behavior and unknown uncertainties, such as model uncertainties and external disturbances. Fortunately, there are many good results about controllers for robotic manipulators, such as adaptive control [1], robust control [2], and sliding mode control [3]. One of the powerful existing controller is the finite-time control [4] that presents finite-time convergence, which provides fast response and high precision. Thus far, there are many finite-time control methods, such as the finite-time stabilization approach for homogeneous systems [5,6], finite-time Lyapunov stabilization approach [7,8,9,10], terminal sliding mode approach [11,12,13,14,15,16,17], and super-twisting algorithm [18,19]. In particular, Ali Abooee et al. proposed a chattering-free second order fast nonsingular terminal sliding mode controller for robotic manipulators with unknown disturbances [15]. Yassine Kali and Maarouf Sadd proposed a high-accuracy trajectory tracking controller for robotic manipulators with uncertainties and unexpected disturbances based on the super-twisting algorithm [19], but it only ensured that the selected linear sliding surface converged to zero in a finite time. Su and Zheng proposed a finite-time tracking controller for robotic manipulators by using nonlinear exponential-like errors and inverse dynamics control [20]. Mirosław Galicki proposed an absolutely continuous terminal sliding mode controller for robotic manipulators based on first and second-order sliding mode control techniques [21]. In these results, the super-twisting algorithm and terminal sliding mode control scheme presented stronger robustness to uncertainties, but in the process of the control design, there was no discussion about the relationship between robustness and the control parameters. Recently, Liu and Zhang [22] discussed this relationship and proposed a finite-time H_∞ controller for uncertain robotic manipulators. However, the controller is also complex due to the requirements of the dynamics mode, especially for more than four-degrees of freedom in robotic manipulators. For this reason, the time delay estimation is used to simplify the controller design [18,19]; however, the work in References [18,19] only guarantee that the closed-loop system is asymptotically convergent.

Motivated by the above works, this work will propose a robust finite-time output feedback controller for uncertain manipulators as follows: (1) The time delay estimation is used to estimate the robot dynamics and to simplify the controller structure, which is simpler to implement in practice; (2) the closed-loop system is not only finite-time stable, but also has the L₂ gain less than or equal to γ, so there is no need to solve the complex Hamilton–Jacobi equation or the Riccati equation; and (3) the high-gain observer is employed to estimate joint velocities, which in practice makes lower in cost.

The rest of paper is organized as follows. Section 2 shows preliminaries, such as the robot dynamic model and the relative finite-time stability theorems. Section 3 presents the main results from the controller design. Section 4 gives the simulations on a two-link robot. Finally, Section 5 provides some conclusions.

2. Preliminaries

2.1. Relative Theorems

The following finite-time H_∞ control theorem can be used.

Lemma 1

[22]. Consider the nonlinear system $\dot{x}=f(x,u),z=h(x)$. Suppose that there is a C¹ function V(x) defined in a neighborhood $\widehat{U}\subset R^n$ of the origin and real numbers c > 0 and 0 < α < 1, such that

(i)

V(x) is positive definite in $\widehat{U}$;

(ii)

$\dot{V}(x)+c{V}^{\alpha }(x)\le \frac{1}{2}({\gamma }^2{\Vert w\Vert }^2-{\Vert z\Vert }^2),\forall x\in \widehat{U}\backslash \{0\}.$

Then, the origin of the system $\dot{x}=f(x,u)$ is locally finite-time stable and the system has a L₂ gain less than or equal to γ. If $\widehat{U}=R^n$ and V(x) is radially unbounded (i.e., V(x)→ +∞ as ||x||→ +∞), then the origin of the system (1) is also globally finite-time stable.

Obviously, it is important and difficult to design a robust controller u and find a satisfied Lyapunov function V(x).

2.2. Problem Formulation

The n-DOF robotic manipulator dynamic [23] is given in the form of

$$M(q)\ddot{q}+C(q,\dot{q})\dot{q}+G(q)=\tau +{\tau }_d$$

(1)

where $q,\dot{q},\ddot{q}\in R^n$ are the joint position, velocity and acceleration vectors, respectively. $M(q)\in R^{n\times n}$ is the inertia matrix, $C(q,\dot{q})\in R^{n\times n}$ is the centrifugal and Coriolis matrix, $G(q)\in R^n$ is the gravitational vector, and ${\tau }_d,\tau \in R^n$ denotes the disturbance and torque input vectors, respectively.

In practice, it is difficult to exactly know the inertia matrix M(q), especially for more than 4 degrees of freedom of robotic manipulators. In order to simplify the controller, a constant matrix is introduced to constitute the inertia matrix, so the dynamic equation of the robotic manipulator is expressed as

$$\overline{M}\ddot{q}+H(q,\dot{q},\ddot{q})=\tau$$

(2)

where

$$H(q,\dot{q},\ddot{q})=[M(q)-\overline{M}]\ddot{q}+C(q,\dot{q})\dot{q}+G(q)-{\tau }_d$$

(3)

Define the desired trajectory $q_d\in R^n$, and $e=q-q_d$ is defined as the tracking error. The main objective of this paper is to design a robust controller $\tau$ so that the tracking error e can convergence to zero in a finite time, even in the presence of uncertainties and external disturbances, and the L₂ gain of the system is less than or equal to given γ, i.e., $e\to 0$ when $t\to T$.

3. Main Results

Define $x_1=q-q_d\in R^n$, $x_2=\dot{q}-{\dot{q}}_d={\dot{x}}_1\in R^n$, the (2) can be rewritten as

$$\{\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2={\overline{M}}^{-1}\tau -{\ddot{q}}_d+w\end{array}$$

(4)

where $w(t)=-{\overline{M}}^{-1}H(q,\dot{q},\ddot{q})$ can be seen as uncertainties. In practice, the $w(t)$ is impossible to know, but $w(t)$ can be estimated using a time delay estimation (TDE) [24] as:

$$\widehat{w}(t)\approx w(t-L)={\dot{x}}_2(t-L)-M^{-1}\tau (t-L)$$

(5)

Design a following controller

$$\tau =\overline{M}(v+{\ddot{q}}_d-\widehat{w})$$

(6)

where $v$ will be designed in the following.

Combine Equations (4) and (6), we can obtain

$$\{\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=v+\tilde{w}\end{array}$$

(7)

where $\tilde{w}=w-\widehat{w}$ is the TDE error, and $\tilde{w}$ is bounded, the proof will be in Appendix A.

In order to improve the robustness to uncertainties, the L₂ gain will be set as γ, γ > 0.

Define auxiliary vector ${\rho }_1(x_1)\in R^n$ with ${\rho }_1(0)=0$, and

$${\eta }_1=x_2-{\rho }_1(x_1)$$

(8)

If we design the following functions:

$$\begin{array}{l}{\rho }_1(x_1)=-L_0{x}_1-L_{1}Si{g}^{\xi }(x_1)\\ {\rho }_2({\eta }_1)=-L_{2}Si{g}^{\xi }({\eta }_1)\end{array}$$

(9)

where L₀ = diag (l₀₁, l₀₂, …, l_0n), L₁ = diag (l₁₁, l₁₂, …, l_1n), L₂ = diag (l₂₁, l₂₂,…,l_2n), all the elements are positive, and 0 < ξ < 1.

Then, select the following evaluation signal of performance:

$$z=\left[\begin{array}{l}{\lambda }_1{x}_1\\ {\lambda }_2{\eta }_1\end{array}\right]$$

(10)

where λ₁ > 0, and λ₂ > 0 are defined as weighted coefficients.

In order to obtain a robust H_∞ finite-time control law, the $v$ is designed as

$$v={\rho }_2({\eta }_1)-x_1-(\frac{1}{2{\gamma }^2}+\frac{{\lambda }_2^2}{2}){\eta }_1+{\dot{\rho }}_1(x_1)$$

(11)

where l₀ = min{l_0i}, i = 1,…, n, l₀ ≥ λ₁²/2, γ > 0. Then, the closed-loop system is globally finite-time stable and has a L₂-gain less than or equal to γ.

So we have the following theorem.

Theorem 1.

For the robotic manipulators (4), if we design the controller as

$$\tau =\overline{M}\left[{\ddot{q}}_d+{\rho }_2({\eta }_1)-x_1-\left(\frac{1}{2{\gamma }^2}+\frac{{\lambda }_2^2}{2}\right){\eta }_1+{\dot{\rho }}_1(x_1)-\widehat{w}\right]$$

(12)

Then, the trajectory tracking error can converge to zero in a finite time, and the closed-loop system has L₂-gain less than or equal to γ.

Poof. 

According to Equations (7) and (11), we can obtain the following closed-loop system:

$$\{\begin{array}{l}{\dot{x}}_1={\eta }_1+{\rho }_1(x_1)\\ {\dot{\eta }}_1={\rho }_2({\eta }_1)+\tilde{w}(x)-x_1-\left(\frac{1}{2{\gamma }^2}+\frac{{\lambda }_2^2}{2}\right){\eta }_1\end{array}$$

(13)

So we select the following Lyapunov function

$$V=\frac{1}{2}{x}_1^T{x}_1+\frac{1}{2}{\eta }_1^T{\eta }_1$$

(14)

and differentiate it with time, and combine it with Equations (13) and (19), and we can obtain

$$\begin{array}{ll}\dot{V}& =x_1^T{\dot{x}}_1+{\eta }_1^T{\dot{\eta }}_1\\ & =x_1^T\left({\eta }_1+{\rho }_1(x_1)\right)+{\eta }_1^T\left({\rho }_2({\eta }_1)+\tilde{w}(x)-x_1-\left(\frac{1}{2{\gamma }^2}+\frac{{\lambda }_2^2}{2}\right){\eta }_1\right)\\ & =x_1^T{\rho }_1(x_1)+{\eta }_1^T{\rho }_2({\eta }_1)+{\eta }_1^T\tilde{w}(x)-\left(\frac{1}{2{\gamma }^2}+\frac{{\lambda }_2^2}{2}\right){\eta }_1^T{\eta }_1\\ & =-x_1^T{L}_{1}Si{g}^{\xi }(x_1)-{\eta }_1^T{L}_{2}Si{g}^{\xi }({\eta }_1)-x_1^T{L}_0{x}_1+{\eta }_1^T\tilde{w}(x)-\left(\frac{1}{2{\gamma }^2}+\frac{{\lambda }_2^2}{2}\right){\eta }_1^T{\eta }_1\end{array}$$

(15)

Define the following function

$$\mathsf{\Gamma }=\dot{V}+\frac{1}{2}\left({\Vert z\Vert }^2-{\gamma }^2{\Vert \tilde{w}\Vert }^2\right)$$

(16)

and combine it with Equations (10) and (15), and we can get

$$\begin{array}{lll}\mathsf{\Gamma }& =& \dot{V}+\frac{1}{2}\left({\Vert z\Vert }^2-{\gamma }^2{\Vert \tilde{w}\Vert }^2\right)\\ & =& -x_1^T{L}_{1}Si{g}^{\xi }(x_1)-{\eta }_1^T{L}_{2}Si{g}^{\xi }({\eta }_1)-x_1^T{L}_0{x}_1+{\eta }_1^T\tilde{w}(x)-\left(\frac{1}{2{\gamma }^2}+\frac{{\lambda }_2^2}{2}\right){\eta }_1^T{\eta }_1\\ & & +\frac{1}{2}\left({\Vert z\Vert }^2-{\gamma }^2{\Vert \tilde{w}\Vert }^2\right)\\ & =& -x_1^T{L}_{1}Si{g}^{\xi }(x_1)-{\eta }_1^T{L}_{2}Si{g}^{\xi }({\eta }_1)-x_1^T{L}_0{x}_1+{\eta }_1^T\tilde{w}(x)-\left(\frac{1}{2{\gamma }^2}+\frac{{\lambda }_2^2}{2}\right){\eta }_1^T{\eta }_1\\ & & +\frac{1}{2}\left({\lambda }_1^2{\Vert x_1\Vert }^2+{\lambda }_2^2{\Vert {\eta }_1\Vert }^2-{\gamma }^2{\Vert \tilde{w}\Vert }^2\right)\\ & =& -x_1^T{L}_{1}Si{g}^{\xi }(x_1)-{\eta }_1^T{L}_{2}Si{g}^{\xi }({\eta }_1)-x_1^T{L}_0{x}_1+{\eta }_1^T\tilde{w}(x)-{\eta }_1^T\frac{1}{2{\gamma }^2}{\eta }_1+\frac{1}{2}{\lambda }_1^2{\Vert x_1\Vert }^2-\frac{1}{2}{\gamma }^2{\Vert \tilde{w}\Vert }^2\\ & \le & -x_1^T{L}_{1}Si{g}^{\xi }(x_1)-{\eta }_1^T{L}_{2}Si{g}^{\xi }({\eta }_1)-x_1^T{L}_0{x}_1+\Vert {\eta }_1\Vert \Vert \tilde{w}\Vert -{\eta }_1^T\frac{1}{2{\gamma }^2}{\eta }_1+\frac{1}{2}{\lambda }_1^2{\Vert x_1\Vert }^2-\frac{1}{2}{\gamma }^2{\Vert \tilde{w}\Vert }^2\\ & =& -x_1^T{L}_{1}Si{g}^{\xi }(x_1)-{\eta }_1^T{L}_{2}Si{g}^{\xi }({\eta }_1)-x_1^T{L}_0{x}_1+\frac{1}{2}{\lambda }_1^2{\Vert x_1\Vert }^2-{\left(\frac{1}{\sqrt{2}\gamma }{\eta }_1-\frac{\gamma }{\sqrt{2}}\tilde{w}\right)}^T\left(\frac{1}{\sqrt{2}\gamma }{\eta }_1-\frac{\gamma }{\sqrt{2}}\tilde{w}\right)\\ & \le & -x_1^T{L}_{1}Si{g}^{\xi }(x_1)-{\eta }_1^T{L}_{2}Si{g}^{\xi }({\eta }_1)-x_1^T{L}_0{x}_1+\frac{1}{2}{\lambda }_1^2{\Vert x_1\Vert }^2\\ & \le & -x_1^T{L}_{1}Si{g}^{\xi }(x_1)-{\eta }_1^T{L}_{2}Si{g}^{\xi }({\eta }_1)-\left(l_0-\frac{1}{2}{\lambda }_1^2\right){\Vert x_1\Vert }^2\\ & \le & -x_1^T{L}_{1}Si{g}^{\xi }(x_1)-{\eta }_1^T{L}_{2}Si{g}^{\xi }({\eta }_1)\end{array}$$

(17)

Let $\alpha =(1+\xi )/2$, $1/2<\alpha <1$, $l_{1\min }=\min \left\{l_{1i}\right\}$, $l_{2\min }=\min \left\{l_{2i}\right\}$, ${\tilde{l}}_1=2^{\alpha }{l}_{1\min }$, ${\tilde{l}}_2=2^{\alpha }{l}_{2\min }$, and $\tilde{l}=\min \{{\tilde{l}}_1,{\tilde{l}}_2\}$, and we can obtain

$$\begin{array}{ll}\mathsf{\Gamma }& \le -x_1^T{L}_{1}Si{g}^{\xi }(x_1)-{\eta }_1^T{L}_{2}Si{g}^{\xi }({\eta }_1)\\ & \le -l_{1\min }{\displaystyle \sum _{i=1}^n{\left|x_{1i}\right|}^{1+\xi }}-l_{2\min }{\displaystyle \sum _{i=1}^n{\left|{\eta }_{1i}\right|}^{1+\xi }}\\ & \le -l_{1\min }{\left({\displaystyle \sum _{i=1}^n{x}_{1i}^2}\right)}^{(1+\xi )/2}-l_{2\min }{\left({\displaystyle \sum _{i=1}^n{\eta }_{1i}^2}\right)}^{(1+\xi )/2}\\ & \le -{\tilde{l}}_1{\left(\frac{1}{2}{\displaystyle \sum _{i=1}^n{x}_{1i}^2}\right)}^{\alpha }-{\tilde{l}}_2{\left(\frac{1}{2}{\displaystyle \sum _{i=1}^n{\eta }_{1i}^2}\right)}^{\alpha }\\ & \le -\tilde{l}{V}^{\alpha }\end{array}$$

(18)

Therefore, the following inequality can be established:

$$\dot{V}+\tilde{l}{V}^{\alpha }\le \frac{1}{2}\left({\gamma }^2{\Vert \tilde{w}\Vert }^2-{\Vert z\Vert }^2\right)$$

(19)

Obviously, according to Lemma 1, the system is finite-time stable and L₂ gain is less than or equal to γ. The proof is complete. □

Remark 1.

The robustness of controller can be adjusted by control parameters, so the TDE error cannot affect the tracking accuracy.

Remark 2.

In order to avoid singularity, the derivative of$Si{g}^{\xi }(x_1)$should be modified by the function proposed in Reference [22] as follows:

$$[Si{g}^{\xi }(x_{1i})]{}^{\prime }=\{\begin{array}{ll}\xi {\left|x_{1i}\right|}^{\xi -1}{\dot{x}}_{1i},& if\left|x_{1i}\right|\ge \varsigma and{\dot{x}}_{1i}\ne 0\\ \xi {\left|{\Delta }_{1i}\right|}^{\xi -1}{\dot{x}}_{1i},& if\left|x_{1i}\right|<\varsigma and{\dot{x}}_{1i}\ne 0\\ 0,& if{\dot{x}}_{1i}=0\end{array}$$

(20)

where $\varsigma$ and ${\Delta }_{1i}$ are both small positive constants, x_1i is the ith element of the vector x₁.

Remark 3.

In controller (12), the joint velocities need to be known, but the usage of speed sensors will increase the device cost. Thus, in this study, the joint velocities will be estimated by observers, such as high-gain observers and second-order sliding mode observers.

The high-gain observer is designed as

$$\{\begin{array}{l}{\dot{\widehat{x}}}_1={\widehat{x}}_2+\frac{h_1}{\epsilon }(x_1-{\widehat{x}}_1)\\ {\dot{\widehat{x}}}_2={\overline{M}}^{-1}\widehat{\tau }-{\ddot{q}}_d+\widehat{w}+\frac{h_2}{{\epsilon }^2}(x_1-{\widehat{x}}_1)\end{array}$$

(21)

where h₁ > 0, h₂ > 0, when the matrix

$$\left[\begin{array}{ll}-h_1& 1\\ -h_2& 0\end{array}\right]$$

is Hurwitz [25], and the asymptotic error is convergent. Then, the observer-based controller is rewritten as

$$\widehat{\tau }=\overline{M}\left[{\ddot{q}}_d+{\rho }_2({\widehat{\eta }}_1)-x_1-\left(\frac{1}{2{\gamma }^2}+\frac{{\lambda }_2^2}{2}\right){\widehat{\eta }}_1+{\dot{\rho }}_1(x_1)-\widehat{w}\right]$$

(22)

where ${\widehat{\eta }}_1={\widehat{x}}_2-{\rho }_1(x_1)$.

Then, we have the following theorem.

Theorem 2.

For the robotic manipulators (4), if we design the observer as (21), and the controller as (22), Then, the trajectory tracking error can converge to zero in a finite time, and the closed-loop system has L₂-gain less than or equal to γ.

Proof. 

The separation principle can be used to prove the stability. So here is omitted. □

Remark 4.

The separation principle has significant practical implications because it allows the designer to design the state feedback controller to meet transient response specification and/or constraints on the state or control variables. Moreover, in the case of high-gain observers, it has a unique advantage that is to recover state trajectories by making observer sufficiently fast [25].

Remark 5.

In practice, the performance of the high-gain observer system will be better than state feedback based on measurement in presence of noise, because in that case the observer acts as a low pass filter [26].

4. Simulations

In order to demonstrate the advantages of this study, a two-link robot is used in simulations. The two-link robot dynamic mode is

$$\left[\begin{array}{ll}{m}_{11}& m_{12}\\ m_{12}& m_{22}\end{array}\right]\left[\begin{array}{l}{\ddot{q}}_1\\ {\ddot{q}}_2\end{array}\right]+\left[\begin{array}{ll}-2b{\dot{q}}_2& -b{\dot{q}}_2\\ b{\dot{q}}_1& 0\end{array}\right]\left[\begin{array}{l}{\dot{q}}_1\\ {\dot{q}}_2\end{array}\right]=\left[\begin{array}{l}{\tau }_1\\ {\tau }_2\end{array}\right]+{\tau }_d$$

(23)

where

$$\begin{array}{l}{a}_{11}=(m_1+m_2)r_1^2+m_2{r}_2^2+2m_2{r}_1{r}_2\cos (q_2)+J_1\\ a_{12}=m_2{r}_1^2+m_2{r}_1{r}_2\cos q_2\\ a_{22}=m_2{r}_2^2+J_2\\ b=m_2{r}_1{r}_2\sin q_2\end{array}$$

The parameters values are given in

Table 1. Dynamic parameter values.

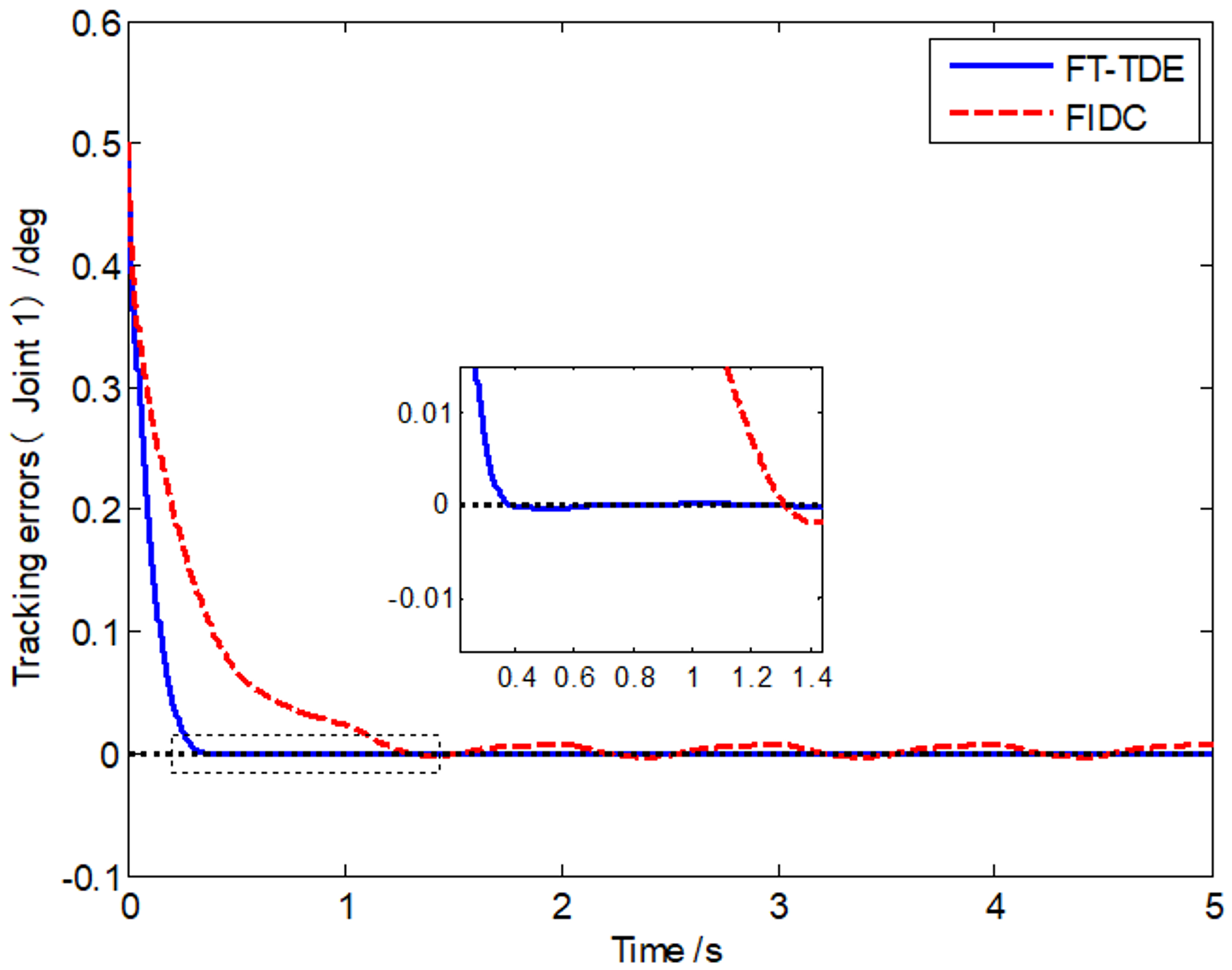
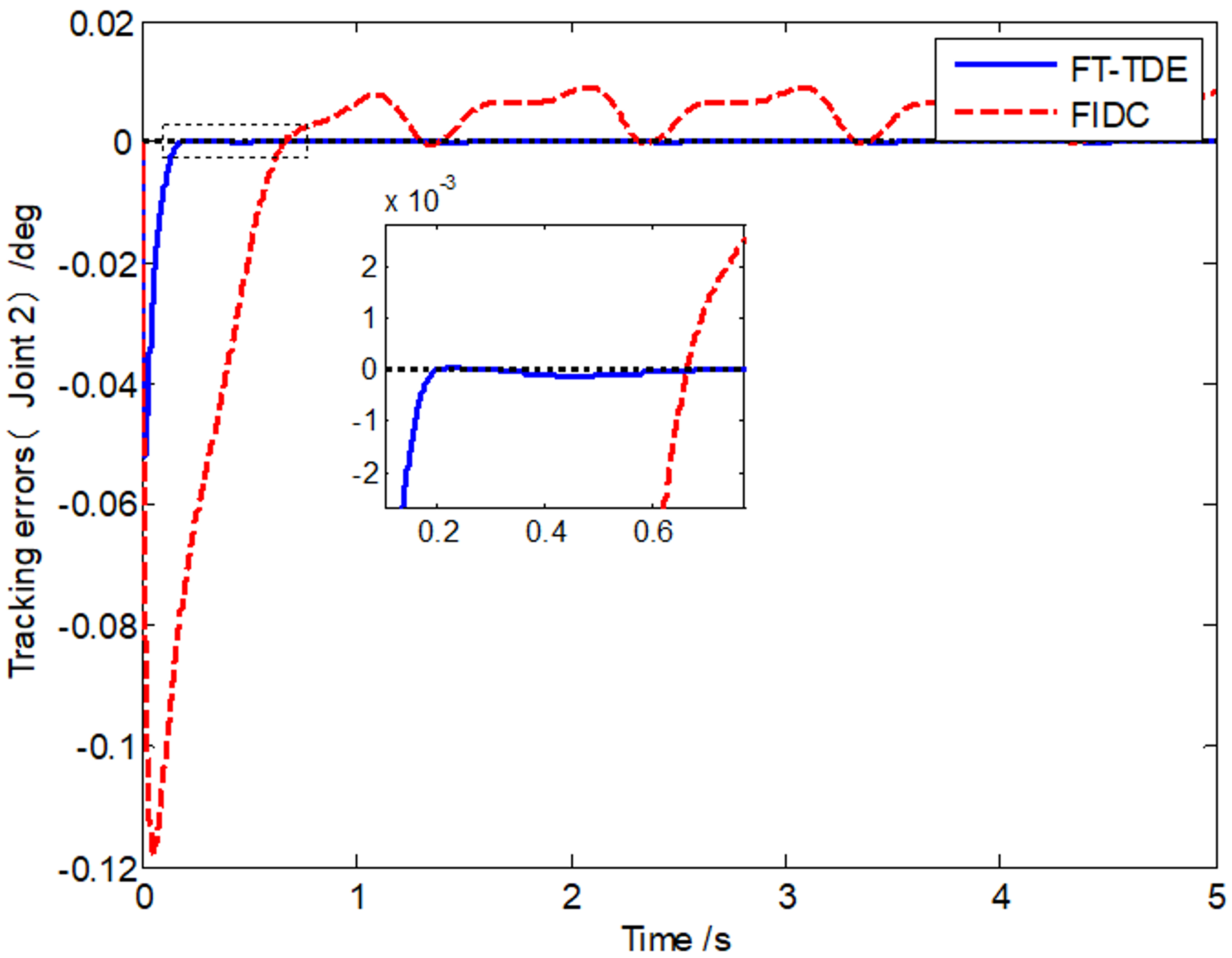
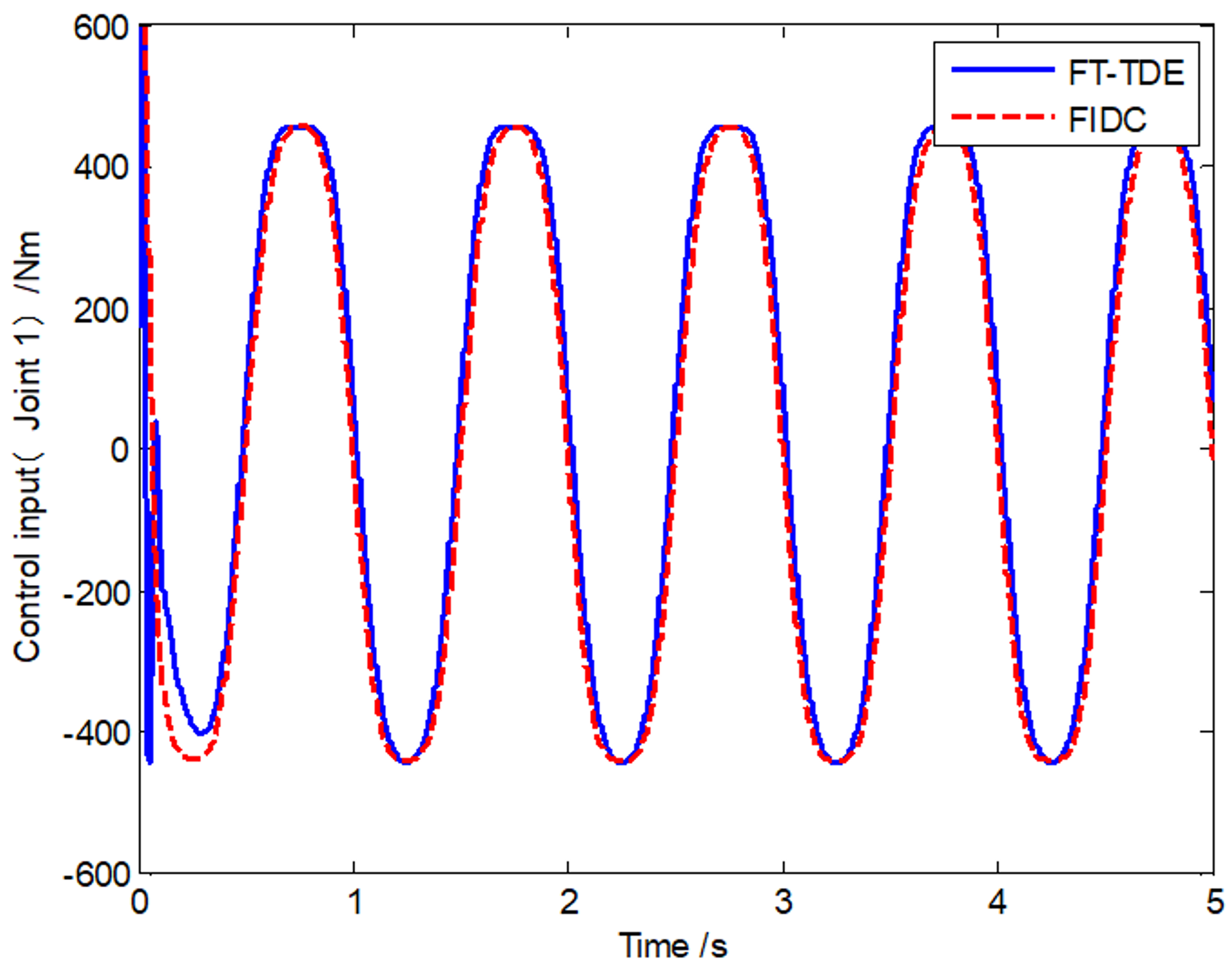
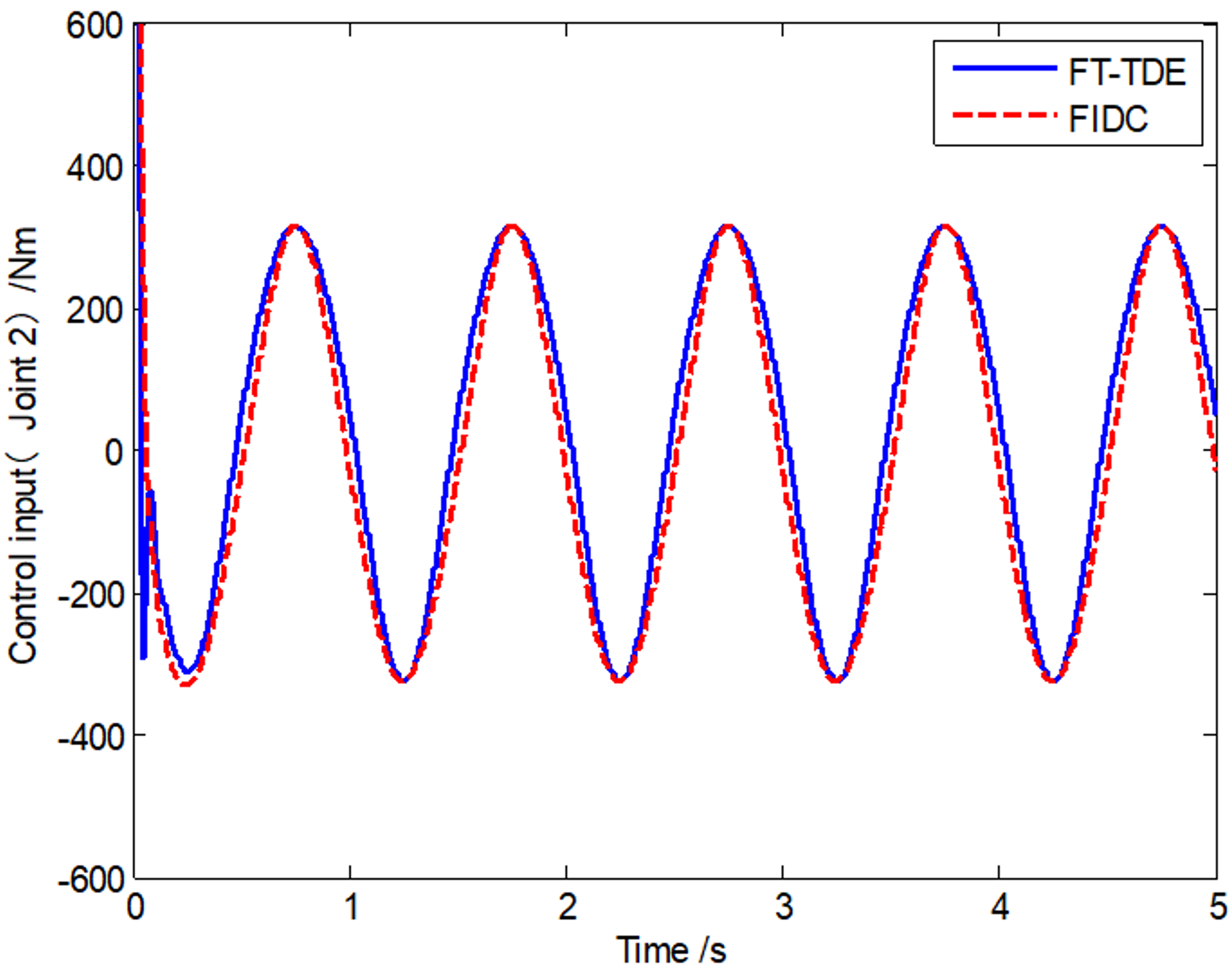
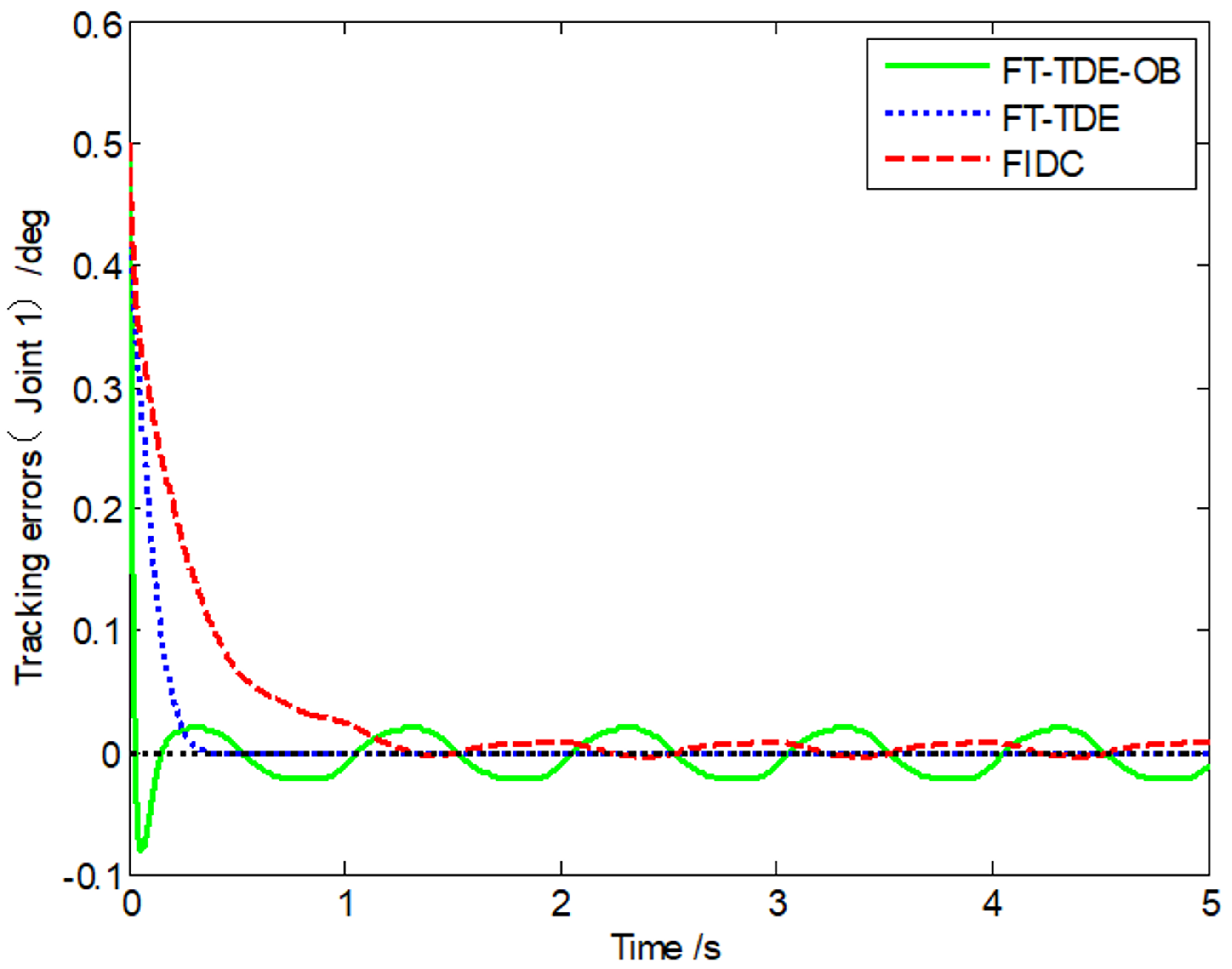
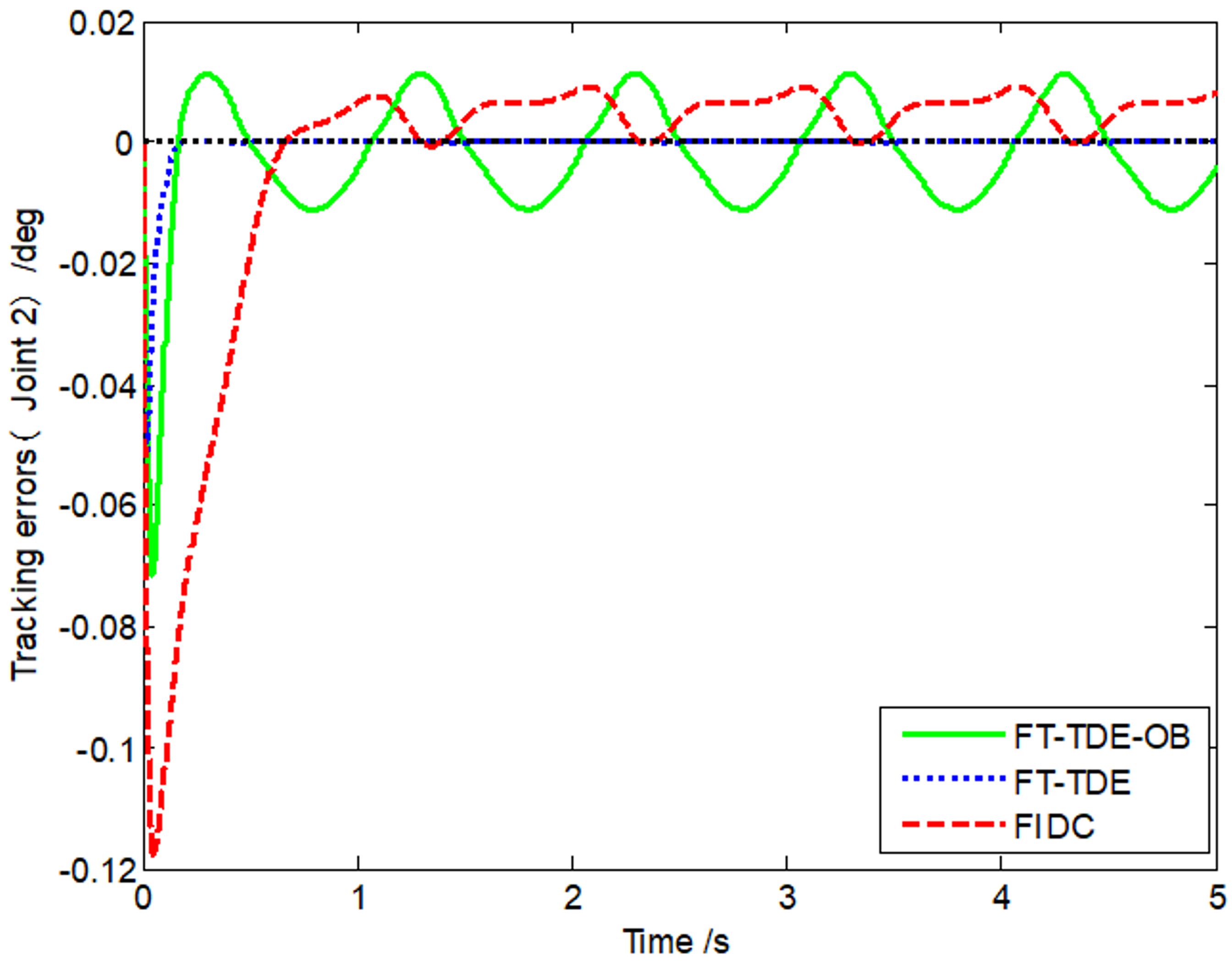
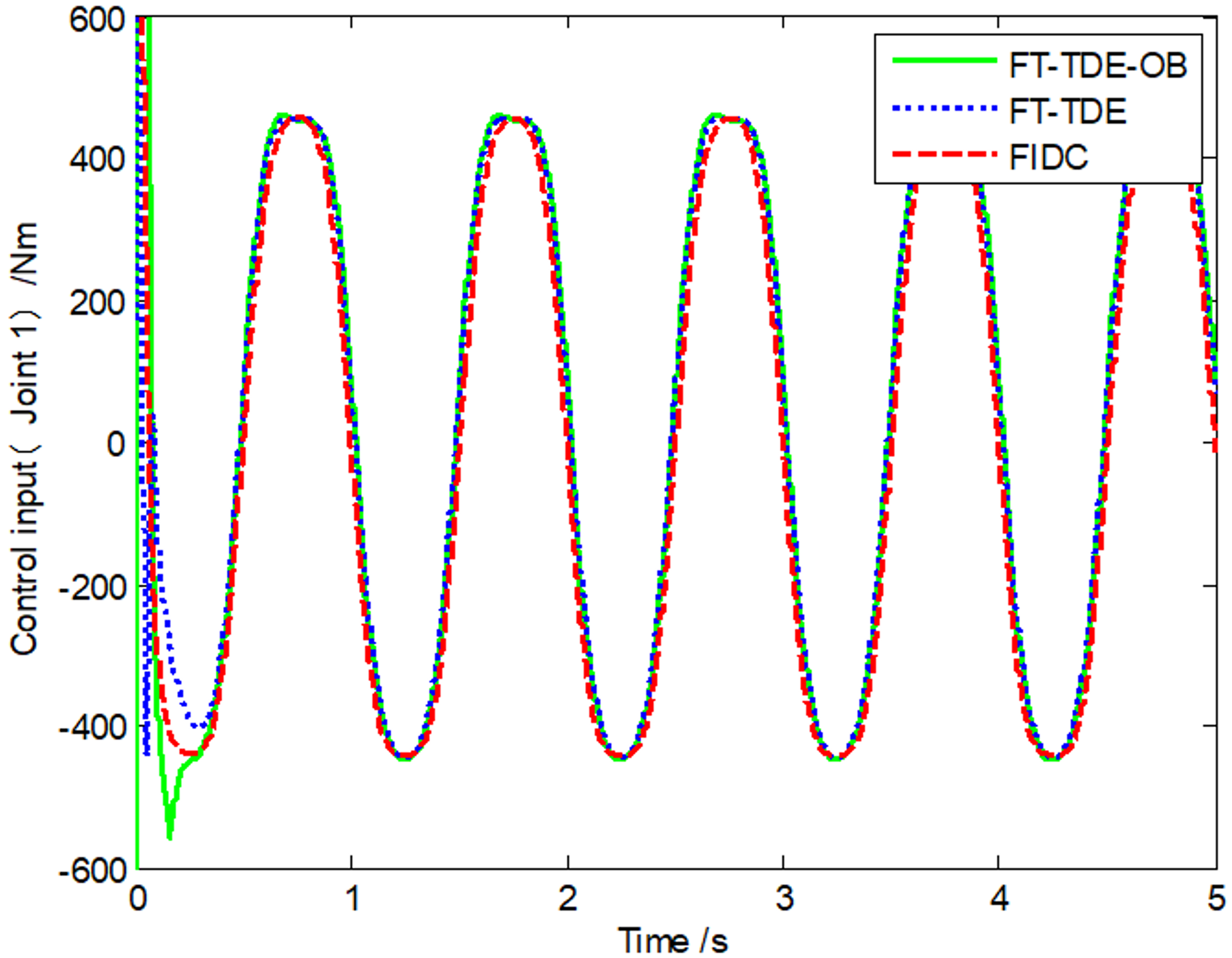
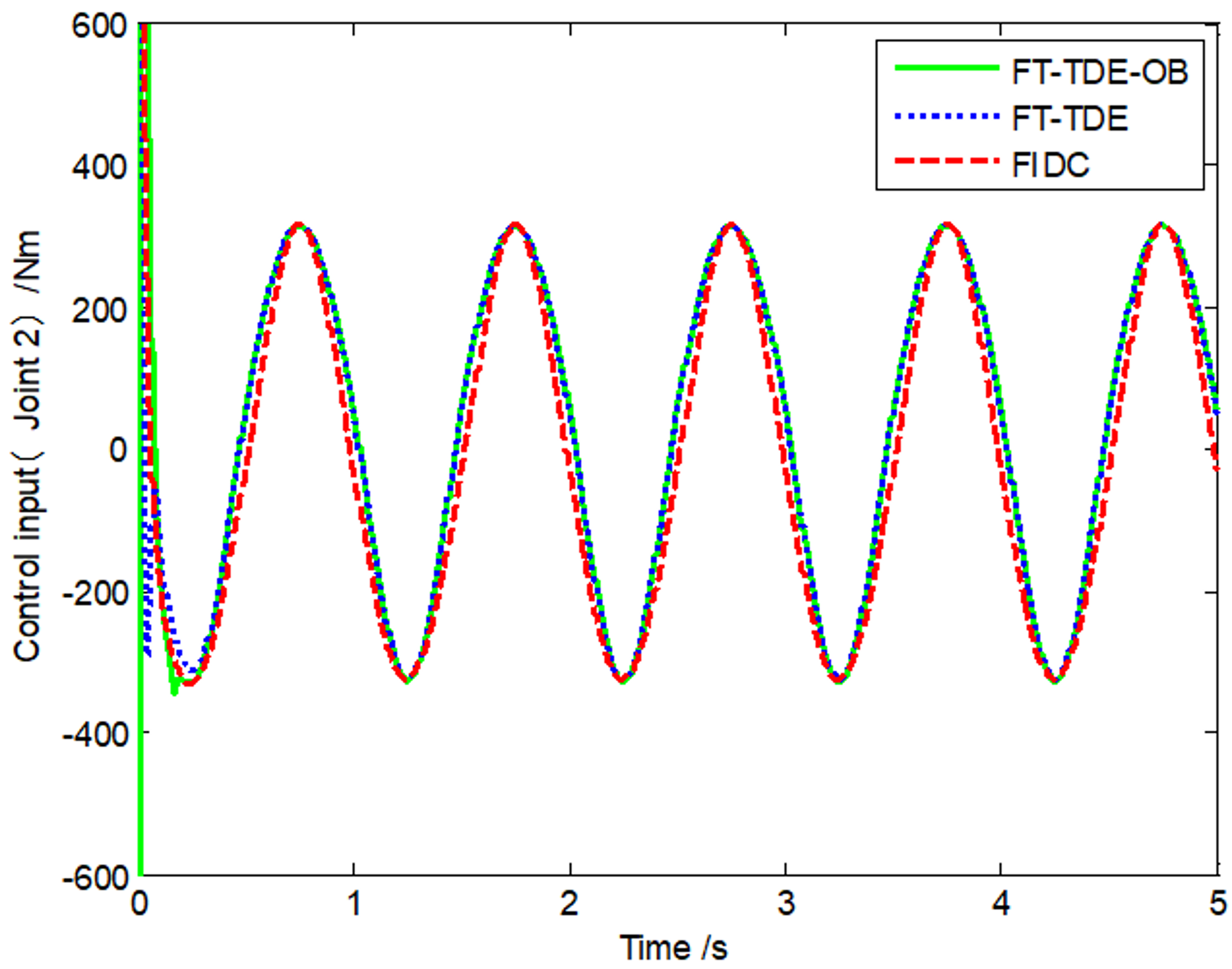
	r1 (m)	r2(m)	J1(kg⋅m2)	J2(kg⋅m2)	m1(kg)	m2 (kg)
Actual values	1	0.8	5	5	0.5	1.5
Nominal values	1.2	0.9	4.5	5.1	0.6	1.3

. The external disturbance ${\tau }_d=0.5{\dot{q}}^2+0.2q+0.1$.The desired trajectory signals are q_d1 = sin(2πt), q_d2 = sin(2πt). The initial states are q₁(0) = 0.2 rad, q₂(0) = 0.2 rad, ${\dot{q}}_1(0)=0$ rad/s, and ${\dot{q}}_2(0)=0$ rad/s.

There are two situations to illustrate the advantages by comparisons with the finite-time inverse tracking controller (FIDC) with state feedback proposed by Su and Zheng [20]. The FIDC is

$$\tau =M_0(q)\left[{\ddot{q}}_d-k_{p}Si{g}^{{\beta }_1}(e)-k_{d}Si{g}^{{\beta }_2}(\dot{e})\right]+C_0(q,\dot{q})\dot{q}+G_0(q)$$

(24)

where k_p = 100, k_d = 50, ${\beta }_1=0.7$ and ${\beta }_2=2{\beta }_1/({\beta }_1+1)=0.82$.

(1) Robust finite-time state feedback control (FT-TDE)

The controller parameters are set as $\xi =0.8$, L₀ = diag (1, 1), L₁ = diag (20, 20), L₂ = diag (50, 50), γ = 1, λ₁ = 1, λ₂ = 1.

The simulation results are shown in Figure 1, Figure 2, Figure 3 and Figure 4. We can easily see that the robustness of FT-TDE is stronger than FIDC, and the response of FT-TDE is faster than FIDC. The response time is less than 0.3 s, and both of the control inputs are nearly smooth and equivalent.

(2) Robust finite-time output feedback control (FT-TDE-OB)

The observer parameters are set as h₁ = 1, h₂ = 1, ε = 0.001. The simulation results are shown in Figure 5, Figure 6, Figure 7 and Figure 8. From Figure 5, Figure 6, Figure 7 and Figure 8, we can see that “FT-TDE-OB” is faster than “FIDC”, but the tracking errors are more than other controllers, which is made by the high-gain observer. In practice, the observer parameters are required to be appropriately chosen, but the high-gain observer is very simple, and acts as a low pass filter.

5. Conclusions

In this paper, the time-delay estimation is used to simplify the robot dynamic model, so that the controller is very simple, and has an L₂-gain, which presents stronger robustness. The high-gain observer is employed to estimate the velocities, which lowers the device cost because there is no speed sensor needed. Simulations demonstrate the effectiveness of the proposed controller; the next work will be that the experiments research on the trajectory tracking control for robotic manipulators, which will be done to assess the control performances, including experiment design, algorithm optimization, performance testing, etc.