Accelerated Life Test Method for the Doubly Truncated Burr Type XII Distribution
Abstract
1. Introduction
1.1. Historical Review and Literature Review
1.2. Motivation and Organization
2. The Doubly Truncated Three-Parameter Burrxii Distribution and ALT Model
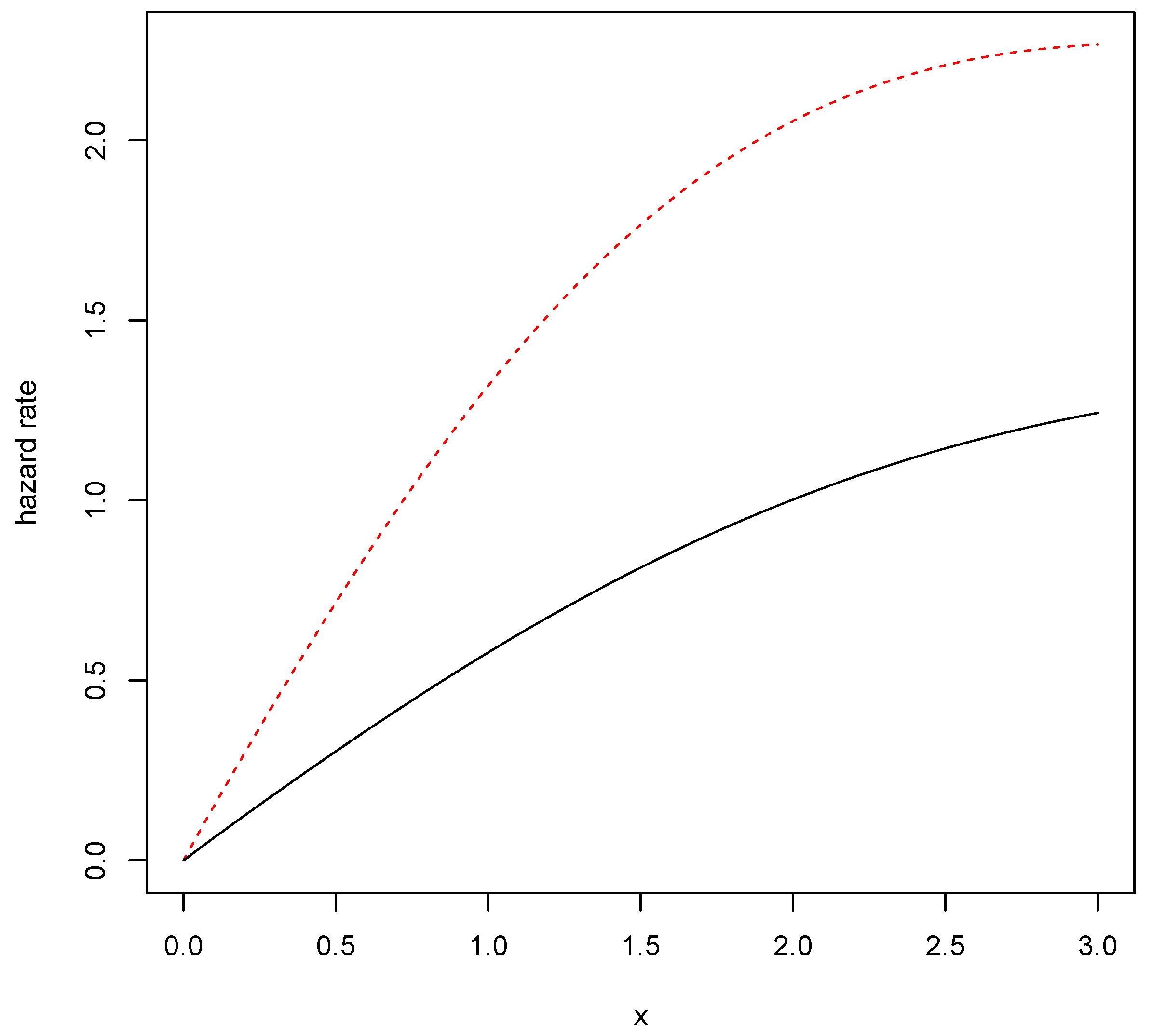
2.1. The Statistical Model
2.2. The ALT Model and Parameter Estimation Methods
- Initial Step:
- Let and , , , , and be the initial states of , , , , and c, respectively.
- Step 1:
- Propose the transition probabilities from to for .
- Step 2:
- Implement Step 2.1 to Step 2.5 N times for , where N is a huge number.
- Step 2.1:
- Generate and , where is the uniform distribution over the domain of (0,1). Update by
- Step 2.2:
- Generate and . Update by
- Step 2.3:
- Generate and . Update by
- Step 2.4:
- Generate and . Update by
- Step 2.5:
- Generate and . Update by
- Step 3:
- The Bayes estimates can be obtained by , and c, where the first chains are used for burn-in and all burn-in chains will be removed from the computation to obtain the Bayes estimates.
| Algorithm 1 The Metropolis-Hastings algorithm via Gibbs sampling. |
|
- Procedure BE-I:
- Let the domain of the model parameters be , , , , and . Uniform distributions over the domains of , , , , and , respectively, are used to be the transition probabilities to implement the Metropolis–Hastings algorithm via Gibbs sampling to obtain Bayes estimates.
- Step 1:
- Obtain 100 sets of Bayes estimates through using procedure BE-I, and denote them by , , , , and . Find the mean of each set of Bayes estimates with 5% of them trimmed from each end. Denote the trimmed mean by , , , , and , respectively.
- Step 2:
- Implement the Metropolis–Hastings algorithm via Gibbs sampling with the normal distributions, , , , , and , as the transition probabilities to obtain Bayes estimates. That is, the MCMC method is implemented based on the knowledge that is obtained from Step 1.
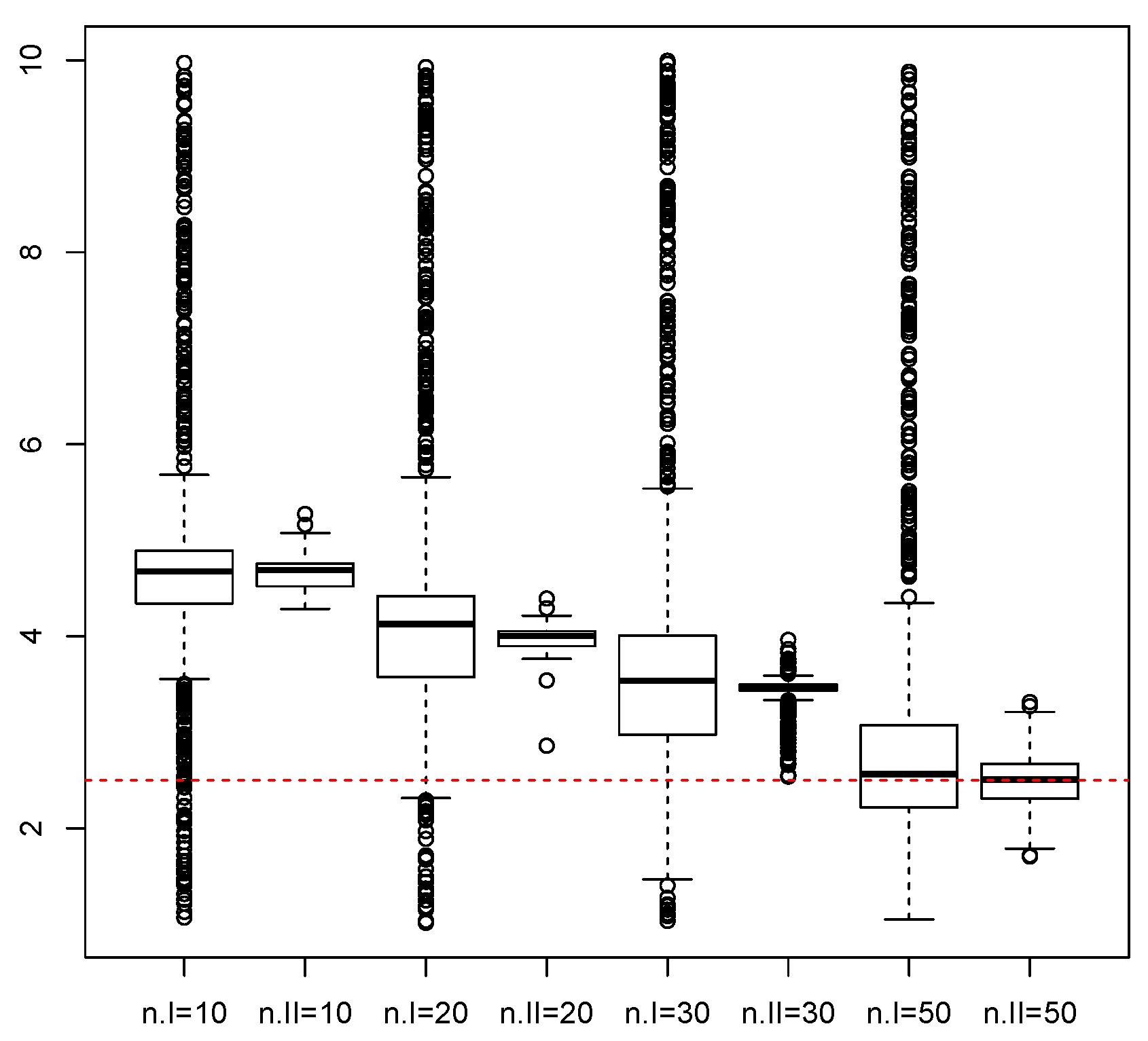
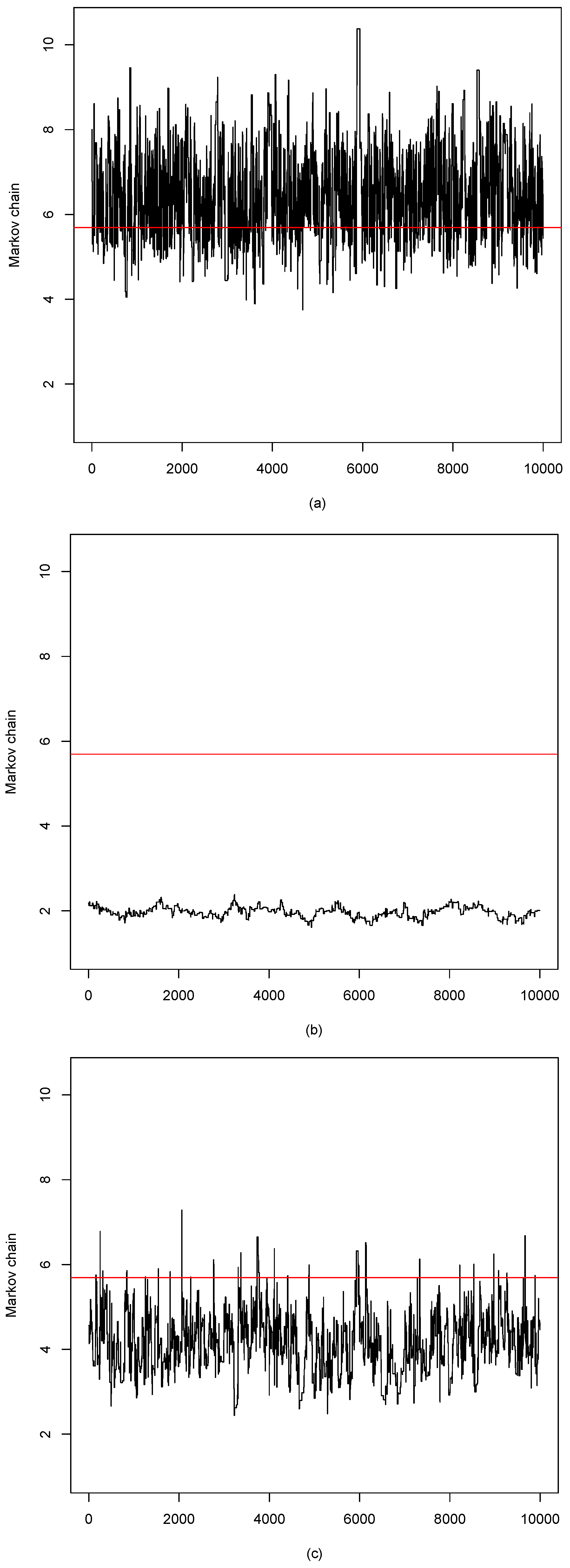
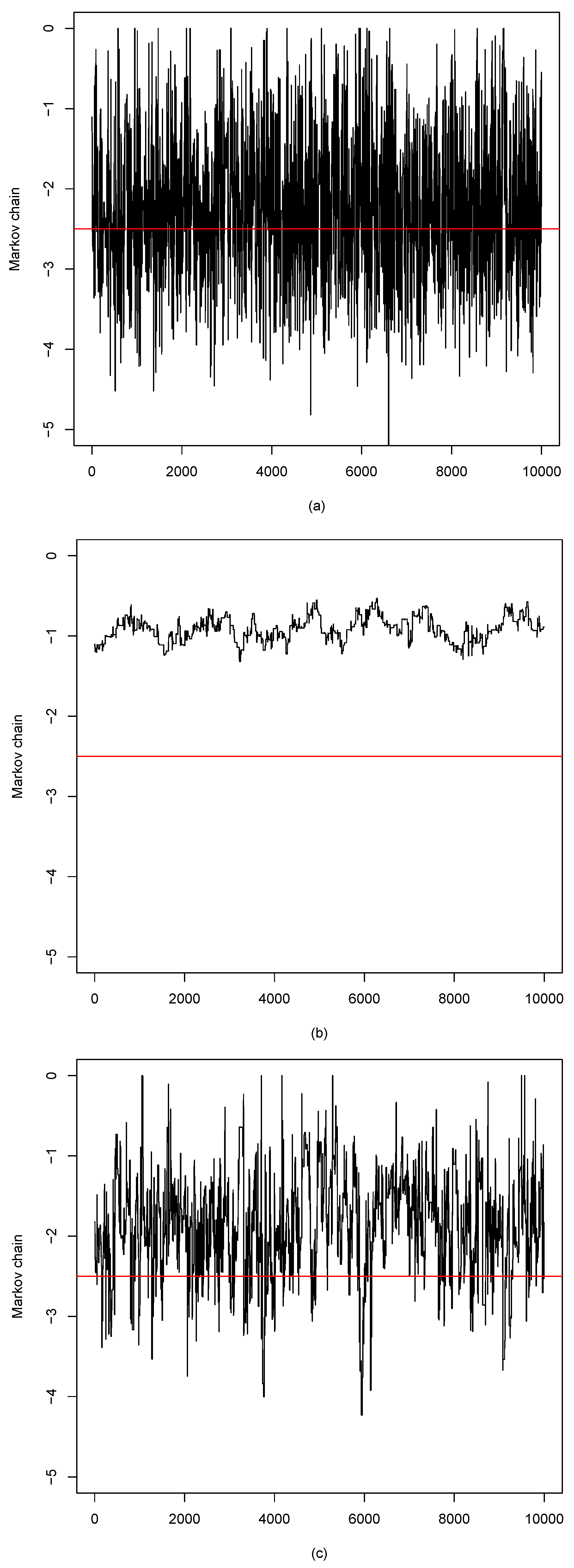
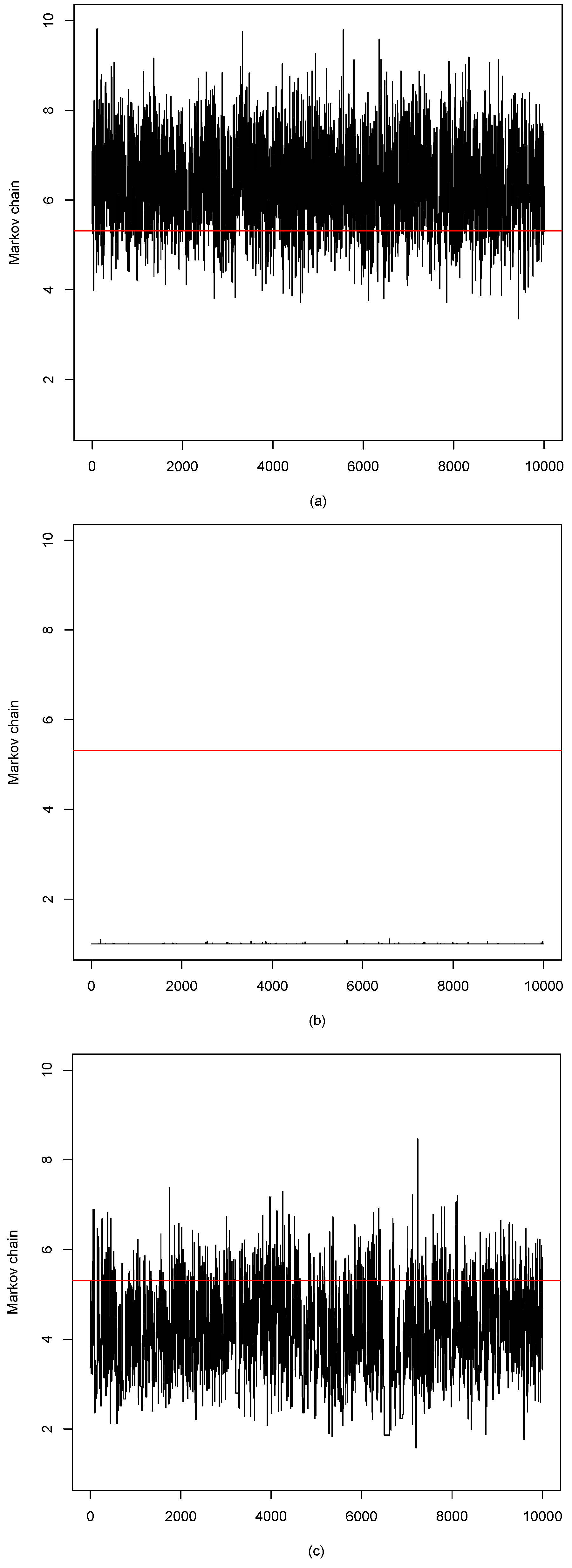
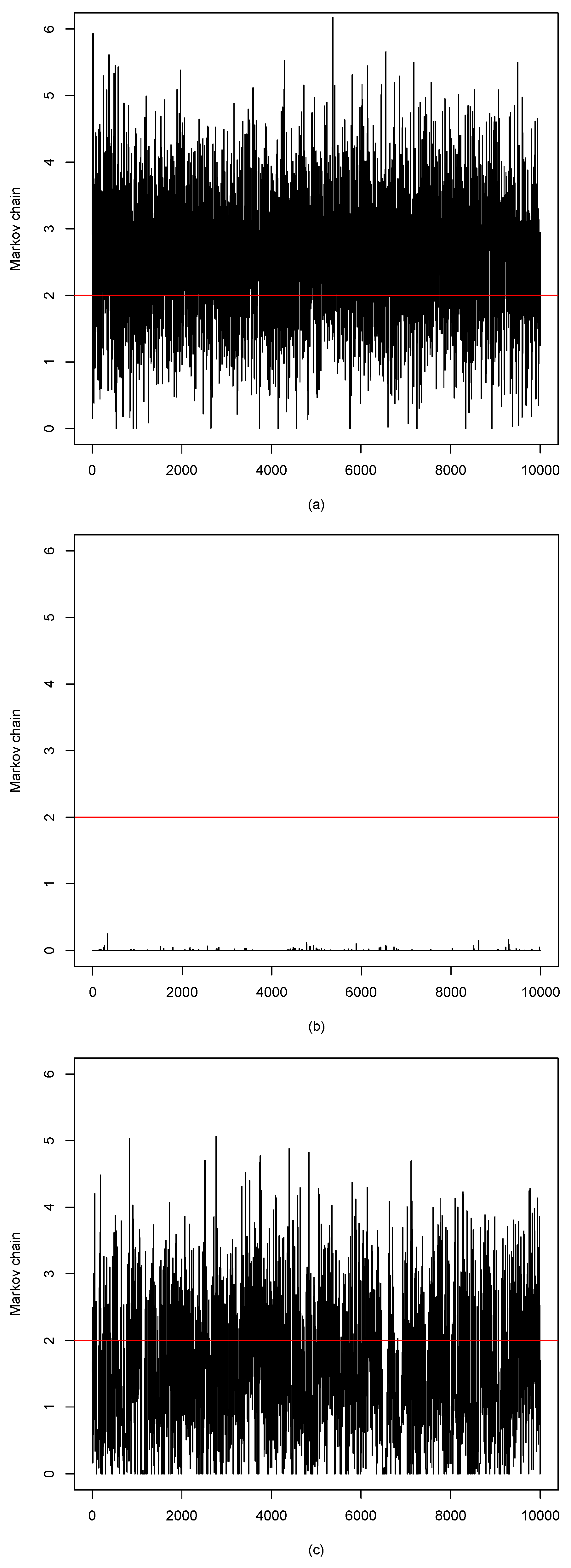
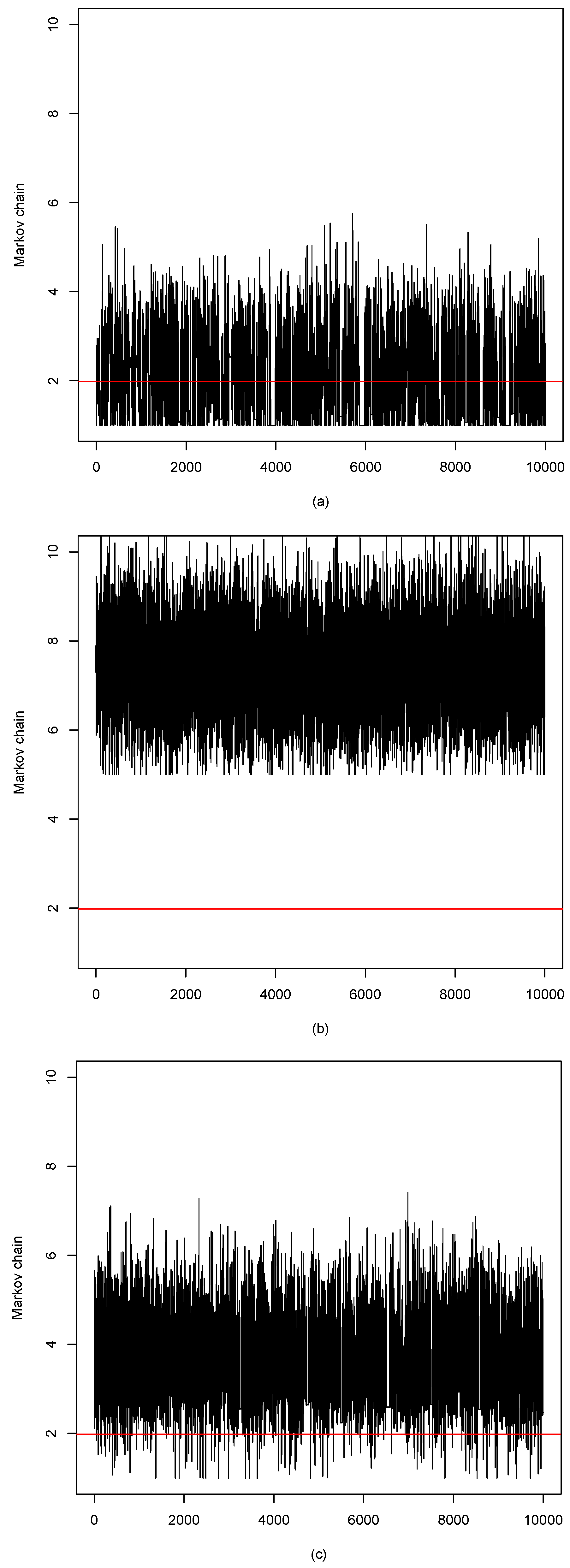
3. Monte Carlo Simulations
4. An Example
5. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Burr, I.W. Cumulative frequency functions. Ann. Math. Stat. 1942, 13, 215–232. [Google Scholar] [CrossRef]
- Tadikamalla, P.R. A look at the Burr and related distribution. Int. Stat. Rev. 1980, 48, 337–344. [Google Scholar] [CrossRef]
- Al-Hussaini, E.K. A characterization of the Burr type XII distribution. Appl. Math. Lett. 1991, 4, 59–61. [Google Scholar] [CrossRef]
- Galambos, J.; Kotz, S. Characterization of Probability Distribution; Lecture Notes in Mathematics; Springer: Berlin, Germany, 1973; Volume 675, pp. 51–53. [Google Scholar]
- Zimmer, W.J.; Keats, J.B.; Wang, F.K. The Burr XII distribution in reliability analysis. J. Qual. Technol. 1998, 30, 386–394. [Google Scholar] [CrossRef]
- Jang, D.-H.; Jung, M.; Park, J.-H.; Kim, C. Bayesian estimation of Burr type XII distribution based on general progressive type XII censoring. Appl. Math. Sci. 2014, 8, 3435–3448. [Google Scholar] [CrossRef]
- Ismail, N.H.; Khalid, A.M. Estimation of 2- and 3-parameter Burr type XII distribution using EM algorithm. Malays. J. Fundam. Appl. Sci. 2014, 10, 74–81. [Google Scholar] [CrossRef][Green Version]
- Thupeng, W.M. Use of the three-parameter Burr type XII distribution for modelling ambient daily maximum nitrogen dioxide concentrations in the Gaborone fire brigade. Am. Sci. Res. J. Eng. Technol. Sci. 2016, 26, 18–32. [Google Scholar]
- Nadar, M.; Papadopoulos, A.S. Bayesian analysis for the Burr type XII distribution based on record values. Statistica 2011, 71, 421–435. [Google Scholar]
- Panahi, H.; Sayyareh, A. Parameter estimation and prediction order statistics for the Burr type XII distribution with type II censoring. J. Appl. Stat. 2014, 41, 215–232. [Google Scholar] [CrossRef]
- Xin, H.; Zhu, J.; Sun, J.; Zheng, C.; Tsai, T.-R. Reliability inference based on three-parameter Burr type XII distribution with type II censoring. Int. J. Reliab. Qual. Saf. Eng. 2018, 25, 1850010. [Google Scholar] [CrossRef]
- Xin, H.; Zhu, J.; Tsai, T.-R. Parameter estimation for the three-parameter Burr-XII distribution under accelerated life testing with type I censoring using particle swarm optimization algorithm. Int. J. Innov. Comput. Inf. Control. 2018, 14, 1959–1968. [Google Scholar]
- Chaturvedi, A.; Belaghi, R.A.; Malhotra, A. Preliminary test estimators of the reliability characteristics for the three parameters Burr XII distribution based on records. Int. J. Syst. Assur. Eng. Manag. 2018, 9, 1260–1278. [Google Scholar] [CrossRef]
- Tahir, M.; Abid, M.; Aslam, M.; Ali, S. Bayesian estimation of the mixture of Burr Type-XII distributions using doubly censored data. J. King Saud-Univ.-Sci. 2019, 31, 1137–1150. [Google Scholar] [CrossRef]
- EL-Sagheer, R.M.; Mahmoud, M.A.W.; Hasaballah, M.H. Bayesian estimations using MCMC approach under three-parameter Burr-XII distribution based on unified hybrid censored scheme. J. Stat. Theory Pract. 2019, 13, 65. [Google Scholar] [CrossRef]
- Byrnes, J.M.; Lin, Y.-J.; Tsai, T.-R.; Lio, Y.L. Bayesian inference of δ=P(X<Y) for Burr type XII distribution based on progressively first failure-censored samples. Mathematics 2019, 7, 794. [Google Scholar] [CrossRef]
- EL-Sagheer, R.M.; Mahmoud, M.A.W.; Hasaballah, M.H. Bayesian inference for the randomly censored three-parameter Burr XII distribution. Appl. Math. Inf. Sci. 2020, 14, 1–11. [Google Scholar]
- Ali Mousa, M.A.M. Empirical Bayes estimators for the Burr type XII accelerated life testing model based on type-II censored data. J. Stat. Comput. Simul. 1995, 52, 95–103. [Google Scholar] [CrossRef]
- Ahmad, N.; Islam, A. Optimal accelerated life test designs for Burr type XII distributions under periodic inspection and type I censoring. Nav. Res. Logist. 1996, 43, 1049–1077. [Google Scholar] [CrossRef]
- Abd-Elfattah, A.M.; Hassan, A.S.; Nassr, S.G. Estimation in step-stress partially accelerated life tests for the Burr type XII distribution using type I censoring. Stat. Methodol. 2008, 5, 502–514. [Google Scholar] [CrossRef]
- Abdel-Hamid, A.H. Constant-partially accelerated life tests for Burr type-XII distribution with progressive type-II censoring. Comput. Stat. Data Anal. 2009, 53, 2511–2523. [Google Scholar] [CrossRef]
- Srivastava, P.W.; Mittal, N. Optimum multi-objective ramp-stress accelerated life test with stress upper bound for Burr type-XII distribution. IEEE Trans. Reliab. 2012, 61, 1030–1038. [Google Scholar] [CrossRef]
- Zhao, J.; Shi, Y.; Yan, W. Inference for constant-stress accelerated life test with Type-I progressively hybrid censored data from Burr-XII distribution. IEEE Signal Process. Lett. 2014, 25, 340–348. [Google Scholar] [CrossRef]
- Ismail, A.A.; Al-Habardi, K. On designing time-censored step-stress life test for the Burr type-XII distribution. Strength Mater. 2017, 49, 699–709. [Google Scholar] [CrossRef]
- Prakash, G. Confidence limits for progressive censored Burr type-XII data under constant-partially ALT. J. Stat. Appl. Probab. 2017, 6, 295–303. [Google Scholar] [CrossRef]
- Ismail, A.A.; Al-Habardi, K. Optimal Plans of step-stress life tests using failure-censored data from Burr type-XII distribution. Strength Mater. 2018, 50, 674–685. [Google Scholar] [CrossRef]
- Okasha, M.K.; Matter, M.Y. On the three-parameter Burr type XII distribution and its application to heavy tailed lifetime data. J. Adv. Math. 2015, 10, 3249–3442. [Google Scholar]
- Kantar, Y.M.; Usta, I. Analysis of the upper-truncated Weibull distribution for wind speed. Energy Convers. Manag. 2015, 96, 81–88. [Google Scholar] [CrossRef]
- Wang, L. Interval estimation for a lower-truncated distribution based on the double type-II censored sample. Commun. Stat.-Theory Methods 2016, 45, 5679–5692. [Google Scholar] [CrossRef]
- He, X.; Hu, X.; Qi, W. Reliability-based optimization design of Mechanical components with truncated normal distributions. In Proceedings of the 2016 5th International Conference on Measurement, Instrumentation and Automation (ICMIA 2016), Shenzhen, China, 17–18 September 2016. [Google Scholar] [CrossRef]
- Dörre, A. Bayesian estimation of a lifetime distribution under double truncation caused by time-restricted data collection. Stat. Pap. 2019. [Google Scholar] [CrossRef]
- Imani, M.; Braga-Neto, U.M. Maximum-likelihood adaptive filter for partially-observed Boolean dynamical systems. IEEE Trans. Signal Process. 2017, 65, 359–371. [Google Scholar] [CrossRef]
- Ducros, F.; Pamphile, P. Bayesian estimation of Weibull mixture in heavily censored data setting. Reliab. Eng. Syst. Saf. 2018, 180, 453–462. [Google Scholar] [CrossRef]
- Jaheen, Z.F.; Okasha, H.M. E-Bayesian estimation for the Burr type XII model based on type-2 censoring. Appl. Math. Model. 2011, 35, 4730–4737. [Google Scholar] [CrossRef]
- Han, M. E-Bayesian estimation and its E-posterior risk of the exponential distribution parameter based on complete and type I censored samples. Commun. Stat.-Theory Methods 2019. [Google Scholar] [CrossRef]
- Afify, A.Z.; Suzuki, A.K.; Zhang, C.; Nassar, M. On three-parameter exponential distribution: Properties, Bayesian and non-Bayesian estimation based on complete and censored samples. Commun. Stat.-Theory Methods 2019, 1–21. [Google Scholar] [CrossRef]
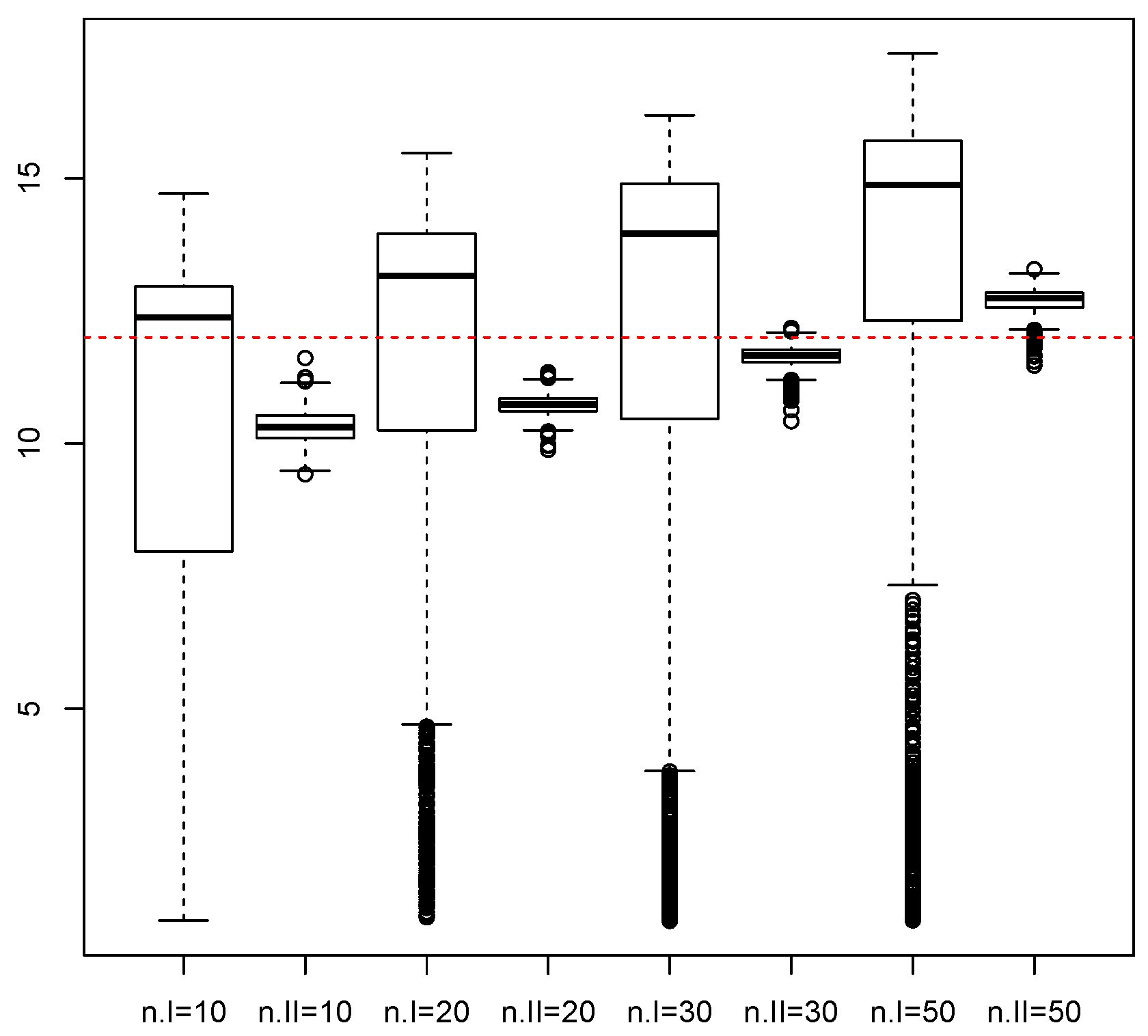
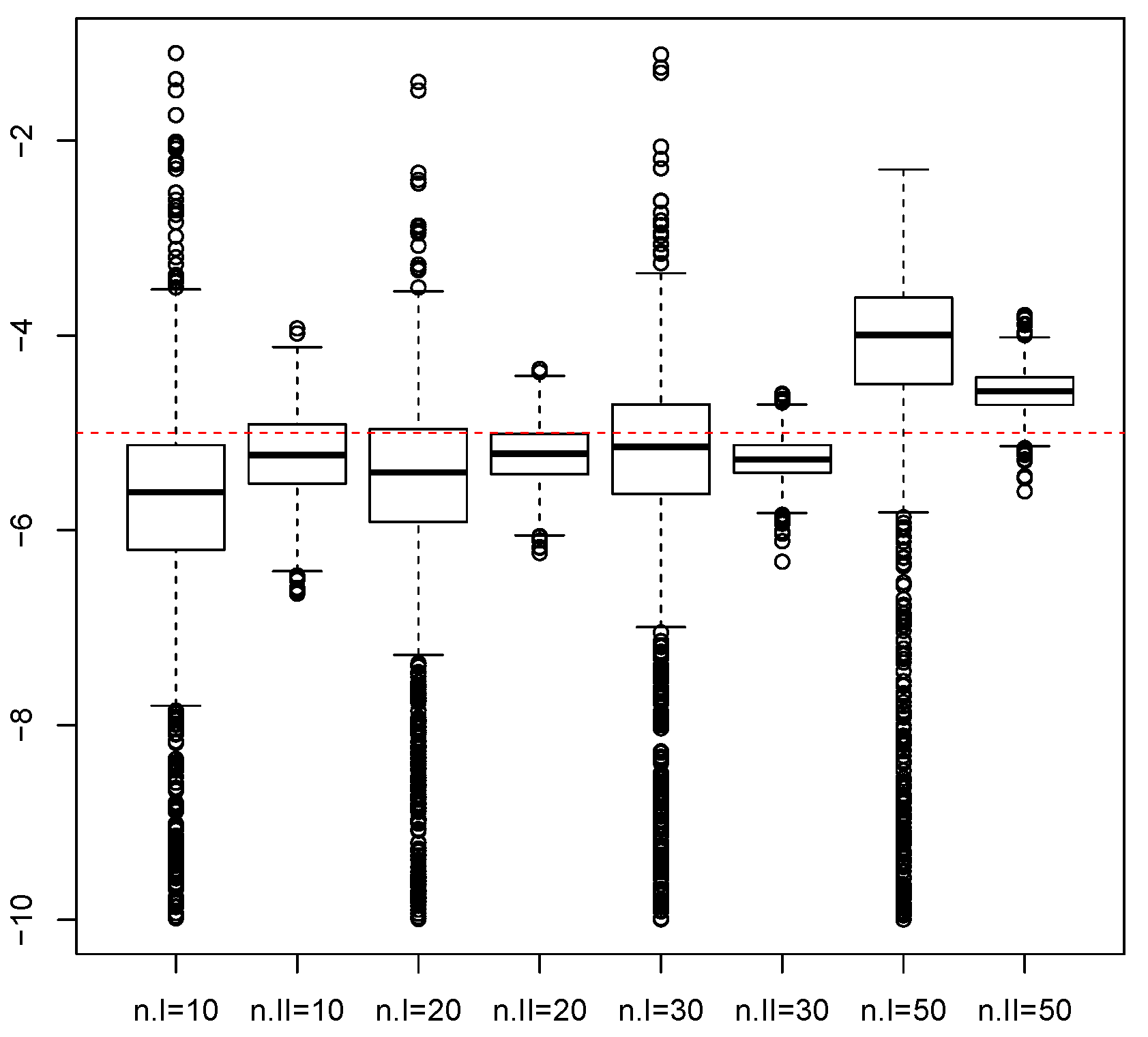
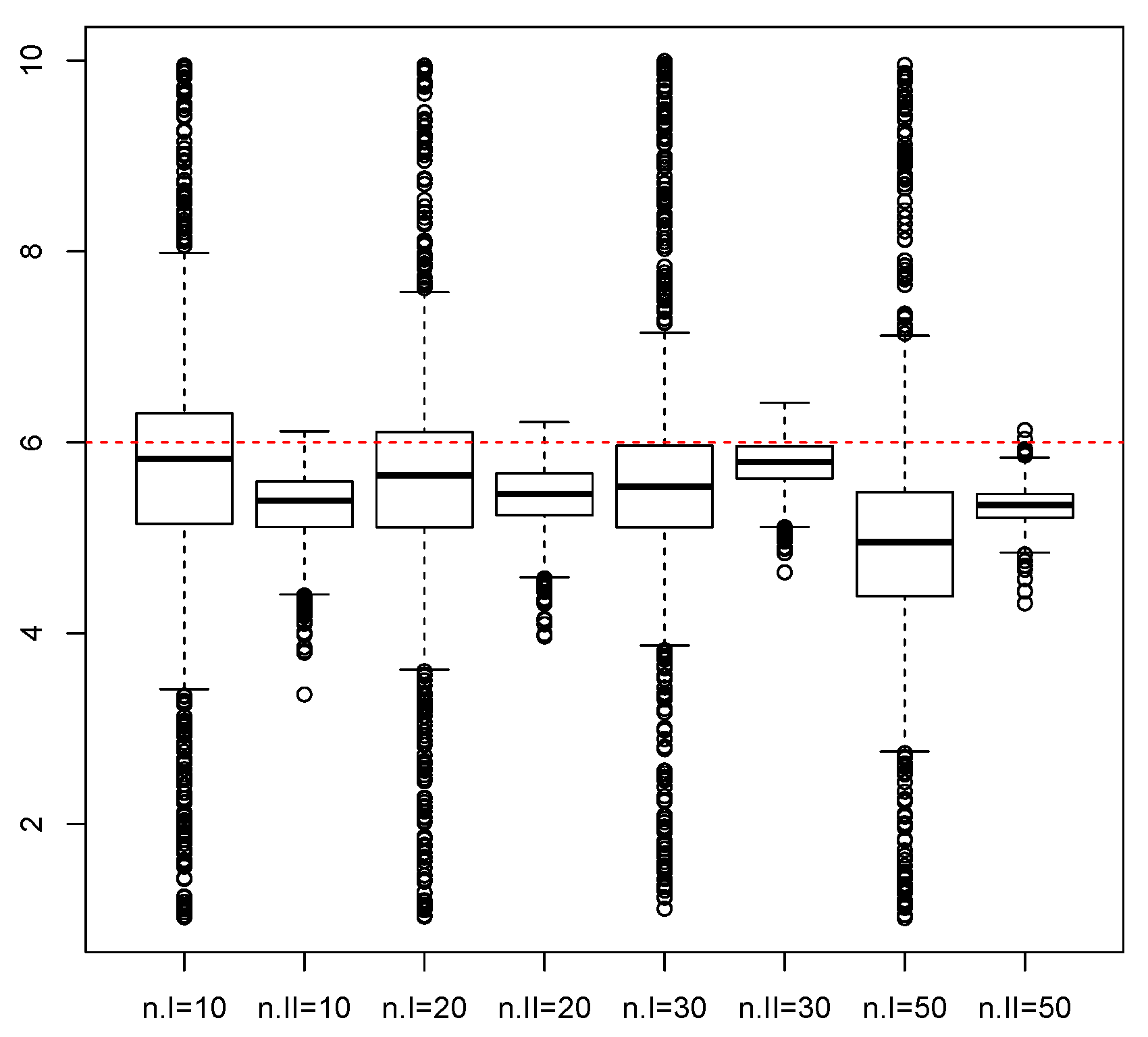
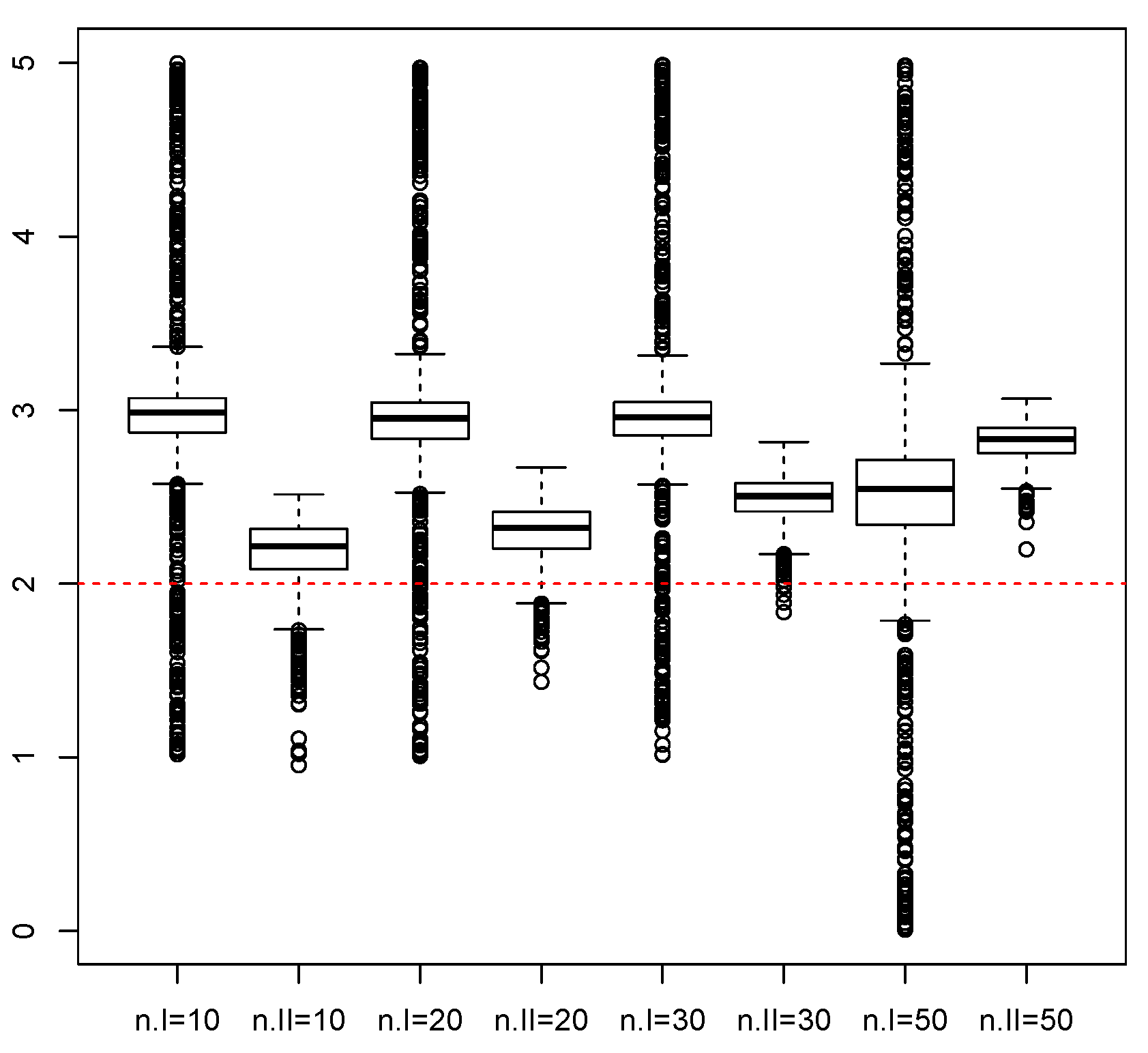

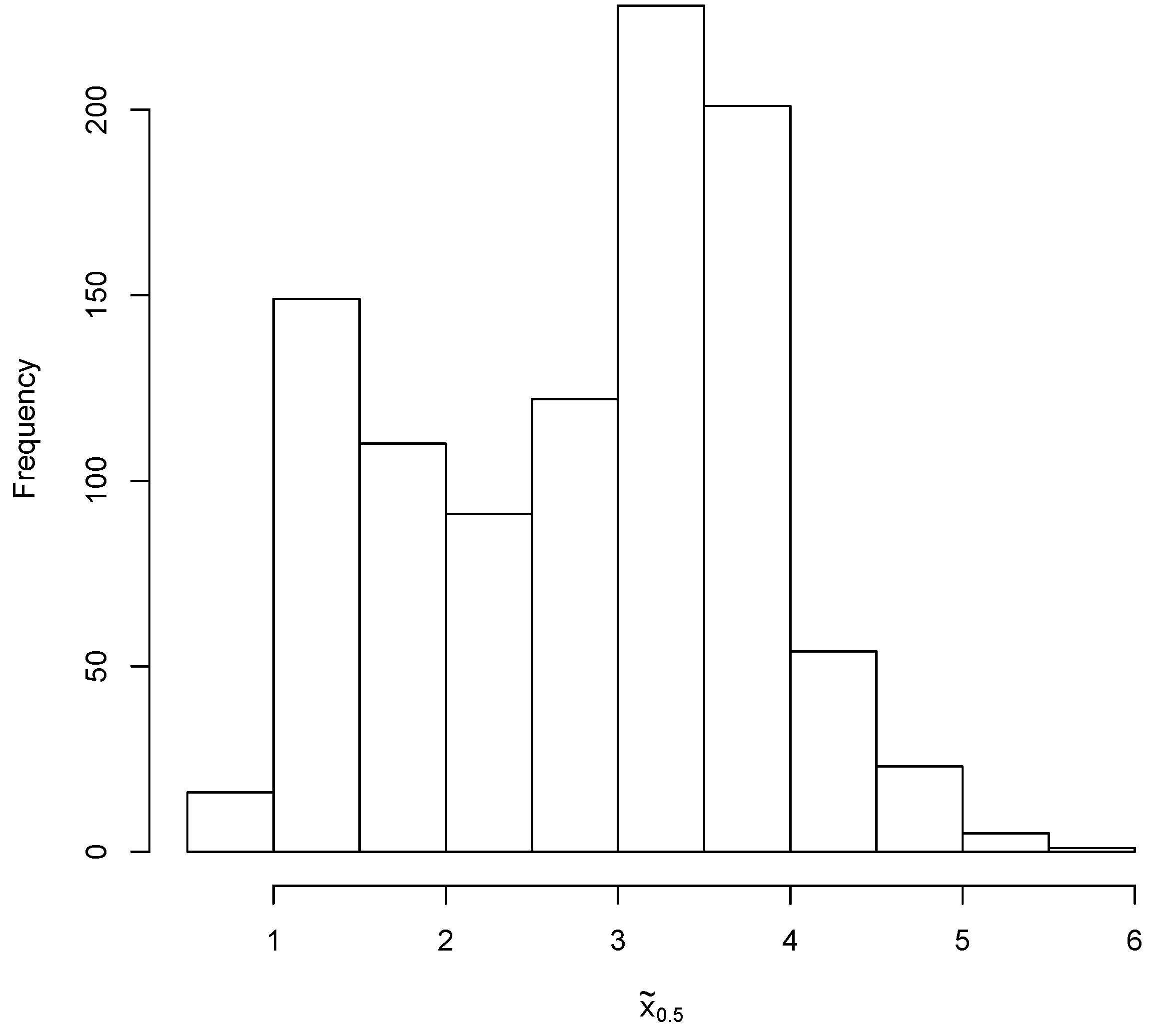
| Procedure | c | |||||
|---|---|---|---|---|---|---|
| (10, 10) | BE-I | −0.1415 | 0.1666 | −0.0540 | 0.5020 | 0.9080 |
| BE-II | −0.1399 | 0.0460 | −0.1136 | 0.0829 | 0.8557 | |
| (20, 20) | BE-I | −0.0710 | 0.1347 | −0.0710 | 0.4849 | 0.7307 |
| BE-II | −0.1060 | 0.0443 | −0.0959 | 0.1443 | 0.5903 | |
| (30, 30) | BE-I | −0.0247 | 0.0924 | −0.0665 | 0.4818 | 0.5595 |
| BE-II | −0.0309 | 0.0545 | −0.0378 | 0.2453 | 0.3749 | |
| (50, 50) | BE-I | 0.0614 | −0.0983 | −0.1629 | 0.2560 | 0.2364 |
| BE-II | 0.0564 | −0.0849 | −0.1117 | 0.4096 | −0.0068 |
| Procedure | c | |||||
|---|---|---|---|---|---|---|
| (10, 10) | BE-I | 0.3578 | 0.3238 | 0.2427 | 0.5961 | 1.0592 |
| BE-II | 0.1422 | 0.0995 | 0.1300 | 0.1372 | 0.8575 | |
| (20, 20) | BE-I | 0.3594 | 0.2971 | 0.2377 | 0.5674 | 0.9505 |
| BE-II | 0.1073 | 0.0756 | 0.1126 | 0.1691 | 0.5916 | |
| (30, 30) | BE-I | 0.3907 | 0.2952 | 0.2339 | 0.5639 | 0.8834 |
| BE-II | 0.0353 | 0.0707 | 0.0586 | 0.2541 | 0.3790 | |
| (50, 50) | BE-I | 0.3921 | 0.3458 | 0.2777 | 0.4370 | 0.7075 |
| BE-II | 0.0601 | 0.0963 | 0.1165 | 0.4134 | 0.1063 |
| Methods | c | |||||
|---|---|---|---|---|---|---|
| RB | Infor-1 | −0.1076 | −0.0824 | −0.2633 | −0.1361 | 0.0195 |
| Infor-2 | −0.1347 | −0.0992 | −0.3210 | −0.1667 | 0.0186 | |
| RsqMSE | Infor-1 | 0.1113 | −0.0910 | 0.2689 | 0.1549 | 0.0593 |
| Infor-2 | 0.1394 | −0.1094 | 0.3283 | 0.1884 | 0.0552 |
| Low Stress |
|---|
| 3.009, 1.434, 3.471, 3.937, 1.605, 2.015, 1.832, 1.501, 1.324, 0.825, |
| 2.055, 2.847, 1.033, 1.612, 2.002, 2.020, 1.603, 1.080, 1.373, 1.849, |
| 0.456, 0.903, 0.990, 1.089, 1.520, 1.151, 3.046, 0.457, 1.966, 0.841, |
| 2.255, 2.542, 2.181, 1.637, 1.252, 0.907, 1.296, 1.304, 2.701, 0.556, |
| 1.552, 3.132, 0.656, 1.097, 0.544, 2.814, 1.759, 1.041, 2.544, 1.853 |
| High Stress |
| 0.498, 1.871, 1.554, 0.679, 1.656, 1.225, 2.027, 1.458, 0.968, 0.667, |
| 0.263, 1.436, 0.664, 2.435, 1.438, 0.638, 1.069, 1.042, 1.293, 0.386, |
| 1.057, 2.197, 0.657, 1.352, 1.115, 0.587, 1.405, 0.635, 1.715, 1.592, |
| 1.886, 0.850, 0.547, 0.783, 0.405, 1.675, 2.150, 0.743, 1.299, 0.766, |
| 0.515, 1.281, 1.738, 2.615, 0.205, 1.058, 0.415, 0.223, 0.594, 1.687 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, H.; Liu, Z.; Lio, Y.; Tsai, T.-R. Accelerated Life Test Method for the Doubly Truncated Burr Type XII Distribution. Mathematics 2020, 8, 162. https://doi.org/10.3390/math8020162
Xin H, Liu Z, Lio Y, Tsai T-R. Accelerated Life Test Method for the Doubly Truncated Burr Type XII Distribution. Mathematics. 2020; 8(2):162. https://doi.org/10.3390/math8020162
Chicago/Turabian StyleXin, Hua, Zhifang Liu, Yuhlong Lio, and Tzong-Ru Tsai. 2020. "Accelerated Life Test Method for the Doubly Truncated Burr Type XII Distribution" Mathematics 8, no. 2: 162. https://doi.org/10.3390/math8020162
APA StyleXin, H., Liu, Z., Lio, Y., & Tsai, T.-R. (2020). Accelerated Life Test Method for the Doubly Truncated Burr Type XII Distribution. Mathematics, 8(2), 162. https://doi.org/10.3390/math8020162






