Abstract
In this paper, an integrated production and distribution problem for perishable products is presented, which is an NP hard problem where a single machine, multi-customers, and homogenous vehicles with capacity constraints are considered. The objective is to minimize the total order weighted delivery time to measure the customer service level, by making two interacted decisions, production scheduling and vehicle routing, simultaneously. An integrated mathematical model is built, and the validity is measured by the linear programming software CPLEX by solving the small-size instances. An improved large neighborhood search algorithm is designed to address the problem. Firstly, a two-stage algorithm is constructed to generate the initial solution, which determines the order production sequence according to the given vehicle routing. Secondly, several removal/insertion heuristics are applied to enlarge the search space of neighbor solutions. Then, a local search algorithm is designed to improve the neighbor solutions, which further generates more chances to find the optimal solution. For comparison purposes, a genetic algorithm developed in a related problem is employed to solve this problem. The computational results show that the proposed improved large neighborhood search algorithm can provide higher quality solutions than the genetic algorithm.
1. Introduction
The usage of perishable products has a negative time sensitivity; that is, the usefulness or value of products decreases with time. The definition of perishable products was proposed by [1]. If at least one of the following conditions occurs during the planning period, goods that are raw materials, intermediate products, or final products can be called perishable products: “(1) its physical status deteriorates obvious, and/or (2) its value decreases in the customer’s perception, and/or (3) some authorities believe that the future functions may be reduced”. Therefore, perishable products have a wide range of definitions, including fresh fruits and vegetables, flowers, food, and other products with a short lifespan, such as blood, drugs, and concrete.
Perishable products should not be delivered long after production, so as to meet customer orders. In addition, companies with such products have employed make-to-order strategies, aiming to reduce the production and delivery lead time [2]. Obviously, for perishable products, it is insufficient to consider the production scheduling or logistics transportation optimization separately. For example, to reduce the value loss of perishable products in delivery, if we make the production start time of the orders as late as possible, it may be difficult to achieve a transportation scheduling of products that is optimal, and the scheduling may be infeasible. In contrast, if only the order transportation optimization is considered, it may lead to excessive production ahead of schedule, leading to a greater value loss. Thus, production scheduling and distribution scheduling decisions should be made jointly at the operational level.
The integrated scheduling of production and distribution has received a lot of attention in recent years [3]. Various problems have been studied for industries such as fashion apparel and toys [4,5], consumer electronics [6], food catering industry [7,8], newspaper [9,10,11], home healthcare [12], and customized furniture [13]. For perishable products, there is less literature on optimizing production and transportation scheduling simultaneously [2,14,15,16,17,18,19,20]. Most of them consider one vehicle to serve all customers, simplifying routing decisions. Therefore, the integrated production and distribution problem for perishable products deserves further study.
In this paper, an integrated production and distribution problem for perishable products (IPDPPP) is presented. As shown in Figure 1, one machine and multi-customer are taken into account. Each customer has only one order, with a different weight according to the importance of each order. The produced products are transported by trucks to customers, without warehousing. In order to make full use of the vehicle capacity, different customers’ orders can be loaded into the same vehicle. Obviously, the IPDPPP has to make two decisions—production scheduling and vehicle routing. Production scheduling means to determine the order production sequence. In addition, the orders must be batched first, and the orders in the same batch are produced in succession. Then, each batch is loaded onto a same vehicle. Vehicle routing aims to determine the optimized routing for each vehicle. While the collaborative scheduling problem usually takes customer response time as the first concern, trying to achieve better customer service with lower logistics costs under limited resource constraints [21], the objective of the IPDPPP is to minimize the total order weighted delivery time by making two decisions simultaneously.
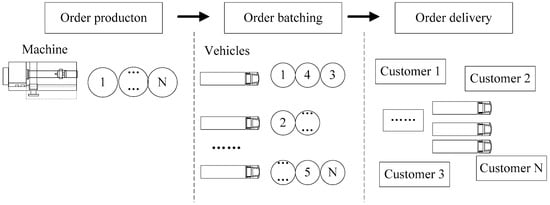
Figure 1.
The integrated production and distribution scheduling procedure.
The main highlights are as follows. Firstly, the vehicle routing decision is considered, except for production scheduling, which is simplified in the majority of literature, with respect to the complexity of the problem. Secondly, the objective of this problem is to minimize the total order weighted delivery time, which is usually applied to measure the customer service level [21]. Thirdly, an improved large neighborhood search algorithm is proposed to address the problem. An initial solution is constructed by a two-stage algorithm. Then, the initial solution is improved by exploring a complex neighborhood, and a local search for improving the neighbor solution is developed. Finally, the experimental results show that the improved large neighborhood search algorithm is effective and efficient. Compared with the results of CPLEX and the published genetic algorithm for the related problem, the optimal or approximate optimal solution can be obtained by the improved large neighborhood search algorithm.
The paper is organized as follows. In Section 2, the relevant literature of the IPDPPP is reviewed. In Section 3, a mathematical model for the integrated problem is built. In Section 4, an improved large neighborhood search algorithm is described to solve the problem, and its performance is analysed in Section 5. Section 6 draws the main conclusions.
2. Literature Review
Recently, the IPDPPP has received considerable attention, but there is not much literature about it. In most of the cases, one customer or infinite vehicles are considered, thus vehicle routing is simplified or ignored [22].
For the IPDPPP without routing decisions, an integrated production–distribution model for a deteriorating inventory item was built [23], where one customer was considered. Thus, the routing of the delivery did not need to be decided. The objective was to minimize the total cost. Although considering multi-customers in [24,25,26,27,28], the vehicle routing problem was simplified by direct delivery, which means that each vehicle only served one customer in one trip. The objectives were to minimize the total cost or total transportation time. The IPDPPP considering items with a short lifetime were studied in [29,30,31,32]. They assumed that transportation is outsourced to third-party-logistics (3PL) providers, and the products are picked up at regular times. The routing decision was ignored by the manufactories, and only the order production scheduling was optimized. The objectives were to minimize the total profit or total cost. A food production and distribution was mentioned in [33], where infinite vehicles were considered for direct delivery. The objective was to minimize the total cost. A nuclear medicine production and delivery problem considering infinite vehicles was studied in [34]. The objective was to minimize the total cost. The infinite vehicles were also considered in [35], and the objective was to minimize the total cost. A chemotherapy production and delivery problem was addressed in [36]. There was one customer and one vehicle. The vehicle could make more than one trip between the pharmacy production unit and the patient location. The objective to minimize was the maximum tardiness of delivery. Different from the above articles, this paper considers multi-customer and finite vehicles simultaneously; both the order production scheduling and the vehicle routing are optimized. The objective is to minimize the total order weighted delivery time in this paper, which differs from these papers.
The IPDPPP becomes more complex when routing decisions are considered. The IPDPPP with time windows was addressed in [16]. They assumed that the demands of customers are stochastic. The aim was to maximize the expected total profit of the supplier. The IPDPPP considering the time windows and parallel production lines were studied in [18,37], the goals were to minimize the total cost. An integrated supply chain scheduling problem along with the batch delivery consideration was investigated in a series of multi-factory environments [38], while considering the due date of each order. The aims were to reduce the total cost of transportation and the total tardiness. The products with a short lifespan were considered in [2,14,15,17,19,20], as well as the order production sequence and delivery sequence were fixed. A truck that has enough capacity to deliver all of the orders in one trip was mentioned in [14,17]. The goal was to maximize the total demand without violating the production/distribution capacity, the product lifespan, and the delivery time window, by selecting a subset of customers from a given sequence to receive the deliveries. While one truck with a limited capacity for transportation was considered in [2,15], which could travel many trips. The goal was to minimize the maximum delivery time of the orders. Multi-trucks with a limited capacity for transportation was addressed in [19,20], which could travel many trips. Their objectives were to minimize the total cost and makespan, respectively. Comparatively, we relaxed the time windows constraint in this paper, which further increases the complexity of the problem due to an expansion in search space. The time windows constraint was also relaxed in [22], the scheduling of production and delivery were considered in a make-to-order environment considering a single machine, multi-customers, and multi-vehicles. The objective was to minimize the makespan and an improved genetic algorithm was proposed. In this paper, however, the objective is to minimize the total order weighted delivery time, which receives relatively less attention in existing literature.
As a result of the complexity in integrated production scheduling and transportation problems, they were solved, in general, via heuristic algorithms. Such as, the branch-and-bound algorithm [2,14], the genetic algorithm [15], the Nelder–Mead method with a heuristic algorithm [16], a new heuristic algorithm [17], the adaptive large neighborhood search [18], a heuristics algorithm based on evolutionary algorithms [19], a greedy randomized adaptive search procedure with an evolutionary local search [20], a Benders decomposition-based heuristic [36], a novel three-phase methodology [37], and a Pareto approach [38]. What is more, in other areas of combinatorial optimization, new algorithms have emerged, such as multi-criteria optimization [39], and a biased-randomized iterated local search algorithm [40]. In this paper, an improved large neighborhood search algorithm is considered. By applying the proposed algorithm, the neighbors could be enlarged by their removal heuristics and insertion heuristics. Then, the solution space is enlarged, which generates more chances to find the optimal solution.
3. Problem and Model Definition
In this section, a mathematical model of the IPDPPP is developed. In the production phase, one machine is considered to produce products from all of the orders at a plant, with a constant production rate of . The machine will not be able to produce a new order until the order being processed has been completed. denotes the set of the plant and all of the customers, with 0 representing the plant and representing the customers. denotes the set of edges, with each edge having a travelling time of (from the plant to a customer or from a customer to another customer).
Customers are in different geographical locations. Each customer places an order to the plant, and is the set of all orders. denotes the weight of the order, , which presents the importance of the order, . Each order, , has a definite demand, , then the order processing time, , can be calculated according to the formula .
is the set of multiple homogenous vehicles with a capacity of . Each vehicle can be used at the most once, starting and ending at the plant. The loaded order quantity of a vehicle cannot exceed the vehicle’s capacity. Each customer’s demands must be delivered at one time, not in batches. Orders belonging to different customers can be delivered by the same vehicle within one trip. We defined the departure time as the time when the vehicle leaves the plant. The objective is to minimize the total weighted delivery time of the orders, which is clearly influenced by the departure time and the transportation time of each vehicle.
The other notations are defined as follows:
Decision variables:
Variables:
Objective function:
Constraints:
Objection Function (1) aims at minimizing the total weighted delivery time of the orders. Constraint (2) indicates that each customer’s demands must be met at one time. Constraints (3) and (4) ensure that each vehicle can be used once, starting and ending at the plant. Constraint (5) represents that the entering vehicle of a customer must eventually leave that customer. Constraint (6) shows that the vehicle capacity cannot be exceeded. Constraint (7) represents the starting time of a machine. Constraints (8) to (10) ensure that each order has a single predecessor and a single successor in the production phase. Constraints (11) to (12) ensure that each customer has a single predecessor and a single successor in the delivery phase. Constraint (13) ensures that the departure time of each vehicle is greater than or equal to the latest production completion time among the orders onboard the vehicle. Constraint (14) indicates that each customer has to be served. Constraint (15) is the integer conditions.
The IPDPPP is an NP-hard problem, optimizing both production scheduling and vehicle routing [22]. Intelligent algorithms have made great achievements in solving production scheduling [41,42], and vehicle routing problems [43,44]. For the complexity of the integration of the production scheduling and distribution problem, metaheuristic can be an appropriate approach to solve it [38]. Therefore, a heuristic algorithm is developed.
4. An Improved Large Neighborhood Search Algorithm
The specialty of our problem is that production scheduling and vehicle routing are considered jointly, which interplay with each other. Production scheduling determines the production sequence of every order; the vehicle routing problem determines the delivery sequence of each order for every vehicle. It is remarkable that the vehicle routing problem is a weighted traveling repairman problem (TRP), not a traditional traveling salesman problem (TSP), as the aim of this research is to minimize the total order weighted delivery time in this research. The difference between them is that the TRP aims at minimizing the sum of all the customers’ delivery times by taking into account customers’ satisfaction [45,46]; while the TSP aims at minimizing the total distances. For example, for a TRP problem or a weighted TRP, if the sequence of all of the customers in a route is reversed, the objective value would be changed; however, for a TSP problem, the objective value is not affected. Therefore, the heuristics to discuss the integration of production and transportation in the literature, with the goal of total cost or makespan, is not suitable to solve this problem.
With respect to the above special consideration, an improved large neighborhood search (ILNS) algorithm is proposed. The large neighborhood search (LNS) algorithm is a meta-heuristic algorithm, which finds better candidate solutions by exploring complex neighborhoods defined by destroy and repair methods. A destroy method destructs part of the current solution, while a repair method rebuilds the destroyed solution. By alternating between an infeasible solution and a feasible solution through destroy and repair methods, the LNS algorithm has been widely used in various combinatorial optimization problems, and has been proved effectively, such as for vehicle routing problems [47,48,49], machine scheduling problems [50,51], supply chain network design [52], satellites scheduling [53], and exam scheduling problems [54]. By applying the LNS algorithm to solve our problem, the neighbors could be enlarged, so as to solve the solution space. Compared with the traditional LNS algorithm, in addition to the above benefits, the improved large neighborhood search (ILNS) algorithm proposed in this paper uses a two-stage algorithm to construct the initial solution, and proposes a local search to improve the neighbor solution, which generates more chances to find the optimal solution. The ILNS algorithm includes the following five stages, and the major procedure of the ILNS algorithm is shown in Figure 2.
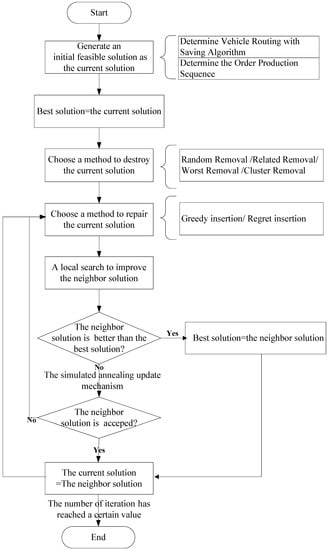
Figure 2.
The major procedure of the improved large neighborhood search algorithm.
Stage 1: Initial solution generation. A two-stage algorithm is developed in the generation. The vehicle routing is determined with the savings algorithm first. Then, the order production sequence is determined by a certain rule, and the objective value of the solution is computed. The constructed initial solution is used as the current solution. The best solution is also equal to the initial solution at this stage.
Stage 2: Neighbor solution generation. A neighborhood is defined implicitly by a destroy and a repair method. In this paper, the destroy method consists of four removals, and the repair method consist of two insertion algorithms. Every time a neighbor solution is derived with the current solution, a certain removal and insertion algorithm is chosen with a certain rule. Each time the vehicle routing is generated, the order production sequence is determined, and the objective value of the neighbor solution is computed.
Stage 3: Local search. A local optimization algorithm is employed to improve the quality of the generated neighbor solutions.
Stage 4: Acceptance rule. If the newly derived neighbor solution is better than the best solution, we update the best solution and set it to be the new current solution; otherwise, the judgement criterion of the simulated annealing algorithm will be used to decide whether to accept the neighbor solution as the new current solution or not.
Stage 5: Stopping criterion. Such an iteration process (Stages 2 and 4) will be repeated until the defined number is reached.
4.1. Construction of an Initial Solution
A two-stage algorithm is proposed to construct the initial solution. First, the vehicle routing is determined with a savings algorithm. When the vehicle routing is given, the orders loaded on each vehicle are called a batch. Second, the production sequence of the orders in each batch is generated based on the vehicle routing. Finally, the objective value is calculated.
4.1.1. Determine Vehicle Routing with a Saving Algorithm
The saving algorithm for the vehicle routing problem is introduced in [55]. For the initial solution, each customer is assigned to a separate route. Then, for each customer i in route and j in route , the savings are calculated as follows: sij = bi0 + b0j − bij; 0 represents the depot and bij represents the cost of edge (i, j). Thus, the value of sij contains the savings of combining two routes and , instead of serving two separate routes. A pseudo-code for the saving algorithm is presented in Algorithm 1.
| Algorithm 1: Saving Algorithm |
| Set X = 1, C = {1,2, …, n}, S = {sij: i,jC} Insert n customers into n empty routes. Calculate the savings sij between any two customers Sequence sij in S in non-increasing order While S is not empty do Mark the largest savings sij If the onboard quantity of vehicle X does not exceed its capacity when i and j are loaded, then Append the arc (i,j) to the end of route X Remove arc (i,j) and other arcs that contain point i or j from set S else X = X + 1 For each customer c in C, do If customer c is not loaded to any route, then Load the order of customer c into the route that has the largest remaining capacity Return to the route of each vehicle |
4.1.2. Determine the Order Production Sequence
As the vehicle routing decision has been made, the transportation time and the orders loaded on each vehicle are determined. The departure time of each vehicle should be reduced, because the objective is to minimize the total weighted delivery time of the orders. The departure time of a vehicle depends on the order production sequence, which is determined as follows.
The rule that the orders onboard the vehicle with the maximum sum of order weighted delivery times are produced first is employed. Assume that the departure times of all of the vehicles are 0. Then, calculate the sum of order weighted delivery times of each vehicle. Finally, arrange the production sequence of each vehicle as per the sum of the order delivery times of all vehicles, sorted in descending order. Assume that the orders that belong to the same order batch are produced successively, and that the production sequence of each order is the same as its delivery sequence; re-calculate the departure time of every vehicle and the sum of order weighted delivery times of each vehicle. Then, the total weighted delivery time of the orders is obtained. The pseudocode to determine the order production sequence is presented in Algorithm 2.
| Algorithm 2: Determine the Order Production Sequence |
|
4.2. Neighborhood Search
Given a current solution, s, several customers are removed and are then reinserted to generate neighbor solutions at each iteration. This is achieved by applying one of several removal and insertion heuristics. Each time a neighbor solution is generated, the objective value of the neighbor solution is calculated as the initial solution.
4.2.1. Four Removal Heuristics
The removal heuristic is to generate destroy neighborhoods by choosing m customers from a current solution, s, and putting them into a request bank, such as random removal, related removal, worst removal, and cluster removal, which can be seen in Figure 3. The black circles denote the removed customers and the dashed lines denote the new generated edges after moving (Figure 3).
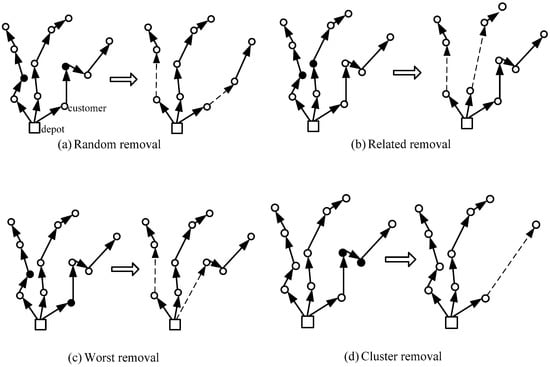
Figure 3.
Four removal heuristics.
(1) Random removal
The simplest removal heuristic randomly selects m customers and deletes them from the current solution, s, which is propitious to diversify the search.
(2) Related removal
The general idea of the related removal heuristic aims to delete somewhat similar customers, as it is considered fairly easy to create new and better solutions [47]. The similarity between two customers, i and j, is calculated by a correlation measure (the distance between two customers), where the lower value means the more similar customers. The related removal heuristic repeatedly chooses a new customer, i, randomly, and the customer ir, having the smallest relatedness with i, removes them from the current solution, s, until m customers have been removed.
(3) Worst removal
This heuristic approach eliminates the customers with a high-cost in the current solution s. Let ; is the cost associated with customer i in the current solution s, and is the cost without customer i in s. The worst removal heuristic repeatedly selects a new customer i, with the highest , until m customers are deleted [56].
(4) Cluster removal
Some instances tested in the computational section contain clusters of customers; it needs to remove clusters of related customers from some routes. For each route, a modified version of Kruskal’s algorithm is applied to divide its customers into two groups, it is stopped when two connected components are left [56]. Then, one of the groups is selected randomly and the customers of the group are removed so that they can be re-inserted appropriately. If more customers need to be removed, one of the removed customers is selected, and a customer is picked from a new route that is closer to the chosen customer. The new route, , is then divided into two clusters, and the process is repeated until m customers are deleted.
4.2.2. Two Insertion Heuristics
The insertion heuristic is used to rebuild the destroyed solution. When the removal heuristics remove customers from the existing routes into a request bank, to generate repair neighborhoods, the insertion heuristic choose m customers from the request bank, inserting them into one or more routes without violating the capacity constraint.
(1) Greedy insertion
Insert customer i into route k in the position that results in the lowest objective value. This process continues until m customers have been inserted. If customer i cannot be reinserted for the capacity constraint, leave it in the request bank. Finally, insert the customers remaining in the request bank into a route randomly, and let the objective value of the new solution be a very large number.
(2) Regret insertion
For each removed customer in the request bank, calculate its regret value, this is equal to the difference in cost between two solutions, in which i is inserted in its best route or in its second-best route [47].
Let denote the change in the objective value by inserting customer i in the route , where customer i can be inserted at a minimum cost. Let denote the change in the objective value by inserting customer i in route , where the customer i can be inserted at the second minimum cost. The regret value of customer i is equal to .
Customer i with the highest regret value is chosen for insertion into the current solution, s, and customer i is deleted from the request bank. Customer i is inserted in its best route. The process is repeated until the request bank is empty.
4.3. A Local Search for Improving the Neighbor Solution
A multiple insertion (MI) algorithm was adapted for parallel machines scheduling [57]. The MI heuristic sorts the jobs in a non-increasing order of the modified processing times, then places each job in the position on the machine with the lowest makespan. In this paper, the MI algorithm is adopted to improve the quality of the neighbor solution. The vehicles can be treated as parallel machines, and the travelling time between customers can be the modified processing times. Thus, sort the customers in a non-increasing order of the travelling time, insert each customer one by one in every position of every route, and then place each customer in the position that results in the lowest objective value.
4.4. Acceptance Rule
The current solution update mechanism determines whether to replace the current solution by the neighbor solution . The acceptance rule of the simulated annealing algorithm is used as the mechanism to accept neighbor solutions [58].
There are two situations that need to be considered. One is that if neighbor solution is superior to the current solution —replace with . Another is that if neighbor solution is inferior to the current solution , the acceptance probability needs to be computed, with that, and are the objective values of the current solution and the neighbor solution, respectively. is the current temperature, which starts at 0.005× (the objective value of the initial solution). At every iteration, similar to [47], decreases linearly to zero, according to a cooling rate fixed to 0.99975. If the acceptance probability is larger than a random number between , accept the neighbor solution and continue searching in the current neighborhood structure; otherwise, turn to the next neighborhood structure to search.
4.5. Stopping Criterion
The removal and insertion heuristics are repeated until the number of iterations reaches 50,000 [47].
5. Computational Results
5.1. Instances Generation
There is no benchmark data for the IPDPPP, the test instances for the computational experiments should be generated according to certain rules. The first set of instances consists of small-sized instances including 5–10 customers and two vehicles. The vehicles are homogenous with a capacity of 20. The coordinates of each customer are randomly generated in [0, 50]. The demand of each customer/order is randomly generated in [1, 10], and the total demands of all of the customers does not exceed 40.
If the order production time is ignored, the problem IPDPPP is simplified to a capacitated vehicle routing problem (CVRP). Thus, the second set of instances consists of larger-sized instances generated from the well-known CVRP benchmarks (A, B, and P series), including 71 instances found on the website http://www.bernabe.dorronsoro.es/vrp/. The instances are composed of 15–100 customers and 2–15 vehicles. The number of customers, customer coordinates, and customers’/orders’ requirements in the set of data are the same as the CVRP benchmark data. The characteristics of the customer coordinates of groups A, B, and P are different. Take the instances A-n32-k5, B-n31-k5, and P-n40-k5 as examples; the customer coordinates of Group A are generated randomly, while that of Group B are clustered and the customer coordinates of Froup C have an almost equal distance, which can be seen in Figure 4.
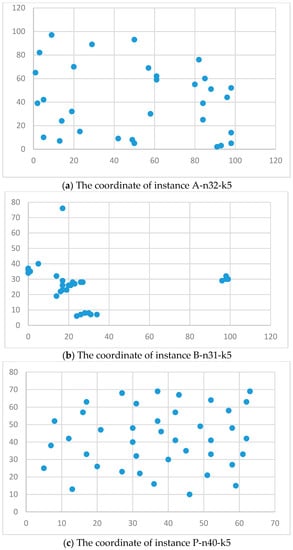
Figure 4.
Examples of the coordinates of instances in Groups A, B, and P.
For each instance, both in first and second set, the order weight is selected from the discrete uniform distribution U [1, 5], at random. For ease of calculation, similar to [15], the production rate is set to 1. In addition, similar to [44], the travel time between two customers or between the plant and a customer is equal to the distance between them.
5.2. Results for Small-Sized Instances
The mathematical model is validated by CPLEX. It should be noted that Constraint (13) in the mathematical model is non-linear; therefore, a new variable with is defined to solve the problem. Then, the following linear Constraints (16) replace Constraint (13).
Table 1 gives the solutions of CPLEX and the improved large neighborhood search (ILNS) algorithm for small-sized cases. The column “Instance” denotes the name of the instance, and “n” and “k” denote the number of customers and the number of vehicles, respectively. The results in Table 1 show that both CPLEX and the ILNS algorithm can get the optimal solution of small-sized test cases, while the running time of the ILNS algorithm is less than that of CPLEX for all of the test cases.

Table 1.
Computational results of CPLEX and the improved large neighborhood search (ILNS) algorithm.
5.3. Results for Larger-Sized Instances
In order to evaluate the effect of the proposed improved ILNS algorithm for larger-sized instances, we compared it with the initial solution (IS) and a genetic algorithm (GA) [22]. Single machine, multi-customers, and multi-vehicles were considered in [22], while the objective was to minimize the makespan, and an improved genetic algorithm was proposed. For a fair comparison, the running time of GA was set to be equal to the ILNS algorithm for each instance. The ILNS algorithm and GA were coded in C++.
Table 2, Table 3 and Table 4 provide the results of the instance of Groups A, B, and P, obtained by algorithms IS, ILNS, and GA for the proposed problem. Column “Instance” denotes the instance name. Columns S1, S2, and S3 denote the results obtained by IS, ILNS algorithm, and GA, respectively. Columns T1 and T2 denote the running times of the IS and ILNS algorithms. The running time of GA is equal to the ILNS algorithm. Columns “Gap1” and “Gap2” denote the percentage gap between the IS and ILNS algorithm results, and the GA and ILNS algorithm results, respectively. They are calculated by and .

Table 2.
Computational results of four algorithms for group A. IS—initial solution; GA—genetic algorithm.

Table 3.
Computational results of four algorithms for Group B.

Table 4.
Computational results of four algorithms for Group C.
Figure 5 provides the tendency in the results of IS, the ILNS algorithm, and GA for instances of Groups A, B and P. It shows that the results of the ILNS algorithm are better than those of IS and GA. Table 2, Table 3 and Table 4 show that the results of the ILNS algorithm are substantially improved based on IS. The average gaps between the IS and ILNS algorithms are 26.20%, 26.04%, and 22.94% for the three instance groups, respectively. At the same time, the computation time of the ILNS algorithm is short. The average running time of the IS is within 0.1 s, and the average running time of the ILNS algorithm is approximately 50 s. This indicates that the performance of the proposed ILNS algorithm is effective and efficient for not only random instances, but also cluster instances and related instances. It also suggests that the removal heuristics and insertion heuristics work well.
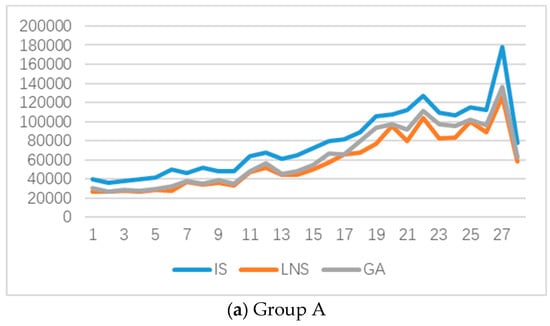
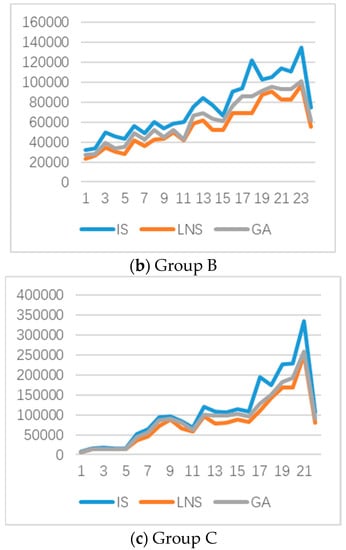
Figure 5.
The tendency in the results of three algorithms (IS, ILNS, and GA).
Moreover, the results of the ILNS algorithm are better than those of the GA. For the three instance groups, the average gaps between the ILNS algorithm and the GA are 7.20%, 11.19%, and 10.91%, respectively. The efficiency of the ILNS algorithm could be explained as follows. For the GA in [22], a method “MUS” which adopts some pre-designed rules to change the order of the customers in a route is defined as a local search algorithm. In their transportation phase, the goal is to minimize the maximum delivery time of the orders of each vehicle, “MUS” is employed to find more shortened routing for each vehicle. However, the objective of this paper is to minimize the sum of the order weighted delivery time. In the transportation phase, the goal is to find a method to minimize the sum time of all of the customers receiving services. Obviously, the local search “MUS” is not suitable for solving this goal. For example, reversing all of the points in a TSP route does not affect the solution of the TSP (traveling salesman problem), but reversing all points in a path of this problem would change the solution. Thus, the local search “MI” applied in this paper is more effective than the “MUS” method for minimizing the sum of the order weighted delivery time.
6. Conclusions
This paper explores an integrated production and transportation scheduling problem for perishable products, which is an NP hard problem, aimed at minimizing the total of the order weight delivery time to improve customer service. In the production stage, a single machine is considered, and the order batching and the production sequence of the orders are determined. In the transportation stage, multiple vehicles and multiple customers are considered, and decisions on vehicle routing are made. An integrated mathematical model is built, and the validity is measured by the linear programming software CPLEX, by solving the small-size instances. An improved large neighborhood search (ILNS) algorithm is proposed to solve the larger-size instances. Firstly, a two-stage algorithm constructs an initial solution. The saving algorithm is developed to determine the vehicle routing, and then the optimal production sequence is decided by a certain rule, according to the given vehicle routing. Secondly, several removal and insertion heuristics are designed to destroy and repair the current solution, to generate extensive neighbor solutions to enlarge the solution space. Then, a local optimization algorithm is used to improve the quality of the generated neighbor solutions, which generates more chances to find the optimal solution. Finally, the acceptance rule of the simulated annealing algorithm is used to determine whether to accept the neighbor solution as the new current solution. To validate and evaluate the effectiveness of the proposed ILNS algorithm, the solutions are compared with the corresponding results obtained by the initial solution and the existing genetic algorithm in the literature. The computational results show that the proposed ILNS algorithm substantially improves the initial solution and is more effective than the genetic algorithm.
In the future, we will explore solving the perishable products’ integrated production and distribution scheduling problem with exact algorithms, and explore the upper or lower bounds. Moreover, from a practical perspective, considering parallel machines and heterogeneous vehicles with time window constraints are also worthy of being addressed as well.
Author Contributions
Formal analysis, L.L.; Methodology, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (no. 71862034, no. 71862035, and no. 71502159), the Scientific Research Funding of Yunnan Department of Education (no. 2017ZZX004), and the Basic Research Foundation of Yunnan Province (no. 2019FB085).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Amorim, P.; Meyr, H.; Almeder, C.; Almada-Lobo, B. Managing perishability in production-distribution planning: A discussion and review. Flex. Serv. Manuf. J. 2013, 25, 389–413. [Google Scholar] [CrossRef]
- Karaoğlan, İ.; Kesen, S.E. The coordinated production and transportation scheduling problem with a time-sensitive product: A branch-and-cut algorithm. Int. J. Prod. Econ. 2017, 55, 22. [Google Scholar]
- Bashiri, M.; Badri, H.; Talebi, J. A new approach to tactical and strategic planning in production–distribution networks. Appl. Math. Model. 2012, 36, 1703–1717. [Google Scholar] [CrossRef]
- Pundoor, G.; Chen, Z.L. Scheduling a production-distribution system to optimize the tradeoff between delivery tardiness and total distribution cost. Naval Res. Logist. 2005, 52, 571–589. [Google Scholar] [CrossRef]
- Chen, Z.L.; Pundoor, G. Order assignment and scheduling in a supply chain. Oper. Res. 2006, 54, 555–572. [Google Scholar] [CrossRef]
- Li, K.P.; Sivakumar, A.I.; Ganesan, V.K. Complexities and algorithms for synchronized scheduling of parallel machine assembly and air transportation in consumer electronics supply chain. Eur. J. Oper. Res. 2008, 187, 442–455. [Google Scholar] [CrossRef]
- Chen, Z.L.; Vairaktarakis, G.L. Integrated scheduling of production and distribution operations. Manag. Sci. 2005, 51, 614–628. [Google Scholar] [CrossRef]
- Sel, C.; Bilgen, B. Hybrid simulation and mip based heuristic algorithm for the production and distribution planning in the soft drink industry. J. Manuf. Syst. 2014, 33, 385–399. [Google Scholar] [CrossRef]
- Russell, R.; Chiang, W.C.; Zepeda, D. Integrating multi-product production and distribution in newspaper logistics. Comput. Oper. Res. 2008, 35, 1576–1588. [Google Scholar] [CrossRef]
- Chiang, W.C.; Russell, R.; Xu, X.J.; Zepeda, D. A simulation/metaheuristic approach to newspaper production and distribution supply chain problems. Int. J. Prod. Econ. 2009, 121, 752–767. [Google Scholar] [CrossRef]
- Russell, R. A constraint programming approach to designing a newspaper distribution system. Int. J. Prod. Econ. 2013, 145, 132–138. [Google Scholar] [CrossRef]
- Liu, R.; Yuan, B.; Jiang, Z. Mathematical model and exact algorithm for the home care worker scheduling and routing problem with lunch break requirements. Int. J. Prod. Res. 2017, 55, 558–575. [Google Scholar] [CrossRef]
- Mohammadi, S.; Al-e-Hashem, S.M.J.; Rekik, Y. An integrated production scheduling and delivery route planning with multi-purpose machines: A case study from a furniture manufacturing company. Int. J. Prod. Econ. 2020, 219, 347–359. [Google Scholar] [CrossRef]
- Armstrong, R.; Gao, S.; Lei, L. A zero-inventory production and distribution problem with a fixed customer sequence. Ann. Oper. Res. 2008, 159, 395–414. [Google Scholar] [CrossRef]
- Geismar, H.N.; Laporte, G.; Lei, L.; Sriskandarajah, C. The integrated production and transportation scheduling problem for a product with a short lifespan. J. Comput. 2008, 20, 21–33. [Google Scholar] [CrossRef]
- Chen, H.K.; Hsueh, C.F.; Chang, M.S. Production scheduling and vehicle routing with time windows for perishable food products. Comput. Oper. Res. 2009, 36, 2311–2319. [Google Scholar] [CrossRef]
- Viergutz, C.; Knust, S. Integrated production and distribution scheduling with lifespan constraints. Ann. Oper. Res. 2014, 213, 293–318. [Google Scholar] [CrossRef]
- Belo-Filho, M.A.F.; Amorim, P.; Almada-Lobo, B. An adaptive large neighbourhood search for the operational integrated production and distribution problem of perishable products. Int. J. Prod. Res. 2015, 53, 1–19. [Google Scholar] [CrossRef]
- Devapriya, P.; Ferrell, W.; Geismar, N. Integrated Production and Distribution Scheduling with a Perishable Product. Eur. J. Oper. Res. 2017, 259, 906–916. [Google Scholar] [CrossRef]
- Lacomme, P.; Moukrim, A.; Quilliot, A.; Vinot, M. Supply chain optimisation with both production and transportation integration: Multiple vehicles for a single perishable product. Int. J. Prod. Res. 2018, 56, 4313–4336. [Google Scholar] [CrossRef]
- Chen, Z.L. Integrated production and outbound distribution scheduling: Review and extensions. Oper. Res. 2010, 58, 130–148. [Google Scholar] [CrossRef]
- Zou, X.; Liu, L.; Li, K.; Li, W. A coordinated algorithm for integrated production scheduling and vehicle routing problem. Int. J. Prod. Res. 2018, 56, 5005–5024. [Google Scholar] [CrossRef]
- Yan, C.; Banerjee, A.; Yang, L. An integrated production–distribution model for a deteriorating inventory item. Int. J. Prod. Econ. 2011, 133, 228–232. [Google Scholar] [CrossRef]
- Garcia, J.M.; Lozano, S.; Canca, D. Coordinated scheduling of production and delivery from multiple plants. Robot. Comput. Integr. Manuf. 2004, 20, 191–198. [Google Scholar] [CrossRef]
- Garcia, J.M.; Lozano, S. Production and delivery scheduling problem with time windows. Comput. Ind. Eng. 2005, 48, 733–742. [Google Scholar] [CrossRef]
- Asbach, L.; Dorndorf, U.; Pesch, E. Analysis, modeling and solution of the concrete delivery problem. Eur. J. Oper. Res. 2009, 193, 820–835. [Google Scholar] [CrossRef]
- Schmid, V.; Doerner, K.F.; Hartl, R.F.; Stoecher, S.W. A hybrid solution approach for ready-mixed concrete delivery. Transp. Sci. 2009, 43, 70–85. [Google Scholar] [CrossRef][Green Version]
- Schmid, V.; Doerner, K.F.; Hartl, R.F.; Salazar-González, J.J. Hybridization of very large neighborhood search for ready-mixed concrete delivery problems. Comput. Oper. Res. 2010, 37, 559–574. [Google Scholar] [CrossRef]
- Huo, Y.; Leung, Y.T.; Wang, X. Integrated production and delivery scheduling with disjoint windows. Discret. Appl. Math. 2009, 158, 921–931. [Google Scholar] [CrossRef][Green Version]
- Geismar, H.N.; Dawande, M.; Sriskandarajah, C. Pool-point distribution of zero-inventory products. Prod. Oper. Manag. 2011, 20, 737–753. [Google Scholar] [CrossRef]
- Amorim, P.; Günther, H.O.; Almada-Lobo, B. Multi-objective integrated production and distribution planning of perishable products. Int. J. Prod. Econ. 2012, 138, 89–101. [Google Scholar] [CrossRef]
- Farahani, P.; Grunow, M.; Günther, H.-O. Integrated production and distribution planning for perishable food products. Flex. Serv. Manuf. J. 2012, 24, 28–51. [Google Scholar] [CrossRef]
- Kopanos, G.M.; Puigjaner, L.; Georgiadis, M.C. Simultaneous production and logistics operations planning in semicontinuous food industries. Omega 2012, 40, 634–650. [Google Scholar] [CrossRef]
- Lee, J.; Kim, B.I.; Johnson, A.L.; Lee, K. The nuclear medicine production and delivery problem. Eur. J. Oper. Res. 2014, 236, 461–472. [Google Scholar] [CrossRef]
- Geismar, H.N.; Murthy, N.M. Balancing Production and Distribution in Paper Manufacturing. Prod. Oper. Manag. 2015, 24, 1164–1178. [Google Scholar] [CrossRef]
- Kergosien, Y.; Gendreau, M.; Billaut, J.C. A Benders decomposition-based heuristic for a production and outbound distribution scheduling problem with strict delivery constraints. Eur. J. Oper. Res. 2017, 262, 287–298. [Google Scholar] [CrossRef]
- Neves-Moreira, F.; Almada-Lobo, B.; Cordeau, J.F.; Guimarães, L. Solving a large multi-product production-Routing problem with delivery time windows. Omega 2019, 86, 154–172. [Google Scholar] [CrossRef]
- Gharaei, A.; Jolai, F. A Pareto approach for the multi-factory supply chain scheduling and distribution problem. Oper. Res. 2019, 1–32. [Google Scholar] [CrossRef]
- Sawik, B.; Faulin, J.; Pérez-Bernabeu, E. Multi-Criteria Optimization for Fleet Size with Environmental Aspects. Transp. Res. Procedia 2017, 27, 61–68. [Google Scholar] [CrossRef]
- Kizys, R.; Juan, A.A.; Sawik, B.; Calvet, L. A Biased-Randomized Iterated Local Search Algorithm for Rich Portfolio Optimization. Appl. Sci. 2019, 9, 3509. [Google Scholar] [CrossRef]
- Jiang, T.H. Cat swarm optimization for solving flexible job shop scheduling problem. Computer Engineering and Applications. Comput. Eng. Appl. 2018, 54, 259–270. [Google Scholar]
- Rossi, F.L.; Nagano, M.S. Heuristics for the mixed no-idle flowshop with sequence-dependent setup times. J. Oper. Res. Soc. 2019, 1–27. [Google Scholar] [CrossRef]
- Caceres-Cruz, J.; Arias, O.; Guimarans, D.; Riera, D.; Angel, A.J. Rich vehicle routing problem: Survey. ACM Comput. Surv. 2015, 42, 1–28. [Google Scholar] [CrossRef]
- Liu, L.; Li, K.; Liu, Z. A capacitated vehicle routing problem with order available time in e-commerce industry. Eng. Optim. 2017, 49, 449–465. [Google Scholar] [CrossRef]
- Salehipour, A.; Sörensen, K.; Goos, P.; Bräysy, O. Efficient GRASP+VND and GRASP+VNS metaheuristics for the traveling repairman problem. 4OR 2011, 9, 189–209. [Google Scholar] [CrossRef]
- Liu, L.; Li, W.L.; Li, K.P.; Zou, X.X. A coordinated production and transportation scheduling problem with minimum sum of order delivery times. J. Heuristics 2019, 1–26. [Google Scholar] [CrossRef]
- Ribeiro, G.M.; Laporte, G. An adaptive large neighborhood search heuristic for the cumulative capacitated vehicle routing problem. Comput. Oper. Res. 2012, 39, 728–735. [Google Scholar] [CrossRef]
- Smith, S.L.; Imeson, F. Glns: An effective large neighborhood search heuristic for the generalized traveling salesman problem. Comput. Oper. Res. 2017, 87, 1–19. [Google Scholar] [CrossRef]
- Grimault, A.; Bostel, N.; Lehuédé, F. An adaptive large neighborhood search for the full truckload pickup and delivery problem with resource synchronization. Comput. Oper. Res. 2017, 88, 1–14. [Google Scholar] [CrossRef]
- Rifai, A.P.; Nguyen, H.T.; Dawal, S.Z.M. Multi-objective adaptive large neighborhood search for distributed reentrant permutation flow shop scheduling. Appl. Soft Comput. 2016, 40, 42–57. [Google Scholar] [CrossRef]
- He, L.; de Weerdt, M.; Yorke-Smith, N. Time/sequence-dependent scheduling: The design and evaluation of a general purpose tabu-based adaptive large neighbourhood search algorithm. J. Intell. Manuf. 2019, 1–28. [Google Scholar] [CrossRef]
- Eskandarpour, M.; Dejax, P.; Péton, O. A large neighborhood search heuristic for supply chain network design. Comput. Oper. Res. 2017, 80, 23–37. [Google Scholar] [CrossRef]
- He, L.; Liu, X.L.; Laporte, G.; Chen, Y.W.; Chen, Y.G. An improved adaptive large neighborhood search algorithm for multiple agile satellites scheduling. Comput. Oper. Res. 2018, 100, 12–25. [Google Scholar] [CrossRef]
- Haddadi, S.; Cheraitia, M. Iterated local and very-large-scale neighborhood search for a novel uncapacitated exam scheduling model. Int. J. Manag. Sci. Eng. Manag. 2018, 13, 286–294. [Google Scholar] [CrossRef]
- Clarke, G.; Wright, J.W. Scheduling of vehicles from a central depot to a number of delivery points. Oper. Res. 1964, 12, 568–581. [Google Scholar] [CrossRef]
- Ropke, S.; Pisinger, D. A unified heuristic for a large class of vehicle routing problems with backhauls. Eur. J. Oper. Res. 2006, 171, 750–775. [Google Scholar] [CrossRef]
- Kurz, M.E.; Askin, R.G. Heuristic scheduling of parallel machines with sequence-dependent set-up times. Int. J. Prod. Res. 2001, 39, 23. [Google Scholar] [CrossRef]
- Hemmelmayr, V.C. Sequential and parallel large neighborhood search algorithms for the periodic location routing problem. Eur. J. Oper. Res. 2015, 243, 52–60. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).