One Parameter Optimal Derivative-Free Family to Find the Multiple Roots of Algebraic Nonlinear Equations

Abstract

In this study, we construct the one parameter optimal derivative-free iterative family to find the multiple roots of an algebraic nonlinear function. Many researchers developed the higher order iterative techniques by the use of the new function evaluation or the first-order or second-order derivative of functions to evaluate the multiple roots of a nonlinear equation. However, the evaluation of the derivative at each iteration is a cumbersome task. With this motivation, we design the second-order family without the utilization of the derivative of a function and without the evaluation of the new function. The proposed family is optimal as it satisfies the convergence order of Kung and Traub’s conjecture. Here, we use one parameter a for the construction of the scheme, and for $a=1$, the modified Traub method is its a special case. The order of convergence is analyzed by Taylor’s series expansion. Further, the efficiency of the suggested family is explored with some numerical tests. The obtained results are found to be more efficient than earlier schemes. Moreover, the basin of attraction of the proposed and earlier schemes is also analyzed.

1. Introduction

One of the challenging tasks of the scientific and engineering field is to solve nonlinear equations. Many problems like the design of electric circuits, the parachutist problem, and the ideal gas law [1] are formulated in the form of nonlinear equations. Due to their significance, sometimes, it is difficult to solve scalar equations with the help of analytical methods. This leads to the development of modern numerical methods. Many scholars [2,3,4,5,6,7,8,9,10] constructed higher order iterative techniques to solve nonlinear equations. Here, we concentrate on the multiple root finding of a function $g:\mathbb{D}\subset \mathbb{R}\to \mathbb{R}$ such that $g\left(x_r\right)=g^{\prime }\left(x_r\right)=g^{″}\left(x_r\right)=g^{″}\left(x_r\right)=\cdots =0$ and $g^m\left(x_r\right)\ne 0$, where $x_r$ is the exact root of function g with multiplicity m.

One of the relevant and basic methods to find the multiple root of a function is the modified Newton’s method ($MNM$) [11] defined as:

$$x_{k+1}=x_k-m\frac{g\left(x_k\right)}{g^{\prime }\left(x_k\right)},k=0,1,2,\cdots .$$

(1)

where m is the multiplicity of root $x_r$ and $g^{\prime }\left(x_k\right)$ is the first derivative of function g. The convergence order of $MNM$ is quadratic if the multiplicity is known. Another important iterative technique to find multiple roots of nonlinear equations is the Schröder method [12] defined as:

$$x_{k+1}=x_k-\frac{g^{\prime }\left(x_k\right)g\left(x_k\right)}{{\left(g^{\prime }\left(x_k\right)\right)}^2-g\left(x_k\right)g^{″}\left(x_k\right)},k=0,1,2,\cdots .$$

(2)

For this scheme, the multiplicity of the root is not required in advance, but it involves the first-order and second-order derivative of a function at each step. Many more researchers [13,14,15,16,17,18,19,20,21,22] developed the higher order iterative schemes involving the first-order derivative to find the multiple roots of a scalar equation. The evaluation of derivatives at each step is time consuming and sometimes a difficult job for any complex problem. Therefore, some authors [23,24,25,26] introduced the derivative-free iterative techniques to find the multiple roots of an equation using second-order the modified Traub–Steffensen method ($TM$) [12], which is defined as:

$$\begin{array}{cc}\hfill w_k& =x_k+\beta g\left(x_k\right),\hfill \\ \hfill x_{k+1}& =x_k-m\frac{g\left(x_k\right)}{g[w_k,x_k]},\beta \in \mathbb{R}-\left\{0\right\},k=0,1,2,\cdots ,\hfill \end{array}$$

(3)

where $g[w_k,x_k]=\frac{g\left(w_k\right)-g\left(x_k\right)}{w_k-x_k}.$ The order of convergence of the modified Traub–Steffensen method is maintained without the evaluation of any derivative.

Very recently, Kumar et al. [26] developed the optimal second-order scheme represented as:

$$x_{k+1}=x_k-G\left(\theta \right),k=0,1,2,\cdots .$$

(4)

where $G\left(\theta \right):\mathbb{D}\subset \mathbb{C}\to \mathbb{C}$ is a weight function and $\theta =\frac{g\left(x_k\right)}{g[w_k,x_k]}$. On the other hand, the construction of iterative methods with less function evaluation plays a key role. For this, the optimal methods are introduced that satisfy the Kung–Traub conjecture [27], meaning the order of convergence is $2^{n-1}$ where n represents the number of function evaluations per iteration. Motivated by this, we suggest a second- order optimal derivative-free iterative family. The salient features of the proposed family are its simple body structure, no new evaluation of the function, consisting of one parameter, and without the computation of the derivative. The proposed work is introduced as follows. Section 2 elaborates on the construction and convergence analysis of the proposed family. The numerical performance of the suggested family is shown in Section 3. The basin of attraction of the suggested methods and the methods available in the literature are exhibited in Section 4. Finally, conclusions are made in Section 5.

2. Construction of the Second-Order Scheme

Here, we construct an optimal second-order family of the iterative method for multiple zeros $m\ge 2$, which is defined by:

$$\begin{array}{cc}\hfill w_k& =x_k+\beta g\left(x_k\right),\hfill \\ \hfill x_{k+1}& =x_k-m\frac{(1-a)g\left(w_k\right)+ag\left(x_k\right)}{g[w_k,x_k]},k=0,1,2,\cdots a\in \mathbb{R}.\hfill \end{array}$$

(5)

For $a=1$, the modified Traub method is special case of the scheme (5).

Convergence Analysis

Using the following Lemmas 1 and 2 and Theorem 1, we illustrate that the constructed family (5) attains the maximum second-order of convergence for all $a\in \mathbb{R}$ without evaluating any extra evaluation of the function or its derivative.

Lemma 1.

Suppose $x_r$ is a solution of multiplicity $m=2$ of the function g. Consider that a function $g:\mathbb{D}\subset \mathbb{C}\to \mathbb{C}$ is analytic in $\mathbb{D}$ surrounding the required zero $x_r$. Then, the proposed scheme (5) has second-order convergence with the following error equation:

$$\begin{array}{cc}\hfill e_{k+1}=& \frac{1}{4}\left(2C_1+(3-4a)\beta g^2\right)e_k^2+\frac{1}{16}\left(-{\beta }^2{g}^4-12C_1^2+16C_2+8\beta (1-2a)C_1{g}^2\right)e_k^3+O\left(e_k^4\right).\hfill \end{array}$$

where $C_i=\frac{2!}{(2+i)!}\frac{g^{(2+i)}\left(x_r\right)}{g^{\left(2\right)}\left(x_r\right)},i=1,2,\dots$.

Proof. 

Let $e_k=x_k-x_r$ be the error in the kth iteration. We use Taylor’s series expansions for function $g\left(x_k\right)$ around $x=x_r$ with the assumption $g\left(x_r\right)=g^{\prime }\left(x_r\right)=0$ and $g^{″}\left(x_r\right)\ne 0$, which are given by:

$$g\left(x_k\right)=\frac{g^{{}^{″}}\left(x_r\right)}{2!}{e}_k^2\left(1+C_1{e}_k+C_2{e}_k^2+C_3{e}_k^3+C_4{e}_k^4+O\left(e_k^5\right)\right).$$

(6)

Set $e_w=w_k-x_r$, and take the Taylor series of a function g about the point $w_k$. We have:

$$g\left(w_k\right)=\frac{1}{2!}{g}^2{e}_k^2+\frac{1}{2!}\left(C_1{g}^2-\beta g^4\right)e_k^3+\frac{1}{8}\left({\beta }^2{g}^6-10\beta C_1{g}^4+4C_2{g}^2\right)e_k^4+O\left(e_k^5\right).$$

(7)

Now,

$$\begin{array}{cc}\hfill g[w_k,x_k]& =\frac{g\left(w_k\right)-g\left(x_k\right)}{w_k-x_k},\hfill \\ \hfill & =g^2{e}_k-\frac{1}{4}\left(g^2\left(\beta g^2-6C_1\right)\right)e_k^2-g^2\left(\beta C_1{g}^2-2C_2\right)e_k^3+O\left(e_k^4\right).\hfill \end{array}$$

(8)

Substitute the values of Equations (6)–(8) into the scheme (5). One obtains the following error equation:

$$\begin{array}{cc}\hfill x_{k+1}-x_r& =x_k-x_r-m\frac{(1-a)g\left(w_k\right)+ag\left(x_k\right)}{g[w_k,x_k]},\hfill \\ \hfill e_{k+1}& =e_k-m\frac{(1-a)g\left(w_k\right)+ag\left(x_k\right)}{g[w_k,x_k]},\hfill \\ \hfill & =\frac{1}{4}\left(2C_1+(3-4a)\beta g^2\right)e_k^2+\hfill \\ \hfill & \frac{1}{16}\left(-{\beta }^2{g}^4-12C_1^2+16C_2+8\beta (1-2a)C_1{g}^2\right)e_k^3+O\left(e_k^4\right).\hfill \end{array}$$

(9)

Hence, the scheme (5) has second-order convergence for $m=2$. □

Lemma 2.

Assuming the same hypotheses of Lemma 1, the scheme given by (5) is of second-order convergence for $m=3$. It satisfies the following error equation:

$$e_{k+1}=\frac{1}{3}\left(b_1\right)e_k^2+\frac{1}{18}\left(-8b_1^2+12b_2+(6-9a)\beta g^3\right)e_k^3+O\left(e_k^4\right).$$

Proof. 

Let $e_k=x_k-x_r$ be the error in the kth iteration. We use the Taylor series expansions for function $g\left(x_k\right)$ around $x=x_r$ with the assumption $g\left(x_r\right)=g^{\prime }\left(x_r\right)=g^{″}\left(x_r\right)=0$ and $g^{‴}\left(x_r\right)\ne 0$, which are given by:

$$g\left(x_k\right)=\frac{g^{{}^{‴}}\left(x_r\right)}{3!}{e}_k^2\left(1+b_1{e}_k+b_2{e}_k^2+b_3{e}_k^3+b_4{e}_k^4+O\left(e_k^5\right)\right),$$

(10)

where $b_i=\frac{3!}{(3+i)!}\frac{g^{(3+i)}\left(x_r\right)}{g^{\left(3\right)}\left(x_r\right)},i=1,2,\dots$.

Set $e_w=w_k-x_r$, and take the Taylor series of a function g about the point $w_k$. We have:

$$g\left(w_k\right)=\frac{1}{3!}{g}^3{e}_k^3+\frac{1}{3!}{b}_1{g}^3{e}_k^4+O\left(e_k^5\right).$$

(11)

Now,

$$\begin{array}{cc}\hfill g[w_k,x_k]& =\frac{g\left(w_k\right)-g\left(x_k\right)}{w_k-x_k},\hfill \\ \hfill & =\frac{1}{2!}{g}^3{e}_k^2+\frac{4}{3!}{b}_1{g}^3{e}_k^3+\left(\frac{5b_2{g}^3}{6}-\frac{\beta g^6}{12}\right)e_k^4+O\left(e_k^5\right).\hfill \end{array}$$

(12)

Substitute the values of Equations (10)–(12) into the scheme (5). One obtains the following error equation:

$$\begin{array}{cc}\hfill x_{k+1}-x_r& =x_k-x_r-m\frac{(1-a)g\left(w_k\right)+ag\left(x_k\right)}{g[w_k,x_k]},\hfill \\ \hfill e_{k+1}& =e_k-m\frac{(1-a)g\left(w_k\right)+ag\left(x_k\right)}{g[w_k,x_k]},\hfill \\ \hfill & =\frac{1}{3}\left(b_1\right)e_k^2+\frac{1}{18}\left(-8b_1^2+12b_2+(6-9a)\beta g^3\right)e_k^3+O\left(e_k^4\right).\hfill \end{array}$$

(13)

Hence, the scheme (5) has second-order convergence for $m=3$. □

Theorem 1. 

Assuming the same hypotheses of Lemma 1, the scheme given by (5) is of second-order convergence for $m\ge 3$. It converges to the following error equation:

$$e_{k+1}=\frac{1}{m}\left(C_1\right)e_k^2+O\left(e_k^3\right).$$

Proof. 

Let $e_k=x_k-x_r$ be the error in the kth iteration. We use the Taylor series expansions for function $g\left(x_k\right)$ around $x=x_r$ with the assumption $g\left(x_r\right)=g^{\prime }\left(x_r\right)=g^{″}\left(x_r\right)=g^{″}\left(x_r\right)=\cdots =0$ and $g^m\left(x_r\right)\ne 0$, which are given by:

$$g\left(x_k\right)=\frac{g^m\left(x_r\right)}{m!}{e}_k^2\left(1+C_1{e}_k+C_2{e}_k^2+C_3{e}_k^3+C_4{e}_k^4+O\left(e_k^5\right)\right),$$

(14)

where $C_i=\frac{m!}{(m+i)!}\frac{g^{(m+i)}\left(x_r\right)}{g^{\left(m\right)}\left(x_r\right)},i=1,2,\dots$.

Set $e_w=w_k-x_r$, and take the Taylor series of a function g about the point $w_k$. We have:

$$g\left(w_k\right)=\frac{1}{m!}{g}^m{e}_k^m+\frac{1}{m!}{C}_1{g}^m{e}_k^{m+1}+O\left(e_k^{m+2}\right).$$

(15)

Now,

$$\begin{array}{cc}\hfill g[w_k,x_k]& =\frac{g\left(w_k\right)-g\left(x_k\right)}{w_k-x_k},\hfill \\ \hfill & =\frac{1}{(m-1)!}{g}^m{e}_k^{m-1}+\frac{m+1}{m!}{C}_1{g}^m{e}_k^m+O\left(e_k^{m+1}\right).\hfill \end{array}$$

(16)

Substitute the values of Equations (10)–(12) into the scheme (5). One obtains the following error equation:

$$\begin{array}{cc}\hfill x_{k+1}-x_r& =x_k-x_r-m\frac{(1-a)g\left(w_k\right)+ag\left(x_k\right)}{g[w_k,x_k]},\hfill \\ \hfill e_{k+1}& =e_k-m\frac{(1-a)g\left(w_k\right)+ag\left(x_k\right)}{g[w_k,x_k]},\hfill \\ \hfill & =\frac{1}{m}\left(C_1\right)e_k^2+O\left(e_k^3\right).\hfill \end{array}$$

(17)

Hence, the scheme (5) has second-order convergence with multiplicity $m\ge 3$. □

3. Numerical Illustration

In this section, the derivative-free proposed schemes (5) for different values of parameter a are verified on some numerical problems. Here, we take $a=\frac{6}{7},\frac{2}{3},\frac{3}{4},$ and $\frac{5}{6}$ and denote the proposed methods as $P{M}_1,P{M}_2,P{M}_3,$ and $P{M}_4$ respectively. The results are compared with other existing methods, the modified Traub method [12] and the Kumar method [26], as shown below.

The modified Traub method is presented as $TM$:

$$\begin{array}{cc}\hfill w_k& =x_k-\beta g\left(x_k\right),\hfill \\ \hfill x_{k+1}& =x_k-m\frac{g\left(x_k\right)}{g[w_k,x_k]}.\hfill \end{array}$$

(18)

The Kumar methods:

$$\begin{array}{cc}\hfill \theta & =\frac{g\left(x_k\right)}{g[w_k,x_k]},\hfill \\ \hfill x_{k+1}& =x_k-G\left(\theta \right).\hfill \end{array}$$

(19)

The function $G\left(\theta \right)$ can be found in the Table 1.

Table 1. The Kumar methods.

Method Representation	$\mathit{G}\left(\mathit{\theta }\right)$
$D{M}_1$	$m\theta (1+\frac{1}{10}\theta )$
$D{M}_2$	$\frac{m\theta }{1+\frac{1}{4}\theta }$
$D{M}_3$	$\frac{m\theta }{1+m\frac{1}{10}\theta }$
$D{M}_4$	$m{e}^{\theta }-1$
$D{M}_5$	$mlog(\theta +1)$
$D{M}_6$	$\frac{\theta }{{\left(\sqrt{(}\frac{1}{m})+\frac{1}{10}\theta \right)}^2}$
$D{M}_7$	$\frac{{\theta }^2+\theta }{\frac{1}{m}+\frac{1}{5}\theta }$

In all numerical problems, the parameter $\beta =-0.01$ is considered. The numerical problems were performed with Mathematica 10 using 1000 multiple precision digits of the mantissa with stopping criterion $|x_k-x_{k-1}|+|g\left(x_k\right)|<=100$. To check the better performance of the proposed method, we display the error between two consecutive iterations $e_k=|x_{k+1}-x_k|$, functional error $\left|g\right(x_k\left)\right|$ at the $\left(k\right)$th iteration, and the approximate computational order of convergence (ACOC) denoted as $\rho$ in Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7. The following formula is used to evaluate the ACOC:

$$\rho =\frac{ln\frac{|x_{k+1}-x_k|}{|x_k-x_{k-1}|}}{ln\frac{|x_k-x_{k-1}|}{|x_{k-1}-x_{k-2}|}},\mathrm{for} \mathrm{each} k=2,3,\dots$$

(20)

Table 2. Numerical results of Example 1.

Schemes	$|{\mathit{x}}_5-{\mathit{x}}_4|$	$|{\mathit{x}}_6-{\mathit{x}}_5|$	$|{\mathit{x}}_7-{\mathit{x}}_6|$	$\left|\mathit{g}\right({\mathit{x}}_7\left)\right|$	$\mathit{\rho }$
$TM$	$1.9(-8)$	$6.2(-15)$	$6.3(-28)$	$1.4(-108)$	$2.000$
$D{M}_1$	$1.8(-8)$	$5.4(-15)$	$4.9(-28)$	$4.8(-109)$	$2.000$
$D{M}_2$	$2.2(-8)$	$8.4(-15)$	$1.2(-27)$	$1.7(-107)$	$2.000$
$D{M}_3$	$2.2(-8)$	$7.9(-15)$	$1.1(-27)$	$1.0(-107)$	$2.000$
$D{M}_4$	$1.4(-8)$	$3.2(-15)$	$1.7(-28)$	$7.3(-111)$	$2.000$
$D{M}_5$	$2.6(-8)$	$1.1(-14)$	$2.2(-27)$	$2.1(-106)$	$2.000$
$D{M}_6$	$2.3(-8)$	$8.8(-15)$	$1.3(-27)$	$2.4(-107)$	$2.000$
$D{M}_7$	$1.3(-8)$	$2.9(-15)$	$1.3(-28)$	$2.7(-111)$	$2.000$
$P{M}_1$	$1.9(-8)$	$6.2(-15)$	$6.3(-28)$	$1.4(-108)$	$2.000$
$P{M}_2$	$1.9(-8)$	$6.2(-15)$	$6.3(-28)$	$1.4(-108)$	$2.000$
$P{M}_3$	$1.9(-8)$	$6.2(-15)$	$6.3(-28)$	$1.4(-108)$	$2.000$
$P{M}_4$	$1.9(-8)$	$6.2(-15)$	$6.3(-28)$	$1.4(-108)$	$2.000$

It is clear from the above table that our proposed methods are equally competent as the existing ones.

Table 3. Numerical results of Example 2.

Schemes	$|{\mathit{x}}_5-{\mathit{x}}_4|$	$|{\mathit{x}}_6-{\mathit{x}}_5|$	$|{\mathit{x}}_7-{\mathit{x}}_6|$	$\left|\mathit{g}\right({\mathit{x}}_7\left)\right|$	$\mathit{\rho }$
$TM$	$6.0(-10)$	$3.3(-26)$	$1.0(-40)$	$5.5(-242)$	$2.000$
$D{M}_1$	$6.7(-10)$	$5.7(-20)$	$4.2(-40)$	$5.9(-238)$	$2.000$
$D{M}_2$	$4.5(-11)$	$2.0(-23)$	$4.1(-48)$	$2.8(-289)$	$2.000$
$D{M}_3$	$1.3(-10)$	$1.1(-22)$	$8.1(-47)$	$4.3(-282)$	$2.000$
$D{M}_4$	$1.1(-13)$	$2.9(-27)$	$2.2(-54)$	$1.1(-322)$	$2.000$
$D{M}_5$	$2.9(-8)$	$6.1(-17)$	$2.7(-34)$	$8.5(-204)$	$2.000$
$D{M}_6$	$1.2(-9)$	$3.0(-20)$	$2.0(-41)$	$4.1(-248)$	$2.000$
$D{M}_7$	$3.4(-11)$	$2.6(-22)$	$1.5(-44)$	$7.4(-264)$	$2.000$
$P{M}_1$	$8.4(-17)$	$6.7(-34)$	$4.1(-68)$	$2.2(-406)$	$2.000$
$P{M}_2$	$1.5(-21)$	$2.0(-43)$	$3.7(-87)$	$1.2(-520)$	$2.000$
$P{M}_3$	$8.8(-16)$	$7.2(-32)$	$4.8(-64)$	$5.5(-382)$	$2.000$
$P{M}_4$	$1.2(-16)$	$1.2(-33)$	$1.4(-67)$	$3.9(-403)$	$2.000$

From the above numerical results, we conclude that our proposed method $P{M}_2$ is faster among all the above-mentioned schemes because it has the lowest residual error.

Table 4. Numerical results of Example 3.

Schemes	$|{\mathit{x}}_5-{\mathit{x}}_4|$	$|{\mathit{x}}_6-{\mathit{x}}_5|$	$|{\mathit{x}}_7-{\mathit{x}}_6|$	$\left|\mathit{g}\right({\mathit{x}}_7\left)\right|$	$\mathit{\rho }$
$TM$	$6.0(-13)$	$8.5(-26)$	$1.7(-51)$	$1.8(-407)$	$2.000$
$D{M}_1$	$5.1(-13)$	$6.9(-26)$	$1.2(-51)$	$2.3(-408)$	$2.000$
$D{M}_2$	$5.2(-13)$	$4.7(-26)$	$3.8(-52)$	$3.5(-413)$	$2.000$
$D{M}_3$	$3.2(-13)$	$1.4(-26)$	$2.6(-53)$	$6.8(-423)$	$2.000$
$D{M}_4$	$8.4(-14)$	$2.5(-27)$	$2.3(-54)$	$1.2(-429)$	$2.000$
$D{M}_5$	$2.0(-13)$	$4.6(-27)$	$2.4(-54)$	$1.6(-431)$	$2.000$
$D{M}_6$	$3.0(-13)$	$1.3(-26)$	$2.2(-53)$	$1.5(-423)$	$2.000$
$D{M}_7$	$2.9(-13)$	$2.5(-26)$	$1.7(-52)$	$4.8(-415)$	$2.000$
$P{M}_1$	$8.3(-15)$	$1.6(-29)$	$6.5(-59)$	$7.7(-467)$	$2.000$
$P{M}_2$	$1.5(-22)$	$5.2(-45)$	$6.4(-90)$	$7.1(-715)$	$2.000$
$P{M}_3$	$2.7(-17)$	$1.8(-34)$	$7.3(-69)$	$2.0(-546)$	$2.000$
$P{M}_4$	$3.1(-15)$	$2.3(-30)$	$1.3(-60)$	$1.8(-480)$	$2.000$

Based on the above computational results, we find that our method $P{M}_2$ has the lowest residual error among all the other mentioned methods.

Table 5. Numerical results of Example 4.

Schemes	$|{\mathit{x}}_5-{\mathit{x}}_4|$	$|{\mathit{x}}_6-{\mathit{x}}_5|$	$|{\mathit{x}}_7-{\mathit{x}}_6|$	$\left|\mathit{g}\right({\mathit{x}}_7\left)\right|$	$\mathit{\rho }$
$TM$	$4.0(-15)$	$5.2(-30)$	$9.1(-60)$	$1.8(-473)$	$2.000$
$D{M}_1$	$4.6(-15)$	$7.1(-30)$	$1.7(-59)$	$2.3(-471)$	$2.000$
$D{M}_2$	$8.4(-15)$	$2.4(-29)$	$2.0(-58)$	$8.7(-463)$	$2.000$
$D{M}_3$	$2.3(-14)$	$1.8(-28)$	$1.1(-56)$	$9.1(-449)$	$2.000$
$D{M}_4$	$5.4(-14)$	$1.1(-27)$	$3.9(-55)$	$2.7(-436)$	$2.000$
$D{M}_5$	$4.3(-14)$	$6.7(-28)$	$1.6(-55)$	$2.0(-439)$	$2.000$
$D{M}_6$	$2.4(-14)$	$2.0(-28)$	$1.4(-56)$	$6.4(-448)$	$2.000$
$D{M}_7$	$9.3(-15)$	$2.9(-29)$	$2.9(-58)$	$1.9(-461)$	$2.000$
$P{M}_1$	$8.9(-17)$	$2.7(-33)$	$2.3(-66)$	$3.3(-526)$	$2.000$
$P{M}_2$	$6.0(-22)$	$1.2(-43)$	$4.9(-87)$	$1.2(-691)$	$2.000$
$P{M}_3$	$8.6(-19)$	$2.4(-37)$	$2.0(-74)$	$9.3(-591)$	$2.000$
$P{M}_4$	$3.9(-17)$	$5.0(-34)$	$8.3(-68)$	$8.6(-538)$	$2.000$

It is clear from the above table that our methods namely $P{M}_1,P{M}_2,P{M}_3$, and $P{M}_4$, perform far better than the existing methods in terms of the absolute difference between two consecutive iterations and absolute residual errors. Scheme $P{M}_2$ has the fastest convergence towards the required root among all the other mentioned methods.

Table 6. Numerical results of Example 5.

Schemes	$|{\mathit{x}}_5-{\mathit{x}}_4|$	$|{\mathit{x}}_6-{\mathit{x}}_5|$	$|{\mathit{x}}_7-{\mathit{x}}_6|$	$\left|\mathit{g}\right({\mathit{x}}_7\left)\right|$	$\mathit{\rho }$
$TM$	$9.9(-23)$	$1.3(-46)$	$2.3(-94)$	$9.8(-379)$	$2.000$
$D{M}_1$	$2.3(-20)$	$3.3(-41)$	$7.0(-83)$	$2.0(-331)$	$2.000$
$D{M}_2$	$6.5(-17)$	$4.7(-34)$	$2.5(-18)$	$9.8(-273)$	$2.000$
$D{M}_3$	$3.6(-18)$	$1.1(-36)$	$1.1(-73)$	$2.7(-294)$	$2.000$
$D{M}_4$	$6.7(-21)$	$1.2(-41)$	$3.7(-83)$	$2.7(-331)$	$2.000$
$D{M}_5$	$5.4(-13)$	$6.8(-26)$	$1.1(-51)$	$1.8(-205)$	$2.000$
$D{M}_6$	$3.0(-16)$	$1.2(-32)$	$1.7(-65)$	$3.0(-261)$	$2.000$
$D{M}_7$	$5.7(-16)$	$1.0(-31)$	$3.2(-63)$	$2.2(-251)$	$2.000$
$P{M}_1$	$4.4(-22)$	$3.7(-45)$	$2.6(-91)$	$3.7(-366)$	$2.000$
$P{M}_2$	$1.8(-21)$	$8.9(-44)$	$2.2(-88)$	$3.5(-354)$	$2.000$
$P{M}_3$	$1.0(-21)$	$2.5(-44)$	$1.5(-89)$	$6.2(-359)$	$2.000$
$P{M}_4$	$5.4(-22)$	$5.8(-45)$	$6.9(-91)$	$2.0(-364)$	$2.000$

Our methods perform better than the existing methods (except $TM$) in terms of the absolute difference between two consecutive iterations and the absolute residual errors. They are equally competent for the scheme $TM$.

Table 7. Numerical results of Example 6.

Schemes	$|{\mathit{x}}_5-{\mathit{x}}_4|$	$|{\mathit{x}}_6-{\mathit{x}}_5|$	$|{\mathit{x}}_7-{\mathit{x}}_6|$	$\left|\mathit{g}\right({\mathit{x}}_7\left)\right|$	$\mathit{\rho }$
$TM$	$2.2(-10)$	$1.4(-20)$	$5.6(-41)$	$2.5(-406)$	$2.000$
$D{M}_1$	$1.2(-9)$	$3.8(-19)$	$3.8(-38)$	$3.4(-378)$	$2.000$
$D{M}_2$	$2.4(-14)$	$1.9(-28)$	$1.3(-56)$	$1.7(-562)$	$2.000$
$D{M}_3$	$2.1(-13)$	$1.6(-26)$	$9.9(-53)$	$3.2(-523)$	$2.000$
$D{M}_4$	$2.8(-8)$	$1.4(-16)$	$3.5(-33)$	$2.2(-329)$	$2.000$
$D{M}_5$	$4.8(-14)$	$8.9(-28)$	$3.0(-55)$	$2.2(-548)$	$2.000$
$D{M}_6$	$1.8(-14)$	$1.2(-28)$	$5.1(-57)$	$3.4(-566)$	$2.000$
$D{M}_7$	$2.2(-10)$	$1.4(-20)$	$5.6(-41)$	$2.5(-406)$	$2.000$
$P{M}_1$	$3.7(-15)$	$3.9(-30)$	$4.2(-60)$	$1.4(-597)$	$2.000$
$P{M}_2$	$1.2(-11)$	$4.2(-23)$	$4.9(-46)$	$6.0(-457)$	$2.000$
$P{M}_3$	$1.1(-14)$	$3.3(-29)$	$3.0(-58)$	$4.1(-579)$	$2.000$
$P{M}_4$	$1.9(-17)$	$1.0(-34)$	$2.9(-69)$	$3.7(-689)$	$2.000$

It is clear from the above table that our methods namely, $P{M}_1,P{M}_2,P{M}_3$, and $P{M}_4$, perform far better than the existing methods in terms of the absolute difference between two consecutive iterations and absolute residual errors. Scheme $P{M}_4$ has the fastest convergence towards the required root among all the other mentioned methods.

Notice that the meaning of $b(\pm a)$ is $b\times {10}^{\pm a}$ in all the tables.

Example 1.

Consider the van der Waals equation of the ideal gas [1]:

$$(P+\frac{a{n}^2}{V^2})(V-nb)=nRT$$

which explains the nature of the real gas by taking the parameters $a,b$ of a particular gas. Other parameters $n,R,T$ are obtained with parameters $a,b$. Therefore, we have nonlinear equations in terms of the volume of gas (V), which is represented as x in the following equation:

$$g_1\left(x\right)=x^3-5.22x^2+9.0825x-5.2675.$$

The desired root is $x_r=1.75$ of multiplicity $m=2$. Table 2 depicts the performance of different schemes with initial guess $x_0=1.8$.

Example 2.

Here, we consider the following nonlinear function of multiplicity $m=3$:

$$g_2\left(x\right)={\left(x^2-e^x-3x+2\right)}^3.$$

The nonlinear equation is tested on the proposed methods and the methods introduced in [26] by taking the initial guess $x_0=1.2$. The proposed methods converge to the desired root $x_r=0.257530285439860\dots$, and the computational results are shown in Table 3.

Example 3.

Finding the eigenvalues of a large matrix whose order is greater than four, we need to solve its characteristic equation. The determination of the roots of such a higher order characteristic equation is a difficult task if we apply the linear algebra approach. Therefore, one of the best ways is to use the numerical techniques. Now, consider the following square matrix of order nine.

$$A=\frac{1}{8}\left(\begin{array}{ccccccccc}-12& 0& 0& 19& -19& 76& -19& 18& 437\\ -64& 24& 0& -24& 24& 64& -8& 32& 376\\ -16& 0& 24& 4& -4& 16& -4& 8& 92\\ -40& 0& 0& -10& 50& 40& 2& 20& 242\\ -4& 0& 0& -1& 41& 4& 1& 2& 25\\ -40& 0& 0& 18& -18& 104& -18& 20& 462\\ -84& 0& 0& -29& 29& 84& 21& 42& 501\\ 16& 0& 0& -4& 4& -16& 4& 16& -92\\ 0& 0& 0& 0& 0& 0& 0& 0& 24\end{array}\right),$$

whose characteristic equation is modeled as a nonlinear equation as:

$$g_3\left(x\right)=x^9-29x^8+349x^7-2261x^6+8455x^5-\mathrm{17,663}{x}^4+\mathrm{15,927}{x}^3+6993x^2-{\mathrm{24,732}}^x+\mathrm{12,960}.$$

The root of this equation is $x_r=3$ with multiplicity $m=4$. Table 4 depicts the better performance of the proposed scheme in comparison to existing techniques by taking initial guess $x_0=2.5$.

Example 4.

Consider another standard nonlinear equation as follows:

$$g_4\left(x\right)=x(x^2+1)(2e^{x^2+1}+x^2-1)cos{h}^2\left(\frac{\pi x}{2}\right),$$

which has root $x_r=i$ of multiplicity four. The results are obtained on initial guess $x_0=1.5i$ and shown in Table 5.

Example 5.

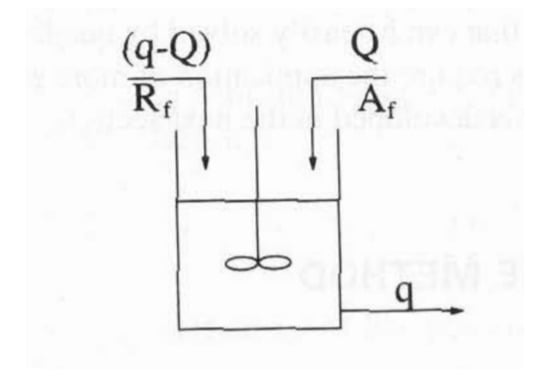
Finally, we consider the problem of a continuous stirred tank reactor [28] shown in the Figure 1.

Figure 1. Continuous stirred tank reactor.

Here, components A and R are fed to the reactor at rates of Q and $q-Q$, respectively. The reaction schemes developed in these reactors are:

$$\begin{array}{c}A+R\to B\\ B+R\to C\\ C+R\to D\\ D+R\to E\end{array}$$

Douglas [29] converted this problem into a mathematical expression:

$$K_c\frac{2.98(t+2.25)}{(t+1.45){(t+2.85)}^2(t+4.35)}=-1.$$

(21)

where $K_c$ is the gain of the proportional controller. This control system is stable for the values of $K_c$. If we take $K_c=0$, we obtain the poles of the open-loop transferred function as the solutions of the following uni-variate equation:

$$g_5\left(x\right)=x^4+11.50x^3+47.49x^2+83.06325x+51.23266875=0.$$

(22)

Clearly, function $g_5\left(x\right)$ has three roots $-1.45,-2.85$, and $-4.35$. One of the roots $-2.85$ has multiplicity $m=2$. The computational results are demonstrated in Table 6. It can be concluded that the results are better for the suggested methods in terms of less residual and functional error with the similar utilization of the number of iterations for the methods developed by Traub and Kumar.

Example 6.

Next, we consider the study of the multi-factor effect in which the trajectory of an electron in the air gap between two parallel plates [30] is defined as:

$$y\left(t\right)=y_0+(v_0+e\frac{E_0}{m_a\omega }sin(\omega t_0+\theta ))(t-t_0)+e\frac{E_0}{m_a{\omega }^2}\left(cos(\omega t+\theta )+sin(\omega t+\theta )\right),$$

(23)

$e,m_a,y_0,v_0$, and $E_{0}sin(\omega t+\theta )$ are the charge of the electron at rest, the mass of the electron at rest, the position and velocity of the electron at time $t_0$, and the RF electric field between the plates, respectively. By choosing particular values of these parameters, we have the following expression:

$$g_6\left(x\right)={\left(x-\frac{1}{2}cos\left(x\right)+\frac{\pi }{4}\right)}^5.$$

(24)

This problem has root $x_r=-0.30909\dots$ with multiplicity $m=5$. We tested the problem at initial guess $x_0=1.2$, and the results are shown in Table 7.

4. Basin of Attraction

In this section, we explored the convergence behavior of the proposed family and earlier developed techniques for finding multiple roots of a nonlinear equation in the complex plane with the basin of attraction. A basin of attraction is a significant tool that depicts the stability behavior of methods on the complex plane. It provides a wide range of initial guesses to find the roots of an equation, which leads to better understanding of the performance behavior of iterative techniques. Many researchers [31,32,33,34,35,36] have opted for the basin of attraction idea to check the effectiveness of the developed iterative techniques.

The function $R:\widehat{\mathbb{C}}\to \widehat{\mathbb{C}}$, where $\widehat{\mathbb{C}}$ is the Riemann sphere, the orbit of a point $z_0\in \widehat{\mathbb{C}}$, is defined by:

$$\{z_0,R\left(z_0\right),R^2\left(z_0\right),...,R^n\left(z_0\right),...\}.$$

A point $z_0\in \overline{\mathcal{C}}$ is called a fixed point of $R\left(z\right)$ if it verifies that $R\left(z\right)=z$. Moreover, $z_0$ is called a periodic point of period $p>1$ if it is a point such that $R^p\left(z_0\right)=z_0$, but $R^k\left(z_0\right)\ne z_0$, for each $k<p$. Moreover, a point $z_0$ is called pre-periodic if it is not periodic, but there exists a $k>0$ such that $R^k\left(z_0\right)$ is periodic.

There exist different types of fixed points depending on their associated multiplier $|R^{\prime }\left(z_0\right)|$. Taking the associated multiplier into account, a fixed point $z_0$ is called:

• a superattractor if $|R^{\prime }\left(z_0\right)|=0$
• an attractor if $|R^{\prime }\left(z_0\right)|<1$
• a repulsor if $|R^{\prime }\left(z_0\right)|>1$
• and parabolic if $|R^{\prime }\left(z_0\right)|=1$.

The fixed points that do not correspond to the roots of the polynomial $p\left(z\right)$ are called strange fixed points. On the other hand, a critical point $z_0$ is a point that satisfies that $R^{\prime }\left(z_0\right)=0$.

The basin of attraction of an attractor $\alpha$ is defined as:

$$\mathcal{A}\left(\alpha \right)=\{z_0\in \widehat{\mathbb{C}}:R^n\left(z_0\right)\to \alpha ,n\to \infty \}.$$

The Fatou set of the rational function R, $\mathcal{F}\left(R\right),$ is the set of points $z\in \widehat{\mathbb{C}}$ whose orbits tend to an attractor (fixed point, periodic orbit, or infinity). Its complement in $\widehat{\mathbb{C}}$ is the Julia set, $\mathcal{J}\left(R\right)$. That means that the basin of attraction of any fixed point belongs to the Fatou set, and the boundaries of these basins of attraction belong to the Julia set.

In this direction, we consider the nonlinear equation $p\left(z\right)$ in interval or boundary $[-3,3]$ with $300\times 300$ mesh points. Each mesh point is used as the initial value to analyze the convergence behavior for suggested methods $P{M}_1,P{M}_2,P{M}_3$, and $P{M}_4$ and for comparison methods $TM,D{M}_1,D{M}_2,D{M}_3,D{M}_4,D{M}_5,D{M}_6$, and $D{M}_7$, respectively. The different colors (red, green, yellow, ...) are considered to represent the roots of $p\left(z\right)$. Choosing one mesh point, if schemes converge to any root of the equation, then it is represented as colors like red, green, and yellow under a tolerance of less than ${10}^{-3}$ and a number of iterations less than 100. Otherwise, black color is assigned, which means that the mesh point does not converge to the required root. The following problems of multiple roots are studied.

Problem 1.

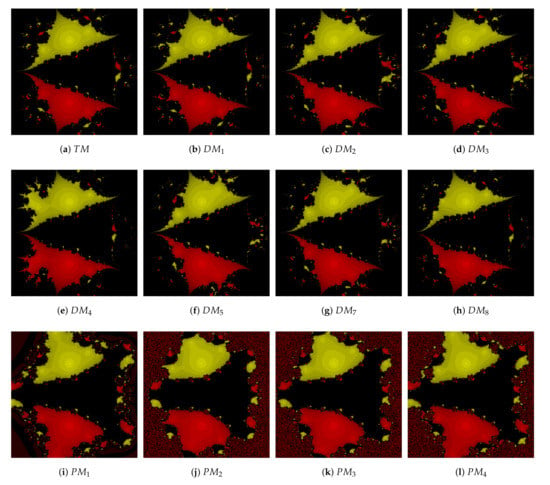
Consider the polynomial equation $p\left(z\right)={(z^2+2z-1)}^3$. The roots of this equation are $0.-1.61803I,0.+1.I,0.+0.618034I$ with multiplicity $m=3$. It is clear from Figure 2 that the suggested methods $P{M}_1,P{M}_2,P{M}_3$, and $P{M}_4$ have more convergence area as compared with methods $TM,D{M}_1,D{M}_2,D{M}_3,D{M}_4,D{M}_5,D{M}_6$, and $D{M}_7$, respectively.

Figure 2. Comparisons of the convergence plane at $\beta =-0.01$ for Problem 1.

Problem 2.

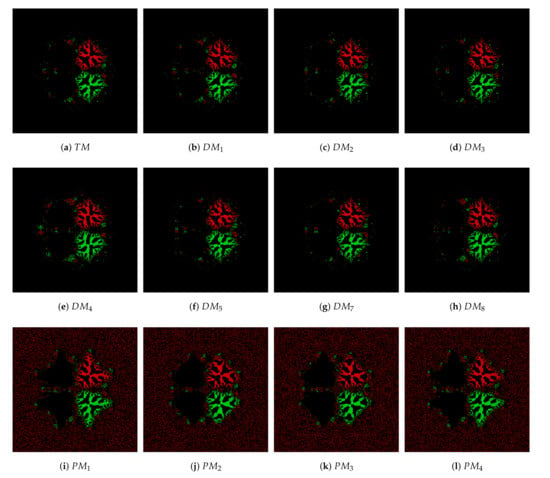
Here, we consider a non-polynomial $p\left(z\right)={(z^3+\frac{1}{z})}^m$ whose roots are $-0.707107+0.707107I,-0.707107-0.707107I,0.707107+0.707107I,0.707107-0.707107I$. The basins of Problem 2 are plotted with multiplicity $m=4$ and $m=3$ in Figure 3 and Figure 4, respectively. It is observed that suggested methods $P{M}_1,P{M}_2,P{M}_3$, and $P{M}_4$ converge to the root shown as red color, and the less divergence region is presented as the black region, whereas method $TM$ shows all divergence region in Figure 3. Similarly, methods $D{M}_1,D{M}_2,D{M}_3,D{M}_4,D{M}_5,D{M}_6$, and $D{M}_7$ do not converge at at least one point, so their graph is not shown here. Moreover, Figure 4 reveals that for multiplicity $m=3$, the proposed methods have more convergence points than the earlier methods.

Figure 3. Comparisons of the convergence plane at $\beta =-0.01$ for Problem 2 with $m=4$.

Figure 4. Comparisons of the convergence plane at $\beta =-0.01$ for Problem 2 with $m=3$.

Problem 3.

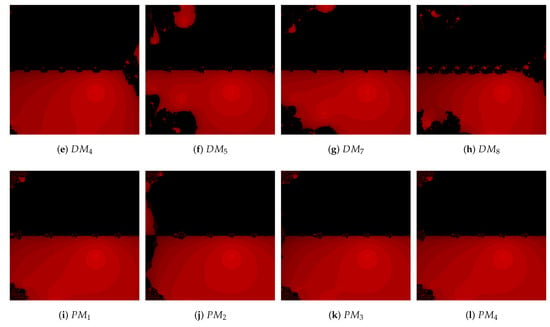
Lastly, we examine $p\left(z\right)={({(z-1)}^2+1)}^2$ with roots $1+I,1-I$, and multiplicity $m=2$. The basins of attraction for the proposed schemes demonstrate equally better convergence performance than the earlier methods in Figure 5.

Figure 5. Comparisons of the convergence plane at $\beta =-0.01$ for Problem 3.

5. Conclusions

The new second-order optimal derivative-free family for the root finding of nonlinear equations is suggested. On the basis of parameter a, some new optimal methods are generated. The well known modified Traub method is a special case for $a=1$. The convergence order is analyzed. Moreover, the efficiency of the proposed methods are verified by testing some numerical illustrations. The results are compared with the modified Traub method and other existing methods. Finally, the obtained results of the developed methods are better in the comparisons of the earlier developed schemes. The basin of attraction of the proposed schemes also shows better stability.