Semiparametric Semivariogram Modeling with a Scaling Criterion for Node Spacing: A Case Study of Solar Radiation Distribution in Thailand

Abstract

Geostatistical interpolation methods, sometimes referred to as kriging, have been proven effective and efficient for the estimation of target quantity at ungauged sites. The merit of the kriging approach relies heavily on the semivariograms in which the parametric functions are prevalently used. In this work, we explore the semiparametric semivariogram where no close-form semivariogram is required. By additionally enforcing the monotonicity condition in order to suppress the presence of spurious oscillation, a scaling of the nodes of the semiparametric kriging is proposed. To this end, the solar radiation estimates across extensive but unmeasured regions in Thailand using three different semivariogram models are undertaken. A cross validation analysis is carried out in order to justify the performance of each approach. The best results are achieved by the semiparametric model with an improvement of around 7–13% compared to those obtained from the parametric semivariograms.

1. Introduction

1.1. Motivation and Related Work

Spatial interpolation methods are essential tools for manipulating available but inadequate data to infill missing information. A wide spectrum of spatial interpolation approaches applied to several disciplines can be found in the literature [1,2,3]. Although most techniques are somewhat similar in the sense that estimations are calculated as the weighted average of known locations, they can be classified into two categories according to their mathematical underlying concepts; deterministic and stochastic methods. Prominent examples of deterministic approaches include spline functions [4], inverse distant weight [5], multiple linear regression [6]. Whilst those of stochastic-based methods which are usually regarded as kriging are ordinary kriging, universal kriging and regression kriging. Several studies attempted to compare between these two interpolation classes [7,8]. In general, it appears that if we take accuracy as a prime concern, kriging interpolation is a preferable option for reliable estimation. This stochastic-based process model has been applied to numerous types of climate variables including temperature [9], rainfall [10], soil properties [11] and solar radiation [12,13].

Kriging is a geostatistical method where an attribute value from each location is interpreted as a single realization of some random field [14,15]. Under this assumption, statistical properties such as unbiased estimator and minimum variance can be used for the estimation of the attribute at the non-observed locations. An estimate at an unknown location is a combination of trend and residual components. There have been various types of kriging approaches depending upon their treatment of both components. The trend, also called the drift term, presents a deterministic structure of the target variable which can be expressed in several ways; either simply an unknown constant or a function of explanatory variables. On the contrary, the residual term involves the weight determination which can be quantified via the semivariogram from input point data. It, therefore, becomes important to choose an appropriate model of semivariogram that correctly presents a spatial dependence structure of the data. The customary procedure is by initially constructing an empirical semivariogram and later imposing a prior assumption regarding semivariogram shape: for instance, exponential, Gaussian, and spherical models. The inferred kriging coefficients are subsequently found by means of any curve-fitting techniques where weighted least-squares method [16] and maximum likelihood estimation [17] are two commonly used. The effort has also been made in order to find other techniques to facilitate the identification of semivariogram parameters. This includes the utilization of heuristic optimization tools, particularly the genetic algorithm (GA). For example, Yeh et al. [18] applied factorial kriging along with GA for the groundwater monitoring network design. Zhang et al. [19] couples GA with ordinary kriging with the aim to minimize the objective function so that the optimal pole structure of switched reluctance motor can be gained.

Although the prescribed semivariogram is relatively convenient, one tends to employ a dissimilar parametric class of functions concerning semivariogram structures for different time and regions. Another complication of such a model is that if the empirical semivariogram cannot be described by any classes of parametric functions, this can ultimately lead to a severely biased prediction. The nonparametric semivariogram is an alternative approach introduced by Shapiro and Botha [20]. Based on the well known Bochner’s theorem [21,22], the spectral representation of any positive definite function can be adopted for covariance function leading to a nonparametric form of semivariogram. This method allows us to estimate the semivariogram flexibly because a fixed functional form of semivariogram needs not to be acquired. However, it is acknowledged that a choice of nodes should be carefully selected otherwise this can give rise to spurious oscillations. Gorsich and Genton [23,24] suggested that the nodes should be roots of the Bessel functions. The series expansion of the nonparametric covariogram estimator accordingly has a similar form to Fourier-Bessel expansion which ultimately guarantees covariogram estimator being positive thoroughly. Later, based on the nonparametric structure and some certain type of parametric models, Carmack et al. [25] developed a semiparametric estimator which is an extension of nonparametric semivariograms. This is principally done by introducing a tuning parameter $\alpha$ in the scaling of lag distance. Nevertheless, some theoretical properties, for example, monotonicity or concavity, were not under consideration in which can potentially cause a bias in the estimate.

1.2. Contribution

The objectives of this paper are outlined as follows:

• The node selection criterion in the semiparametric semivariogram is proposed in accordance with the enforced monotonicity constraint so that the estimator fulfills the additional theoretical properties as well as eliminate spurious fluctuation due to node misspecification.
• A performance of semiparametric semivariogram is conducted and compared with parametric models in the case of the estimation of the spatial distribution of the monthly average daily solar radiation in Thailand.
• The GA is employed as a means to automate the search for optimal parameter values via the objective function.

1.3. Article Structure

The rest of the paper is organized as follows. Section 2 provides a brief description of seimvariogram estimators, both parametric and nonparametric models, and corresponding ordinary kriging method. A mathematical framework for the semiparametric semivariogram and our proposed node selection criterion are presented in Section 3. In Section 4, a case study of Thailand’s solar radiation is adopted to illustrate and compare the performance of three distinct semivariograms. The conclusion and discussion are given in Section 5.

2. Theoretical Background

2.1. Ordinary Kriging

Due to insufficient information about the variable of interest, kriging exploits the probabilistic concept where the uncertainty should be introduced in the description of the target quantity. Suppose that $\{Z\left(\mathbf{s}\right):\mathbf{s}\in D\subset {\mathbb{R}}^d\}$ is a spatial random process where D is the spatial domain and $d\ge 1$. The random variable $Z\left(\mathbf{s}\right)$ can be writte as

$$Z\left(\mathbf{s}\right)=\mu \left(\mathbf{s}\right)+R\left(\mathbf{s}\right)$$

(1)

where $\mu \left(\mathbf{s}\right)$ is the trend component of $Z\left(\mathbf{s}\right)$, and $R\left(\mathbf{s}\right)$ is the residual component with zero mean and stationary covariance.

Let $\{Z\left({\mathbf{s}}_1\right),Z\left({\mathbf{s}}_2\right),\dots ,Z\left({\mathbf{s}}_n\right)\}$ be a collection of samples at locations ${\mathbf{s}}_1,{\mathbf{s}}_2,\dots ,{\mathbf{s}}_n$. The kriging estimate, $Z^{*}\left(\mathbf{s}\right)$, at any location $\mathbf{s}$ can be expressed as a linear combination of available n observations

$$Z^{*}\left(\mathbf{s}\right)=\sum _{i=1}^n{\lambda }_{i}Z\left({\mathbf{s}}_i\right),$$

(2)

where ${\lambda }_i$ indicates the kriging weight assigned to $Z\left({\mathbf{s}}_i\right)$. Particularly, the ordinary kriging assumes the random process to be intrinsically stationary. This leads to the expected difference of the samples being zero and the variance of the estimation can be formulated in terms of the semivariogram

$$Var[Z^{*}\left(\mathbf{s}\right)-Z\left(\mathbf{s}\right)]=-\sum _{j=1}^n\sum _{i=1}^n{\lambda }_j{\lambda }_i\gamma ({\mathbf{s}}_i-{\mathbf{s}}_j)+2\sum _{i=1}^n{\lambda }_i\gamma ({\mathbf{s}}_i-\mathbf{s}).$$

(3)

To evaluate the minimum variance of estimation (3) subject to the unbiasedness constraint ${\sum }_{i=1}^n{\lambda }_i=1$ [26], we apply the Lagrange multiplier method to this optimization problem which gives

$$\sum _{j=1}^n{\lambda }_j\gamma ({\mathbf{s}}_i-{\mathbf{s}}_j)+\mu =\gamma ({\mathbf{s}}_i-\mathbf{s}),$$

(4)

where $\mu$ is the Lagrange multiplier. Our goal is to determine the kriging weights in the Equation (2) which can be accomplished by using the semivariogram model described in the following subsection.

2.2. Semivariogram

The semivariogram quantifies the covariance structures of measured sample points with distance. The widely used semivariogram estimate, $\widehat{\gamma }\left(\mathbf{h}\right)$, was put forth by [14]

$$\widehat{\gamma }\left(\mathbf{h}\right)={\displaystyle \frac{1}{2N\left(\mathbf{h}\right)}}\sum _{j=1}^{N\left(\mathbf{h}\right)}{(Z\left({\mathbf{s}}_j\right)-Z({\mathbf{s}}_j+\mathbf{h}))}^2,$$

(5)

where $N\left(\mathbf{h}\right)$ denotes the number of distinct pairs at a separation lag vector $\mathbf{h}$. Henceforward, we assume the isotropy thereby leading to the semivariogram estimator, $\widehat{\gamma }\left(\mathbf{h}\right)$ being replaced by $\widehat{\gamma }\left(h\right)$ where h is the Euclidean norm of $\mathbf{h}$. Based on this resulting empirical semivariogram, the continuous spatial variability across the domain can be assumedly represented by smooth functions which is known as parametric semivariograms. Various prescribed functions including exponential, spherical and Gaussian functions have been exploited [27,28]. In this work, we employ two parametric krigings for the two dimensional space. One is the exponential model which is explicitly represented by

$$\gamma (h,\mathbf{\theta })=\left\{\begin{array}{cc}{c}_0+c_1\left(1-exp\left(-{\displaystyle \frac{h}{c_2}}\right)\right)\hfill & h>0\hfill \\ 0\hfill & h=0\hfill \end{array}\right.$$

(6)

and the spherical model

$$\gamma (h,\mathbf{\theta })=\left\{\begin{array}{cc}0\hfill & h=0\hfill \\ c_0+c_1\left(1.5\left({\displaystyle \frac{h}{c_2}}\right)-0.5{\left({\displaystyle \frac{h}{c_2}}\right)}^3\right)\hfill & 0<h\le c_2\hfill \\ c_0+c_1\hfill & h>c_2\hfill \end{array}\right.$$

(7)

where $\mathbf{\theta }=(c_0,c_1,c_2)$. The parameter $c_0$ represents the nugget value induced by the spatial error when the distance smaller than the shortest imposed lag distance. Whereas the variance of the process is denoted by $c_1$ and a combination between $c_0$ and $c_1$ is referred to as sill. The parameter $c_2$ is the range in which it indicates a distance from the origin to the point of sill achieved. A choice of these parameters undoubtedly has a considerable impact upon the accuracy of kriging estimators.

As opposed to the parametric semivariogram, a specification of the nonparametric semivariogram model is not required, this therefore provides a flexibility to compute estimate at any location. Under the isotropic and second-order stationary assumptions, the nonparametric semivariogram estimate can be written as a series from Yaglom’s representation of Bochner’s theorem [21,22]. In two-dimensional space, the approximated semivariogram can be expressed as

$${\gamma }^{*}(h;\mathbf{p})=p_0-\sum _{j=1}^m{p}_j{J}_0\left(t_{j}h\right),$$

(8)

where $\mathbf{p}=(p_0,p_1,p_2,\dots ,p_m)$ is a vector of nonnegative coefficients, the scalars $t_j$, for $j=1,2,\dots ,m$, are the jump points or nodes and $J_0$ is the Bessel function of the first kind of order zero. A goal is to find a vector $\mathbf{p}$ so that it can minimize the weighted sum squared errors (WSSE) [29]

$$Q\left(\mathbf{p}\right)=\sum _{i=1}^L{w}_i{\left(\widehat{\gamma }\left(h_i\right)-{\gamma }^{*}(h_i;\mathbf{p})\right)}^2,$$

(9)

where L is the number of discrete lags. The weight is defined as

$$w_i=N\left(h_i\right)/{\left({\gamma }^{*}(h_i;\mathbf{p})\right)}^2,$$

(10)

in which this weight manifestation suggests that the short-lag spatial correlations induces strong weights. The Equation (9) is subject the following constraint

$$p_0-\sum _{j=1}^m{p}_j=b,$$

(11)

where the nonnegative value b corresponds to the nugget effect.

2.3. Genetic Algorithm

Genetic algorithm primarily introduced by John Holland [30] is a class of stochastic optimization technique wherein its underlying principles are inspired by the biological evolution of living organisms. Besides its main contribution to the optimization and search problems, the method is often used as a tool for parameter identification. The process is carried out by a population of chromosomes which represents a collection of solutions to a problem. The chromosomes at each generation are assigned fitness values which indicate how likely they can survive. To produce a population of chromosomes for the subsequent generation with a higher probability of achieving optimal solutions, there are three genetic operations involved; selection, crossover and mutation. The process of chromosome evolution based on such operations is repeated until acceptable criteria are satisfied. The generic procedure of GA can be illustrated in Figure 1.

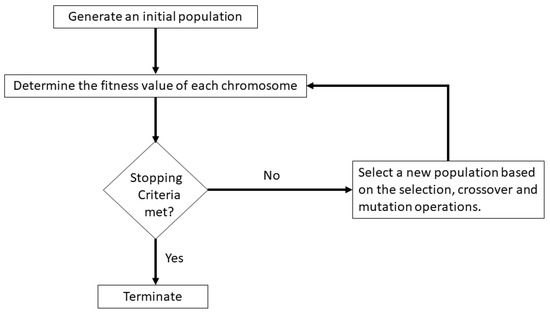
Figure 1. Flowchart of genetic algorithm.

3. Semiparametric Semivariogram and Node Selection Criterion

On the other hand, by considering the semivariogram structures of both parametric and nonparametric models, Carmack et al. [25] purposed the semiparametric semivariogram where h in the nonparametric model is replaced by $h^{\alpha }$, for $\alpha \in [0,1].$ This gives rise to the semivariogram estimate

$${\gamma }_{\alpha }^{*}(h;\mathbf{p})=p_0-\sum _{j=1}^m{p}_j{J}_0\left(t_j{h}^{\alpha }\right).$$

(12)

An imperative part of the nonparametric semivariogram is to choose the right choice of node selection,$t_j$ in the Equation (8). Shapiro and Botha [20] and Cherry [31] utilized improptu means by using regularly spaced nodes so that $t_j=\delta j$ for $j=1,2,\dots ,m$ where $\delta$ is the positive number which can be chosen. However, it appears that equispaced nodes can lead to spurious oscillations due to the fact that estimators are not guaranteed to be positive definite in continuum [24]. Another ubiquitous suggestion for the node selection was made by Gorsich and Genton ([23,24]) who proposed that the nodes should be the roots of Bessel functions. This node representation results in the coefficients in Equation (8) being nonnegative as well as the convergence being ensured. Whilst Carmack et al. adopted the concept of the first root of the Bessel function of the first kind of order zero, $t_2^{*}$ to define the nodes in the semiparametric kriging so that $t_j=t_2^{*}/h_j^{\alpha }$, for $j=1,2,\dots ,m$.

Despite the fact that, in practice, semivariogram structure can possess the hole effect whereby fitted semivariogram exhibits sinusoidal-wave form [32], we here restrict our study to a generally intuitive perception in which objects that are physically close to each other, should have a stronger correlation than those farther away. Given this assumption, the fitted semiparametric semivariogram might not be necessarily satisfied in some certain situations as illustrated in Figure 2. An alternative way for the node scaling is thus proposed by considering the monotonicity requirement for the fitted semivariogram. This precondition implies the first derivative of the estimated semivariogram (12) should be nonnegative, that is

$$\sum _{j=1}^m\alpha p_j{t}_j{h}_i^{\alpha -1}{J}_1\left(t_j{h}_i^{\alpha }\right)\ge 0$$

(13)

for $i=1,2,\dots ,L$, where $J_1$ is the Bessel function of the first kind of order one. By assuming the node scaling in an adhoc manner

$$t_j={\left({\displaystyle \frac{h_1}{h_L}}\right)}^{\alpha }{\displaystyle \frac{t_{\beta }^{*}}{h_j^{\alpha }}}$$

(14)

for $i=1,2,\dots ,L$, where $t_{\beta }^{*}$ is the first root of $J_1$, $h_1$ and $h_L$ are the first and final separation lag distances respectively. Since $0<\alpha <1$ and $0<h_1<h_2<\cdots <h_m<\cdots <h_L$, it consequently gives

$${\displaystyle 0<{\left({\displaystyle \frac{h_i}{h_m}}\right)}^{\alpha }<{\left({\displaystyle \frac{h_i}{h_{m-1}}}\right)}^{\alpha }<\cdots <{\left({\displaystyle \frac{h_i}{h_1}}\right)}^{\alpha }\le {\left({\displaystyle \frac{h_L}{h_1}}\right)}^{\alpha }.}$$

(15)

This leads to

$${\displaystyle 0<{\left({\displaystyle \frac{h_i}{h_m}}\right)}^{\alpha }{\left({\displaystyle \frac{h_1}{h_L}}\right)}^{\alpha }{t}_{\beta }^{*}<{\left({\displaystyle \frac{h_i}{h_{m-1}}}\right)}^{\alpha }{\left({\displaystyle \frac{h_1}{h_L}}\right)}^{\alpha }{t}_{\beta }^{*}<\cdots <{\left({\displaystyle \frac{h_i}{h_1}}\right)}^{\alpha }{\left({\displaystyle \frac{h_1}{h_L}}\right)}^{\alpha }{t}_{\beta }^{*}\le t_{\beta }^{*},}$$

(16)

which ultimately results in

$${\displaystyle 0<J_1\left({\left({\displaystyle \frac{h_i}{h_{m-k}}}\right)}^{\alpha }{\left({\displaystyle \frac{h_1}{h_L}}\right)}^{\alpha }{t}_{\beta }^{*}\right)}$$

(17)

for $i=1,2,\dots ,L$ and $k=0,1,\dots ,m-1$. By defining $t_j$ as in Equation (14), the Equation (13) can be written in terms of a series expansion:

$$\begin{array}{cc}\hfill {\displaystyle \sum _{j=1}^m\alpha p_j{t}_j{h}_i^{\alpha -1}{J}_1\left(t_j{h}_i^{\alpha }\right)}& =\alpha p_1{t}_1{h}_i^{\alpha -1}{J}_1\left(t_1{h}_i^{\alpha }\right)+\alpha p_2{t}_2{h}_i^{\alpha -1}{J}_1\left(t_2{h}_i^{\alpha }\right)\hfill \\ \hfill & +\cdots +\alpha p_m{t}_m{h}_i^{\alpha -1}{J}_1\left(t_m{h}_i^{\alpha }\right)\hfill \\ \hfill & =\alpha p_1{t}_1{h}_i^{\alpha -1}{J}_1\left({\left({\displaystyle \frac{h_1}{h_L}}\right)}^{\alpha }{\displaystyle \frac{t_{\beta }^{*}}{h_1^{\alpha }}}{h}_i^{\alpha }\right)+\alpha p_2{t}_2{h}_i^{\alpha -1}{J}_1\left({\left({\displaystyle \frac{h_1}{h_L}}\right)}^{\alpha }{\displaystyle \frac{t_{\beta }^{*}}{h_2^{\alpha }}}{h}_i^{\alpha }\right)\hfill \\ \hfill & +\cdots +\alpha p_m{t}_m{h}_i^{\alpha -1}{J}_1\left({\left({\displaystyle \frac{h_1}{h_L}}\right)}^{\alpha }{\displaystyle \frac{t_{\beta }^{*}}{h_m^{\alpha }}}{h}_i^{\alpha }\right)\hfill \\ \hfill & =\alpha p_1{t}_1{h}_i^{\alpha -1}{J}_1\left({\left({\displaystyle \frac{h_i}{h_1}}\right)}^{\alpha }{\left({\displaystyle \frac{h_1}{h_L}}\right)}^{\alpha }{t}_{\beta }^{*}\right)+\alpha p_2{t}_2{h}_i^{\alpha -1}{J}_1\left({\left({\displaystyle \frac{h_i}{h_2}}\right)}^{\alpha }{\left({\displaystyle \frac{h_1}{h_L}}\right)}^{\alpha }{t}_{\beta }^{*}\right)\hfill \\ \hfill & +\cdots +\alpha p_m{t}_m{h}_i^{\alpha -1}{J}_1\left({\left({\displaystyle \frac{h_i}{h_m}}\right)}^{\alpha }{\left({\displaystyle \frac{h_1}{h_L}}\right)}^{\alpha }{t}_{\beta }^{*}\right)\hfill \\ \hfill & \ge 0.\hfill \end{array}$$

(18)

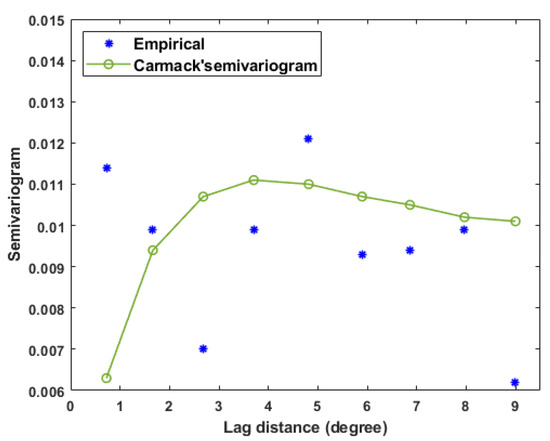
Figure 2. An illustration when the monotonicity constraint is not imposed in the semivariogram.

By this node restriction, the monotonicity condition is proven to be satisfied and this can ultimately prevent noisy behavior in the estimation.

4. A Case Study: An Estimation of Solar Radiation Distribution in Thailand

Renewable energy deployment has grown rapidly in the power sector in the last decade. In an attempt to maintain energy security and environmental sustainability over the coming years, the Thai government sets up a blueprint for 20-year Thailand’s energy plan which is known as the Alternative Energy Development Plan-AEDP (2015–2036). By 2036, renewable energies are planned to account for 30% of net power generation capacity. In particular, giving its location in the equatorial regions, solar energy power has been an undoubtedly favorable renewable source in Thailand due to a large amount of incoming solar radiation all over the country throughout the year. Solar energy production is targeted to reach around 10 gigawatts or nearly 50% of the total alternative energy power capacity by 2036.

To attain the optimal benefits of such resource, one of the key factors for efficient planning and management is to examine the availability of spatially continuous data over the region of interest. Nonetheless, in practice, direct measurements are typically scarce and derived from point sources that are irregularly distributed. For these reasons, spatial interpolation techniques capable of quantitatively capturing the distribution of solar radiation are of great importance.

4.1. Data Description

The kriging technique with different types of semivariograms previously described has been applied to the estimation of solar radiation in Thailand. The study region is carried out across the whole country which extends over the area around 518,000 km${}^2$. The latitude ranges from $5^{\circ }{37}^{\prime }$ N to ${20}^{\circ }{27}^{\prime }$ N, whereas longitude ${97}^{\circ }{22}^{\prime }$ E to ${105}^{\circ }{37}^{\prime }$ E. In this study, a variation of solar radiation characteristics in Thailand is classified according to seasonal periods, namely the summer season (March–June), rainy season (July–October) and winter season (November–February).

The source of solar radiation is obtained from the website of the department of alternative energy development and efficiency, www.dede.go.th. Instead of using a collection of hourly solar radiation data to justify our models, we use monthly averages of daily solar radiation which took place during the period from January 2015 to December 2015, hereby covering changes in annual radiation. In this dataset, the radiation intensity is within the spectral range 14 to 24 MJ/m${}^2$day${}^{-1}$ in summer. Whilst those in the rainy and winter seasons are around 8–20 MJ/m${}^2$day${}^{-1}$ and 11–23 MJ/m${}^2$day${}^{-1}$ respectively. The number of solar radiation monitoring stations is 37 sites that are sparsely situated across Thailand as shown in Figure 3 and details of station positions are displayed in Appendix A.

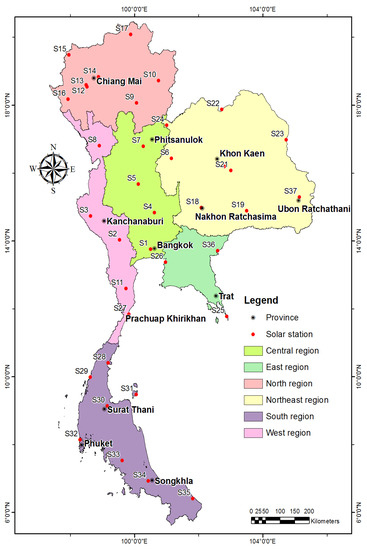
Figure 3. A map of solar radiation monitoring stations in Thailand.

4.2. Accuracy Assessment

Quantitative evaluation of the estimation ability of each approach is performed by using the classical k-fold cross-validation method [33]. The dataset is chronologically divided into 9 folds. On each iteration, about 10% of the data is chosen for the validation, while the remaining data are used for the training. The process is repeated until all folds are picked as a validation set. This implies every individual data is utilized for both training and validating steps.

A combination of these two conventional statistics, the root mean squared error (RMSE) and the mean absolute percentage error (MAPE), are utilised for the evaluation of the quality of forecasting models. They are defined as follows:

$$\begin{array}{cc}\hfill \mathrm{RMSE}& =\sqrt{{\displaystyle \frac{1}{M}}\sum _{i=1}^M{\left(\tilde{Z}\left({\mathbf{s}}_i\right)-Z^{*}\left({\mathbf{s}}_i\right)\right)}^2}\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill \mathrm{MAPE}& ={\displaystyle \frac{1}{M}}\sum _{i=1}^M\left|{\displaystyle \frac{\tilde{Z}\left({\mathbf{s}}_i\right)-Z^{*}\left({\mathbf{s}}_i\right)}{\tilde{Z}\left({\mathbf{s}}_i\right)}}\right|\times 100,\hfill \end{array}$$

(20)

where M is the number of validation sites and $\tilde{Z}\left({\mathbf{s}}_i\right)$ and $Z^{*}\left({\mathbf{s}}_i\right)$ are the actual and estimated (kriged) solar radiation values at site ${\mathbf{s}}_i$ respectively. Despite its popularity for the assessment of model performance in climate and environmental studies, having to compute the RMSE value through the square of the discrepancies between observed and interpolated values can lead to significant weights being placed on outliers. On the contrary, the MAPE is a scale-independent measure resulting in an ease of interpretability. Some problems associated with the MAPE can be arisen due to a division by close-to-zero value. It is accordingly required to apply at least two metrics in order to guarantee consistency in evaluation.

In our numerical experiment, three different semivariogram models are compared; exponential model, spherical model and semiparametric model. Following the recommendation by [20], the number m in the Equation (8) is chosen to be equal to $L-1$. For a fair comparison, all these distinct semivariograms are fitted based on the weighted sum squared errors in Equation (9) and GA is applied to identify the optimal set of parameters. The GA configuration is as follows: a population size of 30, a crossover probability of 0.8, a mutation probability of 0.2 and 5000 maximum generations. A section operator is chosen to be a stochastic uniform with a scattered crossover and Gaussian mutation mechanisms. The computational simulations of all approaches are performed in the MATLAB. Furthermore, when an optimal set of parameters of parametric models are found using GA, the nugget value, $c_0$, always approaches zero. To simplify the time-intensive computation, we thus set the value of the nugget being zero for all semivariograms.

To evaluate the overall performances of different kriging approaches for each month, the MAPE and RMSE values obtained from nine folds are averaged and their corresponding standard deviation is also computed. Table 1 shows the mean and standard deviation of MAPE derived from three different semivariograms. According to the MAPE index, all approaches provide excellent performances as the mean values of MAPE in almost every month are less than 10% with standard deviation ranging from 1.7067% to 4.9115 %, except in July. Especially, the semiparametric semivariogram consistently outperforms both parametric models with a relative improvement in MAPE ranging from around 2% to 28 %. The maximum improvement can be marked in March with MAPE values of 6.0779% for the semiparametric model and 7.6585% and 8.4843% for exponential and spherical models respectively.

Table 1. The mean and standard deviation of mean absolute percentage error (MAPE) of three semivariograms.

Month	Exponential Model		Spherical Model		Semiparametric Model
	Mean (%)	SD (%)	Mean (%)	SD (%)	Mean (%)	SD (%)
January	6.2217	3.2702	6.6655	3.5482	5.2774	2.5521
February	5.3176	1.8502	6.3025	2.2107	4.6256	1.8649
March	7.6585	2.6567	8.4843	2.1647	6.0779	2.2083
April	4.1333	2.0254	4.2075	2.0846	3.9667	1.7067
May	6.9756	4.9115	6.6495	4.4706	6.4628	4.5425
June	5.5709	3.2096	6.0532	3.0307	5.1745	3.2838
July	13.5531	11.1182	13.3897	11.5499	11.7869	10.3217
August	8.1833	3.9285	8.6704	4.5225	7.4525	4.0728
September	6.2838	4.8167	6.1497	4.5305	6.0345	4.6262
October	7.5245	3.6046	7.1737	3.3985	6.8993	2.9198
November	8.4253	4.5760	8.2861	4.8189	8.1190	4.3054
December	6.9176	2.4222	7.6550	2.4751	6.4925	2.5497
Average	7.2304	4.0325	7.4739	4.0671	6.5308	3.7461

As presented in Table 2, similar patterns can be observed for the RMSE values where the semiparametric model exhibits lower RMSE values than other methods for almost every month. This can also be elucidated by the average values of the means in which both parametric semivariograms present higher average values of every month being above 2 MJ/m${}^2$day${}^{-1}$ whereas that of the semiparametric model is 1.8700 MJ/m${}^2$day${}^{-1}$.

Table 2. The mean and standard deviation of root mean squared error (RMSE) of three semivariograms.

Month	Exponential Model		Spherical Model		Semiparametric Model
	Mean (MJ/m${}^2$day${}^{-1}$)	SD (MJ/m${}^2$day${}^{-1}$)	Mean (MJ/m${}^2$day${}^{-1}$)	SD (MJ/m${}^2$day${}^{-1}$)	Mean (MJ/m${}^2$day${}^{-1}$)	SD (MJ/m${}^2$day${}^{-1}$)
January	1.6379	0.9343	1.4910	0.7892	1.2510	0.5902
February	1.4588	0.5254	1.6788	0.6708	1.3034	0.5151
March	2.1150	0.8923	2.3213	0.7933	1.6957	0.8002
April	1.4848	0.4102	1.4099	0.5133	1.3497	0.4626
May	1.9456	0.8488	1.8363	0.8085	1.8220	0.8120
June	1.6121	0.5689	1.7305	0.5652	1.5784	0.5806
July	2.7131	1.2092	2.8761	1.3432	2.5692	1.1359
August	2.1842	0.5334	2.2415	0.6093	2.0698	0.5642
September	1.8844	0.7988	1.8835	0.7460	1.8846	0.7402
October	2.1887	0.5147	2.2186	0.5295	2.1858	0.5099
November	2.6029	0.8561	2.5142	0.8141	2.4596	0.7861
December	2.5024	0.8000	2.4769	0.5723	2.2711	0.6285
Average	2.0275	0.7410	2.0566	0.7296	1.8700	0.6771

Under different seasonal scenarios, relatively low values of the mean and standard deviation of both RMSE and MAPE for all models are produced throughout the summer months. In particular, the lowest mean values of MAPE ranging from 3.9667% to 4.2075% are acquired in April with corresponding standard deviation varying from 1.7067 % to 2.0254 %. This might due to the fact that considerable solar radiation together with high frequencies of the apparent sky are prominent during the dry season, giving rise to low variation in solar radiation across the country. In contrast with the wet season, especially in July when the maximum values of mean error and standard deviation are obtained, the variability between the wet and dry areas throughout the country becomes distinct due to the southwest monsoon together with Inter-Tropical Convergence Zone (ITCZ). This results in significant uncertainty in measurement as well as high fluctuation of solar radiation.

Figure 4 displays a visual comparison of the estimations of solar radiation distribution in March, July and November in Fold 4. The reason for selecting these three months is because each of them represents an individual season in Thailand. Overall, these three semivariograms produce fairly similar distribution patterns of solar radiation with no significant difference among them. A plausible explanation for this might be due to a small local variation of solar radiation, even with a collection of measured data itself. Nonetheless, in Figure 4d–f, little differences can be observed in central Thailand where a relatively higher intensity of solar radiation is predicted by both parametric semivariograms. This similar tendency is also exhibited in November in which lower values of the monthly average of daily solar radiation estimated by exponential and spherical models are found in northern Thailand.

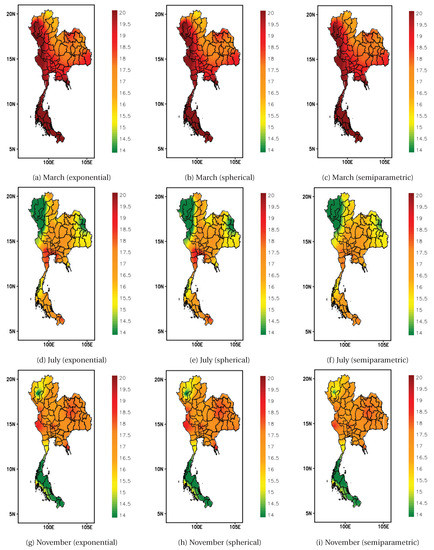
Figure 4. The maps of the predicted montly averages of daily solar radiation for March, July and November using exponential model, spherical model and semiparametric model.

Figure 5 illustrates a comparison regarding the fitted curves generated by each method. Broadly speaking, both exponential and semiparametric curves exhibit somewhat similar trends of behavior for these three selected months. Whereas the fitted curves derived from the spherical model tend to have a steep slope. The above-mentioned observation can be clearly seen in November where the estimated values of sill and range of the exponential semivariogram that are produced by GA are around 0.0260 and 10, while those of the spherical semivariogram are 0.0299 and 9.8739 respectively. On the other hand, the optimal $\alpha$ value of the semiparametric semivariogram appears to be 0.3431.

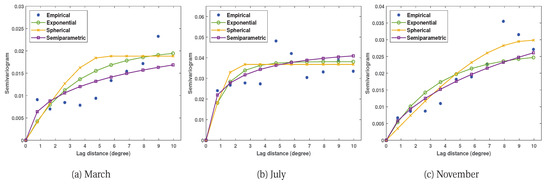
Figure 5. A comparison of three different semivariograms for March, July and November in Fold 4.

It can nevertheless be inconclusive just by examining merely the diagrams attained from each model. Additional investigation is required to assess the model quality. The weighted sum squared errors between empirical and estimated semivariograms are carried out and presented in Table 3. In March and July, the lowest WSSE values are achieved by the semiparametric model, followed by the exponential model while the highest WSSE is obtained from the spherical model.

Table 3. The weighted sum squared errors of three different semivariograms for March, July and November in Fold 4.

Month	Exponential Model	Spherical Model	Semiparametric Model
March	62.8177	88.1736	51.5932
July	17.8280	22.5330	16.9381
November	36.2850	29.6328	25.9583

To investigate the effects of judicious parameter $\alpha$ on kriging estimates, we have varied the values of $\alpha$ in the range of 0.1–0.9 with a spacing of 0.1 (not shown here). It is found that the semiparametric estimates with $\alpha$ being greater than 0.5 result in performance deterioration. This agrees well with the best-tuned $\alpha$ obtained from GA in which it tends to be smaller than 0.5 thoroughly. Figure 6 depicts the results of the empirical semivariogram and the associated semiparametric fits for $\alpha$ being 0.1, 0.5, 0.8 and optimally tuned $\alpha$ derived from the GA.

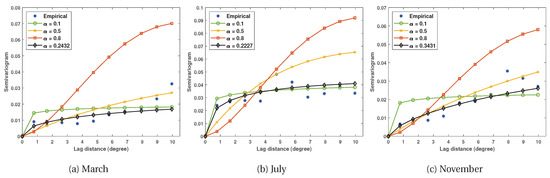
Figure 6. Analysis of the effects of $\alpha$ value in the semiparametric estimators for March, July and November in Fold 4.

In July, the curves obtained from $\alpha =0.1$ and the best-tuned $\alpha$ which is equal to 0.2227 almost coincide with the values of WSSE as shown in Table 4 being 20.0320 and 16.9381, respectively. On the contrary, in November, a suitable choice for $\alpha$ is around 0.3–0.5. The values of WSSE obtained from $\alpha =0.3431$ is 25.9583 and that of $\alpha =0.5$ is 27.4183.

Table 4. The weighted sum squared error of semiparametric semivariogram with different $\alpha$ for March, July and November in Fold 4.

Month	$\mathit{\alpha }=0.1$	$\mathit{\alpha }=0.5$	$\mathit{\alpha }=0.8$	Optimal $\mathit{\alpha }$
March	94.3866	81.6292	268.8628	51.5932
July	20.0320	64.3038	553.6467	16.9381
November	86.1593	27.4183	145.6422	25.9583

5. Conclusions and Discussion

As having been stated earlier, the crucial factor of the traditional nonparametric kriging is to correctly specify the nodes otherwise the method can suffer from spurious oscillation due to the nature of the basis function. The primary objective of this study is to adopt the semiparametric semivariogram which is a variant of the nonparametric model. Regardless of the fact that non-monotonous semivariograms (hole effect) are applicable in some certain cases, the supplementary monotonicity constraint is imposed so that the node selection criterion is established with the aim to meet the theoretical characteristics of semivariograms as well as to prevent the spurious oscillation. This results in the appropriate node space being formulated in terms of the first root of the Bessel function of the first kind of order one, as shown in Equation (14).

The comparison of exponential, spherical and semiparametric models is demonstrated in the case of solar radiation estimation in Thailand. The GA technique is also coupled to all semivariograms for the purpose of identifying optimal parameters. The estimates derived from the semiparametric model are more accurate than those from the other two parametric semivariograms, with a relative improvement of around 7–13% according to the averages values of MAPE and RMSE. Regarding seasonal distribution, high errors are achieved during the monsoon months. This is associated with big changes in cloudiness in some particular areas which causes large fluctuations in solar radiation and ultimately becomes difficult to estimate. Although all three semivariograms produce almost identical maps of solar radiation for the selected months but, from the accuracy measures point of view, it is shown that the best performance is achieved by the semiparametric model. This might due to the fact that irregular patterns of the data arise under different seasonal climatic regimes, so this viable method allows the flexibility to modeling the semivariogram, rather than the predetermined function. Furthermore, following this study, the emphasis is also put on the effect of the tuning parameter $\alpha$ to the semiparametric model. Based on our dataset, the range of fixed values of $\alpha$ that results in sufficiently good estimates is restrained to relatively low values (≤0.5) which agree well with the optimally-tuned $\alpha$ obtained from the GA.