Robust Control Design to the Furuta System under Time Delay Measurement Feedback and Exogenous-Based Perturbation
Abstract
1. Introduction
- (a)
- Design of a nonlinear state-feedback stabiliser for nonlinear systems with random time delays, Lipschitz nonlinearities and parametric uncertainties.
- (b)
- Satisfaction of the asymptotic stabilisation based on Lyapunov–Krasovskii stability theory and LMI approach.
- (c)
- The proposed method is rather straightforward and there is no complexity in the employment of this technique.
- (d)
- Application of the offered method on an experimental device, to prove the efficiency of the method.
2. Notation
3. Robust Delay-Dependent Control Design
- is the state variable.
- is the time delay.
- A, , B, E, C, and are real matrices of appropriate dimensions.
- is the external perturbation.
- is the control input.
- is the output variable.
- is the internal or virtual variable.
4. Random Time Delay Realization
4.1. Nonlinear System Equations
4.2. Formulation
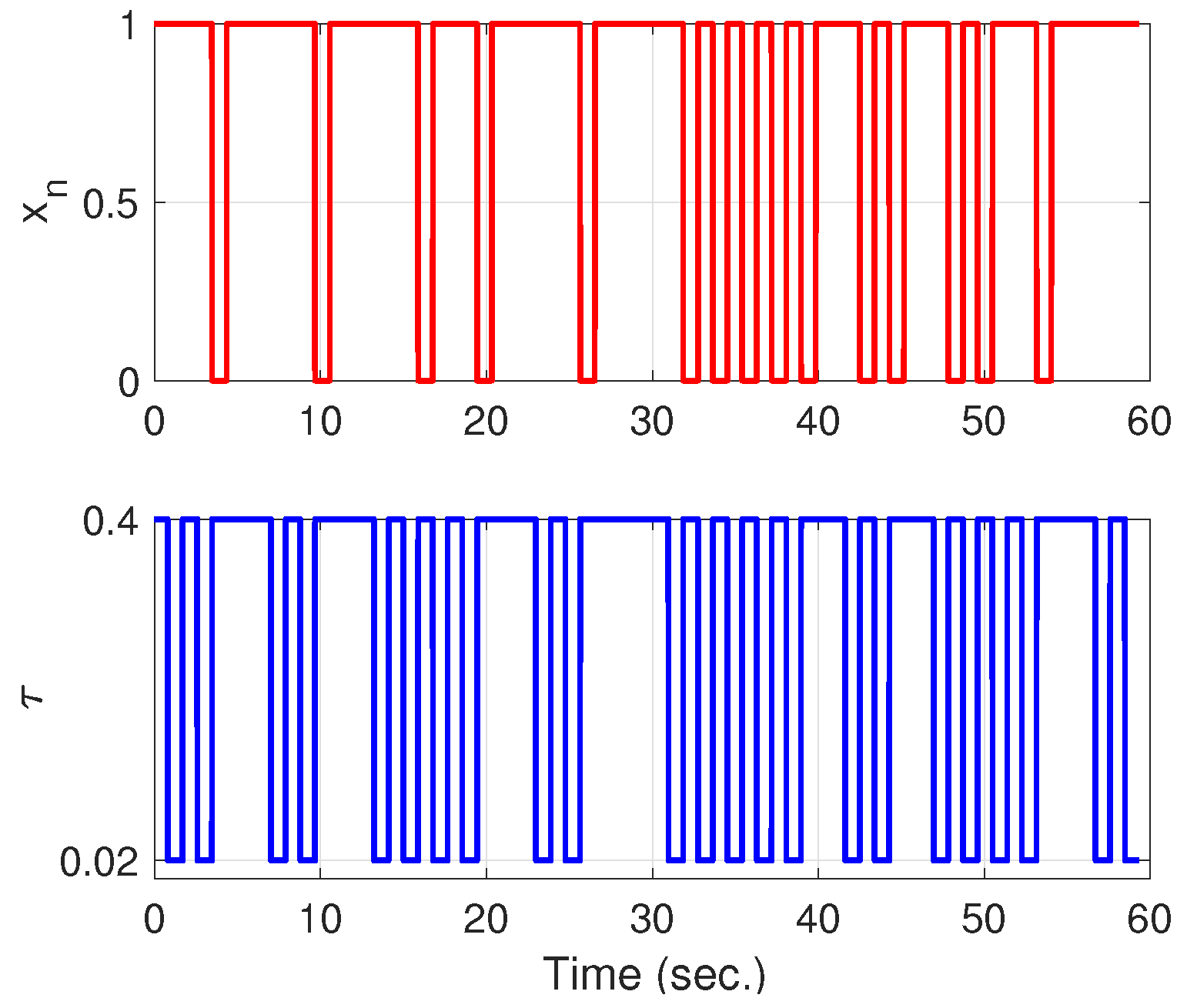
4.3. Random Time Delay Algorithm
| Algorithm 1: Algorithm of the random time delay on the measurements. |
| Initialise xn, xm, r (xn = 0.1, xm = 0, r = 3.7, d1 = 0.23, d2 = 0.45) do xm = r·xn·(1 − xn) if (xm > 0.5) d = d1 else d = d2 endif xn = xm end do |
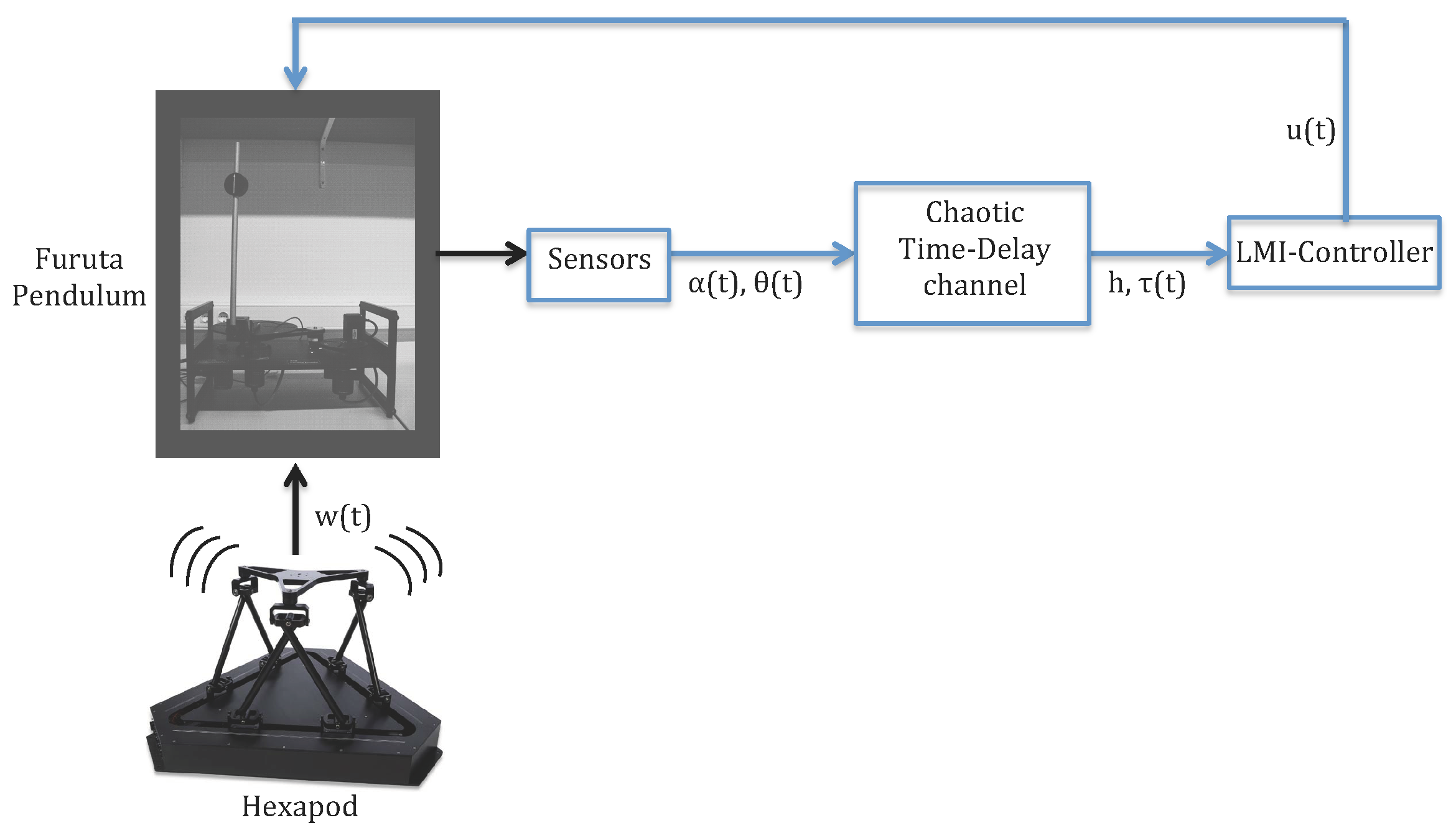
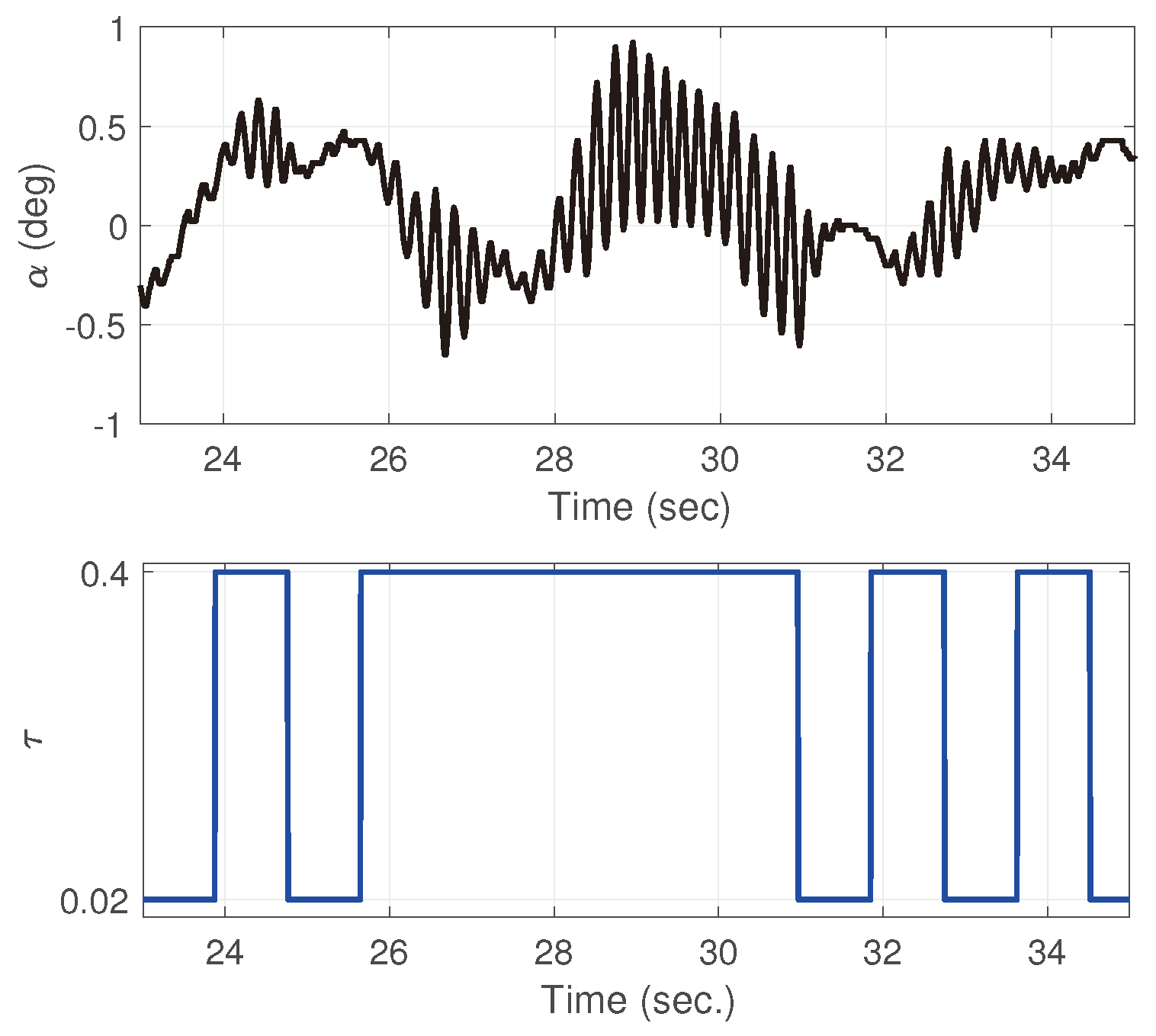
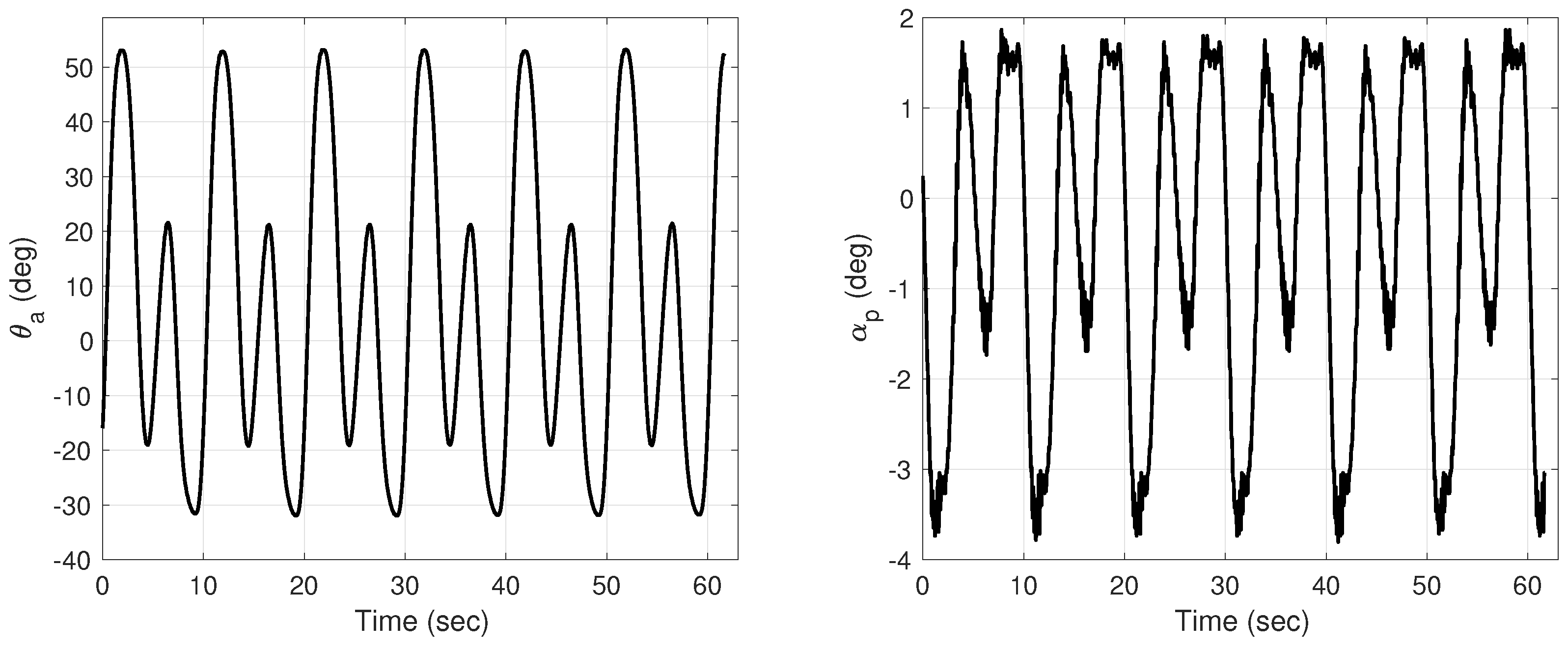
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, R.; Hredzk, B. Distributed Finite-Time Multi-agent Control for DC Micro-grids With Time Delays. IEEE Trans. Smart Grid 2019, 10, 2692–2701. [Google Scholar] [CrossRef]
- Liu, L.; Yin, S.; Zhang, L.; Yin, X.; Yan, H. Improved Results on Asymptotic Stabilization for Stochastic Nonlinear Time-Delay Systems With Application to a Chemical Reactor System. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 195–204. [Google Scholar] [CrossRef]
- Zappatore, A.; Augieri, A.; Bonifetto, R.; Celentano, G.; Savoldi, L.; Vannozzi, A.; Zanino, R. Modeling Quench Propagation in the ENEA HTS Cable-In-Conduit Conductor. IEEE Trans. Appl. Supercond. 2020, 30, 1–7. [Google Scholar] [CrossRef]
- Buzhin, I.G.; Mironov, Y.B. Evaluation of Telecommunication Equipment Delays in Software-Defined Networks. In Proceedings of the 2019 Systems of Signals Generating and Processing in the Field of on Board Communications, Moscow, Russia, 20–21 March 2019. [Google Scholar] [CrossRef]
- Shirai, J.; Yamaguchi, T.; Takaba, K. Remote visual servo tracking control of drone taking account of time delays. In Proceedings of the 56th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Kanazawa, Japan, 19–22 September 2017. [Google Scholar]
- Lim, B.; Lee, J.; Jang, J.; Kim, K.; Park, Y.J.; Seo, K.; Shim, Y. Delayed Output Feedback Control for Gait Assistance With a Robotic Hip Exoskeleton. IEEE Trans. Robot. 2019, 35, 1055–1062. [Google Scholar] [CrossRef]
- Ali, H.; Dasgupta, D. Effects of time delays in the electric power grid. In Proceedings of the 6th International Conference on Critical Infrastructure Protection (ICCIP), Washington, DC, USA, 19–21 March 2012; pp. 139–154. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Seuret, A.; Gouaisbaut, F.; He, Y. Overview of recent advances in stability of linaer systems with time-varying delay. IET Control. Theory Appl. 2019, 13, 1–16. [Google Scholar] [CrossRef]
- Mobayen, S. Optimal LMI-based state feedback stabilizer for uncertain nonlinear systems with time varying uncertainties and disturbances. Complexity 2015, 21, 356–362. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Song, Z.B.; Li, T.; Yang, S.H. Output feedback stabilization for high-order uncertain feedforward time-delay nonlinear systems. J. Frankl. Inst.-Eng. Appl. Math. 2015, 352, 5308–5326. [Google Scholar] [CrossRef]
- Mahmoud, M.S. Recent Progress in Stability and Stabilization of Systems with Time-Delays. Math. Probl. Eng. 2017, 2017, 7354654. [Google Scholar] [CrossRef]
- Li, X.; Cao, J.; Ho, D.W.C. Impulsive Control of Nonlinear Systems With Time-Varying Delay and Applications. IEEE Trans. Cyber. 2020, 50, 2661–2673. [Google Scholar] [CrossRef]
- Briat, C. Linear parameter-varying and time-delay systems. Anal. Obs. Filter. Control. 2014, 3, 5–7. [Google Scholar]
- Li, S.; Ding, L.; Gao, H.; Liu, Y.; Huang, L.; Deng, Z. ADP-Based Online Tracking Control of Partially Uncertain Time-Delayed Nonlinear System and Application to Wheeled Mobile Robots. IEEE Trans. Cybern. 2020, 50, 3182–3194. [Google Scholar] [CrossRef] [PubMed]
- Sayyad-Delshad, S.; Gustafsson, T. H∞ observer design for uncertain nonlinear discrete-time systems with time-delay: LMI optimization approach. Int. J. Robust Nonlinear Control 2015, 25, 1514–1527. [Google Scholar] [CrossRef]
- Krishnamurthy, P.; Khorrami, F. Prescribed-Time Output-Feedback Stabilization of Uncertain Nonlinear Systems with Unknown Time Delays. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 2705–2710. [Google Scholar]
- Tong, S.C.; Sheng, N. Adaptive fuzzy observer back-stepping control for a class of uncertain nonlinear systems with unknown time-delay. Int. J. Autom. Comput. 2010, 7, 236–246. [Google Scholar] [CrossRef]
- Lien, C.H.; Yu, K.W.; Huang, C.T.; Chou, P.Y.; Chung, L.Y.; Chen, J.D. Robust H∞ control for uncertain T-S fuzzy time-delay systems with sampled-data input and nonlinear perturbations. Nonlinear Anal. Hybrid Syst. 2010, 4, 550–556. [Google Scholar] [CrossRef]
- Goodall, D.P.; Postoyan, R. Output feedback stabilization for uncertain nonlinear time-delay systems subject to input constraints. Int. J. Control 2010, 83, 676–693. [Google Scholar] [CrossRef]
- Lakshmanan, M.; Bharathidasan; Senthilkumar, D.V. Dynamics of Nonlinear Time-Delay Systems; Springer Series in Synergetics; Springer: Berlin, Germany, 2011. [Google Scholar]
- Banerjee, T.; Biswas, D. Time-Delayed Chaotic Dynamical Systems; Springer: Berlin, Germany, 2018. [Google Scholar]
- Wang, H.; Wu, J.; Sheng, X.; Wang, X.; Zan, P. A new stability result for nonlinear cascade time-delay system and its application in chaos control. Nonlinear Dyn. 2015, 80, 221–226. [Google Scholar] [CrossRef]
- Zhao, Z.; Lv, F.; Zhang, J.; Du, Y. H∞ synchronization for uncertain time-delay chaotic systems with one-sided Lipschitz nonlinearity. IEEE Access 2018, 6, 19798–19806. [Google Scholar] [CrossRef]
- Park, J.H.; Kwon, O.M. A novel criterion for delayed feedback control of time-delay chaotic systems. Chaos Solitons Fractals 2005, 23, 495–501. [Google Scholar] [CrossRef]
- Sudha, K.R.; Santhi, R.V. Robust decentralized load frequency control of interconnected power system with generation rate constraint using type-2 fuzzy approach. Int. J. Elect. Pow. Energy Syst. 2011, 33, 699–707. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Hu, Q.; Shi, P.; Gao, H. Adaptive variable structure and commanding shaped vibration control of flexible spacecraft. J. Guid. Control Dyn. 2007, 30, 804–815. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, J.; Wang, F.; He, B. Event-triggered adaptive finite-time tracking control for full state constraints nonlinear systems with parameter uncertainties and given transient performance. In ISA Transactions; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Yi, X.; Guo, R.; Qi, Y. Stabilization of Chaotic Systems With Both Uncertainty and Disturbance by the UDE-Based Control Method. IEEE Access 2020, 8, 62471–62477. [Google Scholar] [CrossRef]
- Gritli, H. LMI-Based Robust Stabilization of a Class of Input-Constrained Uncertain Nonlinear Systems with Application to a Helicopter Model. Complexity 2020, 2020, 7025761. [Google Scholar] [CrossRef]
- Xin, Z.; Xiao, C.; Hou, T.; Shen, X. Robust H∞-Control for Uncertain Stochastic Systems with Impulsive Effects. Mathematics 2019, 7, 1169. [Google Scholar] [CrossRef]
- Zhou, K.; Khargonekar, P.P. Robust stabilization of linear systems with norm-bounded time-varying uncertainty. Syst. Control. Lett. 1988, 10, 17–20. [Google Scholar] [CrossRef]
- Xu, S.; Van Dooren, P.; Stefan, R.; Lam, J. Robust stability and stabilization for singular systems with state delay and parameter uncertainty. IEEE Trans. Autom. Control 2020, 47, 1122–1128. [Google Scholar]
- Golestani, M.; Mohammadzaman, I.; Yazdanpanah, M.J.; Vali, A.R. Application of finite-time integral sliding mode to guidance law design. J. Dyn. Syst. Measur. Control 2015, 137, 114501. [Google Scholar] [CrossRef]
- Golestani, M.; Mohammadzaman, I.; Yazdanpanah, M.J. Robust finite-time stabilization of uncertain nonlinear systems based on partial stability. Nonlinear Dyn. 2016, 85, 87–96. [Google Scholar] [CrossRef]
- Barbosa, K.A.; Souza, C.E.; Trofino, A. Robust H2 filtering for uncertain linear systems: LMI based methods with parametric Lyapunov functions. Syst. Control Lett. 2007, 54, 251–262. [Google Scholar] [CrossRef]
- Ngo, P.D.; Shin, Y.C. Modeling of unstructured uncertainties and robust controlling of nonlinear dynamic systems based on type-2 fuzzy basis function networks. Eng. Appl. Artif. Intell. 2016, 53, 74–85. [Google Scholar] [CrossRef]
- Gahinet, P.; Apkarian, P. A linear matrix inequality approach to H∞ control. Int. J. Nonlinear Control 1994, 4, 421–448. [Google Scholar] [CrossRef]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Hilhorst, G.; Pipeleers, G.; Michiels, W.; Swevers, J. Sufficient LMI conditions for reduced-order multi-objective H2/H∞ control of LTI systems. Eur. J. Control 2015, 23, 17–25. [Google Scholar] [CrossRef]
- Zong, G.; Xu, S.; Wu, Y. Robust H∞ stabilization for uncertain switched impulsive control systems with state delay: An LMI approach. Nonlinear Anal.-Hybrid Syst. 2008, 2, 1287–1300. [Google Scholar] [CrossRef]
- Leite, V.J.S.; Tarbouriech, S.; Peres, P.L.D. Robust H∞ state feedback control of discrete-time systems with state delay: An LMI approach. IMA J. Math. Control Info. 2009, 26, 357–373. [Google Scholar] [CrossRef]
- Sootla, A.; Zheng, Y.; Papachristodoulou, A. On the Existence of Block-Diagonal Solutions to Lyapunov and H∞ Riccati Inequalities. IEEE Trans. Aut. Contr. 2020, 65, 3170–3175. [Google Scholar] [CrossRef]
- Mei, W.; Zhao, C.; Ogura, M.; Sugimoto, K. Mixed H2/H∞ control of delayed Markov jump linear systems. IET Control Theory Appl. 2020, 14, 2076–2083. [Google Scholar] [CrossRef]
- Haddad, W.M.; Hui, Q.; Chellaboina, V. H2 optimal semistable control for linear dynamical systems: An LMI approach. J. Frankl. Inst.-Eng. Appl. Math. 2011, 348, 2898–2910. [Google Scholar] [CrossRef]
- Caharija, W.; Pettersen, K.Y.; Bibuli, M.; Calado, P.; Zereik, E.; Braga, J.; Gravdhl, J.T.; Sorensen, A.J. Integral Line-of-Sight Guidance and Control of Underactuated Marine Vehicles, Theory, Simulations, and Experiments. IEEE Trans. Control Syst. Technol. 2016, 24, 1623–1642. [Google Scholar] [CrossRef]
- Mobayen, S.; Pujol-Vazquez, G. A Robust LMI Approach on Nonlinear Feedback Stabilization of Continuous State-Delay Systems with Lipschitzian Nonlinearities: Experimental Validation. Iran J. Sci. Technol. Trans. Mech. Eng. 2019, 43, 549–558. [Google Scholar] [CrossRef]
- Briat, C. Linear Parameter-Varying and Time-Delay Systems: Analysis, Observation, Filtering and Control. In (Section 5.6.7), Advances in Delay and Dynamics 3; Springer: Berlin, Germany, 2015. [Google Scholar]
- Pujol, G. Reliable H∞ control of a class of uncertain interconnected systems: An LMI approach. J. Syst. Sci. 2009, 40, 649–657. [Google Scholar] [CrossRef]
- Model, E.C.P. Manual for A-51 inverted pendulum accessory (Model 220). In Educational Control Products; Ecpsystems: Pleasanton, CA, USA, 2003. [Google Scholar]
- Pujol-Vazquez, G.; Acho, L.; Mobayen, S.; Napoles, A.; Perez, V. Rotary inverted pendulum with magnetically external perturbations as a source of the pendulum’s base navigation commands. J. Frankl. Inst.-Eng. Appl. Math. 2018, 355, 4077–4096. [Google Scholar] [CrossRef]
- Boeing, G. Visual Analysis of Nonlinear Dynamical Systems: Chaos, Fractals, Self-Similarity and the Limits of Prediction. Systems 2016, 4, 37. [Google Scholar] [CrossRef]
- Pareek, N.K.; Patidar, V.; Sud, K.K. Image encryption using chaotic logistic map. Image Vis. Comput. 2006, 24, 926–934. [Google Scholar] [CrossRef]
- Wang, F.; Qian, Z.; Yan, Z.; Yuan, C.; Zhang, W. A Novel Resilient Robot: Kinematic Analysis and Experimentation. IEEE Access 2020, 8, 2885–2892. [Google Scholar] [CrossRef]



Sample Availability: Samples of the compounds are available from the authors. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pujol-Vazquez, G.; Mobayen, S.; Acho, L. Robust Control Design to the Furuta System under Time Delay Measurement Feedback and Exogenous-Based Perturbation. Mathematics 2020, 8, 2131. https://doi.org/10.3390/math8122131
Pujol-Vazquez G, Mobayen S, Acho L. Robust Control Design to the Furuta System under Time Delay Measurement Feedback and Exogenous-Based Perturbation. Mathematics. 2020; 8(12):2131. https://doi.org/10.3390/math8122131
Chicago/Turabian StylePujol-Vazquez, Gisela, Saleh Mobayen, and Leonardo Acho. 2020. "Robust Control Design to the Furuta System under Time Delay Measurement Feedback and Exogenous-Based Perturbation" Mathematics 8, no. 12: 2131. https://doi.org/10.3390/math8122131
APA StylePujol-Vazquez, G., Mobayen, S., & Acho, L. (2020). Robust Control Design to the Furuta System under Time Delay Measurement Feedback and Exogenous-Based Perturbation. Mathematics, 8(12), 2131. https://doi.org/10.3390/math8122131






