Solving Multi-Point Boundary Value Problems Using Sinc-Derivative Interpolation
Abstract
1. Introduction
2. Sinc Preliminaries
3. The Sinc-Derivative Method for MPBVPs
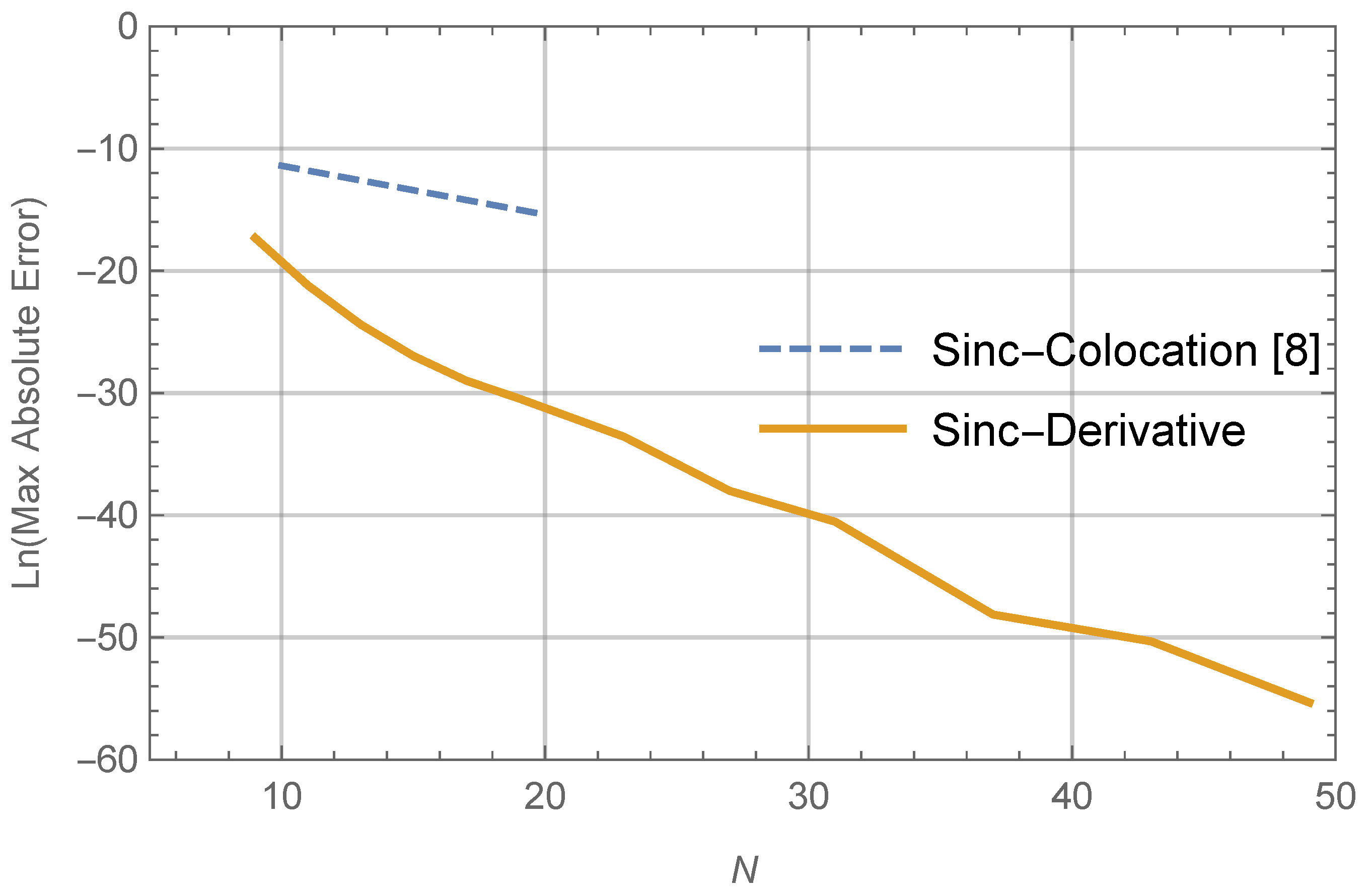
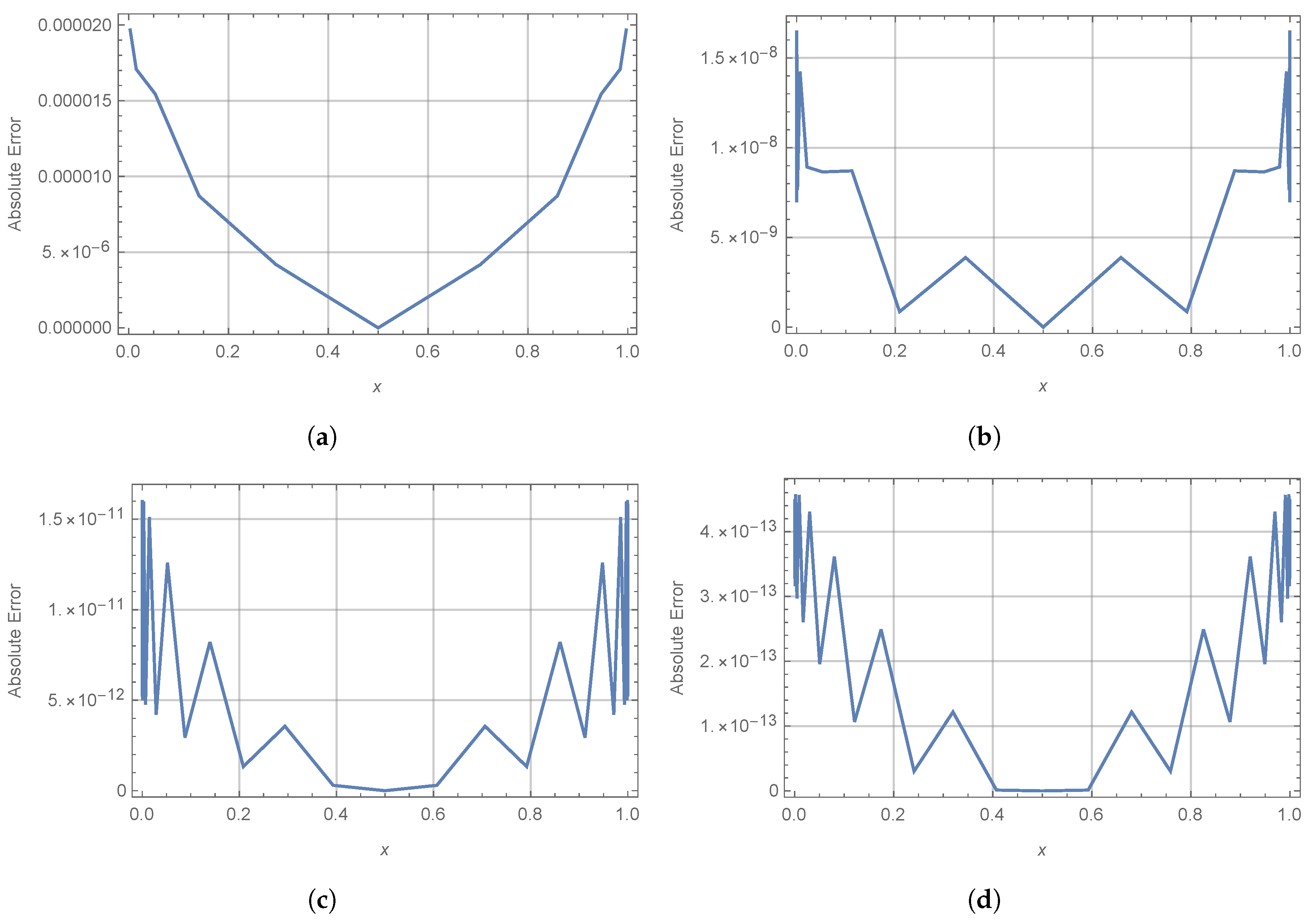
4. Numerical Illustrations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Il’in, V.A.; Moiseev, E.I. Nonlocal boundary value problem of the first kind for a Sturm–Liouville operator in its differential and finite difference aspects. Differ. Equ. 1987, 23, 803–810. [Google Scholar]
- Il’in, V.A.; Moiseev, E.I. Nonlocal boundary value problem of the second kind for a Sturm–Liouville operator. Differ. Equ. 1987, 23, 979–987. [Google Scholar]
- Gupta, C. Solvability of a three-point nonlinear boundary value problem for a second order ordinary differential equation. J. Math. Anal. Appl. 1992, 168, 540–551. [Google Scholar] [CrossRef]
- Ma, R. A survey on nonlocal boundary value problems. Appl. Math. E-Notes 2007, 7, 257–279. [Google Scholar]
- Geng, F.; Cui, M. Multi-point boundary value problem for optimal bridge design. Int. J. Comput. Math. 2010, 87, 1051–1056. [Google Scholar] [CrossRef]
- Moshinsky, M. Sobre los problems de condiciones a la frontiera en una dimension de carac-teristicas discontinuas. Bol. Soc. Mat. Mexicana 1950, 7, 1–25. [Google Scholar]
- Hajji, M.A. Multi-point special boundary-value problems and applications to fluid flow through porous media. In Proceedings of the International Multi-Conference of Engineers and Computer Scientists, Hong Kong, China, 18–20 March 2009. [Google Scholar]
- Saadatmandi, A.; Dehghan, M. The use of Sinc-collocation method for solving multi-point boundary value problems. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 593–601. [Google Scholar] [CrossRef]
- Timoshenko, S. Theory of Elastic Stability; Courier Corporation: Chelmsford, MA, USA, 1961. [Google Scholar]
- Agarwal, R.P.; Thompson, H.B.; Tisdell, C.C. Three-point boundary value problems for second-order discrete equations. Comput. Math. Appl. 2003, 45, 1429–1435. [Google Scholar] [CrossRef]
- Thompson, H.B.; Tisdell, C.C. Three-point boundary value problems for second-order ordinary differential equation. Math. Comput. Model. 2001, 34, 311–318. [Google Scholar] [CrossRef]
- Lepin, A.Y.; Ponomarev, V.D. On a positive solution of a three-point boundary value problem. Differ. Equ. 2006, 42, 291–293. [Google Scholar] [CrossRef]
- Zhang, Z.G.; Liu, L.S.; Wu, C.X. Nontrival solution of third-order nonlinear eigenvalue problems. Appl. Math. Comput. 2006, 176, 714–721. [Google Scholar]
- Pei, M.H.; Chang, S.K. A quasilinearization method for second-order four-point boundary value problems. Appl. Math. Comput. 2008, 202, 54–66. [Google Scholar] [CrossRef]
- Li, X.Y.; Wu, B.Y. A numerical method for solving distributed order diffusion equations. Appl. Math. Lett. 2016, 53, 92–99. [Google Scholar] [CrossRef]
- Dehghan, M. Finite difference procedures for solving a problem arising in modeling and design of certain optoelectronic devices. Math. Comput. Simul. 2006, 71, 16–30. [Google Scholar] [CrossRef]
- Zou, Y.; Hu, Q.; Zhang, R. On numerical studies of multi-point boundary value problems and its fold bifurcation. Appl. Math. Comput. 2007, 185, 527–537. [Google Scholar] [CrossRef]
- Tatari, M.; Dehghan, M. The use of the Adomian decomposition method for solving multi-point boundary value problems. Phys. Scr. 2006, 73, 672–676. [Google Scholar] [CrossRef]
- Urabe, M. Numerical solution of multi-point boundary value problems in Chebyshev series theory of the method. Numer. Math. 1967, 9, 341–366. [Google Scholar] [CrossRef]
- Lentini, M.; Pereyra, V. A variable order finite difference method for nonlinear multipoint boundary value problems. Math. Comput. 1974, 28, 981–1003. [Google Scholar] [CrossRef]
- Ali, J.; Islam, S.; Zaman, G. The solution of multi-point boundary value problems by the optimal homotopy asymptotic method. Comput. Math. Appl. 2010, 59, 2000–2006. [Google Scholar] [CrossRef]
- Li, X.; Wu, B. Reproducing kernel method for singular fourth order four-point boundary value problems. Bull. Malays. Math. Sci. Soc. 2011, 34, 147–151. [Google Scholar]
- Wu, B.; Li, X. Application of reproducing kernel method to third order three-point boundary value problems. Appl. Math. Comput. 2010, 217, 3425–3428. [Google Scholar] [CrossRef]
- Lin, Y.; Cui, M. A numerical solution to nonlinear multi-point boundary value problems in the reproducing kernel space. Math. Methods Appl. Sci. 2011, 34, 44–47. [Google Scholar] [CrossRef]
- Li, X.; Wu, B. Reproducing kernel method for singular multi-point boundary value problems. Math. Sci. 2012, 6, 16–20. [Google Scholar] [CrossRef]
- Azarnavid, B.; Kourosh, P. An iterative reproducing kernel method in Hilbert space for the multi-point boundary value problems. J. Comput. Appl. Math. 2018, 328, 151–163. [Google Scholar] [CrossRef]
- Revelli, R.; Ridolfi, L. Sinc collocation-interpolation method for the simulation of nonlinear waves. Comput. Math. Appl. 2003, 46, 1443–1453. [Google Scholar] [CrossRef]
- Abdella, K.; Yu, X.; Kucuk, I. Application of the Sinc method to a dynamic elasto-plastic problem. J. Comput. Appl. Math. 2009, 223, 626–645. [Google Scholar] [CrossRef][Green Version]
- Parand, K.; Dehghan, M.; Pirkhedri, A. Sinc-collocation method for solving the Blasius equation. Phys. Lett. A 2009, 373, 4060–4065. [Google Scholar] [CrossRef]
- Parand, K.; Pirkhedri, A. Sinc-Collocation method for solving astrophysics equations. New Astron. 2010, 15, 533–537. [Google Scholar] [CrossRef]
- Al-Khaled, K. Numerical approximations for population growth models. Appl. Math. Comput. 2005, 160, 865–873. [Google Scholar] [CrossRef]
- Al-Khaled, K. Numerical study of Fisher’s reaction-diffusion equation by the Sinc collocation method. J. Comput. Appl. Math. 2001, 137, 245–255. [Google Scholar] [CrossRef]
- Winnter, D.F.; Bowers, K.L.; Lund, J. Wind-Driven Currents in a Sea with Variable Eddy Viscosity Calculated via a Sinc-Galerkin Technique. Int. J. Numer. Meth. Fluids 2000, 33, 1041–1073. [Google Scholar] [CrossRef]
- Koonprasert, S.; Bowers, K.L. Block matrix Sinc-Galerkin solution of the wind-driven current problem. Appl. Math. Comput. 2004, 155, 607–635. [Google Scholar] [CrossRef]
- Stenger, F. Numerical Methods Based on Sinc and Analytic Functions; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Lund, J.; Bowers, K.L. Sinc Methods for Quadrature and Differential Equations; Siam: Philadelphia, PA, USA, 1992. [Google Scholar]
- Sugihara, M.; Matsuo, T. Recent developments of the Sinc numerical methods. J. Comput. Appl. Math. 2004, 164, 673–689. [Google Scholar] [CrossRef]
- Sugihara, M. Near optimality of the sinc approximation. Math. Comput. 2003, 72, 767–786. [Google Scholar] [CrossRef]
- Abdella, K. Solving differential equations using Sinc-collocation methods with derivative interpolations. J. Comput. Methods Sci. Eng. 2015, 15, 305–315. [Google Scholar] [CrossRef]
- Burden, R.L.; Faires, J.D. Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Mohseniahouei, Y.; Abdella, K.; Pollanen, M. The application of the Sinc-Collocation approach based on derivative interpolation in numerical oceanography. J. Comput. Sci. 2015, 7, 13–25. [Google Scholar] [CrossRef]
- Abdella, K.; Ross, G.; Mohseniahouei, Y. Solutions to the Blasius and Skiadis problems via sinc-collocation approach. Dyn. Syst. Appl. 2017, 26, 105–120. [Google Scholar]
- Sugihara, M. Double exponential transformation in the Sinc-collocation method. J. Comput. Appl. Math. 2002, 149, 7239–7250. [Google Scholar] [CrossRef]
- Okayama, T.; Matsuo, T.; Sugihara, M. Improvement of a Sinc-collocation method for Fredholm integral equations of the second kind. BIT Numer. Math. 2011, 51, 339–366. [Google Scholar] [CrossRef]
- Rashidinia, J.; Zarebnia, M. Numerical solution of linear integral equations by using sinc-collocation method. Appl. Math. Comput. 2005, 168, 806–822. [Google Scholar] [CrossRef]
- Geng, F.Z. A numerical algorithm for nonlinear multi-point boundary value problems. J. Comput. Appl. Math. 2012, 236, 1789–1794. [Google Scholar] [CrossRef]
- Geng, F.Z. Solving singular second order three-point boundary value problems using Reproduceing kernel Hilbert space method. Appl. Math. Comput. 2009, 215, 2095–2102. [Google Scholar]
- Lie-jun, X.; Cai-lian, Z.; Song, X. A numerical method for third-order non-linear boundary value problems in enginerring. Appl. Math. Comput. 2018, 321, 255–266. [Google Scholar]
- Doha, E.H.; Bhrawy, A.H.; Hafez, R.M. On shifted jacobi spectral method for high-order multi-point boundary value problems. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3802–3810. [Google Scholar] [CrossRef]
- Geng, F.Z.; Qian, S.P. A new reproducing kernel method for linear nonlocal boundary value problems. Appl. Math. Comput. 2014, 248, 421–425. [Google Scholar] [CrossRef]
- Timizi, I.A.; Twizell, E.H.; Islam, S.U. A numerical method for third-order non-linear boundary value problems in enginerring. Int. J. Comput. Math. 2005, 82, 103–109. [Google Scholar] [CrossRef]
- Krajcinvic, D. Sandwitch beam analysis. J. Appl. Mech. 1972, 39, 773–778. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdella, K.; Trivedi, J. Solving Multi-Point Boundary Value Problems Using Sinc-Derivative Interpolation. Mathematics 2020, 8, 2104. https://doi.org/10.3390/math8122104
Abdella K, Trivedi J. Solving Multi-Point Boundary Value Problems Using Sinc-Derivative Interpolation. Mathematics. 2020; 8(12):2104. https://doi.org/10.3390/math8122104
Chicago/Turabian StyleAbdella, Kenzu, and Jeet Trivedi. 2020. "Solving Multi-Point Boundary Value Problems Using Sinc-Derivative Interpolation" Mathematics 8, no. 12: 2104. https://doi.org/10.3390/math8122104
APA StyleAbdella, K., & Trivedi, J. (2020). Solving Multi-Point Boundary Value Problems Using Sinc-Derivative Interpolation. Mathematics, 8(12), 2104. https://doi.org/10.3390/math8122104




