Lorenz Surfaces Based on the Sarmanov–Lee Distribution with Applications to Multidimensional Inequality in Well-Being
Abstract
1. Introduction
2. Preliminary Results
2.1. Univariate Lorenz and Concentration Curves
2.2. The Three Altermative Definitions of Bivariate Lorenz Surface
- The marginal LCs can be obtained as and .
- The bivariate Lorenz surface does not depend on changes of scale in the marginals.
- If is a product distribution function, thenwhich is just the product of the marginal LCs.
- In the case of a product distribution, the two-attribute Gini defined in (4) can be written as,
2.3. Bivariate Lorenz Surface Based on Bivariate Beta-Generated Distributions
2.4. Bivariate Generalized Gini Index
3. The Bivariate Sarmanov–Lee Lorenz Surface
3.1. The Bivariate Sarmanov–Lee Distribution
3.2. The Bivariate Sl Lorenz Surface
3.3. Bivariate Generalized Gini Index
4. Bivariate Lorenz Surface Models
4.1. Bivariate Power Lorenz Surfaces Based on the Fgm Family
4.2. Bivariate Sarmanov–Lee Lorenz Surfaces with Beta and Gb1 Marginals
4.3. Bivariate Sl Lorenz Surfaces with Gamma Marginals
4.4. Bivariate Sl Lorenz Surfaces with Lognormal Marginals
4.5. Other Classes of Bivariate Lorenz Surfaces
5. Extensions to Higher Dimensions and Stochastic Dominance
6. Application: Multidimensional Inequality in Well-Being
6.1. Data and Estimation Methods
- Moments estimation of the marginal distributions. We define,so, point estimates of the couples , are,
- Moment estimation of the dependence parameter. The estimate of w is based on the simple relation . Then, if r denotes the sample linear correlation coefficient, and , the sample standard deviation of the marginal distributions , , the point estimate of w is,
6.2. Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LC | Lorenz curve |
| GB1 | Generalised beta of the first kind |
| FGM | Farlie–Gumbel–Morgenstern |
| SL | Sarmanov–Lee |
| DHS | Demographic and Health Surveys |
| UNDP | United Nations Development Program |
References
- Sen, A. The Concept of Development. In Handbook of Development Economics; Chenery, H., Srinivasan, T.N., Eds.; Elsevier: Amsterdam, The Netherlands, 1988; pp. 9–26. [Google Scholar]
- Sen, A. Development as Capabilities Expansion. J. Dev. Plan. 1989, 19, 41–58. [Google Scholar]
- Sen, A. Development as Freedom; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Jorda, V.; López-Noval, B.; Sarabia, J.M. Distributional dynamics of life satisfaction in Europe. J. Happiness Stud. 2019, 20, 1015–1039. [Google Scholar] [CrossRef]
- Jorda, V.; Sarabia, J.M. International convergence in well-being indicators. Soc. Indic. Res. 2015, 120, 1–27. [Google Scholar] [CrossRef]
- Atkinson, A.B. Multidimensional deprivation: Contrasting social welfare and counting approaches. J. Econ. Inequal. 2003, 1, 51–65. [Google Scholar] [CrossRef]
- Atkinson, A.B.; Bourguignon, F. The comparison of multi-dimensioned distributions of economic status. Rev. Econ. Stud. 1982, 49, 183–201. [Google Scholar] [CrossRef]
- Decancq, K.; Lugo, M.A. Inequality of Wellbeing: A Multidimensional Approach. Economica 2012, 79, 721–746. [Google Scholar] [CrossRef]
- Kolm, S.C. Multidimensional Equalitarianisms. Q. J. Econ. 1977, 91, 1–13. [Google Scholar] [CrossRef]
- Maasoumi, E. The measurement and decomposition of multi-dimensional inequality. Econometrica 1986, 54, 991–997. [Google Scholar] [CrossRef]
- Slottje, D.J. Relative Price Changes and Inequality in the Size Distribution of Various Components. J. Bus. Econ. Stat. 1987, 5, 19–26. [Google Scholar]
- Tsui, K.Y. Multidimensional generalizations of the relative and absolute inequality indices: The Atkinson-Kolm-Sen approach. J. Econ. Theory 1995, 67, 251–265. [Google Scholar] [CrossRef]
- Tsui, K.Y. Multidimensional inequality and multidimensional generalized entropy measures: An axiomatic derivation. Soc. Choice Welf. 1999, 16, 145–157. [Google Scholar] [CrossRef]
- Taguchi, T. On the two-dimensional concentration surface and extensions of concentration coefficient and Pareto distribution to the two-dimensional case-I. Ann. Inst. Stat. Math. 1972, 24, 355–382. [Google Scholar] [CrossRef]
- Taguchi, T. On the two-dimensional concentration surface and extensions of concentration coefficient and Pareto distribution to the two-dimensional case-II. Ann. Inst. Stat. Math. 1972, 24, 599–619. [Google Scholar] [CrossRef]
- Arnold, B.C. Pareto Distributions; International Co-Operative Publishing House: Fairland, MD, USA, 1983. [Google Scholar]
- Koshevoy, G.; Mosler, K. The Lorenz zonoid of a multivariate distribution. J. Am. Stat. Assoc. 1996, 91, 873–882. [Google Scholar] [CrossRef]
- Sarabia, J.M.; Jordá, V. Bivariate Lorenz Curves based on the Sarmanov–Lee Distribution. In Topics in Statistical Simulation, Springer Proceedings in Mathematics & Statistics; Springer: New York, NY, USA, 2014; Volume 114, pp. 447–455. [Google Scholar]
- Lee, M.-L.T. Properties of the Sarmanov Family of Bivariate Distributions. Commun. Stat. Theory Methods 1996, 25, 1207–1222. [Google Scholar]
- Sarmanov, O.V. Generalized Normal Correlation and Two-Dimensional Frechet Classes. Doklady 1966, 168, 596–599. [Google Scholar]
- Gastwirth, J.L. A general definition of the Lorenz curve. Econometrica 1971, 39, 1037–1039. [Google Scholar] [CrossRef]
- Kakwani, N.C. Applications of Lorenz Curves in Economic Analysis. Econometrica 1977, 45, 719–728. [Google Scholar] [CrossRef]
- Taguchi, T. On the structure of multivariate concentration - some relationships among the concentration surface and two variate mean difference and regressions. Comput. Stat. Data Anal. 1988, 6, 307–334. [Google Scholar] [CrossRef]
- Arnold, B.C. Majorization and the Lorenz Curve; Lecture Notes in Statistics 43; Springer: New York, NY, USA, 1987. [Google Scholar]
- Koshevoy, G. Multivariate Lorenz majorization. Soc. Choice Welf. 1995, 12, 93–102. [Google Scholar] [CrossRef]
- Koshevoy, G.; Mosler, K. Multivariate Gini indices. J. Multivar. Anal. 1997, 60, 252–276. [Google Scholar] [CrossRef]
- Mosler, K. Multivariate Dispersion, Central Regions and Depth: The Lift Zonoid Approach; Springer: Berlin, Germany, 2002. [Google Scholar]
- Kleiber, C.; Kotz, S. Statistical Size Distributions in Economics and Actuarial Sciences; John Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Sarabia, J.M.; Prieto, F.; Jordá, V. Bivariate beta-generated distributions with applications to well-being data. J. Stat. Distrib. Appl. 2014, 1, 1–15. [Google Scholar] [CrossRef]
- Alexander, C.; Cordeiro, G.M.; Ortega, E.M.M.; Sarabia, J.M. Generalized beta-generated distributions. Comput. Stat. Data Anal. 2012, 56, 1880–1897. [Google Scholar] [CrossRef]
- Arnold, B.C.; Sarabia, J.M. Analytic Expressions for Multivariate Lorenz Surfaces. Sankhya A Indian J. Stat. 2018, 80, 84–111. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Lai, C.-D. Continuous Bivariate Distributions; Springer: New York, NY, USA, 2009. [Google Scholar]
- Donaldson, D.; Weymark, J.A. A single parameter generalization of the Gin index of inequality. J. Econ. Theory 1980, 22, 67–86. [Google Scholar] [CrossRef]
- Kakwani, N.C. Income Inequality and Poverty, Methods and Estimation and Policy Applications; Oxford University Press: New York, NY, USA, 1980. [Google Scholar]
- Yitzhaki, S. On an extension of the Gini inequality index. Int. Econ. Rev. 1983, 24, 617–628. [Google Scholar] [CrossRef]
- Huang, J.S.; Kotz, S. Modifications of the Farlie-Gumbel-Morgenstern distributions. A tough hill to climb. Metrika 1999, 49, 135–145. [Google Scholar] [CrossRef]
- Bairamov, I.; Kotz, S. On a new family of positive quadrant dependent bivariate distributions. Int. Math. J. 2003, 3, 1247–1254. [Google Scholar]
- Arnold, B.C.; Sarabia, J.M. Majorization and the Lorenz Order with Applications in Applied Mathematics and Economics; Springer: New York, NY, USA, 2018. [Google Scholar]
- McDonald, J.B. Some generalized functions for the size distribution of income. Econometrica 1984, 52, 647–663. [Google Scholar] [CrossRef]
- Sarabia, J.M. Parametric Lorenz Curves: Models and Applications. In Modeling Income Distributions and Lorenz Curves; Chotikapanich, D., Ed.; Springer: New York, NY, USA, 2008; pp. 167–190. [Google Scholar]
- Sarabia, J.M.; Castillo, E.; Pascual, M.; Sarabia, M. Bivariate Income Distributions with Lognormal Conditionals. J. Econ. Inequal. 2007, 5, 371–383. [Google Scholar] [CrossRef]
- Sarabia, J.M.; Castillo, E.; Slottje, D. An Ordered Family of Lorenz Curves. J. Econ. 1999, 91, 43–60. [Google Scholar] [CrossRef]
- Sarabia, J.M.; Castillo, E.; Pascual, M.; Sarabia, M. Mixture Lorenz Curves. Econ. Lett. 2005, 89, 89–94. [Google Scholar] [CrossRef]
- Hlasny, V. Nonresponse Bias in Inequality Measurement: Cross-Country Analysis Using Luxembourg Income Study Surveys. Soc. Sci. Q. 2020, 101, 712–731. [Google Scholar] [CrossRef]
- Jorda, V.; Sarabia, J.M.; Jäntti, M. Estimation of income inequality from grouped data. arXiv 2018, arXiv:1808.09831. [Google Scholar]
- Jenkins, S.P. Pareto models, top incomes and recent trends in UK income inequality. Economica 2017, 84, 261–289. [Google Scholar] [CrossRef]
- Andreoli, F.; Zoli, C. Measuring Dissimilarity; Working Paper Series; Department of Economics University of Verona: Verona, Italy, 2014; Volume 23. [Google Scholar]
- Andreoli, F.; Zoli, C. From unidimensional to multidimensional inequality: A review. Metron 2020, 78, 5–42. [Google Scholar] [CrossRef]
- Stiglitz, J.E.; Sen, A.; Fitoussi, J.P. Report by the Commission on the Measurement of Economic Performance and Social Progress; Citeseer: University Park, PA, USA, 2009. [Google Scholar]
- Hlasny, V.; AlAzzawi, S. Asset inequality in the MENA: The missing dimension? Q. Rev. Econ. Financ. 2019, 73, 44–55. [Google Scholar] [CrossRef]
- Balarajan, Y.; Ramakrishnan, U.; Ozaltin, E.; Shankar, A.H.; Subramanian, S.V. Anaemia in low-income and middle-income countries. Lancet 2011, 378, 2123–2135. [Google Scholar] [CrossRef]
- Scanlon, K.S.; Yip, R.; Schieve, L.A.; Cogswell, M.E. High and low hemoglobin levels during pregnancy: Differential risks for preterm birth and small for gestational age. Obstet. Gynecol. 2000, 96, 741–748. [Google Scholar] [CrossRef]
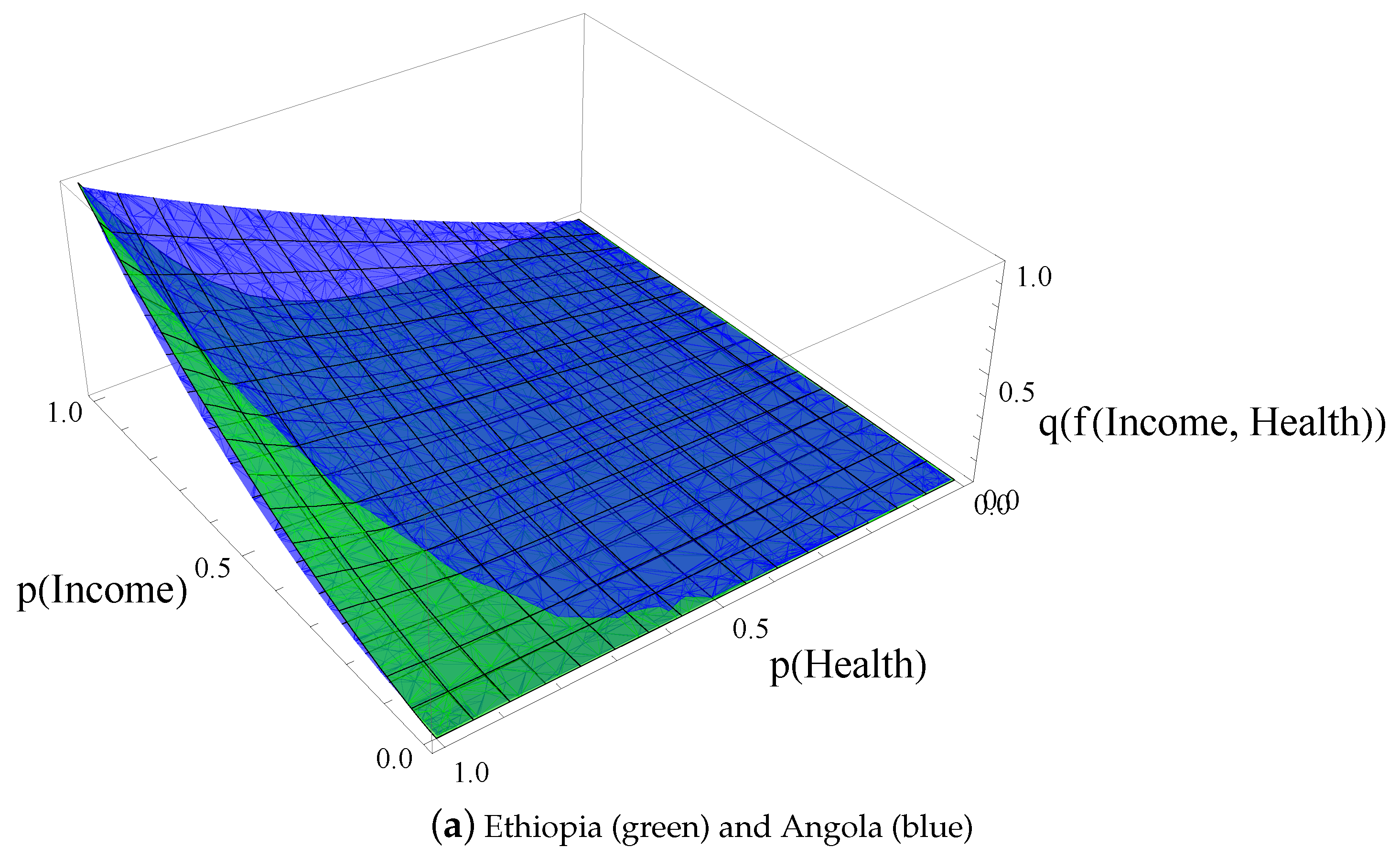
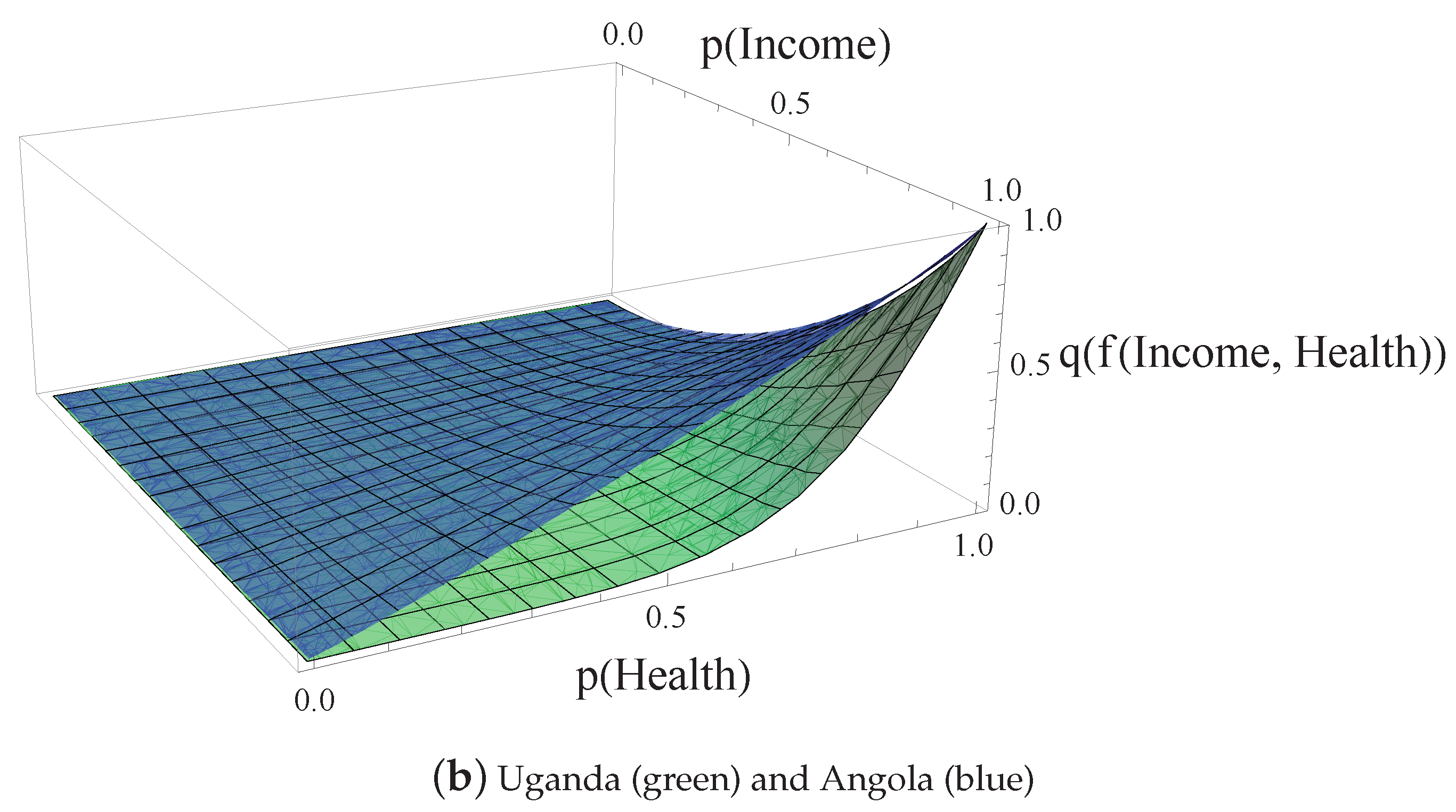
| Income | Health | Dependence | |||
|---|---|---|---|---|---|
| Angola | 1.2660 | 2.0952 | 17.8318 | 29.8269 | 3.6167 |
| (0.0188) | (0.0438) | (1.2273) | (4.2834) | (0.7054) | |
| Ethiopia | 2.8269 | 5.2741 | 0.2338 | 0.6067 | 2.3398 |
| (0.0758) | (0.335) | (0.0147) | (0.027) | (0.114) | |
| Haiti | 1.5794 | 3.8706 | 0.3814 | 1.8932 | 2.8026 |
| (0.0284) | (0.0855) | (0.0231) | (0.0832) | (0.1965) | |
| Nigeria | 0.4532 | 3.1033 | 0.1324 | 0.3306 | 1.1249 |
| (0.012) | (0.0684) | (0.0068) | (0.0144) | (0.1341) | |
| Uganda | 0.9473 | 2.2020 | 0.1994 | 0.6314 | 1.0116 |
| (0.0185) | (0.0539) | (0.0211) | (0.0534) | (0.2055) | |
| Inequality | Equality | |||||
|---|---|---|---|---|---|---|
| Wealth | Health | Bidimensional | Total | Within | Between | |
| Gini | Variables | Variables | ||||
| Angola | 0.3516 | 0.1048 | 0.3943 | 0.6057 | 0.5766 | 0.0291 |
| Ethiopia | 0.2570 | 0.6260 | 0.6921 | 0.3079 | 0.2608 | 0.0471 |
| Haiti | 0.3467 | 0.6214 | 0.7273 | 0.2727 | 0.2294 | 0.0434 |
| Nigeria | 0.6094 | 0.6678 | 0.8640 | 0.1360 | 0.1174 | 0.0186 |
| Uganda | 0.4198 | 0.6680 | 0.7954 | 0.2046 | 0.1799 | 0.0247 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarabia, J.M.; Jorda, V. Lorenz Surfaces Based on the Sarmanov–Lee Distribution with Applications to Multidimensional Inequality in Well-Being. Mathematics 2020, 8, 2095. https://doi.org/10.3390/math8112095
Sarabia JM, Jorda V. Lorenz Surfaces Based on the Sarmanov–Lee Distribution with Applications to Multidimensional Inequality in Well-Being. Mathematics. 2020; 8(11):2095. https://doi.org/10.3390/math8112095
Chicago/Turabian StyleSarabia, José María, and Vanesa Jorda. 2020. "Lorenz Surfaces Based on the Sarmanov–Lee Distribution with Applications to Multidimensional Inequality in Well-Being" Mathematics 8, no. 11: 2095. https://doi.org/10.3390/math8112095
APA StyleSarabia, J. M., & Jorda, V. (2020). Lorenz Surfaces Based on the Sarmanov–Lee Distribution with Applications to Multidimensional Inequality in Well-Being. Mathematics, 8(11), 2095. https://doi.org/10.3390/math8112095





