1. Introduction
The recent decades encountered a tremendous progress in the field of multi-disciplinary simulation tools for continuous time discrete variable systems. A new generation of universal tools and languages for modeling and simulation multi-physical domain applications, such as Modelica [
1], emerged and became widely accepted [
2]; they can be found in commercial and academic high quality implementations and allow to generate large-scale systems of differential algebraic equations (DAEs) automatically. The generated DAEs have many interesting characteristics, such as large scale, high index block structures, which are the major motivation of our work in this paper. In the context of numerical calculation of DAEs, it is well known that a direct numerical simulation without index reduction may not be possible or may provide a bad result [
3,
4]. In brief, higher index DAEs suffer from a rank deficiency in the subset of algebraic equations. The index of a DAE system is a key notion in the theory for measuring the distance from the given system with a singular Jacobian to the corresponding ordinary differential equations with a nonsingular Jacobian. There are various index concepts in the theory of DAEs. The one related to the structural analysis approach is the “structural index”, which is defined by (4). For other indices, we refer the interested readers to [
5,
6]. High-index DAE systems usually need differentiation to reveal all the system’s constraints, which are crucial to determine consistent initial conditions. This procedure is the called “index reduction” of DAEs.
Index reduction in the analysis of DAEs numerical solving is an active technique of research. In [
7], Campbell and Gear gave a derivative-array method to reduce DAEs, which may not be applicable to large-scale nonlinear systems. Pantelides in [
8] constructed a graph-oriented methodology which gives a systematic way to reduce high-index of DAEs with order one to lower index, by selectively adding differentiated forms of the equations already present in the system. In [
9], Mattsson-Söderlind used Pantelides’ method as a preprocessing step, and then differentiated equations in the DAE system with the aid of the information obtained by Pantelides’ method and replaced some derivatives with dummy variables. The dummy method returns a sparse DAEs if the given DAEs is sparse, which can be applied to large-scale DAEs. Pryce in [
10] developed structural analysis method (or Σ method) which is proved to compute the same structural index as Pantelides’ method and is a straightforward method for analyzing the structure of DAEs of any order. This approach is based on solving an assignment problem, which can be formulated as an integer linear programming problem. The idea was generalized to a class of partial differential algebraic equations by Wu et al. [
11]. In [
12,
13], Pryce and Nediakov et al. generalized the structural analysis method to the DAE systems with coarse or fine block-triangular form (BTF), and showed that the difference between the global offsets of signature matrix Σ and the local offsets of each diagonal sub-block in Σ with fine BTF is a constant. They compute the fine BTF for system’s numerical scheme via valid global offset vectors or the local offsets of each separated coarse block. Qin and Tang et al. in [
14] generalized the Σ method for large-scale DAE systems. In addition, there are other index reduction methods for different DAEs [
15,
16,
17,
18,
19,
20,
21]. We focus on structural index reduction method to directly calculate the global canonical offsets of large-scale DAEs with any high order, which are critical for its efficient solution scheme by combing the Pantelides’ method with Pryce’s Σ-method.
The paper is organized as follows. In the next section, we first make necessary preparations and briefly reviews about Pryce’s Σ-method.
Section 3 presents a modified Pantelides’ method derived from Pantelides’ method based on Σ matrix. In
Section 4, we introduce the block triangular forms (BTF) for large-scale DAEs, firstly. Based on our modified Pantelides’ method with parameter, a block Pantelides’ algorithm is proposed to find the canonical offsets of the systems of DAEs. We illustrate the performance of these algorithms via numerical experiments in
Section 5. In the last section, some necessary conclusions are made.
2. Preliminaries
In this section, we give a brief review about the main steps of Pryce’s structural analysis method or Σ-method [
10] and some remarks.
We consider
n dimension DAEs as follows
where
are scalar independent functional variable,
is the derivatives of
,
.
Step 1. Built the
signature matrix
of the DAEs, where
Step 2. Solve an assignment problem to find a highest value transversal (HVT) T, which is a subset of sparsity pattern
S with
n finite entries and describes just one element in each row and each column, such that
is maximized and finite. The sparsity pattern
S of Σ is defined as:
This can be formulated as a Linear Programming Problem, the Primal Problem is:
The problem is equivalent to finding a maximum-weight perfect matching in a bipartite graph whose incidence matrix is the signature matrix, and can be solved by Kuhn-Munkres algorithm [
22] whose time complexity is
.
Step 3. Determine the offsets of the problem, which are the vectors , the smallest such that , for all , and when .
This problem can be formulated as the dual of (2) in the variables
) and
. The Dual Problem is defined as follows:
Step 4. Compute the system Jacobian matrix
, given by
Step 5. Choose a consistent point. If
is nonsingular at that point, then the solution can be computed with Taylor series or numerical homotopy continuation techniques in a neighborhood of that point. And using the canonical offsets
of Problem (3), the structural index is then defined as:
In order to determine the crucial canonical offsets for structural analysis in DAEs system using fixed-point iteration algorithm (FPIA) [
10], we introduce some necessary definitions, firstly. Define a natural semi-ordering of vectors in
, for
,
if
for each
i, the canon of offsets is in the sense of ordering ⪯. Given Σ of DAEs systems and a corresponding transversal
T, for
, we define a mapping
and for
, we define a mapping
Furthermore, we define the composition mapping from to . Then we introduce fixed-point iteration algorithm below.
Remark 1. If the used transversal T is a HVT, Algorithm 1 can find the canonical offsets and for DAE systems by iterations at most, where .
Remark 2. If the Σ matrix of given DAE systems in Problem (3) contains some transversal T, then the canonical dual-optimal pair and can be found in time via the fixed-point iteration algorithm.
| Algorithm 1: Fixed-point Iteration Algorithm (FPIA) |
![Mathematics 08 02057 i001 Mathematics 08 02057 i001]() |
3. A Modified Pantelides’ Method
In this section, we present a modified Pantelides’ method to calculate the canonical offsets for given signature matrix of DAEs system with any high order. Some necessary definitions from are given below.
Definition 1. For and , the Leading Derivative Set is defined asand let denote the set of j indices in the ith row: If I is a set of i-indices, definethat is represents the total set of leading derivatives that appear in the I set of equations. Definition 2 ([
8])
. The set I is structurally singular if has fewer elements than I:where is the cardinality of a set, that is if the I-equations have too few leading derivatives. I is minimal structurally singular if it contains no proper subset. In order to locate the MSS subsets for a given DAEs system, we review the Algorithm 2 (see [
8]) below.
| Algorithm 2: SearchMSS (i,,MARK,MATCH,PATHFOUND) |
![Mathematics 08 02057 i002 Mathematics 08 02057 i002]() |
If Algorithm 2 returns PATHFOUND=TURE, there exists an augmenting path emanating from the i-th equation of DAEs. Otherwise, the MSS subsets was found. MARK is a vector for the functional variables of DAEs. If , this means that the j-th variable has been marked, or it was not unmarked. In addition, MATCH is a matching vector between the equations and the variables of DAEs. MATCH(j) equals 0 which means the j-th variable was not matched. But if MATCH(j) , this means that the j-th variable has been matched with the i-th equation.
Remark 3. If Algorithm 2 returns flag PATHFOUND with value FALSE, then the of equations is MSS with respect to , and .
Based on Algorithm 2, a complete Algorithm 3 below can be constructed to determine an necessary differentiations of system equations.
| Algorithm 3: Modified Pantelides’ Algorithm (MPA) |
![Mathematics 08 02057 i003 Mathematics 08 02057 i003]() |
Lemma 1 ([
10])
. For nonsingular DAE systems, Pantelides’ algorithm gives the same canonical offsets of the DAEs as fixed-point iteration algorithm. Then we are able to give the following theorem.
Theorem 1. For n dimension nonsingular DAE systems with any high order, the modified Pantelides’ algorithm gives the same canonical offsets as the fixed-point iteration algorithm, and the time of the MPA is .
Proof of Theorem 1. Similarly, the proof of the theorem can follow from the Lemma 1 in [
10]. □
Remark 4. From Theorem 1, the modified Pantelides’ algorithm not only is able to calculate the canonical offsets for DAEs with any high order, but also finds a HVT for S(1), which is similar with the Kuhn-Munkres algorithm.
Example 1. The motion of a free pendulum in the Cartesian space can be described by a second-order system of DAEs ,where are constants. From the definition of Σ, labeled by equations and dependent variables, sigma matrix is
where a blank denotes
.
Now, we use Algorithm 3 to compute the canonical offsets of the DAEs and obtain the computational process below.
From
Table 1, we can obtain the canonical offsets
and
, and also get a HVT
via MATCH = (1, 3, 2).
From step 4 in
Section 2, the system Jacobian matrix
is
and
, which means that the modified Pantelides’ algorithm succeeds.
4. Structural Index Reduction Methods for DAEs with Block Structure
In this section, assuming that a given DAE system is structurally nonsingular, i.e., the Σ matrix of the system contains at least one transversal, we can get the block triangular forms of signature matrix
M by permuting its rows and columns [
23,
24],
where the elements in the blanks of
M are
, and the diagonal matrix
is square and irreducible.
The bipartite graph of M or DAE is the undirected graph whose vertices are the n rows and n columns, and which has an edge between row i and column j whenever . We define a structurally nonsingular system of DAE is a coupled system if its graph is connected. In other words, a coupled system does not contains separated subsystems, or the structural analysis can be done in parallel over each subsystem directly and the global canonical offsets of the whole system can be assembled naturally from the local canonical offsets of subsystems.
Next, we propose a block Pantelides’ method for the Σ matrix of a coupled system with BTF whose main idea is to use the modified Pantelies’ method with parameter mentioned below to process each diagonal matrix in block upper triangulated signature matrix from top to bottom in sequence.
4.1. Modified Pantelides’ Method with Parameter
For any given nonnegative parameter , we present a modified Pantelides’ algorithm with parameter (PMPA) just derived from modified Pantelides’ algorithm, and obtain the following Lemma from Theorem 1 easily.
Lemma 2. For a given nonnegative parameter and a nonsingular DAEs system, the modified pantelides’ algorithm with parameter can find the canonical offsets and which satisfies with . And the time of the PMPA is .
It is noted that if for all j, then obtain , which means that the Algorithm 4 is the Algorithm 3.
Example 2. Consider the DAE system from Example 1, and assume parameter , then we also get sigma matrix is Similarly, we use Algorithm 4 to compute the canonical offsets of the DAEs and obtain the computational process below.
From
Table 2, we can obtain the canonical offsets
and
which satisfies with
.
| Algorithm 4: Modified Pantelides’ Algorithm with Parameter (PMPA) |
![Mathematics 08 02057 i004 Mathematics 08 02057 i004]() |
4.2. Block Pantelides’ Method for DAEs with BTF
Since a coupled DAE system is structurally nonsingular, we can obtain the signature matrix M with BTF (13), where and is the order of .
We give some necessary symbols and definitions from [
25] firstly. Assum the parameter vector is
with
ℓ sections, the offsets are
and
, where the dimension of
,
and
are
for
. For any
order matrix
B and
,
n order vector
,
and
,
r order vector
, the mapping
is defined as
, for
; the mapping
is defined via
, for
.
Then we are able to propose Block Pantelides’ algorithm (BPA) for DAEs with block triangular forms by using PMPA.
Lemma 3. Assume that the DAE system is a coupled system, then the block Pantelides’ algorithm gives the same canonical offsets for the system as the modified Pantelides’ algorithm.
Proof of Lemma 3. Similarly, the proof of the Lemma can follow from the Lemma 3.5 in our former article [
25]. □
Moreover, we can obtain the following theorem by Lemma 2 and 3 naturally.
Theorem 2. Assume a system of DAE is a coupled system with BTF (11), then the canonical offsets and of the system can be found in time via the block Pantelides’ algorithm. Furthermore, if for each i, i.e., , then the time is .
Proof of Theorem 2. Combining Remark 2, Lemma 1 with Lemma 3, block Pantelides’ algorithm can obtain the canonical offsets and of the system.
Now, we consider the running time of the algorithm. The time of step 4 in algorithm is
by Lemma 2. For
, the running time of step 6 is
, the time of step 7 and 8 is
, and the running time of step 9 is
by Lemma 2. Thus, the elapsed time of the algorithm is
Therefore, the time complexity of the algorithm is . Moreover, if for each i, then the time is . □
Example 3. Consider a 6 dimension DAEs system as follows,where are constants. Firstly, we get the signature matrix Σ with BTF (19), and use Algorithm 5 to compute the canonical offsets
and
of the DAEs, where
For
,
, then
= PMPA(
) = MPA(
). From Example 1, obtain
and
. For
,
, then
. From Example 2, get
and
. Therefore, we obtain whole canonical offsets
and
for the DAEs.
| Algorithm 5: Block Pantelides’ Algorithm (BPA) |
![Mathematics 08 02057 i005 Mathematics 08 02057 i005]() |
5. Numerical Experimentation
In this section, we do numerical simulation experiments about the running time of structural analysis algorithms for the DAE systems with different scale.
For large-scale or sparse systems produced by multi-domain unified modeling techniques, they always contain several (coupled) subsystems. Considering about the low complexity of block triangulation algorithms [
23], we assume that the signature matrices
M of coupled systems have been changed into the BTFs (13) and that the order of each diagonal block
in
order matrix
M is
r in our experiments, that is
. It is worth noting that the entries of
M are the differential orders in DAEs. We can randomly generate the sparse
M for coupled systems with BTFs simply and properly as follows:
for each element in , randomly select an integer from {0, 1, 2, 3} according to its probability from {0.7, 0.1, 0.1, 0.1}, respectively; and ;
for each element in , randomly select an integer from {-1000, 0, 1, 2} according to its probability from {0.9, 0.05, 0.025, 0.025}, respectively; and ;
the rest elements in M are (means ).
All codes are written in Matlab 2016a under Windows 10 system and run on a personal computer with Intel(R) Core(TM) i5-3570 CPU @
GHz,
GB RAM and 64-bit operating system. We do corresponding random trials for FPIA, extended signature matrix method (ESMM [
14]), MPA and BPA with
and
, and calculate their constants in
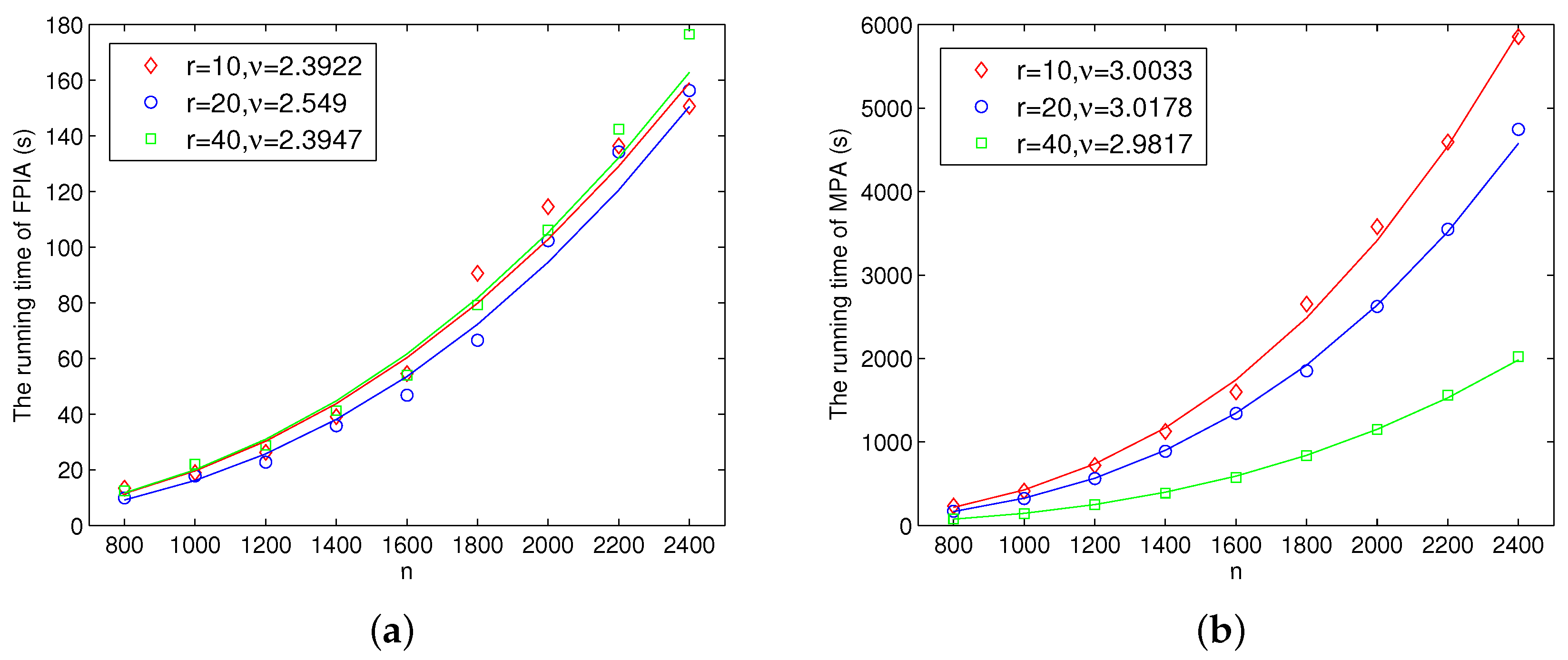
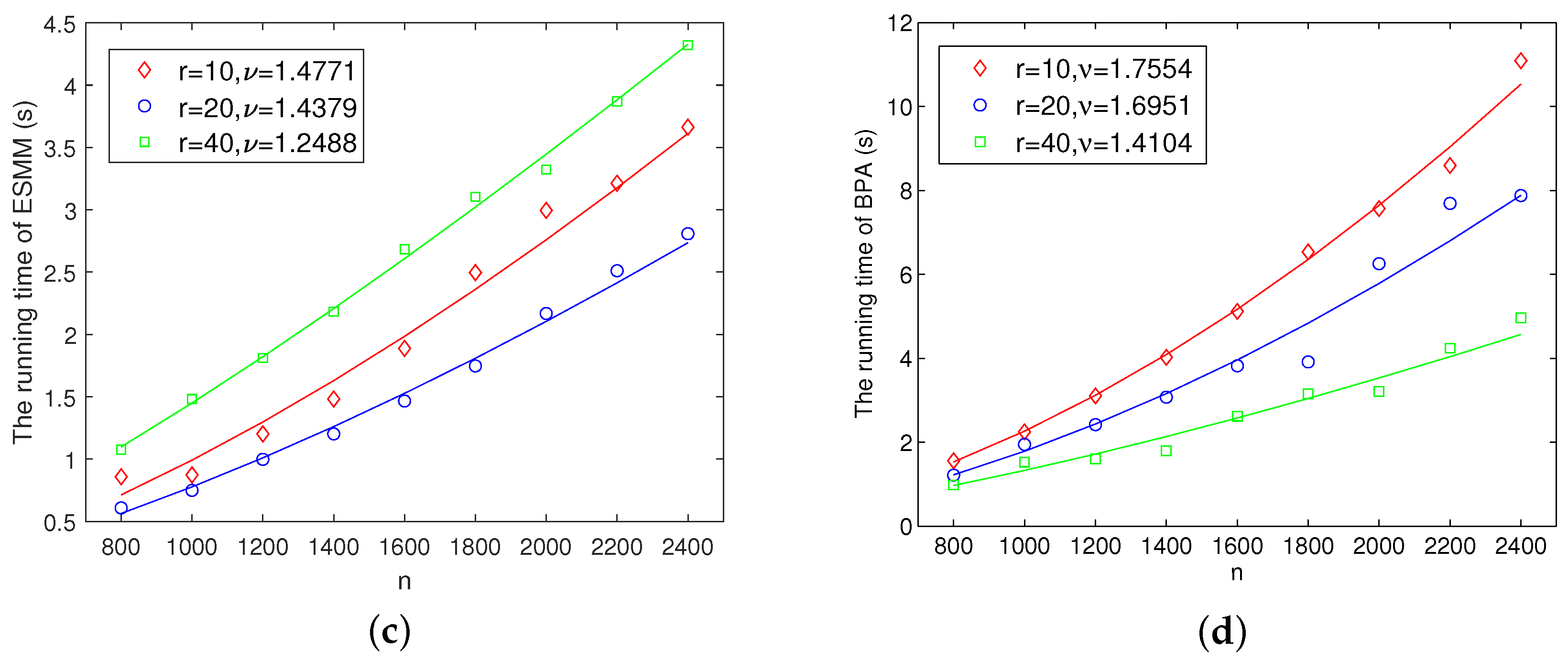
using the standard least-square method. The running times of these algorithms are shown in
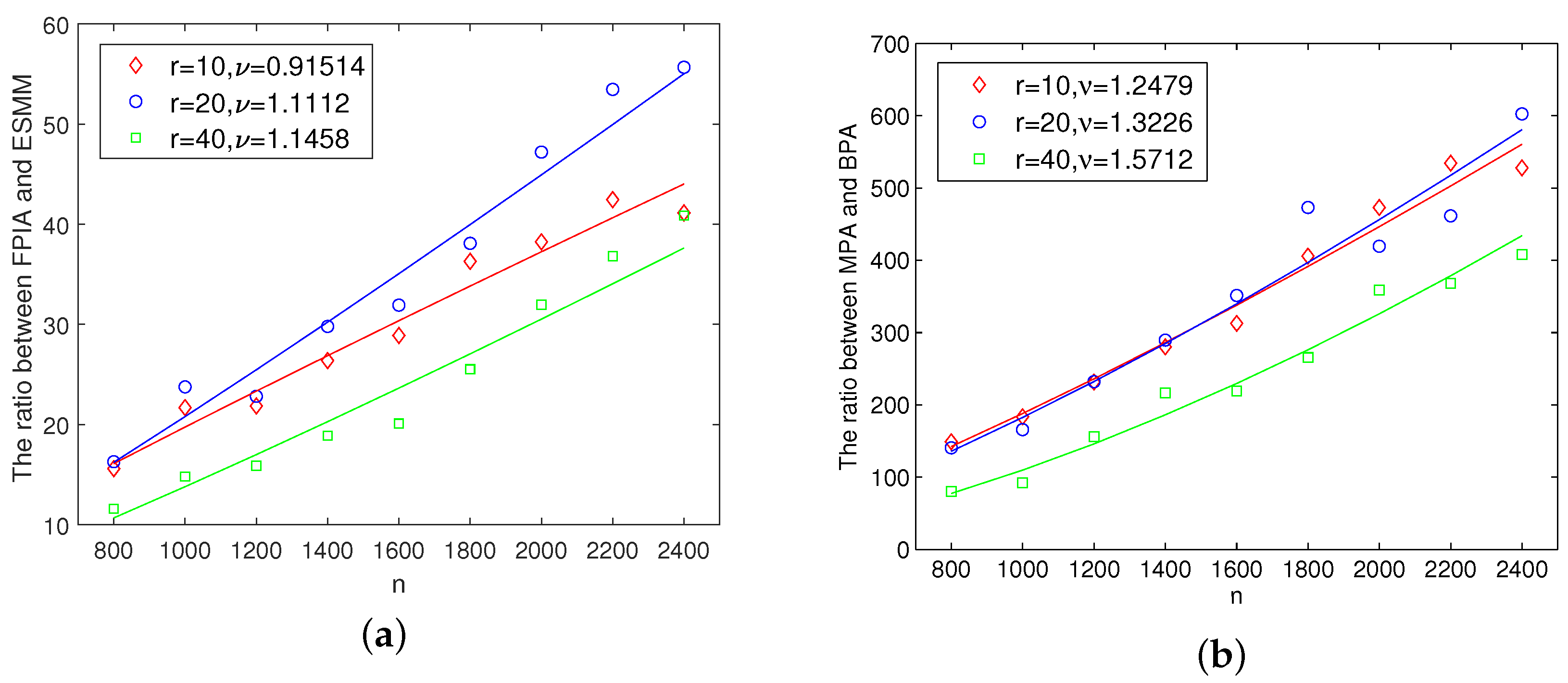
Figure 1, respectively; some ratios of the running times are given in
Figure 2.
As we can observe in
Figure 1, we empirically know that the running times of the BPA for the large-scale DAE systems with different
r are between
and
, FPIA is more like
, and ESMM is between
and
. However, MPA is more like
which is time consuming because of its recursive operations. It is worth noting that the experimental results of the MPA are consistent with Theorem 1.
Observing from
Figure 2, we also know that the ESMM may reduce its running time of large systems for fixed r by nearly
compared to FPIA, while BPA can reduce its running time by at least
(i.e.,
) compared to MPA which is, by and large, consistent with Theorem 2.
In addition, for a fixed n, the running time of the FPIA and ESSM are not influenced basically by the r, while the time of the MPA and BFA decrease with the increase of r. It means that the MPA and BFA may have taken advantage of the intrinsic structure of DAEs.
6. Conclusions
In this article, we first propose a modified Pantelides’ method for any high order DAEs based on its Σ matrix, which is similar to Pryce’s Σ method and also can find a highest value transversal. By introducing a vital parameter vector, a modified Pantelides’ method with parameter has been presented. It leads to a block Pantelides’ method naturally which can be applied to immediately calculate the crucial canonical offsets for large-scale (coupled) systems of DAEs with block-triangular form. The main idea of the block Pantelides’ method is to use the modified Pantelies’ method with parameter to address each diagonal matrix in block upper triangulated signature matrix from top to bottom in sequence. In addition, some examples explain these proposed method clearly, and preliminary numerical experiments show that the time complexity of block Pantelides’ algorithm can be reduced by at least compared to the modified Pantelides’ algorithm.
As the examples showed in [
16,
26,
27], structural index reduction methods including our methods, which ignore numerical information, may fail on some DAEs due to production of a singular Jacobian. Some researchers proposed different index reduction methods [
16,
17,
19,
20] to address this problem for special DAEs which we will consider in the future. Compared with these index reduction methods, our method is able to address a fairly wide class of large-dimension systems of DAEs precisely and efficiently. In the future, the proposed approach will also be applied to exploit some large-scale fractional DAEs [
28] or partial DAEs.