On an Inequality for Legendre Polynomials

Abstract

This paper is concerned with the orthogonal polynomials. Upper and lower bounds of Legendre polynomials are obtained. Furthermore, entropies associated with discrete probability distributions is a topic considered in this paper. Bounds of the entropies which improve some previously known results are obtained in terms of inequalities. In order to illustrate the results obtained in this paper and to compare them with other results from the literature some graphs are provided.

1. Introduction

The classical orthogonal polynomials play an important role in applications of mathematical analysis, spectral method with applications in fluid dynamics and other areas of interest. In the recent years many theoretical and numerical studies about Jacobi polynomials were given. Inequalities for Jacobi polynomials using entropic and information inequalities were obtained in [1]. Bernstein type inequalities for Jacobi polynomials and their applications in many research topics in mathematics were considered in [2]. A very recent conjecture (see [3]) which asserts that the sum of the squared Bernstein polynomials is a convex function in $[0,1]$ was validated using properties of Jacobi polynomials.This conjecture aroused great interest, so that new proofs of it were given (see [4,5]). The main objective of this paper is to obtain upper and lower bounds of Legendre polynomials and to apply these results in order to give lower and upper bounds for entropies. Usually the entropies are described by complicated expressions, then it is useful to establish some bounds of them. The concept of entropy is a measure of uncertainty of a random variable and was introduced by C.E. Shannon in [6]. Later, A. Rényi [7] introduced a parametric family of information measures, that includes Shannon entropy as a special case. The classical Shannon entropy was given using discrete probability distributions. This concept was extended to the continuous case involving the continuous probability distributions. For more details about this topic, the reader is referred to the recent papers [8,9,10,11,12]. This paper is devoted to the entropy associated with discrete probability distribution.

The Jacobi polynomials $P_n^{(\alpha ,\beta )}$ are orthogonal polynomials with respect to the weight ${(1-x)}^{\alpha }{(1+x)}^{\beta }$, $\alpha >-1,\beta >-1$ on the interval $[-1,1]$. Their representation by hypergeometric function is given as follows (see [13,14])

$$P_n^{(\alpha ,\beta )}\left(x\right)=\frac{{(\alpha +1)}_n}{n!}{}_2{F}_1\left(-n,n+\alpha +\beta +1;\alpha +1;\frac{1-x}{2}\right),$$

(1)

where

$${\displaystyle {}_2{F}_1(a,b;c;z)=\sum _{k=0}^{\infty }\frac{{\left(a\right)}_k{\left(b\right)}_k}{{\left(c\right)}_k}·\frac{z^k}{k!},\left|z\right|<1,}$$

and ${\left(a\right)}_k=a(a+1)\dots (a+k-1),k\ge 1$, ${\left(a\right)}_0=1$ is the shifted factorial.

The normalization of $P_n^{(\alpha ,\beta )}$ is effected by

$$P_n^{(\alpha ,\beta )}\left(1\right)={\displaystyle \frac{\Gamma (n+\alpha +1)}{n!\Gamma (\alpha +1)}}.$$

Denote by $R_n^{(\alpha ,\beta )}$ the polynomials:

$$R_n^{(\alpha ,\beta )}\left(x\right)=\frac{P_n^{(\alpha ,\beta )}\left(x\right)}{P_n^{(\alpha ,\beta )}\left(1\right)}.$$

(2)

If $\alpha =\beta =\lambda$, Jacobi’s polynomials $P_n^{(\alpha ,\beta )}\left(x\right)$ are called Gegenbauer polynomials (ultraspherical polynomial). The usual notation and normalization for ultraspherical polynomial is the following (see [15])

$$\begin{array}{cc}\hfill C_n^{\left(\lambda \right)}\left(x\right)& ={\displaystyle \frac{\Gamma (\alpha +1)}{\Gamma (2\alpha +1)}}{\displaystyle \frac{\Gamma (n+2\alpha +1)}{\Gamma (n+\alpha +1)}}{P}_n^{(\alpha ,\alpha )}\left(x\right)\hfill \\ \hfill & ={\displaystyle \frac{\Gamma \left(\lambda +\frac{1}{2}\right)}{\Gamma \left(2\lambda \right)}}{\displaystyle \frac{\Gamma (n+2\lambda )}{\Gamma (n+\lambda +\frac{1}{2})}}{P}_n^{\left(\lambda -\frac{1}{2},\lambda -\frac{1}{2}\right)}\left(x\right),\alpha =\lambda -{\displaystyle \frac{1}{2}}.\hfill \end{array}$$

Note that

$${\displaystyle C_n^{\left(\lambda \right)}\left(x\right)=\frac{{\left(2\lambda \right)}_n}{n!}{R}_n^{(\lambda -\frac{1}{2},\lambda -\frac{1}{2})}\left(x\right)={\displaystyle \frac{{\left(2\lambda \right)}_n}{n!}}{}_2{F}_1\left(-n,n+2\lambda ;\lambda +\frac{1}{2};{\displaystyle \frac{1-x}{2}}\right).}$$

(3)

Some important special cases are the Chebyshev polynomial of the first kind

$$T_n\left(x\right)={\displaystyle \frac{P_n^{\left(-\frac{1}{2},-\frac{1}{2}\right)}\left(x\right)}{P_n^{\left(-\frac{1}{2},-\frac{1}{2}\right)}\left(1\right)}}=R_n^{\left(-\frac{1}{2},-\frac{1}{2}\right)}\left(x\right),$$

(4)

the Chebyshev polynomial of the second kind

$$U_n\left(x\right)=C_n^{\left(1\right)}\left(x\right)=(n+1){\displaystyle \frac{P_n^{\left(\frac{1}{2},\frac{1}{2}\right)}\left(x\right)}{P_n^{\left(\frac{1}{2},\frac{1}{2}\right)}\left(1\right)}}=(n+1)R_n^{\left(\frac{1}{2},\frac{1}{2}\right)}\left(x\right),$$

(5)

and the Legendre polynomial

$$P_n\left(x\right)=C_n^{\left(\frac{1}{2}\right)}\left(x\right)=P_n^{(0,0)}\left(x\right).$$

(6)

2. Preliminary Results

Theorem 1.

Let ${\displaystyle B_{n,k}:=\frac{1}{2^{2n+1}}·\left(\genfrac{}{}{0pt}{}{2k}{k}\right)·\left(\genfrac{}{}{0pt}{}{2n-2k+2}{n-k+1}\right),k,n\in \mathbb{N},k\le n}$. Then, the inequalities

$$\begin{array}{c}{\alpha }_n<B_{n,k}<{\beta }_n,\end{array}$$

(7)

hold for all $n\in \mathbb{N},k\in \mathbb{N}\setminus \left\{0\right\},k\le n$, where

$$\begin{array}{cc}\hfill & {\alpha }_n:=\frac{1}{\pi }·\frac{4}{n+1+\frac{1}{2}+\frac{1}{8(n+1)}},\hfill \\ \hfill & {\beta }_n:=\frac{1}{\pi }·\frac{4\sqrt[4]{46}}{\sqrt{1+(8+\sqrt{46})(n+1)}}.\hfill \end{array}$$

Proof. 

In order to prove the inequalities (7) we use Tóth’s result (see [16]):

$$\frac{1}{\sqrt{\pi (n+\frac{1}{4}+\frac{1}{32n})}}<{\Omega }_n<\frac{1}{\sqrt{\pi (n+\frac{1}{4}+\frac{1}{46n})}},$$

(8)

where ${\displaystyle {\Omega }_n=\frac{1·3···(2n-1)}{2·4···\left(2n\right)}=\frac{1}{4^n}\left(\begin{array}{c}2n\\ n\end{array}\right)}$ for $n\in {\mathbb{N}}^{*}.$

From (8), it follows that

$$\begin{array}{cc}\hfill & \frac{2}{\pi }·\frac{1}{\sqrt{(k+\frac{1}{4}+\frac{1}{32k})\left[n-k+1+\frac{1}{4}+\frac{1}{32(n-k+1)}\right]}}<B_{n,k}\hfill \\ \hfill & <\frac{2}{\pi }·\frac{1}{\sqrt{(k+\frac{1}{4}+\frac{1}{46k})\left[n-k+1+\frac{1}{4}+\frac{1}{46(n-k+1)}\right]}}.\hfill \end{array}$$

(9)

Let $\alpha \in [\frac{1}{46},\frac{1}{32}]$, and consider $f:D\to \mathbb{R}$ a function defined by

$${\displaystyle f(x,y)=\left(x+\frac{1}{4}+\frac{\alpha }{x}\right)\left(y+\frac{1}{4}+\frac{\alpha }{y}\right),}$$

where $D=\{(x,y)\in {\mathbb{R}}^2|x>0,y>0,x+y=n+1\}$.

Further, we determine the extreme points of function f.

We consider $F(x,y)=f(x,y)+\lambda (x+y-n-1)$. From the system

$$\left\{\begin{array}{c}{F}_x^{\prime }=0\hfill \\ F_y^{\prime }=0\hfill \\ F_{\lambda }^{\prime }=x+y-n-1=0,\hfill \end{array}\right.$$

we get

$$\left\{\begin{array}{c}(y-x)·{\displaystyle \frac{4x^2{y}^2-4\alpha xy-4\alpha (x^2+y^2)-4\alpha xy-\alpha (x+y)-4{\alpha }^2}{4x^2{y}^2}}=0,\hfill \\ (y-x)\{4x^2{y}^2-\alpha [4{(n+1)}^2+n+1+4\alpha ]\}=0,\hfill \end{array}\right.$$

Solving the sistem we obtain the following stationary points:

$$A\left(\frac{n+1}{2},\frac{n+1}{2}\right),B\left(\frac{n+1-\sqrt{{\Delta }^{\prime }}}{2},\frac{n+1+\sqrt{{\Delta }^{\prime }}}{2}\right),C\left(\frac{n+1+\sqrt{{\Delta }^{\prime }}}{2},\frac{n+1-\sqrt{{\Delta }^{\prime }}}{2}\right),$$

where ${\Delta }^{\prime }={(n+1)}^2-2\sqrt{\alpha [4{(n+1)}^2+(n+1)+4\alpha ]}.$

We have,

$${\mathrm{d}}^{2}F(x,y)=F_{x^2}^{″}(x,y)\mathrm{d}{x}^2+2F_{xy}(x,y)\mathrm{d}x\mathrm{d}y+F_{y^2}^{″}(x,y)\mathrm{d}{y}^2=[F_{x^2}^{″}(x,y)-2F_{xy}^{″}+F_{y^2}^{″}(x,y)]\mathrm{d}{x}^2.$$

Since ${\mathrm{d}}^{2}F\left(A\right)<0$, it follows that A is a maximum point for f. For $(x,y)\in \{B,C\}$, we have

$$\begin{array}{ccc}\hfill d^{2}F(x,y)& =& \frac{\alpha }{2x^3{y}^3}[4{(n+1)}^2+(n+1)+4\alpha ]\frac{{(n+1)}^4-4\alpha [4{(n+1)}^2+(n+1)+4\alpha ]}{{(n+1)}^2+4xy}\mathrm{d}{x}^2>0.\hfill \end{array}$$

Then f attains its minimum value at the points B and C

We compute

$$\begin{array}{cc}\hfill f\left(B\right)& =\left(\frac{n+1-\sqrt{{\Delta }^{\prime }}}{2}+\frac{1}{4}+\frac{2\alpha }{n+1-\sqrt{{\Delta }^{\prime }}}\right)\left(\frac{n+1+\sqrt{{\Delta }^{\prime }}}{2}+\frac{1}{4}+\frac{2\alpha }{n+1+\sqrt{{\Delta }^{\prime }}}\right)\hfill \\ \hfill & =\sqrt{\alpha }·\sqrt{4{(n+1)}^2+(n+1)+4\alpha }+\frac{4n+5-32\alpha }{16}.\hfill \end{array}$$

We observe that

$$f\left(C\right)=f\left(B\right)>\frac{1}{\sqrt{46}}\sqrt{4{(n+1)}^2+(n+1)+\frac{2}{23}}+\frac{n+1}{4}>\frac{1}{\sqrt{46}}\left(2n+2+\frac{1}{4}\right)+\frac{n+1}{4},$$

$$f\left(B\right)>\frac{1+(8+\sqrt{46})(n+1)}{4\sqrt{46}},f\left(A\right)=\frac{1}{4}{\left(n+1+\frac{1}{2}+\frac{4\alpha }{n+1}\right)}^2.$$

It follows

$$f\left(B\right)\le f(x,y)\le f\left(A\right),$$

$$\frac{1}{\sqrt{f\left(A\right)}}\le \frac{1}{\sqrt{f(x,y)}}\le \frac{1}{\sqrt{f\left(B\right)}},$$

$$\frac{2}{n+1+\frac{1}{2}+\frac{4\alpha }{n+1}}\le \frac{1}{\sqrt{f(x,y)}}\le \frac{2\sqrt[4]{46}}{\sqrt{1+(8+\sqrt{46})(n+1)}}.$$

For ${\displaystyle \alpha \in \left\{\frac{1}{32},\frac{1}{46}\right\}}$ and $k\in \mathbb{N}\setminus \left\{0\right\}$, we obtain (7). □

Remark 1.

The bounds of $B_{n,k}$ for $n\in \mathbb{N}$ and $k=0$ were obtained [16], as follows

$${\displaystyle B_{n-1,0}=\frac{1}{2^{2n-1}}\left(\genfrac{}{}{0pt}{}{2n}{n}\right)\in \left({\displaystyle \frac{2}{\sqrt{\pi \left(n+\frac{1}{4}+\frac{1}{32n}\right)}},\frac{2}{\sqrt{\pi \left(n+\frac{1}{4}+\frac{1}{46n}\right)}}}\right).}$$

(10)

From Theorem 1 and (10), we get

$${\alpha }_n<B_{n,k}<{\gamma }_n,$$

(11)

for all $k=0,1,\cdots ,n$, where ${\gamma }_n:={\displaystyle \frac{2}{\sqrt{\pi \left(n+1+\frac{1}{4}+\frac{1}{46(n+1)}\right)}}}$.

3. Bounds for Legendre Polynomials

Lemma 1.

Let

$${\displaystyle S_n\left(x\right):=\sum _{k=0}^{⌊\frac{n}{2}⌋}{\left[U_{n-2k}\left(\sqrt{\frac{1+x}{2}}\right)\right]}^2,x\in (-1,1),}$$

where $⌊x⌋$ is integer part of positive real number x. The following relation holds

$${\displaystyle S_n\left(x\right)={\displaystyle \frac{1}{2(1-x)}}\left[n+2-U_{n+1}\left(x\right)\right].}$$

(12)

Proof. 

From (1) and (2) the polynomials $R_n^{(\alpha ,\beta )}$ admite the following representation by hypergeometric function

$$R_n^{(\alpha ,\beta )}={}_2{F}_1\left(-n,n+\alpha +\beta +1;\alpha +1;\frac{1-x}{2}\right).$$

(13)

From [14] (eq. 4.7.30, p. 83) we have

$$R_n^{\left(\lambda -\frac{1}{2},\lambda -\frac{1}{2}\right)}\left(x\right)={}_2{F}_1\left(-\frac{n}{2},\frac{n}{2}+\lambda ;\lambda +\frac{1}{2};1-x^2\right).$$

(14)

Therefore,

$$R_{2n}^{(\frac{1}{2},\frac{1}{2})}\left(x\right)={}_2{F}_1\left(-n,n+1;\frac{3}{2};1-x^2\right),$$

$$R_{2n+1}^{(\frac{1}{2},\frac{1}{2})}\left(x\right)={}_2{F}_1\left(-n-\frac{1}{2},n+\frac{3}{2};\frac{3}{2};1-x^2\right).$$

Using the below formula (see [17] ((15.3.3), p. 559))

$${}_2{F}_1(a,b;c;z)={(1-z)}^{c-a-b}{}_2{F}_1(c-a,c-b;c;z),\left|z\right|<1,$$

we obtain

$$R_{2m+1}^{(\frac{1}{2},\frac{1}{2})}\left(x\right)=x{}_2{F}_1(n+2,-n;\frac{3}{2};1-x^2).$$

Then,

$$R_{2n+1}^{(\frac{1}{2},\frac{1}{2})}\left(\sqrt{\frac{1+x}{2}}\right)=\sqrt{\frac{1+x}{2}}{R}_n^{(\frac{1}{2},\frac{1}{2})}\left(x\right).$$

(15)

The link between Chebyshev polynomial of the first and second kind are presented in the following two relations (see [14] (Theorem 4.1, p. 59))

$$\begin{array}{cc}\hfill & T_{2n}\left(x\right)=T_n(2x^2-1),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & 2(1-x^2)U_n^2\left(x\right)=1-T_{2n+2}\left(x\right).\hfill \end{array}$$

(17)

Using relations (15) and (17) we get

$$\begin{array}{cc}\hfill S_{2n+1}\left(x\right)& {\displaystyle =\sum _{k=0}^n{(2n-2k+2)}^2{\left[R_{2n-2k+1}^{\left(\frac{1}{2},\frac{1}{2}\right)}\left(\sqrt{{\displaystyle \frac{1+x}{2}}}\right)\right]}^2}\hfill \\ \hfill & {\displaystyle =\sum _{k=0}^n{(2n-2k+2)}^2{\displaystyle \frac{x+1}{2}}{\left[R_{n-k}^{\left(\frac{1}{2},\frac{1}{2}\right)}\left(x\right)\right]}^2=\sum _{k=0}^{n}2(x+1){\left[U_{n-k}\left(x\right)\right]}^2}\hfill \\ \hfill & {\displaystyle =\sum _{k=0}^n{\displaystyle \frac{1}{1-x}}\left[1-T_{2n-2k+2}\left(x\right)\right]=\sum _{k=0}^n{\displaystyle \frac{1-T_{2k+2}\left(x\right)}{1-x}}.}\hfill \end{array}$$

From relations (16) and (17) it follows

$$\begin{array}{cc}\hfill S_{2n}\left(x\right)& {\displaystyle =\sum _{k=0}^n{\left[U_{2n-2k}\left(\sqrt{{\displaystyle \frac{1+x}{2}}}\right)\right]}^2=\sum _{k=0}^n{\displaystyle \frac{1}{1-x}}\left[1-T_{4n-4k+2}\left(\sqrt{{\displaystyle \frac{1+x}{2}}}\right)\right]}\hfill \\ \hfill & {\displaystyle =\sum _{k=0}^n{\displaystyle \frac{1-T_{2n-2k+1}\left(x\right)}{1-x}}=\sum _{k=0}^n{\displaystyle \frac{1-T_{2k+1}\left(x\right)}{1-x}}.}\hfill \end{array}$$

Using the equalities

$$\sum _{k=0}^n{T}_{2k+1}\left(x\right)=\frac{1}{2}{U}_{2n+1}\left(x\right),\sum _{k=0}^n{T}_{2k}\left(x\right)=\frac{1}{2}\left[1+U_{2n}\left(x\right)\right],$$

we obtain, after a straight forward computation:

$$\begin{array}{cc}\hfill S_{2n+1}\left(x\right)& =\sum _{k=0}^n\frac{1-T_{2k+2}\left(x\right)}{1-x}=\frac{1}{1-x}\left[n+1-\sum _{k=0}^n{T}_{2k+2}\left(x\right)\right]\hfill \\ \hfill & =\frac{1}{1-x}\left[n+1-\sum _{k=1}^{n+1}{T}_{2k}\left(x\right)\right]=\frac{1}{1-x}\left[n+2-\sum _{k=0}^{n+1}{T}_{2k}\left(x\right)\right]\hfill \\ \hfill & =\frac{1}{2(1-x)}\left[2n+3-U_{2n+2}\left(x\right)\right],\hfill \end{array}$$

$$\begin{array}{cc}\hfill S_{2n}\left(x\right)& {\displaystyle =\sum _{k=0}^n{\displaystyle \frac{1-T_{2k+1}\left(x\right)}{1-x}}=\frac{1}{1-x}\left[n+1-\sum _{k=0}^n{T}_{2k+1}\left(x\right)\right]=\frac{1}{2(1-x)}\left[2n+2-U_{2n+1}\left(x\right)\right].}\hfill \end{array}$$

Therefore

$$S_n\left(x\right)=\frac{1}{2(1-x)}[n+2-U_{n+1}\left(x\right)].$$

□

Theorem 2.

Let $P_n$ be the Legendre polynomial of degree $n,n\in \mathbb{N}$. Then, for $x\in (-1,1)$

$${\displaystyle \frac{2}{\pi \left(n+\frac{1}{2}+\frac{1}{8n}\right)}}\left[n+1-U_n\left(x\right)\right]<1-P_n\left(x\right)<{\displaystyle \frac{1}{\sqrt{\pi \left(n+\frac{1}{4}+\frac{1}{46n}\right)}}}\left[n+1-U_n\left(x\right)\right],$$

where $U_n$ is the Chebyshev polynomial of the second kind.

Proof. 

Using the relation (see [18] (p. 713))

$${\displaystyle \sum _{k=0}^n{P}_k^{(\alpha ,0)}\left(x\right)=\sum _{k=0}^{\left[\frac{n}{2}\right]}\frac{{\left(\frac{1}{2}\right)}_k{\left(\frac{\alpha +2}{2}\right)}_{n-k}{\left(\frac{\alpha +3}{2}\right)}_{n-2k}(n-2k)!}{k!{\left(\frac{\alpha +3}{2}\right)}_{n-k}{\left(\frac{\alpha +1}{2}\right)}_{n-2k}{(\alpha +1)}_{n-2k}}{\left[C_{n-2k}^{\left(\frac{\alpha +1}{2}\right)}\left(\sqrt{{\displaystyle \frac{1+x}{2}}}\right)\right]}^2,}$$

we get

$$\begin{array}{cc}\hfill {\displaystyle \sum _{k=0}^n{P}_k^{(1,0)}\left(x\right)}& {\displaystyle =\sum _{k=0}^{\lfloor \frac{n}{2}\rfloor }\frac{{\left(\frac{1}{2}\right)}_k{\left(\frac{3}{2}\right)}_{n-k}}{k!{\left(2\right)}_{n-k}}{\left[C_{n-2k}^{\left(1\right)}\left(\sqrt{{\displaystyle \frac{1+x}{2}}}\right)\right]}^2}\hfill \\ \hfill & {\displaystyle =\sum _{k=0}^{\lfloor \frac{n}{2}\rfloor }{B}_{n,k}{\left[C_{n-2k}^{\left(1\right)}\left(\sqrt{{\displaystyle \frac{1+x}{2}}}\right)\right]}^2.}\hfill \end{array}$$

(18)

The Jacobi polynomials $P_n^{(\alpha ,\beta )},n\in \mathbb{N},\alpha >-1,\beta >-1$ verify the following equality (see [14] ((4.5.4), p. 71)):

$${\displaystyle P_n^{(\alpha +1,\beta )}\left(x\right)=\frac{2}{2n+\alpha +\beta +2}·\frac{1}{1-x}·\left[(n+\alpha +1)P_n^{(\alpha ,\beta )}\left(x\right)-(n+1)P_{n+1}^{(\alpha ,\beta )}\left(x\right)\right].}$$

(19)

From relations (5), (18) and (19) we obtain

$${\displaystyle {\displaystyle \frac{1-P_{n+1}\left(x\right)}{1-x}}=\sum _{k=0}^{\lfloor \frac{n}{2}\rfloor }{B}_{n,k}{\left[U_{n-2k}\left(\sqrt{{\displaystyle \frac{1+x}{2}}}\right)\right]}^2.}$$

Using relation (11), we get

$$\begin{array}{cc}\hfill & {\alpha }_n\sum _{k=0}^{\lfloor \frac{n}{2}\rfloor }{\left[U_{n-2k}\left(\sqrt{{\displaystyle \frac{1+x}{2}}}\right)\right]}^2<\sum _{k=0}^{\lfloor \frac{n}{2}\rfloor }{B}_{n,k}{\left[U_{n-2k}\left(\sqrt{{\displaystyle \frac{1+x}{2}}}\right)\right]}^2<{\gamma }_n\sum _{k=0}^{\lfloor \frac{n}{2}\rfloor }{\left[U_{n-2k}\left(\sqrt{{\displaystyle \frac{1+x}{2}}}\right)\right]}^2.\hfill \end{array}$$

Therefore,

$${\alpha }_n{S}_n<{\displaystyle \frac{1-P_{n+1}\left(x\right)}{1-x}}<{\gamma }_n{S}_n.$$

Consequently,

$$\begin{array}{c}\hfill {\displaystyle \frac{{\alpha }_{n-1}}{2}}\left[n+1-U_n\left(x\right)\right]<1-P_n\left(x\right)<{\displaystyle \frac{{\gamma }_{n-1}}{2}}\left[n+1-U_n\left(x\right)\right],\end{array}$$

(20)

and the Theorem is proved. □

Example 1.

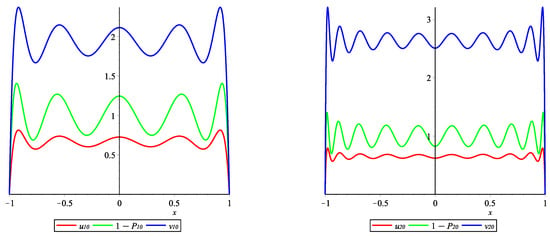
Let $u_n\left(x\right):={\displaystyle \frac{2\left[n+1-U_n\left(x\right)\right]}{\pi \left(n+\frac{1}{2}+\frac{1}{8n}\right)}}$, $v_n\left(x\right):={\displaystyle \frac{\left[n+1-U_n\left(x\right)\right]}{\sqrt{\pi \left(n+\frac{1}{4}+\frac{1}{46n}\right)}}}$. In Figure 1 are given the graphics of the polynomial $1-P_n\left(x\right)$ and the lower and the upper bounds of it obtained in Theorem 2.

Figure 1. Graphs of $u_n$, $v_n$ and $1-P_n$.

4. Bounds for Information Potentials

Let $p\left(x\right)={\left(p_k\left(x\right)\right)}_{k\ge 0}$ be a parameterized discrete probability distribution. The associated information potential is defined by

$${\displaystyle S\left(x\right)=\sum _{k=0}^{\infty }{p}_k^2\left(x\right),x\in T,\mathrm{where}I\mathrm{is}\mathrm{a}\mathrm{real}\mathrm{interval}.}$$

The Rényi entropy of order 2 and the Tsallis entropy of order 2 associated with $p(t,x)$ can be expressed in terms of the information potential $S\left(x\right)$ as follows (see [18] (pp. 20–21)):

$$R\left(x\right):=-logS\left(x\right);T\left(x\right)=1-S\left(x\right).$$

In the following, we consider the binomial distribution $p_{n,k}^{[-1]}$, the Poisson distribution $p_{n,k}^{\left[0\right]}$ and the negative binomial distribution $p_{n,k}^{\left[1\right]}$:

$$\begin{array}{cc}\hfill & p_{n,k}^{[-1]}\left(x\right)=\left(\genfrac{}{}{0pt}{}{n}{k}\right)x^k{(1-x)}^{n-k},x\in [0,1],\hfill \\ \hfill & p_{n,k}^{\left[0\right]}\left(x\right)=e^{-nx}{\displaystyle \frac{{\left(nx\right)}^k}{k!}},x\ge 0,\hfill \\ \hfill & p_{n,k}^{\left[1\right]}\left(x\right)=\left(\genfrac{}{}{0pt}{}{n+k-1}{k}\right)x^k{(1+x)}^{-n-k},x\ge 0.\hfill \end{array}$$

The associated information potentials (index of coincidence) of this distributions are defined as follows:

$$\begin{array}{cc}\hfill & S_{n,-1}\left(x\right):=\sum _{k=0}^n{\left(\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)x^k{(1-x)}^{n-k}\right)}^2,x\in [0,1],\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & S_{n,0}\left(x\right):=e^{-2nx}\sum _{k=0}^{\infty }{\displaystyle \frac{{\left(nx\right)}^{2k}}{{\left(k!\right)}^2}},x\ge 0,\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & S_{n,1}\left(x\right):=\sum _{k=0}^{\infty }{\left(\left({\displaystyle \genfrac{}{}{0pt}{}{n+k-1}{k}}\right)x^k{(1+x)}^{-n-k}\right)}^2,x\ge 0.\hfill \end{array}$$

(23)

From [10] (56) and [12] (21) we know that

$$\begin{array}{cc}\hfill & S_{n,-1}\left(x\right)={\displaystyle \frac{1}{2}}\sum _{k=0}^n{B}_{n-1,k}{(1-2x)}^{2k},\hfill \\ \hfill & S_{n+1,1}\left(x\right)={\displaystyle \frac{1}{2}}\sum _{k=0}^{n-1}{B}_{n-1,k}{(1+2x)}^{-2k-1}.\hfill \end{array}$$

The following lower and upper bounds for the information potential associated to binomial distribution was obtained in [11]:

$${\left[1+(n-3)x(1-x)\right]}^{-\frac{2n}{n-3}}\le S_{n,-1}\left(x\right)\le {\displaystyle \frac{1}{\sqrt{1+4(n-1)x(1-x)}}}.$$

(24)

Using Remark 1 can be obtained new bounds for the information potential $S_{n,-1}$ and $S_{n,1}$ as follows:

Theorem 3.

The following inequalities are satisfied

$${\displaystyle \frac{1}{\pi \left(n+\frac{1}{2}+\frac{1}{8n}\right)}}{\displaystyle \frac{1-{(1-2x)}^{2n+2}}{2x(1-x)}}<S_{n,-1}\left(x\right)<{\displaystyle \frac{1}{\sqrt{\pi \left(n+\frac{1}{4}+\frac{1}{46n}\right)}}}{\displaystyle \frac{1-{(1-2x)}^{2n+2}}{4x(1-x)}},x\in [0,1],$$

(25)

$${\displaystyle \frac{1}{\pi \left(n+\frac{1}{2}+\frac{1}{8n}\right)}}{\displaystyle \frac{1+2x}{2x(1+x)}}\left(1-{\displaystyle \frac{1}{{(1+2x)}^{2n}}}\right)<S_{n+1,1}\left(x\right)$$

$$<{\displaystyle \frac{1}{\sqrt{\pi \left(n+\frac{1}{4}+\frac{1}{46n}\right)}}}{\displaystyle \frac{1+2x}{4x(1+x)}}\left(1-{\displaystyle \frac{1}{{(1+2x)}^{2n}}}\right),x>0.$$

Remark 2.

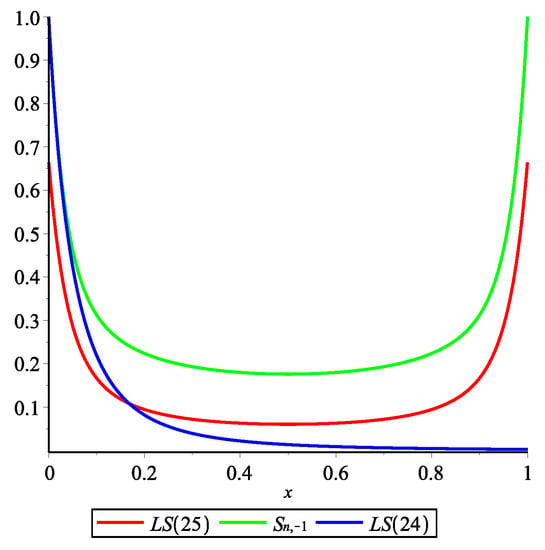
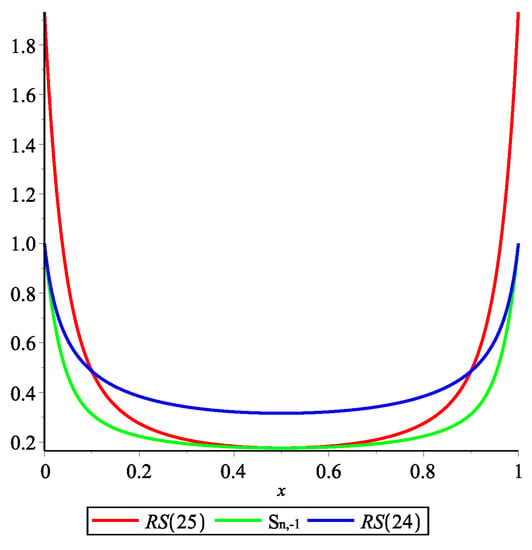
Let $n=10$. In Figure 2 we give a graphical representation of the lower bound of $S_{n,-1}\left(x\right)$ from (24) and (25), respectively. Denote these bounds with LS(24) and LS(25), respectively. In Figure 3 we give a graphical representation of the upper bound of $S_{n,-1}\left(x\right)$ from (24) and (25), respectively. Denote these bounds with RS(24) and RS(25), respectively. Remark that on certain intervals the results obtained in Theorem 3 improve the result from [11].

Figure 2. Graphs of lower bounds of $S_{n,-1}$.

Figure 3. Graphs of upper bounds of $S_{n,-1}$.

5. Conclusions

This paper is devoted to the orthogonal polynomials. Bounds of Legendre polynomials are obtained in terms of inequalities. A more general result in regard with the estimate of the coefficients $B_{n,k}$ is obtained and used in order to give bounds of information potentials associated of the binomial distribution and the negative binomial distribution. The bounds of the entropies are useful especially when they are described by complicated expressions. The results obtained in this paper improve some results from the literature. Motivated by many applications of entropies in secure data transmission, speech coding, cryptography, algorithmic complexity theory, finding such bounds for the entropies will be a topic for future work.