Constrained Mixed-Variable Design Optimization Based on Particle Swarm Optimizer with a Diversity Classifier for Cyclically Neighboring Subpopulations
Abstract
1. Introduction
- (I)
- Most engineering design tasks include multiple real-life physical constraints and thus necessitate PSO techniques that can account for these. Furthermore, such physical constraints are, in general, treated as hard constraints that should be satisfied by any feasible solution found via the optimization procedure.
- (II)
- A large fraction of design problems in engineering fields belong in the category of mixed-integer-discrete-continuous (MIDC) optimization problems and thus particular care has to be taken to find feasible solutions, which makes design tasks more challenging.
2. Engineering Design Problem and Particle Swarm Optimizer
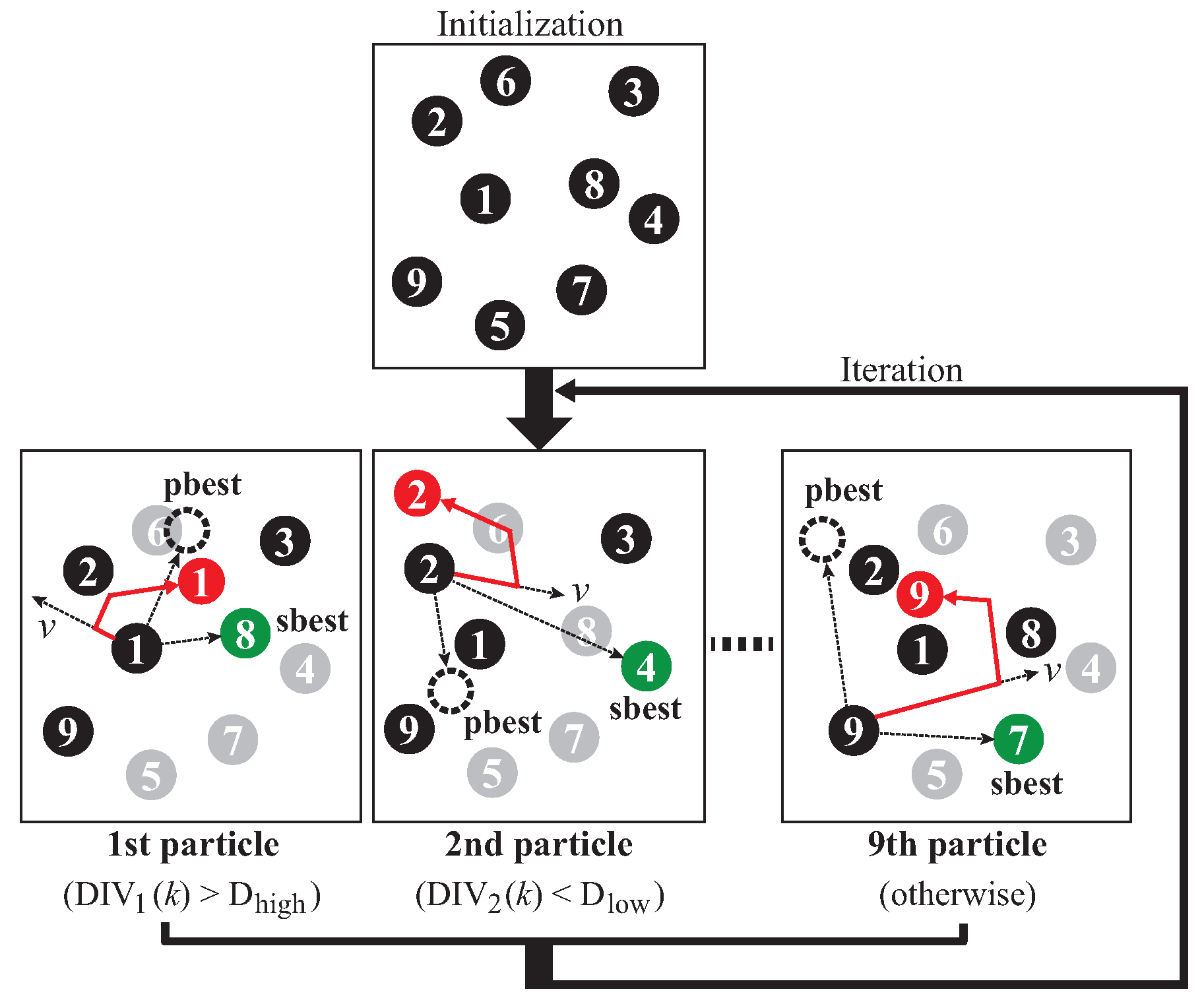
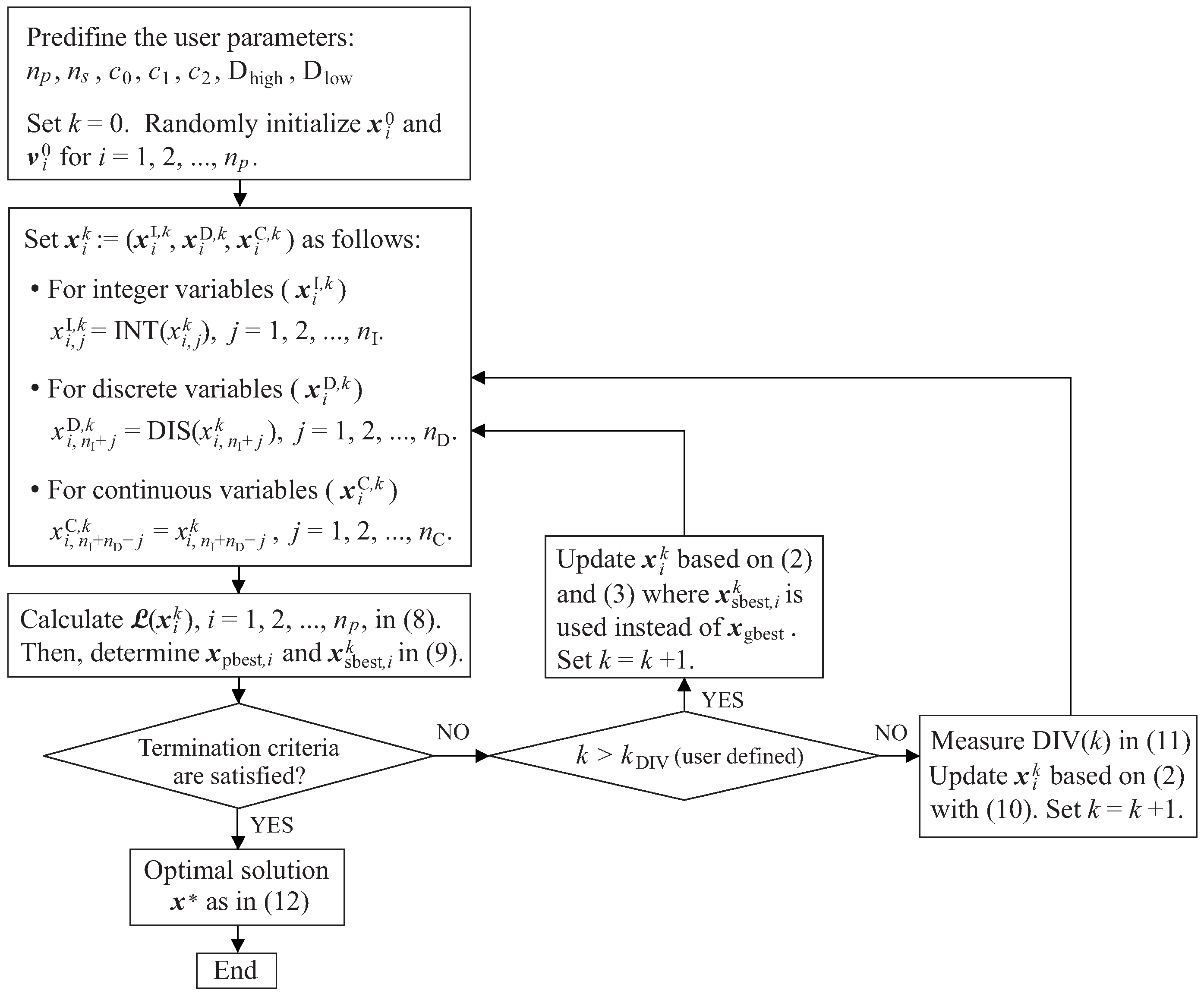
3. PSO with a Diversity Classifier for Cyclically Neighboring Subpopulations
- (I)
- (II)
- For , the variable , which is the jth entry of , denotes the integer design variable and thus must take an integer value. Let denote the nearest integer of . i.e., is rounded to its nearest integer. It then follows that is performed. Similarly, the discrete design variable for takes the value of as . Here, indicates the nearest discrete value that takes in the given data set of discrete design values.
- (III)
4. Numerical Experimentation
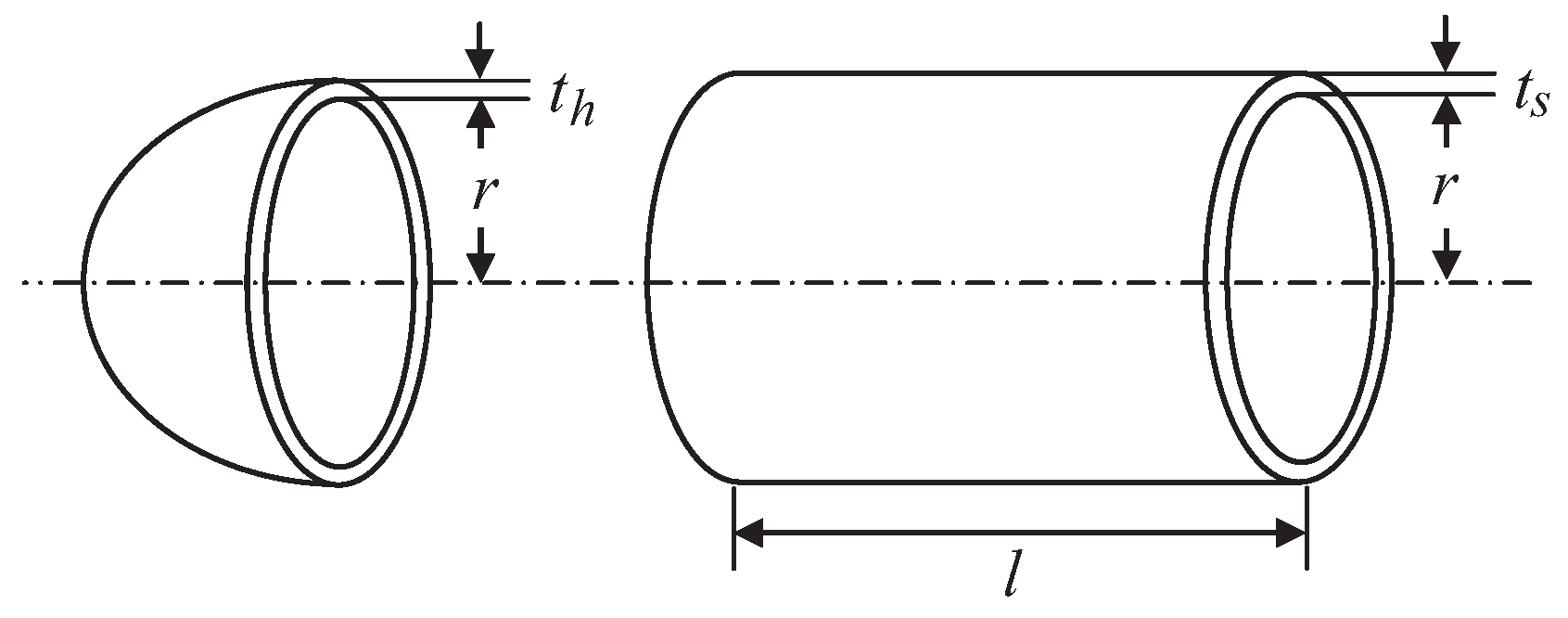
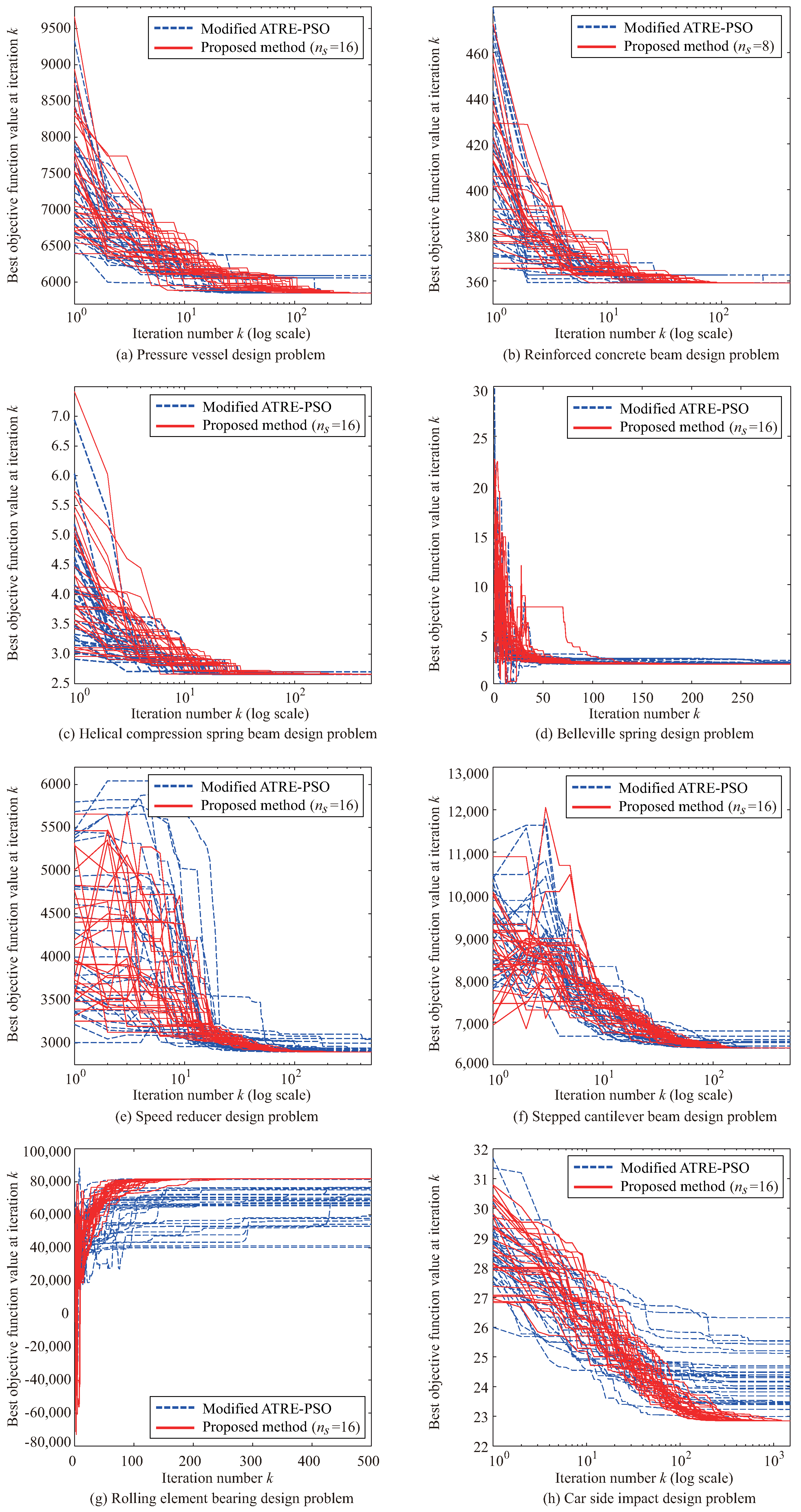
4.1. Optimal Design of Pressure Vessel
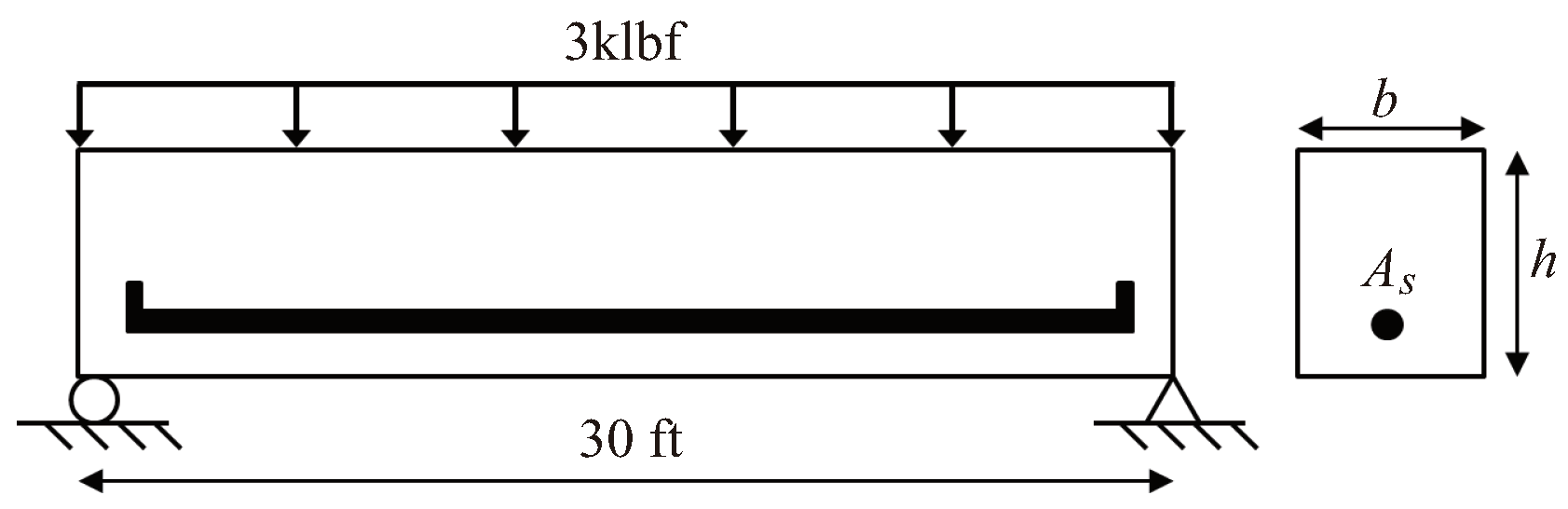
4.2. Optimal Design of Reinforced Concrete Beam
4.3. Optimal Design of Helical Compression Spring
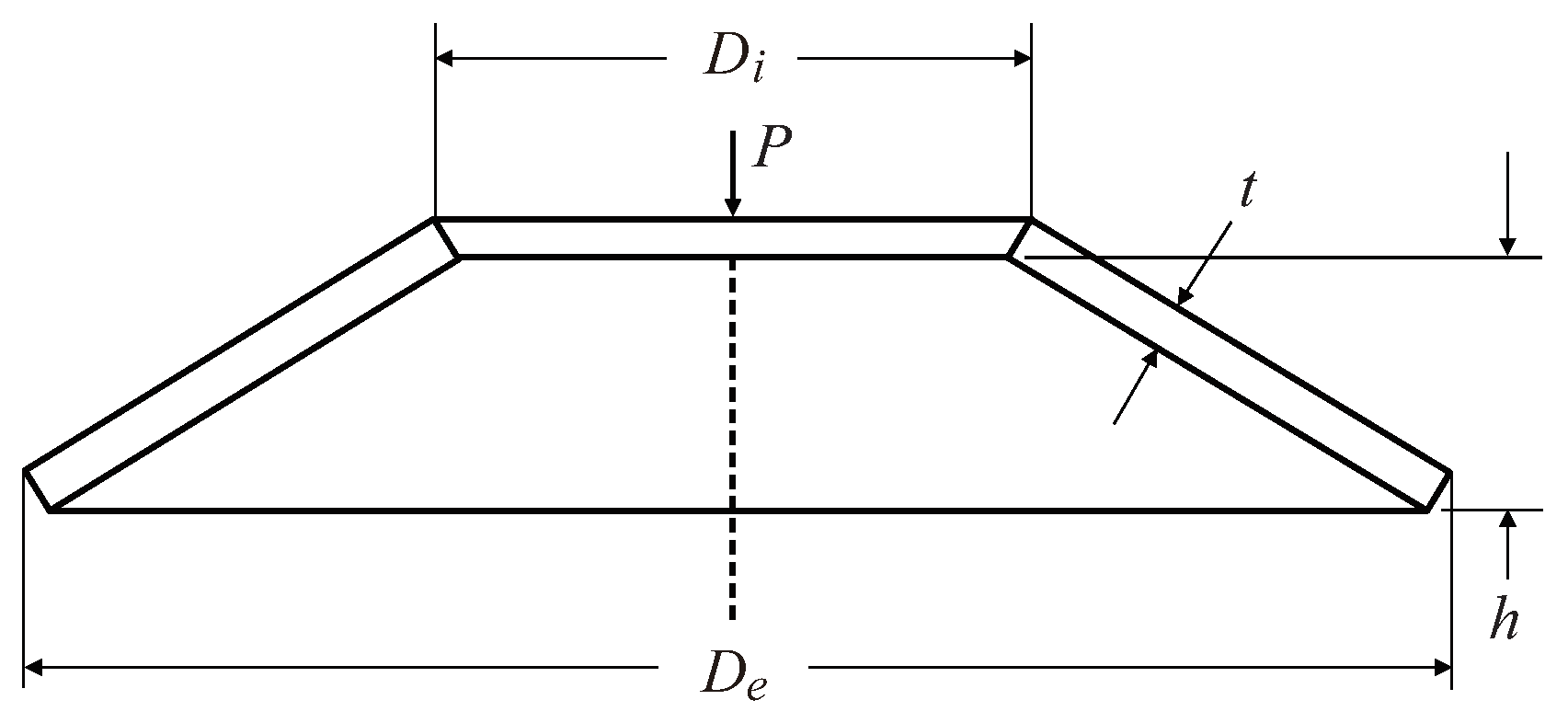
4.4. Optimal Design of Belleville Spring
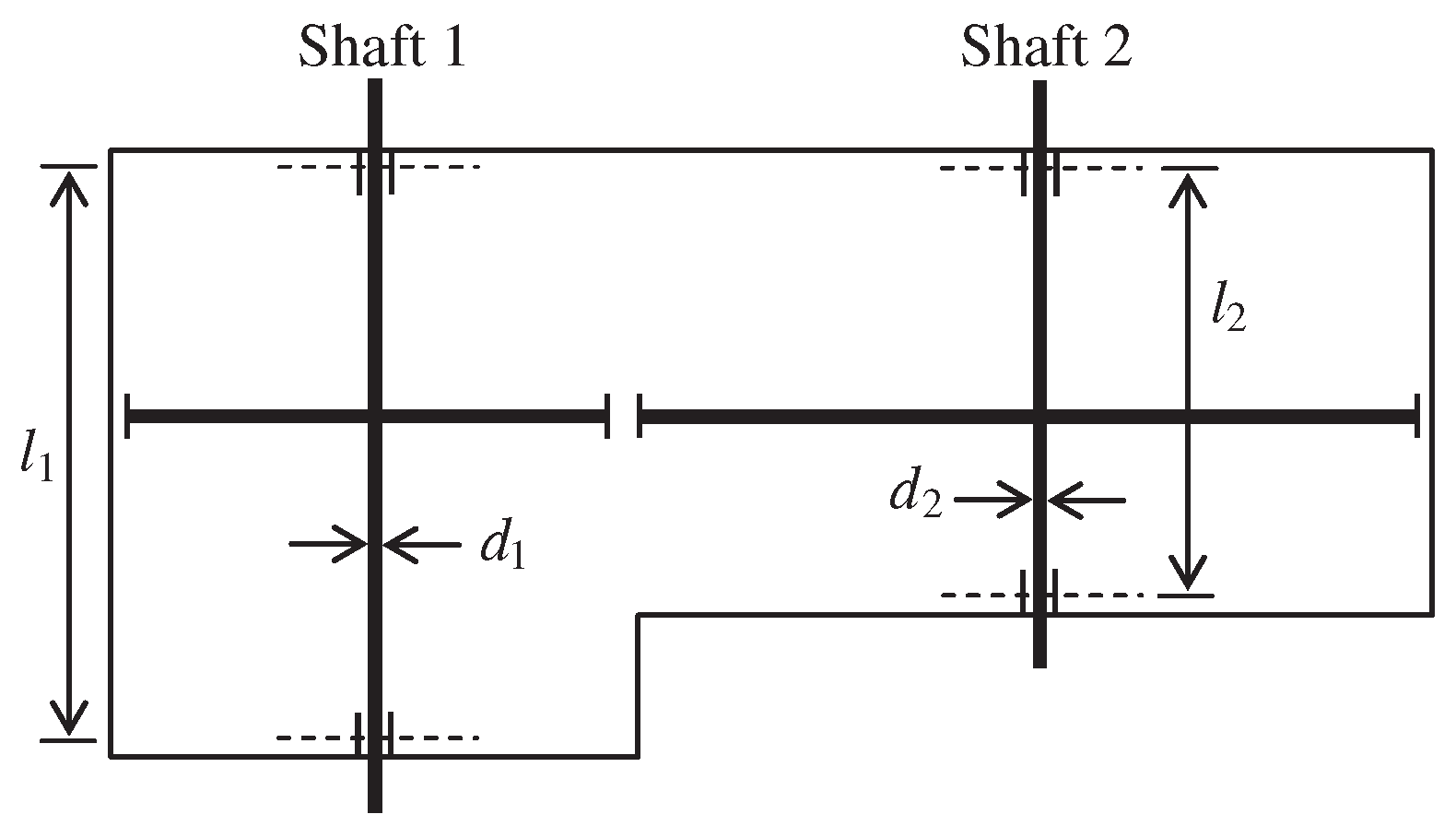
4.5. Optimal Design of Speed Reducer
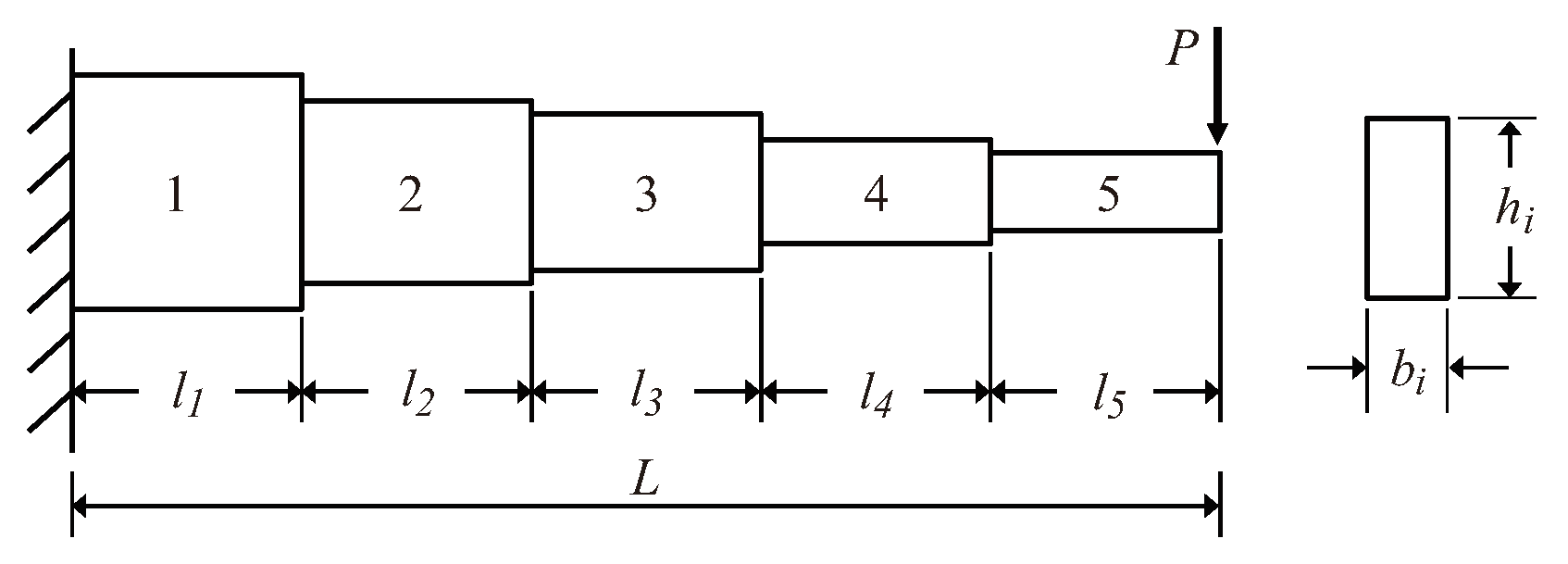
4.6. Optimal Design of Stepped Cantilever Beam
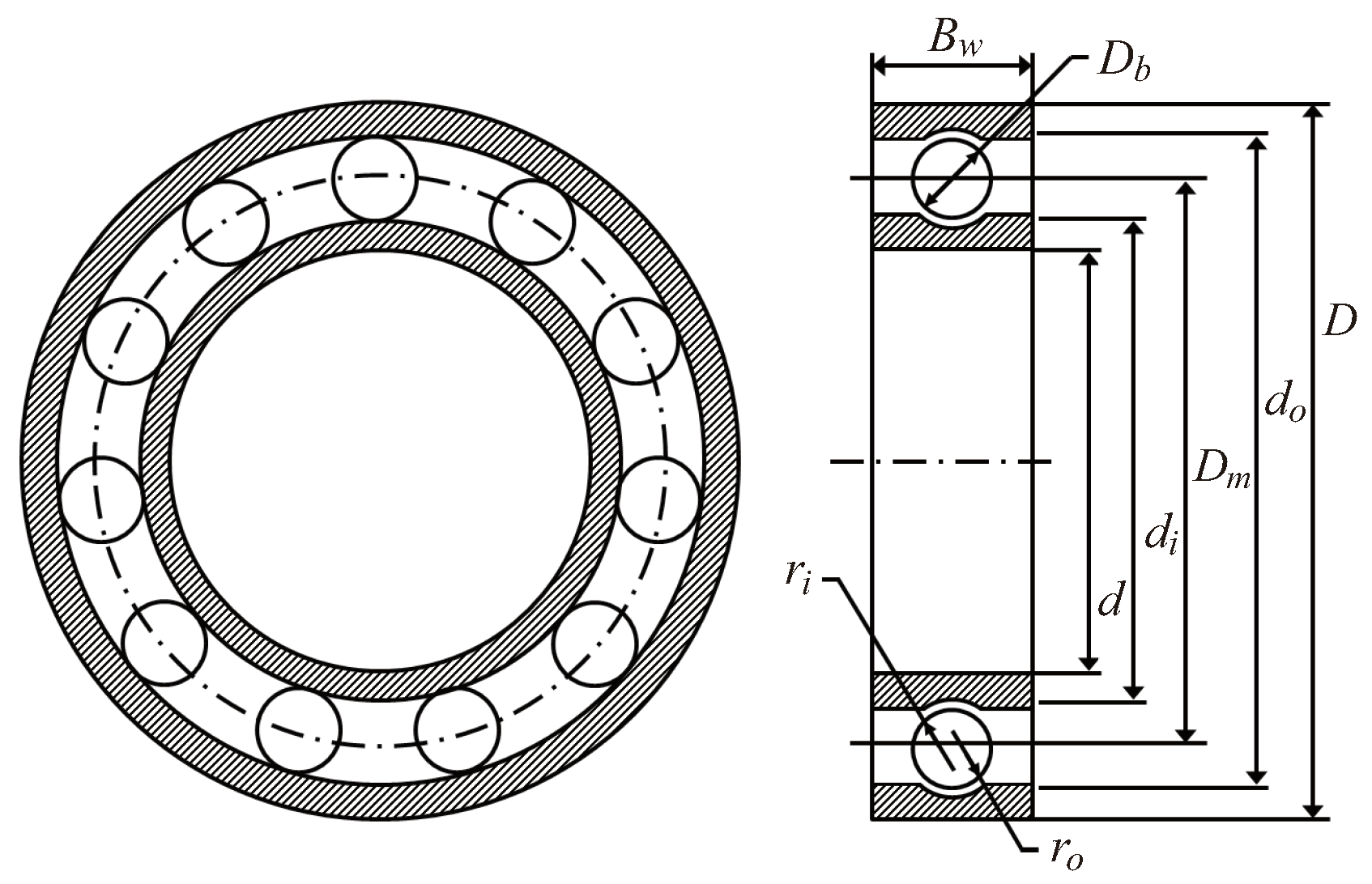
4.7. Optimal Design of Rolling Element Bearing
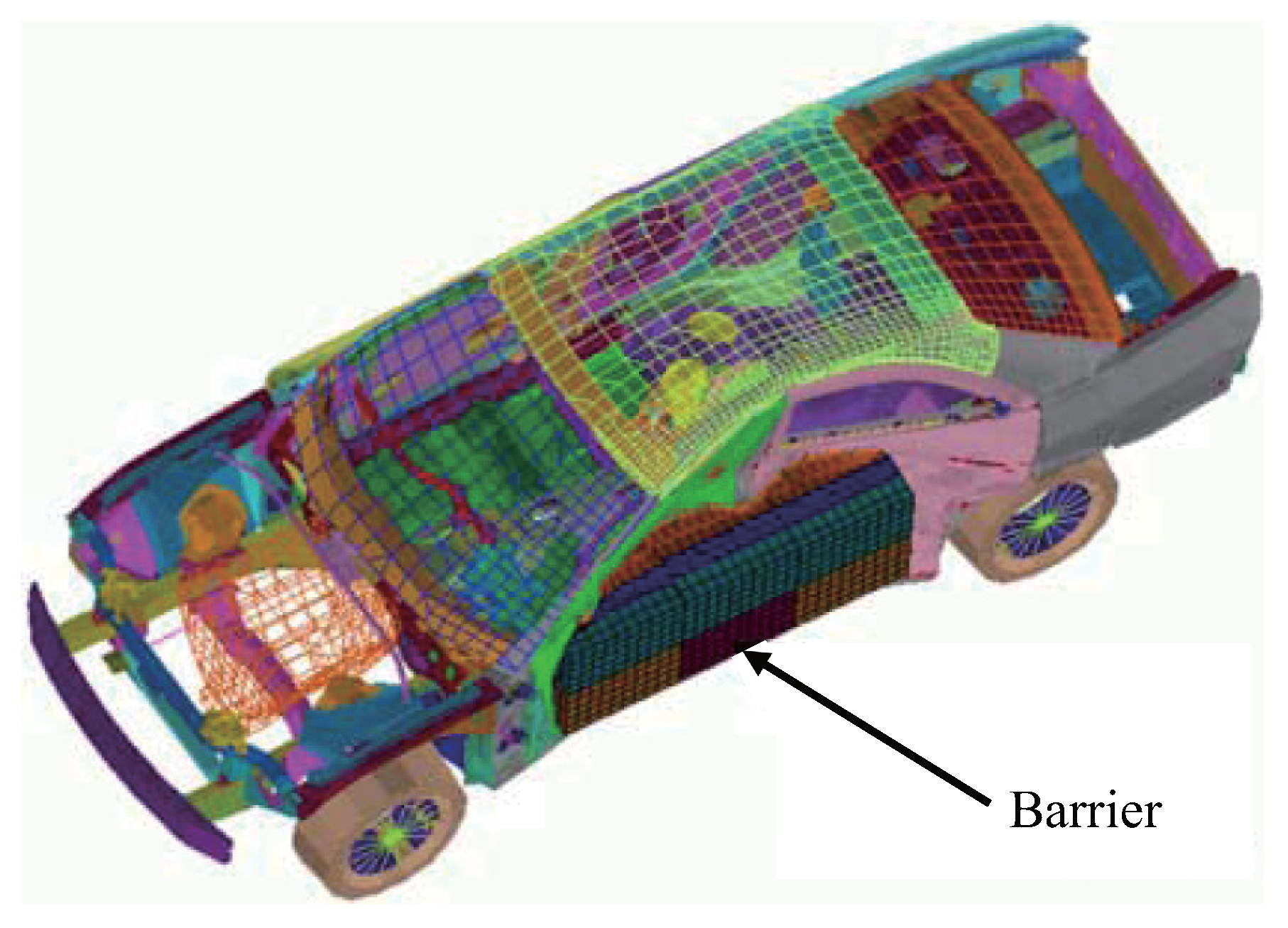
4.8. Car Side Impact Design Problem
4.9. Discussions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Mixed variable structural optimization using firefly algorithm. Comput. Struct. 2011, 89, 2325–2336. [Google Scholar] [CrossRef]
- Datta, D.; Figueira, J.R. A real-integer-discrete-coded particle swarm optimization for design problems. Appl. Soft Comput. 2011, 11, 3625–3633. [Google Scholar] [CrossRef]
- Sadollaha, A.; Bahreininejada, A.; Eskandarb, H.; Hamdia, M. Mine blast algorithm: A new population based algorithm for solving constrained engineering optimization problems. Appl. Soft Comput. 2013, 13, 2592–2612. [Google Scholar] [CrossRef]
- Banks, A.; Vincent, J.; Anyakoha, C. A review of particle swarm optimization. Part I: Background and development. Nat. Comput. 2007, 6, 467–484. [Google Scholar] [CrossRef]
- Banks, A.; Vincent, J.; Anyakoha, C. A review of particle swarm optimization. Part II: Hybridisation, combinatorial, multicriteria and constrained optimization, and indicative applications. Nat. Comput. 2007, 7, 109–124. [Google Scholar] [CrossRef]
- Tomassetti, G. A cost-effective algorithm for the solution of engineering problems with particle swarm optimization. Eng. Optim. 2010, 42, 471–495. [Google Scholar] [CrossRef]
- Pulido, G.T.; Coello, C.A.C. A constraint-handling mechanism for particle swarm optimization. In Proceedings of the 2004 Congress on Evolutionary Computation, Portland, OR, USA, 19–23 June 2004; pp. 1396–1403. [Google Scholar]
- Parsopoulos, K.E.; Vrahatis, M.N. Unified particle swarm optimization for solving constrained engineering optimization problems. In Advances in Natural Computation; Springer: Berlin/Heidelberg, Germany, 2005; pp. 582–591. [Google Scholar]
- Mezura-Montes, E.; Coello Coello, C.A. Constraint-handling in nature-inspired numerical optimization: Past, present and future. Swarm Evol. Comput. 2011, 1, 173–194. [Google Scholar] [CrossRef]
- Chun, S.; Kim, Y.-T.; Kim, T.-H. A diversity-enhanced constrained particle swarm optimizer for mixed integer-discrete-continuous engineering design problems. Adv. Mech. Eng. 2013, 2013, 130750-1–130750-11. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
- Parsopoulos, K.E.; Vrahatisy, M.N. Recent approaches to global optimization problems through particle swarm optimization. Nat. Comput. 2002, 1, 235–306. [Google Scholar] [CrossRef]
- Coelho, L.S. An efficient particle swarm approach for mixed-integer programming in reliability-redundancy optimization applications. Reliab. Eng. Syst. Saf. 2009, 94, 830–837. [Google Scholar] [CrossRef]
- He, S.; Prempain, E.; Wu, Q.H. An improved particle swarm optimizer for mechanical design optimization problems. Eng. Optim. 2004, 36, 585–605. [Google Scholar] [CrossRef]
- Venter, G.; Sobieski, J.S. Particle swarm optimization. AIAA J. 2003, 41, 1583–1589. [Google Scholar] [CrossRef]
- Venter, G.; Sobieski, J.S. Multidisciplinary optimization of a transport aircraft wing using particle swarm optimization. Struct. Multidiscip. Optim. 2004, 26, 121–131. [Google Scholar] [CrossRef]
- Akhtar, S.; Tai, K.; Ray, T. A socio-behavioural simulation model for engineering design optimization. Eng. Optim. 2002, 34, 341–354. [Google Scholar] [CrossRef]
- Cagnina, L.C.; Esquivel, S.C.; Coello Coello, C.A. Solving engineering optimization problems with the simple constrained particle swarm optimizer. Informatica 2008, 32, 319–325. [Google Scholar]
- Coello, C.A.C. Use of a self-adaptive penalty approach for engineering optimization problems. Comput. Ind. 2000, 41, 113–127. [Google Scholar] [CrossRef]
- Hu, X.; Eberhart, R.C.; Shi, Y. Engineering optimization with particle swarm. In Proceedings of the 2003 the IEEE Swarm Intelligence Symposium, Indianapolis, IN, USA, 24–26 April 2003; pp. 53–57. [Google Scholar]
- Lampinen, J.; Zelinka, I. Mixed-integer-discrete-continuous optimization by differential evolution. Part 2. A practical example. In Fifth International Mendel Conference on Soft Computing (MENDEL’99); Brno University of Technology: Brno, Czech Republic, 1999; pp. 77–81. [Google Scholar]
- Liu, H.; Abraham, A.; Zhang, W. A fuzzy adaptive turbulent particle swarm optimization. Int. J. Innov. Comput. Appl. 2007, 1, 39–47. [Google Scholar] [CrossRef]
- Pant, M.; Thangaraj, R.; Abraham, A. Particle swarm optimization: Performance tuning and empirical analysis. In Foundations of Computational Intelligence Volume 3: Global Optimization; Springer: Berlin/Heidelberg, Germany, 2009; pp. 101–128. [Google Scholar]
- Lane, J.; Engelbrecht, A.; Gain, J. Particle swarm optimization with spatially meaningful neighbours. In Proceedings of the 2008 IEEE Swarm Intelligence Symposium, St. Louis, MO, USA, 21–23 September 2008; pp. 1–8. [Google Scholar]
- Richards, M.; Ventura, D. Dynamic sociometry in particle swarm optimization. In Proceedings of the Sixth International Conference on Computational Intelligence and Natural Computing, Cary, NC, USA, 26–30 September 2003; pp. 1557–1560. [Google Scholar]
- Mendes, R.; Neves, J. What makes a successful society? Experiments with population topologies in particle swarms. Lect. Notes Comput. Sci. 2004, 3171, 346–355. [Google Scholar]
- Pant, M.; Radha, T.; Singh, V.P. A simple diversity guided particle swarm optimization. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 3294–3299. [Google Scholar]
- Maruta, I.; Kim, T.-H.; Song, D.H.; Sugie, T. Synthesis of fixed-structure robust controllers using a constrained particle swarm optimizer with cyclic neighborhood topology. Expert Syst. Appl. 2013, 40, 3595–3605. [Google Scholar] [CrossRef]
- Zavala, A.E.M.; Aguirre, A.H.; Diharce, E.V. Robust PSO-based constrained optimization by perturbing the particle’s memory. In Swarm Intelligence: Focus on Ant and Particle Swarm Optimization; I-Tech Education and Publishing: Chicago, IL, USA, 2007; pp. 57–76. [Google Scholar]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput.-Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Mahdavi, M.; Fesanghary, M.; Damangir, E. An improved harmony search algorithm for solving optimization problems. Appl. Math. Comput. 2007, 188, 1567–1579. [Google Scholar] [CrossRef]
- Dimopoulos, G.G. Mixed-variable engineering optimization based on evolutionary and social metaphors. Comput. Methods Appl. Mech. Eng. 2007, 196, 803–817. [Google Scholar] [CrossRef]
- Hedar, A.R.; Fukushima, M. Derivative-free filter simulated annealing method for constrained continuous global optimization. J. Glob. Optim. 2005, 35, 521–649. [Google Scholar] [CrossRef]
- Amir, H.M.; Hasegawa, T. Nonlinear mixed-discrete structural optimization. J. Struct. Eng. 1898, 115, 626–646. [Google Scholar] [CrossRef]
- Shih, C.J.; Yang, Y.C. Generalized Hopfield network based structural optimization using sequential unconstrained minimization technique with additional penalty strategy. Adv. Eng. Softw. 2002, 33, 721–729. [Google Scholar] [CrossRef]
- Mezura-Montes, E.; Hernandez-Ocana, B. Modified bacterial foraging optimization for engineering design. In Intelligent Engineering Systems through Artificial Neural Networks; ASME Press (eBook): New York, NY, USA, 2009; Volume 19, pp. 357–364. [Google Scholar]
- Yun, Y.S. Study on Adaptive Hybrid Genetic Algorithm and Its Applications to Engineering Design Problems. Master’s Thesis, Waseda University, Tokyo, Japan, 2005. [Google Scholar]
- Wu, S.-J.; Chow, P.-T. Genetic algorithms for nonlinear mixed discrete-integer optimization problems via meta-genetic parameter optimization. Eng. Optim. 1995, 24, 137–159. [Google Scholar] [CrossRef]
- Guo, C.; Hu, J.; Ye, B.; Cao, Y. Swarm intelligence for mixed-variable design optimization. J. Zhejiang Univ. Sci. 2004, 5, 851–860. [Google Scholar] [CrossRef]
- Sandgren, E. Nonlinear integer and discrete programming in mechanical design optimization. ASME J. Mech. Des. 1990, 112, 223–229. [Google Scholar] [CrossRef]
- Siddall, J.N. Optimal Engineering Design: Principles and Applications; CRC Press: New York, NY, USA, 1982. [Google Scholar]
- Coello, C.A.C. Treating constraints as objectives for single-objective evolutionary optimization. Eng. Optim. 2000, 32, 275–308. [Google Scholar] [CrossRef]
- Deb, K. GeneAS: A robust optimal design technique for mechanical component design. In Evolutionary Algorithms in Engineering Applications; Springer: Berlin/Heidelberg, Germany, 1997; pp. 497–514. [Google Scholar]
- Liu, H.; Cai, Z.; Wang, Y. Hybridizing particle swarm optimization with differential evolution for constrained numerical and engineering optimization. Appl. Soft Comput. 2010, 10, 629–640. [Google Scholar] [CrossRef]
- Wang, L.; Li, L.P. An effective differential evolution with level comparison for constrained engineering design. Struct. Multidiscip. Optim. 2010, 41, 947–963. [Google Scholar] [CrossRef]
- Chen, T.Y.; Chen, H.C. Mixed-discrete structural optimization using a rank-niche evolution strategy. Eng. Optim. 2009, 41, 39–58. [Google Scholar] [CrossRef]
- Lamberti, L.; Pappalettere, C. Move limits definition in structural optimization with sequential linear programming. Part II: Numerical examples. Comput. Structres 2003, 81, 215–238. [Google Scholar] [CrossRef]
- Thanedar, P.B.; Vanderplaats, G.N. Survey of discrete variable optimization for structural design. J. Struct. Eng. 1995, 121, 301–306. [Google Scholar] [CrossRef]
- Erbatur, F.; Hasancebi, O.; Tutuncu, I.; Kilic, H. Optimal design of planar and space structures with genetic algorithms. Comput. Structres 2000, 75, 209–224. [Google Scholar] [CrossRef]
- Lemonge, A.C.C.; Barbosa, H.J.C. An adaptive penalty scheme for genetic algorithms in structural optimization. Int. J. Numer. Methods Eng. 2004, 59, 703–736. [Google Scholar] [CrossRef]
- Bernardino, H.S.; Barbosa, H.J.C.; Lemonge, A.C.C. A hybrid genetic algorithm for constrained optimization problems in mechanical engineering. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 646–653. [Google Scholar]
- Gupta, S.; Tiwari, R.; Shivashankar, B.N. Multi-objective design optimization of rolling bearings using genetic algorithm. Mech. Mach. Theory 2007, 42, 1418–1443. [Google Scholar] [CrossRef]
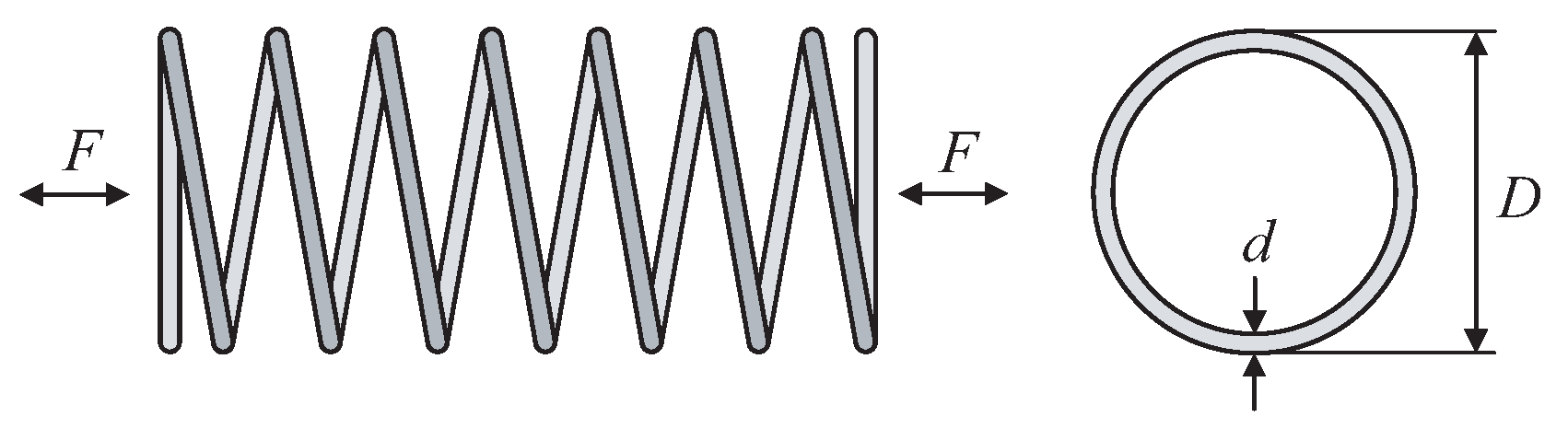

| Method | [32] PSO-GA | [31] HS | [33] SA-DS | [1] FA | [2] PSO | Present Study PSO () |
|---|---|---|---|---|---|---|
| (l) | 221.365487 | 221.36553 | 207.22555 | 221.36547 | 221.365548 | 221.3654714 |
| (r) | 38.860102 | 38.86010 | 39.80962 | 38.86010 | 38.860099 | 38.8601036 |
| () | 0.7500 | 0.75 | 0.7683 | 0.75 | 0.75000 | 0.7500000 |
| () | 0.3750 | 0.375 | 0.3797 | 0.375 | 0.37500 | 0.3750000 |
| −0.0000 | −0.0000 | −0.0000 | −0.0000 | −0.000000 | −0.0000000 | |
| −0.0043 | −0.0043 | −0.0000 | −0.0043 | −0.004275 | −0.0042746 | |
| 0.0446 | 0.2713 | −10.7065 | −0.0134 | −0.000190 | −0.0255540 | |
| −18.6345 | −18.6345 | −32.7744 | −18.6345 | −18.634452 | −18.6345290 | |
| Best objective value | 5850.383064 | 5849.76169 | 5868.76484 | 5850.38306 | 5850.38376 | 5850.38306 |
| Objective deviation a | 1.0 | 1.0 | ||||
| Feasibility | Infeasible | Infeasible | Feasible | Feasible | Feasible | Feasible |
| Worst objective value | N/A b | N/A | 6804.328100 | 6258.96825 | 5850.591797 | 5850.38308 |
| Average objective value | N/A | N/A | 6164. 585867 | 5937.33790 | N/A | 5850.38306 |
| Standard deviation | N/A | N/A | 257.473670 | 164.54747 | N/A | |
| Function evaluations | 100,000 | 200,000 | N/A | 25,000 | 31,436–124,968 | 50,000 |
| Bar Type | () | Bar Type | () | Bar | () | Bar Type | () |
|---|---|---|---|---|---|---|---|
| 1#4 | 0.2 | 6#5 | 1.86 | 9#6 | 3.96 | 12#7 | 7.2 |
| 1#5 | 0.31 | 10#4, 2#9 | 2 | 4#9 | 4 | 13#7 | 7.8 |
| 2#4 | 0.4 | 7#5 | 2.17 | 13#5 | 4.03 | 10#8 | 7.9 |
| 1#6 | 0.44 | 11#4, 5#6 | 2.2 | 7#7 | 4.2 | 8#9 | 8 |
| 3#4, 1#7 | 0.6 | 3#8 | 2.37 | 14#5 | 4.34 | 14#7 | 8.4 |
| 2#5 | 0.62 | 12#4, 4#7 | 2.4 | 10#6 | 4.4 | 11#8 | 8.69 |
| 1#8 | 0.79 | 8#5 | 2.48 | 15#5 | 4.65 | 15#7 | 9 |
| 4#4 | 0.8 | 13#4 | 2.6 | 6#8 | 4.74 | 12#8 | 9.48 |
| 2#6 | 0.88 | 6#6 | 2.64 | 8#7 | 4.8 | 13#8 | 10.27 |
| 3#5 | 0.93 | 9#5 | 2.79 | 11#6 | 4.84 | 11#9 | 11 |
| 5#4, 1#9 | 1 | 14#4 | 2.8 | 5#9 | 5 | 14#8 | 11.06 |
| 6#4, 2#7 | 1.2 | 15#4, 5#7, 3#9 | 3 | 12#6 | 5.28 | 15#8 | 11.85 |
| 4#5 | 1.24 | 7#6 | 3.08 | 9#7 | 5.4 | 12#9 | 12 |
| 3#6 | 1.32 | 10#5 | 3.10 | 7#8 | 5.53 | 13#9 | 13 |
| 7#4 | 1.4 | 4#8 | 3.16 | 13#8 | 5.72 | 14#9 | 14 |
| 5#5 | 1.55 | 11#5 | 3.41 | 10 7, 6#9 | 6 | 15#9 | 15 |
| 2#8 | 1.58 | 8#6 | 3.52 | 14#6 | 6.16 | ||
| 8#4 | 1.6 | 6#7 | 3.6 | 8#8 | 6.32 | ||
| 4#6 | 1.76 | 12#5 | 3.72 | 15#6, 11#7, 7#9 | 6.6 | ||
| 9#4, 3#7 | 1.8 | 5#8 | 3.95 | 9#8 | 7.11 |
| Reference Method | [34] SD-RC a | [35] | [36] BFO | [37] | [1] FA | Present Study PSO () | ||
|---|---|---|---|---|---|---|---|---|
| GHN-ALM b | GHN-EP c | GA | GA-FL | |||||
| () | 7.8 | 6.6 | 6.32 | N/A | 7.20 | 6.16 | 6.32 | 6.32 |
| (b) | 31 | 33 | 34 | N/A | 32 | 35 | 34 | 34 |
| (h) | 7.79 | 8.495227 | 8.637180 | N/A | 8.0451 | 8.7500 | 8.5000 | 8.5000 |
| −0.0205 | −0.1155 | −0.0635 | N/A | −0.0224 | 0 | 0 | 0 | |
| −4.2012 | 0.0159 | −0.7745 | N/A | −2.8779 | −3.6173 | −0.2241 | −0.22409 | |
| Best objective value | 374.2 | 362.2455 | 362.00648 | 376.2977 | 366.1459 | 364.8541 | 359.2080 | 359.2080 |
| Objective deviation | 1.0 | 1.0 | ||||||
| Feasibility | Feasible | Infeasible | Feasible | N/A | Feasible | Feasible | Feasible | Feasible |
| Worst objective value | N/A | N/A | N/A | N/A | N/A | N/A | 669.150 | 359.2080 |
| Average objective value | N/A | N/A | N/A | N/A | 371.5417 | 365.8046 | 460.706 | 359.2080 |
| Standard deviation | N/A | N/A | N/A | N/A | N/A | N/A | 80.73870 | 0.0000 |
| Function evaluations | 396 | N/A | N/A | 100,000 | 100,000 | 30,000 | 25,000 | 20,000 |
| Allowable Wire Diameter (in) | ||||||
|---|---|---|---|---|---|---|
| 0.0090 | 0.0095 | 0.0104 | 0.0118 | 0.0128 | 0.0132 | 0.0140 |
| 0.0150 | 0.0162 | 0.0173 | 0.0180 | 0.0200 | 0.0230 | 0.0250 |
| 0.0280 | 0.0320 | 0.0350 | 0.0410 | 0.0470 | 0.0540 | 0.0630 |
| 0.0720 | 0.0800 | 0.0920 | 0.1050 | 0.1200 | 0.1350 | 0.1480 |
| 0.1620 | 0.1770 | 0.1920 | 0.2070 | 0.2250 | 0.2440 | 0.2630 |
| 0.2830 | 0.3070 | 0.3310 | 0.3620 | 0.3940 | 0.4375 | 0.5000 |
| Notation | Description | Value |
|---|---|---|
| Maximum working load | 1000.0 (lb) | |
| S | Maximum allowable shear stress | (psi) |
| Maximum free length | 14.0 (in) | |
| Minimum wire diameter | 0.2 (in) | |
| Maximum outside spring diameter | 3.0 (in) | |
| Preload compression force | 300.0 (lb) | |
| Maximum allowable deflection | 6.0 (in) | |
| under preload | ||
| Deflection from preload position to | 1.25 (in) | |
| maximum load position | ||
| G | Shear modulus of the material | (psi) |
| Reference Method | [40] NLPA a | [38] GA | [39] HSIA | [21] DE | [14] PSO | [1] FA | [2] PSO | Present Study PSO () |
|---|---|---|---|---|---|---|---|---|
| (D) | 1.180701 | 1.227411 | 1.223 | 1.223041 | 1.223041 | 1.223049 | 1.223041 | 1.223041 |
| (N) | 10 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| (d) | 0.283 | 0.283 | 0.283 | 0.283 | 0.283 | 0.283 | 0.283 | 0.283 |
| 5430.9 | 550.993 | 1008.81 | 1008.8114 | 1008.8114 | 1008.02 | 1008.8059 | 1008.811398 | |
| 8.8187 | 8.9264 | 8.946 | 8.94564 | 8.9456 | 8.946 | 8.945635 | 8.945636 | |
| 0.08298 | 0.0830 | 0.083 | 0.08300 | 0.083 | 0.083 | 0.083000 | 0.083000 | |
| 1.8193 | 1.7726 | 1.77696 | 1.77696 | 1.777 | 1.777 | 1.493959 | 1.493959 | |
| 1.1723 | 1.3371 | 1.32170 | 1.32170 | 1.3217 | 1.322 | 1.321700 | 1.321700 | |
| 5.4643 | 5.4585 | 5.4643 | 5.46429 | 5.4643 | 5.464 | 5.464286 | 5.464286 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0000 | 0 | 0.000000 | 0.000000 | |
| 0.0 | 0.0134 | 0.0 | 0.0 | 0.0000 | 0.0000 | 0.000010 | 0.000000 | |
| Best objective value | 2.7995 | 2.6681 | 2.659 | 2.65856 | 2.65856 | 2.658576 | 2.658559 | 2.658559 |
| Objective deviation | 1.0 | 1.0 | ||||||
| Worst objective value | N/A | N/A | N/A | N/A | N/A | 7.8162919 | N/A | 2.660784 |
| Average objective value | N/A | N/A | N/A | N/A | 2.738024 | 4.3835958 | N/A | 2.658890 |
| Standard deviation | N/A | N/A | N/A | N/A | N/A | 4.6076313 | N/A | 0.000611 |
| Function evaluations | N/A | N/A | N/A | 26,000 | 15,000 | 75,000 | 4784–98,992 | 50,000 |
| a | ≤1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 2.4 | 2.5 | 2.6 | 2.7 | ≥2.8 |
| 0.58 | 1 | 0.85 | 0.77 | 0.71 | 0.66 | 0.63 | 0.6 | 0.56 | 0.55 | 0.53 | 0.52 | 0.51 | 0.51 | 0.5 |
| Reference Method | [42] | [43] | [41] OPTIVAR | [3] NBV | [30] | Present Study PSO () | ||
|---|---|---|---|---|---|---|---|---|
| GeneAS-I | GeneAS-II | ABC | TLBO | |||||
| (t) | 0.208 | 0.205 | 0.210 | 0.204 | 0.204143 | N/A | 0.204143 | 0.204143 |
| (h) | 0.2 | 0.201 | 0.204 | 0.200 | 0.2 | N/A | 0.2 | 0.200000 |
| () | 8.751 | 9.534 | 9.268 | 10.030 | 10.0304732 | N/A | 10.03047 | 10.030473 |
| () | 11.067 | 11.627 | 11.499 | 12.010 | 12.01 | N/A | 12.01 | 12.010000 |
| 2145.4109 | −10.3396 | 2127.2624 | 134.0816 | N/A | ||||
| 39.75018 | 2.8062 | 194.222554 | −12.5328 | N/A | ||||
| 0.00000 | 0.0010 | 0.0040 | 0.0000 | N/A | ||||
| 1.592 | 1.5940 | 1.5860 | 1.5960 | 1.595856 | N/A | 1.595857 | 1.595857 | |
| 0.943 | 0.3830 | 0.5110 | 0.0000 | 0 | N/A | |||
| 2.316 | 2.0930 | 2.2310 | 1.9800 | 1.979526 | N/A | 1.979527 | 1.979527 | |
| 0.21364 | 0.20397 | 0.20856 | 0.19899 | 0.198965 | N/A | 0.198966 | 0.198966 | |
| Best objective value | 2.121964 | 2.01807 | 2.16256 | 1.978715 | 1.979675 | 1.979675 | 1.979675 | 1.979675 |
| Objective deviation | 1.0 | 1.0 | 1.0 | 1.0 | ||||
| Feasibility | Feasible | Infeasible | Feasible | Infeasible | Feasible | N/A | Feasible | Feasible |
| Worst objective value | N/A | N/A | N/A | N/A | 2.005431 | 2.104297 | 1.979757 | 1.979675 |
| Average objective value | N/A | N/A | N/A | N/A | 1.984698 | 1.995475 | 1.979688 | 1.979675 |
| Standard deviation | N/A | N/A | N/A | N/A | 7.78 | 0.07 | 0.45 | 0.000000 |
| Function evaluations | N/A | N/A | N/A | N/A | 15,000 | 150,000 | 150,000 | 50,000 |
| Reference Method | DEDS | DELC | HEAA | MDE | PSO-DE | MBA | Present Study PSO () |
|---|---|---|---|---|---|---|---|
| (b) | 3.5 | 3.5 | 3.500022 | 3.500010 | 3.5000000 | 3.500000 | 3.500000 |
| (m) | 0.7 | 0.7 | 0.70000039 | 0.70000 | 0.700000 | 0.700000 | 0.700000 |
| (n) | 17 | 17 | 17.000012 | 17 | 17.000000 | 17.000000 | 17.000000 |
| () | 7.3 | 7.3 | 7.300427 | 7.300156 | 7.300000 | 7.300033 | 7.300000 |
| () | 7.715319 | 7.715319 | 7.715377 | 7.800027 | 7.800000 | 7.715772 | 7.800000 |
| () | 3.350214 | 3.350214 | 3.350230 | 3.350221 | 3.350214 | 3.350218 | 2.900000 |
| () | 5.286654 | 5.286654 | 5.286663 | 5.286685 | 5.2866832 | 5.286654 | 5.286683 |
| Best objective value | 2994.471066 | 2994.471066 | 2994.499107 | 2996.356689 | 2996.348167 | 2994.482453 | 2896.259285 |
| Objective deviation | 1.0 | ||||||
| Worst objective value | 2994.471066 | 2994.471066 | 2994.752311 | 2996.390137 | 2996.348204 | 2999.652444 | 2896.259380 |
| Average objective value | 2994.471066 | 2994.471066 | 2994.613368 | 2996.367220 | 2996.348174 | 2996.769019 | 2896.259292 |
| Standard deviation | 1.56 | 0.000017 | |||||
| Function evaluations | 30,000 | 30,000 | 40,000 | 24,000 | 54,350 | 25,000 | 50,000 |
| Method | Objective Function | Function | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| () | () | () | () | () | () | () | () | () | () | Best | Deviation | Worst | Mean | Std. Dev. | Evaluations | ||
| [46] | RNES 1 a | 3 | 60 | 3.1 | 55 | 2.6 | 50 | 2.311 | 43.108 | 1.822 | 34.307 | 64269.594 | N/A | 12,000 | |||
| RNES 2 | 3 | 60 | 3.1 | 55 | 2.6 | 50 | 2.267 | 43.797 | 1.849 | 34.282 | 64322.433 | N/A | 12,000 | ||||
| RNES 3 | 3 | 60 | 3.1 | 55 | 2.6 | 50 | 2.348 | 42.804 | 1.783 | 34.753 | 64299.108 | N/A | 12,000 | ||||
| RNES 4 | 3 | 60 | 3.1 | 55 | 2.6 | 50 | 2.491 | 41.51 | 2.113 | 33.231 | 65416.896 | N/A | 12,000 | ||||
| [47] | DOT | N/A | 65391.59 | N/A | N/A | ||||||||||||
| SLP b | N/A | 65451.50 | N/A | N/A | |||||||||||||
| MLD c-SLP | N/A | 65352.20 | N/A | N/A | |||||||||||||
| [48] | C/RU d | 4 | 62 | 3.1 | 60 | 2.6 | 55 | 2.205 | 44.09 | 1.751 | 35.03 | 73555 | N/A | N/A | |||
| PD e | 3 | 60 | 3.1 | 55 | 2.6 | 50 | 2.276 | 45.528 | 1.75 | 34.995 | 64537 | N/A | N/A | ||||
| LAD f | 3 | 60 | 3.1 | 55 | 2.6 | 50 | 2.262 | 45.233 | 1.75 | 34.995 | 64403 | N/A | N/A | ||||
| CAD g | 3 | 60 | 3.1 | 55 | 2.6 | 50 | 2.279 | 45.553 | 1.75 | 35.004 | 64558 | N/A | N/A | ||||
| [49] | GAOS Level 1 | 3 | 60 | 3.1 | 55 | 2.6 | 50 | 2.3 | 45.5 | 1.8 | 35 | 64815 | N/A | 10,000 | |||
| GAOS Level 2 | 3 | 60 | 3.1 | 55 | 2.6 | 50 | 2.27 | 45.25 | 1.75 | 35 | 64447 | N/A | 10,000 | ||||
| [50] | GA-APM h | 3 | 60 | 3.1 | 55 | 2.6 | 50 | 2.2894 | 45.6256 | 1.7931 | 34.593 | 64698.56 | 73931.359 | 68107.046 | N/A | 35,000 | |
| [51] | AIS-GA | 3 | 60 | 3.1 | 55 | 2.6 | 50 | 2.235 | 44.395 | 2.004 | 32.879 | 65559.60 | 77272.78 | 70857.12 | N/A | 35,000 | |
| AIS-GA-C i | 3 | 60 | 3.1 | 60 | 2.6 | 50 | 2.311 | 43.186 | 2.225 | 31.250 | 66533.47 | 76852.86 | 71821.69 | N/A | 35,000 | ||
| [1] | FA | 3 | 60 | 3.1 | 55 | 2.6 | 50 | 2.205 | 44.091 | 1.750 | 34.995 | 63893.52 | 64262.99420 | 64144.75312 | 175.91879 | 50,000 | |
| Present study | PSO () | 3 | 60 | 3.1 | 55 | 2.6 | 50 | 2.20456 | 44.09111 | 1.74976 | 34.99514 | 63893.43 | 1.0 | 63893.43080 | 63893.43080 | 0.00000 | 50,000 |
| Reference Method | [52] GA | [3] MBA | [30] | Present Study PSO (ns = 16) | |
|---|---|---|---|---|---|
| ABC | TLBO | ||||
| () | 125.7171 | 125.7153 | N/A | 125.7191 | 125.719056 |
| () | 21.423 | 21.423300 | N/A | 21.42559 | 21.425590 |
| (Z) | 11 | 11.000 | N/A | 11 | 11.000000 |
| () | 0.515 | 0.515000 | N/A | 0.515 | 0.515000 |
| () | 0.515 | 0.515000 | N/A | 0.515 | 0.515000 |
| () | 0.4159 | 0.488805 | N/A | 0.424266 | 0.411776 |
| () | 0.651 | 0.627829 | N/A | 0.633948 | 0.613510 |
| () | 0.300043 | 0.300149 | N/A | 0.3 | 0.300000 |
| (e) | 0.0223 | 0.097305 | N/A | 0.068858 | 0.059359 |
| () | 0.751 | 0.646095 | N/A | 0.799498 | 0.667473 |
| 0.000821 | 0 | N/A | 0 a | 0.000000 | |
| 13.732999 | 8.630183 | N/A | 13.15257 | 14.026828 | |
| 2.724000 | 1.101429 | N/A | 1.5252 | 0.094509 | |
| −1.107 | 2.040448 | N/A | 0.719056 | −1.401405 | |
| 0.717000 | 0.715366 | N/A | 16.49544 | 0.719056 | |
| 4.857899 | 23.611002 | N/A | 0 | 14.120649 | |
| 0.0021 | 0.000480 | N/A | 0 | 0.000000 | |
| 0.000007 | 0 | N/A | 2.559363 | 0.000000 | |
| 0.000007 | 0 | N/A | 0 | 0.000000 | |
| Best objective value | 81,843.3 | 85,535.9611 b | 81,859.7416 | 81,859.74 | 81,859.7416 |
| Objective deviation | 1.0 | 1.0 | |||
| Feasibility | Feasible | Infeasible | N/A | Infeasible | Feasible |
| Worst objective value | N/A | 84,440.1948 | 78,897.81 | 80,807.8551 | 81,859.7401 |
| Average objective value | N/A | 85,321.4030 | 81,496 | 81,438.987 | 81,859.7415 |
| Standard deviation | N/A | 211.52 | 0.69 | 0.66 | 0.0003 |
| Function evaluations | 225,000 | 50,000 | 10,000 | 10,000 | 50,000 |
| Reference Method | [1] | Present Study PSO () | |||
|---|---|---|---|---|---|
| PSO | DE | GA | FA | ||
| 0.50000 | 0.50000 | 0.50005 | 0.50000 | 0.500000 | |
| 1.11670 | 1.11670 | 1.28017 | 1.36000 | 1.116366 | |
| 0.50000 | 0.5000 | 0.50001 | 0.50000 | 0.500000 | |
| 1.30208 | 1.30208 | 1.03302 | 1.20200 | 1.302197 | |
| 0.50000 | 0.50000 | 0.50001 | 0.50000 | 0.500000 | |
| 1.50000 | 1.50000 | 0.50000 | 1.12000 | 1.500000 | |
| 0.50000 | 0.50000 | 0.50000 | 0.50000 | 0.500000 | |
| 0.34500 | 0.34500 | 0.34994 a | 0.34500 | 0.345000 | |
| 0.19200 | 0.19200 | 0.19200 | 0.19200 | 0.192000 | |
| −19.54935 | −19.54935 | 10.3119 | 8.87307 | −19.561544 | |
| −0.00431 | −0.00431 | 0.00167 | −18.99808 | −0.000190 | |
| Best objective value | 22.84474 | 22.84298 b | 22.85653 | 22.84298 c | 22.842969 |
| Objective deviation | 1.0 | ||||
| Feasibility | Feasible | Feasible | Infeasible | Infeasible | Feasible |
| Worst objective value | 23.21354 | 24.12606 | 26.240578 | 24.06623 | 22.846465 |
| Average objective value | 22.89429 | 23.22828 | 23.51585 | 22.89376 | 22.843136 |
| Standard deviation | 0.15017 | 0.34451 | 0.66555 | 0.16667 | 0.000649 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, T.-H.; Cho, M.; Shin, S. Constrained Mixed-Variable Design Optimization Based on Particle Swarm Optimizer with a Diversity Classifier for Cyclically Neighboring Subpopulations. Mathematics 2020, 8, 2016. https://doi.org/10.3390/math8112016
Kim T-H, Cho M, Shin S. Constrained Mixed-Variable Design Optimization Based on Particle Swarm Optimizer with a Diversity Classifier for Cyclically Neighboring Subpopulations. Mathematics. 2020; 8(11):2016. https://doi.org/10.3390/math8112016
Chicago/Turabian StyleKim, Tae-Hyoung, Minhaeng Cho, and Sangwoo Shin. 2020. "Constrained Mixed-Variable Design Optimization Based on Particle Swarm Optimizer with a Diversity Classifier for Cyclically Neighboring Subpopulations" Mathematics 8, no. 11: 2016. https://doi.org/10.3390/math8112016
APA StyleKim, T.-H., Cho, M., & Shin, S. (2020). Constrained Mixed-Variable Design Optimization Based on Particle Swarm Optimizer with a Diversity Classifier for Cyclically Neighboring Subpopulations. Mathematics, 8(11), 2016. https://doi.org/10.3390/math8112016





