A Robust and Reversible Watermarking Algorithm for a Relational Database Based on Continuous Columns in Histogram
Abstract
1. Introduction
2. Related Work
2.1. HGW Reversible Database Watermarking Method
2.2. NSHGW Reversible Database Watermarking Method
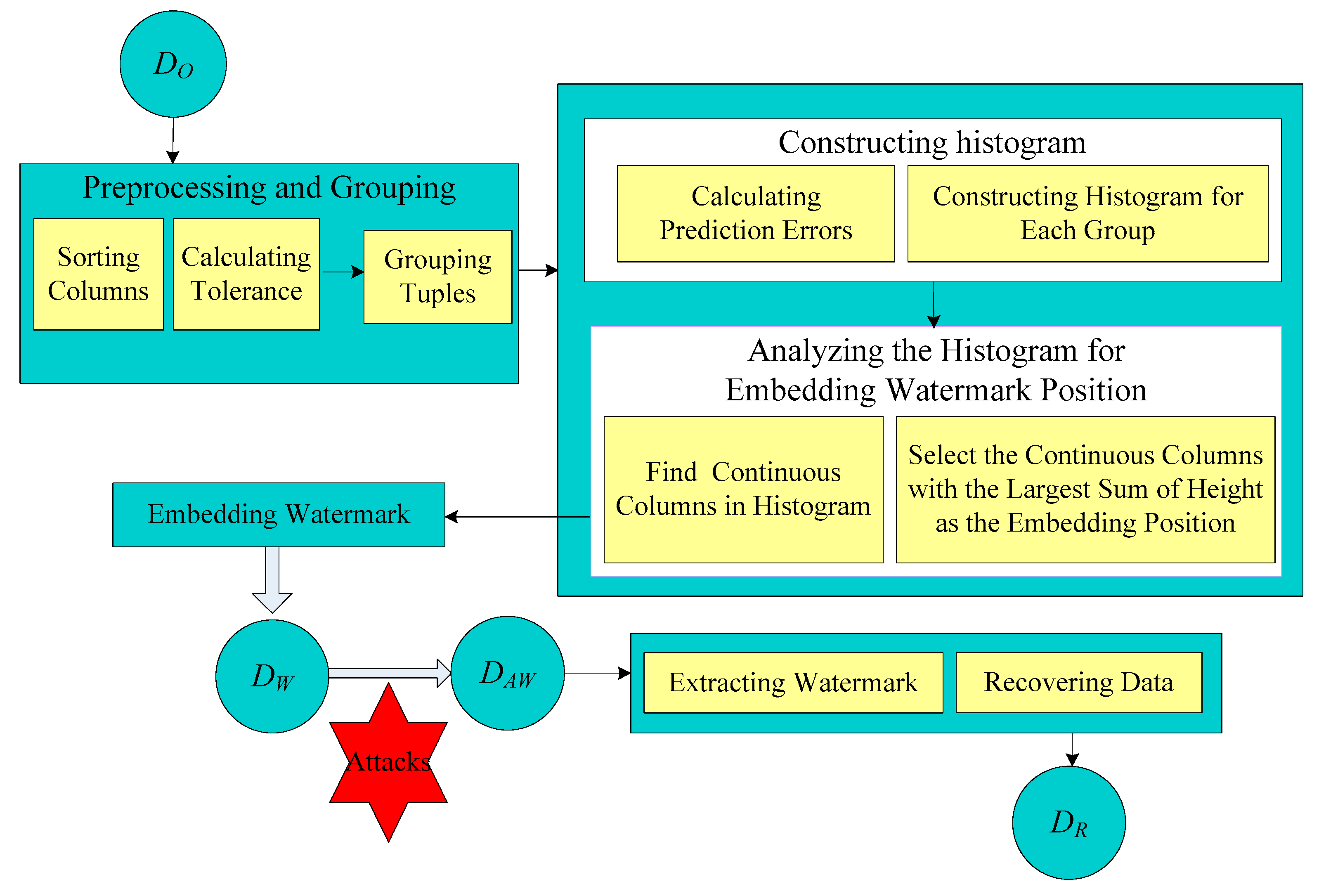
3. The Proposed Method
3.1. Preprocessing and Grouping
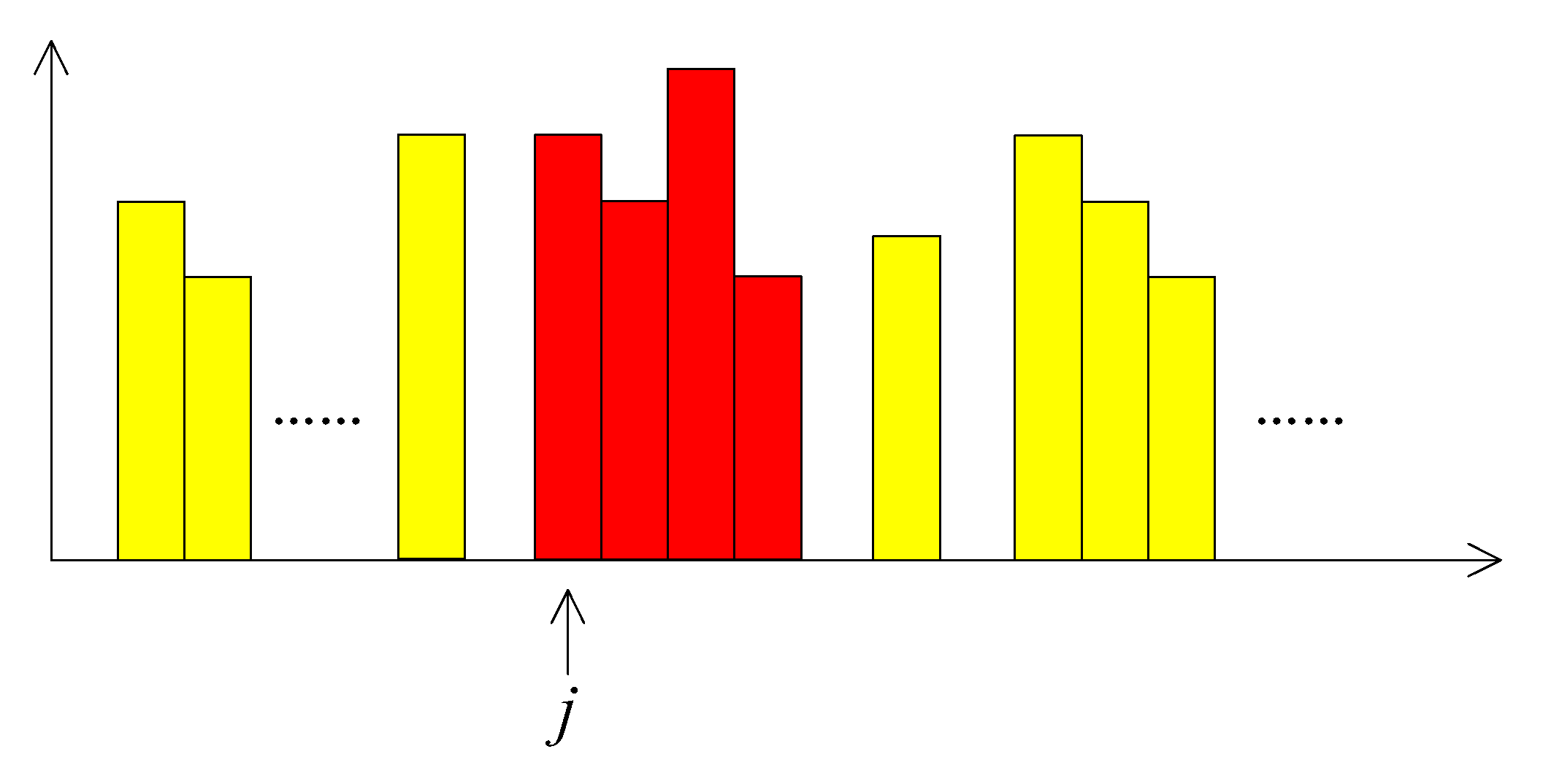
3.2. Construction of Histogram
3.3. Watermark Embedding
3.4. Watermark Extraction and Data Recovery
4. Experimental Results and Analysis
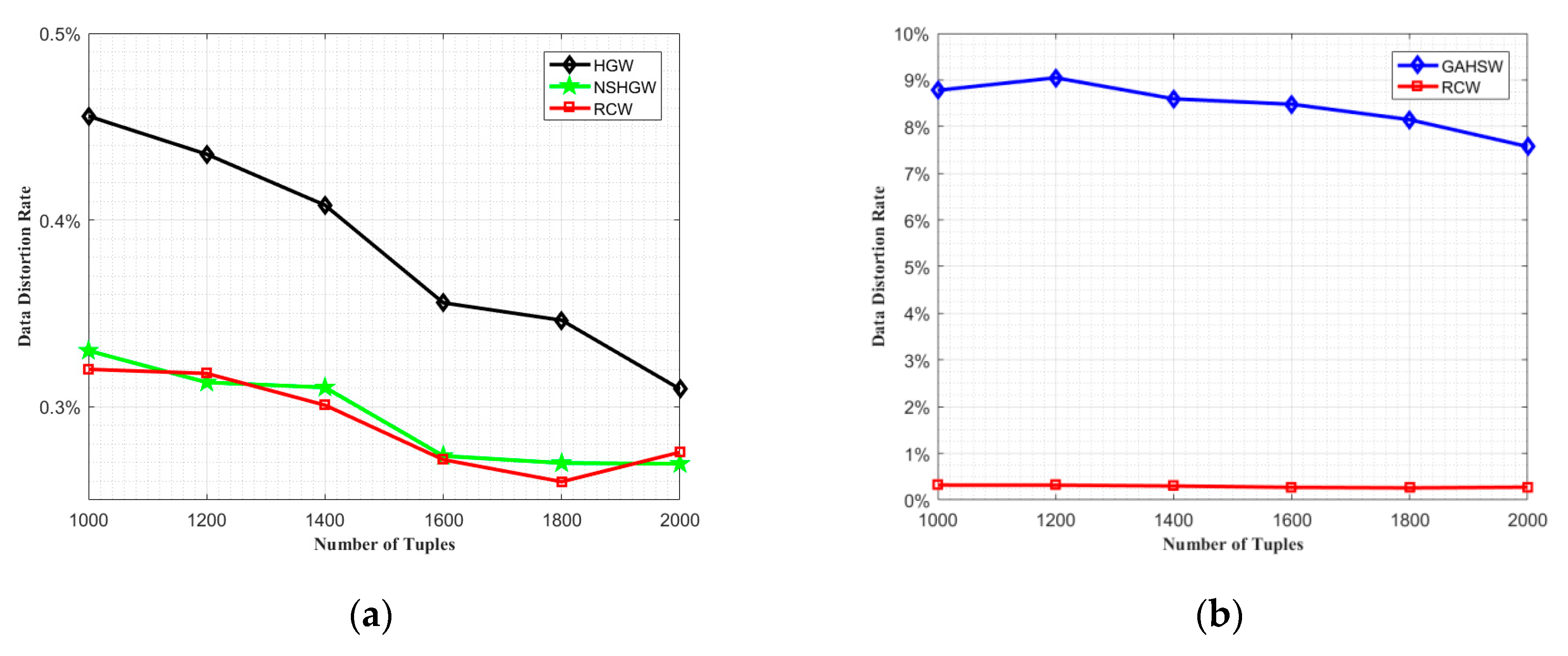
4.1. Comparative Analysis of Data Distortion Effect
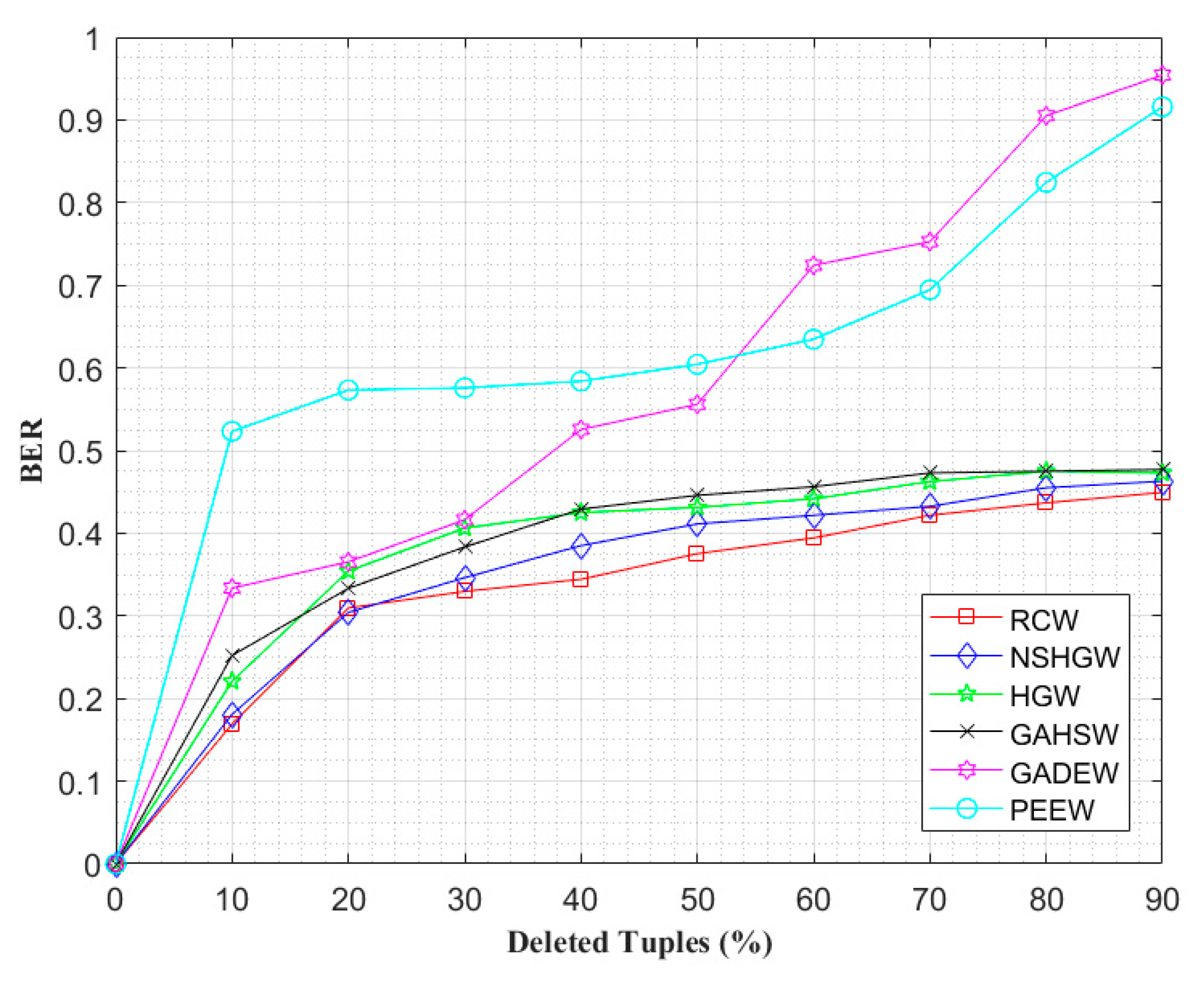
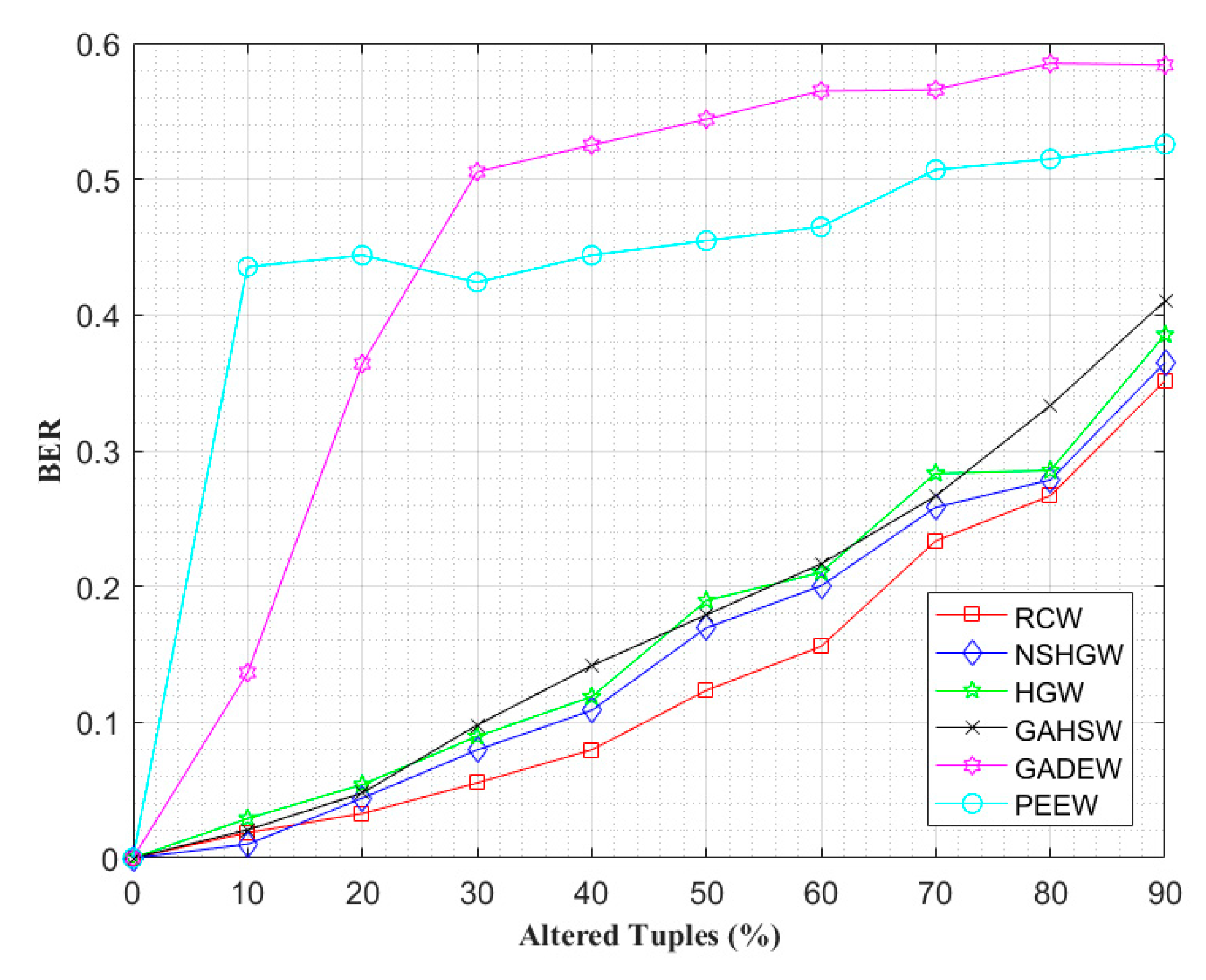
4.2. Watermark Robustness Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gursale, N.; Mohanpurkar, A. A robust, Distortion minimization fingerprinting technique for relational database. Int. J. Recent Innov. Trends Comput. Commun. 2014, 2, 737–1741. [Google Scholar]
- Shehab, M.; Bertino, E.; Ghafoor, A. Watermarking relational databases using optimization-based techniques. IEEE Trans. Knowl. Data Eng. 2008, 20, 116–129. [Google Scholar] [CrossRef]
- Khanduja, V.; Chakraverty, S.; Verma, O. Enabling information recovery with ownership using robust multiple watermarks. J. Inf. Secur. Appl. 2016, 29, 80–92. [Google Scholar] [CrossRef]
- Gupta, G.; Pieprzyk, J. Database relation watermarking resilient against secondary watermarking attacks. In Information Systems Security: 5th International Conference, Proceedings of the Lecture Notes in Computer Science, Volume 5905, Kolkata, India, 14–18 December 2009; Springer: Berlin/Heidelberg, Germany; pp. 222–236.
- Bhattacharya, S.; Cortesi, A. A distortion free watermark framework for relational databases. In Proceedings of the ICSOFT 2009—4th International Conference on Software and Data Technologies, Sofia, Bulgaria, 26–29 July 2009; Volume 2, pp. 229–234. [Google Scholar]
- Iftikhar, S.; Kamran, M.; Anwar, Z. RRW-a robust and reversible watermarking technique for relational data. IEEE Trans. Knowl. Data Eng. 2015, 27, 1132–1145. [Google Scholar] [CrossRef]
- Mo, Q.; Yao, H.; Cao, F. Reversible data hiding in encrypted image based on block classification permutation. Comput. Mater. Contin. 2019, 59, 119–133. [Google Scholar] [CrossRef]
- Wang, B.W.; Kong, W.W.; Li, W. A dual-chaining watermark scheme for data integrity protection in Internet of Things. Comput. Mater. Contin. 2019, 58, 679–695. [Google Scholar] [CrossRef]
- Liu, J.; Li, J.B.; Cheng, J.R. A novel robust watermarking algorithm for encrypted medical image based on DTCWT-DCT and chaotic map. Comput. Mater. Contin. 2019, 61, 889–910. [Google Scholar] [CrossRef]
- Agrawal, R.; Kiernan, J. Watermarking relational databases. In Proceedings of the 28th VLDB Conference, Hong Kong, China, 20–23 August 2002; pp. 155–166. [Google Scholar]
- Sion, R. Proving ownership over categorical data. In Proceedings of the 20th International Conference on Data Engineering, Boston, MA, USA, 2 April 2004; pp. 584–596. [Google Scholar]
- Sion, R.; Atallah, M.; Prabhakar, S. Rights protection for categorical data. IEEE Trans. Knowl. Data Eng. 2005, 17, 912–926. [Google Scholar] [CrossRef]
- Liu, S.Y.; Wang, S.H.; Dengetal, R. A block oriented fingerprinting scheme in relational database. In Information Security and Cryptology—ICISC 2004, Proceedings of the 7th International Conference, Seoul, Korea, 2–3 December 2004; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3506. [Google Scholar]
- Chang, J.; Wu, H. Reversible fragile database watermarking technology using difference expansion based on SVR prediction. In Proceedings of the International Symposium on Computer, Consumer and Control, Taiwan, China, 4–6 June 2012; pp. 690–693. [Google Scholar]
- Zhang, Y.; Yang, B.; Niu, X.M. Reversible watermarking for relational database authentication. J. Comput. 2006, 17, 59–65. [Google Scholar]
- Jawad, K.; Khan, A. Genetic algorithm and difference expansion based reversible watermarking for relational databases. J. Syst. Softw. 2013, 86, 2742–2753. [Google Scholar] [CrossRef]
- Imamoglu, M.B.; Ulutas, M.; Ulutas, G. A new reversible database watermarking approach with firefly optimization algorithm. Math. Probl. Eng. 2017, 2017, 1–14. [Google Scholar] [CrossRef]
- Mahmoud, E.; Farfoura, H.; Wang, X. A novel blind reversible method for watermarking relational databases. J. Chin. Inst. Eng. 2013, 36, 87–97. [Google Scholar]
- Hu, D.H.; Zhao, D.; Zheng, S.L. A new robust approach for reversible database watermarking with distortion control. IEEE Trans. Knowl. Data Eng. 2018, 31, 1024–1037. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.W.; Ge, S.K. A reversible database watermarking method with low distortion. Math. Biosci. Eng. 2019, 16, 4053–4068. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, J.W.; Luo, X.Y. A reversible database watermarking method non-redundancy shifting-based histogram gaps. Int. J. Distrib. Sens. Netw. 2020, 16, 155014772092176. [Google Scholar] [CrossRef]
- Franco-Contreras, J.; Coatrieux, G.; Cuppens, F.; Cuppens-Boulahia, N.; Roux, C. Robust Lossless Watermarking of Relational Databases Based on Circular Histogram Modulation. IEEE Trans. Inf. Forensics Secur. 2017, 9, 397–410. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wang, J.; Jia, H. A Robust and Reversible Watermarking Algorithm for a Relational Database Based on Continuous Columns in Histogram. Mathematics 2020, 8, 1994. https://doi.org/10.3390/math8111994
Li Y, Wang J, Jia H. A Robust and Reversible Watermarking Algorithm for a Relational Database Based on Continuous Columns in Histogram. Mathematics. 2020; 8(11):1994. https://doi.org/10.3390/math8111994
Chicago/Turabian StyleLi, Yan, Junwei Wang, and Hongyong Jia. 2020. "A Robust and Reversible Watermarking Algorithm for a Relational Database Based on Continuous Columns in Histogram" Mathematics 8, no. 11: 1994. https://doi.org/10.3390/math8111994
APA StyleLi, Y., Wang, J., & Jia, H. (2020). A Robust and Reversible Watermarking Algorithm for a Relational Database Based on Continuous Columns in Histogram. Mathematics, 8(11), 1994. https://doi.org/10.3390/math8111994




