Abstract
The problem concerning facilities delocation in the retail sector is addressed in this paper by proposing a novel mixed 0-1 linear optimization model. For this purpose, the aim of the problem is to decide whether to close existing stores or consider an alternative type of store management policy aimed at optimizing the profit of the entire retail network. Each management policy has a different repercussion on the final profit of the stores due to the different margins obtained from the customers. Furthermore, closing stores can cause customers to leave the whole retail network according to their behavior. This behavior is brought about through their tendency to abandon this network. There are capacity constraints imposed depending on the number of stores that should stay open and cease operation costs, customer behavior and final prices. These constraints depend on the type of management policy implemented by the store. Due to the commercial requirements concerning customer behavior, a set of non-linear constraints appears in the definition of the model. Classical Fortet inequalities are used in order to linearize the constraints and, therefore, obtain a mixed 0-1 linear optimization model. As a result of the size of the network, border constraints have been imposed to obtain results in a reasonable computing time. The model implementation is done by introducing smart sets of indices to reduce the number of constraints and variables. Finally, the computational results are presented using data from a real-world case study and, additionally, a set of computational experiments using data randomly generated as shown.
1. Introduction
Facility location problems have been broadly studied in the literature. Their objective is to determine the best place to open new facilities within a region to satisfy the demand of the customers. The best location depends on the criteria considered from a wide range of options. The p-median, p-centre or the capacitated facility location problems are some of the most well-known problems related to the field of location.
There are models available for locating public and retail facilities, emergency services and plants or warehouses, among others. These location issues can be solved by using (integer or continuous) linear optimization, heuristic and meta-heuristic approaches. A comprehensive state of the art in this area can be found in Laporte et al. (2015) [1] among many other interesting references.
The majority of the location problems involve the location or relocation of new facilities. The concept of delocation, defined as the operation cease of existing facilities (see Bhaumik (2010) [2]), has been recently introduced. As shown in ReVelle et al. (2007) [3], there have been several delocation problems in both the private and the public sector. An example of facility closures in the transport sector is provided by Murray and Wu (2003) [4] which details various modelling approaches, that address a reduction of the current number of stops along a bus route in order to promote faster transit speeds and greater geographic coverage given a travel time budget.
Delocation has also been a subject of study for educational organizations. An example can be seen, in Bruno and Andersen (1982) [5] where they present a model to determine school closures in a medium sized school district in California.
As regards the banking sector, the need to address the closure of facilities is shown in Morrison and O’Brien (2001) [6], Wang et al. (2003) [7], Monteiro and Fontes (2005) [8], Ruiz-Hernández (2015) [9] and Ruiz-Hernández (2016) [10] among others. A budget constraint location problem is presented in [7] to locate and relocate bank-branches in a large-sized town. The authors consider both, opening new facilities while at the same time closing some of the existing ones. In [8], a local search heuristic is proposed to address the problem of bank-branch restructuring. In [9], a model for re-sizing the bank network is presented with the aim of maintaining a constant service level, and deciding which branches should continue in business and which should be replaced. More recently, in [10], a stochastic optimization model has been introduced to restructure a network of capacitated bank branch by considering uncertainty in the demand.
Shop closures have also been a topic of concern in the retail sector. Evidence of this fact is shown in Shields and Kures (2007) [11], which investigates the spatial and economic factors that influenced the decision of a major American retailer to close part of its network of stores. A further example on this interest is studied in [3], which introduces two models to reduce the number of facilities in a given area with and without strong competition. In the first case the aim is to reduce the number of facilities to a fixed number, by minimizing the impact on the loss of demand to the competitors. In the second case, the measure of the decline of the service is minimized. On the same line, in [2], a model is presented to downsize an existing distribution network of a firm with known supplier locations. The firm seeks the closure of a fixed number of the supplier nodes. The model assumes that all demand nodes must be served by their respective supplier unless the existing supplier is removed. Recently, in [12], a problem of restructuring bi-level facilities was presented. Here, the aim consists of minimizing costs by opening auxiliary facilities and closing or resizing the existing facilities maintaining an overall coverage.
The underlying problem presented in this paper considers three different elements simultaneously: facilities delocation, modifications on management policies and network restructuring. As stated above, there are many references where some mathematical optimization models have been proposed in order to deal with delocation problems. However, to our knowledge, there are no optimization models that consider all these characteristics together. Then, we present a model that restructures the network of stores of a retail chain by delocating and changing management policy decisions in order to maximize the total profit of the network. As an initial approach, a Mixed 0-1 Non-Linear optimization model is proposed. As a second step, the model is reformulated in order to linearize the non-linear expressions. As a result, a Mixed 0-1 Linear optimization model is proposed. These models have been validated with the real-world data provided by a well-known international company.
The main contributions of this paper are: (1) a novel mathematical optimization model to deal with facility delocation, modifications on management policies and simultaneous network restructuring; (2) its reformulation to an equivalent linear model; and (3) the model has been validated by using real-world data.
The rest of the document is organized as follows: Section 2 is intended to present both the assumptions to be considered and a general description of the problem. Section 3 introduces the notation as well as the Mixed 0-1 Non-Linear optimization model formulation. Section 4 presents the model reformulation to obtain a Linear 0-1 optimization model. In Section 5, the main computational results are reported. Finally, Section 6 concludes and presents future lines of research.
2. Problem Description
The delocation problem has been addressed in the literature for several reasons as discussed in Section 1. In our case, the manager of a retail chain seeks to optimize the management of the network of its stores. The retail chain itself or an external dealer can operate these stores. In these case, the manager would like to know whether it is appropriate to either stop operating the stores or change the management policy.
The network consists of a set of stores all over a specific region. Currently, each store is managed by one of the different management policies considered in the network. Decisions about the change in the management policy are centralized and are mainly based on whether the store generates profits for the company or not. We distinguish two different types of stores in terms of the decisions that can be made about them: non-fixed and fixed stores. The impossibility of delocation or modification of the management policy characterize fixed stores. Then, decisions concerning delocation or modification of the management policy can be made only for non-fixed stores. Consequently, it is the company that decides which store is fixed or non fixed.
The overall benefit is obtained from the purchase of goods made by customers in the stores. Each management policy has different repercussions on the final profit of the stores due to the profit margins imposed by the retail chain or external dealers. The customers of the company can be classified in two different classes: major customers, those who are large-scale consumers (usually professionals) with price fixing agreements, and the rest of the customers that usually have loyalty cards to obtain discounts or other advantages. Each customer consumes in a certain set of stores owing to the customer-store agreements. We can distinguish two types of customer behavior with respect to each store regarding their commitment to the retail chain: customers with a tendency to abandon the network and customers with a tendency to stay in the network. On the one hand, a customer with a tendency to abandon a certain store will leave the network altogether if that store is delocated and, thus, will no longer consume in that retail chain. On the other hand, a customer with a tendency to stay in a certain store will continue consuming in the network in case the store is delocated. Notice that customers with loyalty cards may decide whether to continue consuming in the retail company (in case one of their preferred stores is closed) whereas the major customers will continue to remain in the network. The company knows this aspect beforehand since it is aware of all of the consumer–store agreements. Therefore, a customer will only leave the network if a store where the customer has a tendency to abandon is delocated or if all stores where the customer consumes are delocated. Notice that this behavior occurs particularity in this company chain since it depends on agreements and not on distances. The distances in this problem are not relevant, which is a feature that differs from the rest of the traditional literature. Furthermore, store capacities are not considered since the company is the one responsible for supplying the products to any given store within the network. Finally, the consumption in the delocated stores by those customers that do not leave the network is distributed among the remaining stores where they consume.
In order to maintain a certain service level, the retail chain has imposed a minimum number of stores that must stay open, but not which specific one of them. It is important to point out that the store delocation process has a fixed cost associated to it.
A more precise description of the issues involved, as well as the assumptions for addressing them, is presented below.
2.1. Types of Stores and Management Policies
There are two different types of stores that are considered here: fixed and non-fixed stores. Fixed stores must maintain their management policy and no decisions can be made over them. On the other hand, both decisions, on delocating or modifying management policy, can only be issued on the non-fixed stores. Let us denote as the set of stores in the network, where is the subset of fixed stores and the subset of non-fixed stores. For the stores in the latter set, a delocation cost given by
cj is considered and applied in case of delocation. Notice that .
As stated above, each store
can be run by different management policies. Let us denote as the set of management policies and
the specific set of management policies available for a certain store j.
For each store , the decision made can be either to delocate the facility or to change the management policy within . In the case where the management policy changes from to there will be a variation in the volume of goods consumed, given by a percentage of the initial total consumption of goods which is given, . The extra volume will be charged at the profit margin .
In our case, we consider four different management policies depending on the administration and ownership of the stores. Type A refers to a policy whereby the company both, owns and operates the store. Type B means that the company owns the store but an external dealer operates it. Although one may think this is a franchise arrangement, it is not exactly the case, since a third party operates the store but not with the brand image and other common specifications within the franchise arrangements. Type C implies that an external dealer owns the store but the company operates it (which is usually named a lease agreement) and, finally, if the store is managed by Type D, an external dealer both, owns and operates the store, and the company simply supplies its products. Only the following management changes are allowed. If the store is managed as Type A, then it could be changed to Type B, meaning that an external dealer will operate the store. If the store is managed as Type C, then it could be changed to Type D. Types B and D management policies are not allowed to be modified although those stores can be delocated. Therefore, stores Type B or D must remain unchanged if they are not delocated.
2.2. Customers and Their Behavior
The network is used by a set of customers that can be classified in different ways depending on the types of stores where they consume and their behavior given by the tendency to leave or not the network. This tendency mainly depends on the type of agreement between the company and the customer. For major customers, who have special agreements with the company, due to their large amount of consumption, the tendency to abandon is not common. However, when the agreement is in the form of a loyalty card, the customer may decide whether or not to continue consuming in the retail company if one or some stores are closed. Moreover, a customer may have a subset of stores such that, if one of them is delocated, then, he/she leaves the network due to their dissatisfaction, for instance. This kind of customer is said to have a tendency to abandon the network in each store of this subset. However, if none of these stores is closed but some of the others in which the customers consume are delocated, they remain in the network and distribute their consumption in the delocated stores among those that remain open. The tendency to abandon or not is given and calculated by using machine learning techniques whatever the type of store (fixed or non fixed) where the customer consumes. Taking into account this tendency to abandon, customers will leave the network in the following situations when:
- At least one store in which they have a tendency to abandon is delocated.
- All stores in which they consume are delocated.
The behavior of customers with respect to each store in which they consume, affects the total consumption in the whole network and, thus, the final profit of the retail chain. Notice that the information about the behavior of customers is known in advance for all stores.
Regarding the types of stores where a customer consumes, we can distinguish between customers consuming in at least one non-fixed store and customers that only consume at fixed stores. The latter can be removed from the problem, since they will not change their pattern of consumption even though their incomes should be added to the total income of the company. We therefore assume that all customers in consume in at least one non-fixed store. It is important to analyze the behavior of these customers with respect to the non-fixed stores in which they consume. Then, the following subsets are defined:
- , customers who can leave the network if some of the stores in which they consume are delocated. Three different kinds of customers can be considered here:
- -
- , customers with a tendency to abandon the network in every non-fixed store where they consume. A customer in leaves the network if at least one non-fixed store in which he/she consumes is delocated.
- -
- , customers with a tendency to abandon the network in some, but not all, non-fixed stores where they consume. A customer in leaves the network if at least one store in which he/she has a tendency to abandon is delocated. However, the client does not leave the network in case the stores where they do not have a tendency to abandon are delocated. In the latter case, their consumption in those delocated stores will be distributed among the non-delocated stores in which they still consume.
- -
- , customers consuming only in non-fixed stores and without a tendency to abandon in any of them. A customer in leaves the network if every store in which the client consumes is delocated. However, if at least one store in which they consume remains in the network, their consumption in those delocated stores will be distributed among the non-delocated stores in which he/she consumes.
- , customers who will never leave the network whether or not any of the stores in which they consume are delocated. These customers consume in at least one fixed store and they do not have a tendency to abandon the network in any of the non-fixed stores where they consume. The customer’s consumption in the delocated stores is distributed among the rest of stores where he/she consumes.
Figure 1 shows an example of these sets of customers. Fixed and non-fixed stores are represented by different shapes and each customer is linked by an arrow to the stores where he/she consumes; dotted arrows indicate that the customer has a tendency to abandon the network if the corresponding stores are delocated. Note that , the set of customers that only consume at fixed stores, will be removed from the problem since they have no impact on the optimal solution.
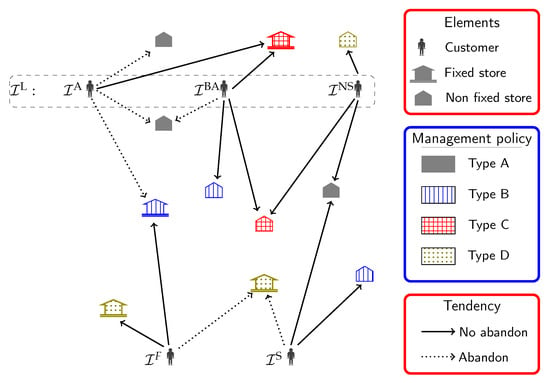
Figure 1.
Classification of the customers.
The amount of goods consumed by each customer in the stores is known in advance, as well as the profit margins that each customer provides to the chain; this profit differs for every customer, store and management policy. When a store is delocated, the customers can either abandon the whole network or keep consuming in the rest of the stores, depending on their behavior. In the latter case, the goods they consumed in the delocating stores are distributed among the remaining stores in a proportional way, given by the amount of goods that each customer is consuming in the stores that remain open. Let us define the increase of goods by customer and store as . In order to illustrate the proportional reassignment of goods, Figure 2 shows one customer which consumes in three different stores, 1, 2 and 6 units, respectively. If the store in which the customer consumes 6 units is delocated, these units will be proportionally distributed in the two remaining stores, hence the final amounts of goods and units, respectively.
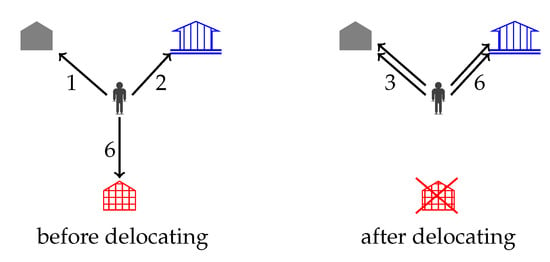
Figure 2.
Proportional reassignment of goods.
In summary, the problem studied considers the following hypotheses:
- The network consists of a set of stores all over a specific region.
- At the present time, each store is managed by one of the four different management policies considered.
- The stores are divided into two groups regarding the decisions that can be made concerning them: non-fixed and fixed stores. Fixed stores are characterized by the impossibility of delocation or modification of management policy. On the other hand, both type of decisions can be made for non-fixed stores.
- The global profit is obtained from the consumption of goods by customers in the stores. Profit margins vary depending on the type of management policy.
- Each customer consumes in a certain set of stores due to customer-store agreements.
- We can distinguish two types of customer behavior: customers with a tendency to abandon a certain store will leave the entire network if that store is delocated, customers with a tendency to stay in a certain store will remain consuming in the network in case the store is delocated. In the latter behavior the consumption in the delocated stores is distributed among the remaining stores where the customer consumes.
- The tendency to abandon or to stay is given as a parameter and calculated by using machine learning techniques for all stores (fixed or non fixed) where the customer consumes.
- This behavior is particularly notable in this company chain since it depends on agreements and not on distances.
- Store capacities are not considered since the company is the one responsible of supplying the products to any store within the network.
- In order to maintain a service level, a minimum number of stores must remain open.
- The store delocation process has a fixed cost associated to it.
3. First Approach: A Mixed 0-1 NonLinear Model
A mathematical Mixed 0-1 NonLinear optimization model is presented as follows, where all the elements are defined.
3.1. Notation
3.1.1. Sets
- ,
- set of stores, divided in two groups: and , set of fixed and non-fixed stores, respectively.
- ,
- set of customers. Note that only customers that consume in at least one non-fixed store are considered here, since, customers consuming only in fixed stores do not imply any change in the company’s profit. Set can be partitioned in the following subsets:
- , customers who may leave the network if some of the stores in which they consume are delocated:
- -
- , customers with a tendency to abandon the network in every non-fixed store where they consume.
- -
- , customers with a tendency to abandon the network in some, but not all, non-fixed stores where they consume.
- -
- , customers consuming only in non-fixed stores without a tendency to abandon any of them.
- , customers consuming in at least one fixed store and without a tendency to abandon any non-fixed stores.
- ,
- set of stores where the customer i consumes in, . is divided in and , the sets of fixed and non-fixed stores, respectively.
- ,
- set of stores where customer i has a tendency to abandon the network (i.e., customer i leaves the network if a store in is delocated), . Note: .
- ,
- set of management policies, such as company ownership, the company operates the store or there is an external dealer for instance. The set of possible management policies for store j will be denoted as ,
3.1.2. Parameters
- service level, given by the number of (fixed and non-fixed) stores that must remain open.
- delocation costs of any store j, .
- percentage of extra volume of goods consumed in store j with management policy k (if there is no profit, ), .
- , profit margin to be applied to the extra volume of goods in store j with management policy k, .
- initial amount of goods consumed by customer i in store j, , .
- unit profit obtained by customer i in store j with management policy k, , , .
- upper bound of the volume of goods consumed by customer i, .
- management policy of any fixed store . Note: .
3.1.3. Decision Variables
- if the (non-fixed) store j is delocated and, 0 otherwise, .
- if the (non-fixed) store j is managed with management policy k and, 0 otherwise, .
- if customer i leaves the network and, 0 otherwise, .
- total amount of goods consumed by customer i in all the delocated stores (must be transferred to the non-delocated stores), .
- increase in the consumption of goods of customer i in store j if at least one of the stores where i consumes is delocated, , .
- increase in the consumption of goods of customer i in store j if the store is managed by policy k, , , .
3.2. Mathematical Formulation
3.2.1. Objective Function
The objective of the problem is to maximize the profit defined as the profit from the sales in the whole network minus the restructuring network costs:
where represents the Profit obtained from the Regular Sales, represents the Profit obtained from the increase of sales in the stores that Remain Open, represents the Profit obtained when there is a Change of Management policy and the Cost due to the Delocation of the stores.
3.2.2. Constraints
The set of constraints in the model are presented below:
Constraints (3) state that a non-fixed store must be either managed with only one policy or be delocated. Constraints (4) ensure a proper service level by maintaining a minimum of p stores open. Constraints (5) force a customer to leave the network if a store in which he/she has a tendency to abandon is delocated; on the other hand, Constraints (6) state that a customer in does not leave the network if none of the stores in which he/she has a tendency to abandon are delocated, that is, if he/she leaves the network, at least one store in which he/she has a tendency to abandon must have been delocated. For customers without a tendency to abandon the network that only consume at non-fixed stores, Constraints (7) ensure those customers remain in the network if at least one of their stores remains open, while Constraints (8) force them to leave the network if all stores where they consume are delocated, that is, if the customer does not abandon the network, then, at least one of the stores in which he/she consumes remains open. Constraints (9) compute, for each customer, the amount of goods that must be transferred from the delocated stores in which he/she consumes to the stores that remain open. Constraints (10)–(13) compute the increase of consumption of goods in some stores for those customers in , thas is, customers that could stay in the network although some of the stores where they consume are delocated. For each customer, goods originally consumed in the delocated stores must be transferred to the non-delocated stores in which the customer continues consuming. The increase in store j will be zero if customer i leaves the network () or if store j is delocated (); otherwise, the total amount of goods consumed in all delocated stores where customer i consumes, , is distributed among the non-delocated stores where the customer consumes in proportion to the quantity that the customer originally consumed in those stores, thas is, . Notice that the denominator in this weighting factor could be 0 for customers that only consume in non-fixed stores if all these stores are delocated; in such a case, Constraints (10) cannot force to be equal to 0, but Constraints (14) and (15), together with (3), will do so. Constraints (14) and (15) relate variables , and to include the increase of goods with the appropriate profit margin depending on the final management policy. These constraints are only defined for non-fixed stores, as they are the only ones whose management policy can be modified. Constraints (16)–(21) define the domain for the variables in the model.
4. Model Reformulation: A Mixed 0-1 Linear Optimization Model
The above described model (M1) contains non-linear expressions. The non-linearities appear in the model through the term (2a) in the objective function and the Constraints (10)–(13). The algorithms developed for these types of models do not provide an optimal solution in a reasonable computing time or even provide any solution at all. Hence we will work with a new Mixed 0-1 Linear optimization model by substituting the non-linear equations in model (M1) with an equivalent linear representation. This model can be solved using Mixed Integer Linear optimizers, that are generally much more efficient.
4.1. Linearization of the Nonlinear Equations
4.1.1. Objective Function
In order to linearize the quadratic term defined by the product of two 0-1 variables in term (2a) of the objective function, new auxiliary 0-1 variables are defined representing product , for , and , such that, if customer i does not leave the network and store j uses management policy k and 0 otherwise.
Variables are computed from the variables and through the following constraints,
4.1.2. Constraints related to increase of goods consumption
Further down we present an equivalent linear formulation to Constraints (10)–(13) in order to obtain a completely linear model, reducing complexity although the dimensions of the model increase.
Constraints (10)–(13) contain a quadratic term in the left hand side (the product of a continuous variable and, a 0-1 variable, ). An equivalent linear representation of this product can be obtained by using Fortet inequalities. The Fortet inequalities are presented in Fortet (1960) [13] and Hammer and Rudeau (1968) [14] and have been recently used in Alonso-Ayuso et al. (2016) [15]. They deal with the linearization of the product involving a binary, say b, and a nonnegative continuous variable, say c. In order to linearize the product , a new nonnegative continuous variable k is introduced, where as well as the following set of constraints
where M is a big enough parameter that should be adjusted to strengthen the linear relaxation of the problem. From this system, if then , and if then, necessarily , which models the product .
Applying Fortet inequalities scheme, product can be replaced with the auxiliary continuous variable , together with the following set of constraints,
where can be set as . With this reformulation, the left hand side is linearized.
The right hand side of the constraints also contains non linear terms that are linearized by using Fortet inequalities one more:
- Constraints (10), defined for and :Constraints (10) contain a cubic term, . A new binary auxiliary variable is introduced to represent the product , such that, if either one of or is equal to 1, then automatically . Then, if customer i does not leave the network and store j is not delocated and 0 otherwiseVariables are computed by using variables and through the following constraints,Replacing this new variable in , the result is . The latter expression is a product of a continuous variable, , and a variable , that can also be linearized using the Fortet inequalities scheme. Therefore, a new continuous variable has to be introduced, , together with the following set of additional constraints:where can be set as .
- Constraints (11), defined for and :These constraints contain a quadratic term, . By using the Fortet inequalities scheme, this product can be replaced by a new continuous variable, , and the following set of additional constraints:where can be set as .
- Constraints (12), defined for and :These constraints contain a quadratic term, . Yet again, the Fortet inequalities scheme can be used to linearize this quadratic term. Therefore, a new continuous variable has to be introduced, , and the following set of additional constraints:where can be set as .
- Constraints (13), defined for and :Once the left hand side of the constraints has been linearized, these constrains become linear.
4.2. Mathematical Formulation
Taking into account all the linearization process performed above, model (1)–(21) can be replaced by an equivalent linear reformulation substituting the non-linear Constraints (2a) and (10)–(13) by their corresponding sets of constraints and auxiliary variables.
Then, the notation for the Mixed 0-1 linear optimization reformulation has the following different elements with respect to Model (M1):
4.2.1. Additional Auxiliary Binary Variables
- if customer leaves the network or store is delocated and 0 otherwise.
- if customer leaves the network or store is operated with management policy and 0 otherwise.
4.2.2. Additional Auxiliary Continuous Variables
- non-negative continuous variables for each customer and stores , .
- non-negative continuous variables for each customer and store .
- non-negative continuous variables for each customer and store .
- non-negative continuous variables for each customer .
4.2.3. New Linear Constraints
- Constraints (11)–(13) must be substituted by their equivalent set of linear constraints:
- The model can be tightened by adding new constraints that allow certain feasible solutions to be cutoff its linear relaxation without eliminating any other feasible solution from the original model:
- Variables’ domain:
5. Study Case Analysis
The model described above was tested by using real-world data taken from a case involving an international company interested in knowing the best management policy for its network of stores. The goal of the company is to choose the most appropriate management policy for each store so as to to maximize the total profit of the company. The possibility of delocating the stores was considered in conjunction with four different types of management policy. However, for confidentiality reasons we are unable to go into detail regarding the instance we are currently using for testing purposes.
The network consisted of 20 stores (six fixed and 14 non fixed). In the initial configuration of the network, the stores belonged to any of types A (owned and operated by the company), C (owned by an external dealer but operated by the company) or D (owned and operated by an external dealer). The model could make decisions on the following management policy changes: if the store was managed as Type A, then it could be replaced with Type B; if the store was managed as Type C, then it could be changed to Type D, and finally, the stores under management Type D must remained under this management policy or otherwise they were delocated. In our experiments, there is no limit in the number of stores that can be delocated.
The network served a number of between 15,000 and 20,000 customers, each of them consuming in one or more stores which were distributed in a region of approximately 1200 km2. On average, each customer consumed in 2.1 different stores. Figure 3a shows the percentage of customers in the network consuming in one store, two stores, etc. Note that almost 60% of the customers visited only one store. There were some customers who visited more than six stores, although they can be considered outliers. Figure 3b shows the percentage of customers that were served by each store. There were five stores attending a high number of customers (more than 3000), but the other 15 had a number of customers, approximately between 1000 and 3000. Table 1 reports the distribution of the customers in the different categories.
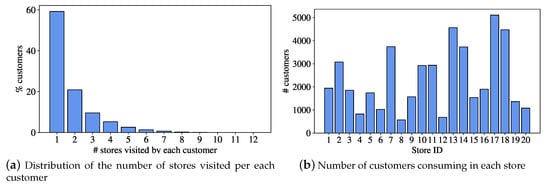
Figure 3.
Distribution of customers in the network.

Table 1.
Distribution (%) of the customers into the different categories.
In order to guarantee the confidentiality of the data, the initial profit given by , and the initial amount of goods sold in the stores given by were both set to 1000. Using this number as a reference, the consumption of goods per customer varied depending on the stores, with an average consumption of 0.05 units. Figure 4 shows the distribution of the consumption per store and customer. Figure 4a shows the distribution of consumption of each customer in the stores. It clearly shows an asymmetric distribution, where most of the customers consumed very little while there were few customers with a much higher level of consumption. Focusing on the stores, for each of the 20 stores we calculated the average consumption that each customer consumed in the store; this amount is represented in Figure 4b. Note that stores #4, #11, #12, and #15 had customers with higher levels of consumption (especially store #4), while there were no significant differences among the rest of the stores.
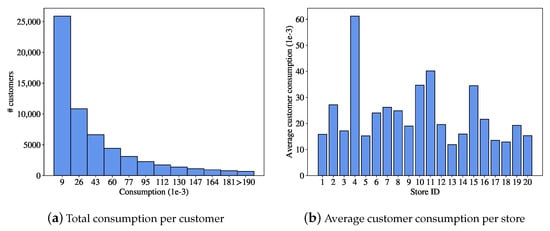
Figure 4.
Distribution of consumption.
The commercial margins were different depending on the customer, the store and the type of management policy, and in some cases they were even found to be negative. Finally, the percentage of customers who had a tendency to leave the network in at least one store was about 75%. This was used to classify the customers in different sets, taking into account their tendency to leave the network and the stores where they consumed.
The model was implemented in the algebraic modelling language AMPL [16] and solved using the optimizer Gurobi v.7.0.0 [17] in a computer with an Intel Core i7-7700HQ, 2.80 GHz, 16 GB RAM, Xubuntu 16.04 SO. The main characteristics of the proposed solution are reported in Table 2.

Table 2.
Results of the case study.
This solution, which was obtained in 310 s, implied the delocation of three stores with a 26.21% increase in the total profit while the 17 remaining stores sold 28.3% less. Furthermore, there was a 19.9% decrease in the number of customers (churn rate).
Table 3 reports more detailed information about the network of stores before and after optimization: whether the store was fixed or not; management policy; amount of product sold and profit of each store before and after the optimization process; and the churn rate (percentage of customers of each store leaving the network).

Table 3.
Characteristics of the stores before and after optimization.
There is evidence that the solution proposed here involved changes in six of the stores. The three stores owned and managed by the company (type A) were put into a dealer operating arrangement (type B), and the three stores of type D (an external dealer both owned and operated the store) were delocated, while the other 14 stores remained in the same situation. Note that the model did not consider the customers’ re-allocation, that is, if a store was delocated, then its customers either left the network or continued to purchase in the remaining stores where they were already consuming, however, they did not start to purchase in new stores. In our case, the delocation of three stores implied that between 84% to 91.8% of their customers left the network, but there were some other customers that continued purchasing in the other stores where they were already consuming.
The distribution of profit that the company obtains at each store before and after the optimization is shown in Figure 5.
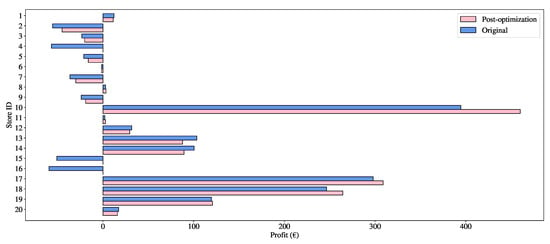
Figure 5.
Distribution of sales profit in the stores.
When comparing the profits before and after the optimization process, we observed that several stores initially had losses. This is due to the fact that some of their customers had a negative commercial margin. After optimization, three of the stores with higher losses were delocated (stores #4, #15 and #16) and overall losses were reduced by 60%. However, there were some stores that also had large losses, store #2 for instance, that continued in the network. The explanation behind this is that even though some of their customers did not provide profits in these stores, the profit they provided in other stores where they also consumed offset the losses. Therefore, although the model focused on individual shops, it proposed a reorganization based on the network as a whole and not only on the shops with losses.
Extended Computational Experiment
Since the company was interested in solving the problem in the future, for a larger network covering all the stores, different instances were solved by increasing the number of facilities. Table 4 reports the results obtained for the different instances. For each instance, the following data are reported: the number of stores and their initial distribution between the different types (A, B, C and D, fixed, non-fixed); an approximation of the number of customers (in thousands), the number of constraints and variables in the optimization model); z, the value of the objective function for the optimal solution (as was previously presented, the initial profit for each instance was set to 1000); the value of the objective function for the linear relaxation of the problem (z), the relative gap between z and z in % (GAP), computed as and the total computing time. Furthermore, the variation (in %) on profit and consumption of the solution is reported as well as the percentage of customers that left the network and the number of stores that were delocated (all of them initially were type D).

Table 4.
Performance of the model for different instances.
The solution obtained included the following changes: all A-stores were changed to B-stores, B and C-stores remained under the same management policy and D-stores remained under the same management policy or they were delocated (see the last column in the table).
The computational time needed to obtain the optimal solution increased as the number of stores increased. The biggest instance solved in a reasonable computing time (less than 24 h, fixed as stopping criterion) had 35 stores. Hence, the model faced a problem when considering larger areas of the network. It should be noted that the higher the dimensions of the problem, the greater the gap between the optimal solution for the continuous linear relaxation and the optimal solution of the problem (see GAP in Table 4). This illustrates the complexity involved in solving large instances. Therefore, other alternative lines of research must be investigated in order to deal with problems of this kind.
6. Conclusions and Future Work
In this paper, a model has been proposed to address the problem of redesigning the network of shops of a retail chain, with the aim of deciding whether the shops should be removed from the network, or whether the type of management policy applied to some of these shops should be modified. Under the proposed mathematical optimization model, simultaneous consideration is given to: the relocation of facilities, changes in management policies, and the restructuring of the network. In addition, customer behavior is also considered. This behavior is based on the type of customers: major customers and the remaining customers who usually have a loyalty card. These customers can decide whether to continue consuming in the company on the basis of their behavior when some of the shops are closed. Moreover, it is possible to adapt this model to different business sectors by considering a network with retail facilities and agreements with their customers.
The model has been tested using a network with real data. In this particular instance the total profit increased by more than 20% and the percentage of non-fixed delocated stores was around . At the same time, it tends to delocate the stores with negative profits as long as it does not cause too many customers to leave. Moreover, it also allows a change in the management policy whenever it brings higher profits to the company.
Our approach has also been tested in different instances, by increasing the number of stores considered. The model achieved results considering up to 35 stores in a reasonable computational time (less than 24 h).
From a business point of view, the application of this model will provide a better management of the network and therefore increase the company’s profits. It will also provide a better knowledge of the network of stores thus facilitating the decision making process.
In order to be able to solve larger instances, a future line of research would be to implement a meta-heuristic approach as for example evolutionary algorithms. In this case, we would consider each store as an individual and the objective function would act as the fitness function.
Uncertainty can arise in the model depending on the customers behavior. Although the tendency to leave the network is given by a parameter 0-1, in reality it is not possible to guarantee what they will eventually do. Consequently, a stochastic model could be studied to take into account this uncertainty, which would consider different scenarios in terms of customer behavior.
From a business perspective it would be interesting to conduct a sensitivity analysis to obtain a clearer understanding of the effect of each of the model’s parameters on the final configuration of the network.
Author Contributions
Conceptualization, M.S.-P., A.A.-A., F.J.M.-C., F.R.-C. and E.L.; data curation, M.S.-P., A.A.-A., F.J.M.-C., F.R.-C. and E.L.; formal analysis, M.S.-P., A.A.-A., F.J.M.-C., F.R.-C. and E.L.; funding acquisition, M.S.-P., A.A.-A., F.J.M.-C., F.R.-C. and E.L.; investigation, M.S.-P., A.A.-A. and F.J.M.-C.; methodology, M.S.-P., A.A.-A., F.J.M.-C., F.R.-C. and E.L.; project administration, M.S.-P., A.A.-A., F.J.M.-C., F.R.-C. and E.L.; resources, M.S.-P., A.A.-A. and F.J.M.-C.; software, M.S.-P., A.A.-A. and F.J.M.-C.; supervision, M.S.-P., A.A.-A. and F.R.-C.; validation, M.S.-P., A.A.-A., F.J.M.-C., F.R.-C. and E.L.; visualization, M.S.-P., A.A.-A. and F.J.M.-C.; writing—original draft, M.S.-P., A.A.-A. and F.J.M.-C.; writing—review editing, M.S.-P., A.A.-A. and F.J.M.-C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Government of the Region of Madrid (M.S.-P., grant IND2018/TIC-9614) and Government of Spain (A.A.-A. and F.J.M.-C., grant RTI2018-094269-B-I00).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Laporte, G.; Nickel, S.; da Gama, F.S. (Eds.) Location Science; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Bhaumik, P. Optimal shrinking of the distribution chain: The facilities delocation decision. Int. J. Syst. Sci. 2010, 41, 271–280. [Google Scholar] [CrossRef]
- ReVelle, C.; Murray, A.; Serra, D. Location models for ceding market share and shrinking services. Int. J. Manag. Sci. 2007, 35, 533–540. [Google Scholar] [CrossRef]
- Murray, T.; Wu, X. Accessibility tradeoffs in public transit planning. J. Geogr. Syst. 2003, 5, 93–107. [Google Scholar] [CrossRef]
- Bruno, J.; Andersen, P. Analytical methods for planning educational facilities in an era of declining enrollments. Socio-Econ. Plan. Sci. 1982, 16, 121–131. [Google Scholar] [CrossRef]
- Morrison, P.; O’Brien, R. Bank branch closures in New Zealand: The application of a spatial interaction model. Appl. Geogr. 2001, 21, 301–330. [Google Scholar] [CrossRef]
- Wang, Q.; Batta, R.; Bhadury, J.; Rump, C. Budget constrained location problem with opening and closing of facilities. Comput. Oper. Res. 2003, 30, 2047–2069. [Google Scholar] [CrossRef]
- Monteiro, M.R.; Fontes, D. Locating and sizing bank-branches by opening, closing or maintaining facilities. In Proceedings of the Operations Research, Bremen, Germany, 7–9 September 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 303–308. [Google Scholar] [CrossRef]
- Ruiz-Hernández, D.; Delgado-Gómez, D.; López-Pascual, J. Restructuring bank networks after mergers and acquisitions: A capacitated delocation model for closing and resizing branches. Comput. Oper. Res. 2015, 62, 316–324. [Google Scholar] [CrossRef]
- Ruiz-Hernández, D.; Delgado-Gómez, D. The stochastic capacitated branch restructuring problem. Ann. Oper. Res. 2016, 246, 77–100. [Google Scholar] [CrossRef]
- Shields, M.; Kures, M. Black out of the blue light: An analysis of Kmart store closing decisions. J. Retail. Consum. Serv. 2007, 14, 259–268. [Google Scholar] [CrossRef]
- Yavari, M.; Mousavi-Saleh, M. Restructuring hierarchical capacitated facility location problem with extended coverage radius under uncertainty. Oper. Res. 2019. [Google Scholar] [CrossRef]
- Fortet, R. Application de l’algebre de boole en recherche operationelle. Rev. Fr. Rech. Oper. 1960, 13, 205–213. [Google Scholar] [CrossRef]
- Hammer, P.L.; Rudeau, S. Boolean Methods in Operations Research and Related Areas, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1968; Volume 7. [Google Scholar] [CrossRef]
- Alonso-Ayuso, A.; Escudero, L.F.; Martín-Campo, F.J. Multiobjective optimization for aircraft conflict resolution. A metaheuristic approach. Eur. J. Oper. Res. 2016, 248, 691–702. [Google Scholar] [CrossRef]
- Fourer, R.; Gay, D.M.; Kernighan, B.W. A Modeling Language for Mathematical Programming. Manag. Sci. 1990, 36, 519–554. [Google Scholar] [CrossRef]
- Gurobi Optimization, Incorporate. Gurobi Optimizer Reference Manual. 2018. Available online: http://www.gurobi.com (accessed on 5 November 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).