State Feedback Regulation Problem to the Reaction-Diffusion Equation †
Abstract
1. Introduction
2. Problem Statement
2.1. Sturm–Liouville Boundary Value Problem
2.2. Abstract Control System Model
2.3. Exogenous System (Exosystem)
3. Regulator Design
3.1. Harmonic Tracking
3.2. Harmonic Disturbance Rejection
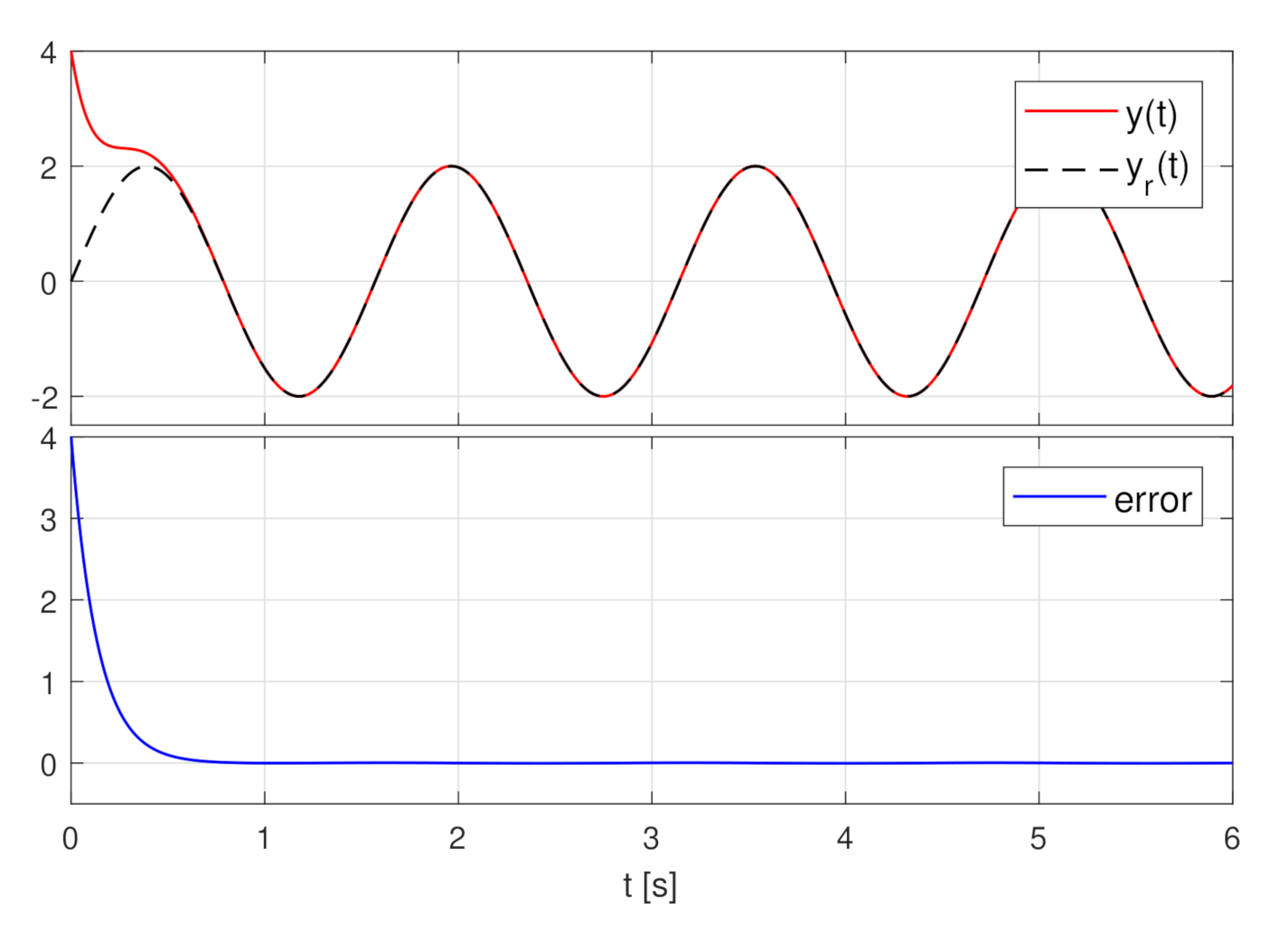
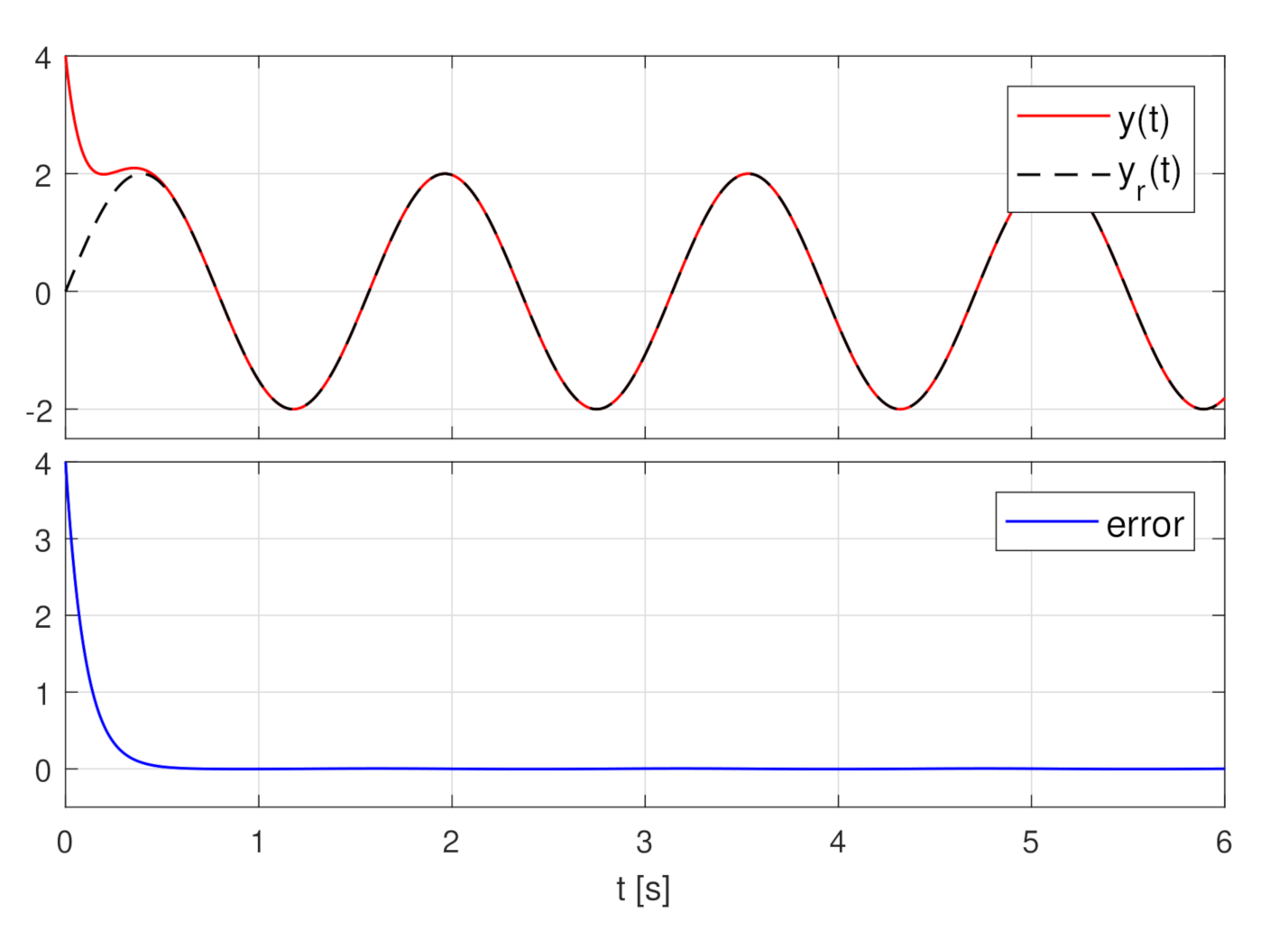
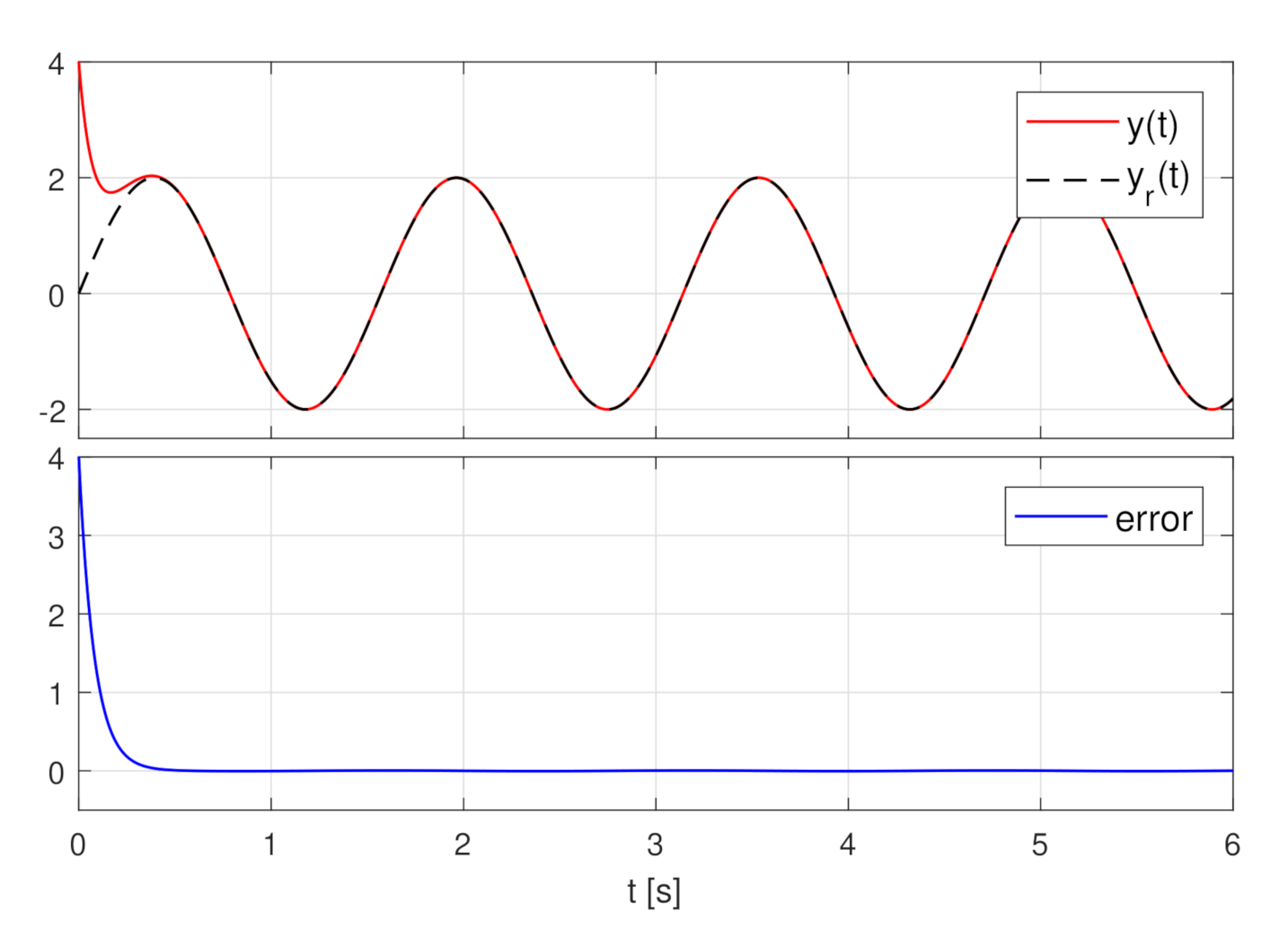
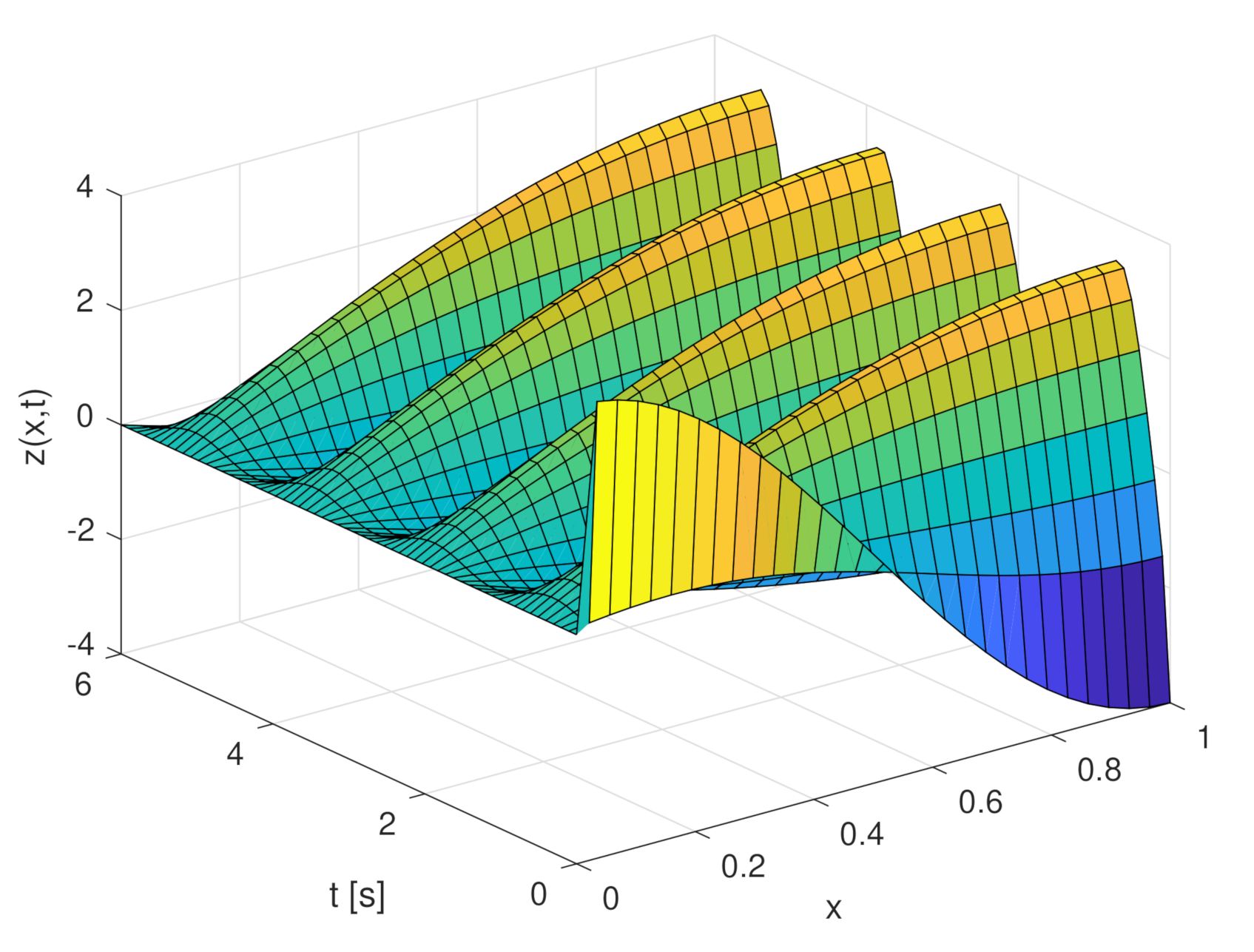
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DPSs | Distributed Parameters Systems |
| EFRP | Error Feedback Regulation Problem |
| ODEs | Ordinary Differential Equations |
| PDEs | Partial Differential Equations |
| R-D | Reaction-Diffusion |
| SFRP | State Feedback Regulation Problem |
| SLBVP | Sturm-Liouville Boundary Value Problem |
| SLDO | Sturm-Liouville Differential Operator |
References
- Morris, K. Control of Systems Governed by Partial Differential Equations in The Control Handbook, 2nd ed.; Levine, W.S., Ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Isidori, A. Nonlinear Control Systems; Springer: London, UK, 1995. [Google Scholar]
- Isidori, A.; Byrnes, C.I. Output Regulation of Nonlinear Systems. IEEE Trans. Autom. Control 1990, 35, 131–140. [Google Scholar] [CrossRef]
- Francis, B.A.; Wonham, W.M. The Internal Model Principle of Control Theory. Automatica 1976, 12, 457–465. [Google Scholar] [CrossRef]
- Francis, B.A. The Linear Multivariable Regulator Problem. SIAM J. Control Optim. 1977, 15, 486–505. [Google Scholar] [CrossRef]
- Wonham, W.M. Linear Multivariable Control: A Geometric Approach; Springer: New York, NY, USA, 1985. [Google Scholar]
- Hautus, M.L.J. Linear Matrix Equations with Applications to the Regulator Problem. In Outils et modèles Mathématiques Pour L’automatique: L’analyse de Systèmes et le Traitement du Signal; Editions du Centre National de la Recherche Scientifique: Paris, France, 1982. [Google Scholar]
- Knobloch, H.W.; Isidori, A.; Flockerzi, D. Topics in Control Theory; Birkhäuser Verlag: Basel, Switzerland, 1993. [Google Scholar]
- Pohjolainen, S.A. On The Asymptotic Regulation Problem for Distributed Parameter Systems. Control Distrib. Parameter Syst. 1983, 197–201. [Google Scholar] [CrossRef]
- Pohjolainen, S.A. Robust Multivariable PI–Controller for Infinite Dimensional Systems. IEEE Trans. Autom. Control 1982, 27, 17–30. [Google Scholar] [CrossRef]
- Schumacher, J.M. Dynamic Feedback in Finite- and Infinite-Dimensional Linear Systems; Mathematisch Centrum Tracts Centrum Voor Wiskunde en Informatica: Amsterdam, The Netherlands, 1981; Volume 143. [Google Scholar]
- Schumacher, J.M. Finite-Dimensional Regulators for a Class of Infinite–Dimensional Systems. Syst. Control Lett. 1983, 3, 7–12. [Google Scholar] [CrossRef]
- Byrnes, C.I.; Laukó, I.G.; Gilliam, D.S.; Shubov, V.I. Output Regulation for Linear Distributed Parameter Systems. IEEE Trans. Autom. Control 2000, 45, 2236–2252. [Google Scholar]
- Müller, P.H.; Kato, T. Perturbation theory for linear operators (Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen mit besonderer Berücksichtigung der Anwendungsgebiete, Band 132) XX+ 592 S. m. 3 Fig. Springer–Verlag. Preis geb. DM 79, 20. Z. Angew. Math. Und Mech. 1967, 47. [Google Scholar] [CrossRef]
- Curtain, R.F.; Zwart, H. An Introduction to Infinite-Dimensional Linear Systems Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Aulisa, E.; Gilliam, D. A Practical Guide to Geometric Regulation for Distributed Parameter Systems; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Natarajan, V.; Gilliam, D.S.; Weiss, G. The State Feedback Regulator Problem for Regular Linear Systems. IEEE Trans. Autom. Control 2014, 59, 2708–2723. [Google Scholar] [CrossRef]
- Xu, X.; Dubljevic, S. Output and Error Feedback Regulator Designs for Linear Infinite-Dimensional Systems. Automatica 2017, 83, 170–178. [Google Scholar] [CrossRef]
- Deutscher, J. A Backstepping Approach to the Output Regulation of Boundary Controlled Parabolic PDEs. Automatica 2015, 57, 56–64. [Google Scholar] [CrossRef]
- Deutscher, J. Finite-Time Output Regulation for Linear 2 × 2 Hyperbolic Systems using Backstepping. Automatica 2017, 75, 54–62. [Google Scholar] [CrossRef]
- Zhou, H.C.; Guo, B.Z. Performance Output Tracking for One-Dimensional Wave Equation Subject to Unmatched General Disturbance and Non-Collocated Control. Eur. J. Control 2018, 39, 39–52. [Google Scholar] [CrossRef]
- Humaloja, J.; Kurula, M.; Paunonen, L. Approximate Robust Output Regulation of Boundary Control Systems. IEEE Trans. Autom. Control 2019, 64, 2210–2223. [Google Scholar] [CrossRef]
- Rebarber, R.; Weiss, G. Internal Model based Tracking and Disturbance Rejection for Stable Well-Posed Systems. Automatica 2003, 39, 1555–1569. [Google Scholar] [CrossRef]
- Jin, F.F.; Guo, B.Z. Boundary Output Tracking for an Euler–Bernoulli Beam Equation with Unmatched Perturbations from a Known Exosystem. Automatica 2019, 109, 108507. [Google Scholar] [CrossRef]
- Xu, X.; Dubljevic, S. Output Regulation for a Class of Linear Boundary Controlled First–Order Hyperbolic PIDE Systems. Automatica 2017, 85, 43–52. [Google Scholar] [CrossRef]
- Logan, J.D. An Introduction to Nonlinear Partial Differential Equations; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Smoller, J. Shock Waves and Reaction-Diffusion Equations; Springer: New York, NY, USA, 1983. [Google Scholar]
- Murray, J.D. Mathematical Biology I: An Introduction; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Murray, J.D. Mathematical Biology II: Spatial Models and Biomedical Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Tveito, A.; Winther, R. Introduction to Partial Differential Equations A Computational Approach; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Banks, H.T.; Tran, H.T. Mathematical and Experimental Modeling of Physical and Biological Processes; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Gahn, M.; Neuss-Radu, M.; Knabner, P. Homogenization of Reaction-Diffusion Processes in a Two-Component Porous Medium with Nonlinear Flux Conditions at the Interface. SIAM J. Appl. Math. 2016, 76, 1819–1843. [Google Scholar] [CrossRef]
- Cardone, G.; Perugia, C.; Timofte, C. Homogenization Results for a Coupled System of Reaction-Diffusion Equations. Nonlinear Anal. 2019, 188, 236–264. [Google Scholar] [CrossRef]
- Karafyllis, I.; Krstic, M. Input-to-State Stability for PDEs; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Krstic, M.; Smyshlyaev, A. Boundary Control of PDEs A Course on Backstepping Designs; SIAM: Philadelphia, PA, USA, 2008. [Google Scholar]
- Ramírez, A.A.; Jurado, F. Tracking Regulator Design with Disturbance Rejection to the Reaction–Diffusion Equation. In Proceedings of the 2019 16th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Mexico City, Mexico, 11–13 September 2019. [Google Scholar]
- Seidman, T.I. Control of the Heat Equation in The Control Handbook, 2nd ed.; Levine, W.S., Ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Strauss, W.A. Partial Differential Equations an Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Mathews, J.; Walker, R.L. Mathematical Methods of Physics; The Benjamin/Cummings Publishing Co.: Menlo Park, CA, USA, 1970. [Google Scholar]
- Boyce, W.E.; DiPrima, R.C.; Meade, D.B. Elementary Differential Equations and Boundary–Value Problems; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Kreyszig, E. Advanced Engineering Mathematics; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Farlow, S.J. Partial Differential Equations for Scientists and Engineers; Dover Publications: New York, NY, USA, 1993. [Google Scholar]
- Holland, S.S., Jr. Applied Analysis by the Hilbert Space Method, an Introduction with Applications to the Wave, Heat, and Schrödinger Equations; Dover Publications: Mineola, NY, USA, 1990. [Google Scholar]
- Kaplan, K. Advanced Calculus; Pearson Education: Boston, MA, USA, 2003. [Google Scholar]
- Pazy, A. Semigroups of Linear Operators and Applications to Partial Differential Equations; Springer: New York, NY, USA, 1983. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jurado, F.; Ramírez, A.A. State Feedback Regulation Problem to the Reaction-Diffusion Equation. Mathematics 2020, 8, 1983. https://doi.org/10.3390/math8111983
Jurado F, Ramírez AA. State Feedback Regulation Problem to the Reaction-Diffusion Equation. Mathematics. 2020; 8(11):1983. https://doi.org/10.3390/math8111983
Chicago/Turabian StyleJurado, Francisco, and Andrés A. Ramírez. 2020. "State Feedback Regulation Problem to the Reaction-Diffusion Equation" Mathematics 8, no. 11: 1983. https://doi.org/10.3390/math8111983
APA StyleJurado, F., & Ramírez, A. A. (2020). State Feedback Regulation Problem to the Reaction-Diffusion Equation. Mathematics, 8(11), 1983. https://doi.org/10.3390/math8111983





