Generalized Finite Difference Method for Plate Bending Analysis of Functionally Graded Materials
Abstract
1. Introduction
2. Numerical Model
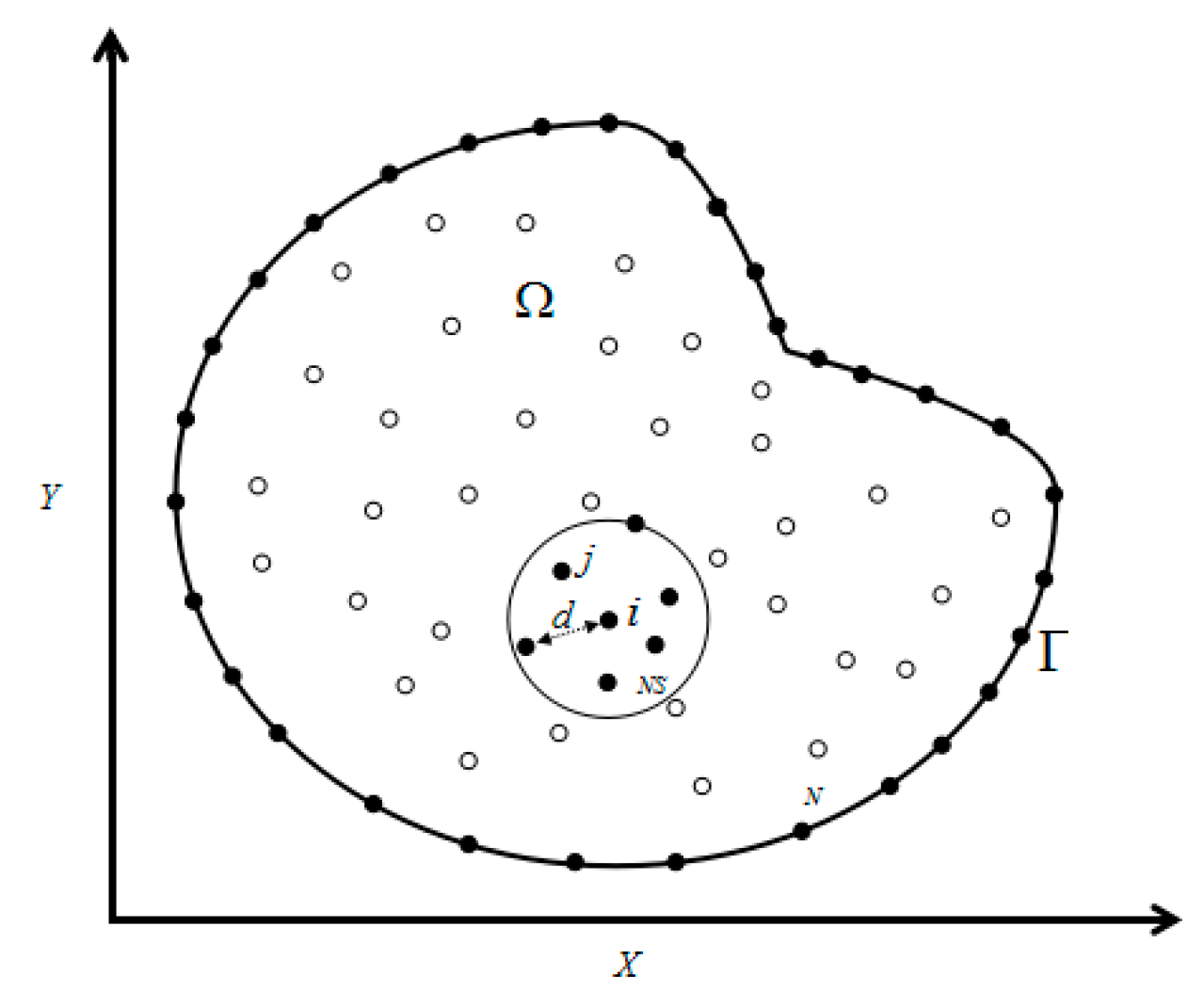
3. Generalized Finite Difference Method
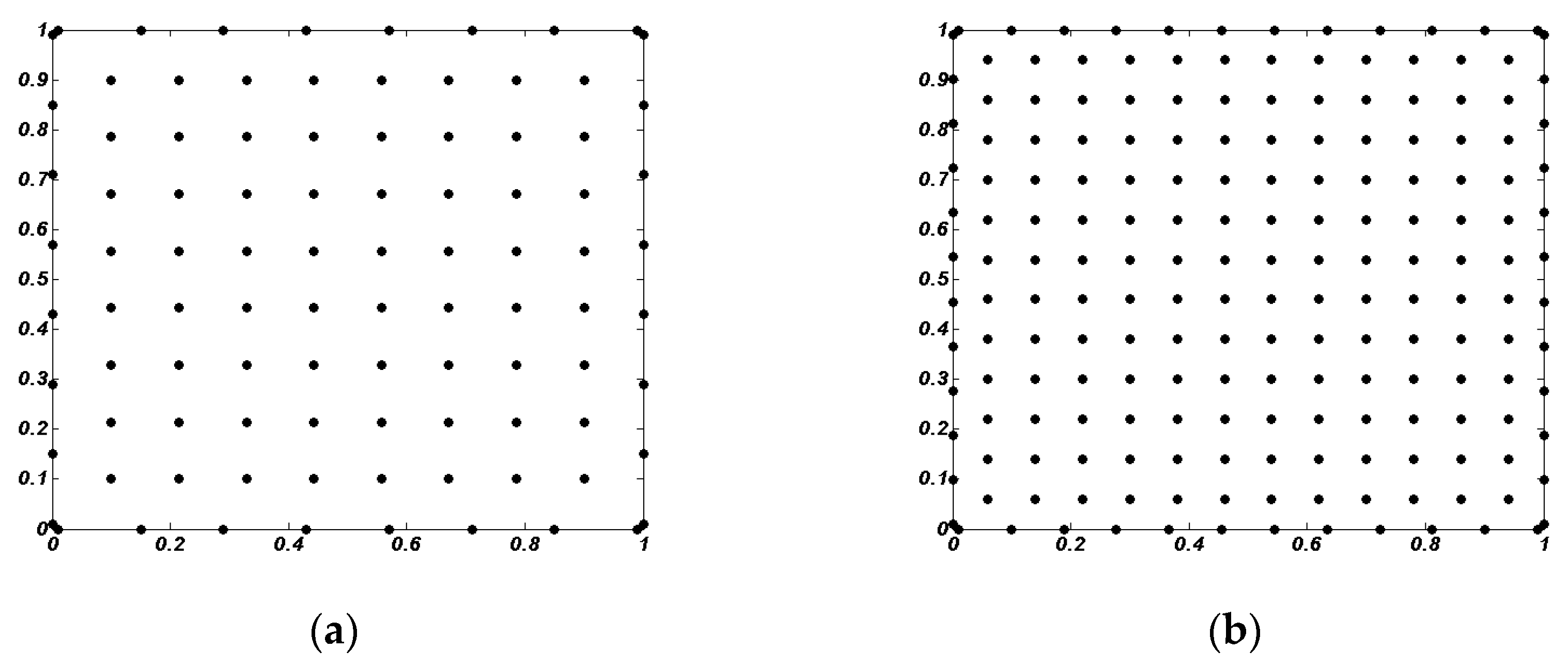
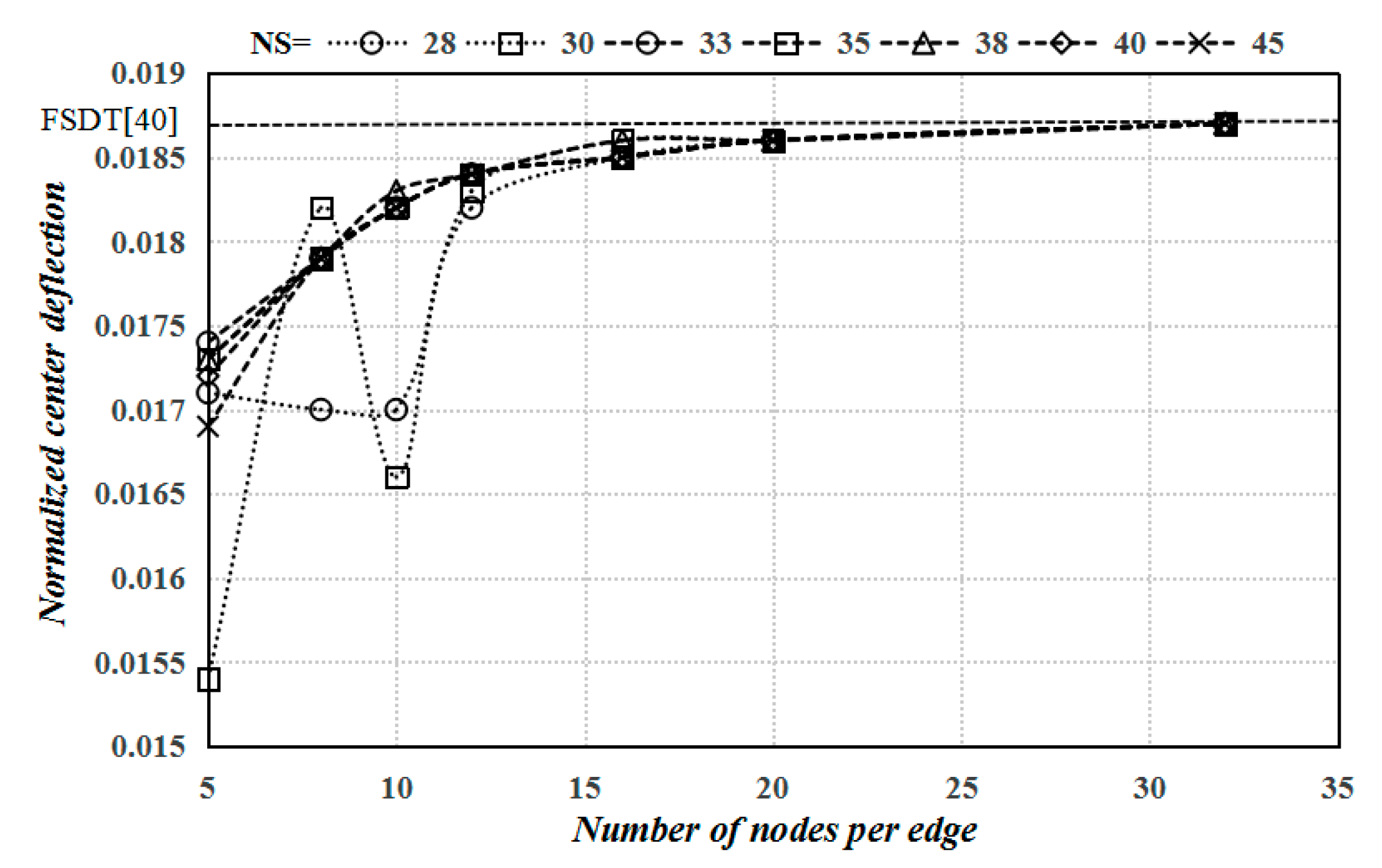
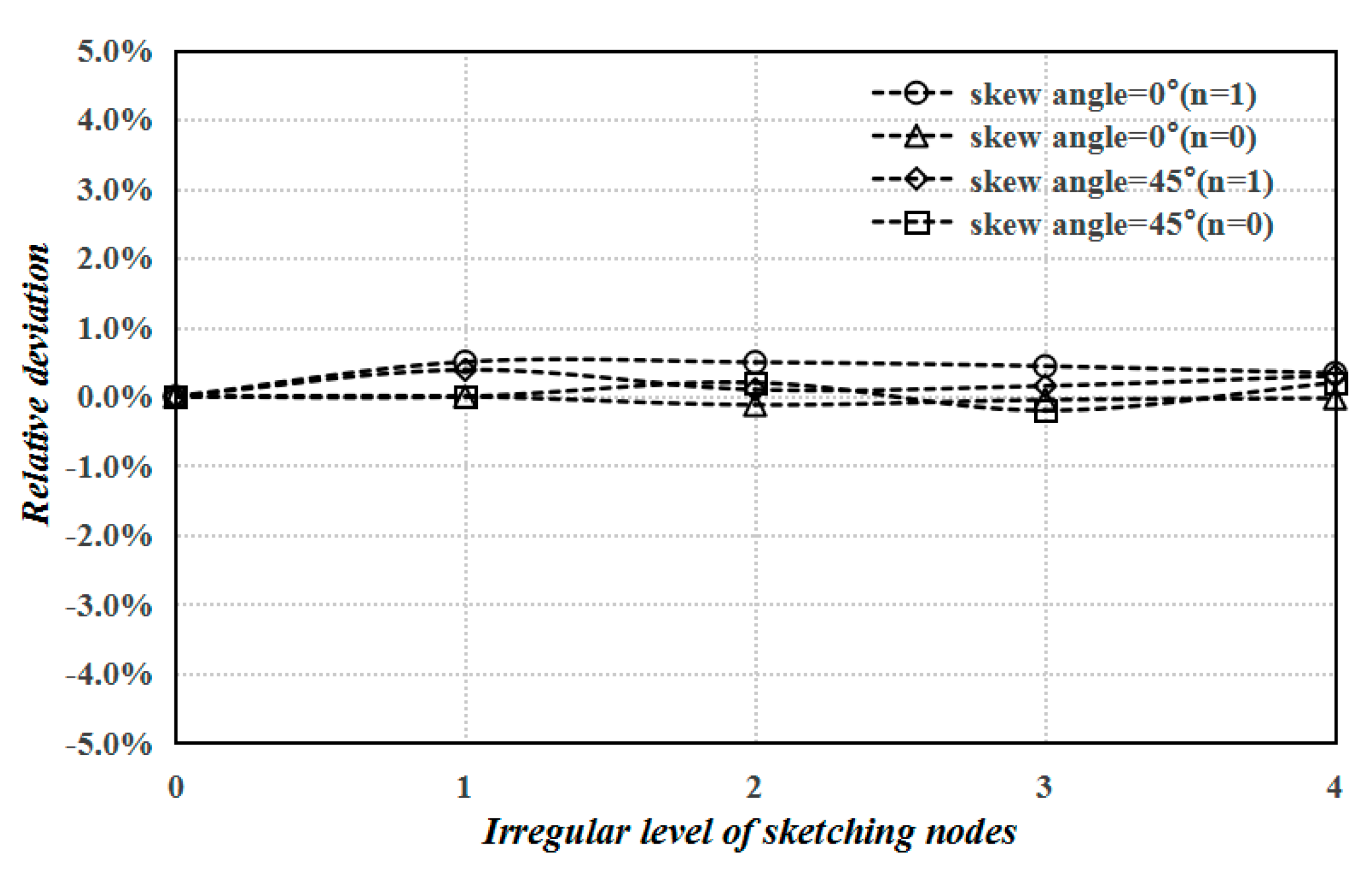
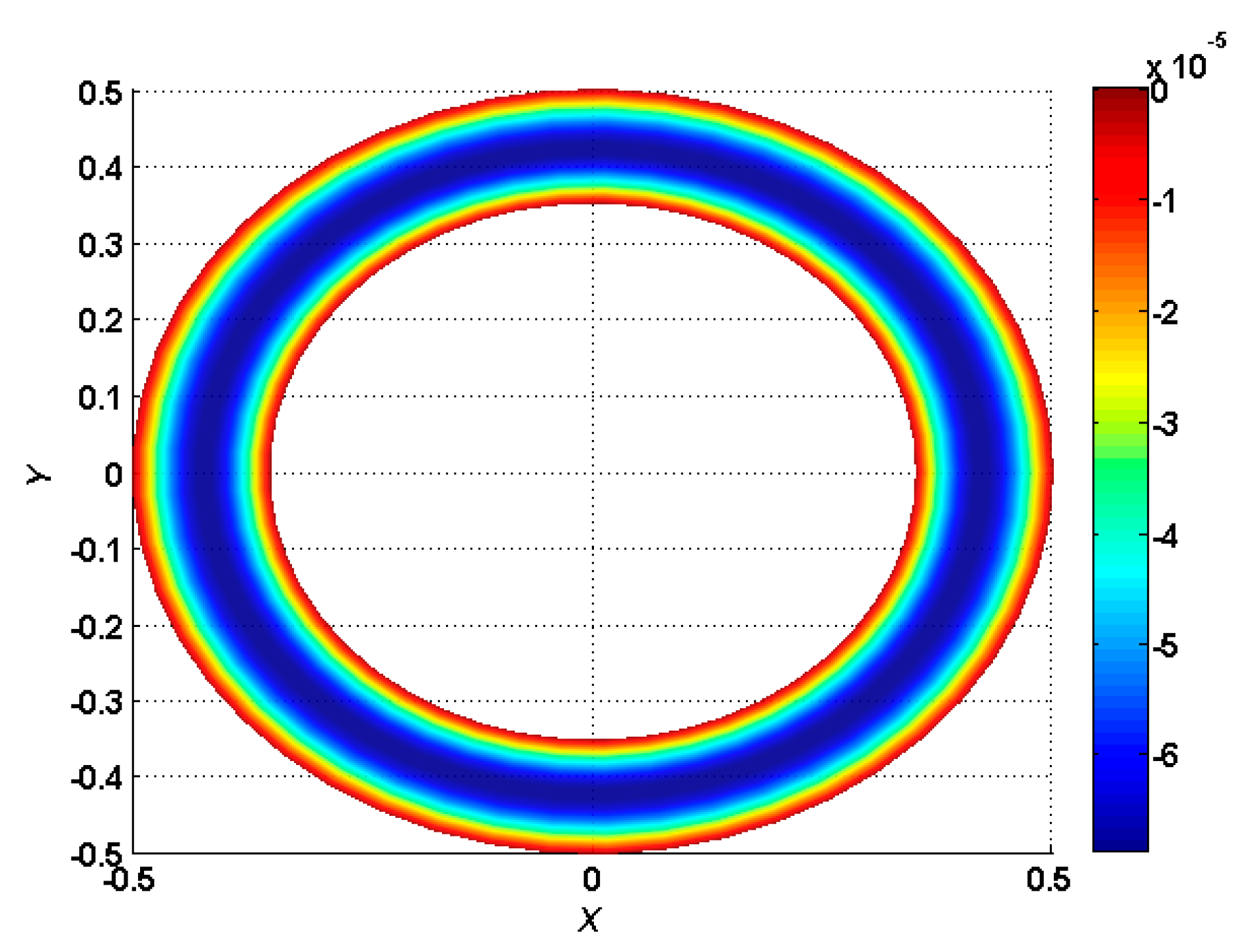
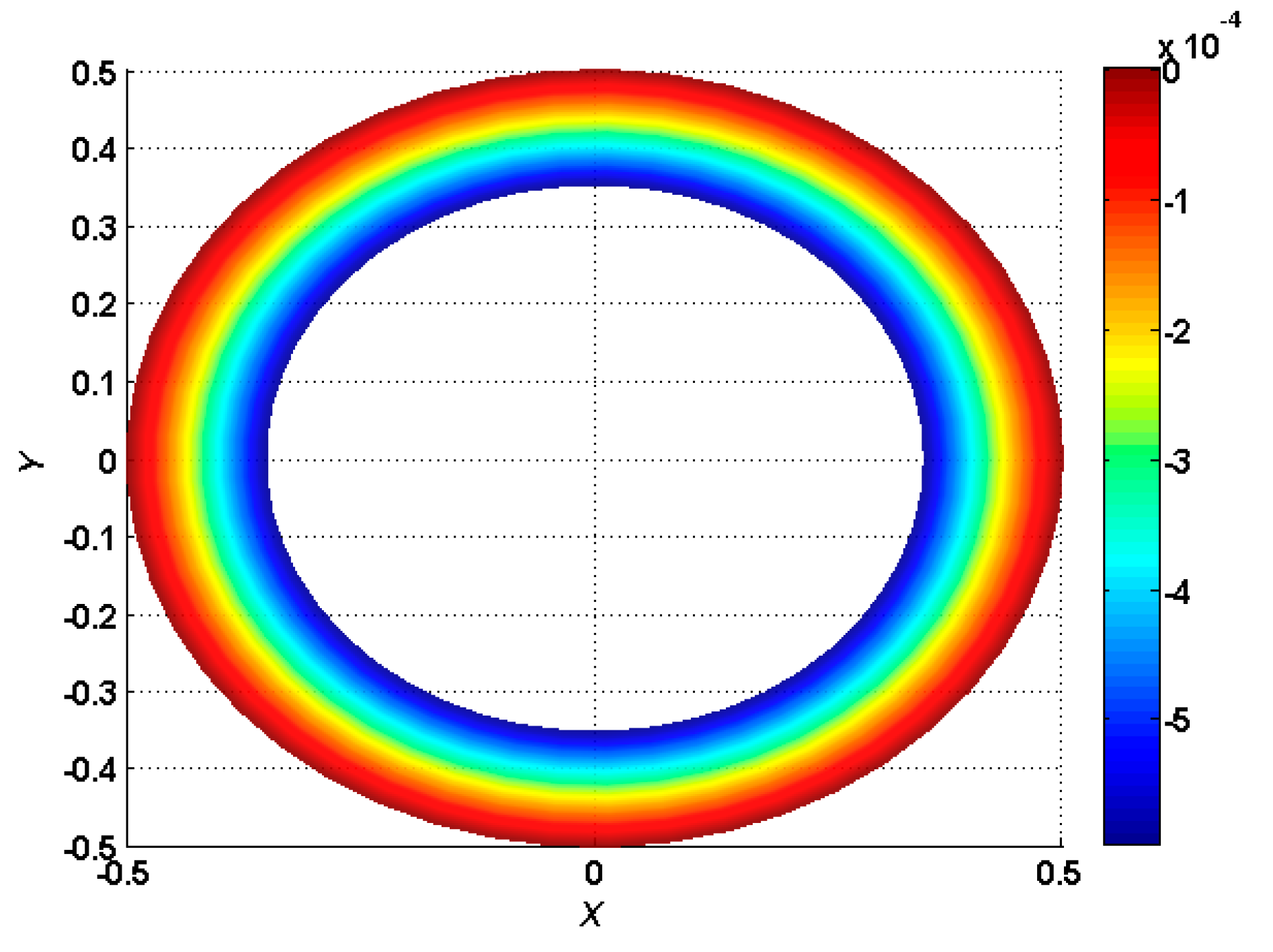
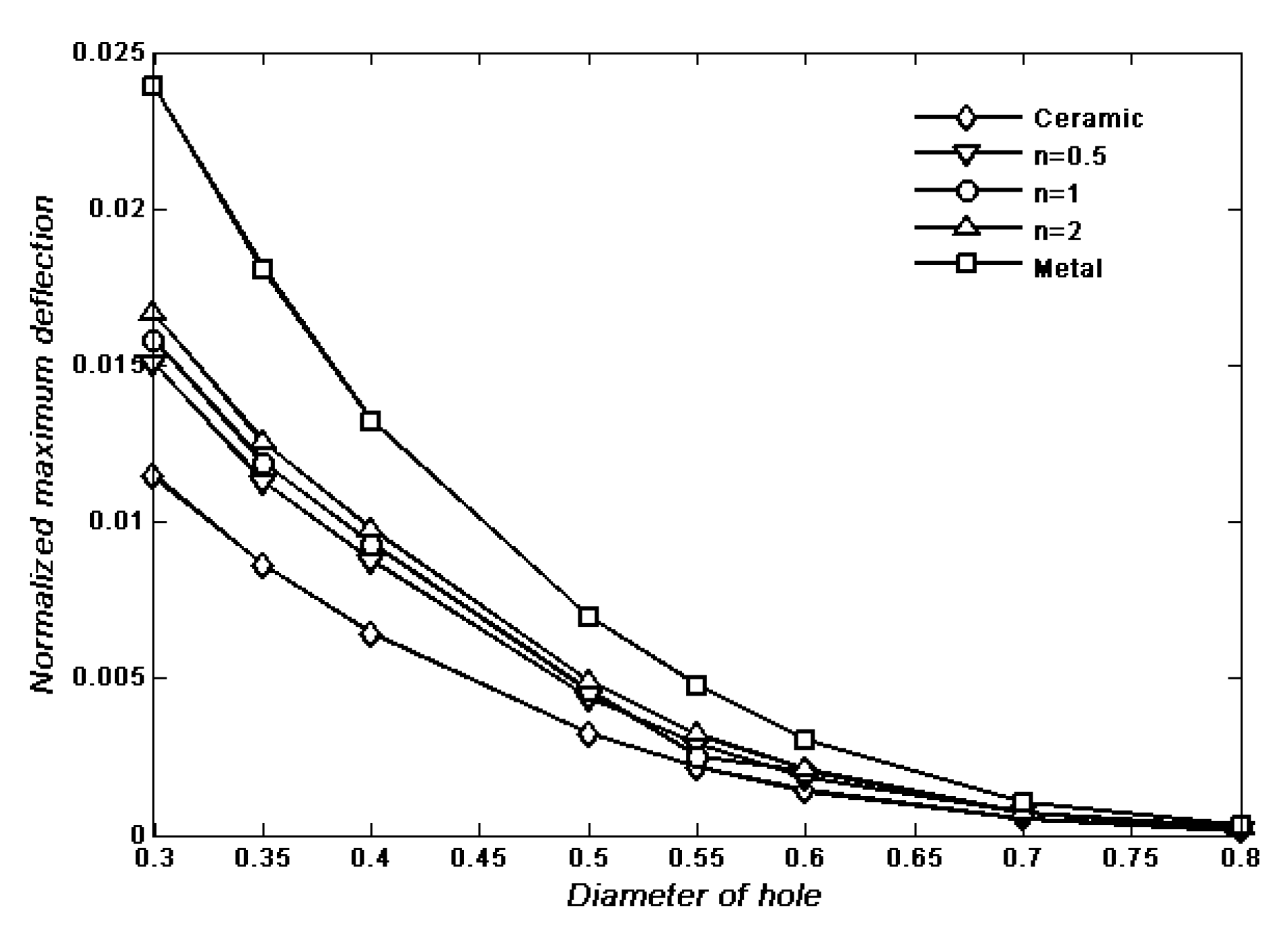
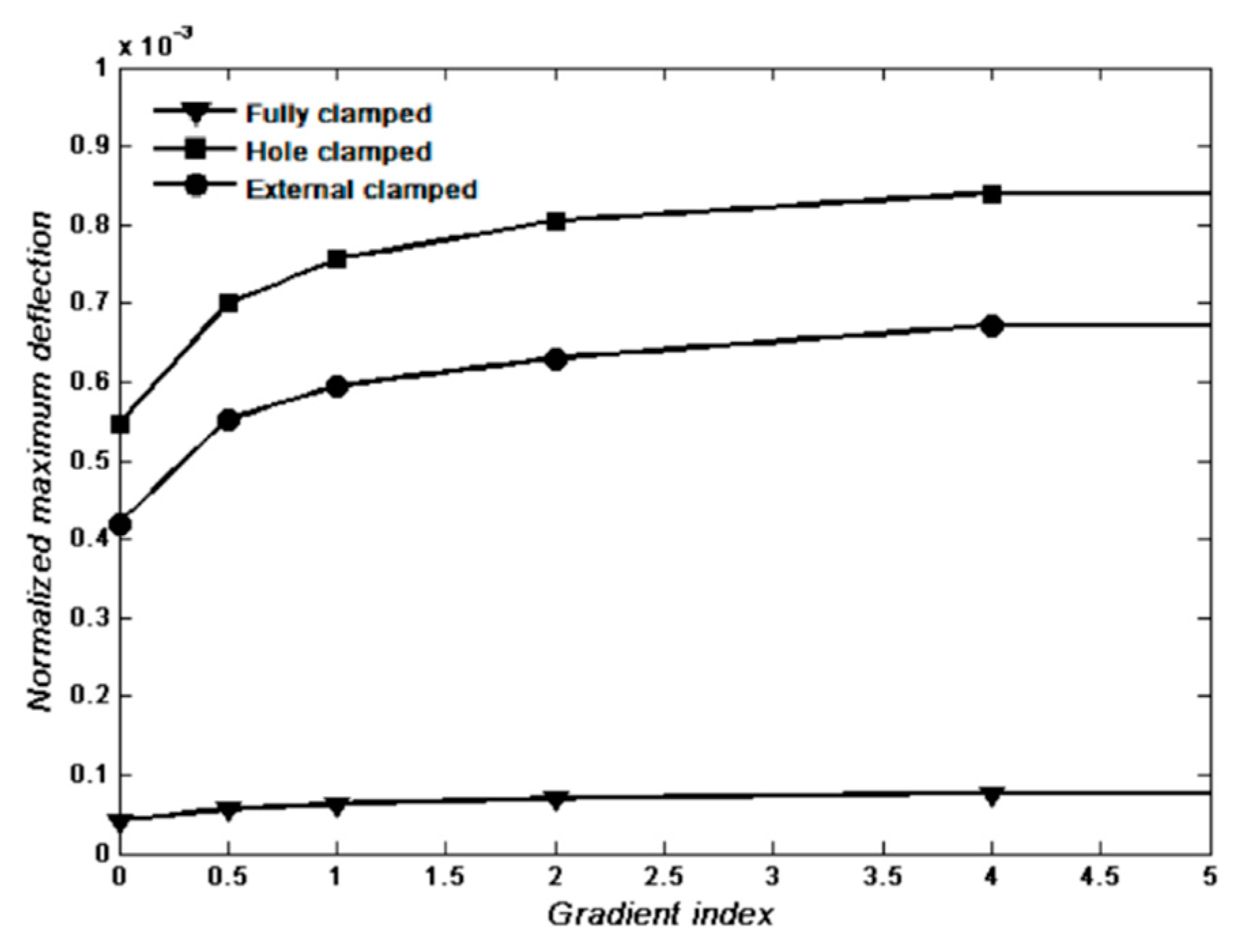
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zenkour, A.M.; Hafed, Z.S.; Radwan, A.F. Bending analysis of functionally graded nanoscale plates by using nonlocal mixed variational formula. Mathematics 2020, 8, 1162. [Google Scholar] [CrossRef]
- Chashmi, M.J.; Fathi, A.; Shirzad, M.; Jafari-Talookolaei, R.A.; Bodaghi, M.; Rabiee, S.M. Design and analysis of porous functionally graded femoral prostheses with improved stress shielding. Designs 2020, 4, 12. [Google Scholar] [CrossRef]
- Scheithauer, U.; Weingarten, S.; Johne, R.; Schwarzer, E.; Abel, J.; Richter, H.-J.; Moritz, T.; Michaelis, A. Ceramic-based 4D components: Additive manufacturing (AM) of ceramic-based functionally graded materials (FGM) by thermoplastic 3D printing (T3DP). Materials 2017, 10, 1368. [Google Scholar] [CrossRef] [PubMed]
- Bodaghi, M.; Noroozi, R.; Zolfagharian, A.; Fotouhi, M.; Norouzi, S. 4D printing self–morphing structures. Materials 2019, 12, 1353. [Google Scholar] [CrossRef] [PubMed]
- Bodaghi, M.; Damanpack, A.R.; Liao, W.-H. Adaptive metamaterials by functionally graded 4D printing. Mater. Des. 2017, 135, 26–36. [Google Scholar] [CrossRef]
- Reddy, B.; Reddy, A.; Kumar, J.; Reddy, K. Bending analysis of laminated composite plates using finite element method. Int. J. Eng. Sci. Technol. 2012, 4, 177–190. [Google Scholar] [CrossRef]
- Pham, Q.H.; Pham, T.D.; Trinh, Q.V.; Phan, D.H. Geometrically nonlinear analysis of functionally graded shells using an edge-based smoothed MITC3 (ES-MITC3) finite elements. Eng. Comput. 2020, 36, 1069–1082. [Google Scholar] [CrossRef]
- Bui, T.Q.; Nguyen, M.N. A moving Kriging interpolation-based meshfree method for free vibration analysis of Kirchhoff plates. Comput. Struct. 2011, 89, 380–394. [Google Scholar] [CrossRef]
- Bui, T.Q.; Nguyen, M.N. Eigenvalue Analysis of Thin Plate with Complicated Shapes by A Novel Mesh-free Method. Int. J. Appl. Mech. 2011, 3, 21–46. [Google Scholar] [CrossRef]
- Bui, T.Q.; Nguyen, M.N.; Zhang, C. An efficient meshfree method for vibration analysis of laminated composite plates. Comput. Mech. 2011, 48, 175–193. [Google Scholar] [CrossRef]
- Dinis, L.M.J.S.; Jorge, R.M.N.; Belinha, J. An Unconstrained Third-Order Plate Theory Applied to Functionally Graded Plates Using a Meshless Method. Mech. Adv. Mater. Struct. 2010, 17, 108–133. [Google Scholar] [CrossRef]
- Wu, C.-P.; Yang, S.-W.; Wang, Y.-M.; Hu, H.-T. A meshless collocation method for the plane problems of functionally graded material beams and plates using the DRK interpolation. Mech. Res. Commun. 2011, 38, 471–476. [Google Scholar] [CrossRef]
- Zhu, P.; Liew, K.M. Free vibration analysis of moderately thick functionally graded plates by local Kriging meshless method. Compos. Struct. 2011, 93, 2925–2944. [Google Scholar] [CrossRef]
- Zhou, H.; Qin, G.; Wang, Z. Heat conduction analysis for irregular functionally graded material geometries using the meshless weighted least-square method with temperature-dependent material properties. Numer. Heat Transf. Part B Fundam. 2019, 75, 1–13. [Google Scholar] [CrossRef]
- Krysl, P.; Belytschko, T. Analysis of thin plates by the element-free Galerkin method. Comput. Mech. 1995, 17, 26–35. [Google Scholar] [CrossRef]
- Liu, G.R.; Chen, X.L.; Reddy, J.N. Buckling of Symmetrically Laminated Composite Plates Using the Element-free Galerkin Method. Int. J. Struct. Stab. Dyn. 2002, 2, 281–294. [Google Scholar] [CrossRef]
- Gilhooley, D.F.; Batra, R.C.; Xiao, J.R. Analysis of thick functionally graded plates by using higher-order shear and normal deformable plate theory and MLPG method with radius basis functions. Compos. Part B 2008, 39, 414–427. [Google Scholar] [CrossRef]
- Sahraee, S.; Saidi, A.R. Axisymmetric bending analysis of thick functionally graded circular plates using fourth-order shear deformation theory. Eur. J. Mech. A/Solids 2009, 28, 974–984. [Google Scholar] [CrossRef]
- Fu, Z.-J.; Chen, W. A truly boundary-only meshfree method applied to Kirchhoff plate bending problem. Adv. Appl. Math. Mech. 2009, 1, 341–352. [Google Scholar]
- Fu, Z.-J.; Chen, W.; Yang, W. Winkler plate bending problems by a truly boundary-only boundary particle method. Comput. Mech. 2009, 44, 757–763. [Google Scholar] [CrossRef]
- Benito, J.J.; Urena, F.; Gavete, L. Influence of several factors in the generalized finite difference method. Appl. Math. Model. 2001, 25, 1039–1053. [Google Scholar] [CrossRef]
- Gavete, L.; Gavete, M.L.; Benito, J.J. Improvements of generalized finite difference method and comparison with other meshless method. Appl. Math. Model. 2003, 27, 831–847. [Google Scholar] [CrossRef]
- Mitchell, A.R.; Griffiths, D.F. The Finite Difference Method in Partial Differential Equations; John Wiley: Hoboken, NJ, USA, 1980. [Google Scholar]
- Belytschko, T.; Lu, Y.-Y.; Gu, L. Element-free Galerkin methods. Int. J. Numer. Meth. Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Ureña, F.; Salete, E.; Benito, J.J. Solving third- and fourth-order partial differential equations using GFDM: Application to solve problems of plates. Comput. Mech. 2012, 89, 366–376. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, L.; Chen, W. Application of the meshless generalized finite difference method to inverse heat source problems. Int. J. Heat Mass Transf. 2017, 108, 721–729. [Google Scholar] [CrossRef]
- Li, P.-W.; Fu, Z.-J.; Gu, Y. The generalized finite difference method for the inverse Cauchy problem in two-dimensional isotropic linear elasticity. Int. J. Solids Struct. 2019, 174, 69–84. [Google Scholar] [CrossRef]
- Li, P.-W.; Chen, W.; Fu, Z.-J. Generalized finite difference method for solving the double-diffusive natural convection in fluid-saturated porous media. Eng. Anal. Bound. Elem. 2018, 95, 175–186. [Google Scholar] [CrossRef]
- Fu, Z.-J.; Xie, Z.-Y.; Ji, S.-Y. Meshless generalized finite difference method for water wave interactions with multiple-bottom-seated-cylinder-array structures. Ocean Eng. 2020, 195, 106736. [Google Scholar] [CrossRef]
- Fu, Z.-J.; Tang, Z.-C.; Zhao, H.-T. Numerical solutions of the coupled unsteady nonlinear convection-diffusion equations based on generalized finite difference method. Eur. Phys. J. Plus 2019, 134, 134. [Google Scholar] [CrossRef]
- Li, P.-W.; Fan, C.-M. Generalized finite difference method for two-dimensional shallow water equations. Eng. Anal. Bound. Elem. 2017, 80, 58–71. [Google Scholar] [CrossRef]
- Vua, T.V.; Nguyenb, N.H.; Khosravifardc, A. A simple FSDT-based meshfree method for analysis of functionally graded plates. Eng. Anal. Bound. Elem. 2017, 79, 1–12. [Google Scholar] [CrossRef]
- Yu, T.T.; Yin, S.H.; Tinh, Q.B. A simple FSDT-based isogeometric analysis for geometrically nonlinear analysis of functionally graded plates. Finite Elem. Anal. Des. 2015, 96, 1–10. [Google Scholar] [CrossRef]
- Mantari, J.L.; Granados, E.V. An original FSDT to study advanced composites on elastic foundation. Thin-Walled Struct. 2016, 107, 80–89. [Google Scholar] [CrossRef]
- Mantari, J.L.; Granados, E.V. A refined FSDT for the static analysis of functionally graded sandwich plates. Thin-Walled Struct. 2015, 90, 150–158. [Google Scholar] [CrossRef]
- Yin, S.H.; Jack, S.H.; Yu, T.T. Isogeometric locking-free plate element: A simple first order shear deformation theory for functionally graded plates. Compos. Struct. 2014, 118, 121–138. [Google Scholar] [CrossRef]
- Nguyen, X.H.; Tran, L.V.; Nguyen, T.T. Analysis of functionally graded plates using an edge-based smoothed finite element method. Compos. Struct. 2011, 93, 3019–3039. [Google Scholar] [CrossRef]
- Nguyen, X.H.; Tran, L.V.; Thai, H. Analysis of functionally graded plates by an efficient finite element method with node-based strain smoothing. Thin Walled Struct. 2012, 54, 1–18. [Google Scholar] [CrossRef]
- Valizadeh, N.; Natarajan, S.; Gonzalez-Estrada, O.A.; Rabczuk, T.; Bui, T.Q.; Bordas, S.P.A. NURBS-based finite element analysis of functionally graded plates: Static bending, vibration, buckling and flutter. Compos. Struct. 2013, 99, 309–326. [Google Scholar] [CrossRef]
- Reddy, J.N. Analysis of functionally graded plates. Int. J. Numer. Methods Eng. 2000, 47, 663–684. [Google Scholar] [CrossRef]
- Singha, M.K.; Prakash, T.; Ganapathi, M. Finite element analysis of functionally graded plates under transverse load. Finite Elem. Anal. Des. 2011, 47, 453–460. [Google Scholar] [CrossRef]
- Zenkour, A.M. Generalized shear deformation theory for bending analysis of functionally graded plates. Appl. Math. Model. 2006, 30, 67–84. [Google Scholar] [CrossRef]

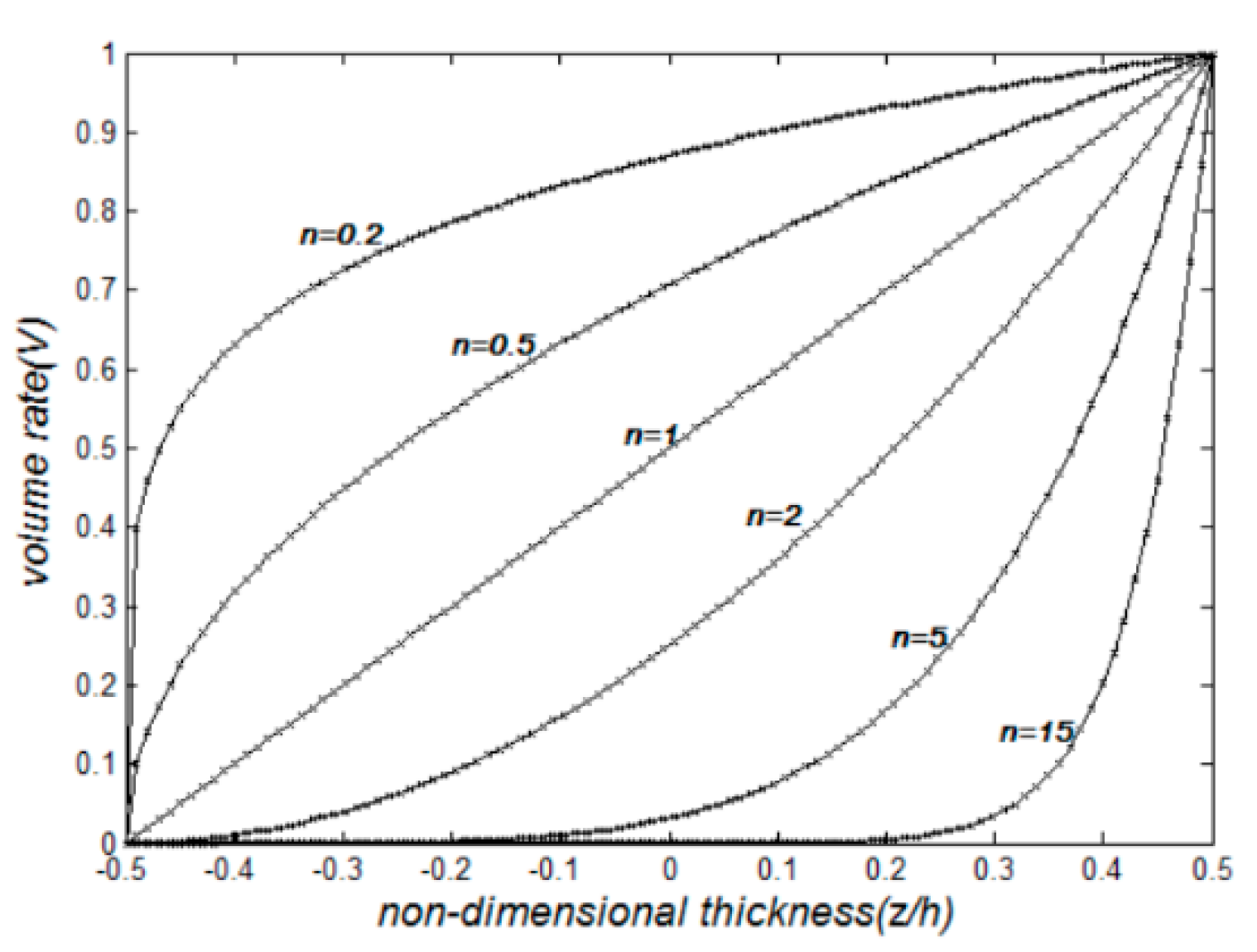



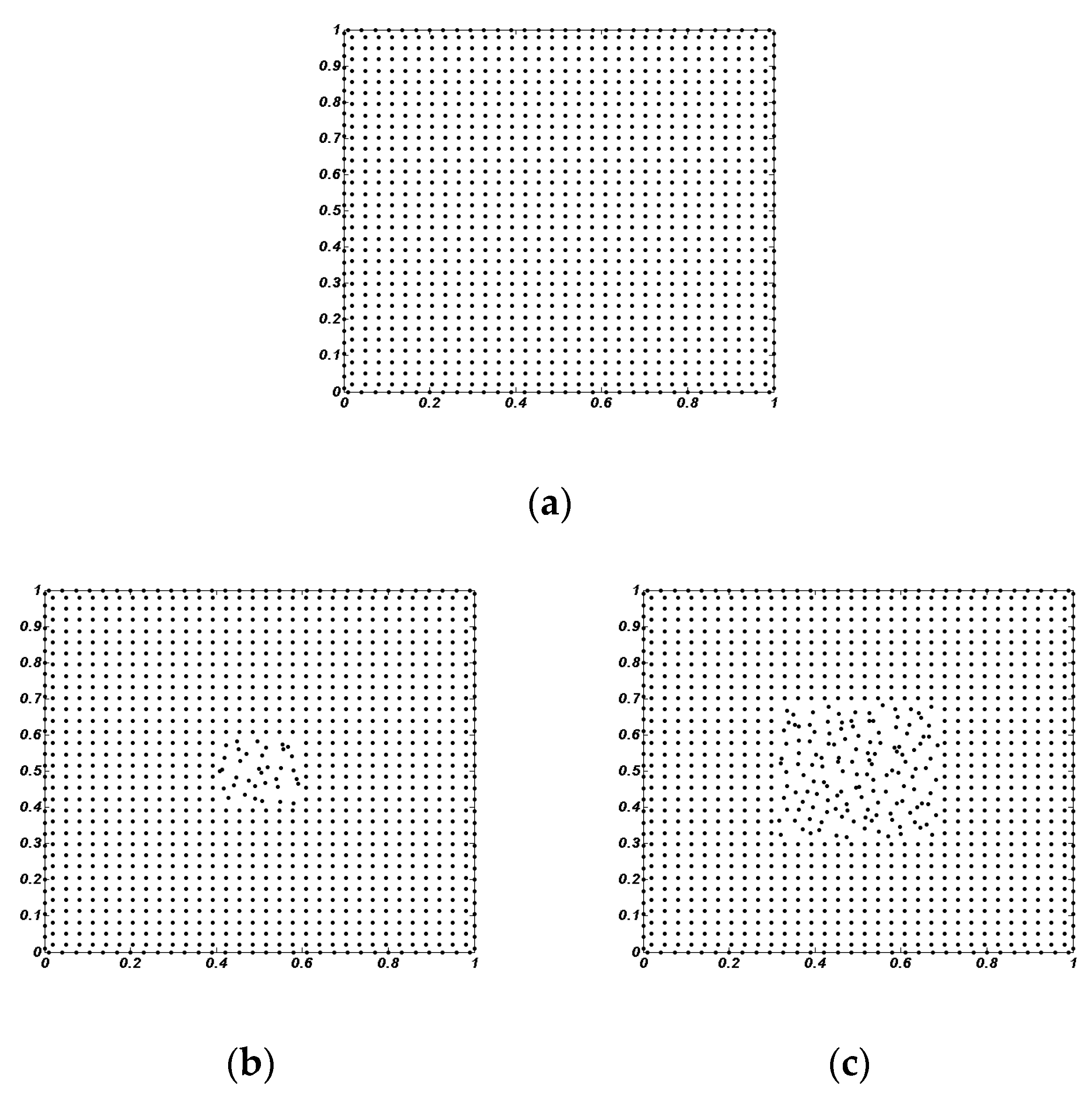




| Properties | Ceramic | |||
|---|---|---|---|---|
| 70 | 380 | 200 | 150 | |
| 0.3 | 0.3 | 0.3 | 0.3 | |
| 2707 | 3800 | 5700 | 5240 |
| Boundary Condition | Method | |||||
|---|---|---|---|---|---|---|
| SSSS | 5 | IGA [36] | 0.0187 | 0.0253 | 0.0295 | 0.0340 |
| ES-DSG [37] | 0.0186 | 0.0243 | 0.0275 | 0.0308 | ||
| MK [32] | 0.0188 | 0.0254 | 0.0297 | 0.0340 | ||
| present | 0.0187 | 0.0248 | 0.0286 | 0.0328 | ||
| 20 | IGA [36] | 0.0157 | 0.0214 | 0.0252 | 0.0285 | |
| MK [32] | 0.0159 | 0.0217 | 0.0253 | 0.0286 | ||
| present | 0.0157 | 0.0213 | 0.0242 | 0.0270 | ||
| SFSS | 5 | IGA [36] | 0.0345 | 0.0469 | 0.0551 | 0.0630 |
| MK [32] | 0.0348 | 0.0472 | 0.0550 | 0.0627 | ||
| present | 0.0347 | 0.0460 | 0.0546 | 0.0621 | ||
| 20 | IGA [36] | 0.0306 | 0.0419 | 0.0551 | 0.0631 | |
| MK [32] | 0.0308 | 0.0422 | 0.0549 | 0.0627 | ||
| present | 0.0303 | 0.0415 | 0.0538 | 0.0618 | ||
| CCCC | 5 | ES-DSG [38] | 0.0083 | 0.0110 | 0.0128 | 0.0149 |
| MITC4 [38] | 0.0082 | 0.0110 | 0.0127 | 0.0149 | ||
| IGA [39] | 0.0082 | 0.0110 | 0.0129 | 0.0149 | ||
| MLPG [17] | 0.0079 | 0.0117 | 0.0137 | 0.0157 | ||
| present | 0.0083 | 0.0110 | 0.0130 | 0.0156 |
| Method | |||||
|---|---|---|---|---|---|
| Uniformly distributed load | |||||
| Singha [41] | 0.0086 | 0.0172 | 0.0221 | 0.0257 | - |
| Zenkour [42] | 0.0085 | 0.0170 | 0.0218 | 0.0253 | - |
| present | 0.0086 | 0.0168 | 0.0215 | 0.0248 | 0.0466 |
| Lateral sinusoidal load | |||||
| Singha [41] | 0.0055 | 0.0109 | 0.0141 | 0.0164 | 0.0296 |
| Zenkour [42] | 0.0054 | 0.0107 | 0.0138 | 0.0161 | 0.0296 |
| present | 0.0054 | 0.0106 | 0.0135 | 0.0158 | 0.0296 |
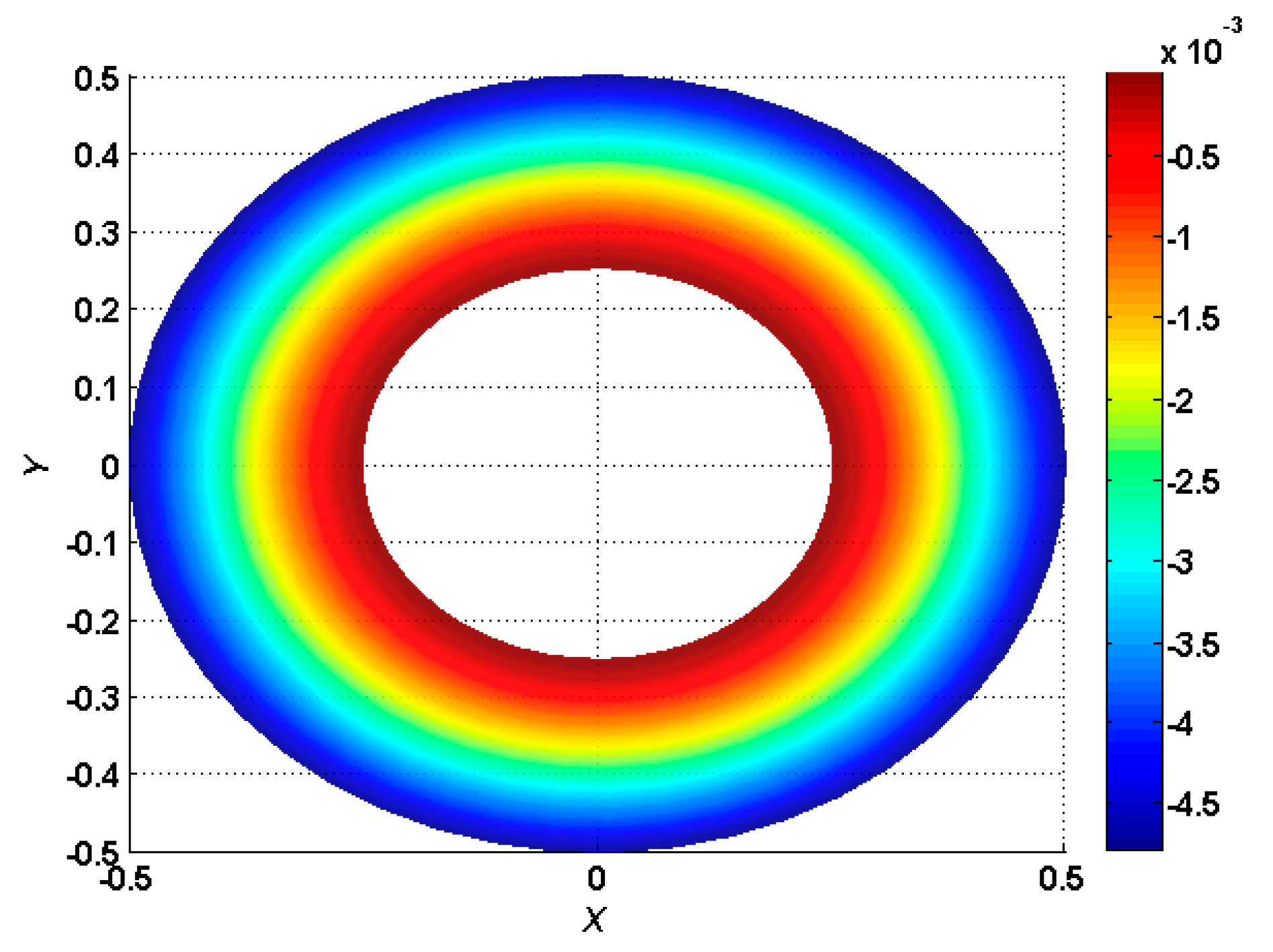
| (ceramic) |  |  |  |  |
 |  |  |  | |
 |  |  | 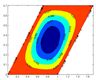 | |
| (metal) |  |  |  | 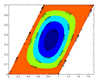 |
Sample Availability: The datasets analyzed during the current study are available from the corresponding author and the first author upon reasonable request. | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.-D.; Tang, Z.-C.; Fu, Z.-J. Generalized Finite Difference Method for Plate Bending Analysis of Functionally Graded Materials. Mathematics 2020, 8, 1940. https://doi.org/10.3390/math8111940
Li Y-D, Tang Z-C, Fu Z-J. Generalized Finite Difference Method for Plate Bending Analysis of Functionally Graded Materials. Mathematics. 2020; 8(11):1940. https://doi.org/10.3390/math8111940
Chicago/Turabian StyleLi, Yu-Dong, Zhuo-Chao Tang, and Zhuo-Jia Fu. 2020. "Generalized Finite Difference Method for Plate Bending Analysis of Functionally Graded Materials" Mathematics 8, no. 11: 1940. https://doi.org/10.3390/math8111940
APA StyleLi, Y.-D., Tang, Z.-C., & Fu, Z.-J. (2020). Generalized Finite Difference Method for Plate Bending Analysis of Functionally Graded Materials. Mathematics, 8(11), 1940. https://doi.org/10.3390/math8111940







