Soliton Solutions for a Nonisospectral Semi-Discrete Ablowitz–Kaup–Newell–Segur Equation
Abstract
1. Introduction
2. Bilinear Form and Multisoliton Solutions for nsd-AKNS Equation (3)
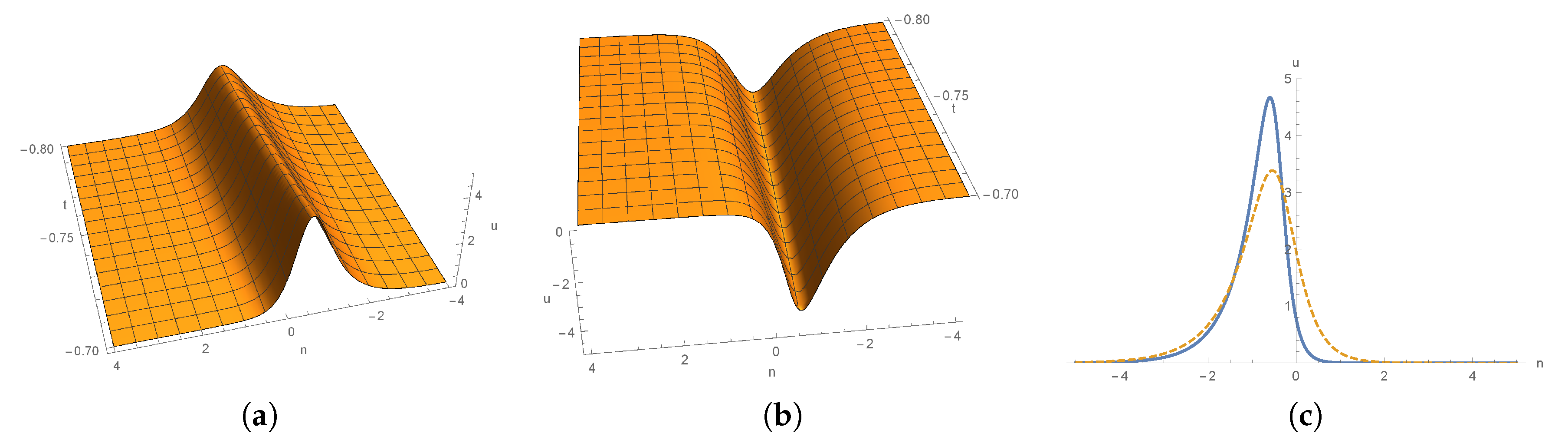
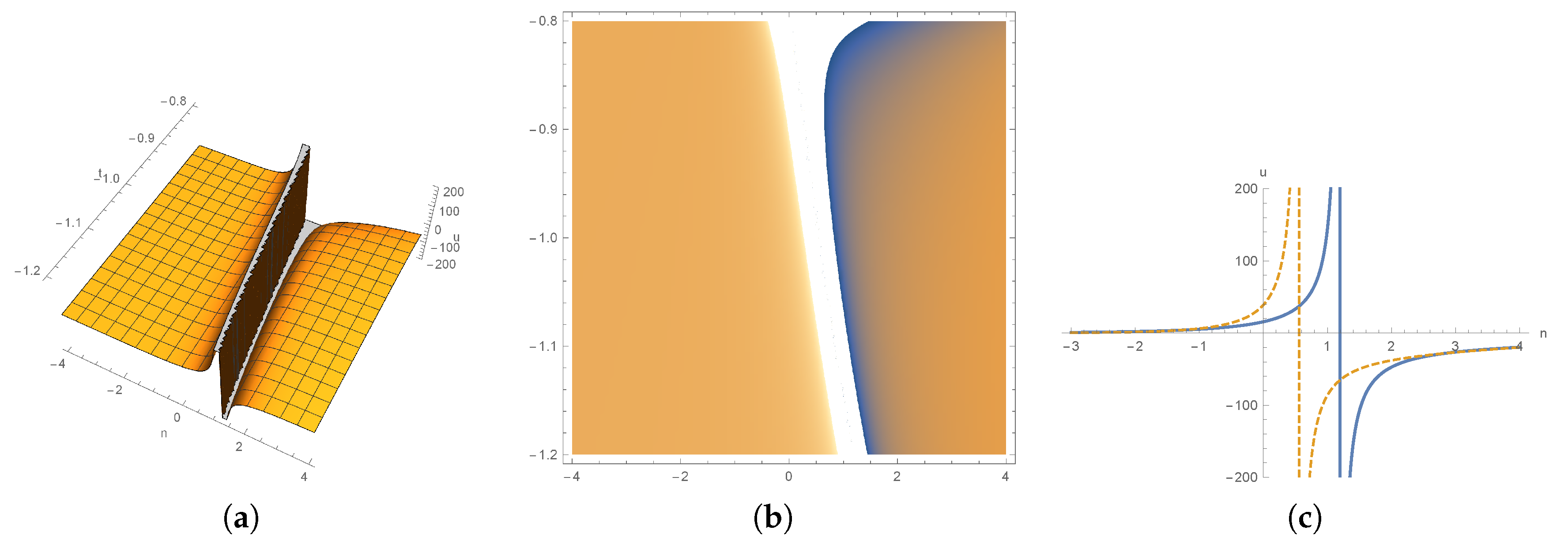
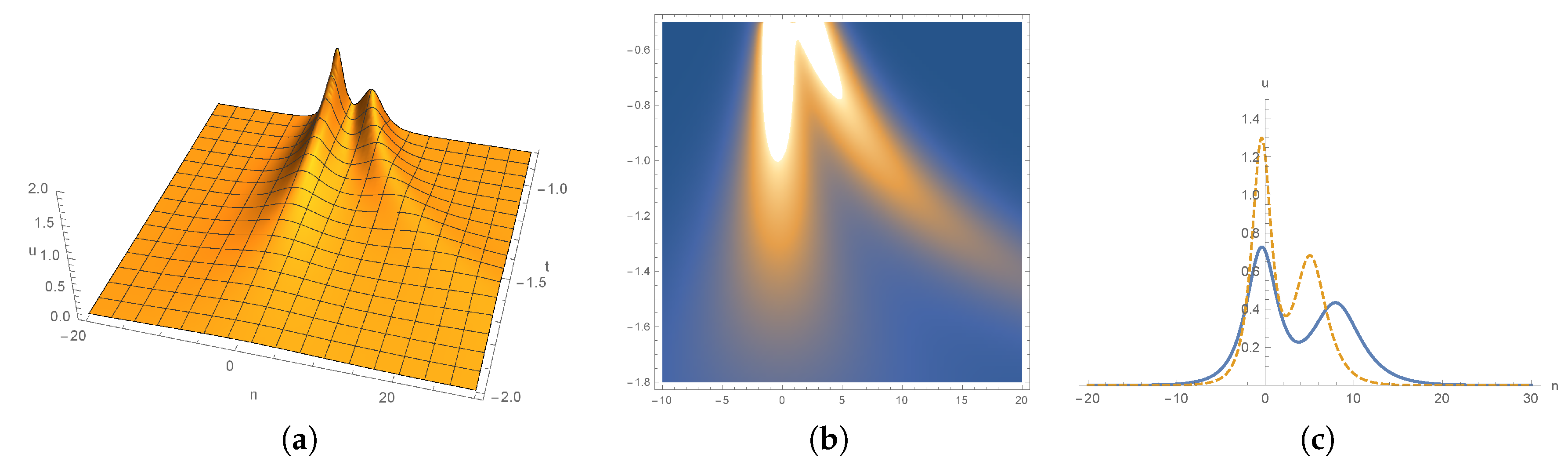
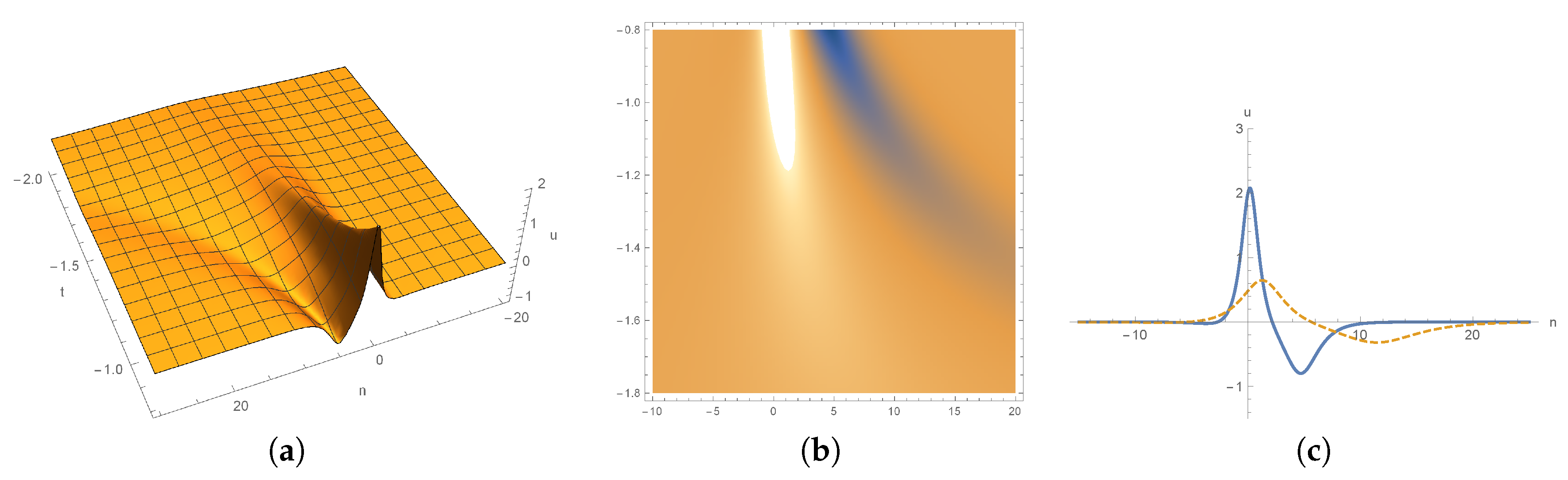
3. Dynamics of 1-Soliton Solution and 2-Soliton Solutions
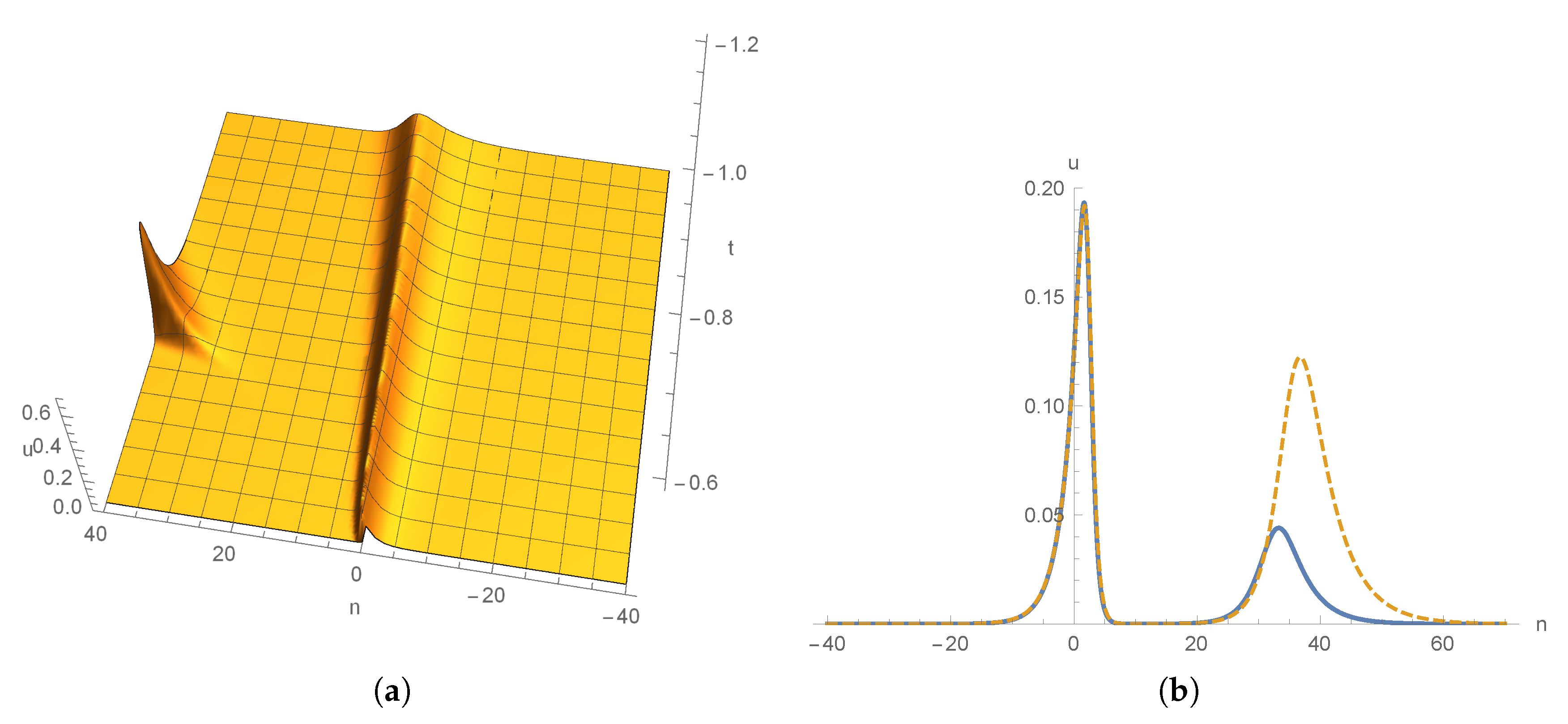
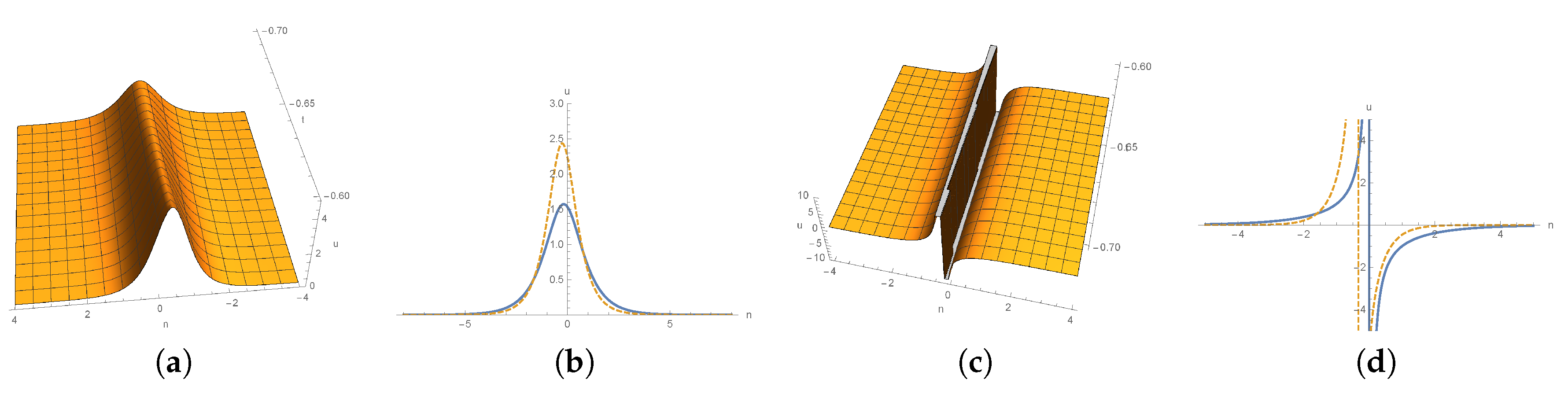
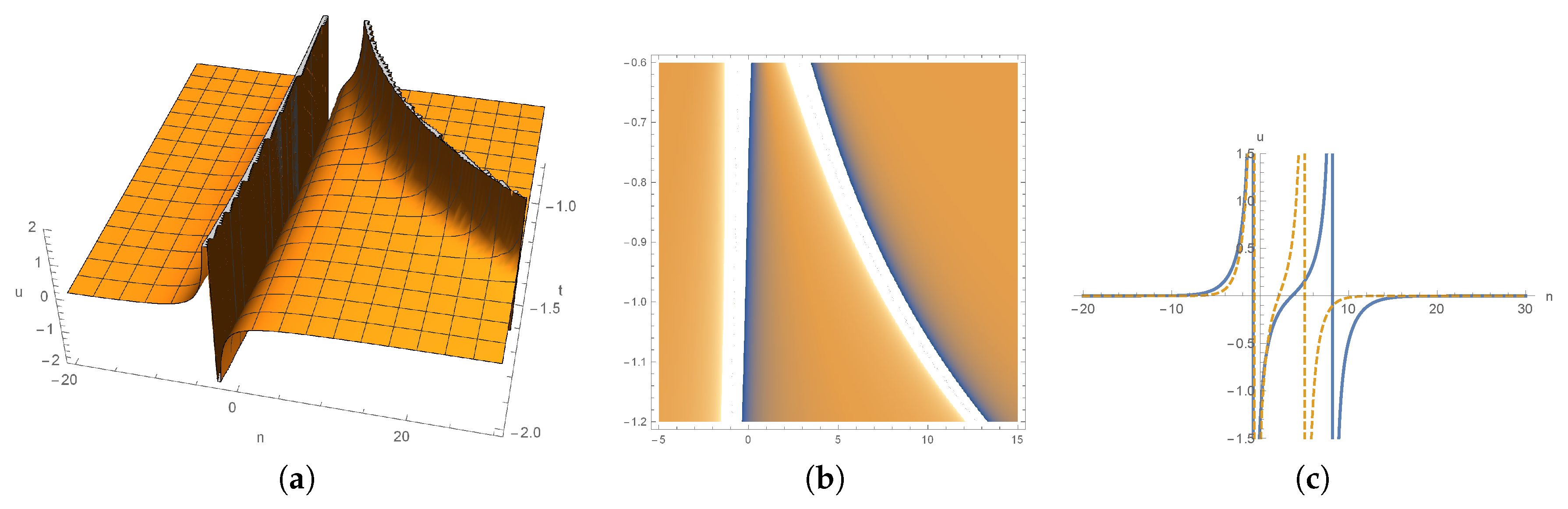
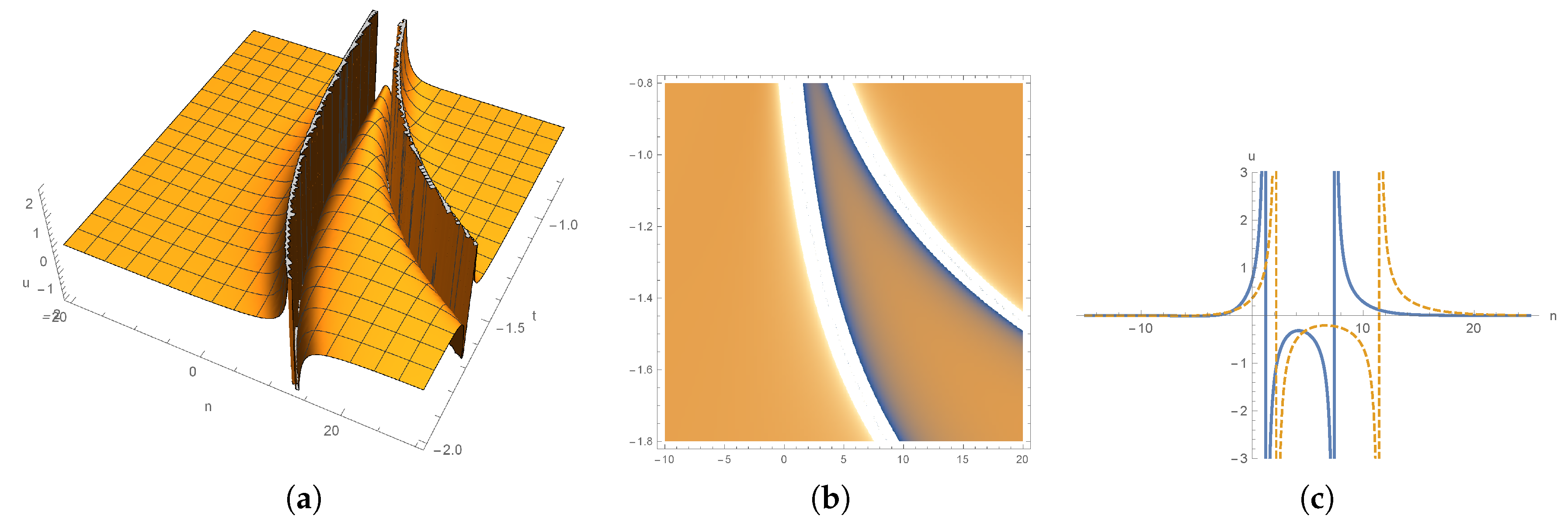
4. Multisoliton Solutions for nsd-mKdV Equation (4) and Dynamics
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, H.; Liu, C.S. Solitons in nonuniform media. Phys. Rev. Lett. 1976, 37, 693–697. [Google Scholar] [CrossRef]
- Hirota, R.; Satsuma, J. N-soliton solution of the KdV equation with loss and nonuniformity terms. J. Phys. Soc. Jpn. 1976, 41, 2141–2142. [Google Scholar] [CrossRef]
- Calogero, F.; Degasperis, A. Conservation laws for classes of nonlinear evolution equations solvable by the spectral transform. Commun. Math. Phys. 1978, 63, 155–176. [Google Scholar] [CrossRef]
- Ma, W.X. An approach for constructing nonisospectral hierarchies of evolution equations. J. Phys. A Gen. Math. 1992, 25, L719–L726. [Google Scholar] [CrossRef]
- Ma, W.X. The algebraic structure of zero curvature representations and application to coupled KdV systems. J. Phys. A Gen. Math. 1993, 26, 2573–2582. [Google Scholar] [CrossRef]
- Ma, W.X. A simple scheme for generating nonisospectral flows from the zero curvature representation. Phys. Lett. A 1993, 179, 179–185. [Google Scholar] [CrossRef]
- Fuchssteiner, B. Master symmetries, higher order time-dependent symmetries and conserved densities of nonlinear evolution equations. Prog. Theor. Phys. 1983, 70, 1508–1522. [Google Scholar] [CrossRef]
- Ma, W.X.; Fuchssteiner, B. Algebraic structure of discrete zero curvature equations and master symmetries of discrete evolution equations. J. Math. Phys. 1999, 40, 2400–2418. [Google Scholar] [CrossRef]
- Gupta, M.R. Exact inverse scattering solution of a nonlinear evolution equation in a nonuniform media. Phys. Lett. A 1979, 72, 420–422. [Google Scholar] [CrossRef]
- Burtsev, S.P.; Zakharov, V.E.; Mikhailov, A.V. Inverse scattering method with variable spectral parameter. Theor. Math. Phys. 1987, 70, 227–240. [Google Scholar] [CrossRef]
- Zhang, D.J.; Chen, D.Y. Negatons, positons, rational-like solutions and conservation laws of the KdV equation with loss and nonuniformity terms. J. Phys. A Gen. Math. 2004, 37, 851–865. [Google Scholar] [CrossRef]
- Zhao, S.L.; Zhang, D.J.; Chen, D.Y. N-soliton solutions of non-isospectral derivative nonlinear Schrödinger equation. Chin. Phys. Lett. 2009, 26, 030202. [Google Scholar]
- Silem, A.; Zhang, C.; Zhang, D.J. Dynamics of three nonisospectral nonlinear Schrödinger equations. Chin. Phys. B 2019, 28, 020202. [Google Scholar] [CrossRef]
- Eilbeck, J.C.; Lomdah, P.S.; Scott, A.C. The discrete self-trapping equation. Physica D 1985, 16, 318–338. [Google Scholar] [CrossRef]
- Laedke, E.W.; Spatschek, K.H.; Turitsyn, S.K. Stability of discrete solitons and quasicollapse to intrinsically localized modes. Phys. Rev. Lett. 1994, 73, 1055–1059. [Google Scholar] [CrossRef]
- Cao, C.W.; Zhang, G.Y. Integrable symplectic maps associated with the ZS-AKNS spectral problem. J. Phys. A Math. Theor. 2012, 45, 265201. [Google Scholar] [CrossRef]
- Xue, L.L.; Liu, Q.P. A supersymmetric AKNS problem and its Darboux-Bäcklund transformations and discrete systems. Stud. Appl. Math. 2015, 135, 35–62. [Google Scholar] [CrossRef]
- Zhao, S.L. A discrete negative AKNS equation: Generalised Cauchy matrix approach. J. Nonlinear Math. Phys. 2016, 23, 544–562. [Google Scholar] [CrossRef]
- Chen, K.; Deng, X.; Zhang, D.J. Symmetry constraint of the differential-difference KP hierarchy and a second discretization of the ZS-AKNS system. J. Nonlinear Math. Phys. 2017, 24, 18–35. [Google Scholar] [CrossRef]
- Zhao, S.L.; Shi, Y. Discrete and semidiscrete models for AKNS equation. Z. Naturforsch. A 2017, 72, 281–290. [Google Scholar] [CrossRef]
- Zhao, S.L. Discrete potential Ablowitz–Kaup–Newell–Segur equation. J. Differ. Equ. Appl. 2019, 25, 1134–1148. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Ladik, J.F. Nonlinear differential-difference equations. J. Math. Phys. 1975, 16, 598–603. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Prinari, B.; Trubatch, A.D. Discrete and Continuous Nonlinear Schrödinger Systems; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ablowitz, M.J.; Kaup, D.J.; Newell, A.C.; Segur, H. Nonlinear-evolution equations of physical significance. Phys. Rev. Lett. 1973, 31, 125–127. [Google Scholar] [CrossRef]
- Zhang, D.J.; Ning, T.K.; Bi, J.B.; Chen, D.Y. New symmetries for the Ablowitz–Ladik hierarchies. Phys. Lett. A 2006, 359, 458–466. [Google Scholar] [CrossRef]
- Zhang, D.J.; Chen, S.T. Symmetries for the Ablowitz–Ladik hierarchy: II. Integrable discrete nonlinear Schrödinger equations anddiscrete AKNS hierarchy. Stud. Appl. Math. 2010, 125, 419–443. [Google Scholar] [CrossRef]
- Li, Q.; Chen, D.Y.; Zhang, J.B.; Chen, S.T. Solving the non-isospectral Ablowitz–Ladik hierarchy via the inverse scattering transform and reductions. Chaos Soliton Fractals 2012, 45, 1479–1485. [Google Scholar] [CrossRef]
- Li, Q.; Duan, Q.Y.; Zhang, J.B. Soliton solutions of the mixed discrete modified Korteweg Cde Vries hierarchy via the inverse scattering transform. Phys. Scr. 2012, 86, 065009. [Google Scholar] [CrossRef]
- Chen, S.T.; Chen, D.Y.; Li, Q.; Cheng, J.W. N-soliton-like and double Casoratian solutions of a nonisospectral Ablowitz–Ladik equation. Int. J. Mod. Phys. B 2016, 30, 1640008. [Google Scholar] [CrossRef]
- Chen, X.M.; Chang, X.K.; Su, J.Q.; Hu, X.B.; Yeh, Y.N. Three semi-discrete integrable systems related to orthogonal polynomials and their generalized determinant solutions. Nonlinearity 2015, 28, 2279–2306. [Google Scholar] [CrossRef]
- Chen, X.M.; Hu, X.B.; Hoissen, F.M. Non-isospectral extension of the Volterra lattice hierarchy, and Hankel determinants. Nonlinearity 2018, 31, 4393–4422. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Zhang, D.J.; Ji, J.; Zhao, S.L. Soliton scattering with amplitude changes of a negative order AKNS equation. Physica D 2009, 238, 2361–2367. [Google Scholar] [CrossRef]
- Hietarinta, J. Scattering of solitons and dromions. In Scattering: Scattering and Inverse Scattering in Pure and Applied Science; Pike, R., Sabatier, P., Eds.; Academic Press: London, UK, 2002; pp. 1773–1791. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.-L. Soliton Solutions for a Nonisospectral Semi-Discrete Ablowitz–Kaup–Newell–Segur Equation. Mathematics 2020, 8, 1889. https://doi.org/10.3390/math8111889
Zhao S-L. Soliton Solutions for a Nonisospectral Semi-Discrete Ablowitz–Kaup–Newell–Segur Equation. Mathematics. 2020; 8(11):1889. https://doi.org/10.3390/math8111889
Chicago/Turabian StyleZhao, Song-Lin. 2020. "Soliton Solutions for a Nonisospectral Semi-Discrete Ablowitz–Kaup–Newell–Segur Equation" Mathematics 8, no. 11: 1889. https://doi.org/10.3390/math8111889
APA StyleZhao, S.-L. (2020). Soliton Solutions for a Nonisospectral Semi-Discrete Ablowitz–Kaup–Newell–Segur Equation. Mathematics, 8(11), 1889. https://doi.org/10.3390/math8111889




