Surface Motion of a Half-Space Containing an Elliptical-Arc Canyon under Incident SH Waves

Abstract

The existence of local terrain has a great influence on the scattering and diffraction of seismic waves. The wave function expansion method is a commonly used method for studying terrain effects, because it can reveal the physical process of wave scattering and verify the accuracy of numerical methods. An exact, analytical solution of two-dimensional scattering of plane SH (shear-horizontal) waves by an elliptical-arc canyon on the surface of the elastic half-space is proposed by using the wave function expansion method. The problem of transforming wave functions in multi-ellipse coordinate systems was solved by using the extra-domain Mathieu function addition theorem, and the steady-state solution of the SH wave scattering problem of elliptical-arc depression terrain was reduced to the solution of simple infinite algebra equations. The numerical results of the solution are obtained by truncating the infinite equation. The accuracy of the proposed solution is verified by comparing the results obtained when the elliptical arc-shaped depression is degraded into a semi-ellipsoidal depression or even a semi-circular depression with previous results. Complicated effects of the canyon depth-to-span ratio, elliptical axis ratio, and incident angle on ground motion are shown by the numerical results for typical cases.

1. Introduction

Scattering and diffraction occur when local seismic waves propagate in media with irregular topography (such as canyons, valleys, hills). This discovery plays a vital role in ground vibration during earthquakes, known as the “topographic effect”. When the wavelength of the seismic wave is comparable to the size of the irregular terrain, amplification or attenuation can be observed. This phenomenon of topographic effects was first observed during the San Fernando earthquake on a steep ridge near the abutment of the Pacoima dam, and was subsequently widely recognized [1,2,3,4,5]. The understanding of topographic effects can provide profound insights into the interpretation of strong ground motions and is conducive to seismic design of large-span structures.

In order to understand and reveal the properties of seismic wave topographic effect, a lot of research work on seismic wave scattering has been done by numerical and analytical methods. The numerical methods used mainly include the finite element method [6,7] and the boundary element method [8,9,10,11], and the analysis methods used are mainly the wave function expansion method. However, in a relatively simple case, the use of the analysis method is of great value not only for revealing the basic mathematical and physical characteristics of the solution to the wave scattering problem but also for testing the accuracy of all numerical methods. The wave function expansion method can provide a closed-form solution, and many two-dimensional scattering problems of plane SH waves are solved by this method, such as horizontally stratified surface layers, semi-cylindrical canyon [12], semi-elliptical canyon [13], multi-layered inhomogeneous semi-cylindrical canyon [14], semi-cylindrical hill [15], cylindrical canyon of the circular-arc cross section [2], cylindrical hill of the circular-arc cross section [16], elliptic-arc canyon in the corner [17], semi-elliptical hill [3,18], and semi-elliptical hill with a concentric elliptical tunnel [19].

From the SH wave scattering problem solved by the wave function expansion method mentioned above, it can be seen that the scattering problem of cylindrical terrain has experienced a process from semi-cylindrical valley to semi-cylindrical hill, circular-arc canyon to circular-arc hill. This is a process from simple to complex. Compared with the circular section, the elliptical section has more geometric generality and can be changed by changing its axial ratio, so the elliptical cylinder can effectively approach kinds of geometric shapes. However, the research on the scattering problem of elliptical cylindrical terrain is not as smooth as that of cylindrical terrain. Due to mathematical difficulties, the research only progressed from semi-elliptical canyon to semi-elliptical hills.

The Mathieu function is an effective method to solve the elliptical boundary value problem. With the maturity of numerical calculation and computing ability, it has been widely used in physics, electromagnetism, and microwave technology. The Mathieu function addition theorem is the bridge of function transformation between different elliptic coordinate systems. The theorem can be divided into extra-domain theorems and intra-domain theorems, and have different expressions [20]. The former is usually used to study the scattering of multi-envelope elliptical structures, while the latter is usually used to study the scattering of multi-elliptical structures [21,22,23,24]. In order to improve the understanding of the influence of the elliptical cylinder topography, this article takes the elliptical-arc canyon under the action of incident plane SH (shear-horizontal) waves as the research object, and proposes a strict analytical solution. Through the application of the extra-domain Mathieu function addition theorems, the problem of transforming wave functions between elliptic coordinate systems is dealt with. Due to the geometric generality of the elliptical section, the model can be adapted to more practical problems. Additionally, the accurate solution proposed can be used as a new benchmark for numerical methods.

2. The Model

The two-dimensional model to be studied is shown in Figure 1. It represents an elastic, isotropic, and homogeneous half-space from which a portion of an elliptical cylinder was removed to form a canyon. The half-space defined by the horizontal boundary Γ and the elliptical-arc boundary L is the region to be analyzed. For the elliptical-arc canyon, the elliptical coordinate system can greatly simplify the free surface boundary conditions around the canyon, so it is more suitable. Therefore, in addition to the global elliptical coordinate system $\left(\xi ,\eta \right)$ defined at the center of the elliptical cylinder, another elliptical coordinate system $\left({\xi }_q,{\eta }_q\right)$ is defined at the midpoint of the horizontal boundary extension line above the canyon. The corresponding Cartesian coordinate systems $\left(x,y\right)$ and $\left(x_q,y_q\right)$ are established, in which the $x$ axis, $y$ axis, $x_q$ axis, and $y_q$ axis are along the $\eta =0$, $\eta =\pi /2$, ${\eta }_q=0$, and ${\eta }_q=\pi /2$, respectively.

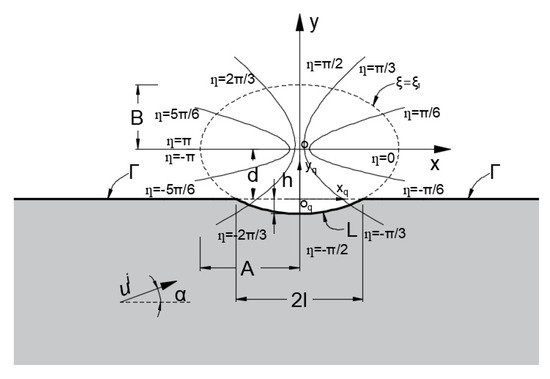
Figure 1. The two-dimensional half-space model containing an elliptical-arc canyon.

Therefore, the horizontal boundary Γ can be defined as $\left\{\left(x_q,y_q\right)|y_q=0\right\}$ or $\left\{\left({\xi }_q,{\eta }_q\right)|{\eta }_q=0\cup {\eta }_q=\pi \right\}$, and the elliptical-arc boundary L can be defined as $\left\{\left(\xi ,\eta \right)|\xi ={\xi }_0\right\}$ with $y_q\le 0$. The hypothesis parameters are as follows:

The rigidity and the shear wave velocity of the medium: μ, β;

The lengths of the semi-major axis and semi-minor axis of the ellipse where the elliptical-arc is located are: A, B;

The focal length of the ellipse where the elliptical-arc is located is: c;

Span of the canyon: 2l;

Depth of the canyon: h;

Distance between the origins of the two coordinate systems: d.

An incident plane wave excites, with time dependence and frequency ω, at an angle α with respect to the positive direction of the $x_q$-axis, while the direction of propagation is perpendicular to the z-axis, i.e.:

$$u_z^i=u_0{e}^{ik(x_q\cos \alpha +y_q\sin a)-i\omega t},$$

(1)

where $u_0$ is the amplitude of the incident wave and k is the shear wavenumber ($\omega /\beta$). It can be represented in the elliptical coordinates system by Mathieu functions [13] (the time factor $e^{-i\omega t}$ was omitted here):

$$u_z^i=2{\displaystyle \sum _{m=0}^{\infty }{i}^{m}c{e}_m({\eta }_q,q_q)M{c}_m^{(1)}}({\xi }_q,q_q)c{e}_m(\alpha ,q_q)+2{\displaystyle \sum _{m=1}^{\infty }{i}^{m}s{e}_m({\eta }_q,q_q)M{s}_m^{(1)}}({\xi }_q,q_q)s{e}_m(\alpha ,q_q),$$

(2)

where $q_q=c_q{}^2{k}^2/4$, $c_q=0.1c$, and $u_0=1$. In addition, $c{e}_m(·)$ and $s{e}_m(·)$ are an even angular Mathieu function and an odd angular Mathieu function, respectively, with order m; $M{c}_m^{(1)}(·)$ and $M{s}_m^{(1)}(·)$ are the even and odd functions of the first modified Mathieu function of order m, respectively.

In the absence of a canyon, the incident wave is reflected on the horizontal free surface ($y_q=0$), and the incident wave $u_z^i$ and the reflected wave $u_z^r$ interfere to give the final wave field $u_z^{i+r}$ in the half-space. $u_z^{i+r}$ can be identified as:

$$u_z^{i+r}=u_z^i+u_z^r=4{\displaystyle \sum _{m=0}^{\infty }{i}^{m}c{e}_m({\eta }_q,q_q)M{c}_m^{(1)}}({\xi }_q,q_q)c{e}_m(\alpha ,q_q).$$

(3)

Close to the canyon, the incident wave $u_z^i$ and the reflected wave $u_z^r$ are scattered and diffracted by the elliptical-arc surface, and one more group of plane waves is generated. The waves are scattered and diffracted outgoing waves $u_z^s$, which can be expressed as the series of elliptic wave functions, as follows:

$$u_z^s={\displaystyle \sum _{m=0}^{\infty }\left[a_{m}c{e}_m({\eta }_q,q_q)M{c}_m^{(3)}({\xi }_q,q_q)\right]}+{\displaystyle \sum _{m=1}^{\infty }\left[b_{m}s{e}_m({\eta }_q,q_q)M{s}_m^{(3)}({\xi }_q,q_q)\right]},$$

(4)

where $a_m$ and $b_m$ are the unknown coefficients to be determined. $M{c}_m^{(3)}(·)$ and $M{s}_m^{(3)}(·)$ are the even and odd functions of the third kind Mathieu function of order m, respectively. The total displacement field $u_z^{total}$ is the superposition of the incident wave, the reflected wave, and the scattered wave, i.e., $u_z^{total}=u_z^i+u_z^r+u_z^s$. $u_z^{total}$ should satisfy the following boundary conditions:

Traction free at Γ:

$${{\sigma }_{{\eta }_{q}z}^{total}|}_{\Gamma }={\partial u_z^{total}/\partial {\eta }_q|}_{\Gamma }=0,$$

(5)

Traction free at L:

$${{\sigma }_{\xi z}^{total}|}_L={\partial u_z^{total}/\partial \xi |}_L=0,$$

(6)

where $J^2=\left(\cosh 2{\xi }_0-\cos 2\eta \right)/2$.

Since ${ds{e}_m({\eta }_q,q_q)/d{\eta }_q|}_{{\eta }_q=0,\pm \pi }\ne 0$, the unknown coefficients $b_m$ must be equal to 0. Then, $u_z^s$ can be expressed as:

$$u_z^s={\displaystyle \sum _{m=0}^{\infty }{a}_{m}c{e}_m({\eta }_q,q_q)M{c}_m^{(3)}({\xi }_q,q_q)}.$$

(7)

3. Application of Mathieu Function Addition Theorem

To adapt to the boundary conditions, the total displacement field $u_z^{total}$ in the local coordinate (${\xi }_q,{\eta }_q$) must be represented by the global coordinate ($\xi ,\eta$). The Mathieu function addition theorem is an effective tool for transforming functions between different elliptical coordinate systems. The Mathieu function addition theorem can be divided into two types: intra-domain and extra-domain. According to [20,22], the extra-domain Mathieu function addition theorem is adopted, which is expressed as follows:

$$c{e}_m({\eta }_q,q_q)M{c}_m^{(t)}({\xi }_q,q_q)={\displaystyle \sum _{l=0}^{\infty }W{E}_{elm}c{e}_l(\eta ,q)M{c}_l^{(t)}(\xi ,q)}+{\displaystyle \sum _{l=1}^{\infty }W{O}_{elm}s{e}_l(\eta ,q)M{s}_l^{(t)}(\xi ,q)},$$

(8)

$$s{e}_m({\eta }_q,q_q)M{s}_m^{(t)}({\xi }_q,q_q)={\displaystyle \sum _{l=0}^{\infty }W{E}_{olm}c{e}_l(\eta ,q)M{c}_l^{(t)}(\xi ,q)}+{\displaystyle \sum _{l=1}^{\infty }W{O}_{olm}s{e}_l(\eta ,q)M{s}_l^{(t)}(\xi ,q)},$$

(9)

where:

$$\begin{array}{l}W{E}_{elm}=\frac{\pi i^{l-m}}{N{e}_l(q)}{\displaystyle \sum _{j=0}^{\infty }{\displaystyle \sum _{p=0}^{\infty }{(-i)}^{j+p}{A}_j^m}}(q_q)A_p^l(q)(J_{p-j}(kd)\cos {\phi }^{-}+{(-1)}^j{J}_{p+j}(kd)\cos {\phi }^{+}),\\ W{O}_{elm}=-\frac{\pi i^{l-m}}{N{o}_l(q)}{\displaystyle \sum _{j=0}^{\infty }{\displaystyle \sum _{p=0}^{\infty }{(-i)}^{j+p}{A}_j^m}}(q_q)B_p^l(q)(J_{p-j}(kd)\sin {\phi }^{-}-{(-1)}^j{J}_{p+j}(kd)\sin {\phi }^{+}),\\ W{E}_{olm}=\frac{\pi i^{l-m}}{N{e}_l(q)}{\displaystyle \sum _{j=0}^{\infty }{\displaystyle \sum _{p=0}^{\infty }{(-i)}^{j+p}{B}_j^m}}(q_q)A_p^l(q)(J_{p-j}(kd)\sin {\phi }^{-}+{(-1)}^j{J}_{p+j}(kd)\sin {\phi }^{+}),\\ W{O}_{olm}=\frac{\pi i^{l-m}}{N{o}_l(q)}{\displaystyle \sum _{j=0}^{\infty }{\displaystyle \sum _{p=0}^{\infty }{(-i)}^{j+p}{B}_j^m}}(q_q)B_p^l(q)(J_{p-j}(kd)\cos {\phi }^{-}-{(-1)}^j{J}_{p+j}(kd)\cos {\phi }^{+}),\\ {\phi }^{+}=j{\phi }_q+p\phi ,\end{array}$$

where $J_{p+j}(·)$ denotes Bessel function, $\phi$ is the angle between line $o{o}_q$ and the positive $x$ axis, and ${\phi }_q$ is the angle between line $o_{q}o$ and the positive $x_q$ axis. The coefficients $A_j^m$ and $B_p^l$ are the Fourier series coefficients of the Mathieu functions, and $N{o}_l$ and $N{e}_l$ are normalized constants. In addition, although $W{E}_{elm}$, $W{O}_{elm}$, $W{E}_{olm}$, and $W{O}_{olm}$ are not all used in this article, they are listed for the sake of formula integrity. The theorem can be accurate in a region outside the circle $C$ of radius d within the circle $C_q$ of radius $A_q$, that is, the region outside the shadow in Figure 2. By reasonably changing $\phi$ and ${\phi }_q$, it is possible to obtain an elliptical-arc canyon at any angle to the horizontal boundary. Because it is tedious to discuss the elliptical-arc canyon at various angles, only the case where the long axis of the ellipse where the elliptical-arc canyon is located is parallel to the horizontal boundary is discussed in this article. The case is $\phi =3\pi /2$ and ${\phi }_q=\pi /2$.

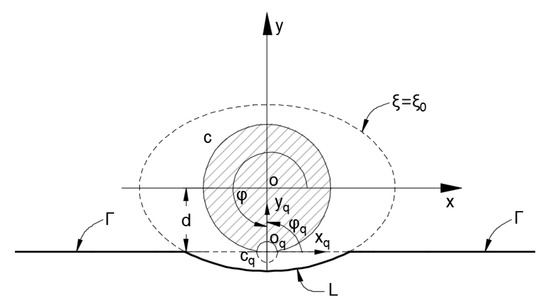
Figure 2. The scope of application of the extra-domain Mathieu function addition theorem.

By applying the extra-domain Mathieu function addition theorem, we can obtain the expressions of $u_z^{i+r}$ and $u_z^s$ in the global coordinate ($\xi ,\eta$), as follows:

$$u_z^{i+r}=4{\displaystyle \sum _{m=0}^{\infty }{i}^{m}c{e}_m(\alpha ,q_q)\left[{\displaystyle \sum _{l=0}^{\infty }W{E}_{elm}c{e}_l(\eta ,q)M{c}_l^{(1)}(\xi ,q)}+{\displaystyle \sum _{l=1}^{\infty }W{O}_{elm}s{e}_l(\eta ,q)M{s}_l^{(1)}(\xi ,q)}\right]},$$

(10)

$$u_z^s={\displaystyle \sum _{m=0}^{\infty }{a}_m\left[{\displaystyle \sum _{l=0}^{\infty }W{E}_{elm}c{e}_l(\eta ,q)M{c}_l^{(3)}(\xi ,q)}+{\displaystyle \sum _{l=1}^{\infty }W{O}_{elm}s{e}_l(\eta ,q)M{s}_l^{(3)}(\xi ,q)}\right]}.$$

(11)

4. Algebra Equations

The sum of waves $u_z^{i+r}$ and $u_z^s$ satisfying the stress-free boundary condition Equation (6) can be written as:

$$\begin{array}{l}{\displaystyle \sum _{m=0}^{\infty }{a}_m\left[{\displaystyle \sum _{l=0}^{\infty }W{E}_{elm}c{e}_l(\eta ,q)M{c}_l^{(3)}{}^{\prime }({\xi }_0,q)}+{\displaystyle \sum _{l=1}^{\infty }W{O}_{elm}s{e}_l(\eta ,q)M{s}_l^{(3)}{}^{\prime }({\xi }_0,q)}\right]}=\\ -{\displaystyle \sum _{m=0}^{\infty }4i^{m}c{e}_m(\alpha ,q_q)\left[{\displaystyle \sum _{l=0}^{\infty }W{E}_{elm}c{e}_l(\eta ,q)M{c}_l^{(1)}{}^{\prime }({\xi }_0,q)}+{\displaystyle \sum _{l=1}^{\infty }W{O}_{elm}s{e}_l(\eta ,q)M{s}_l^{(1)}{}^{\prime }({\xi }_0,q)}\right]}\end{array}$$

(12)

where ‘,’ on the radial Mathieu functions designates differentiation with respect to ξ. Multiplying Equation (12) with $c{e}_n(\eta ,q)$ for n = 0,1,2,3…, integrating over the interval $\left(0,2\pi \right)$ gives:

$${\displaystyle \sum _{m=0}^{\infty }{a}_{m}W{E}_{enm}M{c}_n^{(3)}{}^{\prime }({\xi }_0,q)}=-{\displaystyle \sum _{m=0}^{\infty }4i^{m}c{e}_m(\alpha ,q_q)W{E}_{enm}M{c}_n^{(1)}{}^{\prime }({\xi }_0,q)}.$$

(13)

Equation (13) can be combined in an infinite matrix form as follows:

$$\left[A\right]\left[x\right]=\left[y\right],$$

(14)

where $\left[x\right]$ and $\left[y\right]$ are the unknown coefficients and excitation column vector, respectively, and can be given by:

$$\left[x\right]={\left[\begin{array}{cccc}{a}_1& a_2& \cdots & a_m\end{array}\right]}^T,$$

(15)

$$\left[y\right]={\left[\begin{array}{cccc}{y}_1& y_2& \cdots & y_n\end{array}\right]}^T,$$

(16)

with $y_n={\displaystyle \sum _{m=0}^{\infty }4i^{m}c{e}_m(\alpha ,q_q)W{E}_{enm}M{c}_n^{(1)}{}^{\prime }({\xi }_0,q)}$.

The infinite matrix $\left[A\right]$ can be given by:

$$\left[A\right]=\left[\begin{array}{cccc}{A}_{11}& A_{12}& \cdots & A_{1m}\\ A_{21}& A_{22}& \cdots & A_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ A_{n1}& A_{n2}& \cdots & A_{nm}\end{array}\right],$$

(17)

with $A_{nm}=W{E}_{enm}M{c}_n^{(3)}{}^{\prime }({\xi }_0,q)$.

In theory, if the matrix equation of infinity can be solved, the exact solution of the problem can be obtained by substituting the solved unknowns into the expressions of stress and displacement. However, in practice, this is obviously impossible, so the matrix equation should be solved by truncation.

5. Model Verification

Since boundary $\Gamma$ is a traction-free boundary, the accuracy of the analysis method can be checked by the residual error of dimensionless stress on the canyon surface. According to Wong [13] and Yuan [2], if the maximum residual stress is limited to less than 5%, the accuracy of displacement can be guaranteed. In this paper, in the case of $ETA=1$, the truncation term $m=n=50$ is sufficient to achieve the accuracy of ${10}^{-3}$ for the residual error of dimensionless stress. The following results are obtained when the maximum stress residue is reduced to less than 1% by using the appropriate truncation term m.

To verify the model and the analytical solution, two past exact elastic solutions for a semi-cylindrical canyon and a semi-elliptical canyon are employed. It is convenient to define displacement amplitude $\left|u_z\right|$ as $\left|u_z\right|=\sqrt{\mathrm{Re}{(u_z)}^2+\mathrm{Im}{(u_z)}^2}$. Additionally, the results can be displayed with the dimensionless parameter $ETA$, which is defined as follows: $ETA=2A/\lambda$. $d=0$ can make the local coordinate system coincide with the global coordinate system, which makes the elliptical-arc canyon model simplified to a semi-elliptical canyon model. The results at this time can be compared with the classic results of the semi-ellipse model obtained by Wong [13].

Figure 3 depicts the comparison between the results obtained under conditions $ETA=1.0$, $B/A=0.7$, and $d=0$ and the results of a semi-elliptical canyon. The general trend is that our numerical results are consistent with those given by Wong [13]. Due to the geometric generality of the ellipse, when ${\xi }_0$ tends to infinity, the semi-elliptical canyon tends to a semi-circular one. At this time, our numerical results can be compared with the results obtained by Trifunac [12]. The displacement amplitudes for $ETA=1.25$, $B/A=0.7$, and $d=0$ when $a=0°$, $30°$, $60°$, and $90°$ are presented in Figure 4. It can be clearly seen that their trends are almost the same. After careful comparison, it can be seen that the maximum value of the displacement difference is only very small: less than 1%. The above differences may be due to the different functions used in each problem on the one hand, and because the axis ratio of the ellipse is 0.99 instead of 1 on the other hand. The results in other cases are equally consistent but are not listed here for brevity. Thus, the accuracy and usability of the method proposed in this paper were verified.

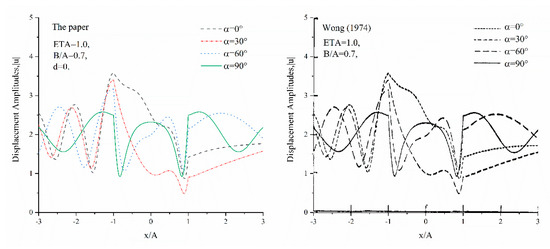
Figure 3. Comparison with the case of a semi-elliptical canyon by Wong [13].

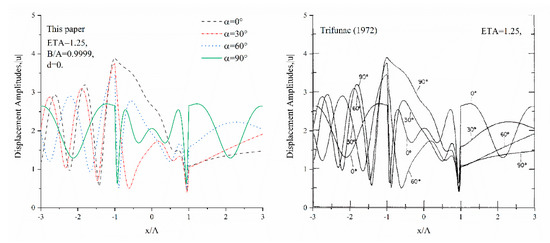
Figure 4. Comparison with the case of a semi-circular canyon by Trifunac [12].

6. Numerical Results and Analysis

In order to study the effects of local terrain irregularities, the amplitude of ground motion at different points is important. With the aid of numerical results, we can examine the magnification mode of the SH-wave in the elliptical-arc canyon under the effect of terrain, so that we can have a clearer understanding of such problems. As expected, the level of magnification and terrain changes in canyons or near canyons are strongly influenced. Since we assume that the excitation consists of an infinite SH-wave with an amplitude of 1, in the absence of a canyon, the amplitude of the ground motion is 2. However, in the case of canyons, due to the interference of scattered waves, the amplitude of ground motion may be different from that of 2.

Therefore, we would like to analyze and discuss the amplitude of ground motion in the elliptical-arc canyon or near the canyon. The calculation accuracy of the Mathieu function calculation program in this paper is ${10}^{-9}$ and the program compiled with the addition formula has an accuracy of ${10}^{-5}$. The elliptical minor-to-major axes ratio, the depth-to-span of the elliptical-arc canyon, and incident angle are considered as the influencing factors on the ground motion. For easy calculation, the dimensionless depth is $h^{*}=h/A$, the dimensionless distance between the origins of two coordinate systems $d^{*}=d/A$ (or $d^{*}=B/A-h^{*}$).

First at all, we calculated the displacement amplitude of the elliptical-arc canyon that approximates the circular-arc canyon ($B/A=0.99$). Figure 5 illustrates the displacement amplitudes for an almost-circular elliptical canyon ($B/A=0.99$) and the dimensionless parameter $ETA$ equal to 1. Additionally, the figure shows three-dimensional plots of displacement amplitudes at different incident angles $a=0°$, $30°$, $60°$, and $90°$ vs. the distance x/A on and around the canyon and the dimensionless distance $d^{*}$ varying within the range [0, 0.9]. It can be seen that when the waves are oblique incidence and grazing incidence, the ground motion near the illuminated surface of the canyon terrain produces violent fluctuations. Obviously, this is due to the reflection of the canyon’s illuminated surface against the waves. In the area of $x/A>0$, due to the barrier effect of the canyon terrain, the ground motion is significantly weakened, and the response is also very smooth. As the value of $d^{*}$ increases, the barrier effect of the canyon terrain still exists, but the movement of the entire surface tends to be gentle, and the amplitude of the response becomes smaller.

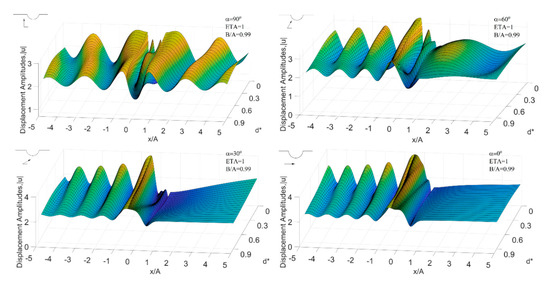
Figure 5. Displacement amplitude for $ETA=1$ and $B/A=0.99$ when $\alpha =0°$, $30°$, $60°$, and $90°$.

Then, we reduced $B/A$ to 0.6. The three-dimensional plots of displacement amplitudes at different incident angles $a=0°$, $30°$, $60°$, and $90°$ vs. the distance x/A on and around the canyon dimensionless distance $d^{*}$ varying within the range [0, 0.5] are shown in Figure 6. It can be seen that the change trend of the entire surface at this time is roughly the same as when $B/A=0.99$, but the displacement amplitude decreases obviously.

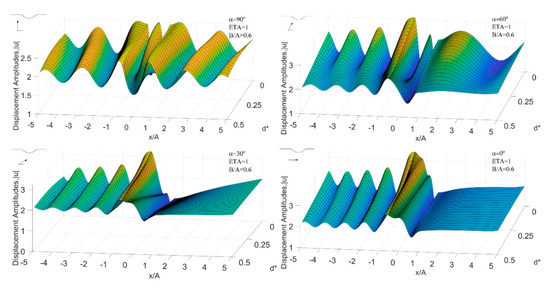
Figure 6. Displacement amplitude for $ETA=1$ and $B/A=0.6$ when $\alpha =0°$, $30°$, $60°$, and $90°$.

To further demonstrate the novelty of this model and method, examples of different elliptical-arc canyons with the same depth-to-span ratio are presented. As shown in Figure 7, although these canyons have the same depth-to-span ratio, they belong to different ellipses. The scattering of SH waves by these canyons with the same depth-to-span ratio and belonging to different ellipses and the differences between them are exactly what can be solved by the method and model in this paper.

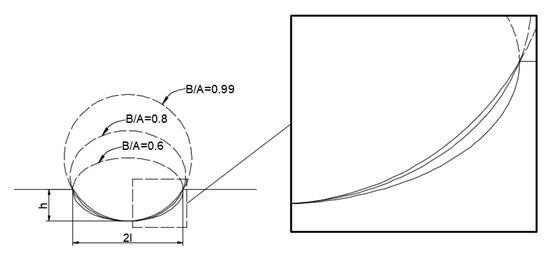
Figure 7. Different elliptical-arc canyons with the same depth-to-span ratio.

Since the ellipse where the elliptical-arc canyon is located is different, the value of $ETA$ is different under the same wavenumber, so we further define the dimensionless parameter $ET{A}^{*}=2l/\lambda$ and the depth-to-span ratio $l^{*}=h/2l$. As shown in Figure 8, under the conditions of $l^{*}=0.3$ and $ET{A}^{*}=1$, the comparison of displacement amplitudes of canyons with an axis ratio of 0.99, 0.8, and 0.6 are presented. It should be noted that when $B/A=0.6$, the elliptical-arc canyon is exactly a semi-elliptical canyon, and when $B/A=0.99$, the elliptical-arc canyon is an almost circular-arc canyon. It can be obviously found that the variation trends of the displacement amplitude under different axial ratios are substantially consistent at the same incident angle. However, the maximum value of the displacement amplitude and the position of the maximum value are obviously different, which is obvious when $\alpha =90°$, and not so obvious when $\alpha =0°$. This can be observed at $l^{*}=0.2$ even more obviously, as shown in Figure 9. Therefore, the difference between the scattering problems caused by the elliptical arc canyon with the same depth-to-span ratio and different axis ratio is worth noting.

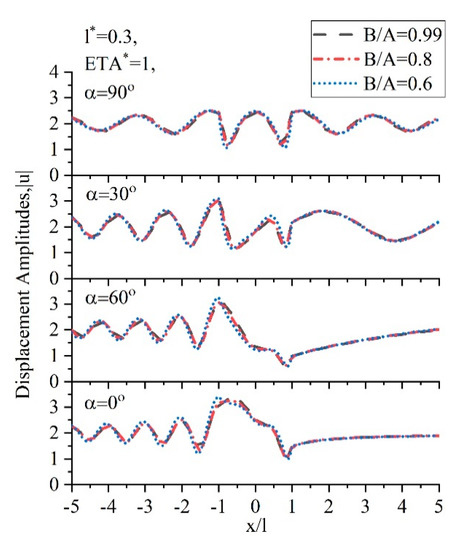
Figure 8. Comparison of displacement amplitudes of canyons belonging to ellipses with different axial ratios when $l^{*}=0.3$ and $ET{A}^{*}=1$.

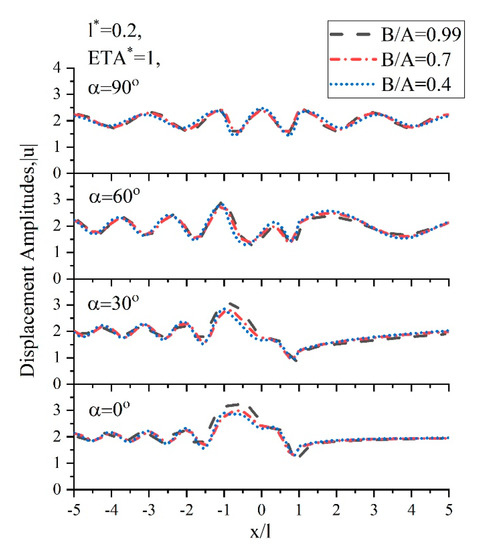
Figure 9. Comparison of displacement amplitudes of canyons belonging to ellipses with different axial ratios when $l^{*}=0.2$ and $ET{A}^{*}=1$.

7. Conclusions

An analytical solution using the method of wave-function series expansion for the scattering of steady-state SH waves in half space with an elliptical-arc canyon was presented. In the process of solving the problem, the extra-domain Mathieu function addition theorem was applied. The elliptical-arc canyon was degraded into a semi-elliptical canyon and an almost semi-circular canyon by utilizing the ellipse’s geometric characteristics. The results were compared with those of Wong [13] and Trifunac [12], respectively, and the validity of the method was verified. By comparing the displacement amplitudes caused by the elliptical-arc canyon under the same depth-to-span ratio and different axial ratios, it was found that the maximum value of the displacement amplitude and the position of the maximum value are obviously different. This was obvious when the SH-wave is incident horizontally. Although the truncation of the infinite equation is inevitable, the accuracy of the numerical results was carefully checked. In addition, based on the method proposed in this paper, it can be further used to study the more practical problems of shallow valleys or shallow hills on incident plane SH waves.