Mathematical Modeling of Linear Fractional Oscillators
Abstract
1. Introduction
2. Preliminary Material on Fractional Calculus
3. Generalization of Newton’s Second Law
4. Formulation of the Problem
5. Solution Method
5.1. Explicit Non-Local Finite-Difference Scheme
- ,
- ,
- .
5.2. Fractional Adams–Bashforth–Moulton Method
5.3. Computational Accuracy Analysis
6. Forced Oscillations of Linear Fractional Oscillators
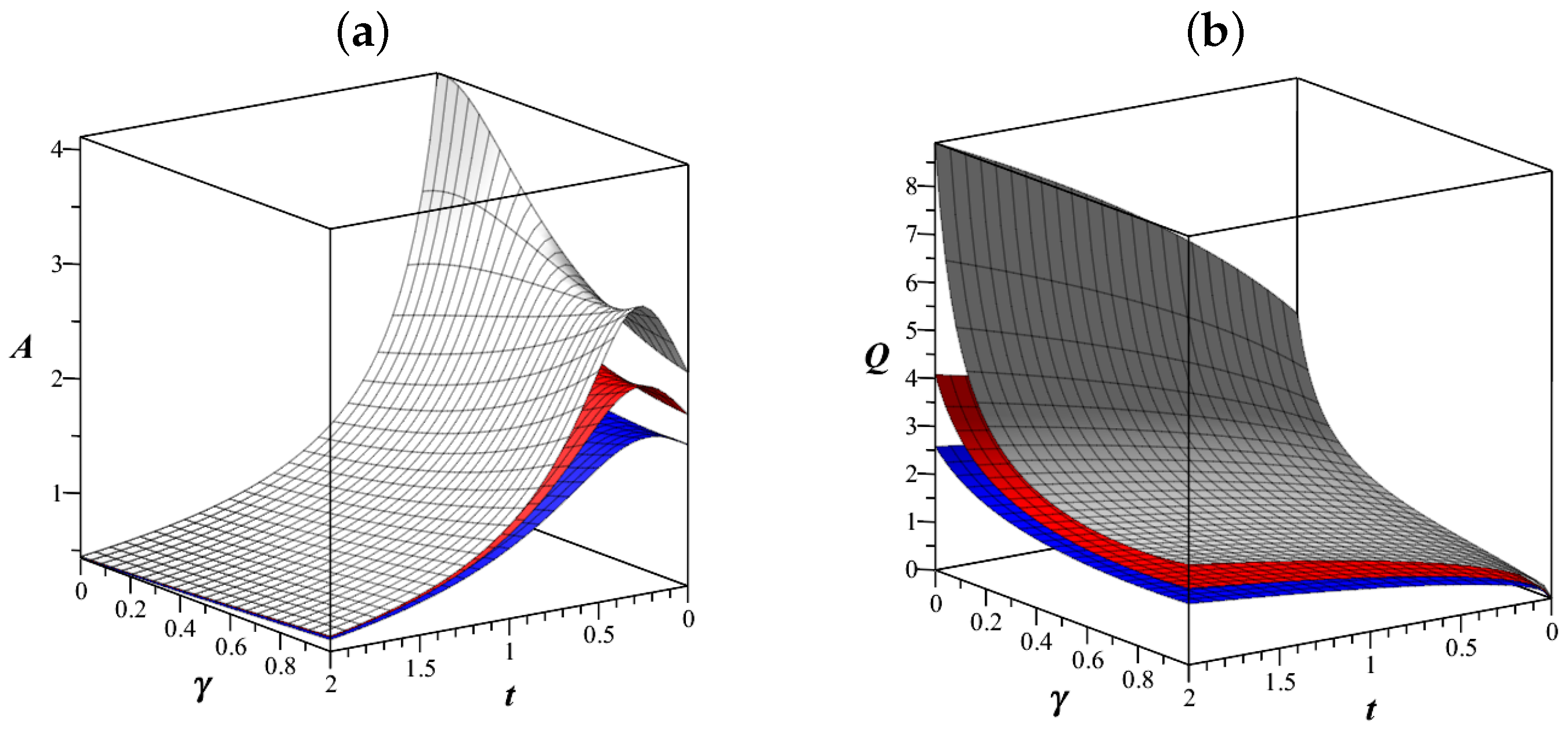
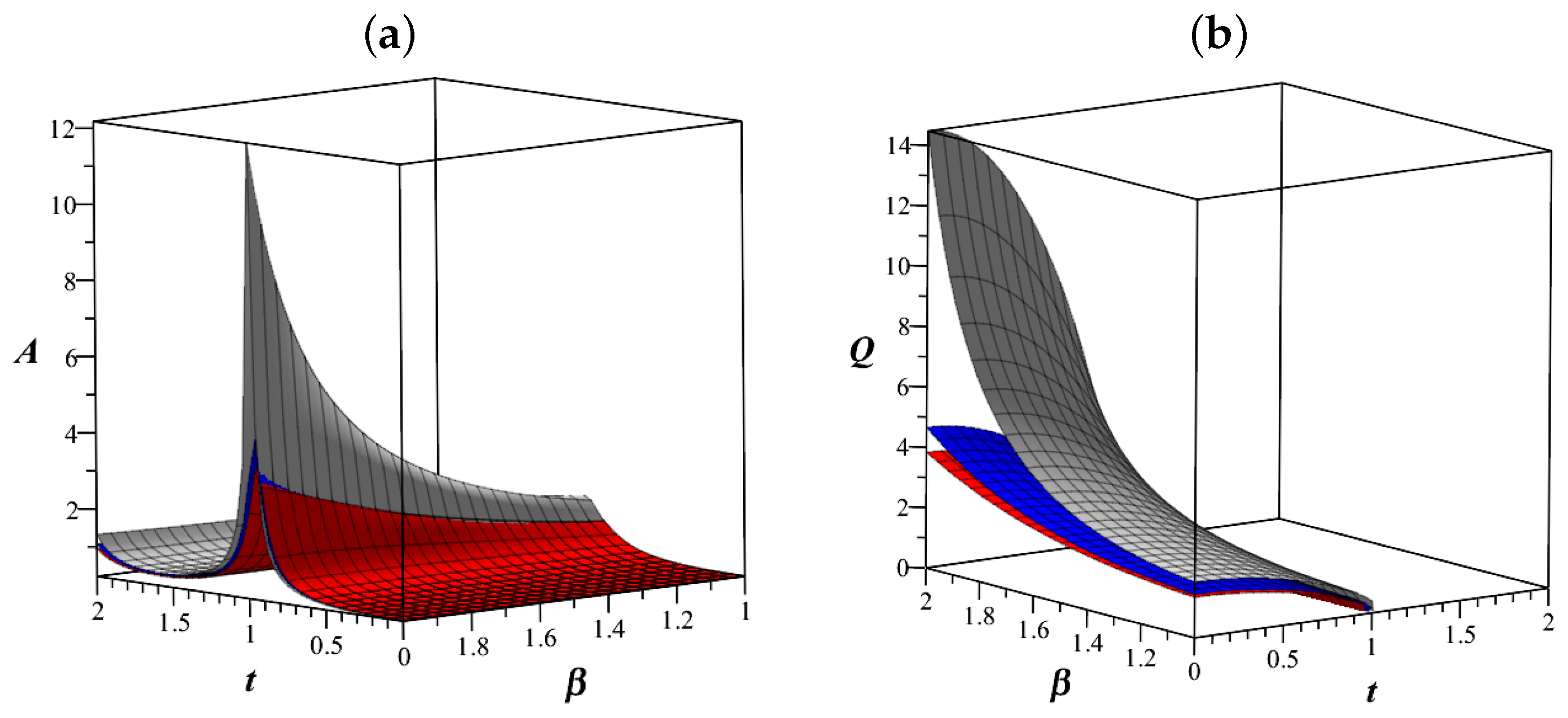
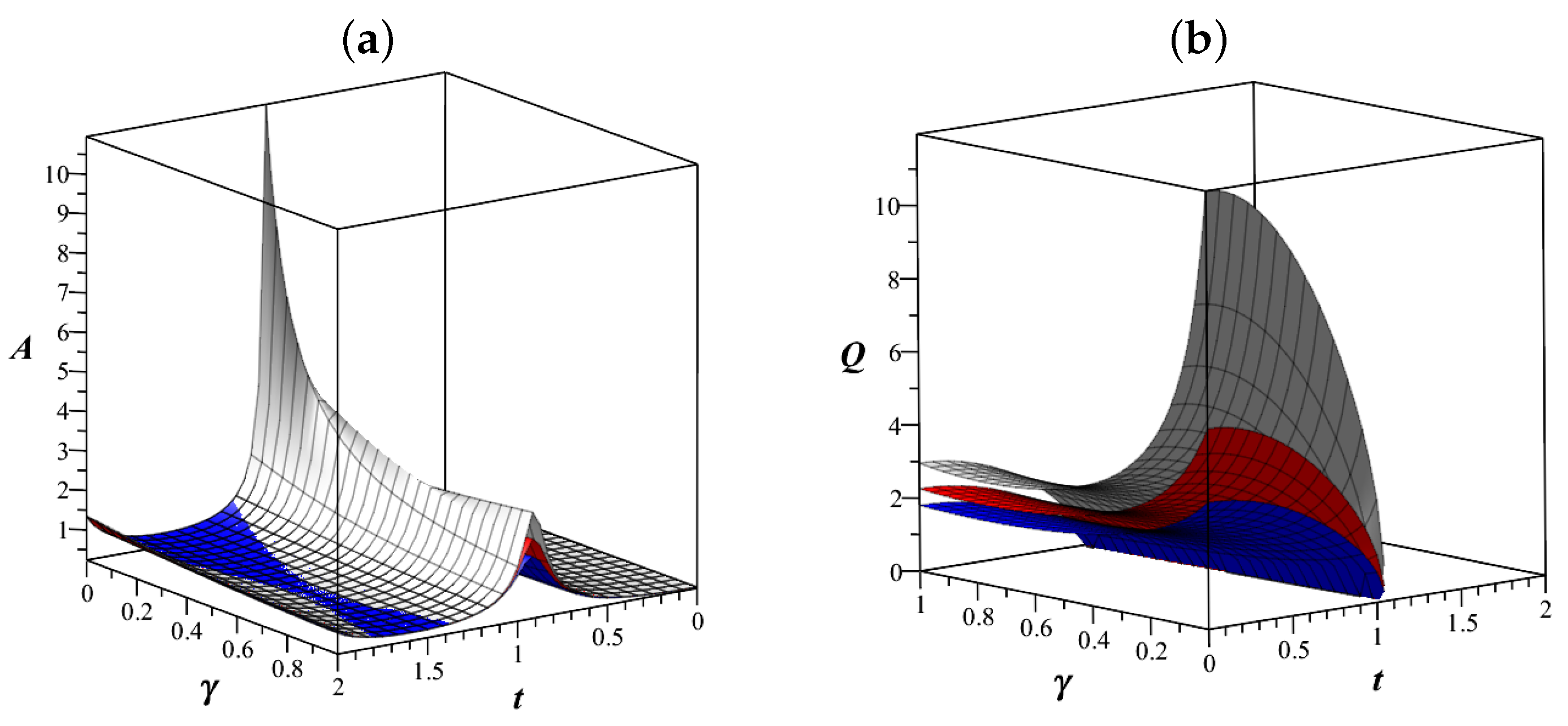
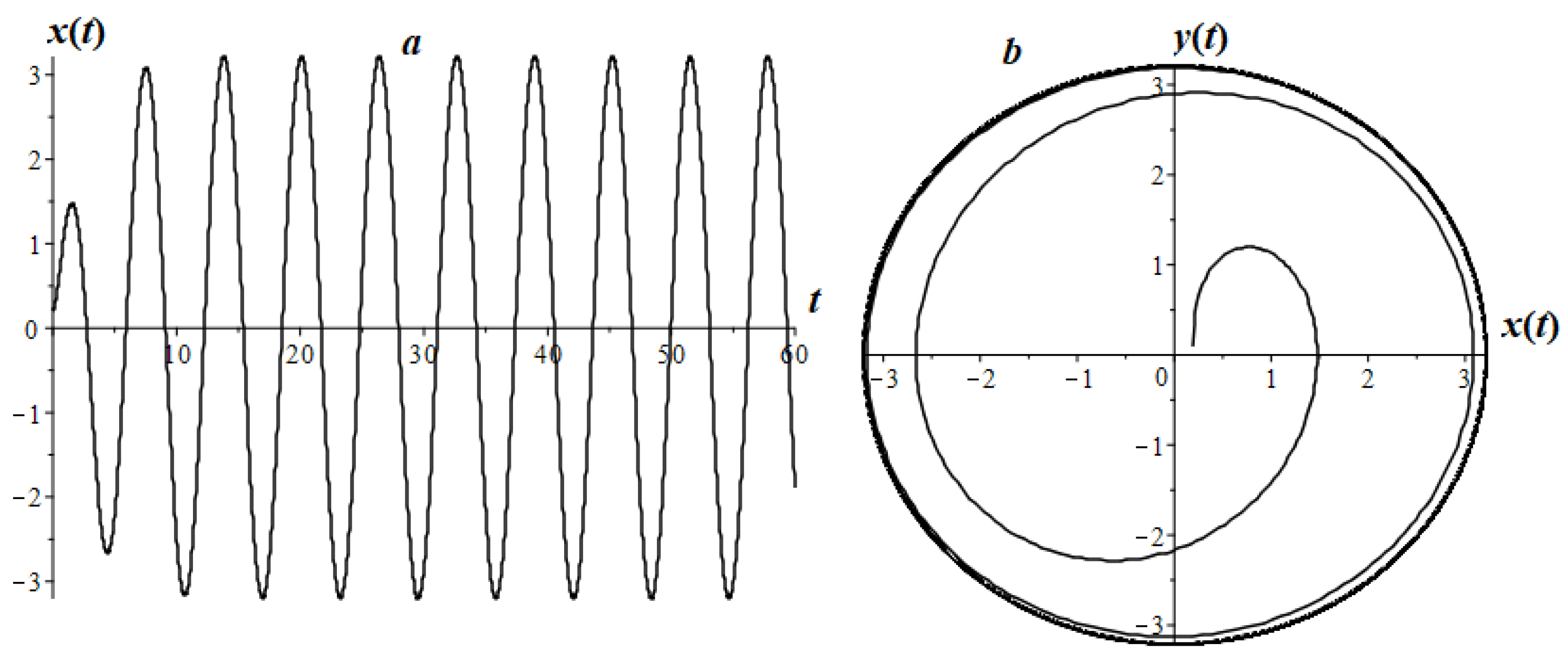
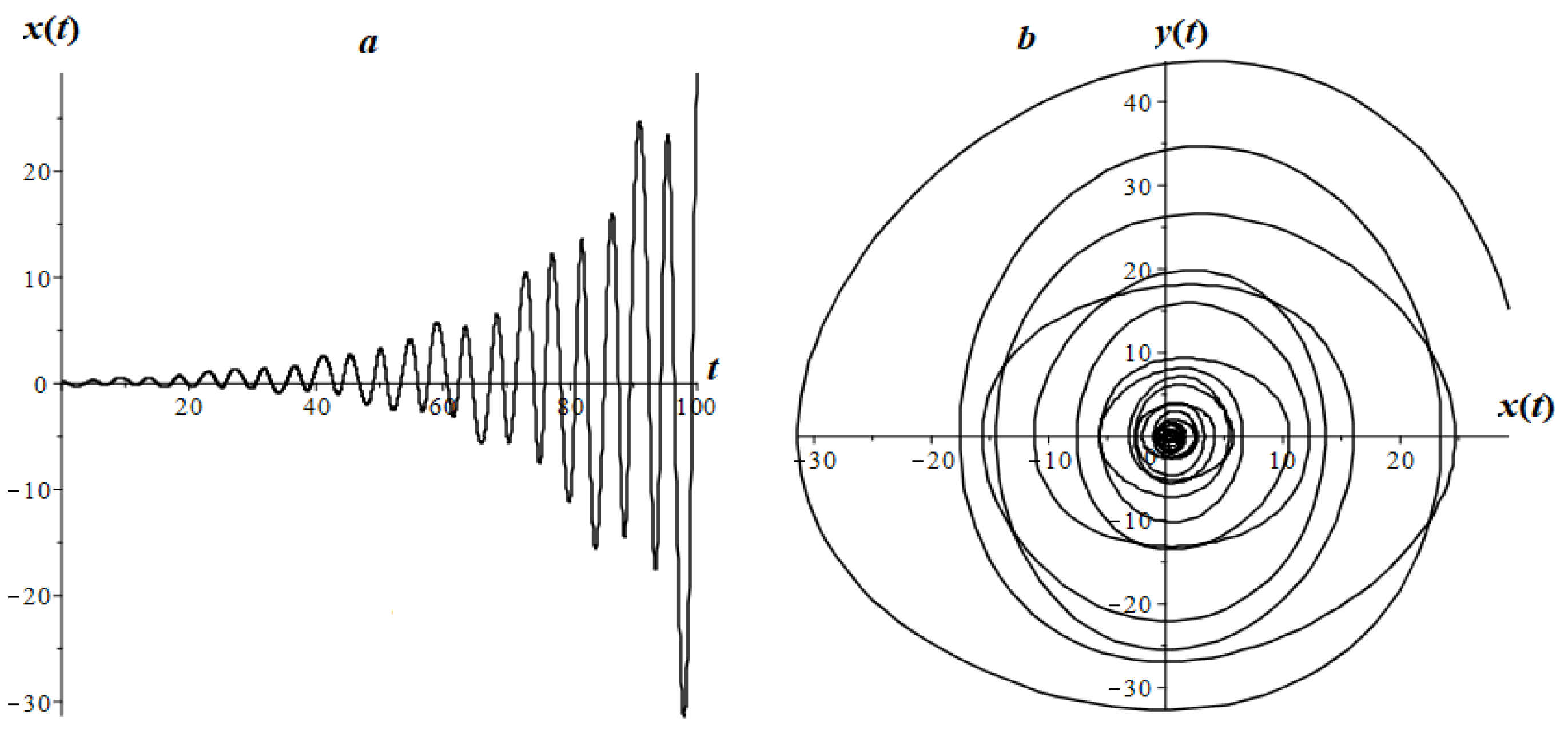
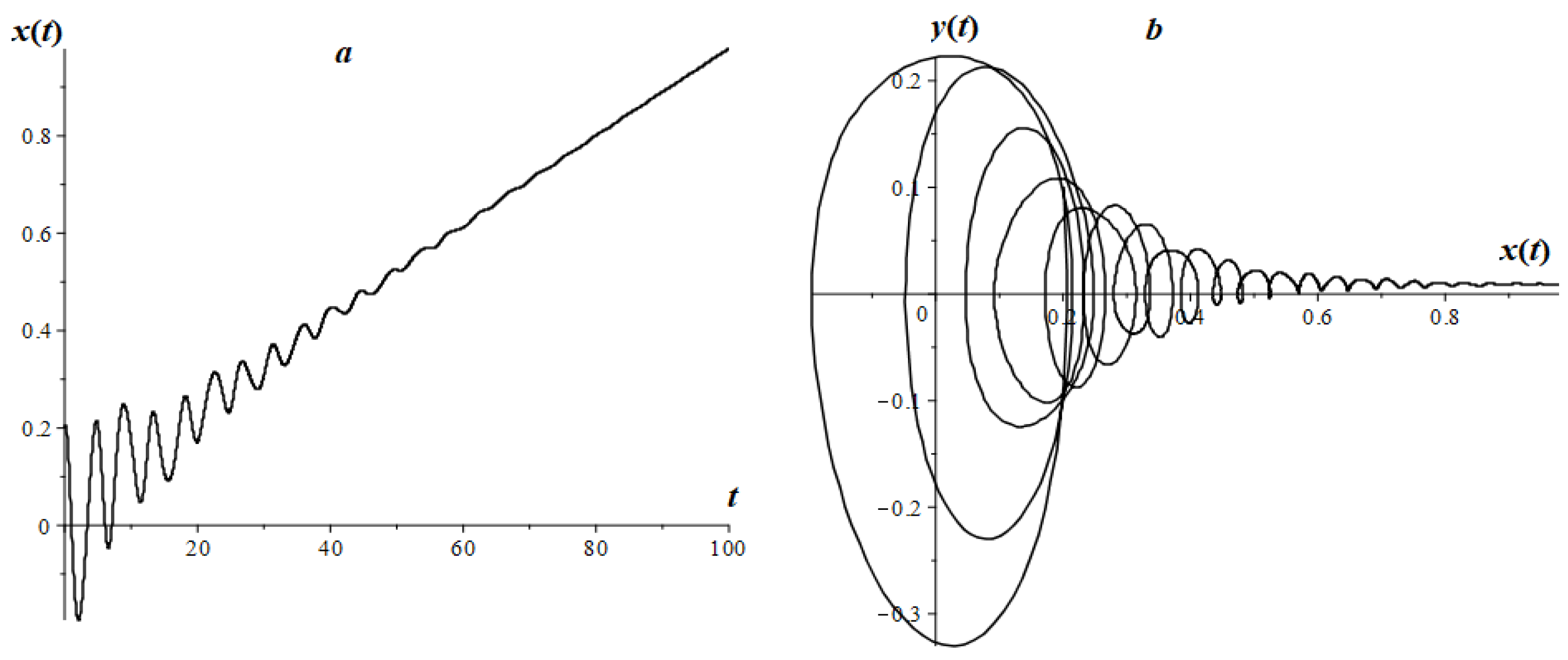
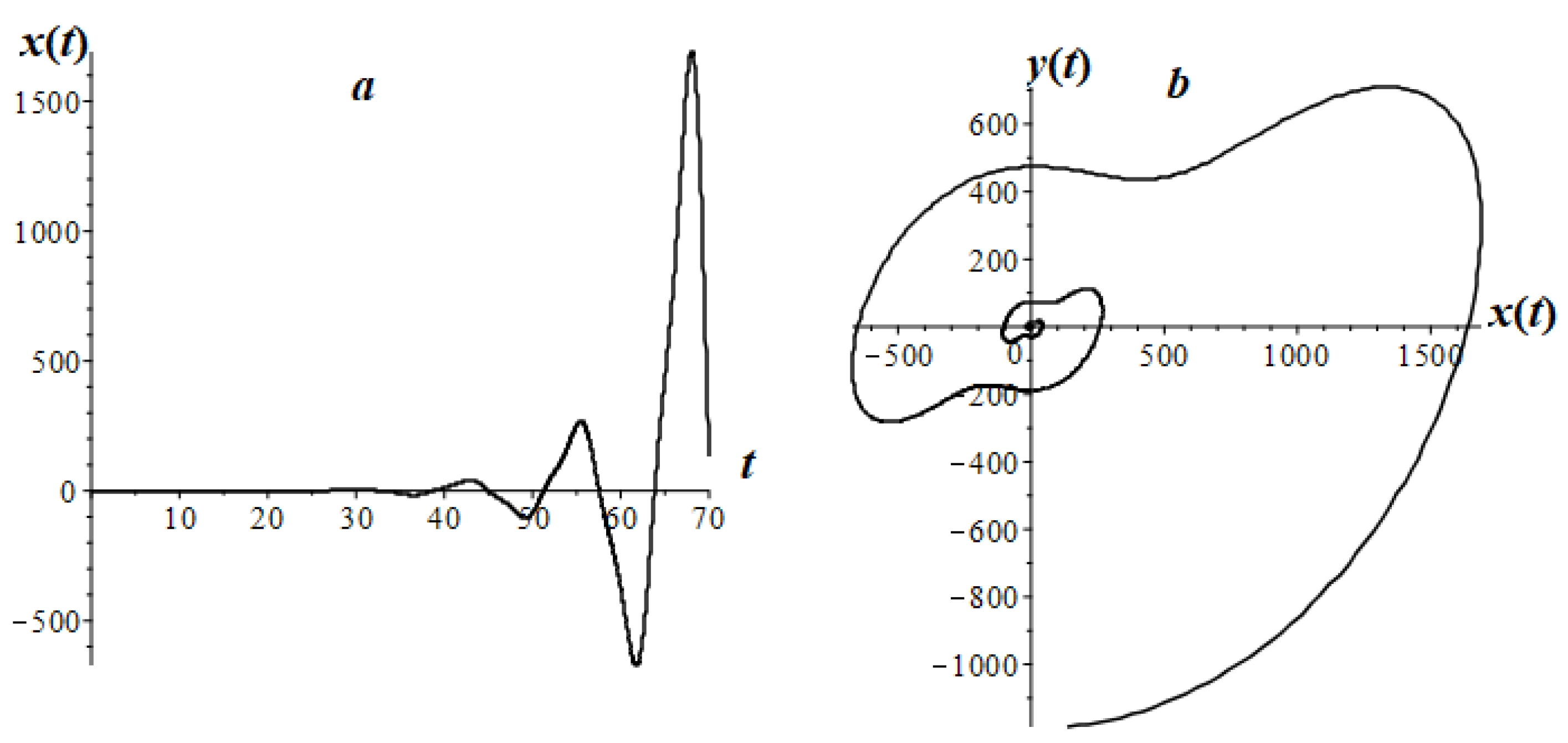
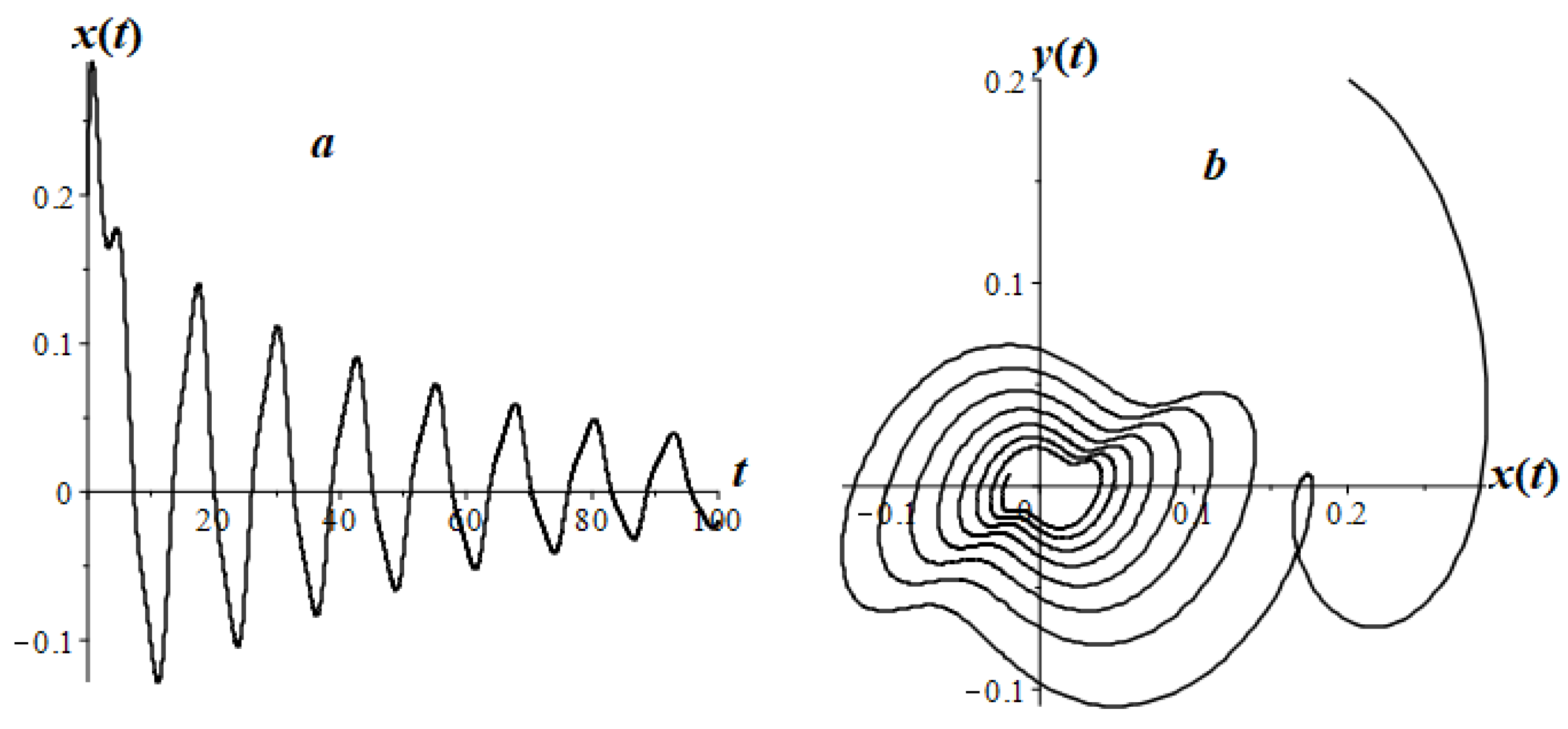
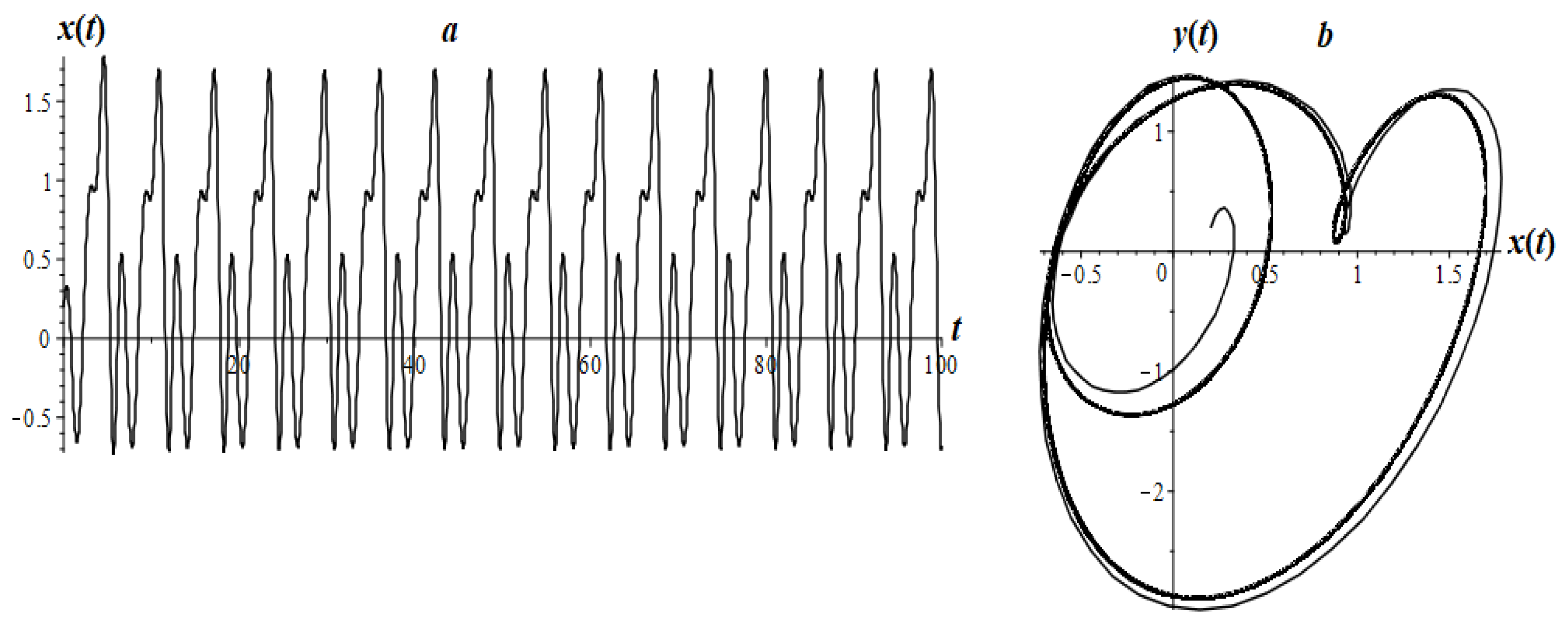
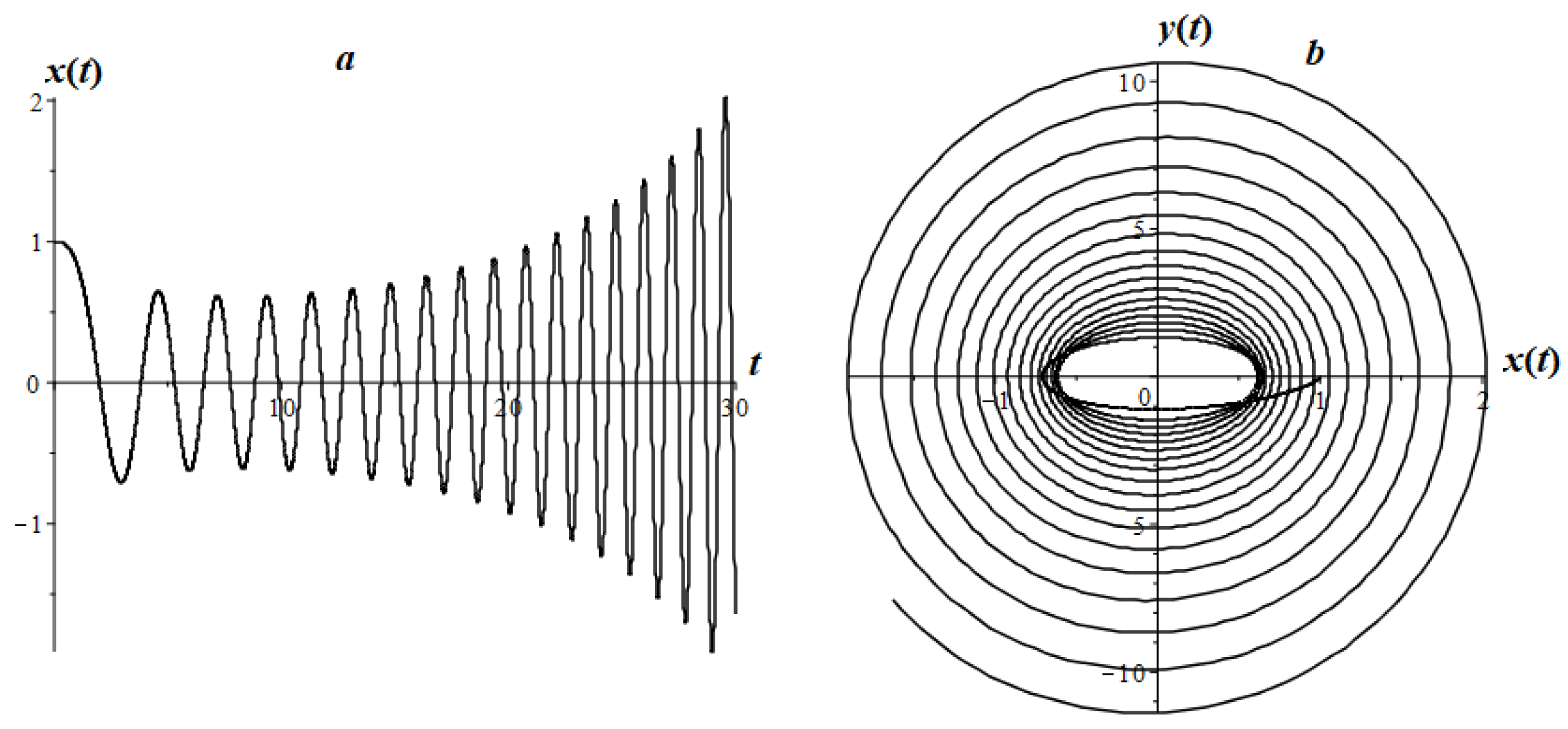
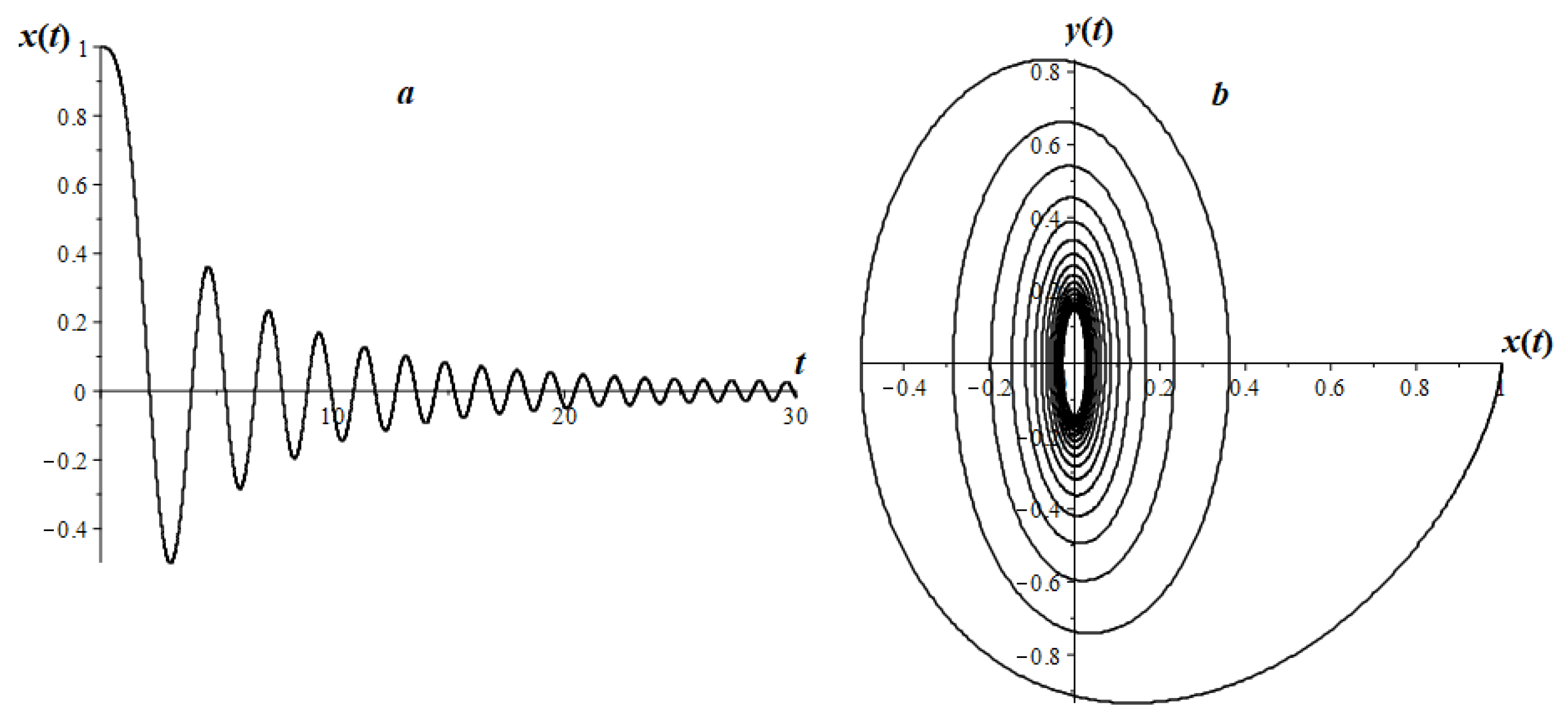
7. Research of Some Types of LFO
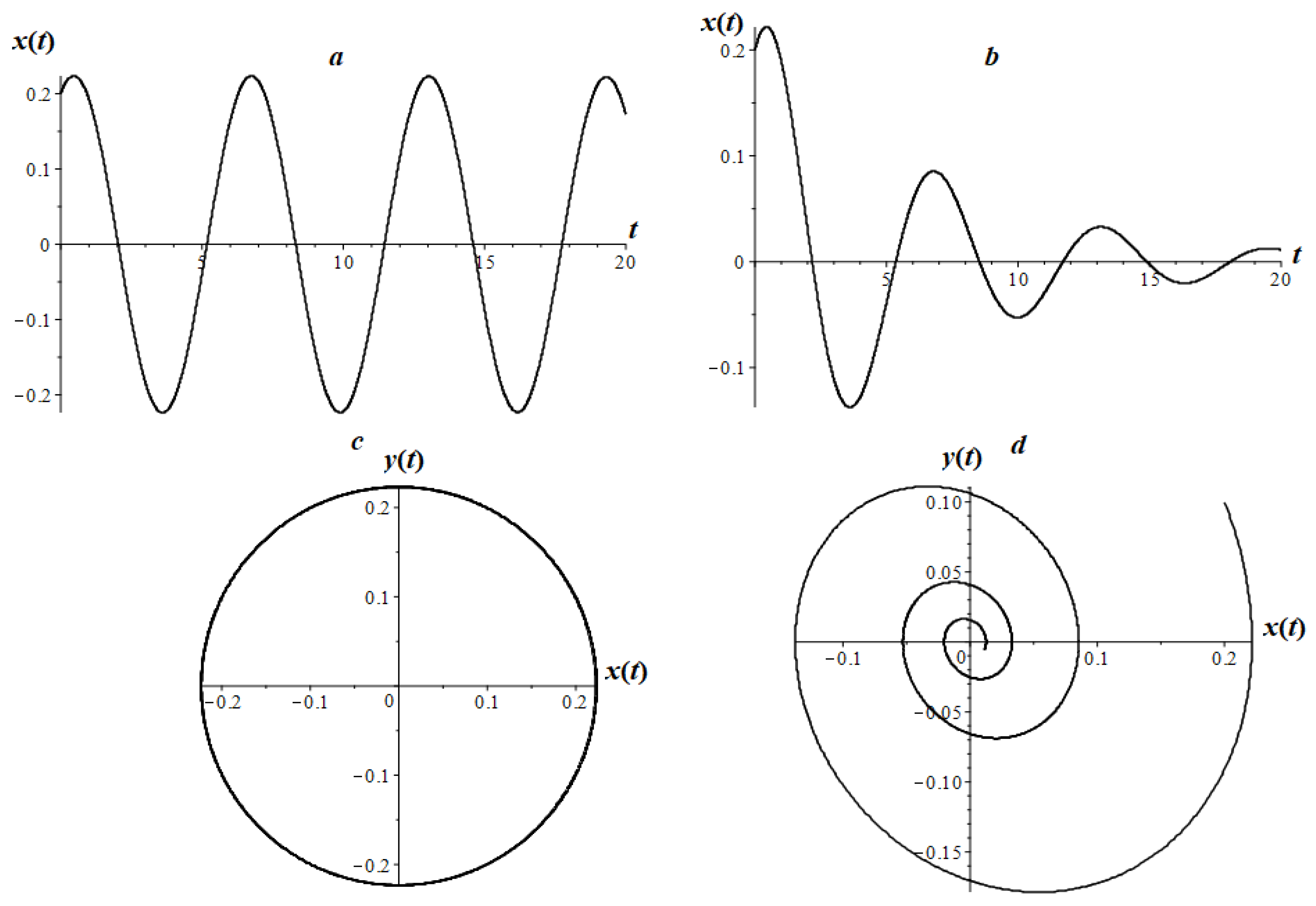
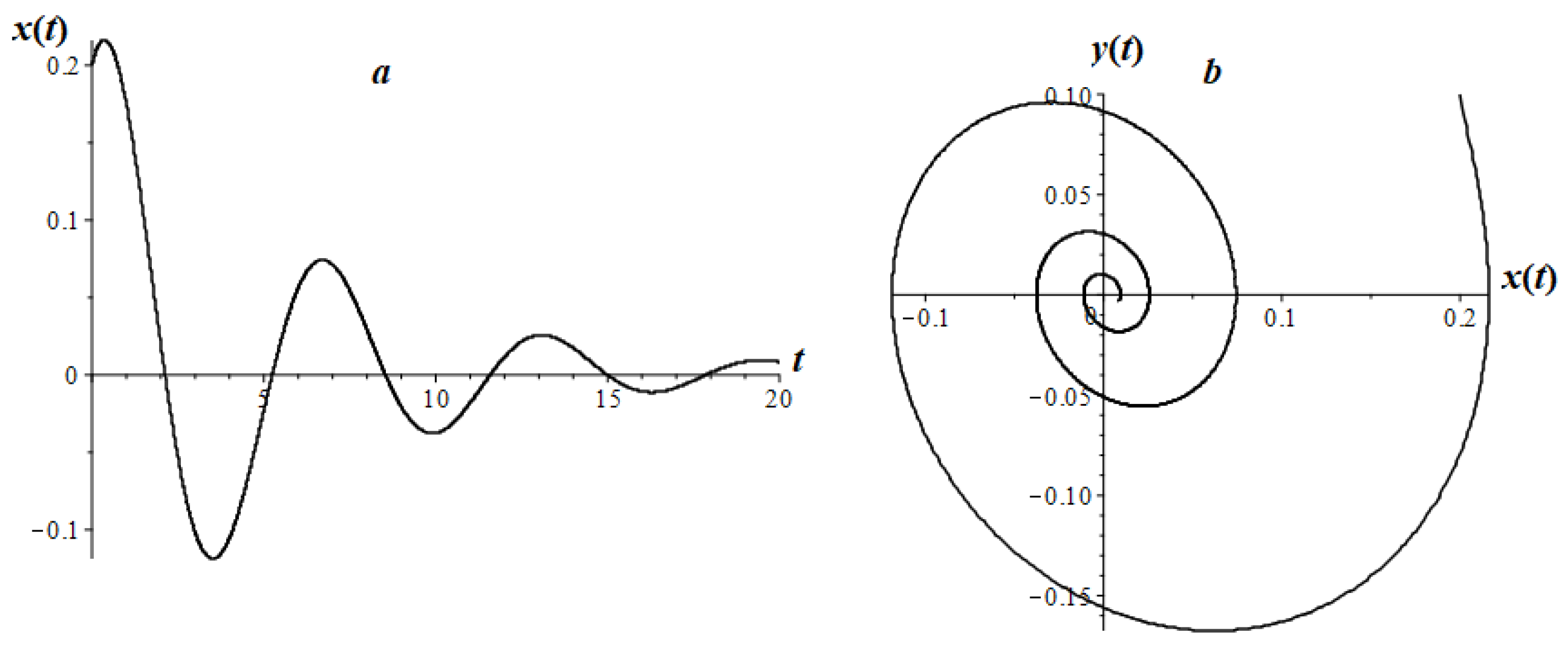
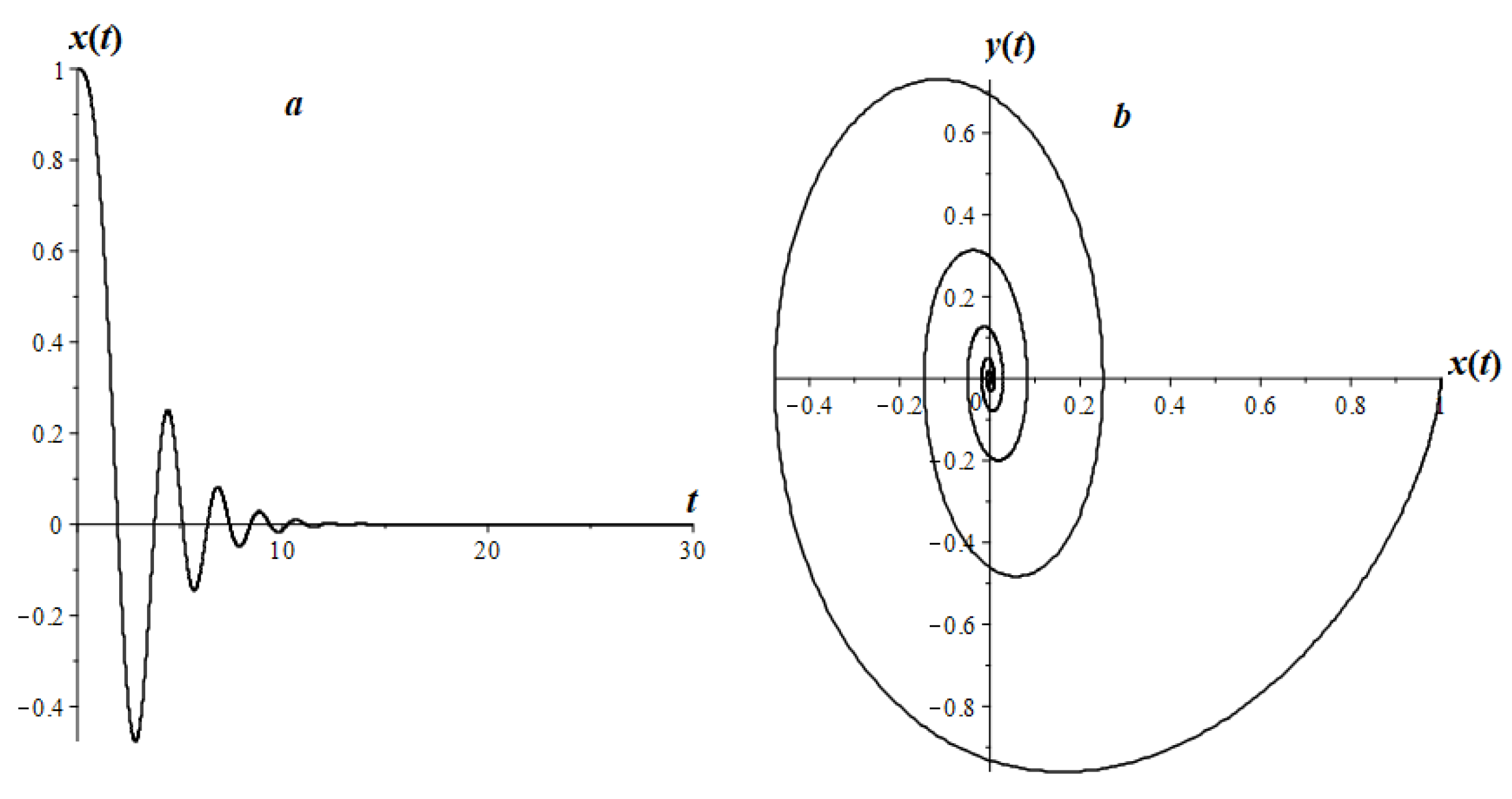
7.1. An Analogue of a Harmonic Oscillator
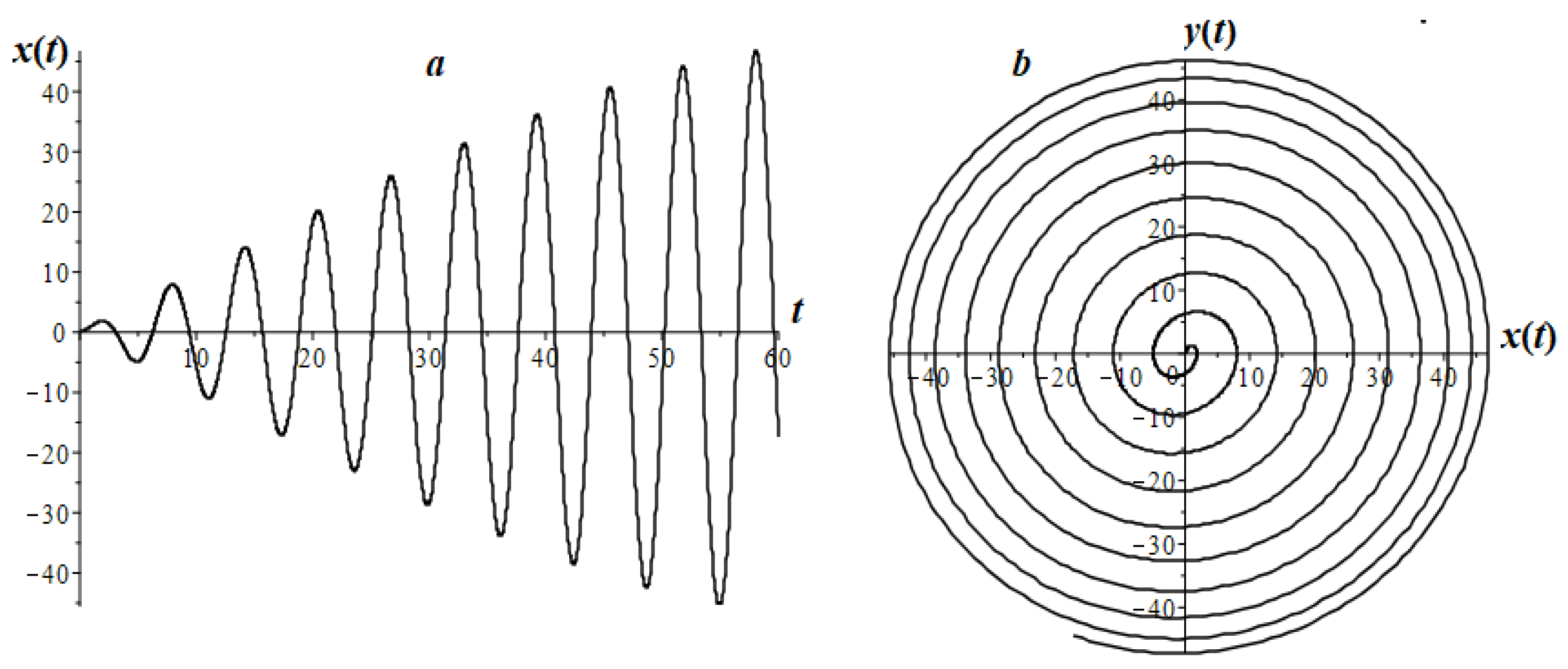
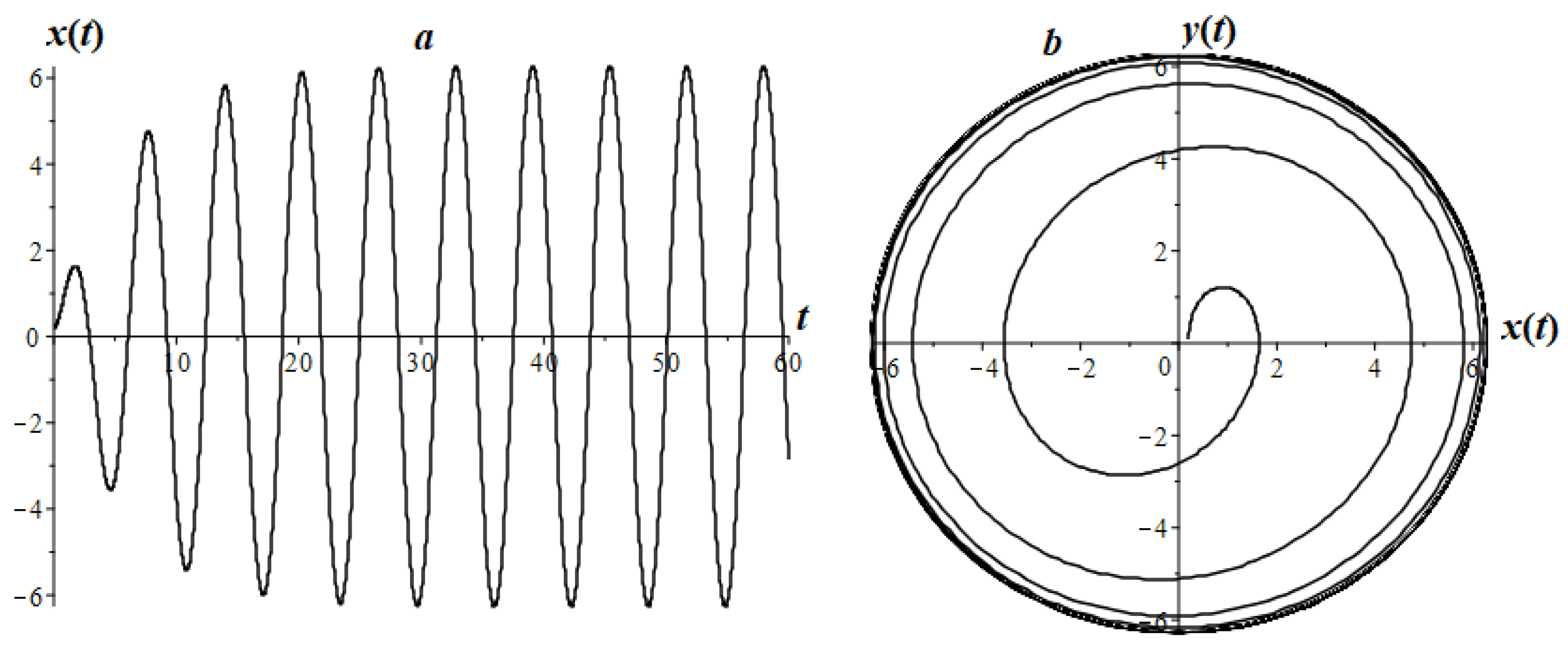
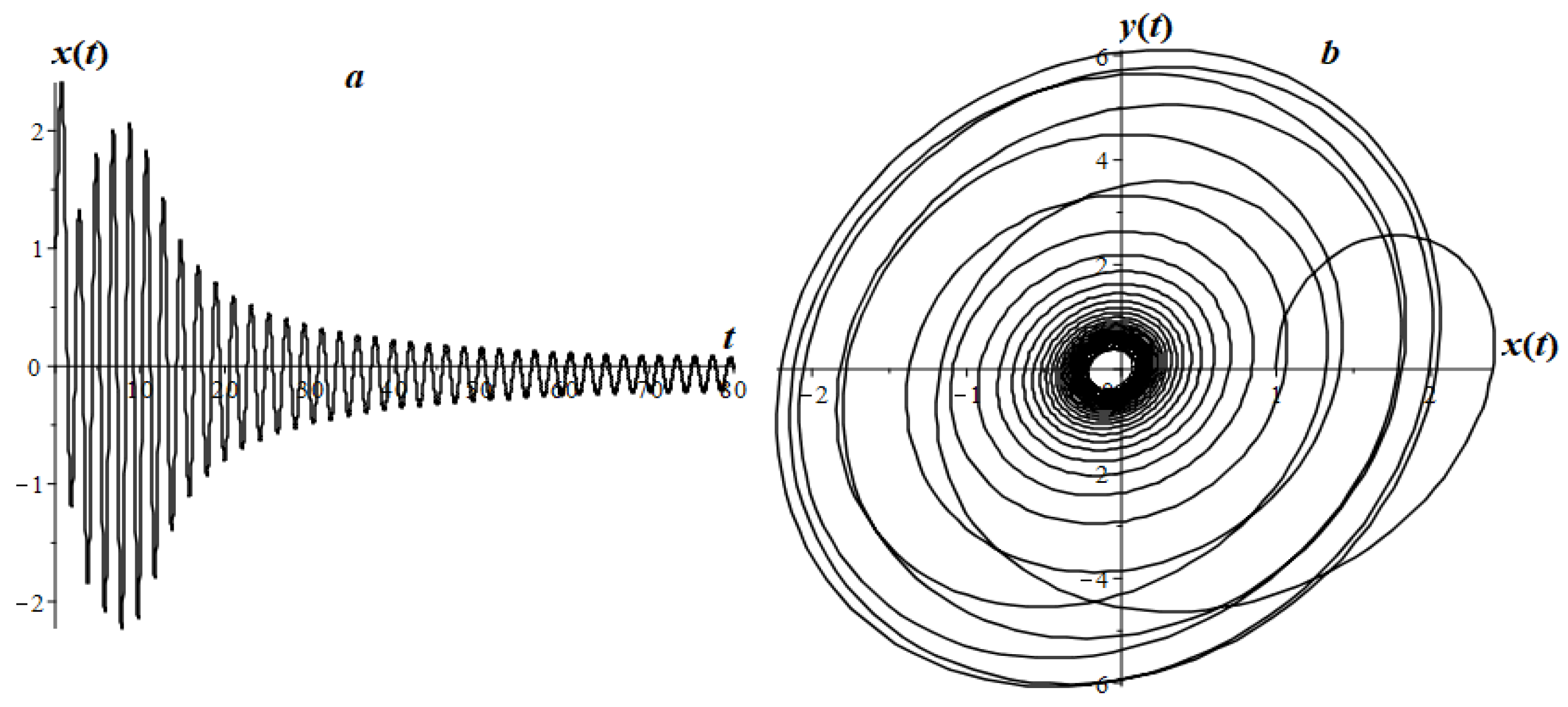
7.2. Fractional Oscillator Mathieu
7.3. Airy Fractional Oscillator
8. Discussion
9. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| LHO | Linear Hereditary Oscillator |
| ENFDS | Explicit Non-local Finite-Difference Scheme |
| ABM | Adams–Bashforth–Moulton method |
| ES | Exact Solution |
| LFO | Linear Fractional Oscillators |
| AFC | Amplitude–Frequency Characteristics |
| PFC | Phase-Frequency Characteristics |
| Q-factor | Quality Factor |
References
- Andronov, A.; Vitt, A.; Khaikin, S. Theory of Oscillators: Adiwes International Series in Physics; Elsevier: Amsterdam, The Netherlands, 2013; Volume 4, p. 848. [Google Scholar]
- Danylchuk, H.; Kibalnyk, L.; Serdiuk, O. Study of critical phenomena in economic systems using a model of damped oscillations. SHS Web Conf. 2019, 65, 06008. [Google Scholar] [CrossRef]
- Li, Z.; Yang, Q. Systems and synthetic biology approaches in understanding biological oscillators. Quant Biol. 2018, 6, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Volterra, V. Sur les equations integro-differentielles et leurs applications. Acta Math. 1912, 35, 295–356. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204, p. 523. [Google Scholar]
- Oldham, K.; Spanier, J. The Fractional Calculus. Theory and Applications of Differentiation and Integration to Arbitrary Order; Academic Press: London, UK, 1974; p. 240. [Google Scholar]
- Miller, K.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differntial Equations; A Wiley-Interscience Publication: New York, NY, USA, 1993; p. 384. [Google Scholar]
- Pskhu, A.; Rekhviashvili, S. Analysis of Forced Oscillations of a Fractional Oscillator. Tech. Phys. Lett. 2018, 44, 1218–1221. [Google Scholar] [CrossRef]
- Parovik, R. Amplitude-Frequency and Phase-Frequency Perfomances of Forced Oscillations of a Nonlinear Fractional Oscillator. Tech. Phys. Lett. 2019, 45, 660–663. [Google Scholar] [CrossRef]
- Khalouta, A.; Kadem, A. A New Method to Solve Fractional Differential Equations: Inverse Fractional Shehu Transform Method. Appl. Appl. Math. 2019, 14, 926–941. [Google Scholar]
- Momani, S.; Odibat, Z. Numerical comparison of methods for solving linear differential equations of fractional order. Chaos Solitons Fractals 2007, 31, 1248–1255. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.; Freed, A.; Luchko, Y. Algorithms for the fractional calculus: A selection of numerical methods. Comput. Methods Appl. Mech. Eng. 2005, 194, 743–773. [Google Scholar] [CrossRef]
- Parovik, R. Mathematical model of a wide class memory oscillators. Bull. South Ural State Univ. Ser. Math. Model. Program. 2018, 11, 108–122. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical Solution of Fractional Differential Equations: A Survey and a Software Tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef]
- Yang, C.; Liu, F. A computationally effective predictor-corrector method for simulating fractional-order dynamical control system. ANZIAM J. 2006, 47, 168–184. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.; Freed, A. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Rekhviashvili, S.; Pskhu, A.; Agarwal, P.; Jain, S. Application of the fractional oscillator model to describe damped vibrations. Turk. J. Phys. 2019, 43, 236–242. [Google Scholar] [CrossRef]
- Parovik, R. Quality Factor of Forced Oscillations of a Linear Fractional Oscillator. Tech. Phys. 2020, 65, 1015–1019. [Google Scholar] [CrossRef]
- Mathieu, E. Mémoire sur le mouvement vibratoire d’une membrane de forme elliptique. J. Math. Pures Appl. 1868, 13, 137–203. [Google Scholar]
- Butikov, I. Analytical expressions for stability regions in the Ince–Strutt diagram of Mathieu equation. Am. J. Phys. 2018, 86, 257–267. [Google Scholar] [CrossRef]
- Rand, R.; Sah, S.; Suchorsky, M. Fractional Mathieu equation. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 3254–3262. [Google Scholar] [CrossRef]
- Parovik, R. Fractal parametric oscillator as a model of a nonlinear oscillation system in natural mediums. Int. J. Commun. Netw. Syst. Sci. 2013, 6, 134–138. [Google Scholar] [CrossRef]
- Airy, G. On the intensity of light in the neighbourhood of a caustic. Trans. Camb. Philos. Soc. 1838, 6, 379–402. [Google Scholar]
- Siviloglou, G. Accelerating finite energy Airy beams. Opt. Lett. 2007, 32, 979–981. [Google Scholar] [CrossRef]
- Parovik, R. Explicit finite-difference scheme for the numerical solution of the model equation of nonlinear hereditary oscillator with variable-order fractional derivatives. Arch. Control Sci. 2016, 26, 429–435. [Google Scholar] [CrossRef]
- Zhang, X.G.; Liu, L.S.; Wu, Y.H. Multiple positive solutions of a singular fractional differential equation with negatively perturbed term. Math. Comput. Model. 2012, 55, 1263–1274. [Google Scholar] [CrossRef]
- Zhang, X.G.; Wu, Y.H.; Caccetta, L. Nonlocal fractional order differential equations with changing-sign singular perturbation. Appl. Math. Model. 2015, 39, 6543–6552. [Google Scholar] [CrossRef]
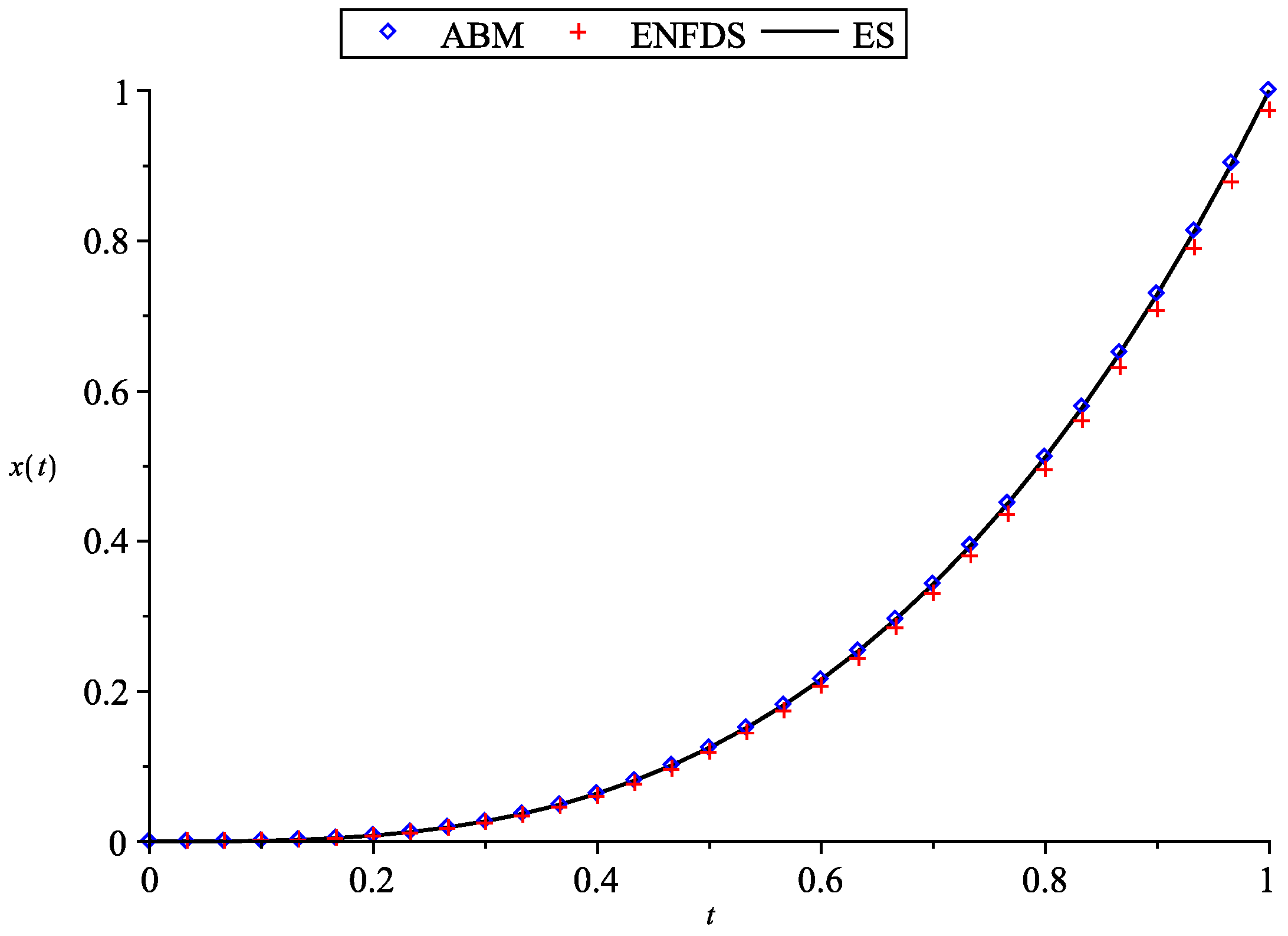
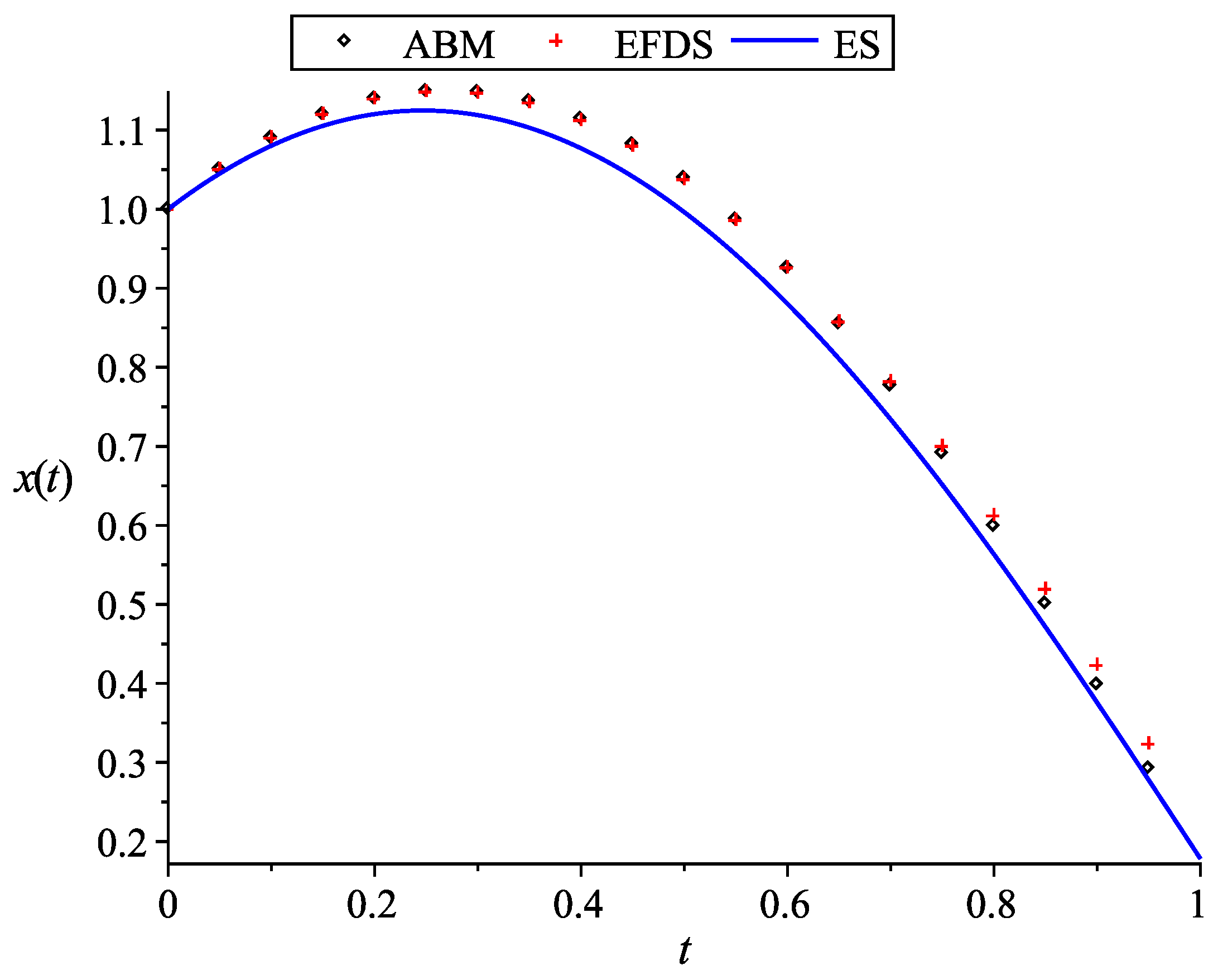
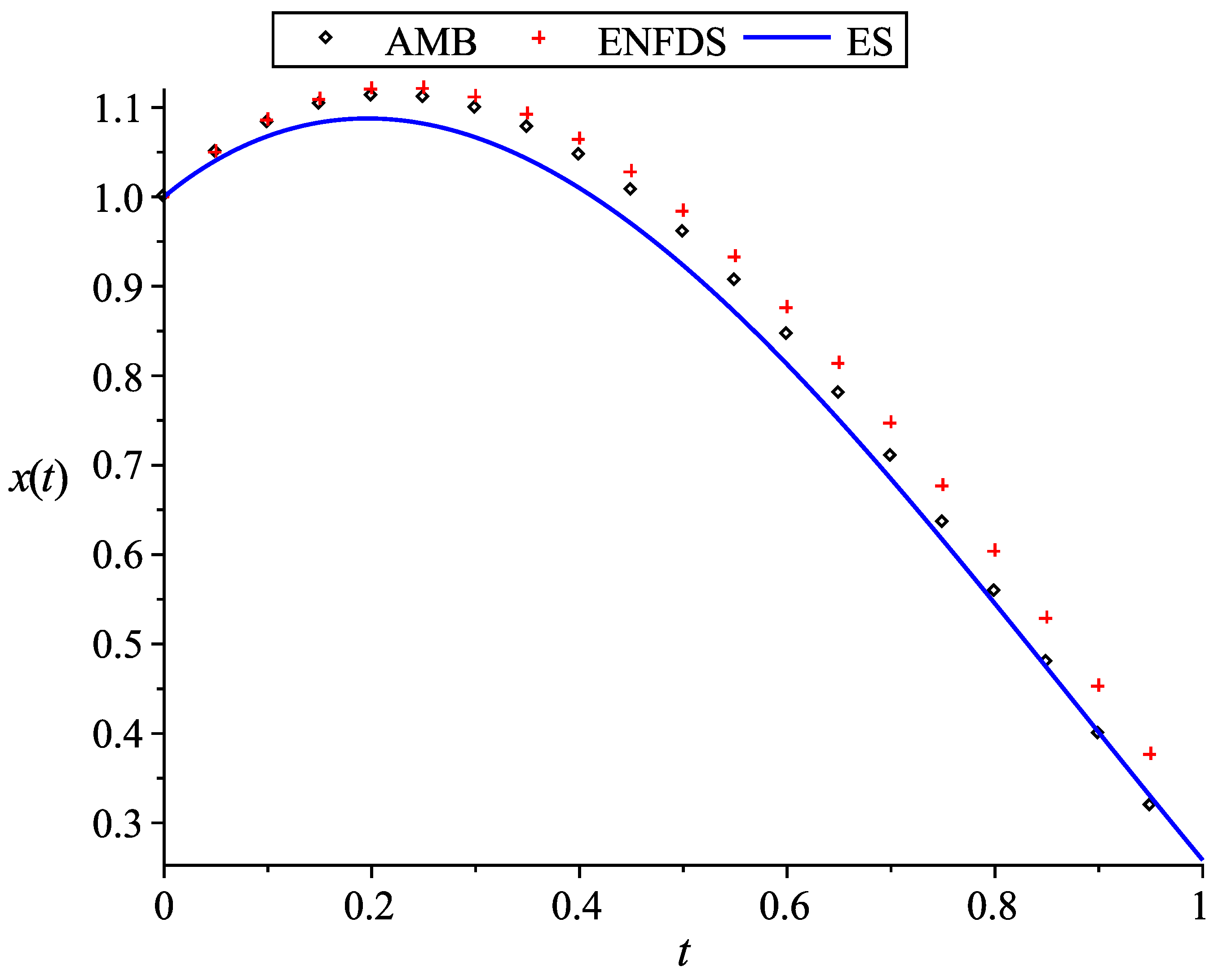

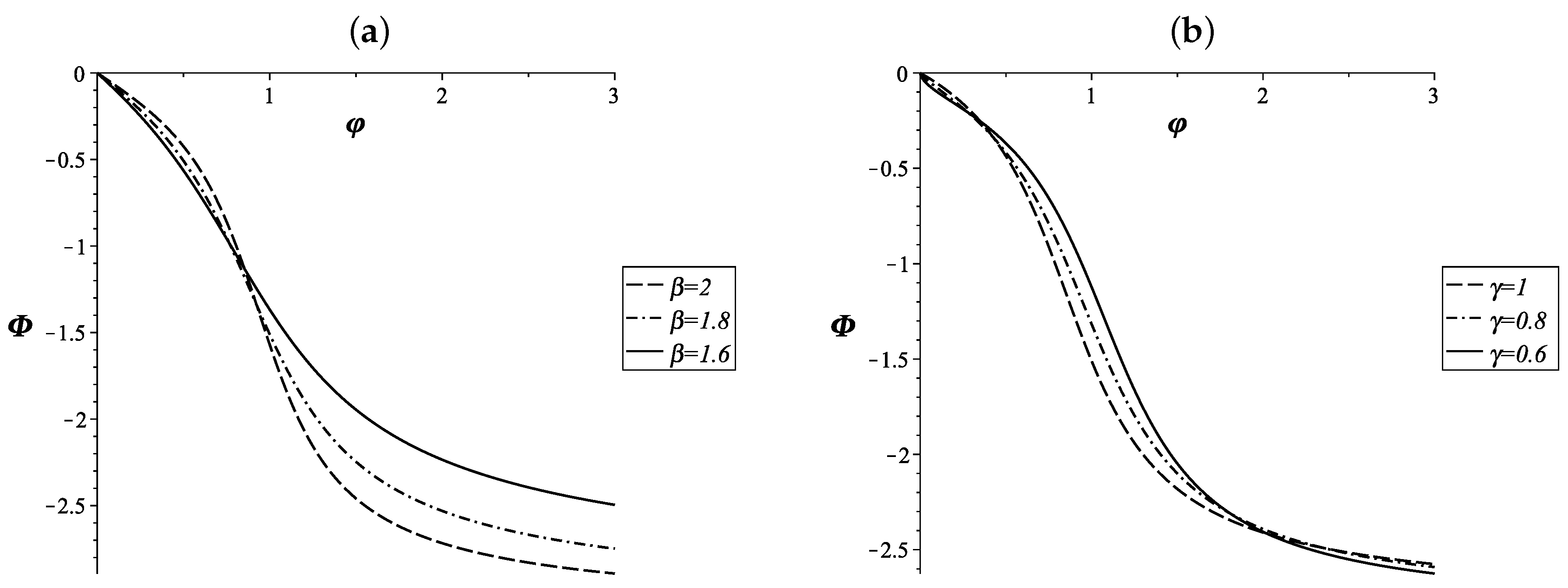
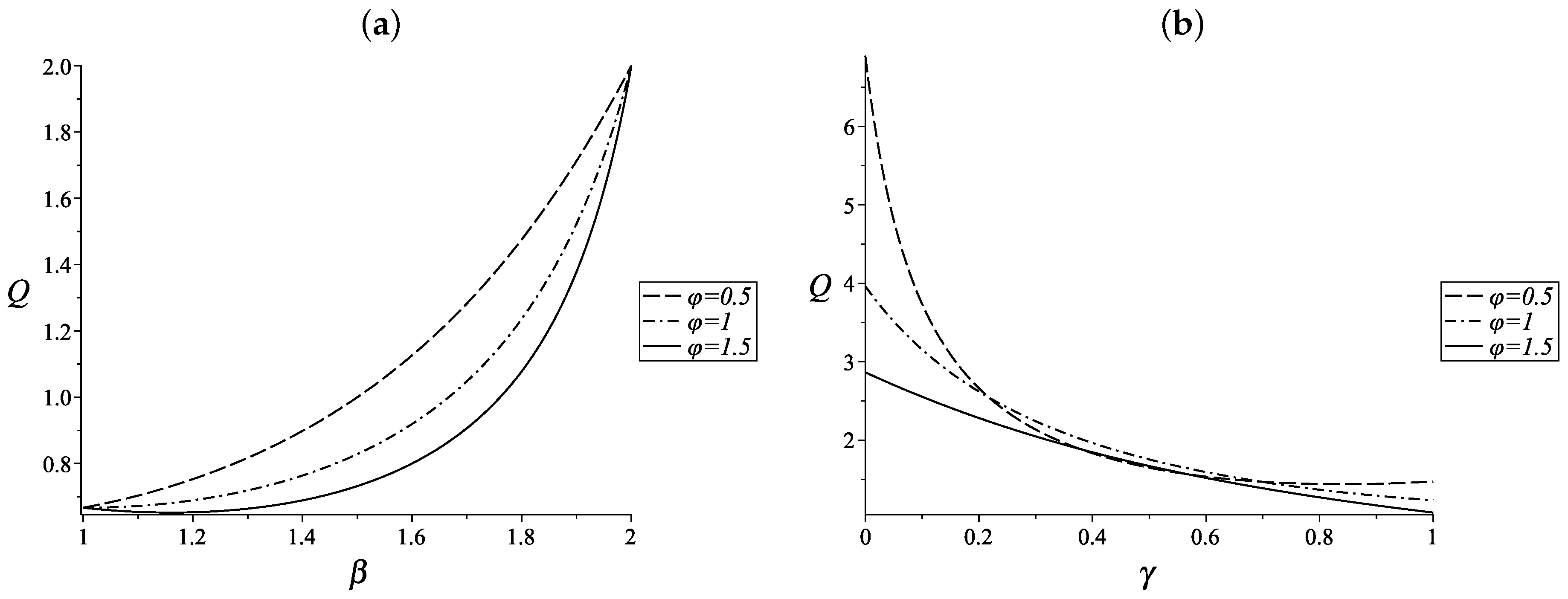

| N | h | ||||
|---|---|---|---|---|---|
| 10 | 1/10 | 0.0561528 | 0.0039560 | - | - |
| 20 | 1/20 | 0.0340440 | 0.0009317 | 0.721956135 | 2.0861050 |
| 40 | 1/40 | 0.0195531 | 0.0002362 | 0.800003094 | 1.9798565 |
| 80 | 1/80 | 0.0108341 | 0.0000628 | 0.851815427 | 1.9100427 |
| 160 | 1/160 | 0.0058603 | 0.0000171 | 0.886538801 | 1.8748556 |
| 320 | 1/320 | 0.0031176 | 0.0000047 | 0.910518254 | 1.8577979 |
| 640 | 1/640 | 0.0016380 | 0.0000014 | 0.92851899 | 1.7975624 |
| N | h | ||||
|---|---|---|---|---|---|
| 10 | 1/10 | 0.025634 | 0.0011076 | - | - |
| 20 | 1/20 | 0.015479 | 0.0002546 | 0.727709917 | 2.120946173 |
| 40 | 1/40 | 0.008987 | 0.0000635 | 0.784362481 | 2.004652815 |
| 80 | 1/80 | 0.005045 | 0.0000167 | 0.832949245 | 1.923159876 |
| 160 | 1/160 | 0.002761 | 0.0000045 | 0.86953863 | 1.881091919 |
| 320 | 1/320 | 0.001484 | 0.0000013 | 0.895926947 | 1.860912083 |
| 640 | 1/640 | 0.000786 | 0.0000004 | 0.916645745 | 1.78891439 |
| N | h | ||||
|---|---|---|---|---|---|
| 10 | 1/10 | 0.00758 | 0.001049 | - | - |
| 20 | 1/20 | 0.00253 | 0.000232 | 1.585196 | 2.179457 |
| 40 | 1/40 | 0.00093 | 0.000054 | 1.445025 | 2.093444 |
| 80 | 1/80 | 0.00038 | 0.000013 | 1.296494 | 2.046768 |
| 160 | 1/160 | 0.00017 | 0.000003 | 1.177333 | 2.023954 |
| 320 | 1/320 | 0.00008 | 0.0000008007 | 1.100742 | 2.012096 |
| 640 | 1/640 | 0.00003739 | 0.0000001994 | 1.058277 | 2.005656 |
| N | h | ||||
|---|---|---|---|---|---|
| 10 | 1/10 | 0.0962543446 | 0.0974594278 | - | - |
| 20 | 1/20 | 0.0483529972 | 0.0450644425 | 0.993246342 | 1.112812209 |
| 40 | 1/40 | 0.0243287977 | 0.0216596566 | 0.990940293 | 1.056979173 |
| 80 | 1/80 | 0.0122257234 | 0.0106471450 | 0.992745193 | 1.024543742 |
| 160 | 1/160 | 0.0061384979 | 0.0052867956 | 0.993962258 | 1.010001173 |
| 320 | 1/320 | 0.0030783418 | 0.0026378633 | 0.995732241 | 1.003023747 |
| 640 | 1/640 | 0.0015461838 | 0.0013190516 | 0.993441601 | 0.9998688 |
| N | h | ||||
|---|---|---|---|---|---|
| 10 | 1/10 | 0.1220802888 | 0.0833919341 | - | - |
| 20 | 1/20 | 0.0632933442 | 0.0376498054 | 0.947704578 | 1.147265441 |
| 40 | 1/40 | 0.0326304379 | 0.0179210448 | 0.955835448 | 1.070987659 |
| 80 | 1/80 | 0.0167613673 | 0.0087578726 | 0.961078508 | 1.033002381 |
| 160 | 1/160 | 0.0085801061 | 0.0043373867 | 0.966072448 | 1.013754391 |
| 320 | 1/320 | 0.0043785606 | 0.0021615271 | 0.970538809 | 1.004775148 |
| 640 | 1/640 | 0.0022275871 | 0.0010803221 | 0.974974836 | 1.000589405 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parovik, R. Mathematical Modeling of Linear Fractional Oscillators. Mathematics 2020, 8, 1879. https://doi.org/10.3390/math8111879
Parovik R. Mathematical Modeling of Linear Fractional Oscillators. Mathematics. 2020; 8(11):1879. https://doi.org/10.3390/math8111879
Chicago/Turabian StyleParovik, Roman. 2020. "Mathematical Modeling of Linear Fractional Oscillators" Mathematics 8, no. 11: 1879. https://doi.org/10.3390/math8111879
APA StyleParovik, R. (2020). Mathematical Modeling of Linear Fractional Oscillators. Mathematics, 8(11), 1879. https://doi.org/10.3390/math8111879





