Abstract
The article investigates a mathematical model of the Duffing oscillator with a variable fractional order derivative of the Riemann–Liouville type. The study of the model is carried out using a numerical scheme based on the approximation of the fractional derivative of the Riemann–Liouville type by a discrete analog—the fractional derivative of Grunwald–Letnikov. The adequacy of the numerical scheme is verified using specific examples. Using a numerical algorithm, oscillograms and phase trajectories are constructed depending on the values of the model parameters. Chaotic regimes of the Duffing fractional oscillator are investigated using the Wolf–Bennetin algorithm. The forced oscillations of the Duffing fractional oscillator are investigated using the harmonic balance method. Analytical formulas for the amplitude-frequency, phase-frequency characteristics, and also the quality factor are obtained. It is shown that the fractional Duffing oscillator possesses different modes: regular, chaotic, multi-periodic. The relationship between the order of the fractional derivative and the quality factor of the oscillatory system is established.
Keywords:
Riemann–Liouville derivative; Grunwald–Letnikov derivative; Lyapunov exponents; Runge rule; phase trajectories; amplitude-frequency characteristic; phase-frequency characteristic; Q-factor PACS:
45.10.Hj
MSC:
34A08; 70G60
1. Introduction
At present, one of the scientific directions has received wide development—hereditary dynamics, the founder of which is the Italian mathematician Vito Volterra [1]. Hereditarity is a property of a dynamic system in which its current state depends on previous states. Hereditary dynamical systems find their application in hereditary mechanics [2], biology [3], economics [4] and other fields of knowledge.
From the point of view of mathematics, a hereditary dynamical system can be described using integro-differential equations with difference kernels, which are called memory functions [1]. If the memory functions are chosen as exponential, then we turn to equations with derivatives of fractional derivatives, which are studied in the framework of fractional calculus [5,6,7]. Fractional derivatives have many definitions and unique properties, but all of them to some extent describe the memory effect that characterizes information about previous states of the system. This effect determines additional degrees of freedom—orders of fractional derivatives. The orders of fractional derivatives can be constant or functions of time, which in the latter case significantly complicates the study of a dynamical system.
It should be noted that in article [8] the Duffing oscillator with a constant order Riemann–Liouville derivative was considered. Chaotic and regular regimes are investigated using a numerical scheme and various tests. Similar studies were carried out in article [9], but with the Caputo derivative of fractional constant order. In article [10], on the basis of Melnikov’s method, the necessary condition for a chaotic regime of a Duffing oscillator with a fractional order derivative under harmonic excitation is investigated. In article [11], forced oscillations of the Duffing oscillator with a constant-order Caputo derivative were investigated. The amplitude-frequency, phase-frequency characteristics, as well as the bistable mode are investigated.
Article [12] proposes an analytical method for solving the Duffing equation with fractional Caputo derivatives based on a combination of the perturbation and Laplace methods. Paper [13] uses He’s fractional derivative to describe the fractional Duffing equation, which is determined using a variational iterative algorithm. To solve such an equation, a complex fractional transformation was used. In article [14], a solution of the Duffing oscillator with fractional derivatives was obtained using the method of homotopy analysis.
This article proposes a generalization of the Duffing oscillator, a nonlinear oscillatory system with chaotic dynamics. This generalization is based on the introduction of a variable order derivative of the Riemann–Liouville type to describe the energy dissipation of an oscillatory system. This article analyzes the chaotic and regular modes, frequency characteristics of the Duffing oscillator with variable memory, which is a generalization of the research from article [8].
The work is organized as follows. Section 2 gives some definitions from the theory of fractional disappearance; Section 3 presents a statement of the Cauchy problem for the Duffing equation with a fractional variable-order derivative of the Riemann–Liouville type in the dissipative term. It also shows a numerical scheme obtained on the basis of the discrete fractional Grunwald–Letnikov derivative. It is shown on a specific example that the circuit has the first order of accuracy. Section 4 contains an algorithm for calculating the maximum Lyapunov exponents. It is shown with a specific example that chaotic regimes are possible under certain conditions. In Section 5, we studied forced oscillations of the Duffing fractional oscillator. Using the harmonic balance method, formulas are derived for calculating the amplitude-frequency and phase-frequency characteristics, as well as the quality factor. Surfaces of the corresponding characteristics are constructed. The conclusion is given in Section 6.
2. Preliminary Material on Fractional Calculus
Definition 1.
The fractional derivative of variable order of the Riemann–Liouville type has the form:
where is Euler’s gamma function.
Definition 2.
The fractional derivative of variable order of the Grunwald–Letnikov type has the form [15]:
where —binomial coefficient.
Remark 1.
The weighting factor in Formula (2) can be determined as follows:
3. Problem Statement and Numerical Solution
Consider the following Cauchy problem with offset [16]:
where —displacement, solution function, and —given constants, is the coefficient of friction, and are the amplitude and frequency of the external periodic impact, , , —simulation time.
Remark 2.
The variable order of the fractional derivative determines the intensity of energy dissipation in the oscillatory system. If this order is constant and equal to one, then the Cauchy problem (3) becomes the Cauchy problem for the classical Duffing oscillator [4].
Let to achieve the required smoothness. Divide the time interval into N equal parts with a constant step . The solution function will go to the grid function , where , .
Remark 3.
The following relation is valid
The Cauchy problem (3) may be represented as a system:
Let us rewrite the Cauchy problem (5) in the difference setting taking into account the relation (4)
Remark 4.
Let us show the last remark with a specific example.
Example 1.
Consider the case:
Consider the change of the absolute error and computational accuracy of scheme (6) when changing the step h. To calculate the absolute error, we use the Runge rule: —absolute magnitude error, is the numerical solution at the step .
From Table 1, we see that with an increase in the number of nodes in the computational grid, the error e decreases, while the computational accuracy tends to unity.

Table 1.
Results of the study of the computational accuracy of the method (6).
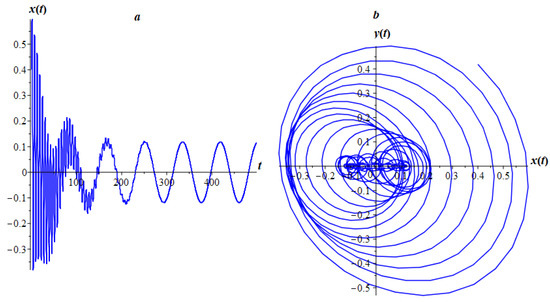
Figure 1.
Oscillogram (a) and phase trajectory (b).
4. Lyapunov Exponents
In the study of nonlinear systems, one of the important tasks is to determine the type of oscillations-periodic, quasi-periodic, random, chaotic. It is especially difficult to distinguish quasiperiodic oscillations from chaotic and random ones, since quasiperiodic oscillations often have a very complex shape that is visually indistinguishable from “random” [17].
A feature of chaotic oscillations is their high sensitivity to small changes in initial conditions. Therefore, one of the most reliable ways to detect chaos is to determine the speed of trajectory run-up, which is estimated using a spectrum of Lyapunov exponents [18].
The geometric meaning of the Lyapunov exponents is that two solutions whose initial values are located in a certain neighborhood of radius will diverge in time T into an n-dimensional ellipsoid along n main semi-axes, and at time t the radii will be determined by the values
where —Lyapunov exponents.
If two trajectories remain close over time, then their change obeys the law
where J is Jacobi matrix, is column vector, —right sides of the system (5). The Formula (7) defines the perturbed equations.
Remark 5.
The presence of at least one positive Lyapunov exponent in the spectrum means the presence of a chaotic regime (asymptotic instability) of the phase trajectory under consideration. A negative reading indicates a limit cycle, while a zero reading indicates that analysis is not enough to draw a conclusion about stability and instability according to Lyapunov. The vectors of the initial conditions for Equation (7) must be orthogonal.
Consider the Benettin–Wolf algorithm for calculating Lyapunov exponents and implement it in the MAPLE environment [19].
- Select the starting point of the vector and together with it we will track the K disturbed trajectories. Let .
- We solve the original equation numerically together with three sets of perturbed equations or equations in variations (7). As the initial vectors for equations in variations, you must select a set of vectors , that are orthogonal and normalized by one.
- After time T, the trajectory will move to the point vector , the perturbation vectors , which we renormalize using the Gram–Schmidt method.
- Next, we continue counting from the point and the perturbation vectors . After a regular time interval T, we get a new set of perturbation vectors , which is subjected to orthogonalization and renormalization.
- Steps 2–4 are repeated M times, and the sums of the calculations are calculated: , which include perturbation vectors before renormalization, but after orthogonalization.
- The estimation of the first three Lyapunov exponents is calculated using the formula:
For a more simplified calculation, take . As a result, we get the following equations:
where solutions of perturbed Equations (9) and (10) according to Formula (7).
Applying the Benettin–Wolf algorithm on Equations (8)–(10), namely steps 3–6, we get the values of the senior Lyapunov exponent. Let us consider the work of the Bennetin–Wolf algorithm using specific examples.
Example 2.
Task parameter values: .
Figure 2 shows the spectrum of Lyapunov exponents relative to the coefficient of dissipation (Figure 2a) and phase trajectories at different values (Figure 2b–d). The figures show that for positive values of Lyapunov exponents, chaotic modes are observed, and the lower the value , the more closely the trajectory approaches that of the classical Duffing oscillator. For negative values of Lyapunov exponents, the phase trajectories are limit cycles, and the greater the modulus of the negative Lyapunov exponent, the more stable the limit cycle will be.
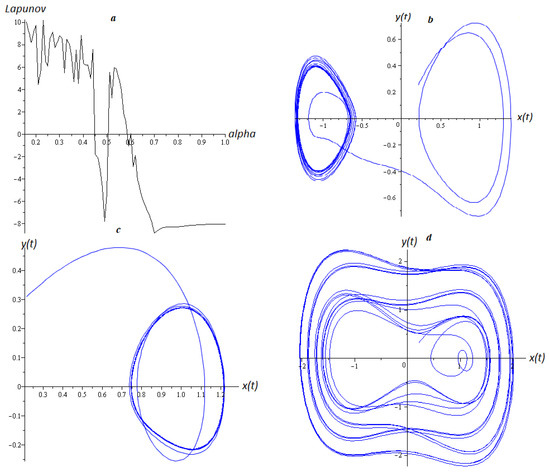
Figure 2.
Range of Lyapunov exponents from (a) and phase trajectories at (b) , (c) and (d) .
Example 3.
Task parameter values: .
Figure 3 shows the spectrum of Lyapunov exponents relative to the fractional derivative q (Figure 3a) and phase trajectories at different values of q (Figure 3b,c). The figures show that for positive values of Lyapunov exponents, chaotic modes are observed, and the closer the value of q is to one, the more closely the trajectory approaches that of the classical Duffing oscillator. With these values of control parameters, the spectrum does not show negative values.
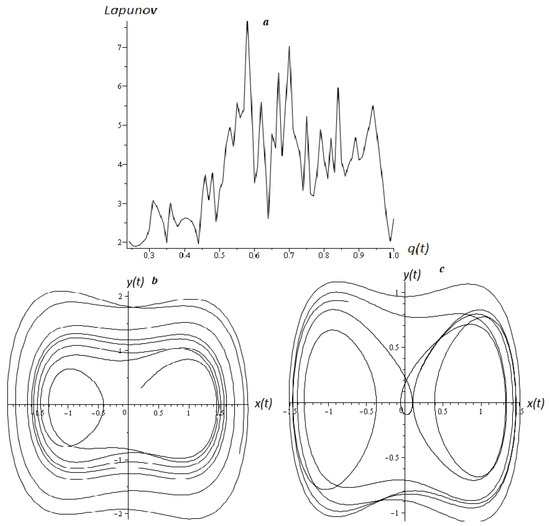
Figure 3.
(a) Range of Lyapunov exponents from q and (b) phase trajectories at and (c) .
5. Forced Oscillations
As shown by the results of articles [20,21], the orders of fractional derivatives in oscillatory systems with memory are associated with the quality factor and are responsible for the intensity of energy dissipation. Therefore, let us investigate the forced oscillations of the Duffing fractional oscillator (3).
Consider the dependence of the amplitude A and phase of steady-state oscillations for operator (1) on the frequency of the external force. To calculate the frequency response and frequency response, we use the harmonic linearization method [21,22,23].
We group expressions by integrals from sine and cosine and differentials from integrals from sine and cosine [21].
Thus, the Riemann–Liouville operator for solution (11) has the form:
In the case of steady oscillations at large times t (), the integrals (12) can be written in the form [23]:
We get the equation [23]:
where
There —digamma function. —the constant of Euler. In practice it is enough to take .
Equation (16) is a classical linear oscillator for which the formulas for the Amplitude-frequency and Phase-frequency characteristics (AFC and PFC) are derived using the harmonic linearization method:
The Q-factor for a fractional Duffing oscillator can be determined from Equation (16) using the formula [21,23]:
where s and p are defined by the Equalities (17) and (18).
Example 4.
Task parameter values: .
Figure 4 shows that when the q parameter is reduced, the quality-factor increases (21). The maximum amplitude corresponds to the maximum Q-factor, and when the frequency decreases, the Q-factor decreases. However, most of all, Q-factor depends on the parameter .
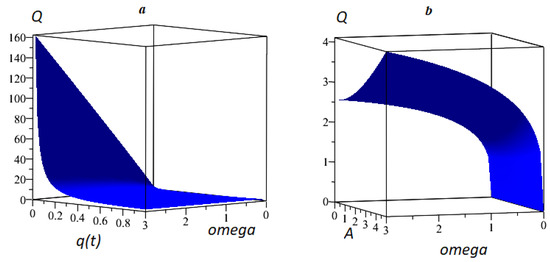
Figure 4.
Q-factor: (a) ; (b) .
Figure 5 shows AFC and PFC versus amplitude and phase versus frequency and the exponent of the derivative . In Figure 5a, we see separate areas from low frequencies to high frequencies.
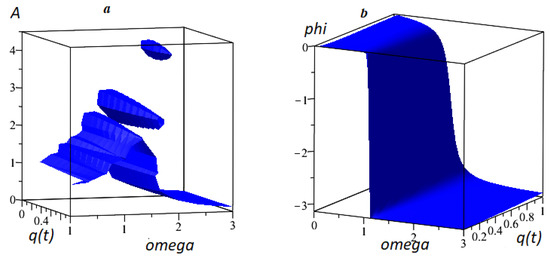
Figure 5.
(a) AFC and (b) PFC with , .
6. Conclusions
The article proposes a mathematical model of a fractional Duffing oscillator with a variable fractional order derivative of the Riemann–Liouville type in the dissipative term. Using the discrete Grunwald–Letnikov derivative, a first-order numerical scheme is constructed. Using Runge’s method, it is shown that with an increase in the number of nodes in the computational grid, the order of computational accuracy tends to unity. A numerical algorithm is proposed for calculating the spectra of the maximum Lyapunov exponents. It is shown that the spectrum of the maximum Lyapunov exponents can contain positive values, which indicates the existence of chaotic regimes. Knowing the conditions for the existence of chaotic regimes, we can investigate regular regimes, for example, regimes of steady oscillations under the action of an external harmonic force. The study of forced vibrations using analytical formulas for the frequency characteristics and quality factor of the oscillatory system showed that the variable order of the fractional derivative determines the intensity of energy dissipation in the system. With an increase in the order, the quality factor of the oscillatory system increases, and with a decrease, it increases. This fact suggests that oscillatory modes can be controlled using the order of the fractional derivative. This fact is very important for the development of applied engineering research. For example, in machine learning and intelligent communications [24].
It is necessary to study the fractional Duffing oscillator with a variable fractional derivative of the Riemann–Liouville type, taking into account different definitions and types of its function [15]. It is of interest to study forced oscillations, resonance curves as in the Figure 5a. Furthermore, also the presence of bistable behavior [11].
It is of interest to study the fractional Duffing oscillator with higher order nonlinearities, for example, by analogy with the article [25].
Author Contributions
Conceptualization, R.P.; methodology, R.P.; software, V.K.; validation, V.K.; formal analysis, V.K.; investigation, V.K.; writing—original draft preparation, V.K.; writing—review and editing, R.P.; visualization, V.K. All authors have read and agreed to the published version of the manuscript.
Funding
The work was carried out according to the Subject AAAA-A17-117080110043-4 «Dynamics of physical processes in the active zones of near space and geospheres» IKIR FEB RAS. The study was carried out with the support of the Russian Foundation for Basic Research within the framework of scientific project No. 19-31-50033. Research topic of Vitus Bering KamSU “Mathematical model of the Duffing oscillator with a derivative of variable fractional order” No. AAAA-A20-120021190004-8.
Acknowledgments
I would like to express my gratitude to Arsen Pskhu for valuable advice, which served to better understand the research results.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AFC | Amplitude–Frequency Characteristics |
| PFC | Phase-Frequency Characteristics |
| Q-factor | Quality Factor |
References
- Volterra, V. Sur les equations integro-differentielles et leurs applications. Acta Math. 1912, 35, 295–356. [Google Scholar] [CrossRef]
- Vlasov, V.; Rautian, N. A Study of Operator Models Arising in Problems of Hereditary Mechanics. J. Math Sci. 2020, 244, 170–182. [Google Scholar] [CrossRef]
- Li, Z.; Yang, Q. Systems and synthetic biology approaches in understanding biological oscillators. Quant Biol. 2018, 6, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Danylchuk, H.; Kibalnyk, L.; Serdiuk, O. Study of critical phenomena in economic systems using a model of damped oscillations. SHS Web Conf. 2019, 65, 06008. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus. Theory and Applications of Differentiation and Integration to Arbitrary Order; Academic Press: London, UK, 1974; p. 240. [Google Scholar]
- Miller, K.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differntial Equations; A Wiley-Interscience Publication: New York, NY, USA, 1993; p. 384. [Google Scholar]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204, p. 523. [Google Scholar]
- Syta, A.; Litak, G.; Lenci, S.; Scheffler, M. Chaotic vibrations of the duffing system with fractional damping. Chaos Interdiscip. J. Nonlinear Sci. 2014, 24, 013107. [Google Scholar] [CrossRef]
- Jiménez, S.; Zufiria, P. Characterizing chaos in a type of fractional Duffing’s equation. Conf. Publ. Am. Inst. Math. Sci. 2015, 2015, 660–669. [Google Scholar] [CrossRef]
- Xing, W.; Chen, E.; Chang, Y.; Wang, M. Threshold for chaos of a duffing oscillator with fractional-order derivative. Shock Vib. 2019, 2019, 1230194. [Google Scholar] [CrossRef]
- Liu, Q.X.; Liu, J.K.; Chen, Y.M. An analytical criterion for jump phenomena in fractional Duffing oscillators. Chaos Solitons Fractals 2017, 98, 216–219. [Google Scholar] [CrossRef]
- Eze, S.C. Analysis of fractional Duffing oscillator. Rev. Mex. Fis. 2019, 66, 187–191. [Google Scholar] [CrossRef]
- Wang, Y.; An, J.Y. Amplitude–frequency relationship to a fractional Duffing oscillator arising in microphysics and tsunami motion. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1008–1012. [Google Scholar] [CrossRef]
- Ejikeme, C.L.; Oyesanya, M.O.; Agbebaku, D.F.; Okofu, M.B. Solution to nonlinear Duffing oscillator with fractional derivatives using homotopy analysis method (HAM). Glob. J. Pure Appl. Math. 2018, 14, 1363–1388. [Google Scholar]
- Atanackovic, T.; Pilipovic, S. Hamilton’s principle with variable order fractional derivatives. Fract. Calc. Appl. Anal. 2011, 14, 94–109. [Google Scholar] [CrossRef]
- Kim, V.A. Duffing oscillator with external harmonic action and variable fractional Riemann–Liouville derivative characterizing viscous friction. Bull. KRASEC Phys. Math. Sci. 2016, 13, 46–49. [Google Scholar]
- Oseledets, V.I. A Multiplicative ergodic theorem. Characteristic Lyapunov exponents of dynamical systems. Proc. Mosc. Math. Soc. 1968, 19, 197–231. [Google Scholar]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Physica 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Kim, V.A.; Parovik, R.I. Calculation of maximal Lyapunov exponents for an oscillatory Duffing system with power memory. Bull. KRASEC Phys. Math. Sci. 2018, 23, 98–105. [Google Scholar] [CrossRef]
- Pskhu, A.; Rekhviashvili, S. Analysis of Forced Oscillations of a Fractional Oscillator. Tech. Phys. Lett. 2018, 44, 1218–1221. [Google Scholar] [CrossRef]
- Parovik, R.I. Amplitude-frequency and phase-frequency performances of forced oscillations of a nonlinear fractional oscillator. Tech. Phys. Lett. 2019, 45, 660–663. [Google Scholar] [CrossRef]
- Parovik, R. Mathematical Modeling of Linear Fractional Oscillators. Mathematics 2020, 8, 1879. [Google Scholar] [CrossRef]
- Kim, V.A.; Parovik, R.I. Investigation of forced oscillations of a Duffing oscillator with a derivative of a variable fractional Riemann–Liouville order. Izv. Kabard. Balkar Sci. Cent. Russ. Acad. Sci. 2020, 93, 46–56. [Google Scholar] [CrossRef]
- Huang, X.L.; Ma, X.; Hu, F. Machine learning and intelligent communications. Mob. Netw. Appl. 2018, 23, 68–70. [Google Scholar] [CrossRef]
- Pirmohabbati, P.; Sheikhani, A.R.; Najafi, H.S.; Ziabari, A.A. Numerical solution of full fractional Duffing equations with Cubic-Quintic-Heptic nonlinearities. AIMS Math. 2020, 5, 1621–1641. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).