Finite Difference Method for Two-Sided Two Dimensional Space Fractional Convection-Diffusion Problem with Source Term
Abstract
1. Introduction
2. Preliminary Remarks
- 1.
- .
- 2.
- .
- 3.
- 4.
- 5.
- .
- Left Riemann-Liouville fractional derivative:
- Right Riemann-Liouville fractional derivative:
3. Numerical Approximation for One Dimensional Two-Sided Convection-Diffusion Problem with Source Term
4. Formulation and Discretization of Two-Dimensional Riesz Space Fractional Convection Diffusion Equation with CNADI-WSGD Scheme
- Algorithm 1:
- The first step is to solve the problem in the x-direction for each fixed to find an intermediate solution in the form:
- Algorithm 2:
- The next step is to solve the problem in y-direction for each fixed as:
- Algorithm 3:
- We need to apply the homogeneous Dirichlet boundary conditions:
5. CNADI-WSGD Scheme for Theoretical Analysis of 2D-RSFCDE with Source Term
5.1. Stability and Convergence Analysis of CNADI-WSGD Scheme
5.2. Stability Analysis of the CNADI-WSGD Method
5.3. Convergence Analysis of CNADI-WSGD Scheme
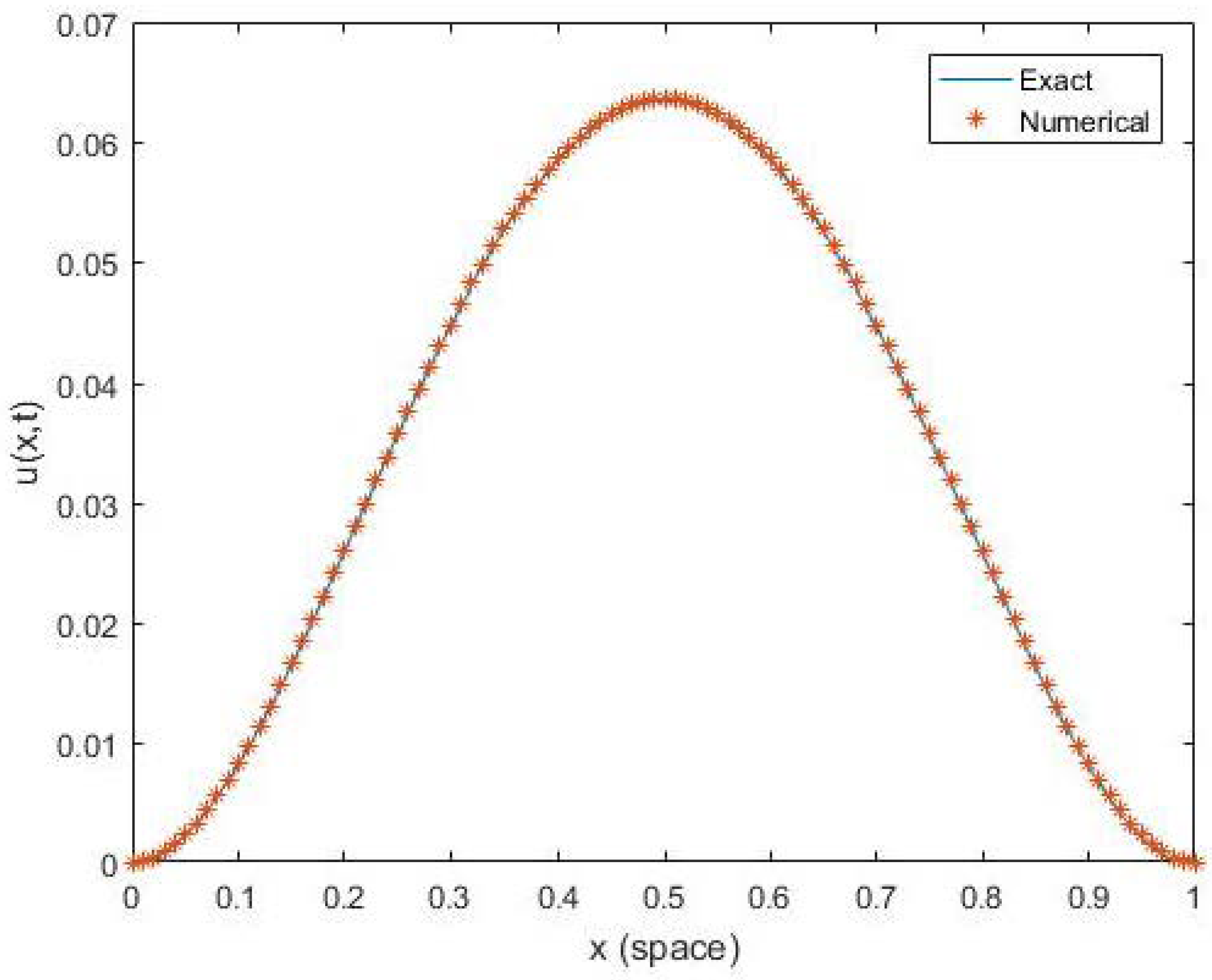
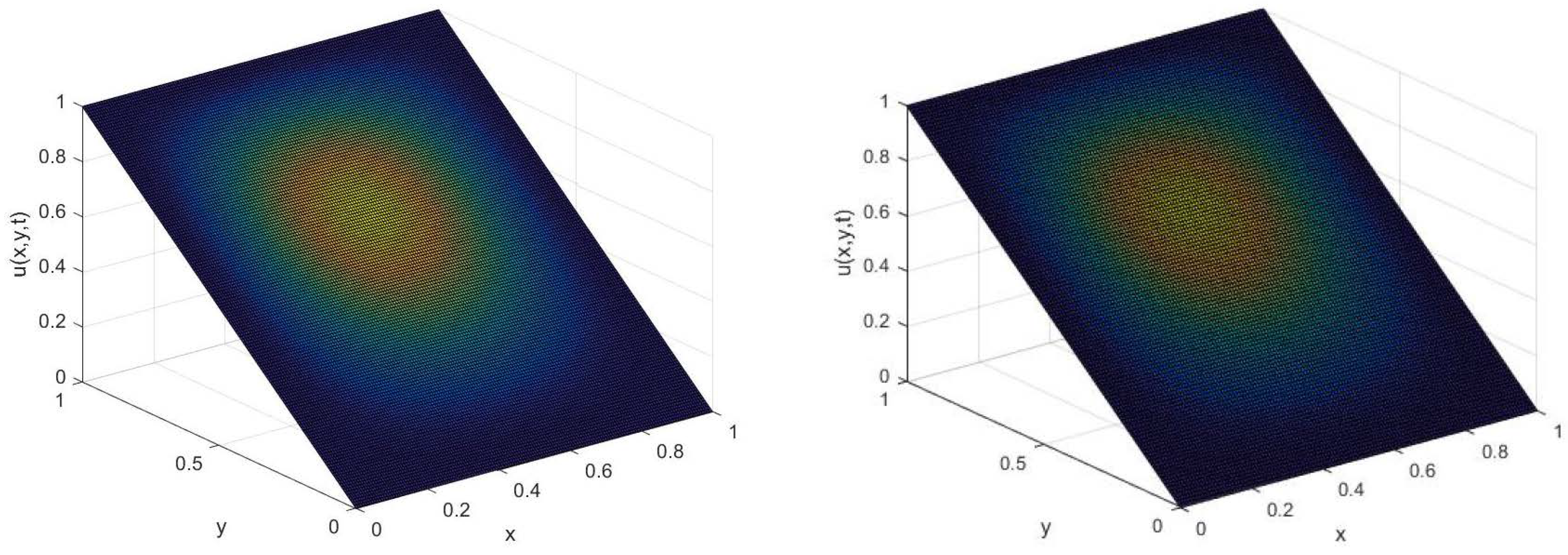
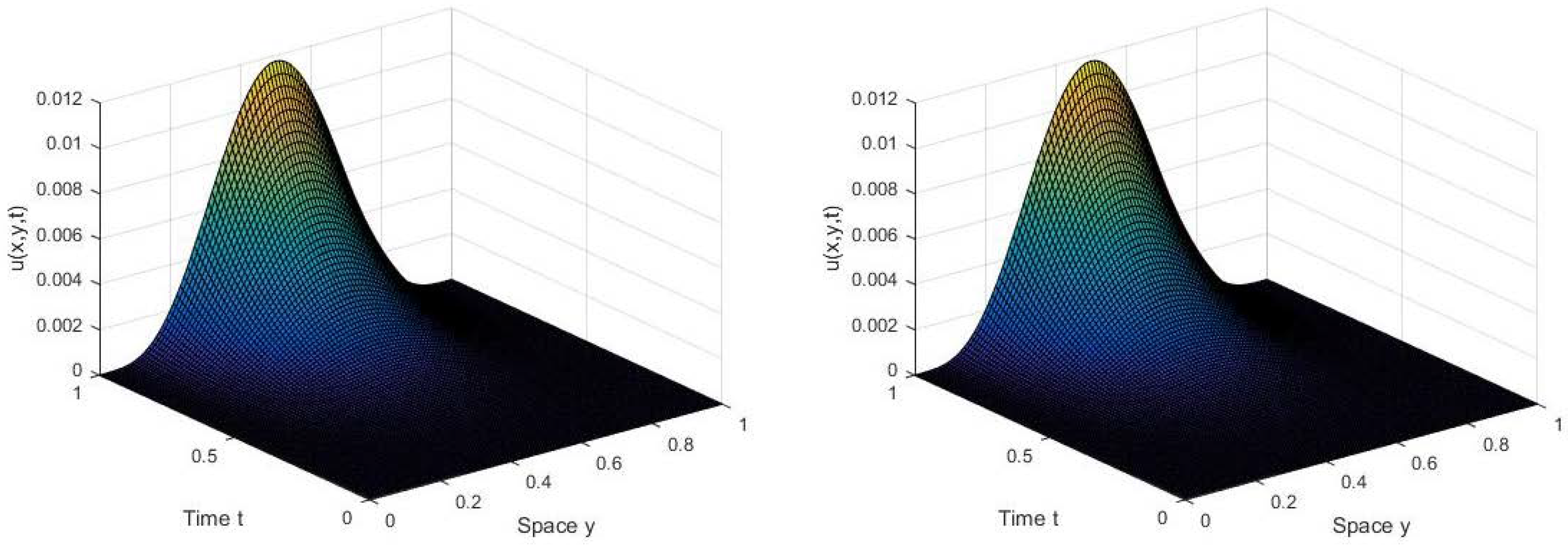
6. Numerical Simulations
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| CN | Crank-Nicolson scheme. |
| ADI | Alternating direction implicit method. |
| CNADI | Crank-Nicolson alternating direction implicit method. |
| WSGD | Weighted shifted Grünwald-Letnikov difference operator. |
| RSFCDE | Riesz space fractional convection–diffusion equation. |
| 2D-RSFCDE | Two-dimensional Riesz space fractional convection–diffusion equation. |
References
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: New York, NY, USA, 1998; Volume 198. [Google Scholar]
- Li, C.; Zeng, F. Finite difference methods for fractional differential equations. Int. J. Bifurcat. Chaos 2012, 22, 1230014. [Google Scholar] [CrossRef]
- Diethelm, K. The Analysis of Fractional Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Fomin, S.; Chugunov, V.; Hashida, T. Application of fractional differential equations for modeling the anomalous diffusion of contaminant from fracture into porous rock matrix with bordering alteration zone. Trans. Porous Med. 2010, 81, 187–205. [Google Scholar] [CrossRef]
- Salman, W.; Gavriilidis, A.; Angeli, P. A model for predicting axial mixing during gas–liquid Taylor flow in microchannels at low Bodenstein number. Chem. Eng. J. 2004, 101, 391–396. [Google Scholar] [CrossRef]
- Berkowitz, B.; Cortis, A.; Dror, I.; Scher, H. Laboratory experiments on dispersive transport across interfaces. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Cortis, A.; Berkowitz, B. Computing “anomalous” contaminant transport in porous media. Ground Water 2005, 43, 947–950. [Google Scholar] [CrossRef]
- Wang, K.; Wang, H. A fast characteristic finite difference method for fractional advection–diffusion equations. Adv. Water. Resour. 2011, 34, 810–816. [Google Scholar] [CrossRef]
- Singh, J.; Swroop, R.; Kumar, D. A computational approach for fractional convection–diffusion equation via integral transforms. Ain Shams Eng. J. 2016, 9, 1019–1028. [Google Scholar] [CrossRef]
- Wang, Y.M. A compact finite difference method for a class of time fractional convection–diffusion-wave equations with variable coefficients. Numer. Algorithms 2015, 70, 625–651. [Google Scholar] [CrossRef]
- Gu, X.M.; Huang, T.Z.; Ji, C.C.; Carpentieri, B.; Alikhanov, A.A. Fast iterative method with a second-order implicit difference scheme for time-space fractional convection–diffusion equation. J. Sci. Comput. 2017, 72, 957–985. [Google Scholar] [CrossRef]
- Cui, M. Combined compact difference scheme for the time fractional convection–diffusion equation with variable coefficients. Appl. Math. Comput. 2014, 246, 464–473. [Google Scholar] [CrossRef]
- Tian, W.; Deng, W.; Wu, Y. Polynomial spectral collocation method for space fractional advection–diffusion equation. Numer. Methods Partial Differ. Equ. 2014, 30, 514–535. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Baleanu, D. A spectral Legendre–Gauss–Lobatto collocation method for a space-fractional advection–diffusion equations with variable coefficients. Rep. Math. Phys. 2013, 72, 219–233. [Google Scholar] [CrossRef]
- Saadatmandi, A.; Dehghan, M.; Azizi, M.R. The Sinc-Legendre collocation method for a class of fractional convection–diffusion equations with variable coefficients. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4125–4136. [Google Scholar] [CrossRef]
- Parvizi, M.; Eslahchi, M.R.; Dehghan, M. Numerical solution of fractional advection-diffusion equation with a nonlinear source term. Numer. Algorithms 2015, 68, 601–629. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; Chapman and Hall/CRC: Boca Raton, FL, USA, 2015. [Google Scholar]
- Jin, B.; Lazarov, R.; Zhou, Z. A Petrov–Galerkin finite element method for fractional convection–diffusion equations. SIAM J. Numer. Anal. 2016, 54, 481–503. [Google Scholar] [CrossRef]
- Aboelenen, T. A direct discontinuous Galerkin method for fractional convection–diffusion and Schrödinger-type equations. Eur. Phys. J. Plus 2018, 133, 316. [Google Scholar] [CrossRef]
- Xu, Q.; Hesthaven, J.S. Discontinuous Galerkin method for fractional convection–diffusion equations. SIAM J. Numer. Anal. 2014, 52, 405–423. [Google Scholar] [CrossRef]
- Gao, F.; Yuan, Y.; Du, N. An upwind finite volume element method for nonlinear convection–diffusion problem. AJCM 2011, 1, 264. [Google Scholar] [CrossRef]
- Badr, M.; Yazdani, A.; Jafari, H. Stability of a finite volume element method for the time-fractional advection-diffusion equation. Numer. Methods Partial Differ. Equ. 2018, 34, 1459–1471. [Google Scholar] [CrossRef]
- Ding, H.F.; Zhang, Y.X. New numerical methods for the Riesz space fractional partial differential equations. Comput. Math. Appl. 2012, 63, 1135–1146. [Google Scholar]
- Anley, E.F.; Zheng, Z. Finite Difference Approximation Method for a Space Fractional Convection–Diffusion Equation with Variable Coefficients. Symmetry 2020, 12, 485. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Sun, Z.Z. Alternating direction implicit schemes for the two-dimensional fractional sub-diffusion equation. J. Comput. Phys. 2011, 230, 8713–8728. [Google Scholar] [CrossRef]
- Tadjeran, C.; Meerschaert, M.M. A second-order accurate numerical method for the two-dimensional fractional diffusion equation. J. Comput. Phys. 2007, 220, 813–823. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Scheffler, H.P.; Tadjeran, C. Finite difference methods for two-dimensional fractional dispersion equation. J. Comput. Phys. 2006, 211, 249–261. [Google Scholar] [CrossRef]
- Valizadeh, S.; Borhanifar, A.; Malek, A. Compact ADI method for solving two-dimensional Riesz space fractional diffusion equation. arXiv 2018, arXiv:1802.02015. [Google Scholar]
- Wang, H.; Basu, T.S. A fast finite difference method for two-dimensional space-fractional diffusion equations. SIAM J. Sci. Comput. 2012, 34, A2444–A2458. [Google Scholar] [CrossRef]
- Yin, X.; Fang, S.; Guo, C. Alternating-direction implicit finite difference methods for a new two-dimensional two-sided space-fractional diffusion equation. Adv. Diff. Equ. 2018, 2018, 389. [Google Scholar] [CrossRef]
- Bu, W.; Tang, Y.; Yang, J. Galerkin finite element method for two-dimensional Riesz space fractional diffusion equations. J. Comput. Phys. 2014, 276, 26–38. [Google Scholar] [CrossRef]
- Li, J.; Liu, F.; Feng, L.; Turner, I. A novel finite volume method for the Riesz space distributed-order diffusion equation. Comput. Appl. 2017, 74, 772–783. [Google Scholar] [CrossRef]
- Chen, H.; Lv, W.; Zhang, T. A Kronecker product splitting preconditioner for two-dimensional space-fractional diffusion equations. J. Comput. Phys. 2018, 360, 1–14. [Google Scholar] [CrossRef]
- Liu, F.; Chen, S.; Turner, I.; Burrage, K.; Anh, V. Numerical simulation for two-dimensional Riesz space fractional diffusion equations with a nonlinear reaction term. Cent. Eur. J. Phys. 2013, 11, 1221–1232. [Google Scholar] [CrossRef]
- Zeng, F.; Liu, F.; Li, C.; Burrage, K.; Turner, I.; Anh, V. A Crank–Nicolson ADI spectral method for a two-dimensional Riesz space fractional nonlinear reaction-diffusion equation. SIAM J. Numer. Anal. 2014, 52, 2599–2622. [Google Scholar] [CrossRef]
- Balasim, A.T.; Ali, N.H.M. New group iterative schemes in the numerical solution of the two-dimensional time fractional advection-diffusion equation. Cogent Math. 2017, 4, 1412241. [Google Scholar] [CrossRef]
- Zhao, Y.; Bu, W.; Huang, J.; Liu, D.Y.; Tang, Y. Finite element method for two-dimensional space-fractional advection–dispersion equations. Appl. Math. Comput. 2015, 257, 553–565. [Google Scholar] [CrossRef]
- Pang, G.; Chen, W.; Sze, K.Y. A comparative study of finite element and finite difference methods for two-dimensional space-fractional advection–dispersion equation. Adv. Appl. Math. Mech. 2016, 8, 166–186. [Google Scholar] [CrossRef]
- Li, J.; Liu, F.; Feng, L.; Turner, I. A novel finite volume method for the Riesz space distributed-order advection–diffusion equation. Appl. Math. Model. 2017, 46, 536–553. [Google Scholar] [CrossRef]
- Chen, M.; Deng, W. A second-order numerical method for two-dimensional two-sided space fractional convection- diffusion equation. Appl. Math. Model. 2014, 38, 3244–3259. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Sun, Z.Z.; Zhao, X. Compact alternating direction implicit scheme for the two-dimensional fractional diffusion-wave equation. SIAM J. Numer. Anal. 2012, 50, 1535–1555. [Google Scholar] [CrossRef]
- Benson, D.A.; Wheatcraft, S.; Meerschaert, M.M. Application of a fractional advection–dispersion equation. Water Resour. Res. 2000, 36, 1403–1412. [Google Scholar] [CrossRef]
- Zhang, Y.; Meerschaert, M.M.; Neupauer, R.M. Backward fractional advection dispersion model for contaminant source prediction. Water Resour. Res. 2016, 52, 2462–2473. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach Science Publisher: Yverdon, Switzerland, 1993; Volume 1. [Google Scholar]
- Podlubny, I. Fractional Differential Equations Academic; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Tian, W.; Zhou, H.; Deng, W. A class of second order difference approximations for solving space fractional diffusion equations. Math. Comp. 2015, 84, 1703–1727. [Google Scholar] [CrossRef]
- Liu, F.; Zhuang, P.; Anh, V.; Turner, I.; Burrage, K. Stability and convergence of the difference methods for the space–time fractional advection–diffusion equation. Appl. Math. Comput. 2007, 191, 12–20. [Google Scholar] [CrossRef]
- Feng, L.; Zhuang, P.; Liu, F.; Turner, I.; Li, J. High-order numerical methods for the Riesz space fractional advection-dispersion equations. arXiv 2020, arXiv:2003.13923. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, F.; Turner, I. Numerical methods for fractional partial differential equations with Riesz space fractional derivatives. Appl. Math. Model. 2010, 34, 200–218. [Google Scholar] [CrossRef]
- Shen, S.; Liu, F.; Anh, V.; Turner, I. The fundamental solution and numerical solution of the Riesz fractional advection–dispersion equation. IMA J. Appl. Math. 2008, 73, 850–872. [Google Scholar] [CrossRef]
- Laub, A.J. Matrix Analysis for Scientists and Engineers; SIAM: Philadelphia, PA, USA, 2005; Volume 91. [Google Scholar]
- Isaacson, E.; Keller, H.B. Analysis of Numerical Methods; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
| 1/10 | – | – | – | ||||
| 1/20 | 1.9156 | 1.9189 | 1.9500 | ||||
| 1/40 | 1.9907 | 1.9851 | 2.0000 | ||||
| 1/80 | 2.0030 | 1.9941 | 1.9782 | ||||
| 1/160 | 2.0086 | 2.0008 | 1.9972 | ||||
| 1/10 | – | – | 1.81 | – | |||
| 1/20 | 1.8745 | 1.9098 | 1.9149 | ||||
| 1/40 | 1.9762 | 1.9428 | 2.0000 | ||||
| 1/80 | 1.9786 | 1.9743 | 1.9109 | ||||
| 1/160 | 1.9899 | 1.9867 | 1.9783 |
| 1/10 | – | – | – | ||||
| 1/20 | 1.9827 | 1.9425 | 1.9594 | ||||
| 1/40 | 1.9750 | 2.0055 | 2.0324 | ||||
| 1/80 | 1.9962 | 1.9960 | 1.9567 | ||||
| 1/160 | 1.9989 | 1.9989 | 1.9988 | ||||
| 1/10 | – | – | – | ||||
| 1/20 | 1.9260 | 1.9403 | 1.9231 | ||||
| 1/40 | 1.9702 | 1.9594 | 2.0275 | ||||
| 1/80 | 1.9843 | 1.9839 | 1.9300 | ||||
| 1/160 | 1.9923 | 1.9921 | 1.9918 |
| 1/10 | – | – | – | ||||
| 1/20 | 2.2243 | 2.0283 | 2.2854 | ||||
| 1/40 | 2.4894 | 2.3923 | 2.0056 | ||||
| 1/80 | 2.1565 | 2.2907 | 1.9961 |
| 1/10 | – | – | – | ||||
| 1/20 | 5.7 | 1.8110 | 1.7766 | 2.0087 | |||
| 1/40 | 1.7454 | 1.6828 | 2.1166 | ||||
| 1/80 | 1.9962 | 1.7467 | 2.3213 | ||||
| 1/10 | – | – | – | ||||
| 1/20 | 2.0780 | 2.0426 | 2.0890 | ||||
| 1/40 | 2.2399 | 1.1 | 2.1844 | 2.4595 | |||
| 1/80 | 2.4602 | 2.6189 | 2.4735 | ||||
| 1/160 | 2.4114 | 2.5202 | 2.3420 |
| 1/10 | – | – | – | ||||
| 1/20 | 2.00 | 2.3163 | 1.9 | 2.5203 | 1.6502 | ||
| 1/40 | 1.7791 | 4.8275 | 1.9767 | 2.3581 | |||
| 1/80 | 1.6257 | 1.6542 | 2.3038 | ||||
| 1/10 | – | – | – | ||||
| 1/20 | 2.0656 | 2.0937 | 2.5340 | ||||
| 1/40 | 2.3024 | 2.4197 | 2.1215 | ||||
| 1/80 | 2.3224 | 2.5575 | 2.0861 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anley, E.F.; Zheng, Z. Finite Difference Method for Two-Sided Two Dimensional Space Fractional Convection-Diffusion Problem with Source Term. Mathematics 2020, 8, 1878. https://doi.org/10.3390/math8111878
Anley EF, Zheng Z. Finite Difference Method for Two-Sided Two Dimensional Space Fractional Convection-Diffusion Problem with Source Term. Mathematics. 2020; 8(11):1878. https://doi.org/10.3390/math8111878
Chicago/Turabian StyleAnley, Eyaya Fekadie, and Zhoushun Zheng. 2020. "Finite Difference Method for Two-Sided Two Dimensional Space Fractional Convection-Diffusion Problem with Source Term" Mathematics 8, no. 11: 1878. https://doi.org/10.3390/math8111878
APA StyleAnley, E. F., & Zheng, Z. (2020). Finite Difference Method for Two-Sided Two Dimensional Space Fractional Convection-Diffusion Problem with Source Term. Mathematics, 8(11), 1878. https://doi.org/10.3390/math8111878





