Efficient Numerical Scheme for the Solution of Tenth Order Boundary Value Problems by the Haar Wavelet Method
Abstract
1. Introduction
- We developed HWCM for the numerical solution of linear and nonlinear tenth order BVPs.
- We examine the effectiveness of the HWCM on some examples and compare our results with other methods.
2. Haar Wavelet
3. Haar Wavelet Collocation Method
3.1. Linear Case
3.2. Nonlinear Case
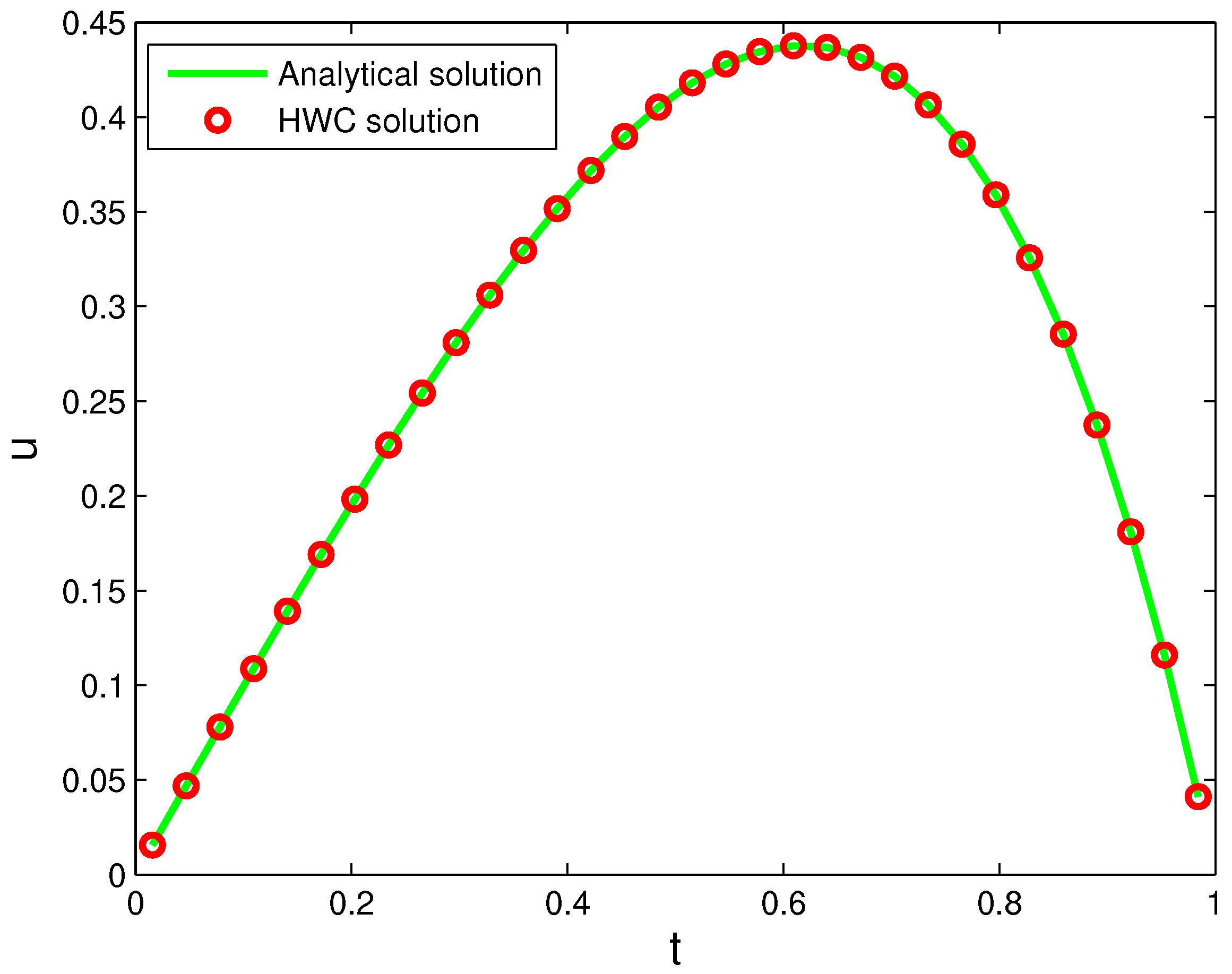
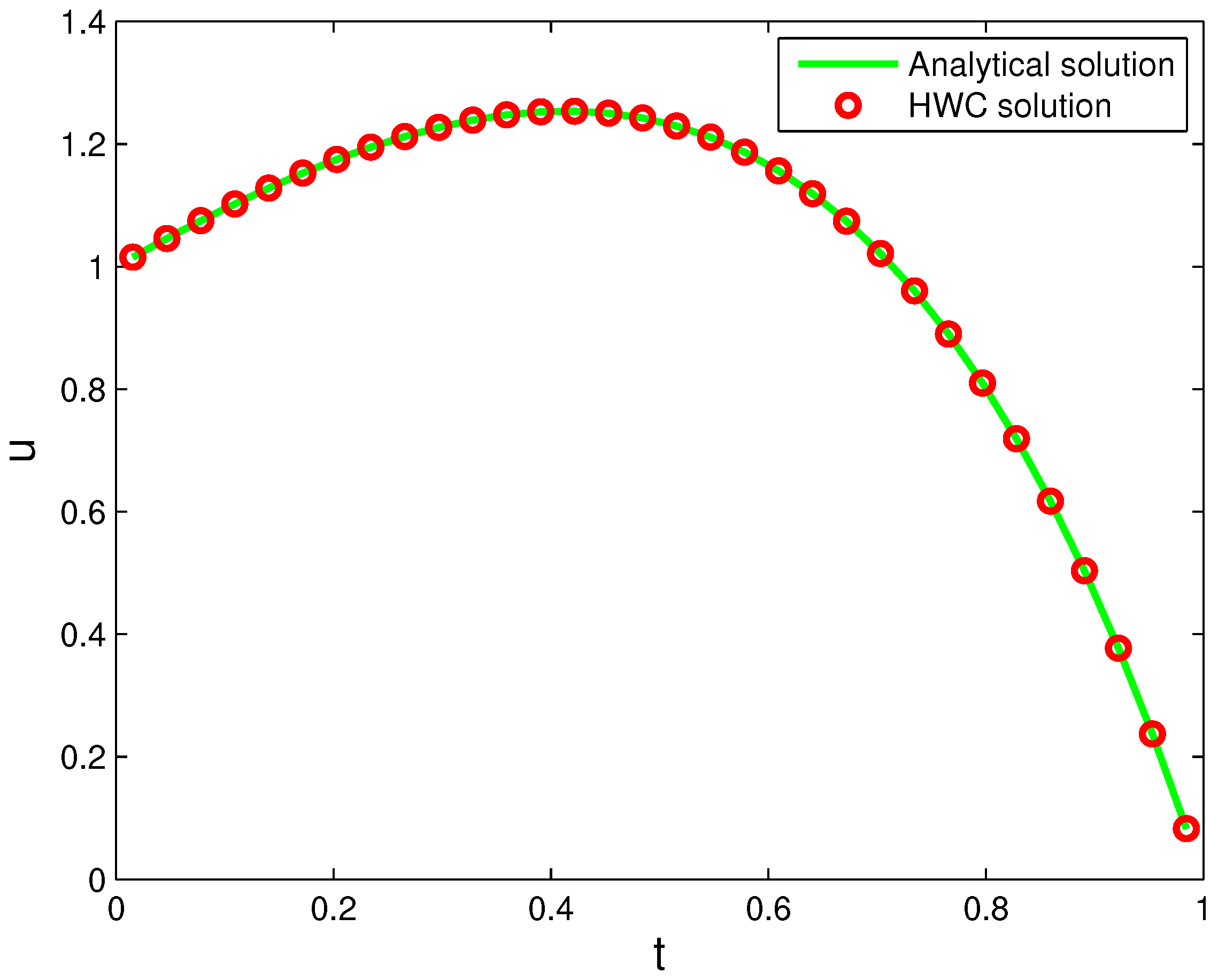
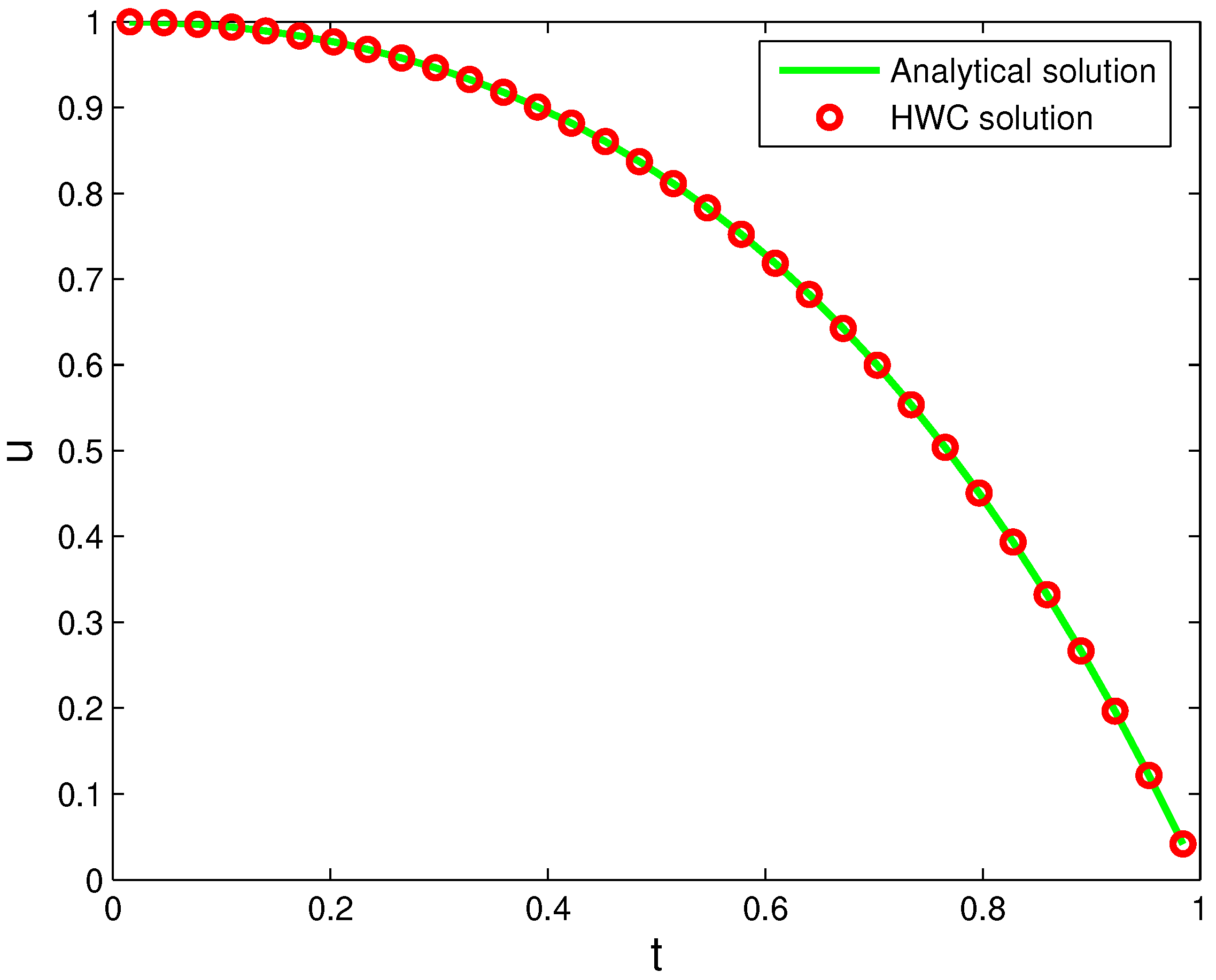
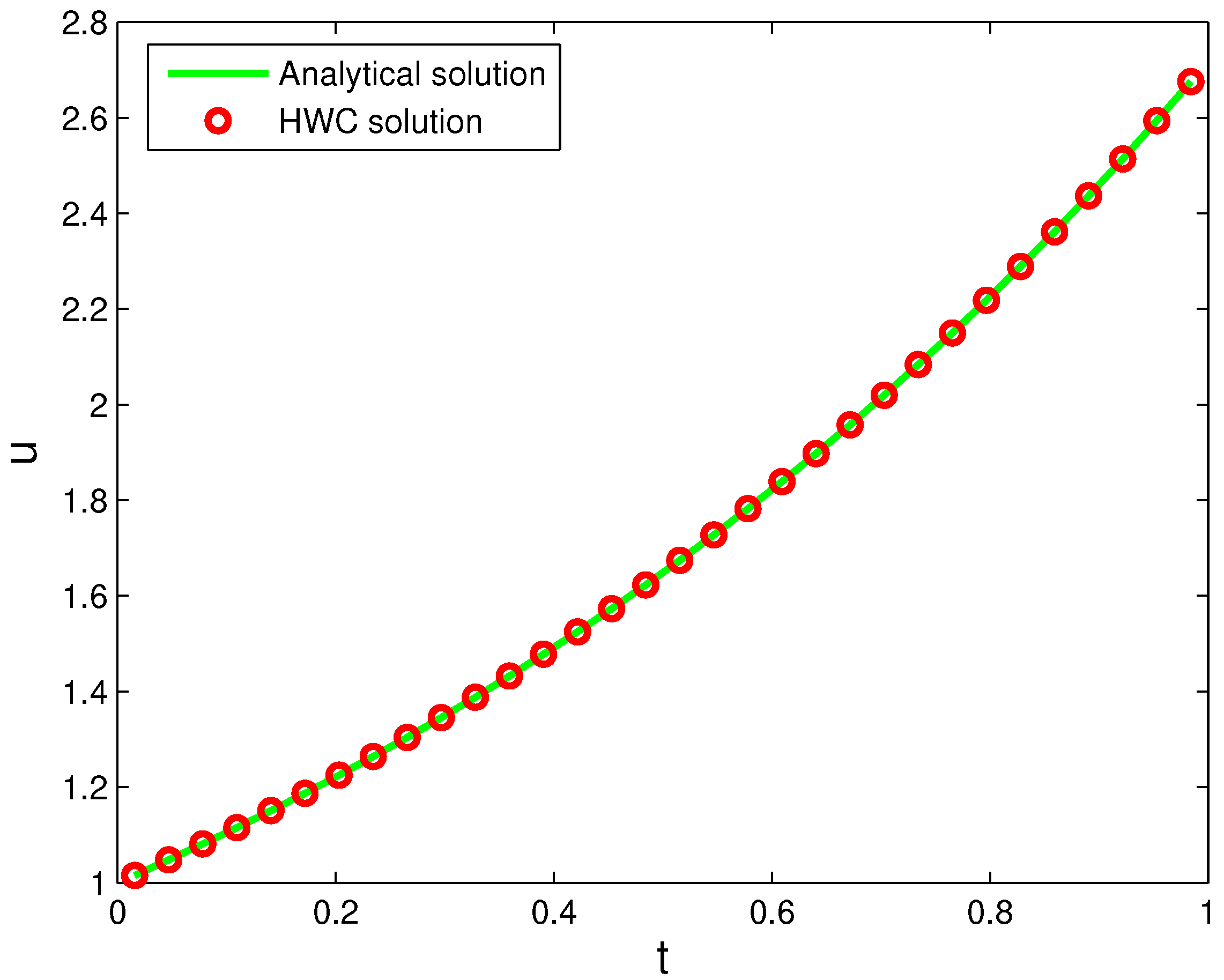
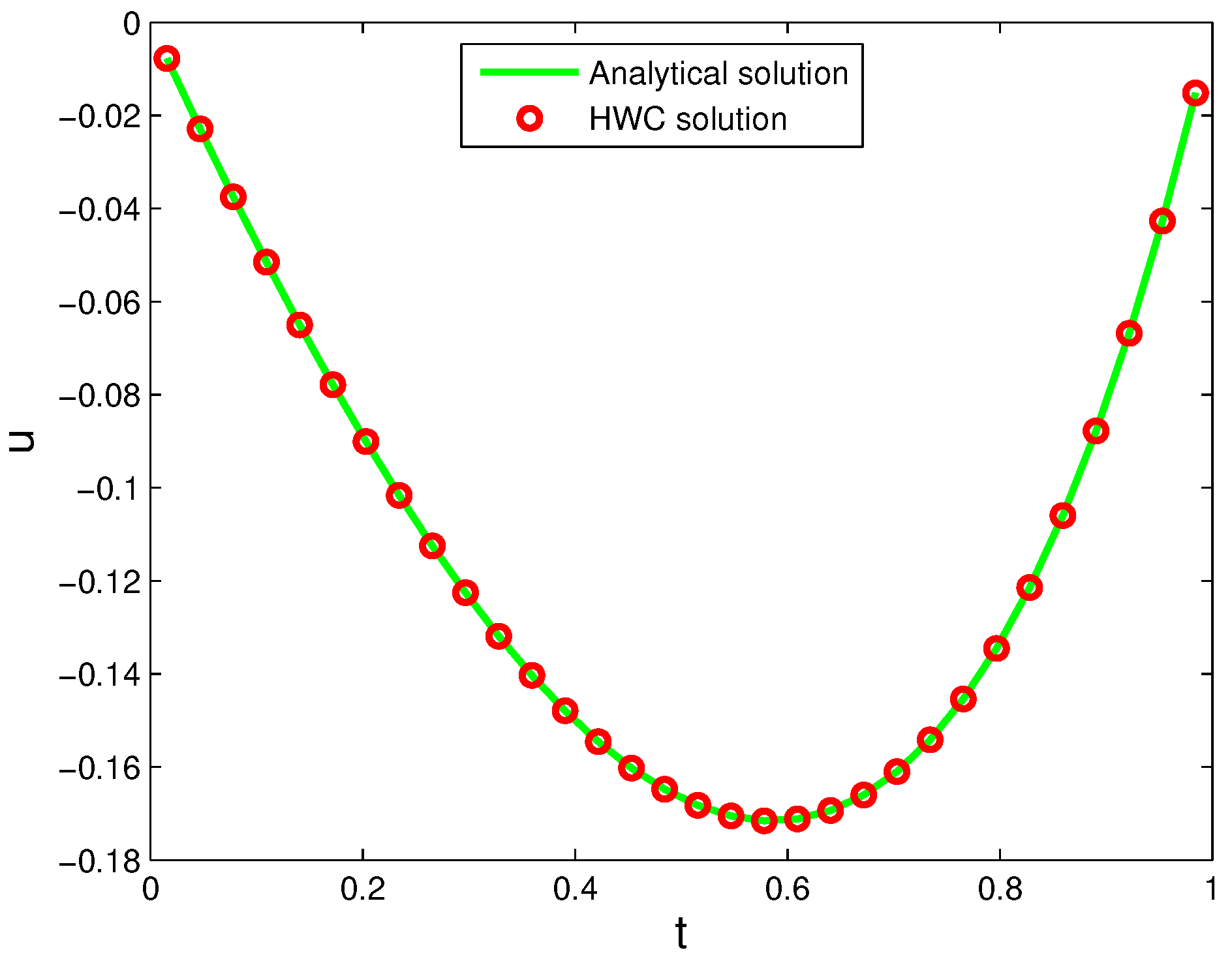
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Iqbal, M.J.; Rehman, S.; Pervaiz, A.; Hakeem, A. Approximations for linear tenth-order boundary value problems through polynomial and non-polynomial cubic spline techniques. Proc. Pak. Acad. Sci. 2015, 52, 389–396. [Google Scholar]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Clarendon Press: Oxford, UK, 1961. [Google Scholar]
- Bishop, R.E.; Cannon, S.M.; Miao, S. On coupled bending and torsional vibration of uni-form beams. J. Sound Vib. 1989, 131, 309–325. [Google Scholar] [CrossRef]
- Akram, G.; Siddiqi, S. Nonic spline solutions of eighth order boundary value problems. Appl. Math. Comput. 2006, 182, 829–845. [Google Scholar] [CrossRef]
- Siddiqi, S.; Akram, G. Solution of eighth-order boundary value problems using the non-polynomial spline technique. Int. J. Comput. Math. 2007, 182, 347–368. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The numerical solutions of special eighth-order boundary value problems by the modified decomposition method. Neural Parallel Sci. Comput. 2000, 8, 133–146. [Google Scholar]
- Siddiqi, S.S.; Twizell, E.H. Spline solutions of linear eighth-order boundary-value problems. Comput. Meth. Appl. Mech. Eng. 1996, 131, 457–464. [Google Scholar] [CrossRef]
- Boutayeb, A.; Twizell, E.H. Finite-difference methods for the solution of special eighth-order boundary-value problems. Int. J. Comput. Math. 1993, 48, 63–75. [Google Scholar] [CrossRef]
- Siddiqi, S.S.; Twizell, E.H. Spline solutions of linear twelfth-order boundary-value problems. Comput. J. Comput. Appl. Math. 1997, 78, 371–390. [Google Scholar] [CrossRef]
- Wu, T.Y.; Liu, G.R. The differential quadrature as a numerical method to solve the differential equation. Comput. Mech. 1999, 24, 197–205. [Google Scholar] [CrossRef]
- Wu, T.Y.; Liu, G.R. A generalized differential quadrature rule for initial-value differential equations. J. Sound Vib. 2000, 233, 195–213. [Google Scholar] [CrossRef]
- Wu, T.Y.; Liu, G.R. The generalized differential quadrature rule for fourth-order differential equations. Int. J. Numer. Meth. Eng. 2001, 50, 1907–1929. [Google Scholar] [CrossRef]
- Wu, T.Y.; Liu, G.R. Application of the generalized differential quadrature rule to sixth-order differential equations. Commun. Numer. Methods Eng. 2000, 16, 777–784. [Google Scholar] [CrossRef]
- Liu, G.R.; Wu, T.Y. Differential quadrature solutions of eighth-order boundary-value differential equations. J. Comput. Appl. Math. 2002, 145, 223–235. [Google Scholar] [CrossRef]
- Geng, F.; Li, X. Variational iteration method for solving tenth-order boundary value problems. J. Math. Sci. 2009, 3, 161–172. [Google Scholar]
- Siddiqi, S.S.; Akram, G.; Zaheer, S. Solution of tenth order boundary value problems using variational iteration technique. Eur. J. Sci. Res. 2009, 30, 326–347. [Google Scholar]
- Siddiqi, S.S.; Akram, G.; Zaheer, S. Solutions of tenth-order boundary value problems using eleventh degree spline. Appl. Math. Comput. 2007, 185, 115–127. [Google Scholar] [CrossRef]
- Siddiqi, S.S.; Twizell, E.H. Spline solutions of linear tenth-order boundary-value problems. Int. J. Comput. Math. 1998, 68, 345–362. [Google Scholar] [CrossRef]
- Twizell, E.H.; Boutayeb, A.; Djidjeli, K. Numerical methods for eighth-, tenth- and twelfth-order eigenvalue problems arising in thermal instability. Adv. Comput. Math. 1994, 2, 407–436. [Google Scholar] [CrossRef]
- Aziz, I.; Amin, R. Numerical solution of a class of delay differential and delay partial differential equations via Haar wavelet. Appl. Math. Model. 2016, 40, 10286–10299. [Google Scholar] [CrossRef]
- Khashan, M.M.; Amin, R.; Syam, M.I. A new algorithm for fractional Riccati type differential equations by using Haar wavelet. Mathematics 2019, 7, 545. [Google Scholar] [CrossRef]
- Amin, R.; Nazir, S.; Magario, I.G. Efficient sustainable algorithm for numerical solution of nonlinear delay Fredholm-Volterra integral equations via Haar wavelet for dense sensor networks in emerging telecommunications. Trans. Emerg. Telecommun. Technol. 2020, 30, 1–12. [Google Scholar] [CrossRef]
- Amin, R.; Nazir, S.; Magario, I.G. A collocation method for numerical solution of nonlinear delay integro-differential equations for wireless sensor network and internet of things. Sensors 2020, 20, 1962. [Google Scholar] [CrossRef]
- Amin, R.; Shah, K.; Asif, M.; Khan, I.; Ullah, F. An efficient algorithm for numerical solution of fractional integro-differential equations via Haar wavelet. J. Comput. Appl. Math. 2021, 381, 113028. [Google Scholar] [CrossRef]
- Akgul, A.; Akgul, E.K.; Baleanu, D.; Inc, M. New numerical method for solving tenth order boundary value problems. Mathematics 2018, 6, 245. [Google Scholar] [CrossRef]
- Siddiqi, S.S.; Iftikhar, M. Numerical solution of higher order boundary value problems. Abstr. Appl. Anal. 2013. [Google Scholar] [CrossRef]
- Lamnii, A.; Mraoui, H.; Sbibih, D.; Tijini, A.; Zidna, A. Spline solution of some linear boundary value problems. Appl. Math. E-Notes 2008, 8, 171–178. [Google Scholar]
- Farajeyan, K.; Maleki, N.R. Numerical solution of tenthorder boundary value problems in off step points. J. Basic Appl. Sci. Res. 2012, 2, 6235–6244. [Google Scholar]
- Oderinu, R.A. On the numerical solution of tenth and twelfth order boundary value problems using weighted residual method (WRM). Gen. Math. Notes 2014, 24, 17–24. [Google Scholar]
| J | ||||||
|---|---|---|---|---|---|---|
| 1 | 4 | 4.278027 × 10 | — | 8.066078 | 2.141112 | 4.034141 |
| 2 | 8 | 2.088323 | 1.0346 | 4.119775 | 7.664428 | 1.493509 |
| 3 | 16 | 7.091844 | 1.5581 | 1.384787 | 2.101769 | 4.025401 |
| 4 | 32 | 2.053994 | 1.7877 | 3.954403 | 5.378154 | 1.020752 |
| 5 | 64 | 5.519342 | 1.8959 | 1.052874 | 1.352397 | 2.559945 |
| 6 | 128 | 1.430068 | 1.9484 | 2.714107 | 3.385924 | 6.404723 |
| 7 | 256 | 3.639369 | 1.9743 | 6.888379 | 8.467896 | 1.601455 |
| 8 | 512 | 9.179565 | 1.9872 | 1.735279 | 2.117167 | 4.003981 |
| 9 | 1024 | 2.305088 | 1.9936 | 4.363176 | 5.293039 | 1.001098 |
| J | ||||||
|---|---|---|---|---|---|---|
| 1 | 4 | 4.706274 | — | 8.873970 | 2.355446 | 4.438198 |
| 2 | 8 | 2.297826 | 1.0343 | 4.534035 | 8.433378 | 1.643689 |
| 3 | 16 | 7.803594 | 1.5581 | 1.524194 | 2.312742 | 4.430672 |
| 4 | 32 | 2.260144 | 1.7877 | 4.352585 | 5.918073 | 1.123549 |
| 5 | 64 | 6.073282 | 1.8959 | 1.158917 | 1.488169 | 2.817759 |
| 6 | 128 | 1.573592 | 1.9484 | 2.987166 | 3.725854 | 7.049689 |
| 7 | 256 | 4.004617 | 1.9743 | 7.580603 | 9.318032 | 1.762671 |
| 8 | 512 | 1.010082 | 1.9872 | 1.907363 | 2.329721 | 4.406964 |
| 9 | 1024 | 2.536421 | 1.9936 | 4.818368 | 5.824435 | 1.103406 |
| Present Method | Homotopy Analysis Technique [26] | Geng and Li [15] | Siddiqi et al. [16] | Siddiqi and Akram [18] |
|---|---|---|---|---|
| 1.103 | 6.42 | 9.08 | 1.97 | 3.28 |
| Siddiqi and Twizell [17] 2.07 | Lamnii et al. [27] 1.86 | Farajeyan and Maleki [28] 1.75 |
| J | ||||||
|---|---|---|---|---|---|---|
| 1 | 4 | 4.282469 | — | 8.078904 | 2.143337 | 4.040556 |
| 2 | 8 | 2.095035 | 1.0315 | 4.142597 | 7.689499 | 1.501796 |
| 3 | 16 | 7.117493 | 1.5575 | 1.394107 | 2.109728 | 4.052754 |
| 4 | 32 | 2.061499 | 1.7877 | 3.982148 | 5.399189 | 1.028014 |
| 5 | 64 | 5.539396 | 1.8959 | 1.060374 | 1.357729 | 2.578336 |
| 6 | 128 | 1.435236 | 1.9484 | 2.735589 | 3.399299 | 6.450834 |
| 7 | 256 | 3.652479 | 1.9743 | 6.938894 | 8.501362 | 1.611802 |
| 8 | 512 | 9.212566 | 1.9872 | 1.743050 | 2.125535 | 4.026448 |
| 9 | 1024 | 2.313387 | 1.9936 | 4.440892 | 5.313967 | 1.017885 |
| J | ||||||
|---|---|---|---|---|---|---|
| 1 | 4 | 4.248266 | — | 8.018031 | 2.126221 | 4.010113 |
| 2 | 8 | 2.082389 | 1.0286 | 4.126033 | 7.643466 | 1.495812 |
| 3 | 16 | 7.077143 | 1.5570 | 1.389999 | 2.098077 | 4.041318 |
| 4 | 32 | 2.049893 | 1.7876 | 3.967937 | 5.369992 | 1.024574 |
| 5 | 64 | 5.508127 | 1.8959 | 1.054712 | 1.350423 | 2.570024 |
| 6 | 128 | 1.427125 | 1.9485 | 2.753353 | 3.381028 | 6.443958 |
| 7 | 256 | 3.631761 | 1.9744 | 7.105427 | 8.454810 | 1.645147 |
| J | ||||||
|---|---|---|---|---|---|---|
| 1 | 4 | 1.376894 | — | 2.335245 | 6.890091 | 1.167937 |
| 2 | 8 | 6.439662 | 1.0964 | 1.004889 | 2.349402 | 3.640074 |
| 3 | 16 | 2.199108 | 1.5501 | 3.235740 | 6.401687 | 9.364978 |
| 4 | 32 | 6.424091 | 1.7754 | 9.156188 | 1.636086 | 2.346317 |
| 5 | 64 | 1.734789 | 1.8887 | 2.434131 | 4.110933 | 5.866305 |
| 6 | 128 | 4.493562 | 1.9488 | 6.274573 | 1.026979 | 1.466562 |
| 7 | 256 | 1.129015 | 1.9928 | 1.592808 | 2.546429 | 3.666386 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amin, R.; Shah, K.; Khan, I.; Asif, M.; Salimi, M.; Ahmadian, A. Efficient Numerical Scheme for the Solution of Tenth Order Boundary Value Problems by the Haar Wavelet Method. Mathematics 2020, 8, 1874. https://doi.org/10.3390/math8111874
Amin R, Shah K, Khan I, Asif M, Salimi M, Ahmadian A. Efficient Numerical Scheme for the Solution of Tenth Order Boundary Value Problems by the Haar Wavelet Method. Mathematics. 2020; 8(11):1874. https://doi.org/10.3390/math8111874
Chicago/Turabian StyleAmin, Rohul, Kamal Shah, Imran Khan, Muhammad Asif, Mehdi Salimi, and Ali Ahmadian. 2020. "Efficient Numerical Scheme for the Solution of Tenth Order Boundary Value Problems by the Haar Wavelet Method" Mathematics 8, no. 11: 1874. https://doi.org/10.3390/math8111874
APA StyleAmin, R., Shah, K., Khan, I., Asif, M., Salimi, M., & Ahmadian, A. (2020). Efficient Numerical Scheme for the Solution of Tenth Order Boundary Value Problems by the Haar Wavelet Method. Mathematics, 8(11), 1874. https://doi.org/10.3390/math8111874









