Abstract
Let G be a graph with no isolated vertex and a function. If f satisfies that every vertex in the set is adjacent to at least one vertex in the set , and if the subgraph induced by the set has no isolated vertex, then we say that f is a total Roman dominating function on G. The minimum weight among all total Roman dominating functions f on G is the total Roman domination number of G. In this article we study this parameter for the rooted product graphs. Specifically, we obtain closed formulas and tight bounds for the total Roman domination number of rooted product graphs in terms of domination invariants of the factor graphs involved in this product.
1. Introduction
The study of domination-related parameters in product graphs is one of the most important and attractive areas of domination theory in graphs. Among the principal attractions of this area, Vizing’s Conjecture [1] is possibly the most popular open problem for the theory of domination in graphs. This conjecture asserts that the domination number of the Cartesian product of two graphs is at least equal to the product of their domination numbers. In recent years, several kinds of domination-related parameters in product graphs have been studied. For instance, we cite the following works: total domination [2] and total Roman domination [3] in direct product graphs; Roman domination in lexicographic product graphs [4]; domination-related parameters like classical domination, Roman domination, independence domination, connected domination, convex domination and super domination in rooted product graphs [5]; and Roman domination in Cartesian and strong product graphs [6]. In this article, we study a very well-known variant of domination (total Roman domination) for the case of rooted product graphs.
We consider as a simple graph. Given a vertex v of a graph G, will denote the open neighborhood of v in G, i.e., the set of vertices of G adjacent to v. The closed neighborhood, denoted by , equals . Given a set , its open neighborhood is the set , and its closed neighborhood is the set . As usual, the graph obtained from G by removing all the vertices in will be denoted by . If , for some vertex v, then we simple write .
The degree of a vertex v in G is . A vertex is universal if . A leaf of G is a vertex v with degree . A support of G is a vertex adjacent to a leaf and a strong leaf is a leaf at distance two from another leaf. The sets of leaves, support vertices and strong leaves are denoted by , and , respectively.
A set is a dominating set of G if . The domination number of G, denoted by , is the minimum cardinality among all dominating sets of G. A dominating set with cardinality is called a -set. A similar agreement will be assumed when referring to optimal functions (or sets) associated to another parameter. Moreover, a dominating set S of G is a total dominating set (TDS) of G if , i.e., every vertex of G is adjacent to at least one vertex in S. The minimum cardinality among all TDSs of G is the total domination number of G, and is denoted . For more information about these two parameters, see the following books [7,8,9].
Let G be a graph and a function. Observe that f induces three sets , and such that for . Hence, we will write instead so as to refer to f. If D is a subset of vertices of G, then . Hence, we define the weight of f as .
One of the domination variants which has been intensively studied in the last two decades concerns the so-called Roman domination, which was formally presented in [10] and was motivated in part by the defensive strategy of the Roman Empire decreed by Constantine (see [11,12]). Several applications of Roman domination were shown in [13]. The Roman domination in graphs is a useful tool for modeling optimization problems such as facility location problems (building a new hospital, fire station, or restaurant), planning of defense strategies, surveillance related problems, communication networks, etc. Given a graph G, a function is called a Roman dominating function (RDF) if every vertex in is adjacent to a vertex in . The minimum weight among all RDFs on G is the Roman domination number, and is denoted . Several well-known results relate the Roman domination number with the (total) domination number. For instance, (see [14]) and (see [10]). Further results on Roman domination can be found for example in [13,14,15,16].
The concept of total Roman domination in graphs was formally presented in [17], although it was previously introduced in [18] in a more general form. A total Roman dominating function (TRDF) on a graph G without isolated vertices is an RDF such that is a total dominating set of G. The minimum weight among all TRDFs on G is the total Roman domination number, and is denoted . As expected, (total) domination number, Roman domination number and total Roman domination number are related. The following relationships are proofs of this: (see [17]) and (see [19]). Further results on total Roman domination can be found for example, in [19,20,21,22].
The complexity of the total Roman domination number was studied in [18]. The authors showed that the decision problem related to total Roman domination number is NP-hard even when restricted to bipartite graphs and chordal graphs. This suggests finding closed formulas or giving tight bounds on this domination invariant for special families of graphs. These studies are attractive, for instance, for the product graphs, and as previously shown, several studies in this regard have been carried out.
Our goal with this paper is to make some contributions to the study of total Roman domination number for the case of rooted product graphs. In that regard, in the next section we state the intervals in which this parameter can be found in a rooted product graph. Furthermore, we obtain closed formulas and tight bounds for this parameter.
2. Main Results in Rooted Product Graphs
Given a graph G of order n and a graph H with root , the rooted product graph is defined as the graph obtained from G and H by taking one copy of G and n copies of H and identifying the -vertex of G with vertex v in the -copy of H for every [23]. Figure 1 shows an example of rooted product graph , where is the path graph of order four.

Figure 1.
The rooted product graph .
For every , will denote the copy of H in containing x. The restriction of any -function f to will be denoted by and the restriction to will be denoted by .
Now, we state some tools, which will be very useful throughout the article.
Lemma 1.
Let H be a graph without isolated vertices and. Then
Moreover, ifthen the following conditions hold.
- (i)
- for every-function f.
- (ii)
- There exists a-functionsatisfying.
- (iii)
- There exists a-functionsatisfying.
Proof.
Let f be a -function and . Let h be a function on H defined as follows: , and whenever . Observe that h is a TRDF on H. Hence, , as desired.
From now on, we assume that . Suppose that there exists such that . In such a case, we deduce that the function , defined by , and whenever , is a TRDF on H. This implies that , which is a contradiction. Thus, . Finally, if , then the function , defined by , and whenever , is a -function. Analogously, the function , defined by , and whenever , is a -function as well, which completes the proof. □
Following is a theorem bounding , for a particular vertex . Before stating this, we shall need the next remark.
Remark 1.
Let H be a graph without isolated vertices. If, then there exists a-function f such that.
Proof.
Let be a -function such that is minimum among all -functions. Let . Since , we have that . If , then . As , it follows that the function , defined by , and whenever is a -function such that , which is a contradiction. Hence, , which implies that . So, and without loss of generality, we can assume that as . Therefore, the proof is complete. □
Theorem 1.
Let H be a graph without isolated vertices. If, then
Proof.
By Remark 1 there exists a -function f such that . Hence, f restricted to is a TRDF on . Thus, . Moreover, let g be a -function and let u be the support vertex associated to v in H. Since , we have that the function , defined by and whenever , is a TRDF on H. So, , which completes the proof. □
Next, we expose a result for the Roman domination number of rooted product graphs given by Kuziak et al. in [5], which will be used later in the paper.
Theorem 2.
[5] Let G be a graph of order . Then for any graph H with root v and at least two vertices,
We continue this section with a useful lemma.
Lemma 2.
Letbe a-function. The following two statements hold for any vertex.
- (i)
- .
- (ii)
- If, then.
Proof.
Let . Observe that every vertex in has a neighbour in and every vertex in has a neighbour in . First, we proceed to prove (i). Suppose that and let . Let g be a function on defined as follows: and whenever . It is easy to see that g is a TRDF on . Hence, , which is a contradiction as . Thus, , which completes the proof of (i).
Now, we proceed to prove (ii). Assume that . Suppose that . Let and we define the function as follows: and whenever . Notice that is a TRDF on such that , which is a contradiction. Thus, . Finally, suppose there exists . In such a case, we define the function as follows: and whenever . As in the case above, is a TRDF on such that , which is again a contradiction. Thus, , and the proof is complete. □
From Lemma 2-(i) we deduce that any -function f generates three sets , , of as follows.
Proposition 1.
Let f be a-function. If, thenand
Proof.
By Lemma 2-(ii), if , then and for every . This implies that , and also that f restricted to is a TRDF on of weight Since , it follows that and . Finally, by Lemma 1 we obtain that , which completes the proof. □
Theorem 3.
Let G and H be two graphs without isolated vertices. Ifand, then the following statements hold.
- (i)
- (ii)
- If, then
Proof.
First, we proceed to prove (i). Notice that, from any -function, we can construct a TRDF on of weight . Thus , which completes the proof of (i).
Finally, we proceed to prove (ii). Assume that . Observe that, from any -function and any -function we can construct a TRDF on of weight at most , which completes the proof. □
The next theorem, which we can consider as one of the main results of this paper, states the intervals in which the total Roman domination number of a rooted product graph can be found.
Theorem 4.
Let G and H be two graphs without isolated vertices. Ifand, then one of the following conditions holds.
- (i)
- .
- (ii)
- .
- (iii)
- .
Proof.
Let be a -function and we consider the sets , and defined above. Now, we analyze the following cases.
- Case 1. . By definition we deduce that for every and, as a consequence, . By Theorem 3, condition (i) follows.
- Case 2. and . By definition we deduce that for every and, as a consequence, . We only need to prove that . Let h be a -function and . From f, u and h, we define a function g on as follows. For every vertex , the restriction of g to is induced from , and we set . Notice that g is a TRDF on of weight , concluding that . Hence, condition (ii) follows.
- Case 3. and . By definition we obtain that
From Lemma 2-(ii) we have that every vertex satisfies that . As , there exists a vertex . This implies that dominates , and as a consequence, is a dominating set of G. Hence, . Combining the inequalities above, we deduce that
On the other hand, by Proposition 1 we have that and that . Moreover, Theorem 3-(ii) leads to . Thus, condition (iii) follows.
- Case 4. and . By Proposition 1 and Theorem 3-(ii) it follows that .
Finally, let us define a set as follows. If then we choose one vertex and set . For the other vertices, if then we set . Now, we will prove that S is a total dominating set of G. By definition of S, if , then x is adjacent to some vertex . Now, by Lemma 2-(ii), if then there exists a vertex , which implies that . If , then it must have a neighbor , otherwise is a TRDF on and so , which is a contradiction. Hence, , which implies that , as required. Therefore, S is a total dominating set of G of cardinality at most and, as a consequence,
So, condition (iii) follows, which completes the proof. □
The bounds given in the theorem above are tight. To see this, we consider the following examples where is the graph shown in Figure 2 (we always assume that G is a graph of order n without isolated vertices). Recall that is the path graph of order n.
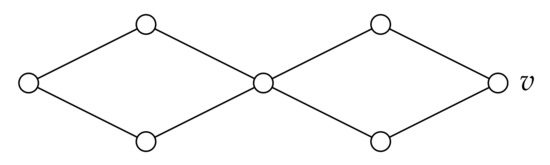
Figure 2.
The graph .
- If , then .
- If , then .
- If and , then .
- .
- Theorem 5 gives some conditions to achieve the equality . In this case we can take H, for example, as the graph given in Figure 3.
 Figure 3. Graphs H, and with different labelings (vertices with no drawn label have label zero) to show that (a), (b) and (c).
Figure 3. Graphs H, and with different labelings (vertices with no drawn label have label zero) to show that (a), (b) and (c).
Next, we analyse some particular cases. First, we consider the case in which .
Theorem 5.
Letbe a graph of order n without isolated vertices. If H is a graph such thatandfor some, then
Proof.
Let be a -function. By Lemma 1-(i), we may assume (without loss of generality) that . From , we define the following function g on H. If then , and . Moreover, let be a -function and we consider the function h on H defined by if , if , and .
Let D be a -set. From D, g and h, we define the following function on . For every , the restriction of to is induced from h. Moreover, if , then the restriction of to is induced from g. By the construction of g and h, it is straightforward to see that is a TRDF on . Thus,
We only need to prove that . Suppose that by some -function f. This implies that , which is a contradiction because (it is easy to see that if and only if ). Therefore, for any -function f. Hence, and by analogy to Cases 3 and 4 in the proof of Theorem 4, we deduce that , which completes the proof. □
Notice that the premises given for the graph H in the previous theorem lead to the existence of a -function f satisfying . Since Lemma 1 does not guarantee the existence of a graph that satisfies such conditions, in Figure 3 we show a graph that does satisfy them.
Theorem 6.
Let G be a graph of order n without isolated vertices and H a graph such thatfor some. Iffor every-function g, then
Proof.
By Theorem 3-(ii) and the equality we have that . To conclude the proof, we only need to prove that . Let be a -function. Let , where and . Since for every -function g, we deduce that (otherwise, if there exists a vertex , then we can obtain a -function g with by giving label 1 to some neighbor of x in , which is a contradiction as ). Moreover, if , then (otherwise, would be a -function with , which contradicts the fact that for every -function g). Now, we define a function on G.
- (i)
- If , then we set .
- (ii)
- If , then we set .
- (iii)
- If , then we choose one vertex not previously labeled (if it exists) and set .
- (iv)
- We set for any other vertex not previously labeled.
We claim that is a TRDF on G. First, we observe that if , then . Hence, there exists a vertex . Since , it follows that , as desired.
We only need to prove that is a total dominating set of G. By definition of h, it is clear to see that every vertex in is adjacent to some vertex in . Now, let . If , then is a TRDF on of weight , which is a contradiction. So, and as f is a TRDF on , there exists a vertex such that . Hence, , as desired.
Thus, we conclude that is a total dominating set of G. So, h is a TRDF on G, and as a consequence, . Therefore,
Therefore, the proof is complete. □
Now, we consider the cases in which either v is a support vertex of H or . Before doing this, we shall need the following useful lemma.
Lemma 3.
Let f be a-function. If there exists a vertexsuch that, then.
Proof.
Let h be a function on defined from f as follows. For every , the restriction of h to is induced from . Notice that h is a TRDF on , which implies that , as desired. □
Theorem 7.
Let G and H be two graphs without isolated vertices and. Ifor, then
Furthermore, if, then.
Proof.
Let be a -function. By Theorem 3-(i) we have that . If , then we are done. In such a sense, we suppose that . This implies that there exists a vertex such that , i.e., . If , then and also is a TRDF on , which implies that , which is a contradiction. Hence, . So, by Lemma 2-(ii) we deduce that , which implies that . Moreover, since , by Lemma 3 we have that .
Now, we proceed to prove that . If , then . This implies that for every vertex . So, by Lemma 2-(ii) we have that , which implies that . Moreover, if , then by hypothesis we have that . So, by contrapositive of Proposition 1. Hence, as above, we deduce that . Therefore, in both cases, the lower bound obtained leads to the equality , as desired.
Furthermore, if , then by Theorem 2 we have that . Since , the result above leads to . □
Observe that if H is a nontrivial star graph or a double star graph (in both cases we consider the root ), then for any graph G of order n without isolated vertices we have that and , respectively. These two particular cases belong to families of graphs that are analyzed in Theorems 9 and 12.
We continue with a result in which or .
Theorem 8.
Let G and H be two graphs without isolated vertices and. Iforand, then
Proof.
Let be a -function and let us consider the function h on H defined as follows. If then , if then , and . Next, we define a function f on from h. For every , the restriction of f to is induced from h. By the construction of h, it is straightforward to see that f is a TRDF on . Thus,
Therefore, Theorem 7 if or Proposition 1 and Lemma 2 if , complete the proof. □
In Figure 4 we show a graph H which satisfies the premises of Theorem 8. In this case, and for any graph G of order n with no isolated vertex, we obtain that .
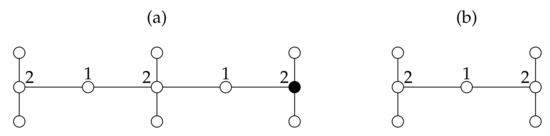
Figure 4.
Graphs H and with different labellings (vertices with no drawn label have label zero) to show that (a) and (b).
Next, we proceed to discuss a particular case when .
Theorem 9.
Let G and H be two graphs without isolated vertices withand. Iforfor every-function g, then
Proof.
Theorem 7 leads to . Hence, we only need to prove that . Let be a -function such that is maximum among all -functions. Now, we analyse the following two cases.
- Case 1. . Let for any . As x and y are adjacent support vertices, it follows that . Hence, is a TRDF on , and as a consequence, . Thus, , as desired.
- Case 2. for every -function g. Since , we have that for every vertex . So, Lemma 2 leads to . If there exists such that , then for every . Thus, the function , defined by , and otherwise, is a -function and satisfies that , which is a contradiction. Therefore, for every . Moreover, if , then there exists a -function g such that , which is a contradiction. Hence, , and as a consequence, , as desired. □
Now, we analyse other cases for the vertex .
Theorem 10.
Let G be a graph without isolated vertices of order n. Let H be a graph such thatfor some. Iffor every-function g, then
Proof.
Let be a -function. With the assumptions given, Proposition 1 leads to . Now, we analyse two cases. First, if , then by analogy to Case 1 in the proof of Theorem 4 we have that .
Second, we suppose that and let . If , then is a TRDF on , which implies that , which is a contradiction. Hence, . If there exists a vertex such that , then is a TRDF on of weight , which is a contradiction. Hence, . Note that the function g, defined by for some vertex and for every , is a TRDF on of weight . So g is a -function and satisfies that , which is again a contradiction. Hence, , and we are done. □
Next, we consider the case in which the root v is a strong leaf vertex of H.
Theorem 11.
Let G and H be two graphs without isolated vertices and. If, then
Proof.
By Theorem 1 we have that . In such a sense, we consider the following two cases.
- Case 1. . Let be a -function. By Proposition 1 we have that . Suppose that and let . If , then is a TRDF on , which implies that , which is a contradiction. Hence, . Let . Since , it follows that . Hence , and so is a TRDF on of weight , which is a contradiction. Therefore, , and so
- Case 2. . First, we prove that . Let u be the support vertex associated to v, i.e., , and let g be any -function. Note that as . So, from g and any -function, we can define a TRDF on of weight at most . Hence, , as desired.
To conclude the proof, we only need to prove that . Let be a -function. Since , we have that for every vertex . Hence, Lemma 2-(ii) leads to . Now, we analyze two subcases.
Subcase 2.1. . In this subcase, by analogy to Case 1 in the proof of Theorem 4, we have that . Therefore, it follows that , which implies that , i.e., (see [10]). Thus, , as desired.
Subcase 2.2. . Let and . As , it follows that . If , then is a TRDF on of weight , which is a contradiction. Hence, , and as a consequence, (otherwise, if , then, as above, is a TRDF on of weight , which is a contradiction). Therefore, and dominates . This implies that f restricted to is an RDF on G, and so, . Now, we suppose that there exists a vertex such that . Let . Since , it follows that . This implies that the function is a -function because . Now, we observe that the function g, defined by and whenever , is a TRDF on . Hence, , which is a contradiction. Therefore, every vertex satisfies that . Thus, as and , we obtain that , which completes the proof. □
The following theorem states the total Roman domination number of the rooted product graph , when the root v is a universal vertex of H.
Theorem 12.
Let G be a graph without isolated vertices of order n. If H is a graph with a universal vertex, then
Proof.
Let f be a function defined as follows: if and whenever . It is clear to see that f is a TRDF on . Hence, . Since , we have that either or . Thus, Theorem 7 leads to the desired result. □
Any corona graph can be expressed as a rooted product graph , where and . Therefore, the following result follows as an immediate consequence of the theorem above.
Theorem 13.
Let G be a graph of order n without isolated vertices andany graph. Then
3. Conclusions and Open Problems
In this paper, we have studied the total Roman domination number of rooted product graphs . In particular, we were able to give the intervals to which belongs. In addition, we have obtained closed formulas for this parameter when certain conditions are imposed on the factor graphs G and H involved in this product.
Next, we propose some open problems, which we consider to be interesting.
- Characterize the graphs G and H (and the root v) that satisfy the following equalities.
- -
- .
- -
- .
- -
- .
- -
- .
- -
- .
- Characterize the graphs G and H (and the root v) such that .
- Given a graph G of order n and a family of n graphs with a set of root vertices , respectively, the generalized rooted product graph is defined as the graph obtained from G and , by identifying the vertex of G with the root vertex of for every . We propose to study the total Roman domination number of generalized rooted product graphs.
Author Contributions
All authors contributed equally to this work. Investigation, A.C.M., S.C.G., A.C.G. and F.A.H.M.; writing—review and editing, A.C.M., S.C.G., A.C.G. and F.A.H.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We would like to thank the anonymous referees for their comments and suggestions towards improving our manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vizing, V.G. The Cartesian product of graphs. Vyčisl. Sist. 1963, 9, 30–43. [Google Scholar]
- Dorbec, P.; Gravier, S.; Klavžar, S.; Špacapan, S. Some results on total domination in direct product graphs. Discuss. Math. Graph Theory 2006, 26, 103–112. [Google Scholar] [CrossRef][Green Version]
- Cabrera Martínez, A.; Kuziak, D.; Peterin, I.; Yero, I.G. Dominating the Direct Product of Two Graphs through Total Roman Strategies. Mathematics 2020, 8, 1438. [Google Scholar] [CrossRef]
- Šumenjak, T.K.; Pavlič, P.; Tepeh, A. On the Roman domination in the lexicographic product of graphs. Discret. Appl. Math. 2012, 160, 2030–2036. [Google Scholar] [CrossRef]
- Kuziak, D.; Lemanska, M.; Yero, I.G. Domination-Related parameters in rooted product graphs. Bull. Malays. Math. Sci. Soc. 2019, 39, 199–217. [Google Scholar] [CrossRef]
- Yero, I.G.; Rodríguez-Velázquez, J.A. Roman domination in cartesian product graphs and strong product graphs. Appl. Anal. Discr. Math. 2013, 7, 262–274. [Google Scholar]
- Haynes, T.W.; Hedetniemi, S.T.; Slater, P.J. Domination in Graphs: Advanced Topics; Chapman and Hall/CRC Pure and Applied Mathematics Series; Marcel Dekker, Inc.: New York, NY, USA, 1998. [Google Scholar]
- Haynes, T.W.; Hedetniemi, S.T.; Slater, P.J. Fundamentals of Domination in Graphs; Chapman and Hall/CRC Pure and Applied Mathematics Series; Marcel Dekker, Inc.: New York, NY, USA, 1998. [Google Scholar]
- Henning, M.; Yeo, A. Total Domination in Graphs, Springer Monographs in Mathematics; Springer: New York, NY, USA, 2013. [Google Scholar]
- Cockayne, E.J.; Dreyer, P.A., Jr.; Hedetniemi, S.M.; Hedetniemi, S.T. Roman domination in graphs. Discrete Math. 2004, 278, 11–22. [Google Scholar] [CrossRef]
- Revelle, C.S.; Rosing, K.E. Defendens imperium romanum: A classical problem in military strategy. Am. Math. Mon. 2000, 107, 585–594. [Google Scholar] [CrossRef]
- Stewart, I. Defend the Roman Empire! Sci. Am. 1999, 28, 136–139. [Google Scholar] [CrossRef]
- Chambers, E.W.; Kinnersley, B.; Prince, N.; West, D.B. Extremal problems for Roman domination. SIAM J. Discrete Math. 2009, 23, 1575–1586. [Google Scholar] [CrossRef]
- Chellali, M.; Haynes, T.W.; Hedetniemi, S.T. Roman and Total Domination. Quaest. Math. 2015, 38, 749–757. [Google Scholar] [CrossRef]
- Favaron, O.; Karami, H.; Khoeilar, R.; Sheikholeslami, S.M. On the Roman domination number of a graph. Discret. Math. 2009, 309, 3447–3451. [Google Scholar] [CrossRef]
- Rao, M.; Talon, A. The 2-domination and Roman domination numbers of grid graphs. Discret. Math. Theor. Comput. Sci. 2019, 21, 9. [Google Scholar]
- Abdollahzadeh Ahangar, H.; Henning, M.A.; Samodivkin, V.; Yero, I.G. Total Roman domination in graphs. Appl. Anal. Discret. Math. 2016, 10, 501–517. [Google Scholar] [CrossRef]
- Liu, C.-H.; Chang, G.J. Roman domination on strongly chordal graphs. J. Comb. Optim. 2013, 26, 608–619. [Google Scholar] [CrossRef]
- Cabrera Martínez, A.; Cabrera García, S.; Carrión García, A. Further results on the total Roman domination number of graphs. Mathematics 2020, 8, 349. [Google Scholar] [CrossRef]
- Amjadi, J.; Sheikholeslami, S.M.; Soroudi, M. On the total Roman domination in trees. Discuss. Math. Graph Theory 2019, 39, 519–532. [Google Scholar] [CrossRef]
- Cabrera Martínez, A.; Rodríguez-Velázquez, J.A. Closed formulas for the total Roman domination number of lexicographic product graphs. 2020. Manuscript. [Google Scholar]
- Campanelli, N.; Kuziak, D. Total Roman domination in the lexicographic product of graphs. Discret. Appl. Math. 2019, 263, 88–95. [Google Scholar] [CrossRef]
- Godsil, C.D.; McKay, B.D. A new graph product and its spectrum. Bull. Aust. Math. Soc. 1978, 18, 21–28. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).