Abstract
In the digital age, the role of information technology and computer processes is growing. This requires refining the development of software by optimizing the communications between program components and seeking effective interaction in the implementation of processes. Complex module structures are usually developed, which require high compatibility between components and their proper functioning. The purpose of this article is to propose an approach for investigation of a set of connected computer processes executed on a macro level by using deterministic modelling. A formal technological procedure for conducting a deterministic investigation of the interaction between processes was developed. It allows for the transition from the object-original to an adequate mathematical model with its program realization. The core of the constructed procedure is the phases “mathematical formalization”, “mathematical description”, and “program realization”. The goal was to present an application of the procedure to investigate all possible realizations of connected processes, presented as nodes in a directed graph scheme of algorithms by determining the reachability. The program language APL2 was used as a tool for program description of the defined mathematical models, which were realized in the software system TryAPL2 for research automation. A preliminary mathematical formalization of interacting processes was made by presenting an example graph scheme and its transformation into an ordered structure. On the basis of the mathematical description, we developed two program models for automation of the transition to an ordered graph scheme and determination of all possible paths in it for activation of sequences of processes. The proposed models are part of a generalized environment for program investigation of the computer processing organization.
1. Introduction
It is known that computer processing is a mathematical (functional) transformation of a set of input data (D) into output results (R), summarized by a global function f: D→R. In this sense, computer data processing is a form of concrete realization of a complex mathematical function in an environment of hardware and software tools and means in different versions—traditional, parallel [1], real-time [2], learning scheduling [3], etc. Regardless of the computer environment realization, the organization of computer processes covers two hierarchical levels related to its program management at a high (macro) level and its machine implementation at low (micro) level. The micro-level presents the organization of elementary operations for machine calculations generated by firmware (concrete sequence of microinstructions from the activated microprogram). An approach for organization of low-level model investigation is discussed in [4], proposing a unified framework for the joint conduct of the classification process and the modelling. The goal is to ensure the effectiveness of model investigation on a micro level (firmware). The firmware analysis permits the determination of correct functionality of processing at the micro level, with the generalized approach being presented in [5], which is directed to identification of firmware modules, its extraction, disassembling, modification, and reprogramming. This approach is particularly relevant in the development of embedded devices for the purpose of the Internet of things (IoT). In this respect, a software technological framework for the continuous execution of binary firmware together with independent testing is proposed in [6], which is not affected by the peripherals (without ignoring them) and processes the input–output data for the firmware on the basis of automatically generated models. An evaluation of this framework is made and good assessment for the effectiveness is obtained. Another actual example of the importance of the investigation of the processing in micro-level (firmware) is the proposed in the method of [7] for security analysis of a memory, which stores micro algorithms for 3G modem control. Testing the method for different versions of the modem has shown good results.
The macro level (as opposite of micro level) in general is a sequence of separate (generally independent) procedures for data stream processing, which are realized by activation of separate algorithms integrated in the frame of symbolic general algorithm, conditionally marked as AG. In both cases, the organization of the processes at each of the two levels is subject to probabilistic parameters and conditions in the computer environment [8]. Formally, from the point of view of formalization, any investigation of processes at the macro level and communications between them is subject to a defined procedure. In this aspect, a generalized scheme of a procedure for analysis and optimization of complex-structured objects during the modelling and algorithms is proposed in [9]. Numerical methods and algorithms for finding the optimal solution are used. Analysis of the features of the management process is carried out to increase the efficiency of using these components of the analyzed system.
The research of information processing in the processes of program module design at a high (macro) level has different applications due to the modern architectures, including distributed computer systems. One of the directions is the formalization of the relationship between the two levels—micro and macro—with the article in [10] proposing an abstract basis for field calculations, which contain several syntactic constructions, and the relationship with the micro level (actions of individual devices and their interaction when performing collective processing) is analyzed. The goal is to facilitate the design of a user interface (API—Application Program Interface) in complex software systems.
Another direction for the application of the analysis of high-level programming processes is the automatic correction of programs, which must ensure reliable implementation of the applied actions through the use of modern tools. In this sense, the study in [11] discusses the problem of locating faults in program codes at the macro level and interactions between programs, including their impact on automatic correction systems. The goal is to analyze the activated procedures, the possibilities for error correction, and the reliable investigation of system performance parameters through analysis at the macro level. The practical use of formal techniques for analysis is discussed in [12], where a pragmatic application of formal method technologies is a purpose of the research. This formal analysis was focused on the controller components of the software implementation for error management and the logic was analyzed by using a technique of model investigation. This helped to analyze the possible situation of a risk and for verification of risk control measures relating to the software components.
The relationships between different software entities can be used for evaluation of the quality of a program, which determines the importance of the tools for computation of their metrics. In this respect, a classification (made by a systematic literature review in software engineering) of the different kinds of coupling relations, together with the metrics to measure them, is presented in [13]. The result of this research is a proposal of suitable tools for software engineering for extracting program metrics united in four groups—structural, dynamic, semantic, and logical. As an addition, this research retrieves tools that extract the metrics belonging to each coupling group. The problem of object monitoring, including software components, is an important one in the processes of relationship evaluation. The communication time between software objects is a critical parameter and is subject to minimization. A set of procedures for effective communication between territorially connected systems is proposed in [14] and an analysis of the effectiveness is made.
One of the applied approaches for investigation of computer processes is mathematical modelling by using formalized descriptions of the investigated object through abstract language (mathematical formal system) or through mathematical relations describing functional behavior. This approach is applicable in different areas—for example, an application in the field of complex electronic systems for various purpose is discussed in [15]. The article proposes a hierarchical method of mathematical and computer modelling of interval-stochastic thermal processes that take into account various physical phenomena in in the considered systems. Different mathematical means can be used for their creation (algebraic, differential, and integral calculus; theoretical systems; etc.). The research presented in [15] is realized by systems of stochastic, unsteady, and nonlinear partial differential equations, and their computer simulation is made by using supercomputer. Another approach is applied in [16], when “a new rumour spreading model in social networks” is proposed that was realized by using discrete mathematical modelling. An optimal control strategy to fight against the spread of the rumor is recommended in the article. Five different perspectives on mathematical modelling are reviewed in [17] because, according to the authors, “there is not a single agreed-on-definition of what mathematical modelling is or how it should be done”. The classification discussed in the article is directed to “realistic modelling, educational modelling, models and modelling perspective, socio-critical modelling, and epistemological modelling”. Finally, a statistical approach for mathematical modelling or solving the problem with minimization of the search time for the necessary information is proposed in [18].
Computer modelling is mathematical modelling in which computer tools are used to create the model and to conduct experiments with it. Mine principles of computer modelling are discussed in [19] and a formal technological scheme for investigation by modelling is proposed. The basic phases of this process are determined: (a) preliminary functional decomposition of the modelled object and a conceptual model formulation, (b) mathematical formalization of structure and relations based on the conceptual model, (c) defining of the functional algorithm, (d) design of the mathematical model, (e) realization of a program model in suitable software system, and (f) organization of experiments with results analysis and conclusions. In addition, a hierarchical procedure for evaluation based on obtained results from modelling with three levels (empirical, analytical, and evaluation) is proposed.
Different language tools (universal and specialized) can be used to create a program model, with thousands of languages having been developed for various applications. In this regard, article [20] proposes an overview of the set of modelling languages, specifically in Industry 4.0. On the basis of this extensive review, the researchers updated the systematic mapping study of modelling languages and modelling techniques. A total of 408 relevant publications were identified on the basis of the study of 3344 candidate publications. One of the article’s goals was to determine the modelling languages in system engineering and knowledge representation. The program language, which can be used for mathematical formal description and model preparation in the area of computing, is APL2 (Array Program Language), which allows for the creation of additional user workspaces with models formed as a separate function or as sequentially called functions. Each defined function (enclosed by symbol ∇) can be executed independently or when calling from another function. Each function has its own definition (header part), which contains its name and its possible arguments (variables), through which data can be exchanged with other functions. There are rules for defining (explicitly or implicitly) local and global variables. Three basic components are connected with the loading—definition of virtual vector (array) for storing items, definition of a relative storage address where the array could be stored, and definition of the virtual distance between subsequent elements [21].
The investigation of processes in data processing is essential for improving the overall organization, both at the macro level and at the low (micro) level. This would allow pre-ensuring the effectiveness of the software and firmware, which is important to minimize the time parameters of execution and communications. The task of ensuring efficient processing is relevant in today’s digital age due to the increased amount of processed data and communications between programs, including cloud computing, Internet of things, and big data analytics. In this respect, the article presents an approach for automation of the process interactions on a macro level on the basis of mathematical description and software realization. A technological scheme of the formal procedure for investigation is proposed. Three phases form the core of this procedure on the basis of which the investigation was conducted—mathematical formalization, mathematical description, and program realization. As a result of their implementation, we performed the following: (1) defining an initial conceptual model by using graph theory, (2) producing a deterministic mathematical formalization for analytical description of the proposed graph scheme and its transformation into an ordered structure, and (3) program realization of the developed mathematical models in the software system TryAPL2 by using the program language APL2. The aim was to propose a formal mathematical approach and tool for evaluation of characteristics of macro-level computer processing. The proposed models are part of a generalized environment for program investigation of the computer processing organization at macro and micro levels.
2. Materials and Methods
The main essence of a model study is to replace the original object ΩO with another object-model ΩM through which the properties or behavior in certain situations of the original are studied by experimenting with the model [22].
The object-original ΩO can be an arbitrary system or process that may not actually exist. Nevertheless, its system properties can be described by finite sets, such as SO—system parameters characterizing the internal state of the real system, its structure, and functioning; YO—quantitative characteristics of system parameters, describing mainly resultant behavioral features that are important in the interaction with other systems; and XO—external actions influencing the behavior of system parameters. In this way, a formal representation of the object-original as a class of finite discrete sets ΩO = {SO, YO, XO} can be made. The peculiarity is that the main sets in the formed class may be too large, which will require the selection of adequate subsets. In this reason, when studying a system, a subset {yo} ∊ YO is usually chosen to be analyzed under the influence of external factors {xo} ∊ XO, and each individual characteristic yoi (i = 1 ÷ K, where K is the total number of elements in the subset of individual characteristics) depends on some subset {so} ∊ SO of system parameters (usually the influence of the other parameters is neglected). This subset of selected system parameters determines the spice of the system, and the characteristics are the data describing its organization and behavior according to the goal of the research. In this sense, each object of study should be considered as a complex of two related parts—static (independent of time) and dynamic (system parameters and characteristics that depend on time).
The object-model ΩM must reproduce with sufficient accuracy the real object under study, being in accordance with the selected goal of the concrete research. The model should comply with the selected conditions for the analysis of the behavior of the original system or process. This determines the need to coordinate the subsets of the class ΩO with appropriate components used for realization of ΩM. In the concrete case, this coordination requires correct transformation of the selected subset in mathematically presented subsets for the model realization. As a result, the following components can be defined: {sm} ∊ SM—parameters of the object-model, {ym} ∊ YM—characteristics of the object-model, and {xm} ∊ XM—external factors of influence for the object-model. The replacement ΩO→ΩM is admissible if the determined model characteristics {ym} ∊ YM sufficiently reflect the respective quantitative characteristics {yo} ∊ YO, defined in the modelling process. In this sense, the modelling is a replacement of a real functional dependence {yo} = ΦO[{so}, {xo}, To], describing the behavior of the original object in time, with a corresponding equivalent dependence {ym} = ΦM[{sm}, {xm}, Tm], where usually the model time Tm is related to the real time To by scaling. The main requirement in modelling is to find such an analytical dependence that describes with sufficient accuracy the behavior of the original in terms of the objectives of the study.
A summary of the information above is made by the formalized scheme of model investigation presented in Figure 1.
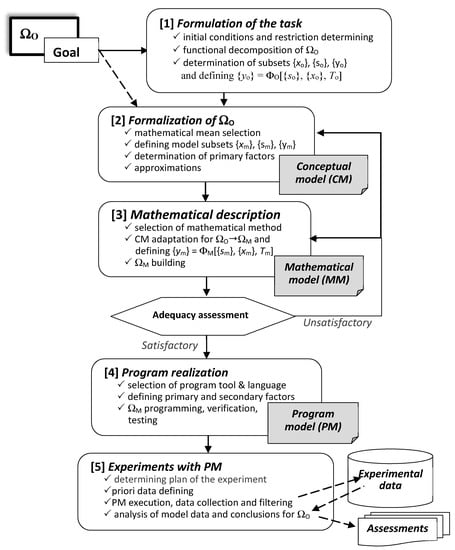
Figure 1.
Generalized formal procedure for organization of model investigation.
The model investigation is related to three basic phases, realizing the successive components of a computer model (conceptual model (CM), mathematical model (MM), program model (PM)) on the basis of mathematical formalization, mathematical description, and program realization of the designed mathematical model in a program source using a suitable software environment. The phase of mathematical formalization is an initial stage, allowing us to make an adequate transition from the formulated task to achieve the goal in the investigation of the object-original (ΩO) to the actual development of a mathematical model (ΩM). The phase of mathematical description is the basic stage in the investigation because it must build a sufficiently adequate model of the real object (process or system). This requires an appropriate mathematical environment to be selected (formal, deterministic, probabilistic, empirical, etc.). The third phase of program realization transforms the mathematical description into a suitable software environment and creates the final result of the modelling, which will be subjected to experiments. A large number of program languages (universal and specialized) can be used to develop the program model, but the choice must take into account the type of mathematical description (ΩM) and the nature of the model investigation—deterministic, probabilistic, simulation, statistical, or heterogeneous. A good opportunity is provided by the APL2 language and the TryAPL2 operating environment, which is relevant to the deterministic model investigation of computer process organization presented in the following sections.
APL is a high-level program language that is suitable for analytical descriptions and for working with vectors and matrices. There is a possibility for parallel execution of several operations, which surpasses in these respects many of the modern universal algorithmic languages. Characteristic features are the specific alphabet, the maintenance of various data structures, the ability to work in dialog and program mode, a wide range of mathematical operations, and the possibility for laconic expression of complex transformations through composite operators. The order of operations in the expressions is from right to left. It is suitable for expressing the subordination between the different parts of the algorithm, allowing parallel execution of several operations. In a sequence of included functions, a variable, determined by a value in an external function, remains with the same value in the internal functions if it is not re-defined in them. The last specified value is actual. The functions use labels interpreted as local, and it is possible to apply recursive calculation.
The language version of APL2, implemented in the TryAPL2 operating environment, allows the creation of additional user workspaces from models formed as a separate function or as sequentially called functions. The function (enclosed by the symbol ∇) can be performed independently or when it is called by another function. Each function has its own definition (header part), which contains its name and its possible arguments (variables), through which data can be exchanged with other functions. There are rules for defining (explicitly or implicitly) local and global variables. A function is executed by calling its name, which can be done on its own in an expression or in the body of another function. Execution requires that the arguments (if any) be real variables or constants. In the environment, system variables and functions with reserved name names (starting with the symbol □) are maintained and used. The organization of work is performed through system commands that serve to manage the work session, store and edit copies of workspaces, and transfer data from one working space to another (file exchange management).
An illustration of the applicability of APL2 in deterministic model investigation is made in Figure 2, which is a program description of a formalized functionality of an idealized computing environment supporting traditional processing in a processor (intensity f1 and number of tasks N1) and k calls to external memory (intensity f2 and number of tasks N2). It is accepted that N = N1 + N2 = const; the task falls in the processor to (k + 1); and the bandwidth p coincides with the intensity for falling f0 into a passive state, which allows for the presentation of the following simple analytical dependences:

Figure 2.
A simple example for analytical model investigation by using APL2—(a) program code, (b) model execution, (c) results interpretation.
To solve the mathematical model, it is necessary to determine the intensity f1(N1), which is based on the following: (a) there is zero intensity for the CPU (Central Processor Unit) load when it does not process a task (N1 = 0), for example, due to an infinitely long time for servicing the tasks in state S2; (b) the service is performed only in one processor and if number of tasks is N1 ≥ 1, the analytical dependence f1(N1 ≥ 1) = const will be saturated and limited to maximum bandwidth (k + 1)/t; (c) to solve the situation 0 < N1 < 1, it is necessary to know f2(N2), which is usually a nonlinear dependence.
The following analytical description can be provided as a result:
The program model is defined as a separate function WORKLOAD for calculating f1(N1) and p, requiring the presentation of of the controllable model parameters (T—fixed processing time for processor, K—number of external memory access). To construct a functional dependence, successive experiments are performed according to a randomized factor plan, for example at values N = 5; T = 10; K = 2, 3, 4, 5. The results of execution of the function at a fixed value for K = 4 and different values (0; 0.2; 0.4; 0.6; 0.8; 1; 2; 4) of the argument N1 are graphically presented in Figure 2c.
3. Mathematical Formalization and Model Construction
In the general case, computer processing can be determined as a set of sequentially executed procedures over data streams. The procedures are implemented on the base of a corresponding algorithm Aj, which can be considered as components of a global functional algorithm AG. Theoretically, the complete algorithm AG can be described logically if the individual algorithms Aj and the conditions for their activation at a specific input information flow are known. This undermines its formal description by a directed graph representing a graph scheme of algorithm (GSA), in which the matrix of connections {cij} describes the existence of an information connection Ai→Aj between two individual algorithms. In an investigation of the computer processes organization, it is possible to apply both approaches—stochastic (if the relationships are defined as probabilities) or deterministic (the matrix of relationships is Boolean).
3.1. Mathematical Formalization
A preliminary formalization of the investigated object ΩO is made on the basis of the requirement of the phase [2] of the general technological procedure presented in Figure 1. In the current case, the object ΩO of model investigation is a global algorithm AG of exemplary computer processing presented as a GSA (Figure 3a). It is a generalized structure of communicating program modules, each of which can be activated by another, depending on the development of the generalized process. In practice, the interactions between different modules and the possible activations of a concrete sequence of them is a probabilistic process, but the task determined for the research allows a deterministic approach to be applied. In this case, the goal is to determine the number and lengths of all possible paths representing the possible realizations of information processing.
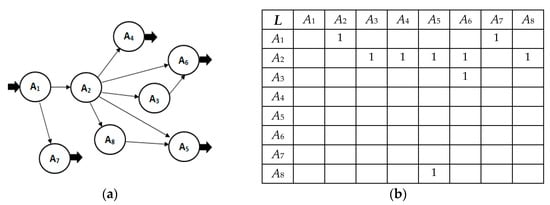
Figure 3.
Mathematical formalization of the investigated object ΩO (a) graph scheme of algorithm (GSA), (b) matrix of connections (conceptual model).
In the deterministic approach, a Boolean matrix of connections L = {lij} is applied, where lij = 1 (if there is a connection) and lij = 0 (in the absence of a connection), as seen in Figure 3b.
The formalization will allow for the construction of a conceptual model (CM) for the model investigation organization, which will formulate the basis for the next mathematical descriptions and the creation of a mathematical model (MM—phase [3] in the Figure 1) on the basis of a graph structure G(A,L).
The object of the investigation is a set of independent algorithms (processes), presented as a final discrete set A = {A1,…,An}, which are executed in different sequences with possible input/output interactions. This allows for the determination of a tree of relations between sequential processes in GSA on the basis of the consequence matrix L—lij:Ai→Aj (i,j ∊ {1,2,…,n}), as shown in Figure 3b. Usually, the investigation is connected with determining the reachability of a given final task (algorithm) from one or several initial tasks. For this purpose, a system of algebraic equations is compiled, describing the presence of edges aij between individual algorithms Ai and Aj:
Solving this system of equations allows for the construction of all directed paths, as well as for the determination of the equivalent paths that lead to the same event in computer processing. The dependence presented above allows to define a graph model (GSA) of the complete processing algorithm G(αA), which will be transformed in an ordered GSA (OGSA) with nodes numbered on the basis of the following condition:
IF ∃ pass(Ai→Aj} ⇒ Ai < Aj; FOR ∀ Ai, Aj (i ≠ j).
The ordering forms layers of information-independent nodes so that (a) the nodes of the first layer have no predecessors and the nodes of the last layer have no successors, and (b) the nodes included in a common layer have no connecting arcs. The rules for the OGSA formation are as follows:
- All initial nodes (without predecessors) are numbered first and included in layer (1).
- A node is numbered and included in the current layer if all its predecessors are already numbered (included in previous determined layers).
- Nodes to be numbered are successors of already numbered nodes.
3.2. Deterministic Mathematical Description
The phase 3 of the procedure shown in Figure 1 recommends making a transition from the formal model to a mathematical description. On the basis of the chosen approach for deterministic mathematical description, we can make the construction of the model ΩM on the basis of the following steps.
Step 1. Formation of a transposed matrix LT by transforming the initial L, where the columns are vectors VAj, describing the successors of each node, fulfilling the condition LT[i,j] ≠ 0 (j = 1 ÷ n), shown in Figure 4a. This can be realized by constructions LT←L & N←ρL [1;] and LT←⌀⊃L.

Figure 4.
Transposed matrix LT (a) and determining the matrix of layers AL (b).
Step 2. Calculation of the elements of a new vector V1 = ∑ VAj (j = 1 ÷ n; n = 8) from LT:
V1[j] = LT[j,1] + LT[j,2] + ... + LT[j,n]; for j = 1 ÷ n.
If V1[j] = 0 ⇒ Aj ∊ Layer(1), node Aj must be included in the layer (1), which is marked in the matrix of layers AL. In this case, it is only V1[1] = 0, which determines that the algorithm A1 must be included in Layer(1) (see column AL1 in Figure 4b).
Step 3. Calculation of elements of the next vector V2 on the basis of vector V1 and row j of LT:
Elements V2[j] = 0 determine algorithms included in the Layer(2)—in our case, algorithms A2 and A7, column AL2 in Figure 4b.
Steps 4, 5, etc. Similar calculation of the next vectors Vq (q = 3, 4, ...) to determine algorithms included in the Layer(q):
For each layer “q”, an added element is marked by AL[j,q] = 1. The steps are performed to obtain a vector with only zero elements ∀Vq[j] = 0 (j= 1 ÷ n).
The result of applying all steps of the procedure is the distribution of the analyzed processes into separate ranks and defining the complete set of final processes (algorithms).
3.3. Possibility for Application of Formalization in Process Dispatching
An example of the proposed approach can be made by extension of the mathematical formalization in the direction of dispatching independent processes in a closed system S for which the processes of the set A do not require additional resources beyond it. It is accepted that the time vector T = {t1, …, tn} for realization of processes Ai (i = 1 ÷ n) is known. If the system of resources has a heterogeneous nature, it is possible for a given process Ai to occupy several devices in succession, staying in each for different times {ti1, ti2, …, tik}. Then, ti = ∑tik and the vector T can be modified in a matrix T* = {tij} with n = |A| rows and m = |S| columns. This will allow for the formalization of the process of creating a dispatching plan for the analyzed processes in the system, which can be presented as a ordered discrete structure p = <S, A, G, T, F>, where S is a set of system resources with |S| = m, A is a final discrete partially ordered set of processes in the environment S with |A| = n, G(A,L) is a directed graph for describing GSA of the processes from set A, T = {t1, …, tn} presents the vector of execution times for all processes in the environment, and F determines a formal criteria (strategy) for process dispatching.
This formalization allows for the presentation of the dispatching as a function D(t) = {d1(t), …, dm(t)} defined in the interval (0, τ) and accepting integer values from the set of indices (1, 2, …, n) of A. Thus, the elements di(t) = j (1 ≤ i ≤ m; 1 ≤ j ≤ n) of the function D will represent the occupation of a resource Si in the moment t during the execution of process Aj.
When defining a static parallel plan, it is usually assumed that the GSA does not take into account the logical connections, but only the information dependence on data transmission. This is mainly related to the requirement to minimize the total execution time of the set A in a fixed structure S. In this case, the nodes of GSA determine times for realization of the processes. An example for application of this approach for formalization is presented in the next section.
4. Program Realization and Experimental Results
4.1. Program Model Realization
This subsection refers to the implementation of phase 4 of the technological procedure from Section 2, with the goal of developing program modules for the formation of a program model based on the performed mathematical description from Section 3. Two program functions were realized by using language APL2 in the operation environment TryAPL2, which are presented below. The model investigation was performed by their execution.
Function GSA—program realization of the deterministic mathematical model ΩM is presented in Figure 5a. The results of the model execution are shown in Figure 5b and include ✓ the Boolean matrix L, describing the initial graph-scheme of the algorithm; ✓ the transposed matrix LT; and ✓ the calculated vectors V[q] (q = 1,2, ...) and the matrix of the layers AL (Table 1), which corresponds to the ordered graph-scheme OGSA (Figure 6). Each of the four defined layers includes procedures that can be performed independently of each other.
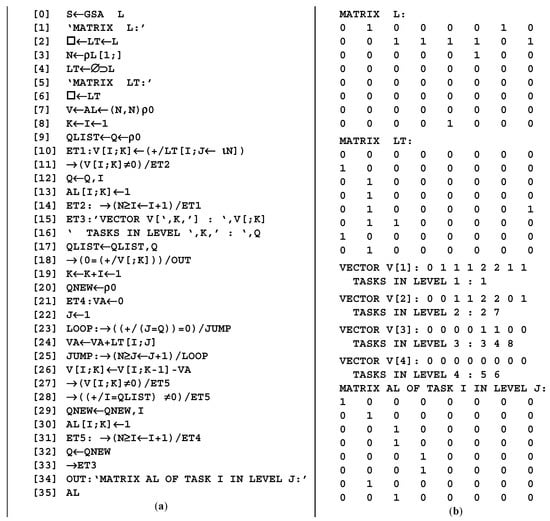
Figure 5.
Program function GSA—(a) program code of the model ΩM; (b) execution.

Table 1.
Separate layers in the matrix AL with the dependence equations for nodes.
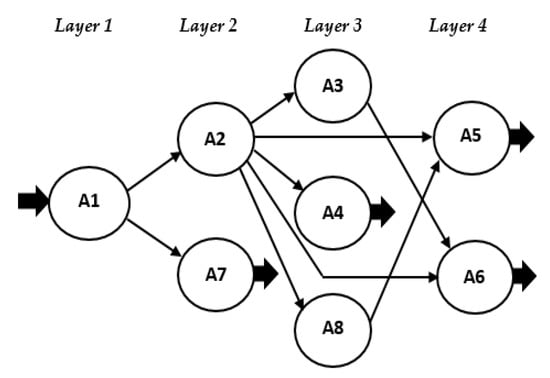
Figure 6.
Ordered graph-scheme OGSA.
When considering the case for dispatching independent processes 1 (Section 3.3), we made an assumption for system resources homogeneity S = {S1, ..., Sm} and equal labor intensity of the processes forming the set A = {A1, …, An}. This means that the mathematical expectation of the times for the realization of the processes were the same, i.e., E[t(Ai)] ≡ E[ti] = const, which allowed for the application of a binary graph to represent the GSA and a fixed time vector T = {ti = τ/i = 1 ÷ n}. In this case, the formed ordered scheme from Figure 6 determined six paths, as the maximum length was 4, which allowed for the definition of a maximum parallel plan with a minimum execution time for this set of eight processes (minimum number of layers). In this case, Table 1 can be transformed into an optimal parallel plan, requiring three independent processor nodes for realization, as shown in Table 2 (u is the total time for parallel form realization).

Table 2.
Determined parallel plan based on the result of GSA execution.
Function PATHS—evaluation of the reachability and determining all paths in the investigated algorithmic structure with argument matrix L (the program code and experimental results are shown in Figure 7).
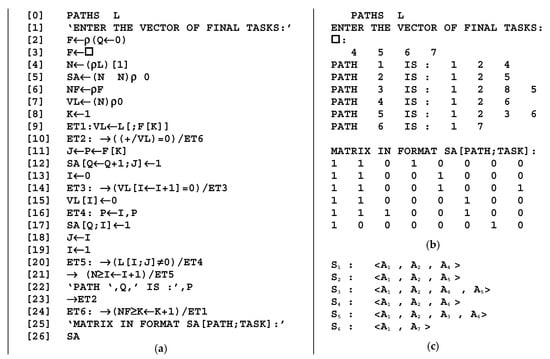
Figure 7.
Program function PATHS—(a) program code; (b) execution; (c) defined paths.
Let us consider a deterministic homogeneous model for the set A = {A1, …, A14} = {1,…, 14}, whose GSA is described below by the existing arcs <Ai→Aj> ≡ “i-j”:
| 1-2, 1-3, 1-4; | 4-7, 4-10; | 8-11; |
| 2-5, 2-8; | 6-9; | 9-11; |
| 3-2, 3-6, 3-12; | 7-9, 7-12; | 10-9; 10-13; 10-14. |
After applying the ranking procedure, we determined five layers (height of the parallel form) for the ordered GSA, which are
G* = {{1}1; {3, 4}2; {2, 6, 7, 10}3; {5, 8, 9, 12, 13, 14}4; {11}5 }
The maximum width of the parallel form was 6, determined by the maximum power of a layer in G * (layer ‘4′). These parameters determined the optimal environment for the realization of the parallel form with |S| = m = 6 processors with a minimum total time for full implementation u = 5τ. The possible paths in ordered graph scheme G * (possible realizations of information processing) are summarized in Table 3.

Table 3.
Defined layers and paths in the ordered GSA.
4.2. Experimental Result Discussion and Examples for Application
The set of final tasks {A4, A5, A6, A7} in GSA and OGSA allowed us to determine all paths from the node A1 presenting possible realization of computer processing. The function performed success transformations to obtain an equation describing the dependence of a final node on one or more initial nodes. For example, two paths, PATH 2 and PATH 3, were determined from the node A1 to the final node A5 (see Figure 7b, which is based on the transformation).
determining the paths <A1→A2→A5> and <A1→A2→A8→A5>. These two paths were equivalent—{S2, S3}, and another couple of equivalent paths were {S4, S5}. The presence of equivalent paths is marked by more than one “1” in the columns for the final tasks in the matrix SA (Figure 7b).
A5 = a25·A2 + a85·A8 = a25·[a12·A1] + a85·[a28·A2] = a25·a12·A1 + a85·a28·a12·A1
The investigated case of dispatching on the basis of the formalization discussed in the end of Section 3.3 considered homogeneous computer systems with times t(Ai) ≡ ti = const for separate resources Sj ∊ S. Communication times for exchange between processors can be ignored if there is shared memory. The weights of the nodes can be transferred along the outgoing arcs of the GSA, which allows for the use of the procedure for finding a path in a graph and defining the optimal plan to relate to the maximum path and the corresponding critical time in the study of parallel planning (maximum path length in GSA; Figure 7c). Weight or binary graphs can be applied, depending on the specific environment for the realization of the parallel processes.
An example graphical description of a dispatch plan for basic parameters S = {1,2,3}, A = {1,2,3,4,5,6,7}, and T = {4,2,2,5,4, 8.5} is given in Figure 8. The applied criteria for dispatching were “general minimization of the time for completion of the set of tasks”. The figure shows the ordered graph scheme formed by the procedure GSA (Figure 5). Four layers were defined, forming information-independent subsets of nodes with corresponding weights ti (i = 1 ÷ 7): {1(4); 2(2)}, {3(2)}, {4(5); 5(4), 6(8)}, {7(5)}, where the notation is i(ti). The maximum processor environment for the implementation of the plan was determined by the maximum power of the layer in the ordered GSA (in this case, three processors).
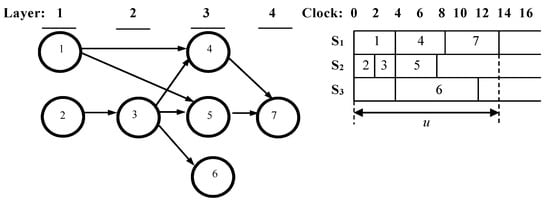
Figure 8.
Graph interpretation of the dispatching plan based on results obtained from GGSA and PATH execution.
The experimental results from the case of 14 processes (Table 3) permitted the analysis of possible realizations of the parallel form at different dispatching strategies, summarized in Table 4.

Table 4.
Possible generated parallel plans for realization of the graph scheme G*.
D1(t)—plan for realization of G* with priority of maximum paths;
D2(t)—modification of the plan D1(t) by taking empty clocks and being reduced while maintaining the priority of the maximum path;
D3(t)—plan for realization of G* with limit m = 3 and sequential traversal of the layers;
D4(t)—plan for realization of G* with limit m = 3 and selection of a process from a given layer according to its maximum repeatability in different paths;
D5(t)—plan for realization of G* with limit m = 2.
A summary of the results of the analysis is presented in Table 5, and a graphical interpretation is given in Figure 9. In addition to the two parameters m = |S| and u presented above, two new characteristics η and χ were defined on the basis of the following expressions:

Table 5.
Evaluation of the parameters of determined dispatching plans.
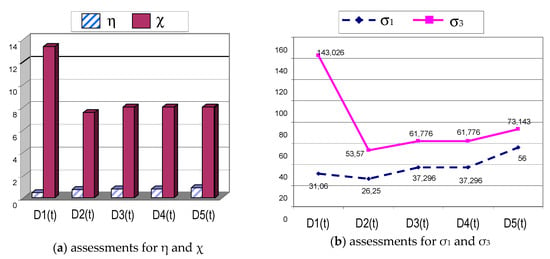
Figure 9.
Graphical interpretation of assessments.
- Relative average resource load factor: ;
- Relative weight of inefficient work (stay): ;
where τ is a separate measure from the plan, which can be effective (τ’) or passive (τ”). The application of different dispatching strategies allowed for the determination of the best result for different plans (marked positions in the table), but in a global aspect as an optimal plan can be determined D2(t).
5. Conclusions
This article discusses problems related to the mathematical formalization of objects, processes, and structures in the computer field for the purposes of research, analysis, and evaluation of parameters of information services. The proposed approach allows automation of the evaluation of certain characteristics of computer processing, presented as a sequence of relatively independent processes. To solve the set goals, we proposed a formalized technological procedure for mathematical model investigation, which had a sufficiently wide field of application, both in studying the implementation of complex software environments and in dispatching various independent processes (homogeneous and heterogeneous). In particular, the basis of the carried out investigation included two main parts—developing an approach for transforming a graph-formalized scheme of structure of algorithms (processes) and automation of the determination of possible sequences of executed processes (all paths in the ordered graph scheme). This allowed for the analysis of selected characteristics of execution and of the dispatching of a set of processes in computer structure—for example, time parameters such as minimum and maximum execution time, and consecutive calls of procedures (algorithms). The choice of the program language was made due to its possibility for parallel calculations and direct work with two-dimensional structures as variables. Program modules for the TryAPL2 operating environment were developed, allowing for the organization of experiments for investigation of developed formal mathematical models. Program experiments were performed, and some experimental results were presented and discussed. The applicability of the designed program tools was extended by additional examples for investigation of dispatching in a computer environment for execution of a sequence of processes. Characteristics for evaluation of the efficiency of the dispatching were defined and used for calculation and comparison of assessments to select the best plan in each of the evaluated dispatch strategies.
The research presented in this article is mainly related to homogeneous processes developing in a homogeneous environment. This can be continued in further research by analyzing processes in micro and macro levels, including in heterogeneous computer spaces, parallel structures, and distributed computer environments. For example, when studying process dispatching in a heterogeneous structure, it will be necessary to determine the time parameters t(Ai) for execution, which in the formalization can be presented by scalar weights of the graph nodes. In this respect, the further research will be directed to an extension of the model investigation to application of a probabilistic approach, which is typical for computer processes. This will be well supported by the capabilities of the software environment TryAPL2 for presentation and executions of stochastic processes.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Bhimani, J.; Ningfang, M.; Leeser, M.; Yang, Z. New performance modeling methods for parallel data processing applications. ACM Trans. Model. Comput. Simul. 2019, 29, 15. [Google Scholar] [CrossRef]
- Habeeb, R.A.A.; Nasaruddin, F.; Gani, A.; Hashem, I.A.T.; Ahmed, E.; Imrah, M. Real-time big data processing for anomaly detection: A survey. Int. J. Inf. Manag. 2019, 45, 289–307. [Google Scholar] [CrossRef]
- Mao, H.; Schwarzkopf, M.; Venkatakrishnan, S.B.; Meng, Z.; Alizadeh, M. Learning scheduling algorithms for data processing clusters. In Proceedings of the ACM Special Interest Group on Data Communication (SIFCOMM’19), Beijing, China, 19–23 August 2019; pp. 270–288. [Google Scholar] [CrossRef]
- Lagrange, A.; Fauvel, M.; May, S.; Dobigeon, N. Hierarchical Bayesian image analysis: From low-level modeling to robust supervised learning. Pattern Recognit. 2019, 85, 26–36. [Google Scholar] [CrossRef]
- TechPats. Firmware Analysis. Available online: https://www.techpats.com/technology/systems-and-software/firmware-analysis/ (accessed on 5 October 2020).
- Feng, B.; Mera, A.; Lu, L. P2IM: Scalable and Hardware-independent Firmware Testing via Automatic Peripheral Interface Modeling. In Proceedings of the 29th USENIX Security Symposium, Boston, MA, USA, 12–14 August 2020; Available online: https://www.usenix.org/system/files/sec20spring_feng_prepub_0.pdf (accessed on 5 October 2020).
- Zhukoskyy, V.; Zhukovska, N.; Vlasyuk, A.; Safonyk, A. Method of forensic analysis for compromising carrier-lock algorithm on 3G modem firmware. In Proceedings of the 2019 IEEE 2nd Ukraine Conference on Electrical and Computer Engineering (UKRCON), Lviv, Ukraine, 2–6 July 2019; pp. 1179–1182. Available online: https://ieeexplore.ieee.org/abstract/document/8879941/authors#authors (accessed on 5 October 2020). [CrossRef]
- Baron, M. Probability and Statistics for Computer Scientists, 3rd ed.; CPC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2019; pp. 135–170. [Google Scholar]
- Lvovich, Y.E.; Tishukov, B.N.; Preobrazhenskiy, A.P.; Kravets, O.J. Complex-structured objects optimization during modelling on the population algorithms adaptation basis. Int. J. Inf. Technol. Secur. 2019, 11, 41–50. [Google Scholar]
- Audrito, G.; Viroli, M.; Damiani, F.; Pianini, D.; Beal, J. A higher-order calculus of computational fields. ACM Trans. Comput. Logic. 2019, 20, 5. [Google Scholar] [CrossRef]
- Liu, K.; Koyuncu, D.; Bissyandé, T.F.; Kim, D.; Klein, J.; Le Traon, Y. You cannot fix what you cannot find! An investigation of fault localization bias in benchmarking automated program repair systems. In Proceedings of the 2019 12th IEEE Conference on Software Testing, Validation and Verification (ICST), Xi’an, China, 22–27 April 2019; pp. 102–113. Available online: https://ieeexplore.ieee.org/document/8730164 (accessed on 5 October 2020). [CrossRef]
- Harrison, M.D.; Freitas, L.; Drinnan, M.; Campos, J.C.; Masci, P.; Costanzo, M.; Whitaker, M. Formal techniques in the safety analysis of software components of a new dialysis machine. Sci. Comput. Program. 2019, 175, 17–34. [Google Scholar] [CrossRef]
- Fregnan, E.; Baum, T.; Palomba, F.; Bacchelli, A. A survey on software coupling relations and tools. Inf. Soft Technol. 2019, 107, 159–178. [Google Scholar] [CrossRef]
- Goryachko, V.V.; Choporov, O.N.; Preobrazhenskiy, A.P.; Kravets, O.J. The use of intellectualization management decision-making in the interaction of territorially connected systems. Int. J. Inf. Technol. Secur. 2020, 12, 87–97. [Google Scholar]
- Madera, A.G. Hierarchical method for mathematical modeling of stochastic thermal processes in complex electronic systems. Comput. Res. Model. 2019, 11, 613–630. [Google Scholar] [CrossRef]
- El Bhih, A.; Ghazzali, R.; Ben Rhila, S.; Rachik, M.; El Alami Laaroussi, A. A discrete mathematical modeling and optimal control of the rumor propagation in online social network. Discret. Dyn. Nat. Soc. 2020, 2020, 4386476. [Google Scholar] [CrossRef]
- Abassian, A.; Safi, F.; Bush, S.; Bostic, J. Five different perspectives on mathematical modeling in mathematical education. Inv. Math. Learn. 2020, 12, 53–65. [Google Scholar] [CrossRef]
- Atlasov, I.V.; Bolnokin, V.E.; Kravets, O.J.; Mutin, D.I.; Nurutdinov, G.N. Statistical models for minimizing the number of search queries. Int. J. Inf. Tech. Secur. 2020, 12, 3–12. [Google Scholar]
- Romansky, R. A formal approach for modelling and evaluation in the field of computing. Int. Trans. Electr. Electron. Comm. Eng. 2012, 2, 1–7. [Google Scholar]
- Wortmann, A.; Barais, O.; Combemale, B.; Wimmer, M. Modeling languages in Industry 4.0: An extended systematic mapping study. Soft Syst. Model. 2020, 19, 67–94. [Google Scholar] [CrossRef]
- Engel, S. Writing circuit histories. Fast Capital. 2018, 15, 19–30. [Google Scholar] [CrossRef]
- Romansky, R.P. Mathematical Formalization and Investigation by Modeling of Structures and Processes for Information Servicing. Ph.D. Dissertation, Technical University of Sofia, Sofia, Bulgaria, 12 March 2013. (In Bulgarian). [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
