1. Introduction
Let
be real Hilbert spaces,
C and
Q be nonempty closed convex subsets of
and
, respectively. Moudafi [
1] introduced the following split equality problem (SEP), which is formulated as finding
where
and
are two bounded linear operators. When
, the SEP reduces to the split feasibility problem (SFP) which was introduced by Censor and Elfving [
2]. The SEP allows asymmetric and partial relations between the variables
x and
y. It has also received much attention due to the application in many disciplines such as medical image reconstruction, game theory, decomposition methods for PDEs and radiation therapy treatment planning; see [
3,
4,
5,
6].
In [
7], Moudafi introduced and studied the following split equality null point problem (SENP): given two set-valued maximal monotone operators
and
, the SENP is formulated as finding
where
is closed and convex, F is set-valued maximal monotone operators [
8]. We note that if
, this problem reduces to the well-known split common null point problem which was originally introduced by Byrne et al. [
9]. For
, let
and
be two families of set-valued maximal monotone operators. The SECNP is formulated as finding
In [
7], Moudafi proposed the following algorithm for solving SENP and obtained a weak convergence theorem:
We note that in the above algorithm, the step-size depends on the operator (matrix) norms and (or the largest eigenvalues of and , where and are the adjoint operators of A and B, respectively). To implement the alternating algorithm (4) for solving SENP (2), we need to compute and , which is generally not an easy task in practice.
To overcome this difficulty, Eslamian [
10] considered an algorithm for solving SECNP for a finite family of maximal monotone operators which does not require any knowledge of the operator norms. In addition, they presented a strong convergence theorem which is more desirable than weak convergence. The algorithm is as follows:
where
and
, the index set
. In addition, the sequences
,
and
satisfy the following conditions: (i)
and
,
, (ii)
and
. It is proved that the sequence
generated by algorithm (5) converges strongly to a solution
of SECNP (3).
Without loss of generality, let
is a family of set-valued maximal monotone operators. Define an operator
by
,
. Let
denote the adjoint operator of
G, then
G and
have the following matrix form
Then the SENP (2) and SECNP (3) can be reformulated as
and
respectively. In addition, the algorithm (5) can be expressed as:
where
,
,
and
,
. In [
10], it has been proved that the sequence
generated by algorithm (8) converges strongly to a solution
of the SECNP (3), and
(
is the solution set of SECNP (7)). However, as with most algorithms, the convergence rate of the iterative sequence (8) is not taken into account.
Recently, the notion of bounded linear regularity has been used to explore the linear convergence of the split equality problems in [
11]. In the present paper, we introduce the bounded linear regularity property of SECNP to consider the linear convergence of the algorithm (8).
The structure of this paper is as follows. In
Section 2, we mainly propose the definition of bounded linear regularity and introduce some lemmas which are very useful in the proof of the main result. In
Section 3, we propose an iterative algorithm and prove its linear convergence in detail, we also use our result to research the split equality optimization problem. In
Section 4, some numerical experiments are given to test the validity of our results.
2. Preliminaries
Throughout this paper, we will denote by
H a real Hilbert space with inner product
and norm
. We denote the unit open ball and unit closed ball with center at origin by
and
, respectively. Let
S be a subset of
H, we denote the interior and relative interior of
S by
, and
, respectively. For
, the classical metric projection of
w onto
S and the distance of
w from
S, denoted by
and
, respectively, and defined by
Let
U be a mapping of
H into
, the effective domain of
U is denoted by
, i.e.,
. The single-valued operator
, which is called the resolvent of
U for
(
) and the resolvent
is firmly nonexpansive [
12]. It is known that
, for all
, and if
, then
Let be a bounded linear operator. The kernel of G is denoted by and the orthogonal complement of is denoted by . Both and are closed subspaces of H.
Recall that a sequence
in
H is said to converge linearly to its limit
(with rate
if there exist
and a positive integer
N such that
Definition 1 ([
13]).
Let be a family of closed convex subsets of a real Hilbert space H, where I is an arbitrary set and . The family is said to be bounded linearly regular if , there exists a constant such that Lemma 1 ([
14]).
Let be a family of closed convex subsets of a real Hilbert space H, where I is an arbitrary set. If , the family is boundedly linearly regular. As we know,
is closed and convex. Throughout this paper, we use
to denote the solution set of SECNP (7), i.e.,
And assume that the SECNP is consistent, thus, is also a closed, convex and nonempty set.
Definition 2. The SECNP is said to satisfy the bounded linear regularity property if, there existssuch that Lemma 2 ([
15]).
Let be a bounded linear operator on H. Then G is injective and has closed range if and only if G is bounded below(i.e., there exists a constant such that , Lemma 3. Letbe bounded linearly regular and G has closed range. Then the SECNP (7) satisfies the bounded linear regularity property.
Proof. Since
is bounded linearly regular,
, there exists
such that
Since
G restricted to
is injective and has closed range, it follows from Lemma 2 that there exists
This completes the proof. □
Lemma 4 ([
16]).
and with the equality holds. Lemma 5 ([
13]).
Let E and F be closed convex subsets of H. Then is bounded linearly regular provided that at least one of the following conditions holds:- (a)
and F is a polyhedron;
- (b)
and E is finite dimensional;
- (c)
and E is finite codimensional.
3. Main Results
Throughout this section we assume that: (1) are real Hilbert spaces, ; (2) for , , and are three families of set-valued maximal monotone operators, where , , and ; (3) , where are any positive real numbers.
3.1. Split Equality Common Null Point Problem
Lemma 6. Forand,
is a solution of SECNP (7) if and only if, Proof. As we know,
, and
are positive real numbers. If
is a solution of SECNP (7), then
, any
we have
Hence we have
, and so
This implies that (10) is true.
Conversely, if
satisfies (10), then we have
Adding up (12) and (13), one gets
Since
, taking
, we have
and
,
. Let
, according to (14) we have
That is is a solution of SECNP (7). This completes the proof. □
Lemma 7. If, where, thenis a nonexpansive mapping.
Proof. Since
is firmly nonexpansive,
, we have
This completes the proof. □
Corollary 1. The SECNP (7) satisfies the bounded linear regularity property if one of the following conditions holds:
- (a)
andare polyhedrons, and G has closed range;
- (b)
,is finite dimensional;
- (c)
,is finite codimensional;
- (d)
, G has closed range and
is finite dimensional;
- (e)
, G has closed range and is finite codimensional.
Next, we establish the linear convergence property for the iterative algorithm under the assumption of bounded linear regularity property for SECNP.
Theorem 1. Assume that the SECNP (7) satisfies the bounded linear regularity property, letbe a sequence generated bywith, where,,andfor, thenconverges to a solutionof SECNP (7) such thatforand, under one of the following conditions: - (a)
- (b)
Proof. Without loss of generality, we assume that
is not in
,
. We now show that
converges to a solution
of SECNP (7) and (17) holds. From
and Lemma 4, we get
As we know,
, then
. According to condition (a) and Lemma 7,
is nonexpansive. In addition, as
, by Lemma 6, we have
. So we can get
For
, since
is firmly nonexpansive and
, we get
Now, we substitute (19) in (18) so we have
Since SECNP (7) satisfies the bounded linear regularity property and
,
, so there exists
such that
. It follows that
Please note that if (a) or (b) holds, then
Since
,
, so there exists
N such that
for
. And,
Observe that
,
is monotone decreasing for
n, hence
Let
, then
As one of (a) and (b) holds, it follows that
is a Cauchy sequence and converges to a solution
of SECNP (7) satisfying
Moreover, if (a) or (b) is assumed, then
. Let
, then
such that
for
. It follows that
where
. Hence,
converges to
linearly.
This completes the proof. □
3.2. The Application of Split Equality Optimization Problem
The so-called split equality optimization problem (SEOP) is formulated as finding
such that
where
and
are two proper, lower semicontinuous, and convex functionals. Let
be a proper, lower semicontinuous, and convex functional. Then SEOP (20) can be reformulated as finding
such that
The subdifferential of
u at
w is the set
Denote by
. It is know that
is maximal monotone operator, so we can define the resolvent
where
, and
Therefore SEOP (21) is equivalent to the SENP (6), then the following corollary can be obtained from Theorem 1 immediately.
Corollary 2. Assume that the solution of SEOP (21)is nonempty where.
In addition, the statements (a) and (b) are consist with Theorem 1. Let the SEOP (21) satisfies the bounded linear regularity property and be a sequence generated bywith, where, and, thenconverges linearly to a solutionof SEOP (21). 4. Numerical Experiments
Let
,
. Let
and
Then are set-valued maximal monotone operators and
Then are set-valued maximal monotone operators and .
Let
are defined by
respectively. Let
and
be defined by
Then is finite codimensional, the range of G is closed, and the solution set of SECNP is . By Corollary 1 we can get that SECNP satisfies the bounded linear regularity property.
Let
. From the algorithm (16), we have
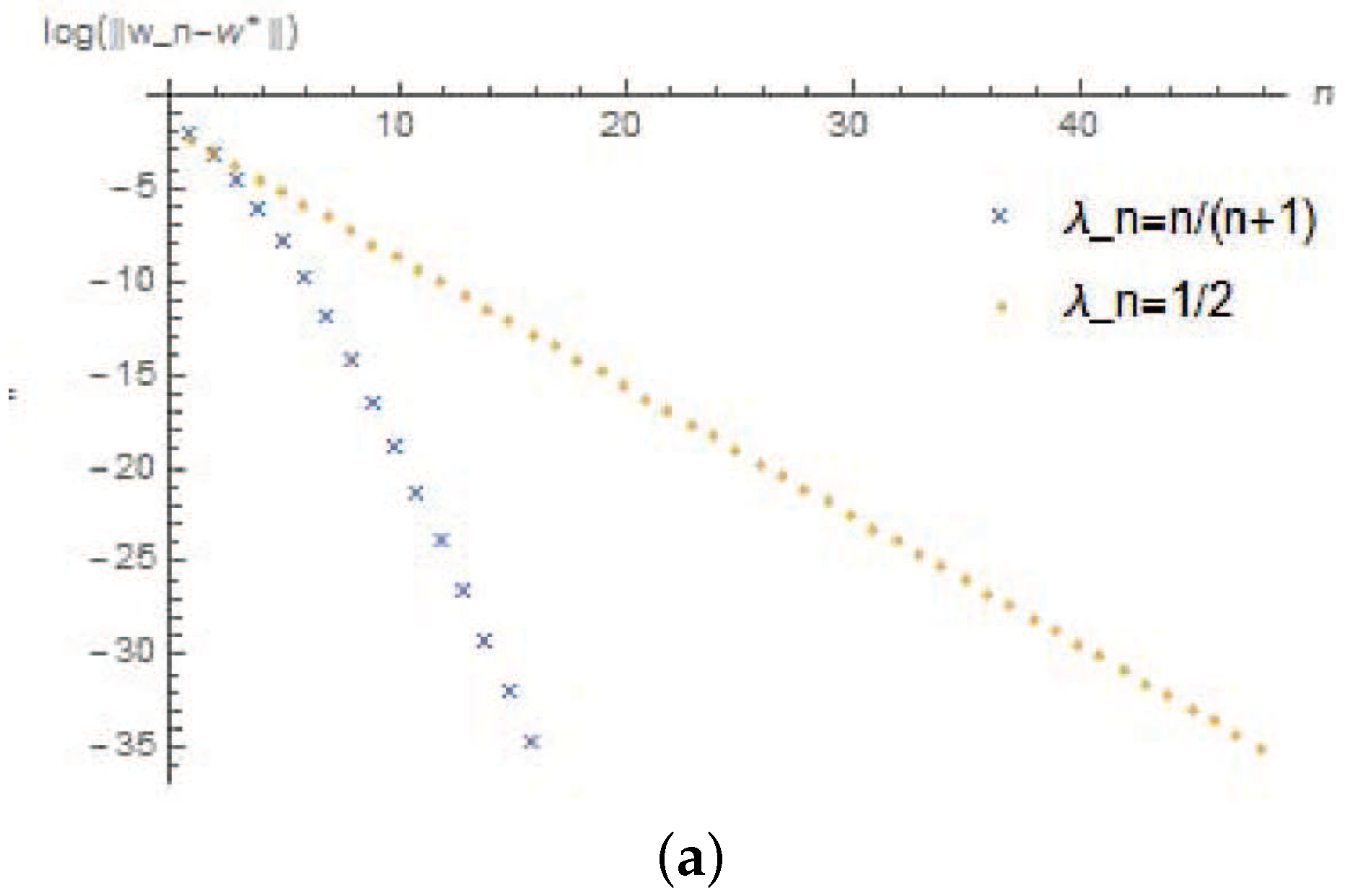
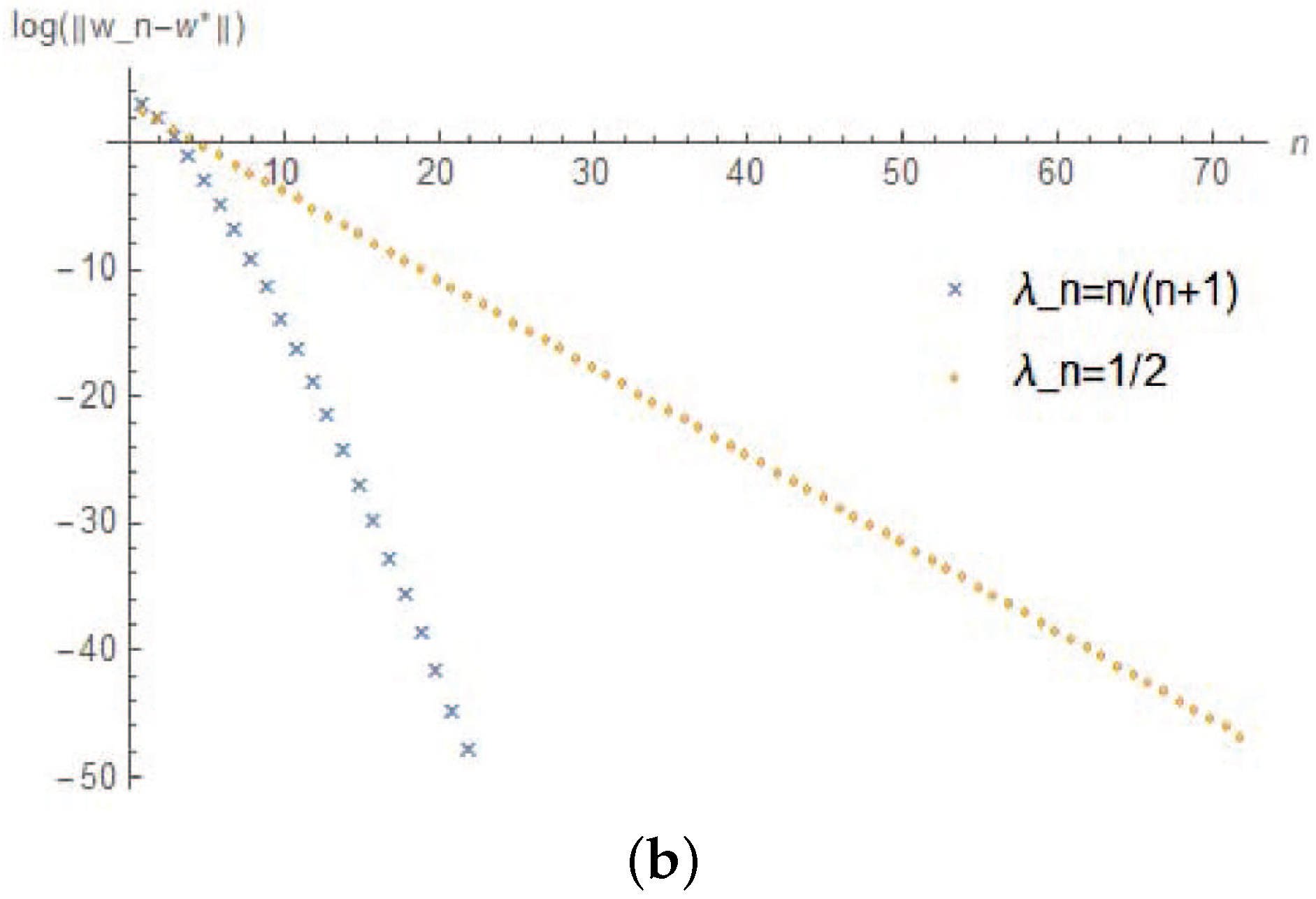
In algorithm (16), we take , respectively. Then we have the following numerical results (the x-coordinate denotes the iteration times, and the y-coordinate denotes the logarithm of the error). The whole program was written in Wolfram Mathematica (version 10.3). All the numerical results were performed on a personal Dell computer with Inter(R) Core(TM) i5-7200 U CPU 2.50 GHz and RAM 4.00 GB.
We choose error to be
, the initial value
and
, according to the algorithm (16), they converges to
and
, respectively (See
Figure 1).