Particle Swarm Optimization for Predicting the Development Effort of Software Projects

Abstract

Software project planning includes as one of its main activities software development effort prediction (SDEP). Effort (measured in person-hours) is useful to budget and bidding the projects. It corresponds to one of the variables most predicted, actually, hundreds of studies on SDEP have been published. Therefore, we propose the application of the Particle Swarm Optimization (PSO) metaheuristic for optimizing the parameters of statistical regression equations (SRE) applied to SDEP. Our proposal incorporates two elements in PSO: the selection of the SDEP model, and the automatic adjustment of its parameters. The prediction accuracy of the SRE optimized through PSO (PSO-SRE) was compared to that of a SRE model. These models were trained and tested using eight data sets of new and enhancement software projects obtained from an international public repository of projects. Results based on statistically significance showed that the PSO-SRE was better than the SRE in six data sets at 99% of confidence, in one data set at 95%, and statistically equal than SRE in the remaining data set. We can conclude that the PSO can be used for optimizing SDEP equations taking into account the type of development, development platform, and programming language type of the projects.

1. Introduction

Software engineering management involves planning [1]. The software project planning includes software prediction, and the most common predicted variables have been size [2] (mainly measured in either source lines of code, or function points [3]), effort (in person-hours or person-months [3]), duration (in months [4]), and quality (in defects [5]).

Software development effort prediction (SDEP), also termed effort estimation or cost estimation [6], is needed for managers to estimate the monetary cost of projects. As reference, in USA the cost by person-month (which is equivalent to 152 person-hours) is of $8000 USD [7].

Unfortunately, those projects taking more time (i.e., time overrun) costing more money (i.e., cost overrun) [8], and cost overrun has been identified as a chronic problem in most software projects [9]; whereas for cost underrun, a portion of the budgeted money is not spent and then money taxes have to be paid. These issues related to costs have been the causes for which a software project has been assessed based upon the ability to achieve the budgeted cost [10,11].

The relevance of the SDEP has been reflected with several publications on systematic reviews published between the years 2007 [6] and 2020 [12] where hundreds of studies on SDEP had been analyzed. The prediction models identified in the systematic reviews have been adaptive ridge regression, association rules, Bayesian networks, case-based reasoning (CBR, also termed analogy-based), decision trees, expectation maximization, fuzzy logic, genetic programming, grey relational analysis, neural networks, principal component analysis, random forest, and support vector regressions.

The proposal of accurate models for SDEP represents a continuous activity of researchers and software managers. On average, software developers spend between 30% and 40% more effort than is predicted when planning any project. The failure attributed to SDEP leads to schedule delays and cost overruns, which can address project failure and affect the reputation and competitiveness. On the other hand, over-predicting the effort of a software project can address ineffective use of resources, which can result in loss of opportunities to fund other projects, and therefore loss of tenders. It can derive, from a social point of view, demotivation of software engineers and their probable search for new job opportunities. These scenarios have motivated researchers for addressing their efforts to determine which prediction technique is most accurate, or to propose new or combined techniques that could provide better predictions [13].

There are several kinds of techniques, which have been applied to SDEP of projects developed individually in academic settings [14] or by teams of practitioners [12]. Our study involves projects developed by teams of practitioners in business environments.

As for metaheuristic algorithms, several studies on them have recently been published between the years 2019 and 2020 being inspired from (a) social behavior of animals, that is, Particle Swarm Optimization (PSO) such as insects, herds, birds and fishes [15], bats [16], butterflies [17], cuckoos [18], elephants [19], fireflies [20], moths [21], and whales [16]; (b) nature (brain [22], differential evolution [16], and genetic algorithm (GA) [23]), (c) physics (cooling of metals [24]), and (d) mathematics (such as sine and cosine operators [24]).

Regarding software engineering field, metaheuristics have also been specifically applied for SDEP. The applied algorithms have been artificial bee colony (ABC) [25], cuckoo search [26], differential evolution [27], GA [28], PSO [29], simulated annealing [30], tabu search [30], and whale optimization algorithm [31].

In those ten studies that we identified where PSO was applied to SDEP (which are analyzed in the Section 2 of the present study), PSO has been used to optimize parameters of models such as Bayesian belief network [32], CBR [33,34,35,36,37], COCOMO statistical equation [38] (whose model was published in the year of 1981 [39]), decision trees [40], fuzzy logic [29], mathematical expressions [25], neural networks [40], and support vector regression [40].

Regarding those five studies where PSO is used for optimizing CBR, in four of them the most similar software projects are selected, and the effort of a new project is predicted through a weighted average obtained from data of those similar projects. These weights are calculated using PSO [34,35,36,37]. In the fifth study, the authors use a hybrid CBR using local and global searches, and a multi-objective PSO is used to minimize two error functions for the searching [33]. As for fuzzy logic, the PSO is used to optimize the parameter values of the membership functions that make up the model [29]. In a different manner, once a set of fuzzy models has been defined, PSO is used to choose that model that best fits the SDEP [38]. PSO has also been used in combination with elements from ABC algorithm to fit the parameters of a predefined SDEP function [25]. Other study uses a classifier committee to make predictions and uses PSO to optimize the parameter values of each of the base classifiers that make up that classifier committee [40]. In a similar perspective, PSO was used within a hybrid model, to estimate the components of a Bayesian network [32]. In our proposal, neither weights nor any CBR model to be optimized are considered.

Unlike the previous proposals, the contribution of our study is the application of the PSO algorithm to optimize the parameters of statistical regression equations (SRE) applied to SDEP (hereafter, termed PSO-SRE), the selection of which is also optimized. Each equation is generated by following a regression analysis, and from data sets of projects selected from an international public repository of recent software projects (i.e., International Software Benchmarking Standards Group, ISBSG release 2018). The software projects were selected based on their type of development (TD), development platform (DP), and programming language type (PLT) as suggested in the guidelines of the ISBSG [41]. The ISBSG has widely been used for SDEP models [42].

The size of a software project is a common variable used for SDEP [3], therefore, our models use it as the independent variable. In our study, the size type is function points, whose value is calculated from nineteen independent variables mentioned in the Section 4 of the present study (i.e., adjusted function points, AFP) [13].

The justification for the comparison between the prediction accuracy of our PSO-SRE with that obtained from SRE is based on the following issues related to SDEP:

(a)

The prediction accuracy of any new proposed model should at least outperform a SRE [43].

(b)

SRE has been the model whose prediction accuracy has mostly been compared to other models such as those based on ML [44,45].

(c)

The prediction accuracy of SRE has outperformed the accuracies obtained from ML models [44].

Owing to a statistical analysis is needed for a validity studies [46], the data preprocessing and our conclusions are based on statistical analysis involving identification of outliers, coefficients of correlation and determination of data, as well as on the suitable statistical test for comparing the prediction accuracy between PSO-SRE and SRE.

A systematic literature review published in 2018 which analyzed studies published between 1981 and 2016 on SDEP models recommends the use of same data sets and a same prediction accuracy measure such that conclusions can be compared to other studies [3]. This recommendation was suggested once they found difficulty to compare the performance among SDEP models due to the wide diversity of data sets and accuracy measures used. Thus, in our study, the models were applied to the same data sets, as well as taking into account a same accuracy measure (i.e., absolute residual, AR). Moreover, they were trained and tested using the same validation method (i.e., a Leave-one-out cross-validation, LOOOV, which is recommended for software effort model evaluation [47]).

In the present study, the null (H₀) and alternative (H₁) hypotheses to be tested are the following:

H₀. 

Prediction accuracy of the PSO-SRE is statistically equal to that of the SRE when these two models are applied to predict the development effort of software projects using the AFP as the independent variable.

H₁. 

Prediction accuracy of the PSO-SRE is statistically not equal to that of the SRE when these two models are applied to predict the development effort of software projects using the AFP as the independent variable.

The remaining of the present study is as follows: Section 2 has been assigned to describe the related studies where PSO has been applied to predict the development effort of software projects. Section 3 describes the Particle Swarm Optimization (PSO) metaheuristic, and our proposal: the PSO-SRE. Section 4 presents the criteria applied to select the data sets of software projects by observing the guidelines of the ISBSG, as well as the data preprocessing. Section 5 presents the results when PSO-SRE is performed and compares its prediction accuracy to SRE once the two models were trained and tested. Section 6 mentions our conclusions. Finally, Section 7 corresponds to a discussion section, which includes the comparison with previous studies, the limitations of our study, validation threats, as well as directions for future work.

2. Related Work

The proposed SDEP techniques have been systematically analyzed in several reviews [3,6,12,44,45,48,49,50,51]. They can be classified in those not based on models, and in those based on models. The first type mentioned is also termed expert judgment [48,52], whereas the latter one can be classified in two categories: statistical [53] and ML models [44,45].

Table 1. Studies on SDEP based on PSO (AR: absolute residual, BRE: mean balanced relative error, IBRE: inverted balanced relative error, LSD: logarithmic standard deviation, LOOCV: Leave-one-out cross validation, MRE: magnitude relative error, r²: coefficient of determination, NS: not specified).

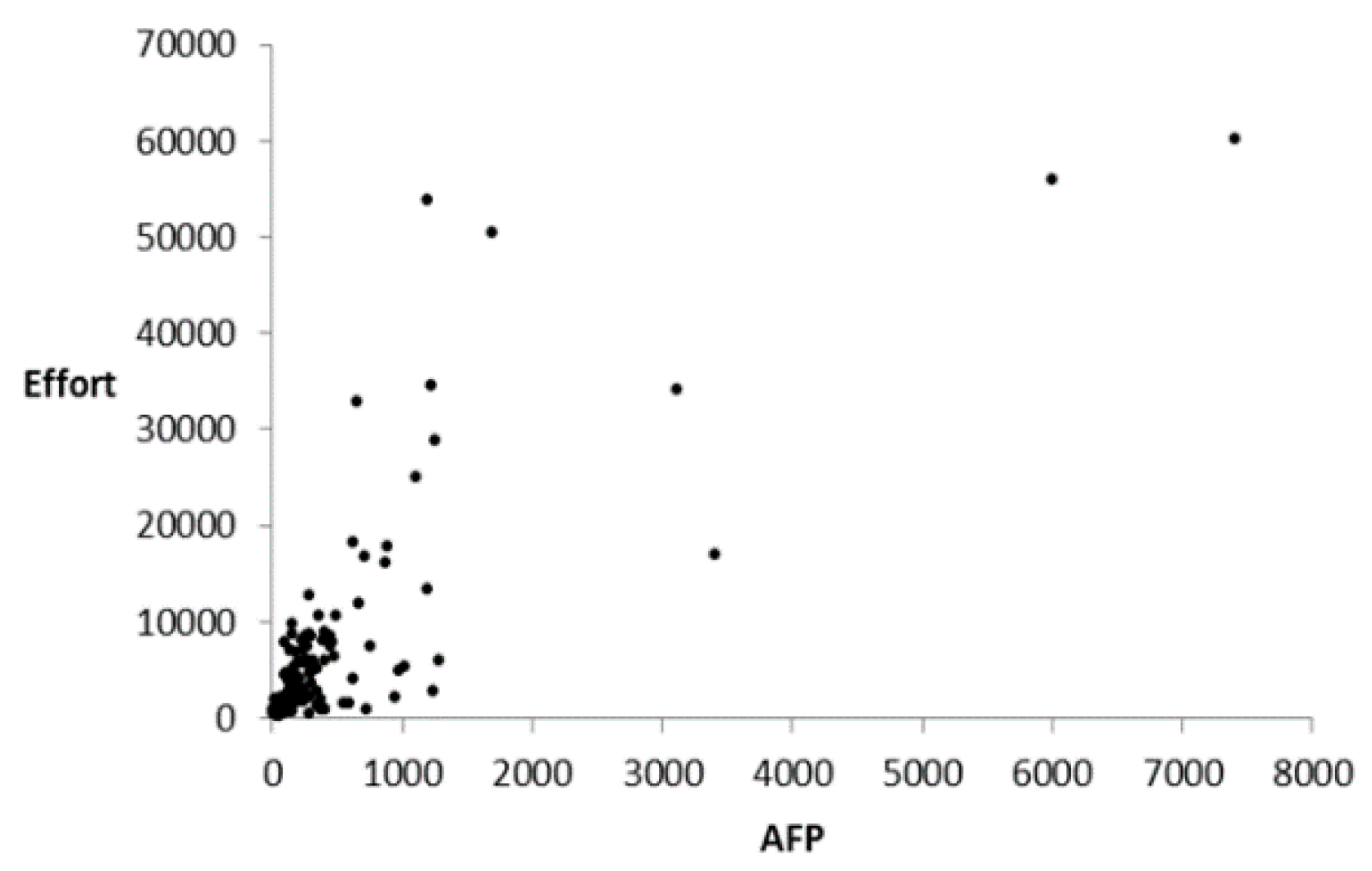
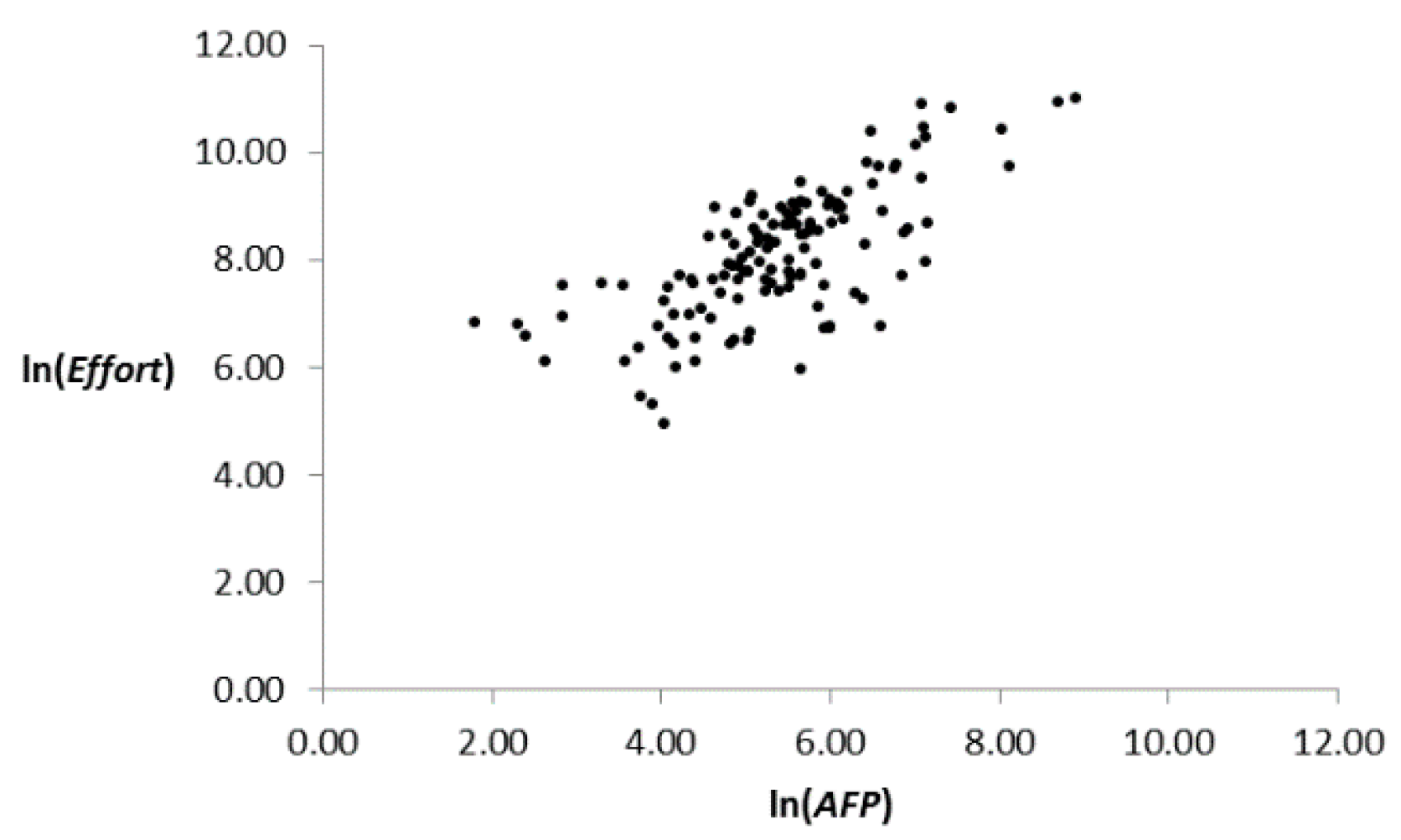
Study	Data Set(s) 1	Prediction Accuracy	Validation Method	Statistical Significance?
[25]	Six software organizations (21)	AR MRE r2	NS	Wilcoxon
[33]	Albrecht (24) Kemerer (15) Nasa (18) ISBSG Release 10 (505) Desharnais (77) Desharnais L1 (44) 3 Desharnais L2 (23) Desharnais L3 (10) Cocomo (63) Cocomo E (28) Cocomo O (24) Cocomo S (11) China (499) Maxwell (62) Telecom (18)	BRE IBRE	LOOCV	ANOVA
[34]	Canadian organization (21) IBM (24) ISBSG Release 11 (134)	MRE	k-fold cross validation (k = 3)	No
[35]	ISBSG Release 2011 (380) Cocomo (63) Maxwell (62)	MRE	k-fold cross validation (k = 10)	Wilcoxon
[29]	Cocomo NASA 2 (93) Cocomo (60)	MRE	NS	No
[40]	Albrecht (24) China (499) COCOMO (252) 2 Desharnais (77) ISBSG Release 8, 2003 (148) Kemerer (15) Miyazaki (48)	AR MRE LSD BRE IBRE	LOOCV	Scott-Knott
[38]	Nasa (18)	MRE	Hold-out	No
[36]	Desharnais (77) Maxwell (62)	MRE	k-fold cross validation (k = 3)	No
[37]	Desharnais (77) Miyazaki (48)	MRE	k-fold cross validation (k = 3)	t-Student
[32]	Cocomo (63)	MRE	Hold-out	No

¹ The parentheses enclose the number of projects by data set. ² It was transformed from 63 into 252 projects. ³ An indented data set means that it is sub set of another one.

shows an analysis of those ten studies identified where PSO was applied to SDEP. It includes the data set(s) of software projects, the number of projects by data set, the prediction accuracy measure, the validation method, as well as if the result was reported based on statistical significance, if so, the name of the statistical test is mentioned. A description including the proposal and results by study is done next:

Azzeh et al. [33] use PSO to find the optimum solutions for variables related to multiple evaluation measures when applied CBR. Their results show that CBR improves when taking into account all variables together.

Bardsiri et al. [34] apply PSO to optimize the CBR weights. The PSO algorithm assigns weights to the features considered in the similarity function. The accuracy of their proposal is compared to those obtained from three types of CBR, as well as to those ones obtained from neural networks, classification and regression tree, and statistical regression models. Results show that the prediction accuracy of the CBR when used PSO was better than all the mentioned models.

Bardsiri et al. [35] use PSO in combination with CBR to design a weighting system in which the project attributes of different clusters of software projects are given different weights. The performance of their proposal is better than the prediction accuracy obtained when neural networks, classification and regression trees, and statistical regression models are applied.

Chhabra and Singh [29] firstly compare the prediction accuracy of three models termed Regression-Based COCOMO, Fuzzy COCOMO, and PSO Optimized Fuzzy COCOMO. In the latter one, they use the PSO to optimize the fuzzy logic model parameters. Then, they also compare the performance of it to that of a GA Optimized Fuzzy COCOMO. Their results show that the PSO Optimized Fuzzy COCOMO has better prediction accuracy than those obtained from the other three models. They concluded that the PSO can be applied as optimizer for a fuzzy logic model.

Hosni et al. [40] apply PSO for setting ensemble parameters of four ML models. They compare the PSO performance to that of grid search. They conclude that PSO and grid search show a same predictive capability when applied to k-nearest neighbor, support vector regression, neural networks, and decision trees.

Khuat and Le [25] propose an algorithm combining the PSO and ABC algorithms for optimizing the parameters of a SDEP formula. This formula is generated by using two independent variables obtained from agile software projects (i.e., final velocity, and story point). The accuracy results by applying this formula are compared to those obtained from four types of neural networks (i.e., general regression neural network, probabilistic neural network, group method of data handling polynomial neural network, and cascade correlation neural network). The performance of the algorithm based on PSO and ABC was better than those obtained from the four mentioned neural networks.

Sheta et al. [38] use PSO for optimizing the parameters of the COCOMO equation (termed PSO-COCOMO). They also build a fuzzy system. The PSO-COCOMO has a better performance than those obtained when the SDEP equations proposed by Halstead, Walston-Felix, Bailey-Basili, and Doty are applied.

Wu et al. [36] use PSO to optimize the CBR weights. They employ Euclidean, Manhattan, and grey relational grade distances as metrics to calculate the similarity measures. Their results show that the weighed CBR generates better prediction accuracy than unweighted CBR methods. They concude that the combined method integrating PSO and CBR improves the performance for the three mentioned measures.

Wu et al. [37] use PSO in combination with six CBR methods. These methods differ by their type of distance measure (i.e., Euclidean, Manhattan, Minkowski, grey relational coefficient, Gaussian, and Mahalanobis). Results show that the combination of methods proposed by them has a better performance than independent methods, and that the weighted mean combination method has a better result.

Zare et al. [32] apply PSO to obtain the optimal updating coefficient of effort prediction based on the concept of optimal control by modifying the predicted value of a Bayesian belief network. Its performance is compared to that obtained when applied GA. Results of their proposed model indicate that optimal updating coefficient obtained by GA increases the accuracy of prediction significantly in comparison with that obtained from PSO.

In accordance with Table 1, only two studies used a non-biased prediction accuracy measure (i.e., AR), only two of them used a deterministic validation method (i.e., LOOCV), the half of them based their conclusions on statistically significance, and none of the them involved any recent repository of software projects: Albrecht was published in the year of 1983, Canadian organization in 1996, COCOMO in 1981, Desharnais in 1988, IBM in 1994, Kemerer in 1987, Maxwell in 1993, Miyazaki in 1994, Nasa in 1981, Telecom in 1997, and the most recent ISBSG release used was published in the year of 2011. Regarding the data set of projects of the six software organizations, it was published in 2012; however, its size is small: 21 projects [25]. Finally, the year of those projects of China was not reported in those studies that have used them [33,40].

In those four studies where the ISBSG data set was used, the releases were 8 [40], 10 [33] and 11 [34,35], whose years of publication and sizes were 2003 with 2000 software projects, 2007 with 4000, and 2009 with 5052, respectively. When the release 8 was used, the authors selected a data set of 148 projects based on the following ISBSG criteria: DT (new), quality rating (“A” and “B” categories), resource level with 1 as value, maximum number of people working on the project, number of business units, and IFPUG as functional sizing method (FSM) type [40]. As for release 10, they selected a data set of 505 projects taking into account only a criterion suggested by the ISBSG: the quality rating (“A”) [33]. As for release 11: (a) they selected a data set of 134 projects based on three ISBSG criteria: quality rating (“A” and “B”), normalized effort ratio of up to 1.2, and “Insurance” value for the type of organization attribute [34], and (b) they selected a data set of 380 projects based on quality rating attribute (“A” and “B”), DT, organization type, DP, normalized effort ratio of up to 1.2, resource level with 1 as value, and IFPUG as FSM [35]. That is, in all of these four studies, only one data set was selected by study, and the type of FSM was not taken into account to select the data set by mixing the IFPUG versions.

In accordance with the analysis of these ten studies, PSO has been used in three fundamental manners: (a) as a tool to support CBR [33,34,35,36,37,40], (b) for the selection of the SDEP model [38], and (c) for the optimization of values of a SDEP model ([25,29,32]). In our opinion, the manner in how PSO was used in these studies has the following disadvantages:

(a)

An increase in the computational cost inherent to CBR models by incorporating the use of optimization techniques.

(b)

Allowing selecting the best SDEP model from a set of predefined models, but without an automatically adjustment of the parameters of the selected model.

(c)

Define a priori the SDEP model to be used, and only adjusting its parameters.

Taking into account these weaknesses, our proposal incorporates the following two elements in PSO:

(1)

The selection of the SDEP model, and

(2)

The automatic adjustment of the SDEP model parameters.

The analysis of the Table 1 also allows us emphasizing our experimental design which involves new and enhancement software projects selected based on their TD, DP, PLT, and FSM. Data of these projects are preprocessed through an outlier analysis, and calculation of two types of coefficients: correlation and determination. The models are trained and tested based on AR while a LOOCV is applied. Finally, the hypotheses of our study are statistically tested.

3. Particle Swarm Optimization (PSO) and PSO-SRE

3.1. PSO

Particle Swarm Optimization (PSO) is an optimization model created in 1995 by Kennedy and Eberhart [54]. It assumes that there is a cloud of particles, which “fly” in a D dimensional space. This original idea was refined three years later considering the introduction of memory into particles [55]. Particles have access to two types of memory: individual memory (the best position occupied by the particle in space) and collective memory (the best position occupied by the cloud in space). The evolution of the original PSO has continuously been analyzed [15].

In PSO, the size of the particle cloud np (number of particles) is considered as a user parameter. In the cloud, each particle $i$ has stored the following three real vectors of D dimensions: the current position vector $x_i$, the vector of the best position reached $p_i$, and the flight speed vector $v_i$. In addition, the cloud or swarm stores the best global position vector $g_{best}$.

The movement of the particles is defined as a change in their position, when adjusting a velocity vector, component by component. To do this, the particles use individual memory and collective memory. The j-th component of the velocity vector of the i-th particle is updated as:

$$v_{i,j}\leftarrow w\ast v_{i,j}+c_1\ast rand\left(0,1\right)\ast \left(p_{ij}-x_{i,j}\right)+c_2\ast rand\left(0,1\right)*\left(g_{best,j}-x_{i,j}\right)$$

(1)

where $w$ is the inertia weight, $c_1$ is the individual memory coefficient, and $c_2$ is the global memory coefficient. The function $rand\left(0,1\right)$ represents the generation of a random number in the [0, 1] interval. If the velocity components exceed the established limits, they are bounded, such that it complied that $V_{min}\le v_{i,j}\le V_{max}$.

Subsequently, the j-th component of the current position vector of the i-th particle is adjusted as:

$$x_{i,j}\leftarrow x_{i,j}+v_{i,j}$$

(2)

This adjusting process on the positions for the particles is repeated until a stop condition is achieved, which is usually settled as a number of algorithm iterations.

The pseudocode of the PSO algorithm described by Shi and Eberhart [55] is shown in Figure 1. It assumes that it is intended to minimize an objective function.

In terms of complexity and time execution, PSO has two external loops that are generation loops and a loop through the entire population. In each loop, the optimization function is computed for each member of the population (particle). Considering $k$ as the cost of computing the optimization function, it can be said that the time of execution of PSO is bounded by $O\left(it\ast np\ast k\right).$

3.2. PSO-SRE

We use a PSO design considering an additional element: the SDEP model. Thus, the 20 functions detailed in

Table 2. Description of the analyzed models.

No.	Model	Equation	Reference
1	Linear equation	$y=a+bx$	[56]
2	Exponential equation	$y=a{e}^{kx}$	[56]
3	Exponential decrease or increase between limits	$y=a{e}^{bx}+c$	[57]
4	Double exponential decay to zero	$y=a{e}^{-bx}+c{e}^{-dx}$	[57]
5	Power	$y=a{x}^b$	[57]
6	Asymptotic equation	$y=a+\frac{b}{x}$	[58]
7	Asymptotic regression model	$y=a-\left(a-b\right)e^{-cx}$	[56]
8	Logarithmic	$y=alnx+b$	[57]
9	“Plateau” curve—Michaelis-Menten equation	$y=\frac{ax}{b+x}$	[57]
10	Yield-loss/density curves	$y=\frac{iX}{1+\frac{iX}{a}}$	[54]
11	Logistic Function	$y=\frac{1}{1+e^{-ax}}$	[57]
12	Logistic curves with additional parameters	$y=\frac{b}{c+e^{-ax}}$	[57]
13	Logistic curve with offset on the y-Axis	$y=\frac{1}{1+e^{b+cx}}+d$	[57]
14	Gaussian curve	$y=\frac{\exp \left[-{\left(x-\mu \right)}^2/2{\sigma }^2\right]}{\sigma \sqrt{2\pi }}$	[57]
15	Log vs. Reciprocal	$y=\left(a-\frac{b}{x}\right)$	[57]
16	Trigonometric functions	$y=a\sin \left(bx+c\right)+d$	[57]
17	Trigonometric functions (2)	$y=\sin ax+\sin bx$	[57]
18	Trigonometric functions (3)	$y=a\sin \left(bx+c\right)+d\sin \left(ex+f\right)+g$	[57]
19	Quadratic polynomial regression	$y=a+bx+c{x}^2$	[57]
20	Cubic polynomial regression	$y=a+bx+c{x}^2+d{x}^3$	[57]

were taken into account to achieve it. The x independent variable used in these 20 functions corresponds to the FSM (i.e., AFP). We add an additional component to each individual, which corresponds to an integer number in the interval [1,20] which represents the SDEP model to be used by the particle. Consequently, each particle has a different number of dimensions, which will vary according to the coefficients of the selected model. This novel modification allows us to simultaneously optimize the SDEP model to be selected, as well as its parameters. Figure 2 shows a swarm of five particles used by our proposed algorithm. The pseudocode of the proposal is shown in Figure 3.

Based on Figure 2, it can be defined that to obtain the final value to be compared for each particle, the first value is taken, which is the one that corresponds to the number of the model shown in Table 2, together with the following n values that correspond to the model parameters. As example, for the particle [1, 0.24, 0.18], the first value (1) would correspond to model 1 of the Table 2 and the next two values (0.24, 0.18) correspond to the parameters a and b to optimize the selected model, which is: $y=a+bx$ obtained by the SDEP model.

We use the first dimension to determine the equation assigned to the particle. By this, we use a dynamic codification, and the particles will have different dimensions, depending on the assigned equation. The dimensions of the particles range from two to five.

To update the velocity vector of a particle, if the value of $g_{best}$ has more dimensions, the ones that are needed are used, and if it has fewer dimensions, we use random numbers instead. The particles have in common that they use mathematical equations to optimize the prediction of the effort of software projects. A particle interacts with itself (updating its best position) and with the best particle of the swarm. Even if a particle and the best particle have different equations, using the coefficients of the best particle helps the particle to move towards a global optimum. If we use random guessing, we do not consider the fitness results. On the other hand, if we use the best particle, we consider the fitness.

We consider that using the proposed codification offers the proposed PSO-SRE more search space capacity (exploration) and allows it to get better out of local optimums. However, for other optimizations problems, this increase in the search capacity of the proposal can be prone to not giving the best results, due to the decrease in the exploitation capacity of the proposal.

The dimension and model will be unique for each data set and, once the stop condition is attained, the test MAR value will be calculated.

A crucial aspect of optimization algorithms such as PSO lies in the selection of the optimization function. In our research, two optimization functions (i.e., the prediction accuracy measures) are evaluated: AR, and the MAR. AR is calculated by ith-project as follows [13]:

$${\mathrm{AR}}_i=\left|{\mathrm{Actual}\mathrm{Effort}}_i-{\mathrm{Predicted}\mathrm{Effort}}_i\right|$$

(3)

And the mean of ARs as follows:

$$MAR=(1/N){\displaystyle \sum A{R}_i}$$

(4)

The median of ARs is denoted by MdAR. The accuracy of a prediction model is inversely proportional to the MAR or MdAR.

The parameter values for the proposed PSO model are: $w=0.1$, $V_{min}=-10$, $V_{max}=10$ and $c_1=c_2=1.5$, this last value was chosen due to it had better results in our experiments, compared to that recommended as a standard value (i.e., $c_1=c_2=2$ [54]). The swarm size was evaluated considering $np$ between 50 and 750, whereas the iteration number was set between 250 and 1500.

As optimization function, we use the MAR of the training set, considering a LOOCV for the corresponding model defined in Table 2.

4. Data Sets of Software Projects

In the present study, the data sets used were obtained from the ISBSG release 2018, which is an international public repository whose data of software projects developed between 1989 and 2016, were reported from 32 countries. Among these countries are Spain, United States, Netherlands, Finland, France, Australia, India, Japan, Canada, and Denmark [59]. The projects were selected observing the ISBSG guidelines by selecting the data sets taking into account the quality of data, FSM, TD, DP, and PLT [41].

Table 3. Criteria for selecting the data sets from the ISBSG (8261 projects).

Attribute	Selected Value(s)	Projects
Adjusted Function Point not null	---	6394
Data quality rating	A, B	6061
Unadjusted Function Point Rating	A, B	5316
Functional sizing methods	IFPUG 4+	4602
Development platform not null	---	3040
Language type not null	---	2711
Resource level	1	2054

describes the number of projects by applying each criterion (the ISBSG classifies the quality data of projects from “A” to “D” types, and “A” and “B” are recommended for statistical analysis). Since IFPUG V4 projects with V4 and post V4 should not be mixed [41], only those projects whose FSM corresponded to IFPUG 4+ were selected. In classifying the final 2054 projects of Table 3 by DT, 618 of them were new, 1416 enhanced and 20 re-development projects. The types of DP reported by the ISBSG are mainframe (MF), midrange (MR), multiplatform (Multi), personal computer (PC), and proprietary, whereas the PLT are second (2GL), third (3GL), fourth (4GL) generation, and application generator (ApG). As for the resource level, the ISBSG classifies it in accordance with how effort is quantified, and the level 1 corresponds to development team effort [41]. Those new and enhancement data sets were selected since they are the larger ones.

The IFPUGV4+ FSM is reported in AFP, which is a composite value calculated from the following nineteen variables: internal logical file, external interface files, external inputs, external outputs, external inquiries, data communications, distributed data processing, performance, heavily used configuration, transaction rate, on-line data entry, end-user efficiency, on-line update, complex processing, reusability, installation ease, operational ease, multiple sites, and facilitate change [13].

Table 4. Projects classified by type of development (TD), development platform (DP), and programming language type (PLT), NSP: Number of software projects.

TD	DP	PLT	NSP
New	MF	2GL	3
	MF	3GL	133
	MF	4GL	28
	MF	ApG	4
	MR	3GL	36
	MR	4GL	22
	Multi	3GL	105
	Multi	4GL	102
	PC	3GL	55
	PC	4GL	118
	Proprietary	5GL	12
Enhancement	MF	2GL	4
	MF	3GL	457
	MF	4GL	48
	MF	ApG	53
	MR	3GL	67
	MR	4GL	53
	Multi	3GL	442
	Multi	4GL	195
	PC	3GL	55
	PC	4GL	42

classifies those final 2034 new and enhancement projects classified in accordance with criteria included in Table 3. Since the χ² statistical normality test to be applied in this study needs at least thirty data, a scatter plot (Effort vs. AFP) was generated by data set whose number of projects in Table 4 was higher or equal than thirty (i.e., fifteen data sets). The scatter plots of these fifteen data sets from the Table 4 showed skewness, heteroscedasticity, and presence of outliers, therefore, in

Table 5. Normal statistical tests by data set (NSP: number of software projects; S-W: Shapiro-Wilk).

TD	DP	PLT	NSP	Variable	Normality Test
					χ2	S-W	Skewness	Kurtosis
New	MF	3GL	133	AFP	0.0000	0.0000	0.0000	0.0000
				Effort	0.0000	0.0000	0.0000	0.0000
	MR	3GL	36	AFP	0.0354	0.0075	0.1836	0.8342
				Effort	0.0000	0.0000	0.0000	0.0000
	Multi	3GL	105	AFP	0.0000	0.0000	0.0000	0.0000
				Effort	0.0000	0.0000	0.0000	0.0000
	Multi	4GL	102	AFP	0.0000	0.0000	0.0000	0.0000
				Effort	0.0000	0.0000	0.0000	0.0000
	PC	3GL	55	AFP	0.0000	0.0000	0.0000	0.0000
				Effort	0.0000	0.0000	0.0000	0.0000
	PC	4GL	118	AFP	0.0000	0.0000	0.0002	0.0158
				Effort	0.0000	0.0000	0.0000	0.0000
Enhancement	MF	3GL	457	AFP	0.0000	0.0000	0.0000	0.0000
				Effort	0.0000	0.0000	0.0000	0.0000
	MF	4GL	48	AFP	0.0000	0.0000	0.0000	0.0000
				Effort	0.0186	0.0000	0.0104	0.0300
	MF	ApG	53	AFP	0.0000	0.0000	0.0000	0.0000
				Effort	0.0000	0.0000	0.0002	0.0000
	MR	3GL	67	AFP	0.0000	0.0000	0.0000	0.0000
				Effort	0.0000	0.0000	0.0000	0.0000
	MR	4GL	53	AFP	0.0000	0.0000	0.0117	0.1535
				Effort	0.0000	0.0000	0.0001	0.0000
	Multi	3GL	442	AFP	0.0000	0.0000	0.0000	0.0000
				Effort	0.0000	0.0000	0.0000	0.0000
	Multi	4GL	195	AFP	0.0000	0.0000	0.0000	0.0000
				Effort	0.0000	0.0000	0.0000	0.0000
	PC	3GL	55	AFP	0.0000	0.0000	0.0003	0.0003
				Effort	0.0000	0.0000	0.0000	0.0000
	PC	4GL	42	AFP	0.0000	0.0000	0.0006	0.0001
				Effort	0.0203	0.0000	0.0047	0.0006

four statistical normality tests are applied for Effort and AFP variables. Table 5 shows that there is at least a p-value lower than 0.01 by data set. It means that can be rejected the idea that Effort and AFP come from a normal distribution with 99% confidence for all of the data sets. Therefore, data are normalized applying them the natural logarithm (ln), which ensures that the resulting model goes through the origin on the raw data scale [43]. As example, Figure 4 and Figure 5 depict those scatter plots corresponding to that data set of Table 4 having 133 new software projects. Figure 4 and Figure 5 depict the raw and transformed data, respectively.

Outliers were identified based on studentized residuals greater than 2.5 in absolute value. The outliers, as well as coefficients of correlation (r) and determination (r²) by data set are included in

Table 6. Normalized data sets of software projects (NSP: number of software projects, NO: number of outliers, FDSS: final data set size).

TD	DP	LT	NSP	NO	FDSS	%	r	r2
New	MF	3GL	133	3	130	2.25	0.7345	0.5396
	MR	3GL	36	6	30	16.6	0.7390	0.5461
	Multi	3GL	105	6	99	5.71	0.7227	0.5223
	Multi	4GL	102	6	96	5.88	0.8513	0.7247
	PC	3GL	55	7	48	12.72	0.7978	0.6365
	PC	4GL	118	6	112	5.08	0.6515	0.4245
Enhancement	MF	3GL	457	17	440	3.86	0.7916	0.6266
	MF	4GL	48	4	44	9.09	0.4751	0.2257
	MF	ApG	53	4	49	8.16	0.6571	0.4318
	MR	3GL	67	3	64	4.68	0.8052	0.6483
	MR	4GL	53	6	47	11.32	0.7127	0.5080
	Multi	3GL	442	14	428	3.16	0.8016	0.6427
	Multi	4GL	195	5	190	2.56	0.7640	0.5838
	PC	3GL	55	2	53	3.77	0.8019	0.6431
	PC	4GL	42	6	36	14.28	0.6418	0.4119

. In accordance with the number of acceptable outliers, a 5% of them by data set was taken as reference [60]. As for a minimum percentage for the coefficient of determination, at least a r² value higher than 0.5 was considered since it has been accepted for SDEP models [61]. Thus, in this study, eight data sets of those fifteen analyzed in Table 6 were selected to generate their corresponding PSO-SRE and SRE. They were finally selected since three of the fifteen had a r² value lower than 0.5, three of them presented a percentage between 11% and 16.6% of outliers, and one of them had a r² = 0.4119 with 14.28% of outliers.

The model for the SRE is linear having the form ln(Effort) = a + b * ln(AFP).

Table 7. SREs for predicting the effort of new and enhancement projects.

TD	DP	LT	SRE
New	MF	3GL	$\ln (Effort)=4.28+0.72*\ln (AFP)$
	Multi	3GL	$\ln (Effort)=3.90+0.73*\ln (AFP)$
	Multi	4GL	$\ln (Effort)=1.69+0.99*\ln (AFP)$
Enhancement	MF	3GL	$\ln (Effort)=3.53+0.83*\ln (AFP)$
	MR	3GL	$\ln (Effort)=4.03+0.67*\ln (AFP)$
	Multi	3GL	$\ln (Effort)=2.13+1.08*\ln (AFP)$
	Multi	4GL	$\ln (Effort)=3.79+0.70*\ln (AFP)$
	PC	3GL	$\ln (Effort)=2.84+0.82*\ln (AFP)$

contains the SRE by data set selected from Table 6. All equations coincide with the assumption of development effort: the higher size (i.e., AFP), the higher effort is.

5. Results

A total of 130, 99, 96, 440, 64, 428, 190 and 53 SREs were generated by data set once a LOOCV was performed.

The proposed PSO-SRE algorithm was executed for each dataset with different configurations in a distributed manner and on a dedicated server for the laboratory, trying to ensure that the execution time was as short as possible and trying to get the best possible result.

After applying the PSO-SRE, it is possible to detail the selected SDEP model (from those ones included in Table 2) by data set.

Table 8. PSO parameters by data set (TD: type of development, DP: development platform LT: programming language, NSP: number of software projects, ID-SRE: unique identifier of the generated SRE) for the Tests (SS: Swarm size, DEDZ: Double exponential decay to zero, LE: Linear equation, Pcu: “Plateau” curve, AE: Asymptotic equation).

TD	DP	LT	NSP	ID SRE	Model Name	Test 1		Test 2		Test 3
						SS	Iterations	SS	Iterations	SS	Iterations
New	MF	3GL	130	1	DEDZ	50	250	150	750	100	500
	Multi	3GL	99	2	LE	50	250	150	750	100	500
	Multi	4GL	96	3	LE	50	250	150	750	100	500
Enhancement	MF	3GL	440	4	LE	250	500	750	1500	500	1000
	MR	3GL	64	5	LE	50	250	150	750	100	500
	Multi	3GL	428	6	Pcu	50	250	150	750	100	500
	Multi	4GL	190	7	Pcu	50	250	150	750	100	500
	PC	3GL	53	8	AE	50	500	150	1500	100	1000

includes the PSO-SRE configuration in terms of the number of iterations, as well as the swarm size for three types of tests described next (the values were selected from those configurations described in the previous paragraph):

• Test 1: Up to 500 iterations, and up to 250 individuals in the swarm;
• Test 2: Up to 1500 iterations, and up to 750 individuals in the swarm;
• Test 3: Up to 1000 iterations, and up to 500 individuals in the swarm.

As for velocity updates, Barrera et al. [62] address the issue of defining velocity limits iteratively. They show that for some optimization functions, the velocity update reported by Shi and Eberhart [55], is susceptible to sub-optimal behavior. However, for predicting the effort of software projects, we obtained good results with the approach of Shi and Eberhart [55].

The number of iterations and swarm size depend on the data set converging in different conditions. In relating the swarm size and iteration number of the three different tests of Table 8 to the prediction accuracy of

Table 9. Prediction accuracies by model.

TD	ID SRE	LT	NSP	SRE		RS		PSO-SRE
								Test 1		Test 2		Test 3
				MAR	MdAR	MAR	MdAR	MAR	MdAR	MAR	MdAR	MAR	MdAR
New	1	3GL	130	0.66	0.60	1.73	1.83	0.54	0.41	0.61	0.51	0.61	0.51
	2	3GL	99	0.62	0.56	1.46	1.35	0.56	0.43	0.61	0.55	0.61	0.55
	3	4GL	96	0.53	0.49	0.74	0.57	0.43	0.32	0.52	0.47	0.52	0.47
Enhancement	4	3GL	440	0.61	0.52	1.99	2.01	0.61	0.50	0.61	0.50	0.61	0.52
	5	3GL	64	0.60	0.50	1.33	1.21	0.53	0.35	0.59	0.49	0.59	0.49
	6	3GL	428	0.56	0.50	1.62	1.60	0.40	0.28	0.55	0.48	0.54	0.46
	7	4GL	190	0.52	0.44	1.37	1.46	0.46	0.41	0.51	0.45	0.51	0.45
	8	3GL	53	0.72	0.70	1.18	1.06	0.48	0.36	0.72	0.70	0.65	0.55

by data set, we can conclude that the increase of swarm size and iteration number degrades the performance of the proposed PSO-SRE algorithm. In accordance with Test 1 data, we can conclude that between 250 and 500 iterations, and a swarm size between 50 and 250 correspond to values which can be suggested for generate better results.

Table 9 includes the prediction accuracy obtained by model. It shows that PSO-SRE had a better MAR than SRE in seven of the eight data sets, and equal than the remaining one for Test 1, that is, when swarm size and number of iterations were lower than those of Test 2 and Test 3. In addition, the MARs for the Test 1 data sets were better than those MARs of Test 2 and Test 3 for all data sets except for one data set in which the MAR resulted equal for the three Tests (MAR = 0.61). Thus, data obtained from Test 1 are used in the present study.

In Table 9, we include a simple Random Search (RS) algorithm, which:

• not have memory of its own nor a search direction,
• repeat the random search of “the best particle” for a number of times that is equal to the number of fitness evaluations in the proposed PSO-SRE,
• compare its best solution with the best solution yielded by PSO-SRE.

Since a MAR is not sufficient to report results in studies on software effort prediction, a suitable statistical test is applied for comparing the accuracies of the two models [46]. The selection of this test should be based in the number of data sets to be compared, data dependence and data distribution. In our study, two data sets will be compared at a time, and they are dependent (because each model was applied to each project by data set). As for data distribution, firstly, a new data set is obtained by each of the eight data sets of Table 9. Each new data set is obtained from the difference between the two ARs by project (an AR of SRE, and an AR of PSO-SRE). Secondly, four normality statistical tests are performed to each new data set. Thirdly, if any of their four p-values is lower than 0.05 or 0.01, then data are non-normally distributed at 95% or 99% of confidence, respectively, and a Wilcoxon test should be applied (the medians of models should be compared to accept/reject the hypothesis), otherwise, a t-paired should be performed (the means of models should then be compared) [63].

Table 10. Statistical tests for data distribution and between models by data set. PSO: (PSO-SRE – SRE), RS: (PSO-SRE – RS).

TD	DP	LT	NSP	Pair	χ2	S-W	Skewness	Kurtosis	p-Value
New	MF	3GL	130	SRE	0.0000	0.0000	0.3410	0.0000	0.0000
				RS	0.0000	0.0000	0.0073	0.9537	0.0000
	Multi	3GL	99	SRE	0.0000	0.0000	0.0000	0.0000	0.0040
				RS	0.1462	0.0160	0.2573	0.6616	0.0000
	Multi	4GL	96	SRE	0.0000	0.0000	0.2251	0.0000	0.0000
				RS	0.2261	0.0387	0.8034	0.0428	0.0000
Enhancement	MF	3GL	440	SRE	0.0000	0.0000	0.6019	0.0000	0.3878
				RS	0.0000	0.0000	0.0000	0.0014	0.0000
	MR	3GL	64	SRE	0.0016	0.5511	0.7769	0.9573	0.0267
				RS	0.7847	0.8470	0.6219	0.9685	0.0000
	Multi	3GL	428	SRE	0.0000	0.0000	0.1028	0.0000	0.0000
				RS	0.0000	0.0000	0.0000	0.5221	0.0000
	Multi	4GL	190	SRE	0.0000	0.0000	0.8475	0.0000	0.0000
				RS	0.0002	0.0000	0.0322	0.1907	0.0000
	PC	3GL	53	SRE	0.0347	0.0002	0.0961	0.0155	0.0000
				RS	0.8419	0.2107	0.5087	0.3184	0.0000

shows that only in two cases the data resulted normally distributed, then, in the resting fourteen cases, a Wilcoxon test was applied, and the medians were used for the fourteen comparisons.

An important issue regarding PSO-SRE is the computational complexity. The server used for performing the tests had the following characteristics: OS: Ubuntu 20.04.1 LTS x86_64, Host: PowerEdge R720, Kernel: 5.4.0-47-generic, CPU: Intel Xeon E5-2620 0 <24> @2.500 GHz, GPU: NVIDIA Tesla K20Xm, GPU: NVIDIA GeForce 210 and Memory: 4828 MiB/64,347 MiB.

We executed the algorithm in a distributed manner (i.e., datasets in parallel), which reduced the execution time. However, we made a sequential set of experiments (i.e., one dataset at the time) to estimate the total time expended in each set of experiments considering the LOOCV used.

Table 11. Execution time of the experiments, using a sequential approach.

TD	DP	LT	NSP	Model Name	Execution Time (Minutes)
					Test 1	Test 2	Test 3	Prediction
New	MF	3GL	130	Double Exponential Decay to Zero	14.5	23.6	36.1	0.28
	Multi	3GL	99	Linear equation	10.8	19.1	30.0	0.30
	Multi	4GL	96	Linear equation	10.7	18.9	28.9	0.30
Enhancement	MF	3GL	440	Linear equation	61.6	122.2	183.6	0.42
	MR	3GL	64	Linear equation	7.1	14.4	17.9	0.28
	Multi	3GL	428	“Plateau” curve	49.8	103.8	165.1	0.39
	Multi	4GL	190	“Plateau” curve	18.9	27.9	49.8	0.26
	PC	3GL	53	Asymptotic equation	5.3	9.2	15.1	0.28

shows the time (sequential) by data set. Its column “Prediction” refers to the time of using the proposed PSO-SRE to predict the effort of a software project for each of the datasets. As shown in Table 11, the proposed PSO-SRE is able to predict the effort of a software project in less than half a minute.

6. Conclusions

The results showed in the Table 9 and Table 10 allow us accepting the following alternative hypothesis formulated in the Section 1 of our study in favor of PSO-SRE for seven of the eight data sets (six of them at 99% of confidence, and the seventh one at 95% of confidence):

Prediction accuracy of the PSO-SRE is statistically not equal to that of the SRE when these two models are applied to predict the development effort of software projects using the AFP as the independent variable.

Regarding the remaining data set, the following null hypothesis is accepted at 99% of confidence:

Prediction accuracy of the PSO-SRE is statistically equal to that of the SRE when these two models are applied to predict the development effort of software projects using the AFP as the independent variable.

As for the comparison between the PSO-SRE and RS, the following hypothesis can be accepted in favor of the PSO-SRE for the eight data sets at 99% of confidence:

Prediction accuracy of the PSO-SRE is statistically not equal to that of the RS when these two models are applied to predict the development effort of software projects using the AFP as the independent variable.

We can conclude that a software manager can apply PSO-SRE for predicting the development effort of a software project taking into account the following TD, DP, and PLT when AFP is used as the independent variable:

(a)

New software projects coded in 3GL and developed in either Mainframe or Multiplatform and coded in 4GL and developed in Multiplatform.

(b)

Software enhancement projects coded in 3GL and developed in Multiplatform, MidRange or personal computer, as well as in those projects coded in 4GL and developed in Multiplatform.

(c)

Since the performance of the PSO-SRE resulted statistically equal than SRE, a software manager could also apply PSO-SRE as alternative to an SRE to software enhancement projects coded in 3GL and developed in Mainframe.

Regarding PSO-SRE optimization, from a general perspective, the best prediction accuracy by data set was obtained when the number of iterations was between 250 and 500, and the swarm size between 50 and 250.

7. Discussion

In software prediction, one of the most common predicted software variables has been effort, which is commonly measured in person-hours or person-month. SDEP is needed for managers to estimate the cost of projects and then for budgeting and bidding; actually, its importance can be showed in the hundreds of studies published in the last forty years. Thus, in the present study, the PSO was applied for optimizing the parameters of SDEP equations. The prediction accuracy of the PSO-SRE was compared to that obtained from SRE. Both types of models were generated based on eight data sets of software projects selected by observing the guidelines of the ISBSG.

In comparing our study with those ten identified ones where PSO has been applied to SDEP and described in Table 1, we identify the following issues:

• None of them generate their models by using a recent repository of software projects.
• Regarding the four studies where the ISBSG is used (1) their releases correspond to those published in the years 2007 and 2009, (2) all of them only select one data set from the ISBSG whose sizes are between 134 and 505, and (3) none of them take into account the version of the FSM to select the data set; whereas in our study, (1) the ISBSG release 2018 was used, (2) eight data sets containing between 53 and 440 projects were selected, and (3) all of them took into account the guidelines suggested by the ISBSG, including the type of FSM, that is, our data sets did not mix IFPUG V4 type with V4 and post V4 one.
• The majority of them base their conclusions on a biased prediction accuracy measure, and on a nondeterministic validation method.
• The half of them bases their conclusions on statistically significance.

We did not find any study having all of the following characteristics as ours when proposed the PSO-SRE:

(1)

The use of PSO incorporating an additional component by allowing automatic completion, in a single step, of the selection of the SDEP model, and automatic adjustment of the parameters of the SDEP model.

(2)

New and enhancement software projects obtained from the ISBSG release 2018.

(3)

Software projects selected taking into account the TD, DP, PLT, and FSM as suggested by the ISBSG.

(4)

Preprocessing of data sets through outliers’ analysis, and correlation and determination coefficients.

(5)

A nonbiased prediction accuracy measure (i.e., AR) to compare the performance between PSO-SRE and SRE models.

(6)

The use of a deterministic validation method for training and testing the models (i.e., LOOCV)

(7)

Selection of a suitable statistical test based on number of data sets to be compared, data dependence, and data distribution for comparing the prediction accuracy between PSO-SRE and SRE by data set.

(8)

Hypotheses tested from statistically significance.

Our manuscript also followed all of the six guidelines when a new SDEP model is proposed [43] by (1) confirming that our PSO-SRE algorithm outperforms a statistical model (i.e., SRE), when PSO-SRE outperformed to SRE in seven of the eight data sets with statistical significance, (2) taking into account the heteroscedasticity, skewness, and heterogeneity of effort and size data of software projects, (3) using statistical tests to compare the performance between prediction models, (4) explaining in detail how our PSO-SRE is applied, (5) justifying the selection of any statistical test we used, and (6) including the criteria followed for selecting the data sets of software projects from the ISBSG.

A first limitation of the present study that reduces the generalization of our conclusions is related to the number of data sets used, that is, in spite of the ISBSG contains more than eight thousands of software projects, we could only select eight data sets observing the guidelines of the ISBSG. A second one is that only 20 prediction models are considered based on simple SRE (Table 2). Finally, a third limitation is that we did not consider other more complex ML prediction models.

As for external threat validity, the prediction accuracy of PSO-SRE will depend on an accurate estimation performed by the practitioner on the independent variable value (i.e., the size measured in AFP).

Another limitation regarding the use of heuristic algorithms (PSO in this paper) is that they prune the search space and can discard useful regions. We are aware that the proposed method, despite its good behavior for predicting the effort of software projects, can have a different performance for other optimization problems.

Future work will be related to the application of other metaheuristics for optimizing the parameters for the SRE. We will intent to use a greater number of datasets, whose data is current and reflecting the heterogenic evolution of these data. Alternative models will also be proposed to predict the effort of new and enhancement software projects such as those based on classifiers [64,65]. Moreover, additional prediction accuracy measure criteria will be take account such as standardized accuracy and effect size [66]. Finally, a modification to the algorithm can be added to take duplicate values into account and to act similarly between them, as well as to apply alternative update mechanisms as in [62] for the velocity update, and test it against the one currently used. We will also explore newer and improved implementations of PSO.