Autonomated Inspection Policy for Smart Factory—An Improved Approach
Abstract
1. Introduction
2. Literature Review
3. Problem Definition, Notation, and Assumptions
3.1. Problem Definition
3.2. Assumptions
- 1.
- 2.
- It is assumed that shortages are not allowed. A single type of item produced at a variable production rate, where production cost depends on the production rate, material cost, die/tool cost for each item, i.e., production cost (Sarkar et al. [54]).
- 3.
- A single type product is first produced without imperfection at the beginning of the production. After some time, the process transfers to the out-of-control state and begins to create faulty products until the production run ends. (Paul et al. [61]).
- 4.
- This model assumes that the probability of defectiveness for the in in-control state must be less than that for the out-of-control state i.e., , as a more general defective production rate in the in-control situation reduces the defective item production in the out-of-control situation (Sarkar et al. [6]).
- 5.
- To maintain industry reputation, the concept of inspection is adopted for both process and searching to ensure high product quality. The faulty or imperfect items are salvaged with some cost . The smart autonomation policy (Dey et al. [8]) is adopted for inspection, and an investment is considered for the autonomated inspection, which provides an error-free inspection process.
- 6.
- A warranty period is considered for non-inspected products, and for that warranty period some warranty cost is implied along with other costs (Lin et al. [62]).
4. Model Formulation
4.1. Some Special Cases
4.1.1. Case I
4.1.2. Case II
4.1.3. Case III
4.1.4. Case IV
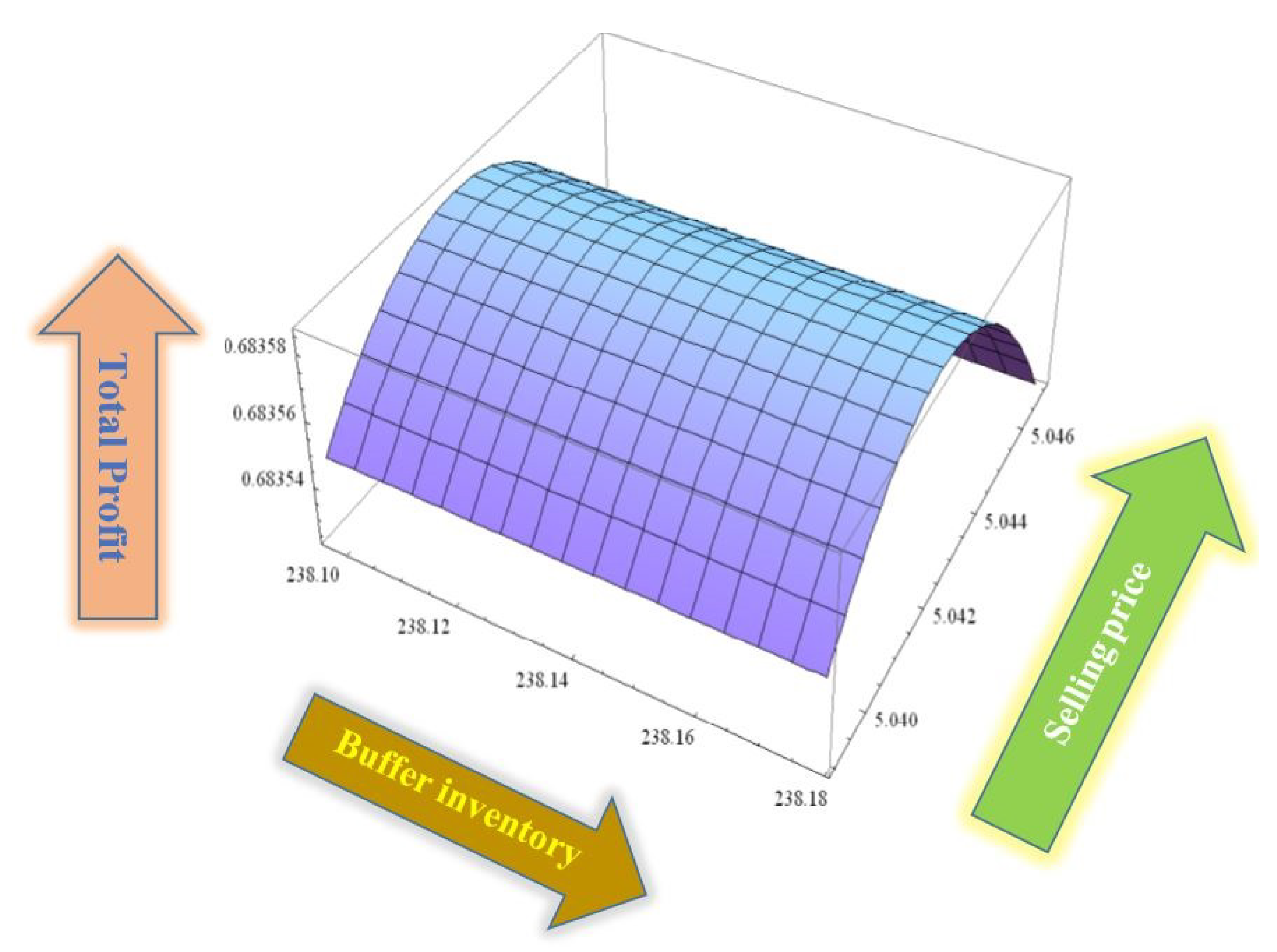
5. Numerical Experiments
6. Discussions
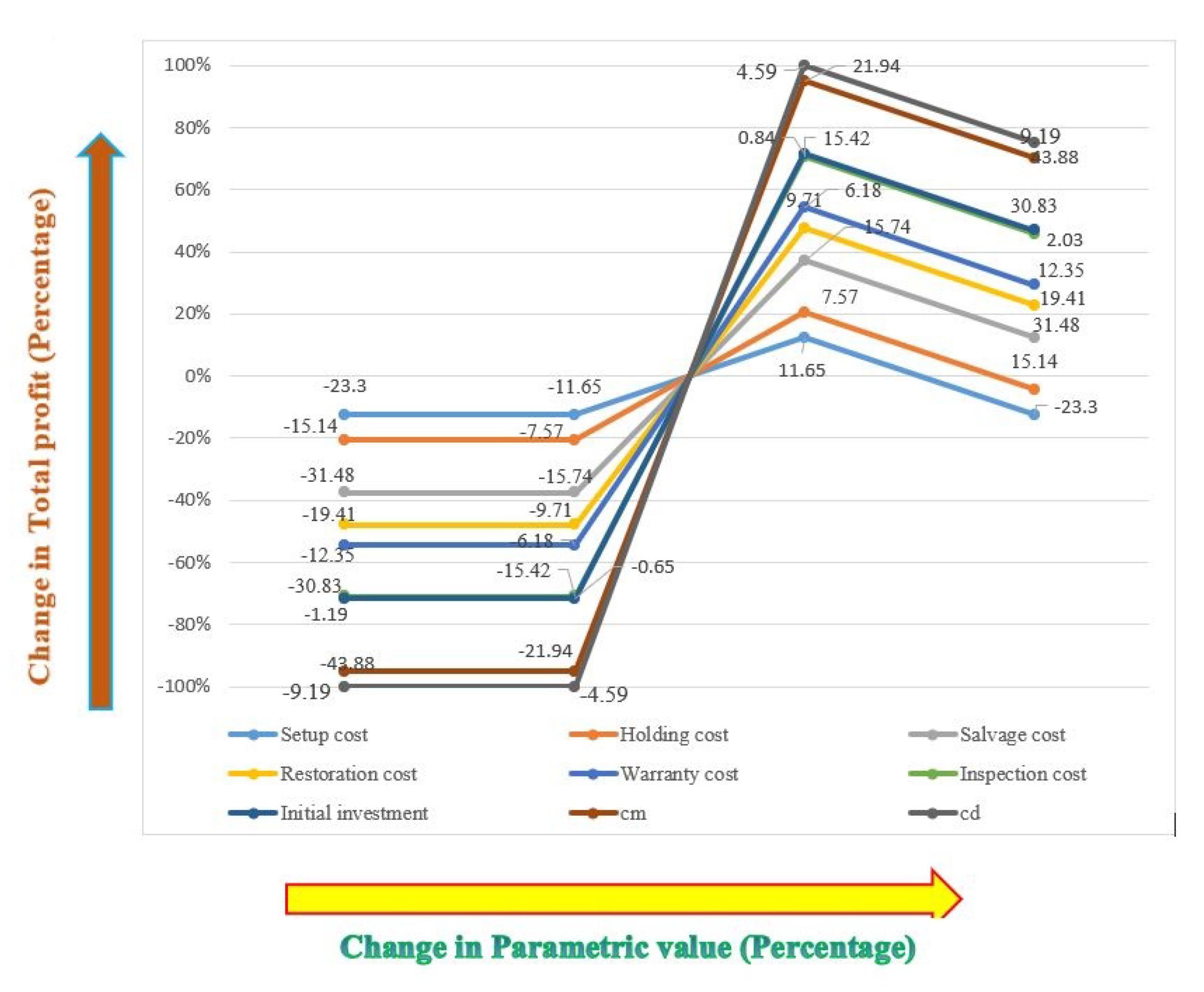
Sensitivity Analysis
- If setup cost increases, the expected total profit per item must decrease. To increase the total profit, the system setup costs can be diminished.
- Table 6 reflects that the increased value of decreases the total profit per item . The holding cost can be diminished by reducing the run length of production . The reduction of the production run length will help to reduce the production and simultaneously reduce the holding cost and increase the total system profit.
- From Table 6, one can find that, if warranty cost, i.e., , increases, the total profit per item decreases. To increase the profit, the manufacturer would have to produce additional perfect items, such that less warranty cost is required, which directly helps to increase the profit of each item.
- Salvage cost has a significant impact on the total profit; this can be observed from Table 6. Table 6 confirms that an increment in salvage cost results in a reduction of the total profit per item . The incrementation of results in an increase in the number of faulty items, which indicates the inspection of huge items, i.e., incrementation of inspection cost, causes low total profit.
- The effect of rework cost on total profit is clearly expressed in Table 6. An increased value of implies more rework cost as well as low profit per item. Therefore, rework cost can be controlled by reducing imperfect items. Additionally, reduced production run time can reduce the total number of imperfect items and cause higher rework cost. Therefore, the production run length decreases as increases.
- If the system is operated at increased inspection cost system, then the total profit per item must decrease. The reduction of the inspection cost to the manufacturer must decrease the inspected fraction batch Therefore, decreases as increases.
- Parameter , i.e., the initial inspection cost for process quality and product is slightly sensitive, which is clear from Table 6. Increments in reduced the profit per item.
- The values of and are significantly sensitive toward the production costs. Increments in these parameters lead to low profit per item.
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Decision Variables | Description |
| length of production-run (unit time) | |
| production rate (unit) | |
| the first fraction of non-inspected items in a batch size (units) | |
| the fraction of second non-inspected for a batch (units) | |
| selling price ($ per unit) | |
| investment for autonomated inspection ($/unit) | |
| Parameters | Description |
| product demand per unit of time, (units/unit time) | |
| cost of stock of products per unit time ($/unit/unit time) | |
| reworking cost of remaking the imperfect products ($/defective lot) | |
| production material cost per item ($/unit) | |
| production percentage of imperfect production in-control situation | |
| tool/die costs of production per item ($/unit) | |
| production percentage of imperfect products in out-of-control situation, | |
| cost of setup for running smooth production ($/setup) | |
| warranty cost of non-searching products defective lots | |
| ($/non-inspected defective lot) | |
| repairing cost to make the system in-control | |
| salvaged cost after inspection for imperfect products ($/defective lot) | |
| development cost for production per item ($/unit) | |
| imperfect cost including the cost of defective lot ($/defective lot); | |
| inspection cost for process checking for maintaining | |
| the present situation of the system ($) | |
| inspection cost per unit ($/unit) | |
| random elapsed time of system in in-control state | |
| probability density function of | |
| lifetime mean value of | |
| distribution function of | |
| scaling parameter related to demand | |
| survival function of i.e., | |
| expected total profit per item ($/unit) |
Appendix A
References
- Angelopoulou, A.; Mykoniatis, K.; Boyapati, N.R. Industry 4.0: The use of simulation for human reliability assessment. Procedia Manuf. 2020, 42, 296–301. [Google Scholar] [CrossRef]
- Bueno, A.; Filho, M.G.; Castagnoli, R. Smart production planning and control in the Industry 4.0 context: A systematic literature review. Comput. Ind. Eng. 2020, 149, 106774. [Google Scholar] [CrossRef]
- Ghosh, D.; Sant, T.G.; Kuiti, M.R.; Swami, S.; Shankar, R. Strategic decisions, competition and cost-sharing contract under industry 4.0 and environmental considerations. Resour. Conserv. Recycl. 2020, 162, 105057. [Google Scholar] [CrossRef]
- Dey, B.K.; Sarkar, B.; Sarkar, M.; Pareek, S. An integrated inventory model involving discrete setup cost reduction, variable safety factor, selling price dependent demand, and investment. Rairo Oper. Res. 2019, 53, 39–57. [Google Scholar] [CrossRef]
- Sarkar, B.; Saren, S. Product inspection policy for an imperfect production system with inspection errors and warranty cost. Eur. J. Oper. Res. 2016, 248, 263–271. [Google Scholar] [CrossRef]
- Sarkar, B.; Sett, B.K.; Sarkar, S. Optimal production run time and inspection errors in an imperfect production system with warranty. J. Ind. Manag. Optim. 2018, 14, 267–282. [Google Scholar] [CrossRef]
- Sett, B.; Sarkar, S.; Sarkar, B. Optimal buffer inventory and inspection errors in an imperfect production system with regular preventive maintenance. Int. J. Adv. Manuf. Technol. 2017, 90, 545–560. [Google Scholar] [CrossRef]
- Dey, B.K.; Pareek, S.; Tayyab, M.; Sarkar, B. Autonomation policy to control work-inprocess inventory in a smart production system. Int. J. Prod. Res. 2020, in press. [Google Scholar] [CrossRef]
- Bettayeb, B.; Bassetto, S.J. Impact of type-II inspection errors on a risk exposure control approach based quality inspection plan. J. Manuf. Syst. 2016, 40, 87–95. [Google Scholar] [CrossRef]
- Hao, S.; Yang, J.; Berenguer, C. Condition-based maintenance with imperfect inspections for continuous degradation processes. Appl. Math. Model. 2020, 86, 311–334. [Google Scholar] [CrossRef]
- Shor, J.; Raz, T. Assessing the impact of human factors on data processing inspection errors. Comput. Ind. Eng. 1988, 14, 503–512. [Google Scholar] [CrossRef]
- Zhang, F.; Shen, J.; Ma, Y. Optimal maintenance policy considering imperfect repairs and non-constant probabilities of inspection errors. Reliab. Eng. Syst. Saf. 2020, 193, 106615. [Google Scholar] [CrossRef]
- Porteus, E.L. Optimal lot sizing, process quality improvement and setup cost reduction. Oper. Res. 1986, 34, 137–144. [Google Scholar] [CrossRef]
- Jamal, A.A.M.; Sarker, B.R.; Mondal, S. Optimal manufacturing batch size with rework process at a single-stage production system. Comput. Ind. Eng. 2004, 47, 77–89. [Google Scholar] [CrossRef]
- Cárdenas-Barrón, L.E. On optimal manufacturing batch size with rework process at single-stage production system. Comput. Ind. Eng. 2007, 53, 196–198. [Google Scholar] [CrossRef]
- Cárdenas-Barrón, L.E. Optimal manufacturing batch size with rework in a single-stage production system—A simple derivation. Comput. Ind. Eng. 2008, 55, 758–765. [Google Scholar] [CrossRef]
- Cárdenas-Barrón, L.E. Economic production quantity with rework process at a single-stage manufacturing system with planned backorders. Comput. Ind. Eng. 2009, 57, 1105–1113. [Google Scholar] [CrossRef]
- Sana, S.S. An economic production lot size model in an imperfect production system. Eur. J. Oper. Res. 2010, 201, 158–170. [Google Scholar] [CrossRef]
- Sana, S.S. A production-inventory model in an imperfect production process. Eur. J. Oper. Res. 2010, 200, 451–464. [Google Scholar] [CrossRef]
- Sana, S.S.; Chaudhuri, K.S. 2010. An EMQ model in an imperfect production process. Int. J. Syst. Sci. 2010, 41, 635–646. [Google Scholar] [CrossRef]
- Sana, S.S. Price-sensitive demand for perishable items–an EOQ model. Appl. Math. Comput. 2011, 217, 6248–6259. [Google Scholar] [CrossRef]
- Sarkar, B.; Moon, I. An EPQ model with inflation in an imperfect production system. Appl. Math. Comput. 2011, 217, 6159–6167. [Google Scholar] [CrossRef]
- Yoo, S.H.; Kim, D.; Park, M.S. Lot size and quality investment with quality cost analyses for imperfect production and inspection processes with commercial return. Int. J. Prod. Econ. 2012, 140, 922–933. [Google Scholar] [CrossRef]
- Sarkar, B.; Cárdenas-Barrón, L.E.; Sarkar, M.; Singgih, M.L. An economic production quantity model with random defective rate, rework process and backorders for a single-stage production system. J. Manuf. Syst. 2020, 33, 423–435. [Google Scholar] [CrossRef]
- Sarkar, B.; Dey, B.K.; Pareek, S.; Sarkar, M. A single-stage cleaner production system with random defective rate and remanufacturing. Comput. Ind. Eng. 2020, 106861. [Google Scholar] [CrossRef]
- Saxena, N.; Sarkar, B.; Singh, S.R. Selection of remanufacturing/ production cycles with an alternative market: A perspective on waste management. J. Clean. Prod. 2020, 245, 118935. [Google Scholar] [CrossRef]
- Tayyab, M.; Sarkar, B. Optimal batch quantity in a cleaner multi-stage lean production system with random defective rate. J. Clean. Prod. 2016, 139, 922–934. [Google Scholar] [CrossRef]
- Lopes, R. Integrated model of quality inspection, preventive maintenance and buffer stock in an imperfect production system. Comput. Ind. Eng. 2018, 126, 650–656. [Google Scholar] [CrossRef]
- Kim, M.S.; Kim, J.S.; Sarkar, B.; Sarkar, M.; Iqbal, M.W. An improved way to calculate imperfect items during long-run production in an integrated inventory model with backorders. J. Manuf. Syst. 2018, 47, 153–167. [Google Scholar] [CrossRef]
- Kang, C.W.; Ullah, M.; Sarkar, B.; Hussain, I.; Akhtar, R. Impact of random defective rate on lot size focusing work-in-process inventory in manufacturing system. Int. J. Prod. Res. 2017, 55, 1748–1766. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Sarkar, B.; Hasani, M. Delayed payment policy in multi-product single-machine economic production quality model with repair failure and partial backordering. J. Ind. Manag. Optim. 2020, 16, 1273–1296. [Google Scholar] [CrossRef]
- Sarkar, M.; Sarkar, B. How does an industry reduce waste and consumed energy within a multi-stage smart sustainable biofuel production system? J. Clean. Prod. 2020, 121200. [Google Scholar] [CrossRef]
- Ullah, M.; Sarkar, B. Recovery-channel selection in a hybrid manufacturing-remanufacturing production model with RFID and product quality. Int. J. Prod. Econ. 2020, 219, 360–374. [Google Scholar] [CrossRef]
- Chryssolouris, G.; Patel, S. In Process Control for Quality Assurance. In Industrial High Technology for Manufacturing; McKee, K., Tijunelis, D., Eds.; Marcel Dekker, Inc.: New York, NY, USA, 1987; pp. 609–643. [Google Scholar]
- Salameh, M.K.; Jaber, M.Y. Economic production quantity model for items with imperfect quality. Int. J. Prod. Econ. 2000, 64, 59–64. [Google Scholar] [CrossRef]
- Wang, C.H.; Sheu, S.H. Simultaneous determination of the optimal production-inventory and product inspection policies for a deteriorating production system. Comput. Oper. Res. 2001, 28, 1093–1110. [Google Scholar] [CrossRef]
- Wang, C.H. Integrated production and product inspection policy for a deteriorating production system. Int. J. Prod. Econ. 2005, 95, 123–134. [Google Scholar] [CrossRef]
- Wang, C.H. Economic offline quality control strategy with two types inspection errors. Eur. J. Oper. Res. 2007, 179, 132–147. [Google Scholar] [CrossRef]
- Wang, C.H.; Meng, F.C. Optimal lot size and offline inspection policy. Comput. Math. Appl. 2009, 58, 1921–1929. [Google Scholar] [CrossRef]
- Lee, T.H. Optimal production run length and maintenance schedule for a deteriorating production system. Int. J. Adv. Manuf. Technol. 2009, 43, 959–963. [Google Scholar] [CrossRef]
- Sarkar, B. Supply chain coordination with variable backorder, inspections, and discount policy for fixed lifetime products. Math. Probl. Eng. 2016, 2016, 6318737. [Google Scholar] [CrossRef]
- Khanna, A.; Gautam, P.; Sarker, B.; Jaggi, C.K. Integrated vendor-buyer strategies for imperfect production systems with maintenance and warranty policy. RAIRO Oper. Res. 2020, 54, 435–450. [Google Scholar] [CrossRef]
- Raouf, A.; Jain, J.K.; Sathe, P.T. A cost-minimization model for multi characteristic component inspection. IIE Trans. 1983, 15, 187–194. [Google Scholar] [CrossRef]
- Duffuaa, S.O.; Khan, M. An optimal repeat inspection plan with several classifications. J. Oper. Res. Soc. 2002, 53, 1016–1026. [Google Scholar] [CrossRef]
- Khanna, A.; Kishore, A.; Sarker, B.; Jaggi, C.K. Inventory and pricing decisions for imperfect quality items with inspection errors, sales returns, and partial backorders under inflation. RAIRO Oper. Res. 2020, 54, 287–306. [Google Scholar] [CrossRef]
- Esmaeilian, B.; Sarkis, J.; Lewis, K.; Behdad, S. Blockchain for the future of sustainable supply chain management in Industry 4.0. Resour. Conserv. Recycl. 2020, 163, 105064. [Google Scholar] [CrossRef]
- Souza, M.L.H.; Costa, C.A.; Ramos, G.O.; Righi, R.R. A survey on decision-making based on system reliability in the context of Industry 4.0. J. Manuf. Syst. 2020, 56, 133–156. [Google Scholar] [CrossRef]
- Büchi, G.; Cugno, M.; Castagnoli, R. Smart factory performance and Industry 4.0. Technol. Forecast. Soc. Chang. 2020, 150, 119790. [Google Scholar] [CrossRef]
- Sana, S.S. Optimal selling price and lotsize with time varying deterioration and partial backlogging. Appl. Math. Comput. 2010, 217, 185–194. [Google Scholar] [CrossRef]
- Khanra, S.; Sana, S.S.; Chudhuri, K. An EOQ model for perishable item with stock and price dependent demand rate. Int. J. Math. Oper. Res. 2010, 2, 320–335. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Kalantari, S.S.; Cárdenas-Barrón, L.E. Pricing and lot sizing for an EPQ inventory model with rework and multiple shipments. TOP 2016, 24, 143–155. [Google Scholar] [CrossRef]
- Pal, B.; Sana, S.S.; Chudhuri, K. Multi-item EOQ model while demand is sales price and price break sensitive. Appl. Math. Comput. 2012, 29, 2283–2288. [Google Scholar] [CrossRef]
- Khouja, M.; Mehrez, A. Economic production lot size model with variable production rate and imperfect quality. J. Oper. Res. Soc. 1994, 4, 1405–1417. [Google Scholar] [CrossRef]
- Sarkar, B.; Sana, S.S.; Chaudhuri, K.S. An imperfect production process for time varying demand with inflation and time value of money—An EMQ model. Expert Syst. Appl. 2011, 38, 13543–13548. [Google Scholar] [CrossRef]
- Sarkar, B.; Majumder, A.; Sarkar, M.; Kim, N.; Ullah, M. Effects of variable production rate on quality of products in a single-vendor multi-buyer supply chain management. Int. J. Adv. Manuf. Technol. 2018, 99, 567–581. [Google Scholar] [CrossRef]
- Majumder, A.; Jaggi, C.K.; Sarkar, B. A multi-retailer supply chain model with backorder and variable production cost. RAIRO Oper. Res. 2018, 52, 943–954. [Google Scholar] [CrossRef]
- Dey, B.K.; Sarkar, B.; Pareek, S. A two-echelon supply chain management with setup time and cost reduction, quality improvement and variable production rate. Mathematics 2019, 7, 328. [Google Scholar] [CrossRef]
- Hu, F.; Zong, Q. Optimal production run time for a deteriorating production system under an extended inspection policy. Eur. J. Oper. Res. 2009, 196, 979–986. [Google Scholar] [CrossRef]
- Sun, Z.; Hupman, A.C.; Abbas, A.E. The value of information for price dependent demand. Eur. J. Oper. Res. 2021, 288, 511–522. [Google Scholar] [CrossRef]
- Chen, C.K.; Lo, C.C.; Weng, T.C. Optimal production run length and warranty period for an imperfect production system under selling price dependent on warranty period. Eur. J. Oper. Res. 2017, 259, 401–412. [Google Scholar] [CrossRef]
- Paul, S.K.; Sarker, R.; Essam, D. Managing disruption in an imperfect production–inventory system. Comput. Ind. Eng. 2015, 84, 101–112. [Google Scholar] [CrossRef]
- Lin, Y.H.; Chen, J.M.; Chen, Y.C. The impact of inspection errors, imperfect maintenance and minimal repairs on an imperfect production system. Math. Comput. Model. 2011, 53, 1680–1691. [Google Scholar] [CrossRef]
- Sarkar, M.; Pan, L.; Dey, B.K.; Sarkar, B. Does the autonomation policy really help in a smart production system for controlling defective production? Mathematics 2020, 8, 1142. [Google Scholar] [CrossRef]
- Tiwari, S.; Kazemi, N.; Modak, N.M.; Cárdenas-Barrón, L.E.; Sarkar, S. The effect of human errors on an integrated stochastic supply chain model with setup cost reduction and backorder price discount. Int. J. Prod. Econ. 2020, 226, 107643. [Google Scholar] [CrossRef]
- Sarkar, M.; Chung, B.D. Flexible work-in-process production system in supply chain management under quality improvement. Int. J. Prod. Res. 2020, 58, 3821–3838. [Google Scholar] [CrossRef]
- Sana, S. Preventive maintenance and optimal buffer inventory for products sold with warranty in an imperfect production system. Int. J. Prod. Res. 2012, 50, 6763–6774. [Google Scholar] [CrossRef]
- Liu, Q.; Dong, M.; Chem, F.; Liu, W.; Ye, C. Multi-objective imperfect maintenance optimization for production system with an intermediate buffer. J. Manuf. Syst. 2020, 56, 452–462. [Google Scholar] [CrossRef]
- Ghaleb, M.; Zolfagharinia, H.; Taghipour, S. Real-time production scheduling in the Industry-4.0 context: Addressing uncertainties in job arrivals and machine breakdowns. Comput. Oper. Res. 2020, 123, 105031. [Google Scholar] [CrossRef]
- Sarkar, B.; Sana, S.S.; Chaudhuri, K.S. An Economic production quantity model with stochastic demand in an imperfect production system. Int. J. Serv. Oper. Manag. 2011, 9, 259–283. [Google Scholar] [CrossRef]
- Mishra, U.; Wu, J.Z.; Sarkar, B. A sustainable production-inventory model for a controllable carbon emissions rate under shortages. J. Clean. Prod. 2020, 256, 120268. [Google Scholar] [CrossRef]
- Tiwari, S.; Ahmed, W.; Sarkar, B. Sustainable ordering policies for non-instantaneous deteriorating items under carbon emission and multi-trade-credit-policies. J. Clean. Prod. 2019, 240, 118–183. [Google Scholar] [CrossRef]
- Gao, J.; Xiao, Z.; Wei, H.; Zhou, G. Dual-channel green supply chain management with eco-label policy: A perspective of two types of green products. Comput. Ind. Eng. 2020, 146, 106613. [Google Scholar] [CrossRef]
- Pakseresht, M.; Shirazi, B.; Mahdavi, I.; Mahdavi-Amiri, N. Toward sustainable optimization with stackelberg game between green product family and downstream supply chain. Sustain. Prod. Consum. 2020, 23, 198–211. [Google Scholar] [CrossRef]
- Sarkar, B.; Tayyab, M.; Kim, N.; Habib, M.S. Optimal production delivery policies for supplier and manufacturer in a constrained closed-loop supply chain for returnable transport packaging through metaheuristic approach. Comput. Ind. Eng. 2019, 135, 987–1003. [Google Scholar] [CrossRef]
- Tayyab, M.; Jemai, J.; Han, L.; Sarkar, B. A sustainable development framework for a cleaner multi-item multi-stage textile production system with a process improvement initiative. J. Clean. Prod. 2020, 246, 119055. [Google Scholar] [CrossRef]
- Pei, Z.; Wooldridge, B.R.; Swimberghe, K.R. Manufacturer rebate and channel coordination in O2O retailing. J. Retail. Consum. Serv. 2021, 58, 102268. [Google Scholar] [CrossRef]

| Author (s) | Production System | Inspection | Demand Depend on | Production Rate | OBP |
|---|---|---|---|---|---|
| Cárdenas-Barrón [17] | Imperfect | NA | NA | Constant | NA |
| Dey et al. [8] | Imperfect | Error-free & Autonomation | Selling Price & Quality | Variable | NA |
| Dey et al. [4] | Integrated | NA | Selling price | Constant | NA |
| Hu and Zong [58] | Imperfect | Manual with extended inspection | NA | Constant | NA |
| Lopes [28] | Imperfect | Manual with two type error | NA | Constant | Yes |
| Sarkar and Saren [5] | Imperfect | Manual with two type error | NA | Constant | NA |
| Sarkar et al. [6] | Imperfect | Manual with two type error | NA | Fixed | Yes |
| Sett et al. [7] | Imperfect | Manual with two type error | NA | Constant | Yes |
| Tayyab and Sarkar [27] | Imperfect Multi-stage | NA | NA | Constant | NA |
| Wang [37] | Imperfect | Manual with warranty | NA | Constant | NA |
| This model | Single-stage and smart | Autonomation & error-free | Selling Price | Controllable | Yes |
| ($/Setup) | ($/Unit/Day) | ($/Unit) | ($/Non-Inspected Lot) | ($/Defective Lot) | ($/Defective Lot) | ($/Defective Lot) | ($/Defective Lot) |
|---|---|---|---|---|---|---|---|
| 180 | 4 | 8 | 3 | 150 |
| a | b | c | ||||||
|---|---|---|---|---|---|---|---|---|
| 25 | 1450 | 15 | 45 |
| Cycle Length | Selling | Investment | Production Rate | Production Cost | Total Profit | ||
|---|---|---|---|---|---|---|---|
| (Day) | (Day) | (Day) | Price($) | ($) | (Unit) | ($/Unit) | ($/Unit) |
| This Model | Sarkar et al. [6] | Sarkar and Saren [5] | Hu and Zong [58] | Wang [37] |
|---|---|---|---|---|
| (1.42,0.12,0.47,5.04,11.30, 397.90) | (2.04,0.058,0.251) | (1.85,0.064) | (2.05,0.062,0.239) | (1.83,0.069) |
| $3.89 | $8.48 | $8.90 | $8.49 | $8.97 |
| Parameters | Change (in %) | Change in TP (%) | Parameters | Change (in %) | Change in TP (%) |
|---|---|---|---|---|---|
| 50% | −23.30 | 50% | −15.14 | ||
| 25% | −11.65 | 25% | −7.57 | ||
| −25% | +11.65 | −25% | +7.57 | ||
| −50% | +23.30 | −50% | +15.14 | ||
| 50% | −31.48 | 50% | −12.35 | ||
| 25% | −15.74 | 25% | −6.18 | ||
| −25% | +15.74 | −25% | +6.18 | ||
| −50% | +31.48 | −50% | +12.35 | ||
| 50% | −30.83 | 50% | −19.41 | ||
| 25% | −15.42 | 25% | −9.71 | ||
| −25% | +15.42 | −25% | +9.71 | ||
| −50% | +30.83 | −50% | +19.41 | ||
| 50% | −1.19 | 50% | −9.19 | ||
| 25% | −0.65 | 25% | −4.59 | ||
| −25% | +0.84 | −25% | +4.59 | ||
| −50% | +2.03 | −50% | +9.19 | ||
| 50% | −43.88 | 50% | −5.77 | ||
| 25% | −21.94 | 25% | +12.09 | ||
| −25% | +21.94 | b | −25% | +14.03 | |
| −50% | +43.88 | −50% | − |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sett, B.K.; Dey, B.K.; Sarkar, B. Autonomated Inspection Policy for Smart Factory—An Improved Approach. Mathematics 2020, 8, 1815. https://doi.org/10.3390/math8101815
Sett BK, Dey BK, Sarkar B. Autonomated Inspection Policy for Smart Factory—An Improved Approach. Mathematics. 2020; 8(10):1815. https://doi.org/10.3390/math8101815
Chicago/Turabian StyleSett, Bimal Kumar, Bikash Koli Dey, and Biswajit Sarkar. 2020. "Autonomated Inspection Policy for Smart Factory—An Improved Approach" Mathematics 8, no. 10: 1815. https://doi.org/10.3390/math8101815
APA StyleSett, B. K., Dey, B. K., & Sarkar, B. (2020). Autonomated Inspection Policy for Smart Factory—An Improved Approach. Mathematics, 8(10), 1815. https://doi.org/10.3390/math8101815







