Evaluation of Enterprise Production Based on Spherical Cubic Hamacher Aggregation Operators

Abstract

In the age of the information-based economy and the rapid advancements of data schemes, business management has been faced with extraordinary difficulties and has entered into a reasonable period where the board’s conventional enterprise execution assessment centers around the interests of investors. Speculators accept money-related information as their basis and focus on the investigation of material fascination, and in the event of the off chance that they do not, they cannot confirm the next economy period. In this way, enterprise execution reflects the interests of investors and business strategists for the needs of partners, which is significant for the forthcoming rivalry. Given that, the collection of data is a significant research tool that has lately been considered by researchers for data examination. In this paper, we have established multi-criteria decision-making methods for the assessment of business execution with spherical fuzzy information. We have applied Hamacher aggregation operators such as the spherical cubic fuzzy Hamacher weighted averaging (SCFHWA) operator, the spherical cubic fuzzy Hamacher ordered weighted averaging (SCFHOWA) operator, the spherical cubic fuzzy Hamacher hybrid averaging (SCFHHA) operator, the spherical cubic fuzzy Hamacher weighted geometric (SCFHWG) operator, the spherical cubic fuzzy Hamacher ordered weighted geometric (SCFHOWG) operator, and the spherical cubic fuzzy Hamacher hybrid geometric (SCFHHG) operator for the appraisal of the best choice of enterprise. We ultimately defend the proposed approach with the existing strategies for possibility and adequacy.

1. Introduction

Monetary administration is a significant part of vital administration examination, which explores how enterprises misuse appropriate methodologies to make and maintain competitiveness benefits. Nowadays, research into rivalry has developed exponentially. It is hard to take genuine trait values seriously in the field of decision conditions, because of their multifaceted nature. The concept of fuzzy set (FS) theory presented by Zadeh [1] in 1965. After that Atanassov [2] proposed intuitionistic fuzzy set (IFS) is the extension of Zadeh fuzzy set, which is characterized by membership and non-membership degrees satisfying the condition that sum of membership and non-membership degrees less or equal to 1. Sinani et al. [3] evaluated a third-party logistics provider and the application of the rough Dombi–Hamy mean operator. Shrivastava et al. [4] concentrated their research on organizational learning forms, and this can offer some knowledge about these distinguished disadvantages. Brockman et al. [5] showed that organization information is the reason for picking and defending competitive benefits and a key variable in the enhancement of firm execution. Some investigations have showed a valuable relationship between learning and rigid execution. For instance, Pamucar et al. [6] discussed the application of a hybrid interval tough weighted power-Heronian operator in multi-criteria decision-making. In [7], the researchers practiced the development proportion of information and faced comparable issues. Enterprise execution estimation is the advancement of a market economy inside a certain time, but it is also a logical strategy and useful tool to regulate enterprises for a nation in terms of how to change its economy, social conditions, and patterns of internationalization. How an arrangement of execution examination that accommodates our monetary improvement is shown carries particularly significant operational significance for upgrading the strength of enterprises, improving the administration level, having the venture intensity, and further improving the monetary development quality. Several MAGDM (multi-attribute group decision making) or multi-criteria decision-making (MCDM) issues (such as business, vital financial administration, and medical diagnosis) have been created with the use of aggregation [8,9] operators under probabilistic conditions. Many researchers have presented an ordered weighted average operator and induced aggregation operators, and have then used these operators to develop the decision-making theory. In [10], the researchers contemplated decision and game theory for execution with intuitionistic fuzzy data. In the next section, we quickly review some fuzzy aggregation functions and their corresponding decision-making problems.

Adrian et al. [11] developed the conceptual model for assessment effect on decision making. In [12] Gigoyic et al. presented the application of hybrid GIS spatial multi-criteria decision making for land sliding susceptibility mapping. Many researchers presented scientific ideas to effectively deal with multi-criteria decision-making (MCDM) [13] issues and multi-criteria group decision making (MCGDM) [14,15] problems. It is known to all that intuitionistic fuzzy sets (IFSs) [16] are extremely intriguing research subjects that have drawn the attention of analysts, in light of the fact that these theories have fruitful applications in various fields, for example, cluster analysis, clinical conclusions, design, and acknowledgement. Numerous researchers have shown intuitionistic fuzzy data in their investigation, such as the following examples. Chen et al. [17] utilized a molecule swarm advancement strategy to address the MCDM issue under IVIF numbers. All of the executions of the criteria for choices and weighted and ordered weighted aggregation operators [18,19,20] have a significant role in the cause of aggregation documents. Garg [21] contributed to the MCDM issue for IVIF conditions using SPA. Kaur et al. [22] proposed generalization of cubic intuitionistic fuzzy aggregation operators using t-norm operations and their applications in group decision-making. Li et al. [23] proposed an MCGDM to construct a closeness co-efficient with a non-linear program strategy using IVIF values, and inclination estimations of the attribute were unclear. Liu et al. [24] proposed to examine the MCDM issue using the VIKOR technique and intuitionistic trapezoidal fuzzy data. The concept of MCDM issues has been studied by defining the accuracy and score function. Ye et al. [25] attempted to break down MCDM using a novel score and accuracy function. As of late, analysts have focused on a model covering-based IF rough set with applications to MCDM issues [26,27]. Li et al. [28,29] created heterogeneous MAGDM issues with (A-IVIF) data, and the application of the proposed strategy was defended with a case of real supplier selection. Xu et al. [30] used weighted aggregation operators to resolve MCGDM issues. As of late, the aggregation of data for operators has been an intriguing research subject, especially in the context of Hamacher operations. The operation presented by Hamacher [31], the Hamacher operation, is a mix of algebraic TCN and TN and of Einstein TCN and TN. Jana et al. [32] proposed the assessment of enterprise performance based on picture fuzzy Hamacher aggregation operators. Huang et al. [33] presented intuitionistic fuzzy Hamacher aggregation and their applications in MCDM. Li et al. [34] introduced the Hamacher aggregation operator for an interval-valued intuitionistic fuzzy set and its application to MACDM issues. In [35], Xiao et al. presented the concept of an ordered weighted geometric operator based on IVF. Garg [36] introduced the intuitionistic fuzzy Hamacher aggregation operators with entropy and their application to multiple-attribute decision making problems. Wei et al. [37] presented Hamacher aggregation on a picture fuzzy set. Zhu et al. [38] presented the idea of hesitant fuzzy linguistic aggregation operators based on the Hamacher t-norm and t-conorm. Harish Garg [39] studied generalized geometric aggregation operators based on T-norm operation for complex intuitionistic fuzzy sets and their application to decision-making. Roychowdhury et al. [40] defined the concept of the generalized Hamacher families of triangle operators.

Even though IVIFSs and IFSs have been effectively applied to resolve practical problems, as a general rule, there are a few conditions that cannot be managed by IFSs. Yager [41] introduced the idea of Pythagorean fuzzy set (PyFS). But in real world problems some problems cannot tackled by IFS and PyFS. To overcome such issues Coung [42] presented the idea of picture fuzzy set. If a human viewpoint including more reactions should be cast, for example, as yes, no abstain, or refusal, it cannot be effectively introduced by established FS and IFS. To prevail in this circumstance, the notion of a spherical fuzzy set (SFS) was introduced by Ashraf et al. [43] as another scientific instrument for computational insight issues. An SFS is distinguished by functions called positive, neutral, and negative membership during the data investigation, with the perspective that it can be considered as a speculation of an IFS, the fuzzy set, and the picture fuzzy sets. Ashraf et al. [44] presented the concept of spherical t-norms and t-conorms and their applications in MAGDM. The investigation of aggregation under various fuzzy conditions is a significant research tool in decision-making problems. Numerous scientists have recently examined SFSs and their applications [45,46,47,48,49]. Wei et al. [50] proposed the idea of similarity measures of spherical fuzzy sets. In [51] Liu et al. presented multi-criteria decision-making approach for project selection problem by utilizing the spherical fuzzy sets. In [52] Gundogdu et al. presented spherical fuzzy TOPSIS method. Barkub et al. [53] introduced a new approach to fuzzy TOPSIS method by utilizing entropy measure under spherical fuzzy information. In the view of some new fuzzy algorithms based on SFS conditions, many researchers have anticipated climate and estimated time series. They contemplated extraordinary sorts of Hamacher aggregation operations under a picture fuzzy set for picture fuzzy Hamacher averaging (PFHA) operators and picture fuzzy Hamacher geometric (PFHG) operators and tackled an MCDM problem with the utility and adaptability of the proposed strategy. In this way, in light of Hamacher operation, how SFS can be aggregated is an exceptionally valuable subject. In [54,55] Muneeza et al. proposed new approach of multi-criteria group decision by utilizing the idea of intuitionistic cubic fuzzy aggregation operators. Khan et al. [56] presented the concept of Pythagorean cubic fuzzy aggregation operators and their applications to multi-criteria decision making problems. Khan et al. [57] given the idea of extended TOPSIS method based on Pythagorean cubic fuzzy multi-criteria decision making with incomplete weight information. In [58], the researchers proposed Pythagorean cubic fuzzy aggregation operators by utilizing level of confidence and its application in multi-criteria decision making process.

In this paper, we characterize spherical cubic Hamacher aggregation operators based on conventional arithmetic, geometric operators, and hybrid operations. The SCFSs (Spherical cubic fuzzy sets) have an incredible ability to display the equivocal and loose data of practical life. In the literature, there is a wide range of works identified with applications of fuzzy aggregation based on Hamacher operations in decision-making issues. With this as inspiration, we used a spherical cubic fuzzy Hamacher weighted averaging (SCFHWA) operator, a spherical cubic fuzzy Hamacher ordered weighted averaging (SCFHOWA) operator, a spherical cubic fuzzy Hamacher hybrid averaging (SCFHHA) operator, a spherical cubic fuzzy Hamacher weighted geometric (SCFHWG) operator, a spherical cubic fuzzy Hamacher ordered weighted geometric (SCFHOWG) operator, and a spherical cubic fuzzy Hamacher hybrid geometric (SCFHHG) operator to determine the best enterprise based on execution assessment. We will obtain more accurate results than TSFSs (T-spherical fuzzy sets).

The significant conversation regarding the selection of the best enterprise is explored in Section 1. In Section 2, the basic ideas of the fuzzy set (FS), intuitionistic fuzzy set (IFS), interval-valued fuzzy set (IVFS), cubic fuzzy set (CFS), and spherical fuzzy set (SFs) are reviewed. Additionally, spherical fuzzy aggregation operators are examined. In Section 3, we present the Hamacher aggregation operators on a spherical fuzzy set. In Section 4, we discuss the new idea of a spherical cubic fuzzy set (SCFS) and its fundamental properties. Hamacher operations on a spherical cubic fuzzy set are presented in Section 5. In Section 6, various spherical cubic fuzzy Hamacher aggregation operators are introduced; the SCFHWA, SCFHOWA, SCFHHA, SCFHWG, SCFHOWG, and SCFHHG operators are examined with their properties. The MCDM method is described in Section 7, and the proposed operators are used to determine an MCDM issue, specifically concerning the selection of the best enterprise. Comparison analysis is conducted in Section 8, wherein a near assessment of other related techniques is presented to show the practicality of the proposed strategies. In Section 9, the conclusion is given.

2. Materials and Methods

In this section, some basic definitions of fuzzy set theory are reviewed.

Definition 1.

[1] Let $X$ be a universal set. A fuzzy set $A$ of $X$ is defined by

$$A=\left\{(x, {\mu }_A(x)) |x\in X\right\}$$

(1)

where ${\mu }_A(x):X\to [0,1]$ is the membership function.

Definition 2.

[2] Let $X$ be non-empty universal set. An IFS $B$ of $X$ is defined as

$$B=\{(x,{\widehat{\mu }}_B(x),{\widehat{\nu }}_B(x)) |x\in X\}$$

(2)

where every element $x$ belongs to $X$ the membership function is defined by ${\widehat{\mu }}_B(x):X\to [0,1]$, and the non-membership function ${\widehat{\nu }}_B(x)$: $X\to [0,1]$ with $0\le {\widehat{\mu }}_B(x)+{\widehat{\nu }}_B(x)\le 1$ for $x$ belongs to $X$. The pair $({\widehat{\mu }}_B(x),{\widehat{\nu }}_B(x))$ is an intuitionistic fuzzy number. The degree of hesitation ${\widehat{\pi }}_B(x)=1-{\widehat{\mu }}_B(x)-{\widehat{\nu }}_B(x)$.

Definition 3.

[2] The distance function of two intuitionistic fuzzy numbers, $B_1=({\widehat{\mu }}_{B_1}(x),{\widehat{\nu }}_{B_1}(x))$ and $B_2=({\widehat{\mu }}_{B_2}(x),{\widehat{\nu }}_{B_2}(x))$, is denoted by $d(B_1,B_2)$ and is defined as follows:

$$d(B_1,B_2)=\left|B_1-B_2\right|=\frac{1}{2}(\left|{\widehat{\mu }}_{B_1}(x)-{\widehat{\mu }}_{B_2}(x)|+|{\widehat{v}}_{B_1}(x)-{\widehat{v}}_{B_2}(x)\right|).$$

Definition 4.

[42] Let $X$ be a universal set. A picture fuzzy set $\widehat{P}$ is defined as follows:

$$\widehat{P}=\left\{({\widehat{u}}_{\widehat{p}}(x),{\widehat{w}}_{\widehat{p}}(x),{\widehat{v}}_{\widehat{p}}(x)) |x\in X\right\}$$

(3)

where ${\widehat{u}}_{\widehat{p}}(x):X\to [0,1]$, ${\widehat{w}}_{\widehat{p}}(x):X\to [0,1]$, and ${\widehat{v}}_{\widehat{p}}(x):X\to [0,1]$ are called positive, neutral, and negative degrees of membership of picture fuzzy set $P$, respectively. Here, $0\le {\widehat{u}}_{\widehat{p}}(x)+{\widehat{w}}_{\widehat{p}}(x)+{\widehat{v}}_{\widehat{p}}(x)\le 1$ for all $x$ belongs to $X$. The degree of hesitation is represented by ${\widehat{\pi }}_B(x)=1-({\widehat{u}}_{\widehat{p}}(x)+{\widehat{w}}_{\widehat{p}}(x)+{\widehat{v}}_{\widehat{p}}(x))$ for all $x$ belongs to $X$. The triplet $({\widehat{u}}_{\widehat{p}}(x),{\widehat{w}}_{\widehat{p}}(x),{\widehat{v}}_{\widehat{p}}(x))$ is called a picture fuzzy number (PFN).

Definition 5.

[43] Let $X$ be a universal set a spherical fuzzy set. The spherical fuzzy set $S$ is defined as follows:

$$\widehat{S}=\left\{({\widehat{u}}_{\widehat{s}}(x),{\widehat{w}}_{\widehat{s}}(x),{\widehat{v}}_{\widehat{s}}(x)) |\in X\right\},$$

(4)

where ${\widehat{u}}_{\widehat{s}}(x):X\to [0,1]$, ${\widehat{w}}_{\widehat{s}}(x):X\to [0,1]$, and ${\widehat{v}}_{\widehat{s}}(x):X\to [0,1]$ are called positive, neutral, and negative degrees of membership of spherical fuzzy set S, respectively. Here, $0\le {({\widehat{u}}_{\widehat{s}}(x))}^2+{({\widehat{w}}_{\widehat{s}}(x))}^2+{({\widehat{v}}_{\widehat{s}}(x))}^2\le 1$. The degree of hesitation or indeterminacy degree of $S$ is defined as ${\widehat{\gamma }}_{\widehat{s}}(x)=\sqrt{1-({({\widehat{u}}_{\widehat{s}}(x))}^2+{({\widehat{w}}_{\widehat{s}}(x))}^2+{({\widehat{v}}_{\widehat{s}}(x))}^2)}$ for all $x\in X$.

Definition 6.

[14] A cubic fuzzy set (CFS) C in $X$ is defined as follows

$$C=\left\{x,[u_C{}^{-}(x),u_C{}^{+}(x)],v_c(x) |x\in X\right\}$$

(5)

where the first element is an interval-valued fuzzy set, which represents the membership degree, and the second element is a simple fuzzy set, which represents the non-membership degree.

Definition 7.

[43] The two spherical cubic fuzzy numbers are ${\widehat{S}}_1=\{({\widehat{u}}_{{\widehat{s}}_1}(x),{\widehat{w}}_{{\widehat{s}}_1}(x),{\widehat{v}}_{{\widehat{s}}_1}(x)) |x\in X\}$ and ${\widehat{S}}_2=\{({\widehat{u}}_{{\widehat{s}}_2}(x),{\widehat{w}}_{{\widehat{s}}_2}(x),{\widehat{v}}_{{\widehat{s}}_2}(x)) |x\in X\}$, and $\mathsf{\gamma }>0$. Therefore, the following operations hold:

$$\begin{array}{c}1.{\widehat{S}}^c=({\widehat{v}}_{\widehat{s}}(x),{\widehat{w}}_{\widehat{s}}(x),{\widehat{u}}_{\widehat{s}}(x));\hfill \\ 2.{\widehat{S}}_2\subseteq {\widehat{S}}_1 \iff {\widehat{u}}_{{\widehat{S}}_2}(x)\le {\widehat{u}}_{{\widehat{S}}_1}(x),{\widehat{w}}_{{\widehat{S}}_2}(x)\le {\widehat{w}}_{{\widehat{S}}_1}(x),{\widehat{v}}_{{\widehat{S}}_2}(x)\ge {\widehat{v}}_{{\widehat{S}}_1}(x);\hfill \\ 3.{\widehat{S}}_2{\displaystyle \cup }{\widehat{S}}_1=\left\{max({\widehat{u}}_{{\widehat{S}}_2}(x),{\widehat{u}}_{{\widehat{S}}_1}(x)),min({\widehat{w}}_{{\widehat{S}}_2}(x),{\widehat{w}}_{{\widehat{S}}_1}(x)),min({\widehat{v}}_{{\widehat{S}}_2}(x),{\widehat{v}}_{{\widehat{S}}_1}(x))\right\};\hfill \\ 4.{\widehat{S}}_2{\displaystyle \cap }{\widehat{S}}_1=\left\{min({\widehat{u}}_{{\widehat{S}}_2}(x),{\widehat{u}}_{{\widehat{S}}_1}(x)),min({\widehat{w}}_{{\widehat{S}}_2}(x),{\widehat{w}}_{{\widehat{S}}_1}(x)),max({\widehat{v}}_{{\widehat{S}}_2}(x),{\widehat{v}}_{{\widehat{S}}_1}(x))\right\};\hfill \\ 5.{\widehat{S}}_2\oplus {\widehat{S}}_1=\left\{\sqrt{{({\widehat{u}}_{{\widehat{s}}_2}(x))}^2+{({\widehat{u}}_{{\widehat{s}}_1}(x))}^2-{({\widehat{u}}_{{\widehat{s}}_2}(x))}^2{({\widehat{u}}_{{\widehat{s}}_1}(x))}^2},{\widehat{w}}_{{\widehat{s}}_2}(x).{\widehat{w}}_{{\widehat{S}}_1}(x),{\widehat{v}}_{{\widehat{S}}_2}(x).{\widehat{v}}_{{\widehat{S}}_1}(x)\right\};\hfill \\ 6.{\widehat{S}}_2⨂{\widehat{S}}_1\left\{\begin{array}{c}{\widehat{u}}_{{\widehat{s}}_2}(x).{\widehat{u}}_{{\widehat{s}}_1}(x),\sqrt{{({\widehat{w}}_{{\widehat{s}}_2}(x))}^2+{({\widehat{w}}_{{\widehat{s}}_1}(x))}^2-{({\widehat{w}}_{{\widehat{s}}_2}(x))}^2{({\widehat{w}}_{{\widehat{s}}_1}(x))}^2},\\ \sqrt{{({\widehat{v}}_{{\widehat{s}}_2}(x))}^2+{({\widehat{v}}_{{\widehat{s}}_1}(x))}^2-{({\widehat{v}}_{{\widehat{s}}_2}(x))}^2{({\widehat{v}}_{{\widehat{s}}_1}(x))}^2}\end{array}\right\}\hfill \end{array}$$

3. Hamacher Aggregation Operators on Spherical Fuzzy Set

In this section, we will discuss Hamacher aggregation operators on the spherical fuzzy set. We will define the aggregation operators on the spherical fuzzy Hamacher weighted averaging (SFHWA) operator, spherical fuzzy Hamacher ordered weighted averaging (SFHOWA), spherical fuzzy Hamacher hybrid averaging (SFHHA), and so on.

Definition 8.

Let$S_p=<c_{S_p}(x),{\dot{c}}_{S_p}(x),{\ddot{c}}_{S_p}(x)>(p=1,2\dots m)$be a collection of spherical fuzzy numbers (SFNs) in$X$. Then, $SFHWA$operator$m$is defined as follows:$SFHW{A}_{\varpi }(S_{p_1},S_{p_2},\dots S_{p_m})={\varpi }_1{S}_{p_1}\oplus {\varpi }_2{S}_{p_2}\oplus \dots \oplus {\varpi }_m{S}_{p_m}$, and the weight vector is represented by$\varpi ={({\varpi }_1,{\varpi }_2,\dots .,{\varpi }_m)}^T$with the specific conditions${\sum }_{p=1}^n{\varpi }_p=1$and${\varpi }_p\in [0,1].$Now, by the law$(6)$of spherical fuzzy set number, the SFWA operator by the induction on$m$ is converted to the form mentioned below.

$$SFHW{A}_{\varpi }\left(S_{p_1},S_{p_2},\dots ,S_{p_m}\right)=\left\{\begin{array}{c}\sqrt{\left(\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right){\left(c_{S_p}\left(x\right)\right)}^2\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-{\left(c_{S_p}\left(x\right)\right)}^2\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right){\left(c_{S_p}\left(x\right)\right)}^2\right)}^{{\varpi }_p}-\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-{\left(c_{S_p}\left(x\right)\right)}^2\right)}^{{\varpi }_p}}\right)},\hfill \\ \left(\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\left({\dot{c}}_{S_p}\left(x\right)\right)}^2\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right){\left({\dot{c}}_{S_p}\left(x\right)\right)}^2\right)}^{{\varpi }_p}-\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-{\left({\dot{c}}_{S_p}\left(x\right)\right)}^2\right)}^{2{\varpi }_p}}}\right),\hfill \\ \left(\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\left({\ddot{c}}_{S_p}\left(x\right)\right)}^2\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right){\left({\ddot{c}}_{S_p}\left(x\right)\right)}^2\right)}^{{\varpi }_p}-\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-{\left({\ddot{c}}_{S_p}\left(x\right)\right)}^2\right)}^{2{\varpi }_p}}}\right),\hfill \end{array}\right\}$$

(6)

Definition 9.

Let$S_p=<c_{S_p}(x),{\dot{c}}_{S_p}(x),{\ddot{c}}_{S_p}(x)>(p=1,2\dots m)$be a collection of SFNs in$X$; then, $SFHOWA$operator$m$ is defined as follows:

$$SFHOW{A}_{\varpi }\left(S_{p_1},S_{p_2},\dots ,S_{p_m}\right)=\left\{\begin{array}{c}\sqrt{\left(\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right){\left(c_{S_{\sigma \left(p\right)}}\left(x\right)\right)}^2\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-{\left(c_{S_{\sigma \left(p\right)}}\left(x\right)\right)}^2\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right){\left(c_{S_{\sigma \left(p\right)}}\left(x\right)\right)}^2\right)}^{{\varpi }_p}-\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-{\left(c_{S_{\sigma \left(p\right)}}\left(x\right)\right)}^2\right)}^{{\varpi }_p}}\right)},\hfill \\ \left(\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\left({\dot{c}}_{S_{\sigma \left(p\right)}}\left(x\right)\right)}^2\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right){\left({\dot{c}}_{S_{\sigma \left(p\right)}}\left(x\right)\right)}^2\right)}^{{\varpi }_p}-\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-{\left({\dot{c}}_{S_{\sigma \left(p\right)}}\left(x\right)\right)}^2\right)}^{2{\varpi }_p}}}\right),\hfill \\ \left(\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\left({\ddot{c}}_{S_p}\left(x\right)\right)}^2\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right){\left({\ddot{c}}_{S_{\sigma \left(p\right)}}\left(x\right)\right)}^2\right)}^{{\varpi }_p}-\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-{\left({\ddot{c}}_{S_{\sigma \left(p\right)}}\left(x\right)\right)}^2\right)}^{2{\varpi }_p}}}\right)\hfill \end{array}\right\}$$

(7)

Here, the permutation $({\sigma }_1,{\sigma }_2\dots {\sigma }_m)$ for all $p$, $S_{\sigma (p-1)}\ge S_{\sigma (p)}$, and the weight vector $\varpi ={({\varpi }_1,{\varpi }_2,\dots .,{\varpi }_m)}^T$ with the specific conditions ${\sum }_{p=1}^n{\varpi }_p=1$ and ${\varpi }_p\in [0,1]$.

Definition 10.

Let$S_p= <c_{S_p}(x),{\dot{c}}_{S_p}(x),{\ddot{c}}_{S_p}(x)>(p=1,2\dots m)$be a collection of SFNs in$X$; then, $SFHHA$operator$m$is defined as follows:$SFHH{A}_{\varpi }(S_{p_{\sigma (1)}},S_{p_{\sigma (2)}},\dots ,S_{p_{\sigma (m)}})={\varpi }_1{S}_{p_{\sigma (1)}}\oplus {\varpi }_2{S}_{p_{\sigma (2)}}\oplus ,\dots ,\oplus {\varpi }_m{S}_{p_{\sigma (m)}},$and the weight vector is represented by$\varpi ={({\varpi }_1,{\varpi }_2,\dots ,{\varpi }_m)}^T$with the specific conditions${\sum }_{p=1}^n{\varpi }_p=1$and${\varpi }_p\in [0,1].$Here, the$jth$largest weighted SFNs${\tilde{S}}_p$is${\tilde{S}}_{\sigma (p)}=m{\varpi }_p{\tilde{S}}_p(x).$

$$SFHH{A}_{\varpi }\left(S_{p_1},S_{p_2},\dots ,S_{p_m}\right)=\left\{\begin{array}{c}\sqrt{\left(\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right){\left({\tilde{c}}_{S_{\sigma \left(p\right)}}\left(x\right)\right)}^2\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-{\left({\tilde{c}}_{S_{\sigma \left(p\right)}}\left(x\right)\right)}^2\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right){\left({\tilde{c}}_{S_{\sigma \left(p\right)}}\left(x\right)\right)}^2\right)}^{{\varpi }_p}-\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-{\left({\tilde{c}}_{S_{\sigma \left(p\right)}}\left(x\right)\right)}^2\right)}^{{\varpi }_p}}\right)},\hfill \\ \left(\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\left({\tilde{\dot{c}}}_{S_{\sigma \left(p\right)}}\left(x\right)\right)}^2\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right){\left({\tilde{\dot{c}}}_{S_{\sigma \left(p\right)}}\left(x\right)\right)}^2\right)}^{{\varpi }_p}-\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-{\left({\tilde{\dot{c}}}_{S_{\sigma \left(p\right)}}\left(x\right)\right)}^2\right)}^{2{\varpi }_p}}}\right),\hfill \\ \left(\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\left({\tilde{\ddot{c}}}_{S_p}\left(x\right)\right)}^2\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right){\left({\tilde{\ddot{c}}}_{S_{\sigma \left(p\right)}}\left(x\right)\right)}^2\right)}^{{\varpi }_p}-\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-{\left({\tilde{\ddot{c}}}_{S_{\sigma \left(p\right)}}\left(x\right)\right)}^2\right)}^{2{\varpi }_p}}}\right)\hfill \end{array}\right\}$$

(8)

The weight vector $\varpi ={({\varpi }_1,{\varpi }_2,\dots .,{\varpi }_m)}^T$ with the specific conditions ${\sum }_{p=1}^n{\varpi }_p=1$ and ${\varpi }_p\in [0,1],$ where $m$ is known as the balancing coefficient.

4. Spherical Cubic Fuzzy Set and Their Operations

In this section, we discuss Hamacher aggregation operators on the spherical cubic fuzzy set. We will define the aggregation operators on the spherical cubic fuzzy Hamacher weighted averaging (SCFHWA) operator, the spherical cubic fuzzy Hamacher ordered weighted averaging (SCFHOWA) operator, the spherical cubic fuzzy Hamacher hybrid averaging (SCFHHA) operator, the spherical cubic fuzzy Hamacher weighted geometric (SCFHWG) operator, the spherical cubic fuzzy Hamacher ordered weighted geometric (SCFHOWG) operator, and the spherical cubic fuzzy Hamacher hybrid geometric (SCFHHG) operator.

Definition 11.

Let$X$be any non-empty set. The spherical cubic fuzzy set$S$in$X$is defined as follows:

$$S=\{x,<c_S,{\dot{c}}_S,{\ddot{c}}_S>|x\in X\}$$

(9)

Here, $<[{\widehat{e}}^{-},{\widehat{e}}^{+}],\widehat{\lambda }>$ represents the membership degree, $<[{\widehat{n}}^{-},{\widehat{n}}^{+}],\widehat{\mu }>$ represents the neutral degree, and $<[{\widehat{r}}^{-},{\widehat{r}}^{+}],\widehat{\delta }>$ represents the non-membership degree of $S$, where $[{\widehat{e}}^{-},{\widehat{e}}^{+}]\subseteq [0,1]$, $[{\widehat{r}}^{-},{\widehat{r}}^{+}]\subseteq [0,1]$, $[{\widehat{n}}^{-},{\widehat{n}}^{+}]\subseteq [0,1]$ and $\widehat{\lambda }:X\to [0,1]$, $\widehat{\mu }:X\to [0,1]$, $\widehat{\delta }:X\to [0,1]$ are under the conditions of $sup[{\widehat{e}}^{-},{\widehat{e}}^{+}]+sup[{\widehat{n}}^{-},{\widehat{n}}^{+}]+sup[{\widehat{r}}^{-},{\widehat{r}}^{+}]\le 1$ and $\widehat{\lambda }+\widehat{\lambda }+\widehat{\delta }\le 1$. We named $(<[{\widehat{e}}^{-},{\widehat{e}}^{+}],\widehat{\lambda }>,<[{\widehat{n}}^{-},{\widehat{n}}^{+}],\widehat{\mu }>,<[{\widehat{r}}^{-},{\widehat{r}}^{+}],\widehat{\delta }>)$ as spherical cubic fuzzy numbers (SCFNs), and the degree of hesitation is defined as $\widehat{\pi }(S)=\{[1-({\widehat{e}}^{-}+{\widehat{n}}^{-}+{\widehat{r}}^{-}),1-({\widehat{e}}^{+}+{\widehat{n}}^{+}+{\widehat{r}}^{+})],<1-(\widehat{\lambda }+\widehat{\mu }+\widehat{\delta })>\}.$

Example 1.

Let$X=(x_1,x_2,x_3)$ be a set of SCFs, defined as follows:

$$S=\left\{\begin{array}{c}(x_1,([0.2,0.4],0.1),([0.1,0.1],0.3),[0.1,0.2],0.1),\hfill \\ (x_2,([0.1,0.1],0.2),([0.1,0.2],0.2),[0.1,0.2],0.3),\hfill \\ (x_3,([0.1,0.2],0.3),([0.1,0.3],0.2),[0.1,0.2],0.2)\hfill \end{array}\right\}.$$

Therefore, $S$ satisfies the definition of SCFs.

Definition 12.

Let$S= (<[{\widehat{e}}^{-},{\widehat{e}}^{+}],\widehat{\lambda }>,<[{\widehat{n}}^{-},{\widehat{n}}^{+}],\widehat{\mu }>,<[{\widehat{r}}^{-},{\widehat{r}}^{+}],\widehat{\delta }>)$be the spherical cubic fuzzy number (SCFN). Therefore, the score function is defined as

$$S_c(S)=(([{({\widehat{e}}^{-},{\widehat{e}}^{+}+\widehat{\lambda })}^2+{({\widehat{n}}^{-},{\widehat{n}}^{+}+\widehat{\mu })}^2-{({\widehat{r}}^{-},{\widehat{r}}^{+}+\widehat{\delta })}^2])/9)$$

(10)

where $S_c(S)\in [-1,1].$

Definition 13.

An accuracy function$A(S)$is defined as

$$A(S)=(([{({\widehat{e}}^{-}+{\widehat{e}}^{+}+\widehat{\lambda })}^2+{({\widehat{n}}^{-}+{\widehat{n}}^{+}+\widehat{\mu })}^2-{({\widehat{r}}^{-}+{\widehat{r}}^{+}+\widehat{\delta })}^2])/9)$$

(11)

where $A(S)\in [0,1].$

Definition 14.

Let$S_2= (<[{\widehat{e}}_2^{-},{\widehat{e}}_2^{+}],{\widehat{\lambda }}_2>,<[{\widehat{n}}_2^{-},{\widehat{n}}_2^{+}],{\widehat{\mu }}_2>,<[{\widehat{r}}_2^{-},{\widehat{r}}_2^{+}],{\widehat{\delta }}_2>)$and$S_1= (<[{\widehat{e}}_1^{-},{\widehat{e}}_1^{+}],{\widehat{\lambda }}_1>,<[{\widehat{n}}_1^{-},{\widehat{n}}_1^{+}],{\widehat{\mu }}_1>,<[{\widehat{r}}_1^{-},{\widehat{r}}_1^{+}],{\widehat{\delta }}_1>)$be two SCFNs. Therefore,

$$\begin{array}{c}1. S_c(S_1)>S_c(S_2)\Rightarrow S_1>S_2,\\ 2. S_c(S_1)<S_c(S_2)\Rightarrow S_1<S_2,\\ 3. S_c(S_1)=S_c(S_2),\\ (i)A(S_1)>A(S_2)\Rightarrow S_1>S_2,\\ (ii) A(S_1)<A(S_2)\Rightarrow S_1<S_2.\end{array}$$

Definition 15.

Let$S_1=\{x,<c_{S_1},{\dot{c}}_{S_1},{\ddot{c}}_{S_1}> | x\in X\}$, $S_2=\{x,<c_{S_2},{\dot{c}}_{S_2},{\ddot{c}}_{S_2}> | x\in X\}$, defined as$S_2= (<[{\widehat{e}}_2^{-},{\widehat{e}}_2^{+}],{\widehat{\lambda }}_2>,<[{\widehat{n}}_2^{-},{\widehat{n}}_2^{+}],{\widehat{\mu }}_2>,<[{\widehat{r}}_2^{-},{\widehat{r}}_2^{+}],{\widehat{\delta }}_2>)$and$S_1= (<[{\widehat{e}}_1^{-},{\widehat{e}}_1^{+}],{\widehat{\lambda }}_1>,<[{\widehat{n}}_1^{-},{\widehat{n}}_1^{+}],{\widehat{\mu }}_1>,<[{\widehat{r}}_1^{-},{\widehat{r}}_1^{+}],{\widehat{\delta }}_1>)$, be two SCFNs in$X$and$\gamma \ge 0$. Therefore, the following operations hold:

$$\begin{array}{c}1.S_1\oplus S_2=\left\{\begin{array}{c}\left(\begin{array}{c}\left[\sqrt{{(\widehat{e}₁{}^{-})}^2+{(\widehat{e}₂{}^{-})}^2-{(\widehat{e}₁{}^{-})}^2{(\widehat{e}₂{}^{-})}^2, }\sqrt{{(\widehat{e}₁{}^{+})}^2+{(\widehat{e}₂{}^{+})}^2-{(\widehat{e}₁{}^{+})}^2{(\widehat{e}₂{}^{+})}^2}\right],\\ \sqrt{{(\widehat{\lambda }₁)}^2+{(\widehat{\lambda }₂)}^2-{(\widehat{\lambda }₁)}^2{(\widehat{\lambda }₂)}^2}\end{array}\right),\\ ([\widehat{n}₁{}^{-}\widehat{n}₂{}^{-},\widehat{n}₁{}^{+}\widehat{n}₂{}^{+}],\widehat{\mu }₁\widehat{\mu }₂)([\widehat{r}₁{}^{-}\widehat{r}₂{}^{-},\widehat{r}₁{}^{+}\widehat{r}₂{}^{+}],\widehat{\delta }₁\widehat{\delta }₂)\end{array}\right\};\hfill \\ 2.S_1\otimes S_2=\left\{\begin{array}{c}\left(\left[\widehat{e}₁{}^{-}\widehat{e}₂{}^{-},\widehat{e}₁{}^{+}\widehat{e}₂{}^{+}\right],\widehat{\lambda }₁\widehat{\lambda }₂\right),\\ \left(\begin{array}{c}[\sqrt{{(\widehat{n}₁{}^{-})}^2+{(\widehat{n}₂{}^{-})}^2-{(\widehat{n}₁{}^{-})}^2{(\widehat{n}₂{}^{-})}^2, }\sqrt{{(\widehat{n}₁{}^{+})}^2+{(\widehat{n}₂{}^{+})}^2-{(\widehat{n}₁{}^{+})}^2{(\widehat{n}₂{}^{+})}^2}],\\ \sqrt{{(\widehat{\mu }₁)}^2+{(\widehat{\mu }₂)}^2-{(\widehat{\mu }₁)}^2{(\widehat{\mu }₂)}^2}\end{array}\right),\\ \left(\begin{array}{c}\left[\sqrt{{\left(\widehat{r}₁{}^{-}\right)}^2+{\left(\widehat{r}₂{}^{-}\right)}^2-{\left(\widehat{r}₁{}^{-}\right)}^2{\left(\widehat{r}₂{}^{-}\right)}^2, }\sqrt{{\left(\widehat{r}₁{}^{+}\right)}^2+{\left(\widehat{r}₂{}^{+}\right)}^2-{\left(\widehat{r}₁{}^{+}\right)}^2{\left(\widehat{r}₂{}^{+}\right)}^2}\right],\\ \sqrt{{\left(\widehat{\delta }₁\right)}^2+{\left(\widehat{\delta }₂\right)}^2-{\left(\widehat{\delta }₁\right)}^2{\left(\widehat{\delta }₂\right)}^2}\end{array}\right)\end{array}\right\};\hfill \\ 3. S^{\gamma }=\left\{\begin{array}{c}\left(\left[{\left(\widehat{e}{}^{-}\right)}^{\gamma },{\left(\widehat{e}{}^{+}\right)}^{\gamma }\right],{\left(\widehat{\lambda }\right)}^{\gamma }\right),\left(\left[{\left(\widehat{n}{}^{-}\right)}^{\gamma },{\left(\widehat{n}{}^{+}\right)}^{\gamma }\right],{\left(\widehat{\mu }\right)}^{\gamma }\right),\\ \left(\left[\sqrt{1-{\left(1-{\left({\widehat{r}}^{-}\right)}^2\right)}^{\gamma }},\sqrt{1-{\left(1-{\left({\widehat{r}}^{+}\right)}^2\right)}^{\gamma }}\right],\sqrt{1-{\left(1-{\left(\widehat{\delta }\right)}^2\right)}^{\gamma }}\right)\end{array}\right\};\hfill \\ 4.\gamma S=\left\{\begin{array}{c}\left(\left[\sqrt{1-{\left(1-{\left(\widehat{e}{}^{-}\right)}^2\right)}^{\gamma }},\sqrt{1-{\left(1-{\left(\widehat{e}{}^{+}\right)}^2\right)}^{\gamma }}\right],\sqrt{1-{\left(1-{\left(\widehat{\lambda }\right)}^2\right)}^{\gamma }}\right),\\ \left(\left[\sqrt{1-{\left(1-{\left(\widehat{n}{}^{-}\right)}^2\right)}^{\gamma }},\sqrt{1-{\left(1-{\left(\widehat{n}{}^{+}\right)}^2\right)}^{\gamma }}\right],\sqrt{1-{\left(1-{\left(\widehat{\mu }\right)}^2\right)}^{\gamma }}\right),\left(\left[{\left({\widehat{r}}^{-}\right)}^{\gamma },{\left({\widehat{r}}^{+}\right)}^{\gamma }\right],{\left(\widehat{\delta }\right)}^{\gamma }\right)\end{array}\right\}\hfill \end{array}$$

Definition 16.

Let$S₂= \left(<\left[\widehat{e}₂{}^{-},\widehat{e}₂{}^{+}\right],\widehat{\lambda }₂>,<\left[\widehat{n}₂{}^{-},\widehat{n}₂{}^{+}\right],\widehat{\mu }₂>,<\left[\widehat{r}₂{}^{-},\widehat{r}₂{}^{+}\right],{\widehat{\delta }}_2>\right)$and$S₁= \left(<\left[\widehat{e}₁{}^{-},\widehat{e}₁{}^{+}\right],\widehat{\lambda }₁>,<\left[\widehat{n}₁{}^{-},\widehat{n}₁{}^{+}\right],\widehat{\mu }₁>,<\left[\widehat{r}₁{}^{-},\widehat{r}₁{}^{+}\right],\widehat{\delta }₁>\right)$be two SCFNs in$X$. Therefore, the distance function of$S₁$and$S₂$is defined as

$$D\left(S₁,S₂\right)=\frac{1}{9}\left(\begin{array}{c}\left|\widehat{e}₁{}^{-}-\widehat{e}₂{}^{-}|+|\widehat{e}₁{}^{+}-\widehat{e}₂{}^{+}|+|\widehat{\lambda }₁-\widehat{\lambda }₂\right|+\\ \left|\widehat{n}₁{}^{-}-\widehat{n}₂{}^{-}|+|\widehat{n}₁{}^{+}-\widehat{n}₂{}^{+}|+|\widehat{\mu }₁-\widehat{\mu }₂\right|+\\ \left|\widehat{r}₁{}^{-}-\widehat{r}₂{}^{-}|+|\widehat{r}₁{}^{+}-\widehat{r}₂{}^{+}|+|\widehat{\delta }₁-{\widehat{\delta }}_2\right|+\end{array}\right)$$

5. Hamacher Operations in SCFs

In this section, we define some new Hamacher operations and properties of SCFs.

Definition 17.

Let$S₁= \left(<\left[\widehat{e}₁{}^{-},\widehat{e}₁{}^{+}\right],\widehat{\lambda }₁>,<\left[\widehat{n}₁{}^{-},\widehat{n}₁{}^{+}\right],\widehat{\mu }₁>,<\left[\widehat{r}₁{}^{-},\widehat{r}₁{}^{+}\right],\widehat{\delta }₁>\right) S₂= \left(<\left[\widehat{e}₂{}^{-},\widehat{e}₂{}^{+}\right],\widehat{\lambda }₂>,<\left[\widehat{n}₂{}^{-},\widehat{n}₂{}^{+}\right],\widehat{\mu }₂>,<\left[\widehat{r}₂{}^{-},\widehat{r}₂{}^{+}\right],{\widehat{\delta }}_2>\right)$be two SCFS in$X$and$\gamma >0$. We determine the following basic Hamacher operators in SCFs, and we determine the following basic Hamacher operators in SCFs.

$$\begin{array}{c}1. S₁\oplus S₂=\left\{\begin{array}{c}\left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{\left(\widehat{e}₁{}^{-}\right)²+\left(\widehat{e}₂{}^{-}\right)²-\left(\widehat{e}₁{}^{-}\right)²\left(\widehat{e}₂{}^{-}\right)²-\left(1-\widehat{f}\right)\left(\widehat{e}₁{}^{-}\right)²\left(\widehat{e}₂{}^{-}\right)²}{1-\left(1-\widehat{f}\right)\left(\widehat{e}₁{}^{-}\right)²\left(\widehat{e}₂{}^{-}\right)²}},\\ \sqrt{\frac{(\widehat{e}₁{}^{+})²+\left(\widehat{e}₂{}^{+}\right)²-\left(\widehat{e}₁{}^{+}\right)²\left(\widehat{e}₂{}^{+}\right)²-\left(1-\widehat{f}\right)\left(\widehat{e}₁{}^{+}\right)²\left(\widehat{e}₂{}^{+}\right)²}{1-\left(1-\widehat{f}\right)\left(\widehat{e}₁{}^{+}\right)²\left(\widehat{e}₂{}^{+}\right)²}}\end{array}\right],\\ \sqrt{\frac{\left(\widehat{\lambda }₁\right)²+\left(\widehat{\lambda }₂\right)²-\left(\widehat{\lambda }₁\right)²\left(\widehat{\lambda }₂\right)²-\left(1-\widehat{f}\right)\left(\widehat{\lambda }₁\right)²\left(\widehat{\lambda }₂\right)²}{1-\left(1-\widehat{f}\right)\left(\widehat{\lambda }₁\right)²\left(\widehat{\lambda }₂\right)²}}\end{array}\right),\left(\begin{array}{c}\left[\begin{array}{c}\frac{\widehat{n}₁{}^{-}\widehat{n}₂{}^{-}}{\sqrt{\widehat{f}+\left(1-\widehat{f}\right)\left(\left(\widehat{n}₁{}^{-}\right)²+\left(\widehat{n}₂{}^{-}\right)²-\left(\widehat{n}₁{}^{-}\right)²\left(\widehat{n}₂{}^{-}\right)²\right)}},\\ \frac{\widehat{n}₁{}^{+}\widehat{n}₂{}^{+}}{\sqrt{\widehat{f}+\left(1-\widehat{f}\right)\left(\left(\widehat{n}₁{}^{+}\right)²+\left(\widehat{n}₂{}^{+}\right)²-\left(\widehat{n}₁{}^{+}\right)²\left(\widehat{n}₂{}^{+}\right)²\right)}}\end{array}\right],\\ \frac{\widehat{\mu }₁\widehat{\mu }₂}{\sqrt{\widehat{f}+\left(1-\widehat{f}\right)\left(\left(\widehat{\mu }₁\right)²+\left(\widehat{\mu }₂\right)²-\left(\widehat{\mu }₁\right)²\left(\widehat{\mu }₂\right)²\right)}}\end{array}\right)\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\widehat{r}₁{}^{-}\widehat{r}₂{}^{-}}{\sqrt{\widehat{f}+\left(1-\widehat{f}\right)\left(\left(\widehat{r}₁{}^{-}\right)²+\left(\widehat{r}₂{}^{-}\right)²-\left(\widehat{r}₁{}^{-}\right)²\left(\widehat{r}₂{}^{-}\right)²\right)}},\\ \frac{\widehat{r}₁{}^{+}\widehat{r}₂{}^{+}}{\sqrt{\widehat{f}+\left(1-\widehat{f}\right)\left(\left(\widehat{r}₁{}^{+}\right)²+\left(\widehat{r}₂{}^{+}\right)²-\left(\widehat{r}₁{}^{+}\right)²\left(\widehat{r}₂{}^{+}\right)²\right)}}\end{array}\right],\\ \frac{\widehat{\delta }₁\widehat{\delta }₂}{\sqrt{\widehat{f}+\left(1-\widehat{f}\right)\left(\left(\widehat{\delta }₁\right)²+\left(\widehat{\delta }₂\right)²-\left(\widehat{\delta }₁\right)²\left(\widehat{\delta }₂\right)²\right)}}\end{array}\right)\end{array}\right\};\hfill \\ 2.S₁\otimes S₂=\left\{\begin{array}{c}\left(\begin{array}{c}\left[\begin{array}{c}\frac{\widehat{e}₁{}^{-}\widehat{e}₂{}^{-}}{\sqrt{\widehat{f}+\left(1-\widehat{f}\right)\left(\left(\widehat{e}₁{}^{-}\right)²+\left(\widehat{e}₂{}^{-}\right)²-\left(\widehat{e}₁{}^{-}\right)²\left(\widehat{e}₂{}^{-}\right)²\right)}},\\ \frac{\widehat{e}₁{}^{+}\widehat{e}₂{}^{+}}{\sqrt{\widehat{f}+\left(1-\widehat{f}\right)\left(\left(\widehat{e}₁{}^{+}\right)²+\left(\widehat{e}₂{}^{+}\right)²-\left(\widehat{e}₁{}^{+}\right)²\left(\widehat{e}₂{}^{+}\right)²\right)}}\end{array}\right],\\ \frac{\widehat{\lambda }₁\widehat{\lambda }₂}{\sqrt{\widehat{f}+\left(1-\widehat{f}\right)\left(\left(\widehat{\lambda }₁\right)²+\left(\widehat{\lambda }₂\right)²-\left(\widehat{\lambda }₁\right)²\left(\widehat{\lambda }₂\right)²\right)}}\end{array}\right),\left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{\left(\widehat{n}₁{}^{-}\right)²+\left(\widehat{n}₂{}^{-}\right)²-\left(\widehat{n}₁{}^{-}\right)²\left(\widehat{n}₂{}^{-}\right)²-\left(1-\widehat{f}\right)\left(\widehat{n}₁{}^{-}\right)²\left(\widehat{n}₂{}^{-}\right)²}{1-\left(1-\widehat{f}\right)\left(\widehat{n}₁{}^{-}\right)²\left(\widehat{n}₂{}^{-}\right)²}},\\ \sqrt{\frac{(\widehat{n}₁{}^{+})²+\left(\widehat{n}₂{}^{+}\right)²-\left(\widehat{n}₁{}^{+}\right)²\left(\widehat{n}₂{}^{+}\right)²-\left(1-\widehat{f}\right)\left(\widehat{n}₁{}^{+}\right)²\left(\widehat{n}₂{}^{+}\right)²}{1-\left(1-\widehat{f}\right)\left(\widehat{n}₁{}^{+}\right)²\left(\widehat{n}₂{}^{+}\right)²}}\end{array}\right],\\ \sqrt{\frac{\left(\widehat{\mu }₁\right)²+\left(\widehat{\mu }₂\right)²-\left(\widehat{\mu }₁\right)²\left(\widehat{\mu }₂\right)²-\left(1-\widehat{f}\right)\left(\widehat{\mu }₁\right)²\left(\widehat{\mu }₂\right)²}{1-\left(1-\widehat{f}\right)\left(\widehat{\mu }₁\right)²\left(\widehat{\mu }₂\right)²}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{\left(\widehat{r}₁{}^{-}\right)²+\left(\widehat{r}₂{}^{-}\right)²-\left(\widehat{r}₁{}^{-}\right)²\left(\widehat{r}₂{}^{-}\right)²-\left(1-\widehat{f}\right)\left(\widehat{r}₁{}^{-}\right)²\left(\widehat{r}₂{}^{-}\right)²}{1-\left(1-\widehat{f}\right)\left(\widehat{r}₁{}^{-}\right)²\left(\widehat{r}₂{}^{-}\right)²}},\\ \sqrt{\frac{(\widehat{r}₁{}^{+})²+\left(\widehat{r}₂{}^{+}\right)²-\left(\widehat{r}₁{}^{+}\right)²\left(\widehat{r}₂{}^{+}\right)²-\left(1-\widehat{f}\right)\left(\widehat{r}₁{}^{+}\right)²\left(\widehat{r}₂{}^{+}\right)²}{1-\left(1-\widehat{f}\right)\left(\widehat{r}₁{}^{+}\right)²\left(\widehat{r}₂{}^{+}\right)²}}\end{array}\right],\\ \sqrt{\frac{\left(\widehat{\delta }₁\right)²+\left(\widehat{\delta }₂\right)²-\left(\widehat{\delta }₁\right)²\left(\widehat{\delta }₂\right)²-\left(1-\widehat{f}\right)\left(\widehat{\delta }₁\right)²\left(\widehat{\delta }₂\right)²}{1-\left(1-\widehat{f}\right)\left(\widehat{\delta }₁\right)²\left(\widehat{\delta }₂\right)²}}\end{array}\right),\end{array}\right\};\hfill \\ 3.\gamma S₁=\left\{\begin{array}{c}\left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{\left(1+\left(\widehat{f}-1\right)\left(\widehat{e}₁{}^{-}\right)²\right)}^{\gamma }-{\left(1-\left(\widehat{e}₁{}^{-}\right)²\right)}^{\gamma }}{{\left(1+\left(\widehat{f}-1\right)\left(\widehat{e}₁{}^{-}\right)²\right)}^{\gamma }+\left(\widehat{f}-1\right){\left(1-\left(\widehat{e}₁{}^{-}\right)²\right)}^{\gamma }}},\\ \sqrt{\frac{{\left(1+\left(\widehat{f}-1\right)\left(\widehat{e}₁{}^{+}\right)²\right)}^{\gamma }-{\left(1-\left(\widehat{e}₁{}^{+}\right)²\right)}^{\gamma }}{{\left(1+\left(\widehat{f}-1\right)\left(\widehat{e}₁{}^{+}\right)²\right)}^{\gamma }+\left(\widehat{f}-1\right){\left(1-\left(\widehat{e}₁{}^{+}\right)²\right)}^{\gamma }}}\end{array}\right],\\ \sqrt{\frac{{\left(1+\left(\widehat{f}-1\right)\left(\widehat{\lambda }₁\right)²\right)}^{\gamma }-{\left(1-\left(\widehat{\lambda }₁\right)²\right)}^{\gamma }}{{\left(1+\left(\widehat{f}-1\right)\left(\widehat{\lambda }₁\right)²\right)}^{\gamma }+\left(\widehat{f}-1\right){\left(1-\left(\widehat{\lambda }₁\right)²\right)}^{\gamma }}}\end{array}\right),\left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{\left(\widehat{n}₁{}^{-}\right)}^{\gamma }}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left(\widehat{n}₁{}^{-}\right)²\right)\right)}^{\gamma }+\left(\widehat{f}-1\right){\left(\widehat{n}₁{}^{-}\right)}^{2\gamma }}},\\ \frac{\sqrt{\widehat{f}}{\left(\widehat{n}₁{}^{+}\right)}^{\gamma }}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left(\widehat{n}₁{}^{+}\right)²\right)\right)}^{\gamma }+\left(\widehat{f}-1\right){\left(\widehat{n}₁{}^{+}\right)}^{2\gamma }}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{\left(\widehat{\mu }₁\right)}^{\gamma }}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left(\widehat{\mu }₁\right)²\right)\right)}^{\gamma }+\left(\widehat{f}-1\right){\left(\widehat{\mu }₁\right)}^{2\gamma }}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{\left(\widehat{r}₁{}^{-}\right)}^{\gamma }}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left(\widehat{r}₁{}^{-}\right)²\right)\right)}^{\gamma }+\left(\widehat{f}-1\right){\left(\widehat{r}₁{}^{-}\right)}^{2\gamma }}},\\ \frac{\sqrt{\widehat{f}}{\left(\widehat{r}₁{}^{+}\right)}^{\gamma }}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left(\widehat{r}₁{}^{+}\right)²\right)\right)}^{\gamma }+\left(\widehat{f}-1\right){\left(\widehat{r}₁{}^{+}\right)}^{2\gamma }}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{\left(\widehat{\delta }₁\right)}^{\gamma }}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left(\widehat{\delta }₁\right)²\right)\right)}^{\gamma }+\left(\widehat{f}-1\right){\left(\widehat{\delta }₁\right)}^{2\gamma }}}\end{array}\right)\end{array}\right\};\hfill \\ 4.S{₁}^{\gamma } =\left\{\begin{array}{c}\left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{\left(\widehat{e}₁{}^{-}\right)}^{\gamma }}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left(\widehat{e}₁{}^{-}\right)²\right)\right)}^{\gamma }+\left(\widehat{f}-1\right){\left(\widehat{e}₁{}^{-}\right)}^{2\gamma }}},\\ \frac{\sqrt{\widehat{f}}{\left(\widehat{e}₁{}^{+}\right)}^{\gamma }}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left(\widehat{e}₁{}^{+}\right)²\right)\right)}^{\gamma }+\left(\widehat{f}-1\right){\left(\widehat{e}₁{}^{+}\right)}^{2\gamma }}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{\left(\widehat{\lambda }₁\right)}^{\gamma }}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left(\widehat{\lambda }₁\right)²\right)\right)}^{\gamma }+\left(\widehat{f}-1\right){\left(\widehat{\lambda }₁\right)}^{2\gamma }}}\end{array}\right),\left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{\left(1+\left(\widehat{f}-1\right)\left(\widehat{n}₁{}^{-}\right)²\right)}^{\gamma }-{\left(1-\left(\widehat{n}₁{}^{-}\right)²\right)}^{\gamma }}{{\left(1+\left(\widehat{f}-1\right)\left(\widehat{n}₁{}^{-}\right)²\right)}^{\gamma }+\left(\widehat{f}-1\right){\left(1-\left(\widehat{n}₁{}^{-}\right)²\right)}^{\gamma }}},\\ \sqrt{\frac{{\left(1+\left(\widehat{f}-1\right)\left(\widehat{n}₁{}^{+}\right)²\right)}^{\gamma }-{\left(1-\left(\widehat{n}₁{}^{+}\right)²\right)}^{\gamma }}{{\left(1+\left(\widehat{f}-1\right)\left(\widehat{n}₁{}^{+}\right)²\right)}^{\gamma }+\left(\widehat{f}-1\right){\left(1-\left(\widehat{n}₁{}^{+}\right)²\right)}^{\gamma }}}\end{array}\right],\\ \sqrt{\frac{{\left(1+\left(\widehat{f}-1\right)\left(\widehat{\mu }₁\right)²\right)}^{\gamma }-{\left(1-\left(\widehat{\mu }₁\right)²\right)}^{\gamma }}{{\left(1+\left(\widehat{f}-1\right)\left(\widehat{\mu }₁\right)²\right)}^{\gamma }+\left(\widehat{f}-1\right){\left(1-\left(\widehat{\mu }₁\right)²\right)}^{\gamma }}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{\left(1+\left(\widehat{f}-1\right)\left(\widehat{r}₁{}^{-}\right)²\right)}^{\gamma }-{\left(1-\left(\widehat{r}₁{}^{-}\right)²\right)}^{\gamma }}{{\left(1+\left(\widehat{f}-1\right)\left(\widehat{r}₁{}^{-}\right)²\right)}^{\gamma }+\left(\widehat{f}-1\right){\left(1-\left(\widehat{r}₁{}^{-}\right)²\right)}^{\gamma }}},\\ \sqrt{\frac{{\left(1+\left(\widehat{f}-1\right)\left(\widehat{r}₁{}^{+}\right)²\right)}^{\gamma }-{\left(1-\left(\widehat{r}₁{}^{+}\right)²\right)}^{\gamma }}{{\left(1+\left(\widehat{f}-1\right)\left(\widehat{r}₁{}^{+}\right)²\right)}^{\gamma }+\left(\widehat{f}-1\right){\left(1-\left(\widehat{r}₁{}^{+}\right)²\right)}^{\gamma }}}\end{array}\right],\\ \sqrt{\frac{{\left(1+\left(\widehat{f}-1\right)\left(\widehat{\delta }₁\right)²\right)}^{\gamma }-{\left(1-\left(\widehat{\delta }₁\right)²\right)}^{\gamma }}{{\left(1+\left(\widehat{f}-1\right)\left(\widehat{\delta }₁\right)²\right)}^{\gamma }+\left(\widehat{f}-1\right){\left(1-\left(\widehat{\delta }₁\right)²\right)}^{\gamma }}}\end{array}\right)\end{array}\right\}.\hfill \end{array}$$

Theorem 1.

Let$S₁=\left\{\right(x,<\left[\widehat{e}₁{}^{-},\widehat{e}₁{}^{+}\right],\widehat{\lambda }₁>,<\left[\widehat{n}₁{}^{-},\widehat{n}₁{}^{+}\right],\widehat{\mu }₁>,<\left[\widehat{r}₁{}^{-},\widehat{r}₁{}^{+}\right],\widehat{\delta }₁>|x\in X)\}$and$S₂= \left(<\left[\widehat{e}₂{}^{-},\widehat{e}₂{}^{+}\right],\widehat{\lambda }₂>,<\left[\widehat{n}₂{}^{-},\widehat{n}₂{}^{+}\right],\widehat{\mu }₂>,<\left[\widehat{r}₂{}^{-},\widehat{r}₂{}^{+}\right],{\widehat{\delta }}_2>\right)$be two SCFS in$X$and$\gamma ₁,\gamma ₂>0$. We have the following properties:

$$\begin{array}{c}1.S₂\oplus S₁=S₁\oplus S₂,\\ 2.S₂\otimes S₁=S₁\otimes S₂,\\ 3.\gamma \left(S₂\oplus S₁\right)=\gamma S₂\oplus \gamma S₁,\\ 4.\gamma \left(S₂\otimes S₁\right)=\gamma S₂\otimes \gamma S₁,\\ 5.\left(\gamma ₁\oplus \gamma ₂\right)S=\gamma ₁S\oplus \gamma ₂S,\\ 6.\left(\gamma ₁\otimes \gamma ₂\right)S=\gamma ₁S\otimes \gamma ₂S.\end{array}$$

Proof: 

Proof is very simple. □

6. Spherical Cubic Fuzzy Hamacher Weighted Averaging (SCFHWA) Aggregation Operators

Now, we will introduce various spherical cubic fuzzy Hamacher aggregation operators and discuss their features.

6.1. SCFHWA Operator

Definition 18.

Let$S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)>$be an SCFN in$X$and let the SCFHWA operator be a mapping of$\Phi ⁿ\to \Phi$, such that$SCFHW{A}_{\varpi }\left(S₁,S₂,\dots ,S_n\right)={\oplus }_{p=1}^m{\varpi }_p{S}_p,$and the weight vector is represented by$\varpi ={\left(\varpi ₁,\varpi ₂\dots {\varpi }_n\right)}^T$with the specific conditions${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right]$. Now, we obtain the following results related to SCFNs and Hamacher operators.

Theorem 2.

Let$S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)>$be an SCFN in$X.$Therefore, the aggregation value of them using the SCFHWA operator is also an SCFN and is defined as

$$SCFHW{A}_{\varpi }\left(S_1,S_2,\dots ,S_n\right)=\left\{\begin{array}{c}\left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}}},\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}}}\end{array}\right],\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{n}}_p{}^{-}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{n}}_p{}^{-}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{n}}_p{}^{-}\right)}^{2{\varpi }_p}}},\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{n}}_p{}^{+}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{n}}_p{}^{+}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{n}}_p{}^{+}\right)}^{2{\varpi }_p}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{\mu }}_p\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\mu }}_p\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{\mu }}_p\right)}^{2{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{r}}_p{}^{-}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{r}}_p{}^{-}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{r}}_p{}^{-}\right)}^{2{\varpi }_p}}}\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{r}}_p{}^{+}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{r}}_p{}^{+}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{r}}_p{}^{+}\right)}^{2{\varpi }_p}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{\delta }}_p\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\delta }}_p\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{\delta }}_p\right)}^{2{\varpi }_p}}}\end{array}\right),\end{array}\right\}$$

(12)

where the weight vector $\varpi ={\left(\varpi ₁,\varpi ₂\dots {\varpi }_n\right)}^T$ with the specific conditions ${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right]$.

Proof. 

We will prove it by mathematical induction.

(i)

When $m=2$, we get

$$\begin{array}{cc}\varpi ₁S₁\oplus \varpi ₂S₂& =\left\{\begin{array}{c}\left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_1{}^{-}\right)²\right)}^{{\varpi }_1}-{\left(1-\left({\widehat{e}}_1{}^{-}\right)²\right)}^{{\varpi }_1}}{{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_1{}^{-}\right)²\right)}^{{\varpi }_1}+\left(\widehat{f}-1\right){\left(1-\left({\widehat{e}}_1{}^{-}\right)²\right)}^{{\varpi }_1}}},\\ \sqrt{\frac{{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_1{}^{+}\right)²\right)}^{{\varpi }_1}-{\left(1-\left({\widehat{e}}_1{}^{+}\right)²\right)}^{{\varpi }_1}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_1{}^{+}\right)²\right)}^{{\varpi }_1}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{e}}_1{}^{+}\right)²\right)}^{{\varpi }_1}}}\end{array}\right],\\ \sqrt{\frac{{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\lambda }}_1\right)²\right)}^{{\varpi }_1}-{\left(1-\left({\widehat{\lambda }}_1\right)²\right)}^{{\varpi }_1}}{{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\lambda }}_1\right)²\right)}^{{\varpi }_1}+\left(\widehat{f}-1\right){\left(1-\left({\widehat{\lambda }}_1\right)²\right)}^{{\varpi }_1}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{\left({\widehat{n}}_1{}^{-}\right)}^{{\varpi }_1}}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{n}}_1{}^{-}\right)²\right)\right)}^{{\varpi }_1}+\left(\widehat{f}-1\right){\left({\widehat{n}}_1{}^{-}\right)}^{2{\varpi }_1}}},\\ \frac{\sqrt{\widehat{f}}{\left({\widehat{n}}_1{}^{+}\right)}^{{\varpi }_1}}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{n}}_1{}^{+}\right)²\right)\right)}^{{\varpi }_1}+\left(\widehat{f}-1\right){\left({\widehat{n}}_1{}^{+}\right)}^{2{\varpi }_1}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{\left({\widehat{\mu }}_1\right)}^{{\varpi }_1}}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\mu }}_1\right)²\right)\right)}^{{\varpi }_1}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{\mu }}_1\right)}^{2{\varpi }_1}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{r}}_1{}^{-}\right)}^{{\varpi }_1}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{r}}_1{}^{-}\right)²\right)\right)}^{{\varpi }_1}+\left(\widehat{f}-1\right){\left({\widehat{r}}_1{}^{-}\right)}^{2{\varpi }_1}}}\\ \frac{\sqrt{\widehat{f}}{\left({\widehat{r}}_1{}^{+}\right)}^{{\varpi }_1}}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{r}}_1{}^{+}\right)²\right)\right)}^{{\varpi }_1}+\left(\widehat{f}-1\right){\left({\widehat{r}}_1{}^{+}\right)}^{2{\varpi }_1}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{\left({\widehat{\delta }}_1\right)}^{{\varpi }_1}}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\delta }}_1\right)²\right)\right)}^{{\varpi }_1}+\left(\widehat{f}-1\right){\left({\widehat{\delta }}_1\right)}^{2{\varpi }_1}}}\end{array}\right)\end{array}\right\}\hfill \\ & \oplus \left\{\begin{array}{c}\left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_2{}^{-}\right)²\right)}^{{\varpi }_2}-{\left(1-\left({\widehat{e}}_2{}^{-}\right)²\right)}^{{\varpi }_2}}{{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_2{}^{-}\right)²\right)}^{{\varpi }_1}+\left(\widehat{f}-1\right){\left(1-\left({\widehat{e}}_2{}^{-}\right)²\right)}^{{\varpi }_1}}},\\ \sqrt{\frac{{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_2{}^{+}\right)²\right)}^{{\varpi }_2}-{\left(1-\left({\widehat{e}}_2{}^{+}\right)²\right)}^{{\varpi }_2}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_2{}^{+}\right)²\right)}^{{\varpi }_2}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{e}}_2{}^{+}\right)²\right)}^{{\varpi }_2}}}\end{array}\right],\\ \sqrt{\frac{{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\lambda }}_2\right)²\right)}^{{\varpi }_2}-{\left(1-\left({\widehat{\lambda }}_2\right)²\right)}^{{\varpi }_2}}{{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\lambda }}_2\right)²\right)}^{{\varpi }_2}+\left(\widehat{f}-1\right){\left(1-\left({\widehat{\lambda }}_2\right)²\right)}^{{\varpi }_2}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{\left({\widehat{n}}_2{}^{-}\right)}^{{\varpi }_2}}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{n}}_2{}^{-}\right)²\right)\right)}^{{\varpi }_2}+\left(\widehat{f}-1\right){\left({\widehat{n}}_2{}^{-}\right)}^{2{\varpi }_2}}},\\ \frac{\sqrt{\widehat{f}}{\left({\widehat{n}}_2{}^{+}\right)}^{{\varpi }_2}}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{n}}_2{}^{+}\right)²\right)\right)}^{{\varpi }_2}+\left(\widehat{f}-1\right){\left({\widehat{n}}_2{}^{+}\right)}^{2{\varpi }_2}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{\left({\widehat{\mu }}_2\right)}^{{\varpi }_2}}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\mu }}_2\right)²\right)\right)}^{{\varpi }_2}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{\mu }}_2\right)}^{2{\varpi }_2}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{r}}_2{}^{-}\right)}^{{\varpi }_2}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{r}}_2{}^{-}\right)²\right)\right)}^{{\varpi }_2}+\left(\widehat{f}-1\right){\left({\widehat{r}}_2{}^{-}\right)}^{2{\varpi }_2}}}\\ \frac{\sqrt{\widehat{f}}{\left({\widehat{r}}_2{}^{+}\right)}^{{\varpi }_2}}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{r}}_2{}^{+}\right)²\right)\right)}^{{\varpi }_2}+\left(\widehat{f}-1\right){\left({\widehat{r}}_2{}^{+}\right)}^{2{\varpi }_2}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{\left({\widehat{\delta }}_2\right)}^{{\varpi }_2}}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\delta }}_2\right)²\right)\right)}^{{\varpi }_2}+\left(\widehat{f}-1\right){\left({\widehat{\delta }}_2\right)}^{2{\varpi }_2}}}\end{array}\right)\end{array}\right\}\hfill \end{array}$$

$$\varpi ₁S₁\oplus \varpi ₂S₂=\left\{\begin{array}{c}\left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{{\displaystyle \prod }}_{p=1}^2{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^2{\left(1-\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^2{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^2{\left(1-\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}}},\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^2{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^2{\left(1-\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^2{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^2{\left(1-\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}}}\end{array}\right],\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^2{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^2{\left(1-\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^2{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^2{\left(1-\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^2{\left({\widehat{n}}_p{}^{-}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^2(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{n}}_p{}^{-}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^2{\left({\widehat{n}}_p{}^{-}\right)}^{2{\varpi }_p}}},\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^2{\left({\widehat{n}}_p{}^{+}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^2(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{n}}_p{}^{+}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^2{\left({\widehat{n}}_p{}^{+}\right)}^{2{\varpi }_p}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^2{\left({\widehat{\mu }}_p\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^2(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\mu }}_p\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^2{\left({\widehat{\mu }}_p\right)}^{2{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^2{\left({\widehat{r}}_p{}^{-}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^2(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{r}}_p{}^{-}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^2{\left({\widehat{r}}_p{}^{-}\right)}^{2{\varpi }_p}}}\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^2{\left({\widehat{r}}_p{}^{+}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^2(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{r}}_p{}^{+}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^2{\left({\widehat{r}}_p{}^{+}\right)}^{2{\varpi }_p}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^2{\left({\widehat{\delta }}_p\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^2(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\delta }}_p\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^2{\left({\widehat{\delta }}_p\right)}^{2{\varpi }_p}}}\end{array}\right),\end{array}\right\}$$

Hence, Equation (12) holds for $m=2$.

(ii)

Let us assume that Equation (12) is true for $m=k$. Therefore, we have

$$SCFHW{A}_{\varpi }\left(S_1,S_2,\dots ,S_k\right)=\left\{\begin{array}{c}\left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{{\displaystyle \prod }}_{p=1}^k{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^k{\left(1-\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^k{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^k{\left(1-\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}}},\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^k{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^k{\left(1-\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^k{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^k{\left(1-\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}}}\end{array}\right],\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^k{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^k{\left(1-\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^k{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^k{\left(1-\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^k{\left({\widehat{n}}_p{}^{-}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^k(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{n}}_p{}^{-}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^k{\left({\widehat{n}}_p{}^{-}\right)}^{2{\varpi }_p}}},\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^k{\left({\widehat{n}}_p{}^{+}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^k(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{n}}_p{}^{+}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^k{\left({\widehat{n}}_p{}^{+}\right)}^{2{\varpi }_p}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^k{\left({\widehat{\mu }}_p\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^k(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\mu }}_p\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^k{\left({\widehat{\mu }}_p\right)}^{2{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^k{\left({\widehat{r}}_p{}^{-}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^k(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{r}}_p{}^{-}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^k{\left({\widehat{r}}_p{}^{-}\right)}^{2{\varpi }_p}}}\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^k{\left({\widehat{r}}_p{}^{+}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^k(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{r}}_p{}^{+}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^k{\left({\widehat{r}}_p{}^{+}\right)}^{2{\varpi }_p}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^k{\left({\widehat{\delta }}_p\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^k(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\delta }}_p\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^k{\left({\widehat{\delta }}_p\right)}^{2{\varpi }_p}}}\end{array}\right)\end{array}\right\}$$

(iii)

Now, for $m=k+1$, we have

(iv)

$$SCFHW{A}_{\varpi }\left(S_1,S_2,\dots ,S_k,S_{k+1}\right)=SCFHW{A}_{\varpi }\left(S_1,S_2,\dots ,S_k\right)\oplus S_{p+1}$$

$$\begin{array}{c}=\left\{\begin{array}{c}\left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{{\displaystyle \prod }}_{p=1}^k{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^k{\left(1-\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^k{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^k{\left(1-\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}}},\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^k{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^k{\left(1-\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^k{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^k{\left(1-\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}}}\end{array}\right],\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^k{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^k{\left(1-\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^k{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^k{\left(1-\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^k{\left({\widehat{n}}_p{}^{-}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^k(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{n}}_p{}^{-}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^k{\left({\widehat{n}}_p{}^{-}\right)}^{2{\varpi }_p}}},\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^k{\left({\widehat{n}}_p{}^{+}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^k(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{n}}_p{}^{+}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^k{\left({\widehat{n}}_p{}^{+}\right)}^{2{\varpi }_p}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^k{\left({\widehat{\mu }}_p\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^k(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\mu }}_p\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^k{\left({\widehat{\mu }}_p\right)}^{2{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^k{\left({\widehat{r}}_p{}^{-}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^k(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{r}}_p{}^{-}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^k{\left({\widehat{r}}_p{}^{-}\right)}^{2{\varpi }_p}}}\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^k{\left({\widehat{r}}_p{}^{+}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^k(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{r}}_p{}^{+}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^k{\left({\widehat{r}}_p{}^{+}\right)}^{2{\varpi }_p}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^k{\left({\widehat{\delta }}_p\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^k(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\delta }}_p\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^k{\left({\widehat{\delta }}_p\right)}^{2{\varpi }_p}}}\end{array}\right)\end{array}\right\}\hfill \\ \oplus \left\{\begin{array}{c}\left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_{k+1}{}^{-}\right)²\right)}^{{\varpi }_{k+1}}-{\left(1-\left({\widehat{e}}_{k+1}{}^{-}\right)²\right)}^{{\varpi }_{k+1}}}{{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_{k+1}{}^{-}\right)²\right)}^{{\varpi }_{k+1}}+\left(\widehat{f}-1\right){\left(1-\left({\widehat{e}}_{k+1}{}^{-}\right)²\right)}^{{\varpi }_{k+1}}}},\\ \sqrt{\frac{{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_{k+1}{}^{+}\right)²\right)}^{{\varpi }_{k+1}}-{\left(1-\left({\widehat{e}}_{k+1}{}^{+}\right)²\right)}^{{\varpi }_{k+1}}}{{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_{k+1}{}^{+}\right)²\right)}^{{\varpi }_{k+1}}+\left(\widehat{f}-1\right){\left(1-\left({\widehat{e}}_{k+1}{}^{+}\right)²\right)}^{{\varpi }_{k+1}}}}\end{array}\right],\\ \sqrt{\frac{{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\lambda }}_{p+1}\right)²\right)}^{{\varpi }_{k+1}}-{\left(1-\left({\widehat{\lambda }}_{p+1}\right)²\right)}^{{\varpi }_{k+1}}}{{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\lambda }}_{p+1}\right)²\right)}^{{\varpi }_{k+1}}+\left(\widehat{f}-1\right){\left(1-\left({\widehat{\lambda }}_{p+1}\right)²\right)}^{{\varpi }_{k+1}}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{\left({\widehat{n}}_{p+1}{}^{-}\right)}^{{\varpi }_{k+1}}}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{n}}_{p+1}{}^{-}\right)²\right)\right)}^{{\varpi }_{k+1}}+\left(\widehat{f}-1\right){\left({\widehat{n}}_{p+1}{}^{-}\right)}^{2{\varpi }_{k+1}}}},\\ \frac{\sqrt{\widehat{f}}{\left({\widehat{n}}_{p+1}{}^{+}\right)}^{{\varpi }_{k+1}}}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{n}}_{p+1}{}^{+}\right)²\right)\right)}^{{\varpi }_{k+1}}+\left(\widehat{f}-1\right){\left({\widehat{n}}_{p+1}{}^{+}\right)}^{2{\varpi }_{k+1}}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{\left({\widehat{\mu }}_{p+1}\right)}^{{\varpi }_{k+1}}}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\mu }}_{p+1}\right)²\right)\right)}^{{\varpi }_{k+1}}+\left(\widehat{f}-1\right){\left({\widehat{\mu }}_{p+1}\right)}^{2{\varpi }_{k+1}}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{\left({\widehat{r}}_{p+1}{}^{-}\right)}^{{\varpi }_{k+1}}}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{r}}_{p+1}{}^{-}\right)²\right)\right)}^{{\varpi }_{k+1}}+\left(\widehat{f}-1\right){\left({\widehat{r}}_{p+1}{}^{-}\right)}^{2{\varpi }_{k+1}}}}\\ \frac{\sqrt{\widehat{f}}{\left({\widehat{r}}_{p+1}{}^{+}\right)}^{{\varpi }_{k+1}}}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{r}}_{p+1}{}^{+}\right)²\right)\right)}^{{\varpi }_{k+1}}+\left(\widehat{f}-1\right){\left({\widehat{r}}_{p+1}{}^{+}\right)}^{2{\varpi }_{k+1}}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{\left({\widehat{\delta }}_{p+1}\right)}^{{\varpi }_{k+1}}}{\sqrt{(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\delta }}_{p+1}\right)²\right)\right)}^{{\varpi }_{k+1}}+\left(\widehat{f}-1\right){\left({\widehat{\delta }}_{p+1}\right)}^{2{\varpi }_{k+1}}}}\end{array}\right)\end{array}\right\}\hfill \end{array}$$

$$SCFHW{A}_{\varpi }\left(S_1,S_2,\dots ,S_{k+1}\right)=\left\{\begin{array}{c}\left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{{\displaystyle \prod }}_{p=1}^{k+1}{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^{k+1}{\left(1-\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^{k+1}{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^{k+1}{\left(1-\left({\widehat{e}}_p{}^{-}\right)²\right)}^{{\varpi }_p}}},\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^{k+1}{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^{k+1}{\left(1-\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^{k+1}{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^{k+1}{\left(1-\left({\widehat{e}}_p{}^{+}\right)²\right)}^{{\varpi }_p}}}\end{array}\right],\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^{k+1}{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^{k+1}{\left(1-\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^{k+1}{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^{k+1}{\left(1-\left({\widehat{\lambda }}_p\right)²\right)}^{{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^{k+1}{\left({\widehat{n}}_p{}^{-}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^{k+1}(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{n}}_p{}^{-}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^{k+1}{\left({\widehat{n}}_p{}^{-}\right)}^{2{\varpi }_p}}},\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^{k+1}{\left({\widehat{n}}_p{}^{+}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^{k+1}(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{n}}_p{}^{+}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^{k+1}{\left({\widehat{n}}_p{}^{+}\right)}^{2{\varpi }_p}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^{k+1}{\left({\widehat{\mu }}_p\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^{k+1}(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\mu }}_p\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^{k+1}{\left({\widehat{\mu }}_p\right)}^{2{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^{k+1}{\left({\widehat{r}}_p{}^{-}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^{k+1}(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{r}}_p{}^{-}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^{k+1}{\left({\widehat{r}}_p{}^{-}\right)}^{2{\varpi }_p}}}\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^{k+1}{\left({\widehat{r}}_p{}^{+}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^{k+1}(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{r}}_p{}^{+}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^{k+1}{\left({\widehat{r}}_p{}^{+}\right)}^{2{\varpi }_p}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^{k+1}{\left({\widehat{\delta }}_p\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^{k+1}(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\delta }}_p\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^{k+1}{\left({\widehat{\delta }}_p\right)}^{2{\varpi }_p}}}\end{array}\right)\end{array}\right\}$$

Therefore, this is true for $m=k+1$. Hence, this holds for all values of $m$. □

Proposition 3.

Let$S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)> \left(p=1,2\dots m\right)$be a collection of SCFNs in$X$and the weight vector of$S_p$be$\varpi ={\left(\varpi ₁,\varpi ₂\dots {\varpi }_m\right)}^T$with the specified condition${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right]$. Therefore, we establish the following properties.

Boundary: 

For every $\varpi$,

$$S^{-}\le SCFHW{A}_{\varpi }\left(S₁,S₂\dots S_n\right)\le S^{+}$$

where

$$\begin{array}{c}{S}^{-}=\left\{\begin{array}{c}\left(\left[min{\widehat{e}}_p^{-},max{\widehat{e}}_p{}^{+}\right],max{\widehat{\lambda }}_p\right),\left(\left[max{\widehat{n}}_p{}^{-},min{\widehat{n}}_p{}^{+}\right],min{\widehat{\mu }}_p\right),\\ \left(\left[max{\widehat{r}}_p{}^{-},min{\widehat{r}}_p{}^{+}\right],min{\widehat{\delta }}_p\right)\end{array}\right\};\\ S^{+}=\left\{\begin{array}{c}\left(\left[max{\widehat{e}}_p^{-},min{\widehat{e}}_p{}^{+}\right],min{\widehat{\lambda }}_p\right),\left(\left[min{\widehat{n}}_p{}^{-},max{\widehat{n}}_p{}^{+}\right],max{\widehat{\mu }}_p\right),\\ \left(\left[min{\widehat{r}}_p{}^{-},max{\widehat{r}}_p{}^{+}\right],max{\widehat{\delta }}_p\right)\end{array}\right\}.\end{array}$$

Idempotency: 

For every $S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)> \left(p=1,2\dots m\right)$ that is same, that is, $S_p =S$, it holds that $SCFHW{A}_{\varpi }\left(S₁,S₂\dots S_n\right)=S.$

Monotonicity: 

Let $S_p{}^{*}= \left(<\left[{\widehat{e}}_p{}^{*-},{\widehat{e}}_p{}^{*+}\right],{\widehat{\lambda }}_p{}^{*}>,<\left[{\widehat{n}}_p{}^{*-},{\widehat{n}}_p{}^{*+}\right],{\widehat{\mu }}_p{}^{*}>,<\left[{\widehat{r}}_p{}^{*-},{\widehat{r}}_p{}^{*+}\right],{\widehat{\delta }}_p{}^{*}>\right)$ be a collection of SCFNs if $[{\widehat{e}}_p^{-},{\widehat{e}}_p^{+}]\le \left[{\widehat{e}}_p{}^{*-},{\widehat{e}}_p{}^{*+}\right],{\widehat{\lambda }}_p\le {\widehat{\lambda }}_p{}^{*};[{\widehat{n}}_p^{-},{\widehat{n}}_p^{+}]\le \left[{\widehat{n}}_p{}^{*},{\widehat{n}}_p{}^{*+}\right],{\widehat{\mu }}_p\le {\widehat{\mu }}_p{}^{*};[{\widehat{r}}_p^{-},{\widehat{r}}_p^{+}]\le \left[{\widehat{r}}_p{}^{*-},{\widehat{r}}_p{}^{*+}\right],{\widehat{\delta }}_p\le {\widehat{\delta }}_p{}^{*}$. For every $p$,

$$SCFHW{A}_{\varpi }\left(S₁,S₂\dots S_n\right)\le SCFHW{A}_{\varpi }\left(S_1{}^{*},S_2{}^{*}\dots S_n{}^{*}\right).$$

This can be verified similarly.

The concept of SCFHWA aggregation operators evaluates SFHWA only. In the MCDM issue, there are conditions whereby the ordering situation of the SCFN resolves issues. For those circumstances, the idea of ordered weighted average operators performs an important role, and the SCFHOWA operator is suggested as follows.

6.2. Spherical Cubic Fuzzy Hamacher Ordered Weighted Averaging (SCFHOWA) Aggregation Operator

Now, we discuss the concept of the SCFHOWA operator and its basic properties, that is, boundary, idempotency, and monotonicity.

Definition 19.

Let$S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)>$be a collection of SCFNs in$X$. Therefore, the$SCFHOWA$operator is mapping$SCFHOWA:{\Phi }^{\mathrm{n}}\to \Phi$and the weight vector$\varpi ={\left(\varpi ₁,\varpi ₂\dots {\varpi }_n\right)}^T$under the specified conditions${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right]$as$SCFHOW{A}_{\varpi }\left(S₁,S₂\dots S_n\right)={\oplus }_{p=1}^m{\varpi }_p{S}_{\sigma \left(p\right)}$for all$p$, $S_{\sigma \left(p-1\right)}\ge S_{\sigma \left(p\right)}$, and the permutation$\left(\sigma ₁,\sigma ₂\dots {\sigma }_m\right)$. Therefore, we obtain the following result related to SCFNs and the Hamacher operator.

Theorem 3.

Let$S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)>$be a collection of SCFNs in$X$. Therefore, the aggregation of SCFHOWA is also an SCFN, and it is defined as follows:

$$SCFHW{A}_{\varpi }\left(S_1,S_2,\dots ,S_n\right)=\left\{\begin{array}{c}\left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)²\right)}^{{\varpi }_p}}},\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)²\right)}^{{\varpi }_p}}}\end{array}\right],\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)²\right)}^{{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)}^{2{\varpi }_p}}},\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)}^{2{\varpi }_p}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)}^{2{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)}^{2{\varpi }_p}}}\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)}^{2{\varpi }_p}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)}^{2{\varpi }_p}}}\end{array}\right)\end{array}\right\}$$

(13)

with ${\left(\varpi ₁,\varpi ₂\dots {\varpi }_m\right)}^T$ under the specified conditions ${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right].$

Proposition 4:

Let$S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)> \left(p=1,2\dots m\right)$be a collection of SCFNs in$X$and the weight vector of$S_p$be$\varpi ={\left(\varpi ₁,\varpi ₂\dots {\varpi }_m\right)}^T$with the specified condition${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right]$. Therefore, we establish the following properties.

Boundary: 

For every $\varpi$

$$S^{-}\le SCFHOW{A}_{\varpi }\left(S₁,S₂\dots S_n\right)\le S^{+}$$

where

$$\begin{array}{c}{S}^{-}=\left\{\begin{array}{c}\left(\left[min{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{-},max{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right],max{\widehat{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right),\left(\left[max{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-},min{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right],min{\widehat{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right),\\ \left(\left[max{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-},min{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right],min{\widehat{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)\end{array}\right\}\\ S^{+}=\left\{\begin{array}{c}\left(\left[max{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{-},min{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right],min{\widehat{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right),\left(\left[min{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-},max{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right],max{\widehat{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right),\\ \left(\left[min{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-},max{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right],max{\widehat{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)\end{array}\right\}\end{array}$$

Idempotency: 

For every $S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)> \left(p=1,2\dots m\right)$ that is the same, that is, $S_p =S$, it holds that $SCFHOW{A}_{\varpi }\left(S₁,S₂\dots S_n\right)=S.$

Monotonicity: 

Let $S^{*}= =\left(<\left[{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\widehat{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}>,<\left[{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\widehat{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}>,<\left[{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\widehat{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}>\right)$ be a collection of SCFNs if $\left[{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{-},{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{+}\right]\le \left[{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\widehat{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\le {\widehat{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{*};\left[{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{-},{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{+}\right]\le \left[{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\widehat{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\le {\widehat{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{*};\left[{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-},{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right]\le \left[{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\widehat{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\le {\widehat{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{*}$. For every $p$,

$$SCFHOW{A}_{\varpi }\left(S₁,S₂\dots S_n\right)\le SCFHOW{A}_{\varpi }\left(S_1{}^{*},S_2{}^{*}\dots S_n{}^{*}\right).$$

6.3. Spherical Cubic Fuzzy Hamacher Hybrid Averaging (SCFHHA) Aggregation Operator

Now, we will discuss the SCFHHA operator and further discuss its basic properties, that is, idempotency, boundary, and monotonicity.

Definition 20.

Let$S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)>$be a collection of SCFNs in$X$. Therefore, the SCFHHA operator is mapping$SCFHHA:\Phi ⁿ\to \Phi$and the weight vector$\varpi ={\left(\varpi ₁,\varpi ₂\dots {\varpi }_m\right)}^T$with the specified condition${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right]$as$SCFHH{A}_{\varpi }\left(S₁,S₂\dots S_n\right)={\oplus }_{p=1}^m{\varpi }_p{S}_{\sigma \left(p\right)}^{*}$for all$p$, where$S_{\sigma \left(p\right)}^{*}$represents the$pth$highest weight SFNs$S$. The weight of$S_p$is${\left(\varpi ₁,\varpi ₂\dots {\varpi }_m\right)}^T$with the specified condition${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right]$for$p=1,2,\dots \dots m.$

$$S_{\sigma \left(p\right)}^{*}=m{\varpi }_p{S}_{\sigma \left(p\right)}=\left(<\left[{\tilde{e}}_{\sigma \left(p\right)}^{*-},{\tilde{e}}_{\sigma \left(p\right)}^{*+}\right],{\tilde{\lambda }}_{\sigma \left(p\right)}^{*}>,<\left[{\tilde{n}}_{\sigma \left(p\right)}^{*-},{\tilde{n}}_{\sigma \left(p\right)}^{*+}\right],{\tilde{\mu }}_{\sigma \left(p\right)}^{*}>,<\left[{\tilde{r}}_{\sigma \left(p\right)}^{*-},{\tilde{r}}_{\sigma \left(p\right)}^{*+}\right],{\tilde{\delta }}_{\sigma \left(p\right)}^{*}>\right).$$

where $\mathrm{m}$ represents the balancing coefficient when $\varpi ={\left(\frac{1}{\mathrm{m}},\frac{1}{\mathrm{m}},\dots ,\frac{1}{\mathrm{m}}\right)}^{\mathrm{T}}$. Therefore, SCFHWA and SCFOHWA operators are considered as special cases of the SCFHHA operator. Now, we will obtain the following result related to the SCFN and the Hamacher operator.

Theorem 4.

Let$S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)>$be a collection of SCFNs in$X$. Therefore, the aggregation of SCFHHA is also an SCFN, and it is defined as

$$SCFHW{A}_{\omega \varpi }\left(S_1,S_2,\dots ,S_n\right)=\left\{\begin{array}{c}\left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)²\right)}^{{\varpi }_p}}},\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)²\right)}^{{\varpi }_p}}}\end{array}\right],\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\tilde{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\tilde{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\tilde{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\tilde{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)²\right)}^{{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)}^{2{\varpi }_p}}},\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)}^{2{\varpi }_p}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\tilde{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\tilde{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\tilde{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)}^{2{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)}^{2{\varpi }_p}}}\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)}^{2{\varpi }_p}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\tilde{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\tilde{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\tilde{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)}^{2{\varpi }_p}}}\end{array}\right)\end{array}\right\}$$

(14)

Now, the weight vector of $S_p$ is ${\left(\varpi ₁,\varpi ₂\dots {\varpi }_m\right)}^T$ with the specified condition ${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right].$

Proposition 4.

Let$S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)> \left(p=1,2\dots m\right)$be a collection of SCFNs in$X$and the weight vector of$S_p$be$\varpi ={\left(\varpi ₁,\varpi ₂\dots {\varpi }_m\right)}^T$with the specified condition${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right]$. Therefore, we establish the following properties.

Boundary: 

For every $\varpi$,

$$S^{-}\le SCFHH{A}_{\varpi }\left(S₁,S₂\dots S_n\right)\le S^{+}$$

where

$$\begin{array}{c}{S}^{-}=\left\{\begin{array}{c}\left(\left[min{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},max{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],max{\tilde{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right),\left(\left[max{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},min{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],min{\tilde{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right),\\ \left(\left[max{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},min{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],min{\tilde{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)\end{array}\right\};\\ S^{+}=\left\{\begin{array}{c}\left(\left[max{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},min{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],min{\tilde{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right),\left(\left[min{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},max{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],max{\tilde{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right),\\ \left(\left[min{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},max{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],max{\tilde{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)\end{array}\right\}.\end{array}$$

Idempotency: 

For every $S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)> \left(p=1,2\dots m\right)$ that is the same, that is, $S_p =S$, it holds that $SCFHH{A}_{\varpi }\left(S₁,S₂\dots S_n\right)=S.$

Monotonicity: 

Let $S^{*}= =\left(<\left[{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\tilde{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}>,<\left[{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\tilde{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}>,<\left[{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\tilde{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}>\right)$ be a collection of SCFNs if $\left[{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{-},{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{+}\right]\le \left[{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\tilde{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\le {\tilde{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*};\left[{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{-},{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{+}\right]\le \left[{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\tilde{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\le {\tilde{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*};\left[{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{-},{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{+}\right]\le \left[{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\tilde{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\le {\tilde{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*};$. For every $p$,

$$SCFHH{A}_{\varpi }\left(S₁,S₂\dots S_n\right)\le SCFHH{A}_{\varpi }\left(S_1{}^{*},S_2{}^{*}\dots S_n{}^{*}\right).$$

The theorem is proved. □

Theorem 5.

The SCFHWA operator is a special case of the SCFHHA operator.

Proof. 

Assume $\varpi ={\left(\frac{1}{m},\frac{1}{m},\dots ,\frac{1}{m}\right)}^T$. Thus, ${\tilde{S}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}=S_{\mathsf{\sigma }\left(\mathrm{p}\right)}$. Therefore,

$$\begin{array}{c}SCFHH{A}_{\omega ,\varpi }\left(S_1,S_2,\dots ,S_n\right)={\varpi }_1{S}_{\mathsf{\sigma }\left(1\right)}\oplus {\varpi }_2{S}_{\mathsf{\sigma }\left(2\right)},\dots ,\oplus {\varpi }_m{S}_{\mathsf{\sigma }\left(\mathrm{m}\right)};\\ =\frac{1}{m}\left(S_{\mathsf{\sigma }\left(1\right)}\oplus S_{\mathsf{\sigma }\left(2\right)}\oplus \dots ,\oplus S_{\mathsf{\sigma }\left(\mathrm{m}\right)}\right);\\ =\varpi ₁S₁\oplus \varpi ₂S₂\dots \oplus {\varpi }_m{S}_n;\\ =SCFHW{A}_{\varpi }\left(S₁,S₂\dots S_n\right)\end{array}$$

The theorem is proved. □

Theorem 6.

The SCFHOWA operator is a special case of the SCFHHA operator.

Proof. 

Assume $\varpi ={\left(\frac{1}{m},\frac{1}{m},\dots ,\frac{1}{m}\right)}^T$. Therefore, ${\tilde{S}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}=S_{\mathsf{\sigma }\left(\mathrm{p}\right)}$. Thus,

$$\begin{array}{c}SCFHH{A}_{\omega ,\varpi }\left(S₁,S₂\dots S_n\right)=\varpi ₁{\tilde{S}}_{\mathsf{\sigma }\left(1\right)}\oplus \varpi ₂{\tilde{S}}_{\mathsf{\sigma }\left(2\right)},\dots ,\oplus {\varpi }_m{\tilde{S}}_{\mathsf{\sigma }\left(\mathrm{m}\right)};\\ =\frac{1}{m}\left(S_{\mathsf{\sigma }\left(1\right)}\oplus S_{\mathsf{\sigma }\left(2\right)}\oplus \dots ,\oplus S_{\mathsf{\sigma }\left(\mathrm{m}\right)}\right);\\ =\varpi ₁S₁\oplus \varpi ₂S₂\dots \oplus {\varpi }_m{S}_n;\\ =SCFHW{A}_{\varpi }\left(S₁,S₂\dots S_n\right).\end{array}$$

The theorem is proved. □

6.4. Spherical Cubic Fuzzy Hamacher Weighted Geometric (SCFHWG) Aggregation Operator

Now, we will define some geometric aggregation operators based on spherical cubic Hamacher operations.

Definition 21.

Let$S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)>$be an SCFN in$X$and let the SCFHWG operator be a mapping of$\Phi ⁿ\to \Phi$such that$SCFHW{G}_{\varpi }\left(S₁,S₂,\dots ,S_n\right)={{\displaystyle \prod }}_{p=1}^m{\varpi }_p{S}_p,$and the weight vector is represented by$\varpi ={\left(\varpi ₁,\varpi ₂\dots {\varpi }_n\right)}^T$with the specific conditions${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right]$. Now we obtain the following results related to SCFNs and Hamacher operators.

Theorem 7.

Let$S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)>$be an SCFN in$X$. Therefore, the aggregation value of them using the SCFHWG operator is also an SCFN and is defined as

$$SCFHW{G}_{\varpi }\left(S_1,S_2,\dots ,S_n\right)=\left\{\begin{array}{c}\left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{e}}_p{}^{-}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{e}}_p{}^{-}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{e}}_p{}^{-}\right)}^{2{\varpi }_p}}},\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{e}}_p{}^{+}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{e}}_p{}^{+}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{e}}_p{}^{+}\right)}^{2{\varpi }_p}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{\lambda }}_p\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\lambda }}_p\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{\lambda }}_p\right)}^{2{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{n}}_p{}^{-}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{n}}_p{}^{-}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{n}}_p{}^{-}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{n}}_p{}^{-}\right)²\right)}^{{\varpi }_p}}},\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{n}}_p{}^{+}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{n}}_p{}^{+}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{n}}_p{}^{+}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{n}}_p{}^{+}\right)²\right)}^{{\varpi }_p}}}\end{array}\right],\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\mu }}_p\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{\mu }}_p\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\mu }}_p\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{\mu }}_p\right)²\right)}^{{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{r}}_p{}^{-}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{r}}_p{}^{-}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{r}}_p{}^{-}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{r}}_p{}^{-}\right)²\right)}^{{\varpi }_p}}},\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{r}}_p{}^{+}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{r}}_p{}^{+}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{r}}_p{}^{+}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{r}}_p{}^{+}\right)²\right)}^{{\varpi }_p}}}\end{array}\right],\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\delta }}_p\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{\delta }}_p\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\delta }}_p\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{\delta }}_p\right)²\right)}^{{\varpi }_p}}}\end{array}\right)\end{array}\right\}$$

(15)

where the weight vector $\varpi ={\left(\varpi ₁,\varpi ₂\dots {\varpi }_{\mathrm{n}}\right)}^{\mathrm{T}}$ with the specific conditions ${\sum }_{\mathrm{p}=1}^{\mathrm{m}}{\varpi }_{\mathrm{p}}=1 \mathrm{and} {\varpi }_{\mathrm{p}}\in \left[0,1\right]$

Proof. 

The proof is similar to Theorem 1, so we will omit the proof here. □

Moreover, the defined SCFHWG aggregation operator fulfills the properties as discussed in Theorem 2.

6.5. Spherical Cubic Fuzzy Hamacher Ordered Weighted Geometric (SCFHOWG) Aggregation Operator

Now, we will discuss the concept of the SCFHOWA operator and its basic properties, that is, boundary, idempotency, and monotonicity.

Definition 22.

Let$S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)>$be a collection of SCFNs in$X$. Therefore, the$SCFHOWA$operator is mapping$SCFHOWG:\Phi ⁿ\to \Phi$and the weight vector$\varpi ={\left(\varpi ₁,\varpi ₂\dots {\varpi }_n\right)}^T$under the specified conditions${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right]$as$SCFHOW{G}_{\varpi }\left(S₁,S₂\dots S_n\right)={{\displaystyle \prod }}_{p=1}^m{\varpi }_p{S}_{\sigma \left(p\right)}$for all$p$, $S_{\sigma \left(p-1\right)}\ge S_{\sigma \left(p\right)}$, and the permutation$\left(\sigma ₁,\sigma ₂\dots {\sigma }_m\right)$. Therefore, we obtain the following result related to SCFNs and the Hamacher operator.

Theorem 8.

Let$S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)>$be a collection of SCFNs in$X$. Therefore, the aggregation of SCFHOWG is also an SCFN and it is defined as follows:

$$SCFHW{G}_{\varpi }\left(S_1,S_2,\dots ,S_n\right)=\left\{\begin{array}{c}\left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)}^{2{\varpi }_p}}},\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)}^{2{\varpi }_p}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\widehat{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\widehat{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\widehat{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)}^{2{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)²\right)}^{{\varpi }_p}}},\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)²\right)}^{{\varpi }_p}}}\end{array}\right],\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)²\right)}^{{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{-}\right)²\right)}^{{\varpi }_p}}},\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}{}^{+}\right)²\right)}^{{\varpi }_p}}}\end{array}\right],\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\widehat{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\widehat{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)²\right)}^{{\varpi }_p}}}\end{array}\right),\end{array}\right\}$$

(16)

with ${\left(\varpi ₁,\varpi ₂\dots {\varpi }_m\right)}^T$ under the specified conditions ${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right].$

Proposition 6.

Let$S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)> \left(p=1,2\dots m\right)$be a collection of SCFNs in$X$and the weight vector of$S_p$be$\varpi ={\left(\varpi ₁,\varpi ₂\dots {\varpi }_m\right)}^T$with the specified condition${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right]$. Therefore, we establish the following properties.

Boundary: 

For every $\varpi$,

$$S^{-}\le SCFHOW{G}_{\varpi }\left(S_1,S_2,\dots ,S_n\right)\le S^{+},$$

where

$$\begin{array}{c}{S}^{-}=\left\{\begin{array}{c}\left(\left[min{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{-},max{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{+}\right],max{\widehat{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right),\left(\left[max{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{-},min{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{+}\right],min{\widehat{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right),\\ \left(\left[max{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{-},min{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{+}\right],min{\widehat{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)\end{array}\right\}\\ S^{+}=\left\{\begin{array}{c}\left(\left[max{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{-},min{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{+}\right],min{\widehat{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right),\left(\left[min{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{-},max{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{+}\right],max{\widehat{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right),\\ \left(\left[min{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{-},max{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{+}\right],max{\widehat{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\right)\end{array}\right\}\end{array}$$

Idempotency: 

For every $S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)> \left(p=1,2\dots m\right)$ that is the same, that is, $S_p =S$, it holds that $SCFHOW{G}_{\varpi }\left(S₁,S₂\dots S_n\right)=S.$

Monotonicity: 

Let $S^{*}= =\left(<\left[{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\widehat{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}>,<\left[{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\widehat{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}>,<\left[{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\widehat{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}>\right)$ be a collection of SCFNs if $\left[{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{-},{{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}}^{+}\right]\le \left[{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\widehat{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\widehat{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\le {{\widehat{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}}^{*};\left[{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{-},{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{+}\right]\le \left[{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\widehat{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\widehat{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\le {{\widehat{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}}^{*};\left[{{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}}^{-},{{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}}^{+}\right]\le \left[{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\widehat{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\widehat{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\le {{\widehat{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}}^{*};$. For every $p$,

$$SCFHOW{G}_{\varpi }\left(S₁,S₂\dots S_n\right)\le SCFHOW{G}_{\varpi }\left(S_1{}^{*},S_2{}^{*}\dots S_n{}^{*}\right).$$

6.6. Spherical Cubic Fuzzy Hamacher Hybrid Geometric (SCFHHG) Aggregation Operator

Now, we will discuss SCFHHG operator and further discuss its basic properties, that is, idempotency, boundary, and monotonicity.

Definition 23.

Let$S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)>$be a collection of SCFNs in$X$. Therefore, the SCFHHG operator is mapping$SCFHHG:\Phi ⁿ\to \Phi$and the weight vector$\varpi ={\left(\varpi ₁,\varpi ₂\dots {\varpi }_m\right)}^T$with the specified condition${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right]$as$SCFHH{G}_{\varpi }\left(S₁,S₂\dots S_n\right)={{\displaystyle \prod }}_{p=1}^m{\varpi }_p{S}_{\sigma \left(p\right)}^{*}$for all$p$, where$S_{\sigma \left(p\right)}^{*}$represented the$pth$highest weight SFNs$S$. The weight of$S_p$is${\left(\varpi ₁,\varpi ₂\dots {\varpi }_m\right)}^T$with the specified condition${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right]$for$p=1,2,\dots m.$

$$S_{\sigma \left(p\right)}^{*}=m{\varpi }_p{S}_{\sigma \left(p\right)}=\left(<\left[{\tilde{e}}_{\sigma \left(p\right)}^{*-},{\tilde{e}}_{\sigma \left(p\right)}^{*+}\right],{\tilde{\lambda }}_{\sigma \left(p\right)}^{*}>,<\left[{\tilde{n}}_{\sigma \left(p\right)}^{*-},{\tilde{n}}_{\sigma \left(p\right)}^{*+}\right],{\tilde{\mu }}_{\sigma \left(p\right)}^{*}>,<\left[{\tilde{r}}_{\sigma \left(p\right)}^{*-},{\tilde{r}}_{\sigma \left(p\right)}^{*+}\right],>\right)$$

where $\mathrm{m}$ represents the balancing coefficient when $\varpi ={\left(\frac{1}{\mathrm{m}},\frac{1}{\mathrm{m}},\dots ,\frac{1}{\mathrm{m}}\right)}^{\mathrm{T}}$. Therefore, SCFHWG and SCFOHWG operators are considered as a special case of SCFHHA operator. Now, we will obtain the following result related to SCFNs and Hamacher operators.

Theorem 9.

Let$S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)>$be a collection of SCFNs in$X$. Therefore, the aggregation of SCFHHG is also an SCFN and it is defined as

$$SCFHW{G}_{\omega \varpi }\left(S_1,S_2,\dots ,S_n\right)=\left\{\begin{array}{c}\left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)}^{2{\varpi }_p}}},\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)}^{2{\varpi }_p}}}\end{array}\right],\\ \frac{\sqrt{\widehat{f}}{{\displaystyle \prod }}_{p=1}^m{\left({\tilde{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)}^{{\varpi }_p}}{\sqrt{{{\displaystyle \prod }}_{p=1}^m(1+\left(\widehat{f}-1\right){\left(\left(1-\left({\tilde{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)²\right)\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left({\tilde{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)}^{2{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)²\right)}^{{\varpi }_p}}},\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)²\right)}^{{\varpi }_p}}}\end{array}\right],\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\tilde{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\tilde{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\tilde{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\tilde{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)²\right)}^{{\varpi }_p}}}\end{array}\right),\\ \left(\begin{array}{c}\left[\begin{array}{c}\sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-}\right)²\right)}^{{\varpi }_p}}},\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right)²\right)}^{{\varpi }_p}}}\end{array}\right],\\ \sqrt{\frac{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\tilde{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)²\right)}^{{\varpi }_p}-{{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\tilde{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)²\right)}^{{\varpi }_p}}{{{\displaystyle \prod }}_{p=1}^m{\left(1+\left(\widehat{f}-1\right)\left({\tilde{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)²\right)}^{{\varpi }_p}+\left(\widehat{f}-1\right){{\displaystyle \prod }}_{p=1}^m{\left(1-\left({\tilde{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)²\right)}^{{\varpi }_p}}}\end{array}\right),\end{array}\right\}$$

(17)

with ${\left(\varpi ₁,\varpi ₂\dots {\varpi }_m\right)}^T$ under the specified conditions ${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right].$

Proposition 7.

Let$S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)> \left(p=1,2\dots m\right)$be a collection of SCFNs in$X$and the weight vector of$S_p$be$\varpi ={\left(\varpi ₁,\varpi ₂\dots {\varpi }_m\right)}^T$with the specified condition${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right].$Therefore, we establish the following properties.

Boundary: 

For every $\varpi$,

$$S^{-}\le SCFHH{G}_{\omega ,\varpi }\left(S₁,S₂\dots S_n\right)\le S^{-}$$

where

$$\begin{array}{c}{S}^{-}=\left\{\begin{array}{c}\left(\left[min{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},max{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],max{\tilde{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right),\left(\left[max{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},min{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],min{\tilde{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right),\\ \left(\left[max{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},min{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],min{\tilde{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)\end{array}\right\},\\ S^{+}=\left\{\begin{array}{c}\left(\left[max{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},min{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],min{\tilde{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right),\left(\left[min{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},max{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],max{\tilde{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right),\\ \left(\left[min{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},max{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],max{\tilde{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}\right)\end{array}\right\}\end{array}$$

Idempotency: 

For every $S_p=<c_{S_p}\left(x\right),{\dot{c}}_{S_p}\left(x\right),{\ddot{c}}_{S_p}\left(x\right)> \left(p=1,2\dots m\right)$ that is the same, that is, $S_p =S$, it holds that $SCFHH{G}_{\omega ,\varpi }\left(S₁,S₂\dots S_n\right)=S.$

Monotonicity: 

Let $S^{*}= =\left(<\left[{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\tilde{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}>,<\left[{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\tilde{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}>,<\left[{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\tilde{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}>\right)$ be a collection of SCFNs if $\left[{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{-},{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{+}\right]\le \left[{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\tilde{e}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\tilde{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\le {\tilde{\lambda }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*};\left[{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{-},{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{+}\right]\le \left[{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\tilde{n}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\tilde{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\le {\tilde{\mu }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*};\left[{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{-},{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{+}\right]\le \left[{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*-},{\tilde{r}}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*+}\right],{\tilde{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}\le {\tilde{\delta }}_{\mathsf{\sigma }\left(\mathrm{p}\right)}^{*}$. For every $p$,

$$SCFHH{G}_{\omega ,\varpi }\left(S₁,S₂\dots S_n\right)\le SCFHH{G}_{\omega ,\varpi }\left(S_1{}^{*},S_2{}^{*}\dots S_n{}^{*}\right).$$

The theorem is hence proved.

7. Model of the MCDM Based on Using Spherical Cubic Hamacher Aggregation Operators

In this part, the SCFHWA operator is used for the MCDM method. Let there be $m$ alternatives $A=\left\{A₁,A₂\dots A_m\right\}$ and n criteria $C=\left\{C₁,C₂\dots C_n\right\}$, assessed with the weight vector $\varpi ={\left(\varpi ₁,\varpi ₂\dots {\varpi }_m\right)}^T$ with the specified condition ${\sum }_{p=1}^m{\varpi }_p=1 and {\varpi }_p\in \left[0,1\right]$. To assess the achievement based on the criteria $C_p$ of the alternative $A_i$, the decision-maker needs to provide not only the statistics about alternative $A_i$, but also those about not fulfilling criteria $C_p$. The ratings of alternatives $A_i$ on criteria $C_p$ given by the choice producer are the SCFNs in $X$. $S_{ip}=<C_{S_{ip}}\left(x\right),{\dot{C}}_{S_{ip}}\left(x\right),{\ddot{C}}_{S_{ip}}\left(x\right)> (i=\left(1,2\dots m\right),\left(p=1,2,\dots n\right).$ Let $c_{S_{ip}}$ be the degree of alternative $A_i$ fulfilling the criteria $C_p$, let ${\dot{c}}_{S_{ip}}$ show the degree of alternative $A_i$ that is alternative, and let ${\ddot{c}}_{S_{ip}}\left(x\right)$ show the degree of alternative $A_i$ not fulfilling the criteria $C_p$, such that $C_{S_{ip}}\left(x\right)=<\left[{\widehat{e}}_{ip}^{-},{\widehat{e}}_{ip}^{+}\right],{\widehat{\lambda }}_{ip}>, {\dot{C}}_{S_{ip}}\left(x\right)=<\left[{\widehat{n}}_{ip}^{-},{\widehat{n}}_{ip}^{+}\right],{\widehat{\mu }}_{ip}>, {\ddot{C}}_{S_{ip}}=<\left[{{\widehat{r}}_{ip}}^{-},{{\widehat{r}}_{ip}}^{+}\right],{\widehat{\delta }}_{ip}>)$ under the specified conditions $\left[{\widehat{e}}_{ip}^{-},{\widehat{e}}_{ip}^{+}\right]\subset \left[0,1\right], \left[{\widehat{n}}_{ip}^{-},{\widehat{n}}_{ip}^{+}\right]\subset \left[0,1\right], \left[{\widehat{r}}_{ip}^{-},{\widehat{r}}_{ip}^{+}\right]\subset \left[0,1\right]and {\widehat{\lambda }}_{ip}:X\to \left[0,1\right],{\widehat{\mu }}_{ip}:X\to \left[0,1\right], {\widehat{\delta }}_{ip}:X\to \left[0,1\right]$ under the condition $sup\left[{\widehat{e}}_{ip}^{-},{\widehat{e}}_{ip}^{+}\right]+sup\left[{\widehat{n}}_{ip}^{-},{\widehat{n}}_{ip}^{+}\right]+sup\left[{\widehat{r}}_{ip}^{-},{\widehat{r}}_{ip}^{+}\right]\le 1 and {\widehat{\lambda }}_{ip}+{\widehat{\mu }}_{ip}+{\widehat{\delta }}_{ip}\le 1. \left(i=1,2\dots m, p=1,2\dots n\right).$

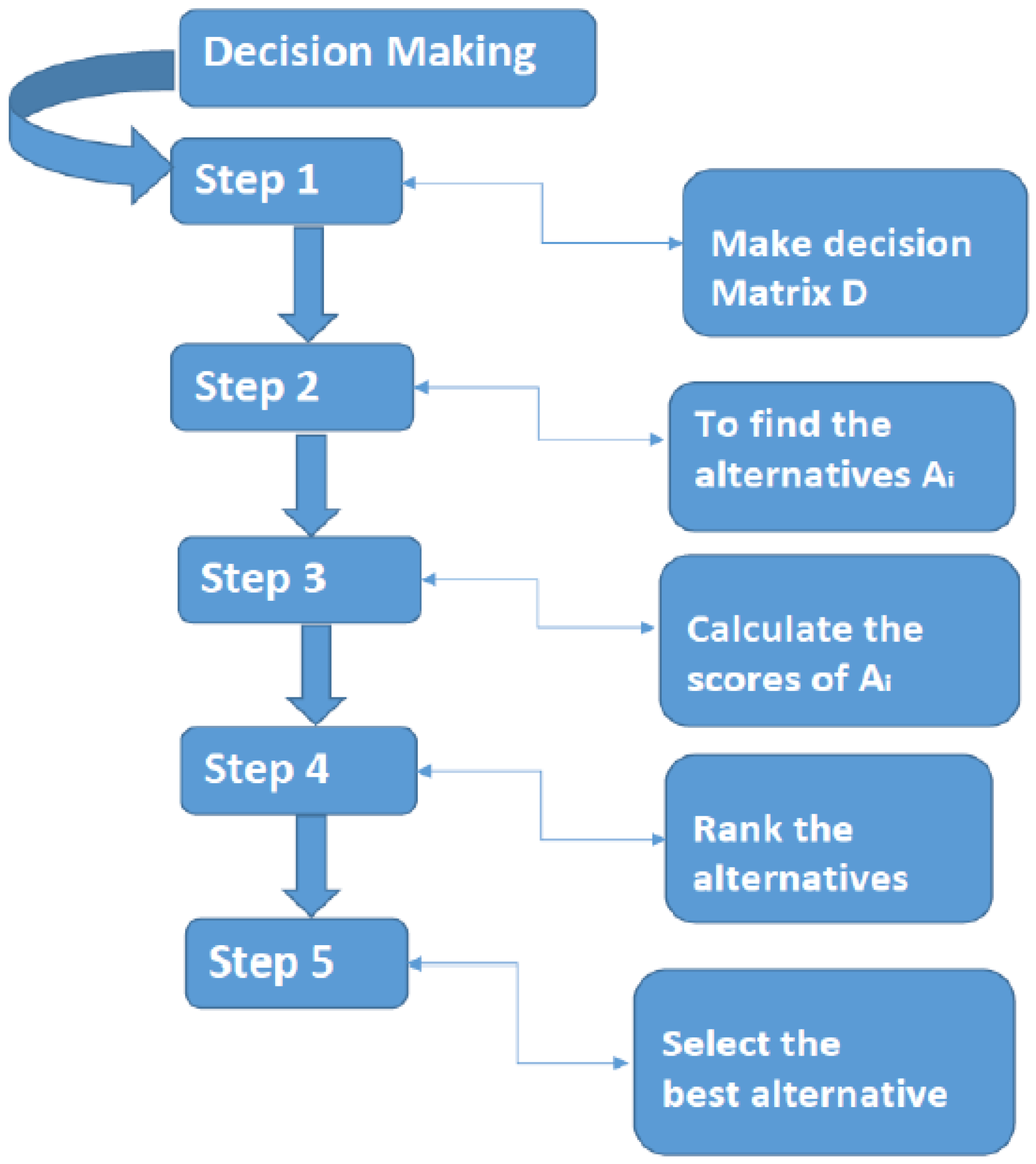
Along these lines, the MCDM issue can be quickly represented in an SCF decision matrix $D={\left(S_{ip}\right)}_{m\times n}={\left(<C_{S_{ip}}\left(x\right),{\dot{C}}_{S_{ip}}\left(x\right),{\ddot{C}}_{S_{ip}}\left(x\right)>\right)}_{m\times n} \left(i=1,2\dots m, p=1,2\dots n\right).$ Further, the accompanying advances are included in the MCDM process.

Step 1:

Settle on the MCDM decision matrix $D={\left(S_{ip}\right)}_{m\times n}={\left(<C_{S_{ip}}\left(x\right),{\dot{C}}_{S_{ip}}\left(x\right),{\ddot{C}}_{S_{ip}}\left(x\right)>\right)}_{m\times n} \left(i=1,2\dots m, p=1,2\dots n\right)$. The criteria are normally delegated to cost and benefit. In the situation that all of the criteria are of a similar kind, there is no need for normalizing the rating values, while the rating estimations of the cost type can be changed into rating estimations of the benefit type by the following normalized formula, if the decision matrix contains both cost and benefit criteria.

$${\widehat{S}}_{ip}=<{\widehat{c}}_{S_{ip}},{\widehat{d}}_{S_{ip}}>=\{\begin{array}{c}{v}_{S_{ip}}, \mathrm{if} \mathrm{the} \mathrm{criteria} \mathrm{is} \mathrm{of} \mathrm{benefit} \mathrm{type}\\ v^c{}_{S_{ip}}, \mathrm{if} \mathrm{the} \mathrm{criteria} \mathrm{is} \mathrm{of} \mathrm{cost} \mathrm{type}\end{array}$$

Here, $v^c{}_{S_{ip}}$ represents the complement of $v_{S_{ip}}$. Along these lines, we obtain the normalization of the SCF decision matrix, which is represented by $D^m$ and given by $D^{m }={\left({\widehat{S}}_{ip}\right)}_{m\times n}={<{\widehat{c}}_{S_{ip}},{\widehat{d}}_{S_{ip}}>}_{m\times n}\left(i=1,2\dots m, p=1,2\dots n\right).$

Next, we will apply the SCFHWA, SCFHOWA, and SCFHHA operators to MCDM, which further requires the following steps.

Step 2:

Utilize the recommended aggregation operators to find the SCFNs $S_i \left(i=1,2\dots m\right)$ for the alternatives $A_i$. The created operators stem the system in general preference values $S_i$ of the alternatives $A_i$, and the weight vector of the criteria here is $\varpi ={\left(\varpi ₁,\varpi ₂\dots {\varpi }_m\right)}^T.$

Step 3:

Utilizing the score functions of the SCFNs, find the score $S_c\left(S_i\right) (i=1,2\dots m)$ of all values $S_i$ to rank all the alternatives $A_i$ to select the best choice $A_i$. In the situation where there is no disparity between $S_c\left(S_i\right)$ and $S_c$ ($S_j$), continue to find the accuracy H($S_i$) and H($S_j$) using SCF information of $S_i$ and $S_j$. Rank the alternative $A_i \left(i=1,2\dots m\right)$ based on the accuracy of H($S_i$) and H($S_j$).

Step 4:

Rank all the alternatives $A_i \left(i=1,2\dots m\right)$ to select the best one.

Numerical Application

The long-term stable advancement of enterprises is hampered because of these issues. The creation, natural contamination, low-quality creation, misuse of assets, and absence of security of the premiums of the representatives cause investors to lose enthusiasm to contribute to wealth, make investments in the organization, and bear speculation chances. Enterprise development and endurance rely upon an enterprise’s capacity and adequate management of the relationships among different inventors. Key administration does not approve of the conduct of enterprises on the off chance that they need to accomplish an objective on investor esteem in the creation of procedures, paying little head to the enthusiasm of different partner’s necessities. From the viewpoint of partners, in a supervision and executive framework, an enterprise’s financial performance depends on an enterprise’s self-observation, self-restraint, and self-assessment; however, there is essential instrumentation to adequately communicate with partners to determine each partner’s benefit, which is a vital administration objective of the enterprise. Right now, we will introduce a project for the selection of best enterprise alternatives based on budgetary performance to research our proposed strategy. Here, we have assessed the overall performance of four enterprises $A_i \left(i=1,2,3,4\right)$. An organization that puts away its cash is looking to boost benefits. It is required to determine the enterprise performance of four possible enterprises to select the best one. The entire dynamic procedure is presented by a stream graph in the following figure. The investment company takes a decision relying upon the following four characteristics.

C₁: Financial Execution, C₂: Customer Execution, C₃: Internal Procedures Execution, C₄: Staff Execution

To keep decision-makers from dominating, they are required to exempt four possible enterprises $A_i \left(i=1,2,3,4\right)$ under the considered attributes, whose weight vector is ${\left(0.2,0.3,0.5\right)}^T$ and criteria weighting vector is ${\left(0.1,0.2,0.3,0.4\right)}^T$ (

Table 1. First decision-maker data.

	${\mathit{C}}_{\mathbf{1}}$	${\mathit{C}}_{\mathbf{2}}$	${\mathit{C}}_{\mathbf{3}}$	${\mathit{C}}_{\mathbf{4}}$
$A_1$	$\left(\begin{array}{c}\left(\left[0.2,0.4\right],0.1\right),\\ \left(\left[0.2,0.1\right],0.4\right),\\ \left(\left[0.2,0.1\right],0.5\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.5,0.2\right],0.6\right),\\ \left(\left[0.3,0.4\right],0.1\right),\\ \left(\left[0.1,0.2\right],0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.4,0.5\right],0.2\right),\\ \left(\left[0.1,0.2\right],0.5\right),\\ \left(\left[0.1,0.2\right],0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.4\right],0.4\right),\\ \left(\left[0.3,0.2\right],0.3\right),\\ \left(\left[0.1,0.2\right],0.2\right)\end{array}\right)$
$A_2$	$\left(\begin{array}{c}\left(\left[0.2,0.4\right],0.1\right),\\ \left(\left[0.2,0.1\right],0.2\right),\\ \left(\left[0.2,0.3\right],0.5\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.2,0.1\right],0.4\right),\\ \left(\left[0.3,0.2\right],0.2\right),\\ \left(\left[0.4,0.1\right],0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.5,0.1\right],0.6\right),\\ \left(\left[0.1,0.2\right],0.1\right),\\ \left(\left[0.1,0.3\right],0.2\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.2\right],0.3\right),\\ \left(\left[0.3,0.2\right],0.2\right),\\ \left(\left[0.1,0.5\right],0.4\right)\end{array}\right)$
$A_3$	$\left(\begin{array}{c}\left(\left[0.1,0.2\right],0.2\right),\\ \left(\left[0.1,0.4\right],0.1\right),\\ \left(\left[0.3,0.2\right],0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.2,0.1\right],0.2\right),\\ \left(\left[0.1,0.2\right],0.2\right),\\ \left(\left[0.1,0.6\right],0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.2,0.1\right],0.4\right),\\ \left(\left[0.1,0.2\right],0.4\right),\\ \left(\left[0.1,0.4\right],0.1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.5\right],0.4\right),\\ \left(\left[0.2,0.1\right],0.3\right),\\ \left(\left[0.1,0.3\right],0.1\right)\end{array}\right)$
$A_4$	$\left(\begin{array}{c}\left(\left[0.1,0.4\right],0.1\right),\\ \left(\left[0.1,0.3\right],0.2\right),\\ \left(\left[0.1,0.2\right],0.5\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.4\right],0.3\right),\\ \left(\left[0.1,0.2\right],0.4\right),\\ \left(\left[0.1,0.3\right],0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.4\right],0.1\right),\\ \left(\left[0.2,0.1\right],0.2\right),\\ \left(\left[0.1,0.2\right],0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.2,0.3\right],0.4\right),\\ \left(\left[0.1,0.2\right],0.2\right),\\ \left(\left[0.1,0.3\right],0.4\right)\end{array}\right)$

,

Table 2. Second decision-maker data.

	${\mathit{C}}_{\mathbf{1}}$	${\mathit{C}}_{\mathbf{2}}$	${\mathit{C}}_{\mathbf{3}}$	${\mathit{C}}_{\mathbf{4}}$
$A_1$	$\left(\begin{array}{c}\left(\left[0.1,0.5\right],0.4\right),\\ \left(\left[0.1,0.2\right],0.1\right),\\ \left(\left[0.2,0.3\right],0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.2,0.6\right],0.3\right),\\ \left(\left[0.1,0.2\right],0.3\right),\\ \left(\left[0.1,0.2\right],0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.2,0.5\right],0.4\right),\\ \left(\left[0.1,0.2\right],0.3\right),\\ \left(\left[0.1,0.2\right],0.2\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.5\right],0.4\right),\\ \left(\left[0.1,0.2\right],0.2\right),\\ \left(\left[0.1,0.2\right],0.1\right)\end{array}\right)$
$A_2$	$\left(\begin{array}{c}\left(\left[0.1,0.5\right],0.1\right),\\ \left(\left[0.1,0.3\right],0.2\right),\\ \left(\left[0.2,0.1\right],0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.2\right],0.3\right),\\ \left(\left[0.3,0.1\right],0.4\right),\\ \left(\left[0.5,0.1\right],0.2\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.2\right],0.4\right),\\ \left(\left[0.2,0.1\right],0.2\right),\\ \left(\left[0.3,0.1\right],0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.2,0.3\right],0.4\right),\\ \left(\left[0.1,0.2\right],0.3\right),\\ \left(\left[0.2,0.1\right],0.1\right)\end{array}\right)$
$A_3$	$\left(\begin{array}{c}\left(\left[0.4,0.2\right],0.5\right),\\ \left(\left[0.1,0.2\right],0.4\right),\\ \left(\left[0.1,0.3\right],0.1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.4\right],0.1\right),\\ \left(\left[0.1,0.2\right],0.2\right),\\ \left(\left[0.3,0.2\right],0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.3\right],0.5\right),\\ \left(\left[0.2,0.4\right],0.4\right),\\ \left(\left[0.1,0.2\right],0.1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.2\right],0.1\right),\\ \left(\left[0.2,0.3\right],0.2\right),\\ \left(\left[0.3,0.4\right],0.3\right)\end{array}\right)$
$A_4$	$\left(\begin{array}{c}\left(\left[0.1,0.3\right],0.5\right),\\ \left(\left[0.3,0.4\right],0.4\right),\\ \left(\left[0.2,0.1\right],0.1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.4\right],0.1\right),\\ \left(\left[0.1,0.2\right],0.4\right),\\ \left(\left[0.3,0.2\right],0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.2\right],0.2\right),\\ \left(\left[0.2,0.4\right],0.3\right),\\ \left(\left[0.3,0.1\right],0.4\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.4\right],0.5\right),\\ \left(\left[0.1,0.3\right],0.2\right),\\ \left(\left[0.1,0.2\right],0.2\right)\end{array}\right)$

and

Table 3. Third decision-maker data.

	${\mathit{C}}_{\mathbf{1}}$	${\mathit{C}}_{\mathbf{2}}$	${\mathit{C}}_{\mathbf{3}}$	${\mathit{C}}_{\mathbf{4}}$
$A_1$	$\left(\begin{array}{c}\left(\left[0.1,0.3\right],0.2\right),\\ \left(\left[0.2,0.3\right],0.1\right),\\ \left(\left[0.1,0.4\right],0.1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.2\right],0.3\right),\\ \left(\left[0.3,0.4\right],0.1\right),\\ \left(\left[0.1,0.2\right],0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.4\right],0.3\right),\\ \left(\left[0.3,0.2\right],0.2\right),\\ \left(\left[0.1,0.4\right],0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.2\right],0.3\right),\\ \left(\left[0.3,0.1\right],0.2\right),\\ \left(\left[0.1,0.4\right],0.3\right)\end{array}\right)$
$A_2$	$\left(\begin{array}{c}\left(\left[0.1,0.2\right],0.5\right),\\ \left(\left[0.3,0.1\right],0.2\right),\\ \left(\left[0.2,0.4\right],0.1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.2\right],0.4\right),\\ \left(\left[0.3,0.1\right],0.3\right),\\ \left(\left[0.2,0.4\right],0.1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.2,0.1\right],0.4\right),\\ \left(\left[0.3,0.2\right],0.1\right),\\ \left(\left[0.1,0.2\right],0.3\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.2\right],0.4\right),\\ \left(\left[0.4,0.1\right],0.2\right),\\ \left(\left[0.2,0.3\right],0.3\right)\end{array}\right)$
$A_3$	$\left(\begin{array}{c}\left(\left[0.5,0.1\right],0.6\right),\\ \left(\left[0.2,0.1\right],0.2\right),\\ \left(\left[0.1,0.2\right],0.1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.3\right],0.4\right),\\ \left(\left[0.4,0.5\right],0.2\right),\\ \left(\left[0.2,0.1\right],0.1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.2\right],0.3\right),\\ \left(\left[0.3,0.4\right],0.2\right),\\ \left(\left[0.2,0.1\right],0.1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.2\right],0.3\right),\\ \left(\left[0.3,0.4\right],0.5\right),\\ \left(\left[0.4,0.3\right],0.2\right)\end{array}\right)$
$A_4$	$\left(\begin{array}{c}\left(\left[0.1,0.2\right],0.3\right),\\ \left(\left[0.2,0.3\right],0.4\right),\\ \left(\left[0.4,0.1\right],0.2\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.3\right],0.4\right),\\ \left(\left[0.2,0.1\right],0.3\right),\\ \left(\left[0.5,0.1\right],0.2\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.2\right],0.2\right),\\ \left(\left[0.3,0.4\right],0.5\right),\\ \left(\left[0.1,0.2\right],0.1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.2\right],0.2\right),\\ \left(\left[0.3,0.4\right],0.2\right),\\ \left(\left[0.4,0.1\right],0.5\right)\end{array}\right)$

).

By spherical cubic fuzzy Hamacher weighted average operator

Step 1:

The data of decision-makers are given in Table 1, Table 2 and Table 3. There is no need to normalize the data. Assume $f=2$ and weight vector $\varpi ={\left(0.2,0.3,0.5\right)}^T,$ using the SCFHWA operator, the aggregated information of the data in Table 1, Table 2 and Table 3 of all the decision-makers, and the data represented in

Table 4. Aggregation of all decision-maker data by the spherical cubic fuzzy Hamacher weighted average (SCFHWA) operator.

	${\mathit{C}}_{\mathbf{1}}$	${\mathit{C}}_{\mathbf{2}}$	${\mathit{C}}_{\mathbf{3}}$	${\mathit{C}}_{\mathbf{4}}$
$A_1$	$\left(\begin{array}{c}\left(\left[0.13,0.39\right],0.27\right),\\ \left(\left[0.11,0.15\right],0.08\right),\\ \left(\left[0.09,0.22\right],0.13\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.26,0.37\right],0.38\right),\\ \left(\left[0.16,0.27\right],0.09\right),\\ \left(\left[0.06,0.14\right],0.28\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.22,0.45\right],0.32\right),\\ \left(\left[0.12,0.11\right],0.021\right),\\ \left(\left[0.06,0.23\right],0.21\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.36\right],0.35\right),\\ \left(\left[0.16,0.09\right],0.16\right),\\ \left(\left[0.06,0.23\right],0.14\right)\end{array}\right)$
$A_2$	$\left(\begin{array}{c}\left(\left[0.13,0.36\right],0.36\right),\\ \left(\left[0.14,0.09\right],0.14\right),\\ \left(\left[0.14,0.19\right],0.15\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.13,0.18\right],0.37\right),\\ \left(\left[0.16,0.36\right],0.07\right),\\ \left(\left[0.25,0.14\right],0.1\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.27,0.14\right],0.45\right),\\ \left(\left[0.15,0.11\right],0.09\right),\\ \left(\left[0.09,0.12\right],0.17\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.14,0.23\right],0.38\right),\\ \left(\left[0.19,0.09\right],0.17\right),\\ \left(\left[0.12,0.18\right],0.17\right)\end{array}\right)$
$A_3$	$\left(\begin{array}{c}\left(\left[0.42,0.16\right],0.52\right),\\ \left(\left[0.09,0.11\right],0.16\right),\\ \left(\left[0.08,0.17\right],0.08\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.13,0.31\right],0.3\right),\\ \left(\left[0.14,0.26\right],0.14\right),\\ \left(\left[0.14,0.12\right],0.23\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.13,0.22\right],0.39\right),\\ \left(\left[0.15,0.3\right],0.3\right),\\ \left(\left[0.09,0.11\right],0.06\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.29\right],0.28\right),\\ \left(\left[0.18,0.22\right],0.3\right),\\ \left(\left[0.22,0.28\right],0.14\right)\end{array}\right)$
$A_4$	$\left(\begin{array}{c}\left(\left[0.1,0.28\right],0.35\right),\\ \left(\left[0.14,0.28\right],0.3\right),\\ \left(\left[0.19,0.07\right],0.14\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.35\right],0.32\right),\\ \left(\left[0.09,0.09\right],0.3\right),\\ \left(\left[0.26,0.18\right],0.09\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.25\right],0.18\right),\\ \left(\left[0.18,0.25\right],0.31\right),\\ \left(\left[0.09,0.11\right],0.13\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.13,0.29\right],0.36\right),\\ \left(\left[0.12,0.27\right],0.14\right),\\ \left(\left[0.14,0.1\right],0.26\right)\end{array}\right)$

. Using the SCFHWA operator, taking $f=2$, the aggregate data in Table 4, and the weight vector $\varpi ={\left(0.1,0.2,0.3,0.4\right)}^T$, we have the alternatives $A_i \left(i=1,2,3,4\right).$

$$\begin{array}{c}A₁=(\left(\left[0.18,0.4\right],0.34\right),\left(\left[0.07,0.06\right],0.07\right),\left(\left[0.3,0.12\right],0.1\right)\\ A₂=(\left(\left[0.19,0.22\right],0.4\right),\left(\left[0.1,0.04\right],0.08\right),\left(\left[0.06,0.08\right],0.08\right)\\ A₃=(\left(\left[0.17,0.26\right],0.35\right),\left(\left[0.08,0.14\right],0.13\right),\left(\left[0.07,0.09\right],0.05\right)\\ A₄=(\left(\left[0.11,0.29\right],0.31\right),\left(\left[0.06,0.12\right],0.13\right),\left(\left[0.07,0.05\right],0.1\right)\end{array}$$

Step 2:

Using the definition of score function S($A_i$) of $A_i$ (i=1,2,3,4), the calculated scores are as follows

$$S_c\left(A_1\right)=0.08, S_c\left(A₂\right)=0.1, S_c\left(A₃\right)=0.1, S_c\left(A₄\right)=0.07.$$

Step 3:

Rank all the scores and choose the best alternative.

$$A₃=A₂>A₁>A₄.$$

Step 4:

$A₃$ is the best choice.

By the spherical cubic fuzzy Hamacher ordered weighted average operator

Step 1:

The aggregated data of three decision-makers are given in Table 4. Using the SCFHOWA operator $f=2$, the aggregated data in Table 4, and the weight vector $\varpi ={\left(0.1,0.2,0.3,0.4\right)}^T$, we have the collective SCFNs for the alternatives $A_i\left(i=1,2,3,4\right).$

$$\begin{array}{c}A₁=(\left(\left[0.16,0.39\right],0.32\right),\left(\left[0.06,0.06\right],0.06\right),\left(\left[0.03,0.12\right],0.1\right);\\ A₂=(\left(\left[0.15,0.26\right],0.38\right),\left(\left[0.1,0.04\right],0.09\right),\left(\left[0.07,0.09\right],0.07\right);\\ A₃=(\left(\left[0.22,0.23\right],0.34\right),\left(\left[0.06,0.13\right],0.1\right),\left(\left[0.07,0.09\right],0.05\right);\\ A₄=(\left(\left[0.11,0.3\right],0.29\right),\left(\left[0.06,0.1\right],0.13\right),\left(\left[0.1,0.04\right],0.13\right).\end{array}$$

Step 2:

Using the definition of score function $S\left(A_i\right)$ of $A_i$(i=1,2,3,4), the calculated scores are as follows.

$$S_c\left(A_1\right)=0.05, S_c\left(A_2\right)=0.06, S_c\left(A_3\right)=0.06, S_c\left(A_4\right)=0.03.$$

Step 3:

Rank all the scores and choose the best alternative.

$$A₃=A₂>A₁>A₄.$$

Step 4:

$A₃$ is the best choice.

By the spherical cubic fuzzy Hamacher hybrid Aggregation operator

The decision-making data are given in Table 1, Table 2 and Table 3. Apply ${\tilde{S}}_p=m{\omega }_p{\widehat{S}}_p=\langle \left[{\tilde{e}}_p{}^{-},{\tilde{e}}_p{}^{+}\left],{\tilde{\lambda }}_p\rangle ,\langle \right[{\tilde{n}}_p{}^{-},{\tilde{n}}_p{}^{+}\left],{\tilde{\mu }}_p\rangle ,\langle \right[{\tilde{\gamma }}_p{}^{-},{\tilde{\gamma }}_p{}^{+}\right],{\tilde{\delta }}_p\rangle$ to the data given in Table 1, Table 2 and Table 3 using the weight vector $\varpi ={\left(0.2,0.3,0.5\right)}^T$ of all the alternatives $A_i$. The aggregated data with the weight vector $\varpi =\left(0.2,0.4,0.4\right)$ using the SCFHHA operator are given in

Table 5. Aggregation of all decision-maker data by the spherical cubic fuzzy Hamacher ordered weight average (SCFHOWA) operator.

	${\mathit{C}}_{\mathbf{1}}$	${\mathit{C}}_{\mathbf{2}}$	${\mathit{C}}_{\mathbf{3}}$	${\mathit{C}}_{\mathbf{4}}$
$A_1$	$\left(\begin{array}{c}\left(\left[0.26,0.37\right],0.38\right),\\ \left(\left[0.16,0.27\right],0.09\right),\\ \left(\left[0.06,0.14\right],0.28\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.2,0.45\right],0.32\right),\\ \left(\left[0.1,0.14\right],0.18\right),\\ \left(\left[0.06,0.23\right],0.16\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.14,0.39\right],0.32\right),\\ \left(\left[0.12,0.14\right],0.12\right),\\ \left(\left[0.06,0.23\right],0.09\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.13,0.36\right],0.31\right),\\ \left(\left[0.14,0.08\right],0.13\right),\\ \left(\left[0.09,0.02\right],0.28\right)\end{array}\right)$
$A_2$	$\left(\begin{array}{c}\left(\left[0.27,0.14\right],0.43\right),\\ \left(\left[0.18,0.11\right],0.1\right),\\ \left(\left[0.11,0.12\right],0.14\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.13,0.31\right],0.4\right),\\ \left(\left[0.16,0.11\right],0.16\right),\\ \left(\left[0.17,0.14\right],0.13\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.2\right],0.38\right),\\ \left(\left[0.21,0.07\right],0.22\right),\\ \left(\left[0.14,0.22\right],0.13\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.16,0.28\right],0.36\right),\\ \left(\left[0.17,0.08\right],0.17\right),\\ \left(\left[0.14,0.16\right],0.18\right)\end{array}\right)$
$A_3$	$\left(\begin{array}{c}\left(\left[0.1,0.35\right],0.43\right),\\ \left(\left[0.23,0.29\right],0.21\right),\\ \left(\left[0.09,0.1\right],0.06\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.43,0.14\right],0.54\right),\\ \left(\left[0.09,0.09\right],0.23\right),\\ \left(\left[0.06,0.2\right],0.16\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.28\right],0.24\right),\\ \left(\left[0.3,0.18\right],0.2\right),\\ \left(\left[0.09,0.11\right],0.06\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.13,0.18\right],0.24\right),\\ \left(\left[0.15,0.27\right],0.14\right),\\ \left(\left[0.14,0.16\right],0.13\right)\end{array}\right)$
$A_4$	$\left(\begin{array}{c}\left(\left[0.1,0.28\right],0.31\right),\\ \left(\left[0.18,0.34\right],0.36\right),\\ \left(\left[0.08,0.11\right],0.09\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.13,0.29\right],0.39\right),\\ \left(\left[0.09,0.22\right],0.23\right),\\ \left(\left[0.14,0.1\right],0.14\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.3\right],0.33\right),\\ \left(\left[0.12,0.12\right],0.26\right),\\ \left(\left[0.26,0.08\right],0.21\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.1,0.32\right],0.16\right),\\ \left(\left[0.14,0.19\right],0.19\right),\\ \left(\left[0.22,0.09\right],0.35\right)\end{array}\right)$

.

Step 1:

Using the formula ${\tilde{S}}_p=m{\omega }_p{\widehat{S}}_p=\langle \left[{\tilde{e}}_p{}^{-},{\tilde{e}}_p{}^{+}\left],{\tilde{\lambda }}_p\rangle ,\langle \right[{\tilde{n}}_p{}^{-},{\tilde{n}}_p{}^{+}\left],{\tilde{\mu }}_p\rangle ,\langle \right[{\tilde{\gamma }}_p{}^{-},{\tilde{\gamma }}_p{}^{+}\right],{\tilde{\delta }}_p\rangle$ with the given data in Table 5, using the weight vector as $\varpi ={\left(0.1,0.2,0.3,0.4\right)}^T,$ the calculated values are given in

Table 6. Aggregation of all decision-maker data by the spherical cubic fuzzy Hamacher ordered weighted geometric (SCFHOWG) operator.

	${\mathit{C}}_{\mathbf{1}}$	${\mathit{C}}_{\mathbf{2}}$	${\mathit{C}}_{\mathbf{3}}$	${\mathit{C}}_{\mathbf{4}}$
$A_1$	$\left(\begin{array}{c}\left(\left[0.26,0.37\right],0.38\right),\\ \left(\left[0.11,0.04\right],0.03\right),\\ \left(\left[0.02,0.05\right],0.05\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.13,0.42\right],0.44\right),\\ \left(\left[0.01,0.01\right],0.01\right),\\ \left(\left[0.01,0.02\right],0.01\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.19,0.3\right],0.33\right),\\ \left(\left[0.16,0.09\right],0.11\right),\\ \left(\left[0.11,0.16\right],0.07\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.08,0.25\right],0.16\right),\\ \left(\left[0.32,0.35\right],0.29\right),\\ \left(\left[0.3,0.38\right],0.33\right)\end{array}\right)$
$A_2$	$\left(\begin{array}{c}\left(\left[0.16,0.29\right],0.47\right),\\ \left(\left[0.02,0.01\right],0.02\right),\\ \left(\left[0.01,0.02\right],0.02\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.26,0.14\right],0.48\right),\\ \left(\left[0.04,0.03\right],0.03\right),\\ \left(\left[0.03,0.03\right],0.04\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.11,0.16\right],0.33\right),\\ \left(\left[0.15,0.08\right],0.16\right),\\ \left(\left[0.15,0.12\right],0.09\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.08,0.22\right],0.2\right),\\ \left(\left[0.34,0.3\right],0.34\right),\\ \left(\left[0.34,0.37\right],0.34\right)\end{array}\right)$
$A_3$	$\left(\begin{array}{c}\left(\left[0.13,0.23\right],0.42\right),\\ \left(\left[0.04,0.07\right],0.05\right),\\ \left(\left[0.03,0.03\right],0.02\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.13,0.33\right],0.33\right),\\ \left(\left[0.02,0.02\right],0.03\right),\\ \left(\left[0.02,0.02\right],0.01\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.26,0.1\right],0.33\right),\\ \left(\left[0.31,0.31\right],0.35\right),\\ \left(\left[0.29,0.35\right],0.29\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.29,0.35\right],0.29\right),\\ \left(\left[0.12,0.16\right],0.11\right),\\ \left(\left[0.11,0.1\right],0.11\right)\end{array}\right)$
$A_4$	$\left(\begin{array}{c}\left(\left[0.15,0.35\right],0.42\right),\\ \left(\left[0.01,0.02\right],0.01\right),\\ \left(\left[0.01,0.01\right],0.02\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.06,0.17\right],0.21\right),\\ \left(\left[0.34,0.39\right],0.4\right),\\ \left(\left[0.37,0.28\right],0.34\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.09,0.32\right],0.26\right),\\ \left(\left[0.09,0.09\right],0.16\right),\\ \left(\left[0.16,0.09\right],0.13\right)\end{array}\right)$	$\left(\begin{array}{c}\left(\left[0.11,0.26\right],0.2\right),\\ \left(\left[0.05,0.06\right],0.07\right),\\ \left(\left[0.03,0.03\right],0.04\right)\end{array}\right)$

. Again, using the SCFHHA operator and weight vector $\varpi ={\left(0.15,0.25,0.31,0.29\right)}^T$, we have the collective alternatives $A_i$ (i=1,2,3,4) as follows.

$$\begin{array}{c}{A}_1=\left(\left(\left[0.18,0.31\right],0.36\right),\left(\left[0.04,0.03\right],0.03\right),\left(\left[0.03,0.05\right],0.03\right)\right);\\ A_2=\left(\left(\left[0.16,0.2\right],0.37\right),\left(\left[0.05,0.03\right],0.04\right),\left(\left[0.04,0.04\right],0.04\right)\right);\\ A_3=\left(\left(\left[0.18,0.24\right],0.33\right),\left(\left[0.04,0.05\right],0.05\right),\left(\left[0.03,0.04\right],0.03\right)\right);\\ A₄=\left(\left(\left[0.1,0.28\right],0.27\right),\left(\left[0.03,0.04\right],0.05\right),\left(\left[0.04,0.03\right],0.04\right)\right).\end{array}$$

Step 2:

Using the definition of score function $S_c\left(A_i\right) of A_i \left(i=1,2,3,4\right),$ the calculated scores are as follows.

$$S_c\left(A_1\right)=0.06, S_c\left(A_2\right)=0.08, S_c\left(A_3\right)=0.08, S_c\left(A₄\right)=0.05.$$

Step 3:

Rank all the scores and choose the best alternative.

$$A₃=A₂>A₁>A₄$$

Step 4:

$A₃$ is the best choice.

By spherical cubic fuzzy Hamacher weighted geometric operator

Step 1:

The data of decision-makers are given in Table 1, Table 2 and Table 3. There is no need to normalize the data. Assume $f=2$ and weight vector $\varpi ={\left(0.2,0.3,0.5\right)}^T$, using the SCFHWG operator, the aggregated information of the data in Table 1, Table 2 and Table 3 of all the decision-makers, and the data represented in Table 4. Using the SCFHWG operator, taking $f=2$, the aggregate data in Table 4, and the weight vector $\varpi ={\left(0.1,0.2,0.3,0.4\right)}^T$, we have the alternatives $A_i \left(i=1,2,3,4\right).$

$$\begin{array}{c}A₁=(\left(\left[0.07,0.19\right],0.2\right),\left(\left[0.2,0.2\right],0.17\right),\left(\left[0.17,0.22\right],0.18\right);\\ A₂=(\left(\left[0.06,0.1\right],0.23\right),\left(\left[0.2,0.17\right],0.2\right),\left(\left[0.2,0.21\right],0.19\right);\\ A₃=(\left(\left[0.08,0.11\right],0.21\right),\left(\left[0.19,0.2\right],0.21\right),\left(\left[0.17,0.2\right],0.17\right);\\ A₄=(\left(\left[0.04,0.16\right],0.15\right),\left(\left[0.18,0.2\right],0.22\right),\left(\left[0.21,0.15\right],0.19\right).\end{array}$$

Step 2:

Using the definition of score function $S_c\left(A_i\right)$ of $A_i$ (i=1,2,3,4), the calculated scores are as follows.

$$S_c\left(A_1\right) = 0.03, S_c\left(A_2\right) = 0.04, S_c\left(A_3\right) = 0.04, S_c\left(A_4\right) = 0.01.$$

Step 3:

Rank all the scores and choose the best alternative.

$$A₃=A₂>A₁>A₄.$$

Step 4:

$A₃$ is the best choice.

By spherical cubic fuzzy Hamacher ordered weighted geometric operator

Step 1:

The aggregated data of the three decision-makers are given in Table 4. Using the SCFHOWG operator, $f=2,$ the aggregated data in Table 4, and the weight vector $\varpi ={\left(0.1,0.2,0.3,0.4\right)}^T$, we have the collective SCFN for the alternatives $A_i\left(i=1,2,3,4\right).$

$$\begin{array}{c}A₁=(\left(\left[0.03,0.2\right],0.13\right),\left(\left[0.23,0.21\right],0.24\right),\left(\left[0.13,0.31\right],0.28\right)\\ A₂=(\left(\left[0.03,0.08\right],0.18\right),\left(\left[0.28,0.15\right],0.25\right),(\left[0.23,0.3\right],0.28\\ A₃=(\left(\left[0.04,0.07\right],0.34\right),\left(\left[0.06,0.13\right],0.1\right),\left(\left[0.07,0.09\right],0.05\right)\\ A₄=(\left(\left[0.03,0.13\right],0.09\right),\left(\left[0.21,0.29\right],0.32\right),\left(\left[0.33,0.17\right],0.33\right).\end{array}$$

Step 2:

Using the definition of score function $S_c\left(A_i\right) of A_i\left(i=1,2,3,4\right)$, the calculated scores are as follows.

$$S_c\left(A_1\right)=0.02, S_c\left(A_2\right)=0.03, S_c\left(A_3\right)=0.03, S_c\left(A_4\right)=0.01.$$

Step 3:

Rank all the scores and choose the best alternative.

$$A₃=A₂>A₁>A₄.$$

Step 4:

$A₃$ is the best choice.

By spherical cubic fuzzy Hamacher Hybrid Aggregation operator

The decision-making data are given in Table 1, Table 2 and Table 3. Apply ${\tilde{S}}_p=m{\omega }_p{\widehat{S}}_p=\langle \left[{\tilde{e}}_p{}^{-},{\tilde{e}}_p{}^{+}\left],{\tilde{\lambda }}_p\rangle ,\langle \right[{\tilde{n}}_p{}^{-},{\tilde{n}}_p{}^{+}\left],{\tilde{\mu }}_p\rangle ,\langle \right[{\tilde{\gamma }}_p{}^{-},{\tilde{\gamma }}_p{}^{+}\right],{\tilde{\delta }}_p\rangle$ to the data given in Table 1, Table 2 and Table 3, using the weight vector $\varpi ={\left(0.2,0.3,0.5\right)}^T$ of all the alternatives $A_i$. The aggregated data with the weight vector $\varpi =\left(0.2,0.4,0.4\right)$ using the SCFHHA operator are given in Table 5.

Step 1:

Using the formula ${\tilde{S}}_p=m{\omega }_p{\widehat{S}}_p=\langle \left[{\tilde{e}}_p{}^{-},{\tilde{e}}_p{}^{+}\left],{\tilde{\lambda }}_p\rangle ,\langle \right[{\tilde{n}}_p{}^{-},{\tilde{n}}_p{}^{+}\left],{\tilde{\mu }}_p\rangle ,\langle \right[{\tilde{\gamma }}_p{}^{-},{\tilde{\gamma }}_p{}^{+}\right],{\tilde{\delta }}_p\rangle$ to the given data in Table 5, using the weight vector $\varpi ={\left(0.1,0.2,0.3,0.4\right)}^T$, the calculated values are given in Table 6. Again, using the SCFHHA operator and weight vector $\varpi ={\left(0.15,0.25,0.31,0.29\right)}^T$, we get the collective alternatives $A_i \left(i=1,2,3,4\right)$ as follows.

Step 2:

Using the definition of score function $S_c\left(A_i\right)$ of $A_i$ (i=1,2,3,4), the calculated score are as follows.

$$S_c\left(A_1\right) = 0.03, S_c\left(A_2\right) = 0.04, S_c\left(A_3\right) = 0.04, S_c\left(A_4\right) = 0.01.$$

Step 3:

Rank all the scores and choose the best alternative.

$$A₃=A₂>A₁>A₄.$$

Step 4:

$A₃$ is the best choice.

8. Discussion

In this section, we compare our recommended developed fuzzy aggregation operations to pre-defined fuzzy aggregation operators and state the conclusion of our research work. Despite that fuzzy set, intuitionistic fuzzy set, and spherical fuzzy set theory have a doubtful impact on various fields, there are real-world issues, the agreements upon which are impractical by SFS and not by any means to be resolved by TSFSs (T-spherical fuzzy sets). In SCFS, each component is comprised of membership, neutral, and non-membership functions. Membership function is characterized as a CFN (cubic fuzzy number), and neutral and non-membership are also defined as cubic fuzzy numbers. In Section 7, we discussed the numerical problem, as the SCFN is the most advanced structure, so it is not feasible for the current fuzzy aggregation operators to resolve the data contained in said issue, which shows that the current aggregation operators have a constrained methodology. In any case, we can effectively understand any issue under the TSFS and ICFS data by adding the information as a neutral membership in the ICFs. Therefore, SCFS is a more general idea than TSFS and provides more accurate results. In this manner, the SCFHA operator is the most impressive for determining eccentric issues.

Moreover, we consider the numerical problem in Section 7. Instead of using the score of SCFNs, we have to use the score function of cubic fuzzy numbers by taking the membership, neutral, and non-membership function of SCFNs as individual CFNs, that is, consider SCFN $\langle \left[{\tilde{e}}^{-},{\tilde{e}}^{+}\left],\tilde{\lambda }\rangle ,\langle \right[{\tilde{n}}^{-},{\tilde{n}}^{+}\left],\tilde{\mu }\rangle ,\langle \right[{\tilde{\gamma }}^{-},{\tilde{\gamma }}^{+}\right],\tilde{\delta }\rangle$ as Group 3 CFNs $C₁=\langle \left[{\tilde{e}}^{-},{\tilde{e}}^{+}\right],\tilde{\lambda }\rangle , C₂=\langle \left[{\tilde{n}}^{-},{\tilde{n}}^{+}\right],\tilde{\mu }\rangle , C₃=\langle \left[{\tilde{\gamma }}^{-},{\tilde{\gamma }}^{+}\right],\tilde{\delta }\rangle$, calculate the score function individually by the score function of CNFs¹³, and then calculate the average by the formula $=1/3\left(S\left(C₁\right)+S\left(C₂\right)+S\left(C₃\right)=1/3\left({\tilde{e}}^{-}+{\tilde{e}}^{+}-\tilde{\lambda }\right)/3\right)+\left({\tilde{n}}^{-}+{\tilde{n}}^{+}-\tilde{\mu }/3\right)+\left({\tilde{\gamma }}^{-}+{\tilde{\gamma }}^{+}-\tilde{\delta }\right)/3\left)\right).$ 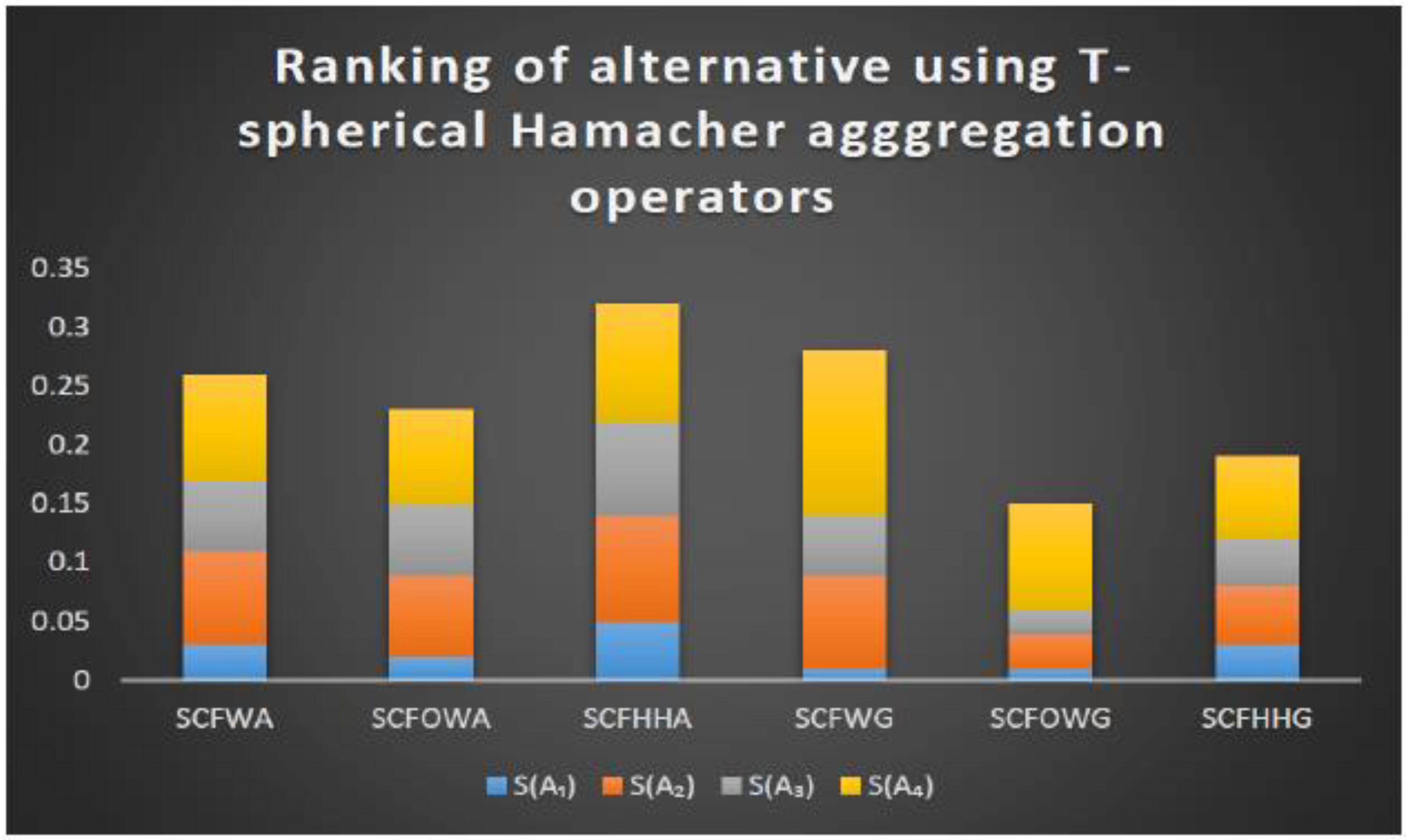From the ranking result of the alternative given in

Table 7. Comparison and ranking of the alternatives.

Operators	$\mathit{S}\left(\mathit{A}\mathbf{₁}\right)$	$\mathit{S}\left(\mathit{A}\mathbf{₂}\right)$	$\mathit{S}\left(\mathit{A}\mathbf{₃}\right)$	$\mathit{S}\left(\mathit{A}\mathbf{₄}\right)$	Ranking
SCFWA	0.08	0.1	0.1	0.07	$\mathit{A}₃=\mathit{A}₂>\mathit{A}₁>\mathit{A}₄$
SCFOWA	0.05	0.06	0.06	0.03	$\mathit{A}₃=\mathit{A}₂>\mathit{A}₁>\mathit{A}₄$
SCFHHA	0.06	0.08	0.08	0.05	$\mathit{A}₃=\mathit{A}₂>\mathit{A}₁>\mathit{A}₄$
SCFWG	0.02	0.05	0.05	0.01	$\mathit{A}₃=\mathit{A}₂>\mathit{A}₁>\mathit{A}₄$
SCFOWG	0.02	0.03	0.03	0.01	$\mathit{A}₃=\mathit{A}₂>\mathit{A}₁>\mathit{A}₄$
SCFHHG	0.03	0.04	0.04	0.01	$\mathit{A}₃=\mathit{A}₂>\mathit{A}₁>\mathit{A}₄$

, and the graphical results shown in Figure 1 and Figure 2, we get the same result obtained from Table 7, which was found using the TSFN score function, that is, $A₃$ is the best choice in all the alternatives, as shown in Figure 1, Figure 2 and Figure 3. This can be seen in different analyses [28,50,51,52]. The calculation utilizing TSFS for MCDM issues cannot deal with them under the same uncertain circumstances, so their proposed calculations may not deliver the precise outcomes in spite of the fact that SCFHWA operators do not have such impediments, and in this manner, can give progressively precise outcomes. The results demonstrate that the proposed system is continuously capable of dealing with the defenselessness of the dynamic appraisal given by the decision-maker. For the given solution to the certified enterprise determination problem, an objection ranking result can be made, and the conditions under which decision-makers show constrained insight can be shown. Additionally, the proposed assessment of the enterprise performance model sufficiently contemplates the distinctive significance of the evaluation criteria, which makes the ranking orders progressively predictable with the situation.

9. Conclusions

Enterprises are significant factors to customers, stockholders, governments, creditors, and other stakeholders. In the production of enterprises, two attributes should be taken into consideration: monetary and society; subsequently, we should think about the partner’s advantage in the execution of enterprise assessment. We set up a presentation assessing a framework based on partner benefits. In this article, we defined the notion of the spherical cubic fuzzy set, which is a generalization of spherical fuzzy sets, intuitionistic cubic fuzzy sets, and Pythagorean cubic fuzzy sets. Some spherical cubic fuzzy operational laws were developed. Furthermore, the score and accuracy degree for the contrast of spherical cubic fuzzy numbers was defined. For the aggregation of spherical cubic fuzzy information, we contemplated the multi-criteria group decision-making problem for emerging enterprise performance technology with spherical cubic fuzzy information. We utilized the concept of the spherical cubic fuzzy Hamacher weighted average (SCFHWA) operator, the spherical cubic fuzzy Hamacher ordered weight average (SCFHOWA) operator, and the spherical cubic fuzzy Hamacher hybrid average (SCFHHA) operator to assess the best enterprise based on performance. We discussed the properties of idempotency, boundary, and monotonicity and presented a relation between these proposed operators. Furthermore, we developed multi-criteria decision making (MCDM) to prove the effectiveness and validity of the proposed methodology. A numerical example showed that the proposed operators can resolve decision making more accurately. We compared these with pre-defined operators to show the validity and effectiveness of the proposed methodology.

In future, we will define other methods with SCFS such as Dombi aggregation operators and introduce the idea of spherical cubic fuzzy Dombi weighted average (SCFDWA), spherical cubic fuzzy Dombi ordered weighted average (SCFDOWA), spherical cubic fuzzy Dombi weighted geometric (SCFDWG), spherical cubic fuzzy Dombi ordered weighted geometric (SCFDOWG), and generalized operators in multi-criteria decision making.