Invariant Means, Complementary Averages of Means, and a Characterization of the Beta-Type Means

Abstract

We prove that whenever the selfmapping $(M_1,\dots ,M_p):I^p\to I^p$, ($p\in \mathbb{N}$ and $M_i$-s are p-variable means on the interval I) is invariant with respect to some continuous and strictly monotone mean $K:I^p\to I$ then for every nonempty subset $S\subseteq \{1,\dots ,p\}$ there exists a uniquely determined mean $K_S:I^p\to I$ such that the mean-type mapping $(N_1,\dots ,N_p):I^p\to I^p$ is K-invariant, where $N_i:=K_S$ for $i\in S$ and $N_i:=M_i$ otherwise. Moreover $min(M_i:i\in S)\le K_S\le max(M_i:i\in S).$ Later we use this result to: (1) construct a broad family of K-invariant mean-type mappings, (2) solve functional equations of invariant-type, and (3) characterize Beta-type means.

1. Preliminaries

In the whole paper $I\subset \mathbb{R}$ stands for an interval, $p\in \mathbb{N},$$p>1$ is fixed, and ${\mathbb{N}}_p:=\{1,\dots ,p\}$.

A function $M:I^p\to I$ is called a mean on I if

$$min\left(x_1,\dots ,x_p\right)\le M\left(x_1,\dots ,x_p\right)\le max\left(x_1,\dots ,x_p\right),x_1,\dots ,x_p\in I,$$

or, briefly, if

$$min\mathbf{x}\le M\left(\mathbf{x}\right)\le max\mathbf{x},\mathbf{x}=\left(x_1,\dots ,x_p\right)\in I^p.$$

The mean M is called strict, if for all nonconstant vectors $\mathbf{x}$ these inequalities are sharp; and symmetric, if $M\left(x_{\sigma \left(1\right)},\dots ,x_{\sigma \left(p\right)}\right)=M\left(x_1,\dots ,x_p\right)$ for all $x_1,\dots ,x_p\in I$ and all permutations $\sigma$ of the set ${\mathbb{N}}_p$. Mean M is monotone if it is increasing in each of its variables. It is important to emphasize that every strictly monotone mean is strict.

A mapping $\mathbf{M}:I^p\to I^p$ is referred to as mean-type if there exist some means $M_i:I^p\to I$, $i\in {\mathbb{N}}_p$, such that $\mathbf{M}=(M_1,\dots ,M_p)$. For a mean-type mapping $\mathbf{M}:I^p\to I^p$ we denote a projection onto the i-th coordinate by ${\left[\mathbf{M}\right]}_i:I^p\to I$. In this case we obviously have ${\left[\mathbf{M}\right]}_i=M_i$ for all $i\in {\mathbb{N}}_p$.

We say that a function $K:I^p\to \mathbb{R}$ is invariant with respect to $\mathbf{M}$ (briefly $\mathbf{M}$-invariant), if $K\circ \mathbf{M}=K$.

Theorem 1

(Invariance Principle, [1]). If $\mathbf{M}:I^p\to I^p$, $\mathbf{M}=(M_1,\dots ,M_p)$ is a continuous mean-type mapping such that

$$max\mathbf{M}\left(\mathbf{x}\right)-min\mathbf{M}\left(\mathbf{x}\right)<max\left(\mathbf{x}\right)-min\left(\mathbf{x}\right),\mathbf{x}\in I^p\backslash \Delta \left(I^p\right),$$

where $\Delta \left(I^p\right):=\left\{\mathbf{x}=\left(x_1,\dots ,x_p\right)\in I^p:x_1=\dots =x_p\right\}$ then there is a unique $\mathbf{M}$-invariant mean $K:I^p\to I$ and the sequence of iterates ${\left({\mathbf{M}}^n\right)}_{n\in \mathbb{N}}$ of the mean-type mapping $\mathbf{M}$ converges to $\mathbf{K}:=\left(K,\dots ,K\right)$ pointwise on $I^p$.

2. A Family of Complementary Means

Let us recall the following result.

Remark 1

(Matkowski [2]). Assume that $K:I^2\to I$ is a symmetric mean which is continuous and monotone.

Then

(i)

for an arbitrary mean $M_1:I^2\to I$ there is a unique mean $M_2:I^2\to I$ such that K is $(M_1,M_2)$-invariant,

$$K\circ (M_1,M_2)=K;$$

${\mathcal{K}}_{M_1}:=M_2,$ is referred to as a K-complementary mean for $M_1;$ and we have

$${\mathcal{K}}_{M_1}=M_2⟺{\mathcal{K}}_{M_2}=M_1;$$

(ii)

if $M_1,M_2:I^2\to I$ are means such that K is $(M_1,M_2)$-invariant, then there exists a unique mean $M:I^2\to I$ such that

$$min\left(M_1,M_2\right)\le M\le max\left(M_1,M_2\right)$$

and

$$K\circ (M,M)=K;$$

moreover

$$M=K.$$

In this case, $p\ge 3$ the counterpart of part (i) of Remark 1 is false which shows the following

Example 1.

Let $I=\mathbb{R}$, and $K=A$ where $A\left(x_1,x_2,x_3\right)=\frac{x_1+x_2+x_3}{3}$. The functions $M_1\left(x_1,x_2,x_3\right)=\frac{x_1+x_2}{2},$$M_2\left(x_1,x_2,x_3\right)=x_2$ are means in $\mathbb{R}$. Then it is easy to see that there is no mean $M_3$ such that

$$A\circ \left(M_1,M_2,M_3\right)=A,$$

but a partial counterpart of part (ii) holds true.

The main result of this section reads as follows.

Theorem 2.

Let $M_1,\dots ,M_p:I^p\to I$ be means. Assume that $K:I^p\to I$ is a continuous and monotone mean which is invariant with respect to the mean type mapping $\mathbf{M}:=(M_1,\dots ,M_p)$.

Then for every nonempty subset $S\subseteq {\mathbb{N}}_p$ there exists a unique mean $K_S\left(\mathbf{M}\right):I^p\to I$ such that K in ${\mathbf{K}}_S\left(\mathbf{M}\right)$-invariant, where ${\mathbf{K}}_S\left(\mathbf{M}\right):I^p\to I^p$ is given by

$${\left[{\mathbf{K}}_S\left(\mathbf{M}\right)\right]}_i:=\left\{\begin{array}{cc}{K}_S\left(\mathbf{M}\right)\hfill & \mathit{for}i\in S,\hfill \\ M_i\hfill & \mathit{for}i\in {\mathbb{N}}_p\backslash S.\hfill \end{array}\right.$$

(1)

Moreover, $min(M_i:i\in S)\le K_S\left(\mathbf{M}\right)\le max(M_i:i\in S)$.

Proof. 

In the case $S={\mathbb{N}}_p$ the ${\mathbf{K}}_S\left(\mathbf{M}\right)$-invariance of K implies $K_S\left(\mathbf{M}\right)=K$ and the statement is obvious. From now on we assume that $S\ne {\mathbb{N}}_p$.

Denote briefly $M_{\vee }:=max\{M_i:i\in S\}$ and $M_{\wedge }:=min\{M_i:i\in S\}$. Fix $\mathbf{x}\in I^n$ arbitrarily. Define a function $T:I\to I^p$ by

$${\left[T\left(\alpha \right)\right]}_i:=\left\{\begin{array}{cc}{M}_i\left(\mathbf{x}\right)\hfill & i\in {\mathbb{N}}_p\backslash S,\hfill \\ \alpha \hfill & i\in S.\hfill \end{array}\right.$$

and $f:I\to I$ by $f\left(\alpha \right):=K\circ T\left(\alpha \right)$. Then, as K is continuous and strictly increasing, so is f. Therefore in view of the equality $K\circ \mathbf{M}\left(\mathbf{x}\right)=K\left(\mathbf{x}\right)$ we obtain $f\left(M_{\vee }\left(\mathbf{x}\right)\right)\ge K\left(\mathbf{x}\right)$ and $f\left(M_{\wedge }\left(\mathbf{x}\right)\right)\le K\left(\mathbf{x}\right)$. Thus, there exists unique number ${\alpha }_{\mathbf{x}}\in [M_{\wedge }\left(\mathbf{x}\right),M_{\vee }\left(\mathbf{x}\right)]$ such that $f\left({\alpha }_{\mathbf{x}}\right)=K\left(\mathbf{x}\right)$. Now, as $\mathbf{x}\in I^n$ was arbitrary we define $K_S\left(\mathbf{M}\right)\left(\mathbf{x}\right):={\alpha }_{\mathbf{x}}$.

Then we have

$$K\left(\mathbf{x}\right)=f\left({\alpha }_{\mathbf{x}}\right)=f\left(K_S\left(\mathbf{M}\right)\left(\mathbf{x}\right)\right)=\left(K\circ T\circ \left(K_S\left(\mathbf{M}\right)\right)\right)\left(\mathbf{x}\right)=\left(K\circ \left({\mathbf{K}}_S\left(\mathbf{M}\right)\right)\right)\left(\mathbf{x}\right),$$

which shows that K is ${\mathbf{K}}_S\left(\mathbf{M}\right)$-invariant.

Now we need to show that $K_S\left(\mathbf{M}\right)$ is uniquely determined. Assume that K is ${\mathbf{K}}_S\left(\mathbf{M}\right)$-invariant and $K_S\left(\mathbf{M}\right)\left(\mathbf{x}\right)\ne {\alpha }_{\mathbf{x}}$ for some $\mathbf{x}\in I^p$. Then, as f is a monomorphism we obtain

$$K\circ \left({\mathbf{K}}_S\left(\mathbf{M}\right)\right)\left(\mathbf{x}\right)=\left(K\circ T\circ \left(K_S\left(\mathbf{M}\right)\right)\right)\left(\mathbf{x}\right)\ne f\left({\alpha }_{\mathbf{x}}\right)=K\left(\mathbf{x}\right)$$

contradicting the ${\mathbf{K}}_S\left(\mathbf{M}\right)$-invariance. □

Let us underline that we do not assume that means $M_1,\dots ,M_P$ are continuous. This is relatively recent approach to invariant property which was studied by the authors in [3].

The intuition beyond this theorem is the following. Once we have a continuous and monotone mean K such that $\mathbf{M}$ is K-invariant mean we can unite a subfamily ${\left(M_s\right)}_{s\in S}$ into a single mean (denoted by $K_S\left(\mathbf{M}\right)$) to preserve the K-invariance. In view of Theorem 1, such a mean is unique. In this connection we propose the following

Definition 1.

Let $K:I^p\to I$ be a continuous and monotone mean which is invariant with respect to the mean type mapping $\mathbf{M}:=(M_1,\dots ,M_p)$.

For each set $S\subset {\mathbb{N}}_p:$

(i) 

the mean $K_S\left(\mathbf{M}\right)$ is called a K-complementary averaging of the means $\{M_i:i\in S\}$ with respect to the invariant mean-type mapping $\mathbf{M}=(M_1,\dots ,M_p)$;

(ii) 

the mean-type mapping ${\mathbf{K}}_S\left(\mathbf{M}\right)$ given by (1) is called a K-complementary averaging of the mean-type mapping $\mathbf{M}=(M_1,\dots ,M_p)$ with respect to the means $\{M_i:i\in S\}$.

Moreover, the set

$$\mathfrak{K}\left(K,\mathbf{M}\right):=\left\{{\mathbf{K}}_S\left(\mathbf{M}\right):S\subseteq {\mathbb{N}}_p,S\ne \varnothing \right\}$$

is called the family of all K-complementary averaging of the mean-type mapping $\mathbf{M}=(M_1,\dots ,M_p).$

We can now reapply this result to the complementary of the establish a K-complementary of ${\mathbf{K}}_S\left(\mathbf{M}\right)$ for the set ${\mathbb{N}}_p\backslash S$. More precisely we obtain

Corollary 1.

Under the assumptions of Theorem 2 there exists unique mean $K_S^{*}\left(\mathbf{M}\right):I^p\to I$ such that K is ${\mathbf{K}}_S^{*}\left(\mathbf{M}\right)$-invariant, where ${\mathbf{K}}_S^{*}\left(\mathbf{M}\right):I^p\to I^p$ is given by

$${\left[{\mathbf{K}}_S^{*}\left(\mathbf{M}\right)\right]}_i:=\left\{\begin{array}{cc}{K}_S\left(\mathbf{M}\right)\hfill & \mathit{for}i\in S,\hfill \\ K_S^{*}\left(\mathbf{M}\right)\hfill & \mathit{for}i\in {\mathbb{N}}_p\backslash S.\hfill \end{array}\right.$$

Moreover, $min(M_i:i\in {\mathbb{N}}_p\backslash S)\le K_S^{*}\left(\mathbf{M}\right)\le max(M_i:i\in {\mathbb{N}}_p\backslash S)$.

Let us underline that the value $K_S^{*}\left(\mathbf{M}\right)$ does not depend on $\mathbf{M}$ explicitly. The whole system of dependences is illustrated in Figure 1.

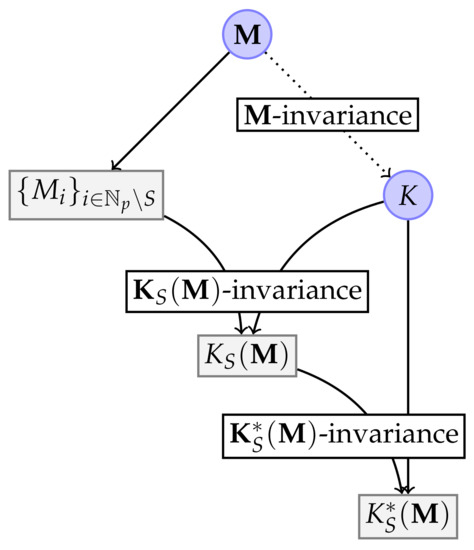
Figure 1. Map of dependencies between means. Rectangle vertexes are dependent on S. Dotted line means that there could exists more $\mathbf{M}$-invariant mean satisfying the conditions of Theorem 2.

Observe that, as the mean $K_S^{*}\left(\mathbf{M}\right)$ is uniquely determined, we obtain

$${\mathbf{K}}_S^{*}\left(\mathbf{M}\right)\in \mathfrak{K}\left(K,\mathbf{M}\right)\iff \mathrm{all}\mathrm{means}(M_i:i\in {\mathbb{N}}_p\backslash S)\mathrm{are}\mathrm{equal}\mathrm{to}\mathrm{each}\mathrm{other}.$$

3. Application in Solving Functional Equations

Theorem 3.

Let $\mathbf{M}=(M_1,\dots ,M_p)$ be a mean-type mapping such that $M_1,\dots ,M_p:{\left(0,\infty \right)}^p\to \left(0,\infty \right)$ are strictly monotonic and homogeneous. Then

(i) 

the sequence $\left({\mathbf{M}}^n:n\in \mathbb{N}\right)$ of iterates of $\mathbf{M}$ converge uniformly on compact subsets to a mean-type mapping $\mathbf{K}=\left(K,\dots ,K\right)$, where K is a unique $\mathbf{M}$-invariant mean.

(ii) 

K is monotone, homogeneous and for every $S\subset {\mathbb{N}}_p$ the iterates of ${\mathbf{K}}_S\left(\mathbf{M}\right)$ converge uniformly on compact subsets to a mean-type mapping $\mathbf{K}=\left(K,\dots ,K\right)$;

(iii) 

a function $F:{\left(0,\infty \right)}^p\to \mathbb{R}$ is continuous on the diagonal $\Delta \left({\left(0,\infty \right)}^p\right):=\left\{\left(x_1,\dots ,x_p\right)\in {\left(0,\infty \right)}^p:x_1=\dots =x_p\right\}$ and satisfies the functional equation

$$F\circ \mathbf{M}=F$$

(2)

if and only if $F=\phi \circ K$, where $\phi :\left(0,\infty \right)\to \mathbb{R}$ is an arbitrary continuous function of a single variable;

(iv) 

a function $F:{\left(0,\infty \right)}^p\to \mathbb{R}$ is continuous on the diagonal $\Delta \left({\left(0,\infty \right)}^p\right)$ and satisfies the simultaneous system of functional equations

$$F\circ {\mathbf{K}}_S\left(\mathbf{M}\right)=F,S\subset {\mathbb{N}}_p;$$

(3)

if and only if $F=\phi \circ K$, where $\phi :\left(0,\infty \right)\to \mathbb{R}$ is an arbitrary continuous function of a single variable (so (2) and (3) are equivalent)

Proof. 

The homogeneity and monotonicity of $M_1,\dots ,M_p$ imply their continuity (cf. ([4], Theorem 2)), so the invariance principle implies (i).

Now we prove that K is monotone. Indeed, take two vectors $v,w\in {(0,\infty )}^p$ such that $v_i\le w_i$ for all $i\in {\mathbb{N}}_p$ and $v_{i_0}<w_{i_0}$ for certain $i_0\in {\mathbb{N}}_p$. Then, as each $M_i$ is monotone, there exists a constant $\theta \in (0,1)$ such that $M_i\left(v\right)\le \theta M_i\left(w\right)$ for all $i\in {\mathbb{N}}_p$.

Then for all $n\in \mathbb{N}$ and $i\in {\mathbb{N}}_p$ we have

$$\begin{array}{cc}\hfill {\left[{\mathbf{M}}^n\left(v\right)\right]}_i& ={\left[{\mathbf{M}}^{n-1}(M_1\left(v\right),\dots ,M_p\left(v\right))\right]}_i\le {\left[{\mathbf{M}}^{n-1}(\theta M_1\left(w\right),\dots ,\theta M_p\left(w\right))\right]}_i\hfill \\ \hfill & =\theta {\left[{\mathbf{M}}^{n-1}(M_1\left(w\right),\dots ,M_p\left(w\right))\right]}_i=\theta {\left[{\mathbf{M}}^n\left(w\right)\right]}_i.\hfill \end{array}$$

In a limit case as $n\to \infty$ in view of the first part of this statement we obtain $K\left(v\right)\le \theta K\left(w\right)<K\left(w\right)$. Thus, K is monotone, which is (ii).

(iii) Assume first that $F:{\left(0,\infty \right)}^p\to \mathbb{R}$ that is continuous on the diagonal $\Delta \left({\left(0,\infty \right)}^p\right)$ and satisfies Equation (2). Hence, by induction,

$$F=F\circ {\mathbf{M}}^n,n\in \mathbb{N},$$

By (ii) the sequence $\left({\mathbf{M}}^n:n\in \mathbb{N}\right)$ converges to $\mathbf{K}=\left(K,\dots ,K\right)$. Since F is continuous on $\Delta \left({\left(0,\infty \right)}^p\right)$, we hence get for all $\mathbf{x}\in {\left(0,\infty \right)}^p$,

$$\begin{array}{ccc}\hfill F\left(\mathbf{x}\right)& =& \underset{n\to \infty }{lim}F\left({\mathbf{M}}^n\left(\mathbf{x}\right)\right)=F\left(\underset{n\to \infty }{lim}{\mathbf{M}}^n\left(\mathbf{x}\right)\right)=F\left(\mathbf{K}\left(\mathbf{x}\right)\right)\hfill \\ & =& F\left(K\left(\mathbf{x}\right),\dots ,K\left(\mathbf{x}\right)\right).\hfill \end{array}$$

Setting

$$\phi \left(t\right):=F\left(t,\dots ,t\right),t\in \left(0,\infty \right),$$

we hence get $F\left(\mathbf{x}\right)=\phi \left(K\left(\mathbf{x}\right)\right)$ for all $\mathbf{x}\in {\left(0,\infty \right)}^p$.

To prove the converse implication, take an arbitrary function $\phi :I\to \mathbb{R}$ and put $F:=\phi \circ K$. Then, for all $\mathbf{x}\in {\left(0,\infty \right)}^p,$ making use of the K-invariance with respect to $\mathbf{M}$, we have

$$F\left(\mathbf{M}\left(\mathbf{x}\right)\right)=\left(\phi \circ K\right)\left(\mathbf{M}\left(\mathbf{x}\right)\right)=\phi \left(K\left(\mathbf{M}\left(\mathbf{x}\right)\right)\right)=\phi \left(K\left(\mathbf{x}\right)\right)=F\left(\mathbf{x}\right),$$

which completes the proof of (iii).

(iv) we omit similar argument. □

Part (ii) of this result gives rise to the following extension.

General Complementary Process

Once we have a mean-type $\mathbf{M}:I^p\to I^p$ and a continuous and monotone mean $K:I^p\to I$ which is $\mathbf{M}$-invariant let ${\mathfrak{K}}^{+}\left(\mathbf{M},K\right)$ be the smallest family of mean-type mappings containing $\mathbf{M}$ which is closed under K-complementary averaging.

More precisely, for every $\mathbf{X}\in {\mathfrak{K}}^{+}\left(\mathbf{M},K\right)$ and nonempty subset $S\subseteq {\mathbb{N}}_p$ we have ${\mathbf{K}}_S\left(\mathbf{X}\right)\in {\mathfrak{K}}^{+}\left(\mathbf{M},K\right)$, too. We also define a family of means

$${\mathfrak{K}}_0\left(\mathbf{M},K\right):=\left\{{\left[\mathbf{X}\right]}_i:\mathbf{X}\in {\mathfrak{K}}^{+}\left(\mathbf{M},K\right)\mathrm{and}i\in {\mathbb{N}}_p\right\}$$

Obviously using notions from Theorem 2 and Corollary 1 we have

$${\mathfrak{K}}^{+}\left(\mathbf{M},K\right)\supseteq {\mathfrak{K}}^{+}\left({\mathbf{K}}_S\left(\mathbf{M}\right),K\right)\supseteq {\mathfrak{K}}^{+}\left({\mathbf{K}}_S^{*}\left(\mathbf{M}\right),K\right)$$

Furthermore, we have the following.

Proposition 1.

Given an interval $I\subset \mathbb{R}$, $p\in \mathbb{N}$, and a mean-type mapping $\mathbf{M}:=(M_1,\dots ,M_p):I^p\to I^p$ which is invariant with respect to some continuous and monotone mean $K:I^p\to I$. Then

$$min(M_1,\dots ,M_p)\le X\le max(M_1,\dots ,M_p)\mathit{for}\mathit{all}X\in {\mathfrak{K}}_0\left(\mathbf{M},K\right).$$

Its inductive proof is obvious in view of Theorem 2 (moreover part).

Now we prove that complementary means preserve symmetry.

Proposition 2.

If a continuous and monotone mean $K:I^p\to I$ is invariant with respect to a mean-type mapping $\mathbf{M}:=(M_1,\dots ,M_p):I^p\to I^p$ such that all $M_i$-s are symmetric, then K and all means in ${\mathfrak{K}}_0\left(\mathbf{M},K\right)$ are symmetric.

Proof. 

Fix a nonconstant vector $x\in I^p$ and a permutation $\sigma$ of ${\mathbb{N}}_p$. First observe that $K\left(x\right)=K\circ \mathbf{M}\left(x\right)=K\circ \mathbf{M}(x\circ \sigma )=K(x\circ \sigma )$, which implies that K is symmetric.

As the family ${\mathfrak{K}}_0\left(\mathbf{M},K\right)$ is generating by complementing, we need to show that symmetry is preserved by a single complement. Therefore, it is sufficient to show that the mean $K_S\left(\mathbf{M}\right)$ defined in Theorem 2 is symmetric. However, using the notions therein, we have

$$K\circ \left({\mathbf{K}}_S\left(\mathbf{M}\right)\right)\left(x\right)=K\left(x\right)=K(x\circ \sigma )=K\circ \left({\mathbf{K}}_S\left(\mathbf{M}\right)\right)(x\circ \sigma ).$$

By monotonicity of K, if $K_S\left(\mathbf{M}\right)\left(x\right)<K_S\left(\mathbf{M}\right)(x\circ \sigma )$ we would have

$$K\circ \left({\mathbf{K}}_S\left(\mathbf{M}\right)\right)\left(x\right)=K\left(x\right)<K\circ \left({\mathbf{K}}_S\left(\mathbf{M}\right)\right)(x\circ \sigma )$$

contradicting the above equality. Similarly we exclude the case $K_S\left(\mathbf{M}\right)\left(x\right)>K_S\left(\mathbf{M}\right)(x\circ \sigma )$. Therefore $K_S\left(\mathbf{M}\right)\left(x\right)=K_S\left(\mathbf{M}\right)(x\circ \sigma )$ which, as x and $\sigma$ were taken arbitrarily, yields the symmetry of $K_S\left(\mathbf{M}\right)$. □

4. An Applications to Beta-Type Means

Following [5], for a given $k\in \mathbb{N}$ we define a p-variable Beta-type mean ${\mathcal{B}}_p:{\mathbb{R}}_{+}^k\to {\mathbb{R}}_{+}$ by

$${\mathcal{B}}_p(x_1,\dots ,x_p):={\left(\frac{p{x}_1\dots x_p}{x_1+\dots +x_p}\right)}^{\frac{1}{p-1}}.$$

This is a particular case of so-called biplanar-combinatoric means (Media biplana combinatoria) defined in Gini [6] and Gini–Zappa [7].

In order to formulate the next results, we adapt the notation that A, G and H are arithmetic, geometric and harmonic means of suitable dimension, respectively.

In [8], the invariance $G\circ \left(A,H\right)=G,$ equivalent to the Pythagorean proportion, has been extended for arbitrary $p\ge 3$. In case $p=3$ it takes the form $G\circ \left(A,F,H\right)=G$, where

$$F\left(x_1,x_2,x_3\right)=:\frac{x_2{x}_3+x_3{x}_1+x_1{x}_2}{x_1+x_2+x_3},x_1,x_2,x_3>0,$$

and $H\le F\le A$. Hence, making use of Corollary 1 with $p=3,$$K=G$, $S=\left\{1,2\right\}$ we obtain the following.

Remark 2.

For all $x_1,x_2,x_3,$ the following inequality holds

$$H\left(x_1,x_2,x_3\right)\le {\mathcal{B}}_3(x_1,x_2,x_p)\le A\left(x_1,x_2,x_3\right),$$

and the inequalities are sharp for nonconstant vectors $x=\left(x_1,x_2,x_3\right)\in {\left(0,\infty \right)}^3$.

Passing to the main part of this section, first observe the following easy-to-see lemma.

Lemma 1.

Let $p\in \mathbb{N}$, $p\ge 2$. Then there exists exactly one mean $M:I^p\to I$ such that $G\circ \left(A,\underset{(p-1)\mathrm{times}}{\underbrace{M,\dots ,M}}\right)=G$. Furthermore $M={\mathcal{B}}_p$.

Its simple proof which is a straightforward implication of Theorem 2 is omitted. Based on this lemma it is natural to define a mean-type mapping $\mathbf{B}:I^p\to I^p$ by ${\left[\mathbf{B}\right]}_1:=A$ and ${\left[\mathbf{B}\right]}_i:={\mathcal{B}}_p$ for all $i\in \{2,\dots ,p\}$. Then we have $G\circ \mathbf{B}=G$, which implies that the geometric mean is the unique $\mathbf{B}$-invariant mean.

We are now going to establish the set ${\mathfrak{K}}^{+}\left(\mathbf{B},G\right)$. It is quite easy to observe that all means in ${\mathfrak{K}}_0\left(\mathbf{B},G\right)$ are of the form ${\mathcal{H}}_{p,\alpha }:I^p\to I$ ($\alpha \in \mathbb{R}$) given by

$${\mathcal{H}}_{p,\alpha }(x_1,\dots ,x_p):={\left(x_1\dots x_p\right)}^{\frac{1-\alpha }{p}}{\left(\frac{x_1+\dots +x_p}{p}\right)}^{\alpha }$$

including ${\mathcal{B}}_p={\mathcal{H}}_{p,-\frac{1}{p-1}}$. In the next lemma we show some elementary properties of the family $\left({\mathcal{H}}_{p,\alpha }\right)$.

Lemma 2.

Let $p\in \mathbb{N}$. Then

1.

${\mathcal{H}}_{p,\alpha }$ is reflexive for all $\alpha \in \mathbb{R}$, that is ${\mathcal{H}}_{p,\alpha }(x,\dots ,x)=x$ for all $x\in {\mathbb{R}}_{+}$,

2.

${\mathcal{H}}_{p,\alpha }$ is continuous for all $\alpha \in \mathbb{R}$ (as a p-variable function),

3.

${\mathcal{H}}_{p,\alpha }$ is a strict mean for all $\alpha \in [-\frac{1}{p-1},1]$,

4.

${\mathcal{H}}_{p,\alpha }$ is a symmetric function for all $\alpha \in \mathbb{R}$, that is ${\mathcal{H}}_{p,\alpha }(x\circ \sigma )={\mathcal{H}}_{p,\alpha }\left(x\right)$ for all $x\in {\mathbb{R}}_{+}^p$ and a permutation σ of ${\mathbb{N}}_p$,

5.

${\mathcal{H}}_{p,1}$ and ${\mathcal{H}}_{p,0}$ are p-variable arithmetic and geometric means, respectively,

6.

${\mathcal{H}}_{p,\alpha }$ is increasing with respect to α, that is ${\mathcal{H}}_{p,\alpha }\left(x\right)<{\mathcal{H}}_{p,\beta }\left(x\right)$ for every nonconstant vector $x\in {\mathbb{R}}_{+}^p$ and $\alpha ,\beta \in \mathbb{R}$ with $\alpha <\beta$.

Proof. 

By the definition of ${\mathcal{H}}_{p,\alpha }$ we can easily verify that (1), (2), (4) and (5) holds.

From now on fix a nonconstant vector $x=(x_1,\dots ,x_p)\in {\mathbb{R}}_{+}^p$. By (4) we may assume without loss of generality that $x_1\le \dots \le x_p$. Denote briefly

$$g:=\sqrt[p]{x_1\dots x_p}\mathrm{and}a:=\frac{x_1+\dots +x_p}{p}.$$

By Cauchy inequality we have $x_1<g<a<x_p$. Moreover, by the definition ${\mathcal{H}}_{p,\alpha }\left(x\right)=a^{\alpha }{g}^{1-\alpha }$. Thus, for all $\alpha <\beta$ we have

$${\mathcal{H}}_{p,\beta }\left(x\right)=a^{\beta }{g}^{1-\beta }=a^{\alpha }{g}^{1-\alpha }{\left(\frac{a}{g}\right)}^{\beta -\alpha }>a^{\alpha }{g}^{1-\alpha }={\mathcal{H}}_{p,\alpha }\left(x\right),$$

which completes the proof of (6). The only remaining part to be proved is (3). However, applying (6), it is sufficient to show that

$${\mathcal{H}}_{p,1}\left(x\right)<max\left(x\right)=x_p\mathrm{and}{\mathcal{H}}_{p,-\frac{1}{p-1}}\left(x\right)>min\left(x\right)=x_1.$$

By (5) we immediately obtain ${\mathcal{H}}_{p,1}\left(x\right)=a<x_p$. For the second part observe that

$$\begin{array}{c}\hfill {\mathcal{H}}_{p,-\frac{1}{p-1}}\left(x\right)=\sqrt[p-1]{\frac{g^p}{a}}=\sqrt[p-1]{\frac{x_1\dots x_p}{a}}>\sqrt[p-1]{\frac{x_1\dots x_p}{x_p}}=\sqrt[p-1]{x_1\dots x_{p-1}}\ge x_1,\end{array}$$

which completes the proof. □

Now we generalize Lemma 1 to the following form

Lemma 3.

Let $p\in \mathbb{N}$, $p\ge 2$ and $\alpha \in {\mathbb{R}}^p$. Then $G\circ ({\mathcal{H}}_{p,{\alpha }_1},\dots ,{\mathcal{H}}_{p,{\alpha }_p})=G$, if and only if ${\alpha }_1+\dots +{\alpha }_p=0$.

Its proof is obvious in view of the identity $G\circ ({\mathcal{H}}_{p,{\alpha }_1},\dots ,{\mathcal{H}}_{p,{\alpha }_p})={\mathcal{H}}_{p,\frac{1}{p}({\alpha }_1+\dots +{\alpha }_p)}$. Having this proved, let us show the next important result.

Theorem 4.

Let $p\ge 2$. Then

$$\begin{array}{cc}\hfill & {\mathfrak{K}}^{+}\left((A,\underset{(p-1)\mathrm{times}}{\underbrace{{\mathcal{B}}_p,\dots ,{\mathcal{B}}_p}}),G\right)\hfill \\ \hfill & \subseteq \left\{({\mathcal{H}}_{p,{\alpha }_1},\dots ,{\mathcal{H}}_{p,{\alpha }_p})\mid {\alpha }_1,\dots ,{\alpha }_p\in \mathbb{Q}\cap [-\frac{1}{p-1},1]\mathit{and}{\alpha }_1+\dots +{\alpha }_p=0\right\}.\hfill \end{array}$$

In particular

$${\mathfrak{K}}_0=\left((A,{\mathcal{B}}_p,\dots ,{\mathcal{B}}_p),G\right)\subseteq \left\{{\mathcal{H}}_{p,\alpha }\mid \alpha \in \mathbb{Q}\cap [-\frac{1}{p-1},1]\right\}.$$

Proof. 

First observe that in view of Lemma 1 G is $\mathbf{B}$-invariant, and thus the set ${\mathfrak{K}}^{+}(\mathbf{B},G)$ is well-defined. Now denote briefly

$$\mathsf{\Lambda }:=\left\{({\mathcal{H}}_{p,{\alpha }_1},\dots ,{\mathcal{H}}_{p,{\alpha }_p})\mid {\alpha }_1,\dots ,{\alpha }_p\in \mathbb{Q}\cap [-\frac{1}{p-1},1]\mathrm{and}{\alpha }_1+\dots +{\alpha }_p=0\right\}.$$

Obviously $\mathbf{B}\in \mathsf{\Lambda }$, so it is sufficient to prove that $\mathsf{\Lambda }$ is closed with respect to G-complementary averaging. To this end take an arbitrary vector $({\alpha }_1,\dots ,{\alpha }_p)$ real numbers such that $\mathbf{H}:=({\mathcal{H}}_{p,{\alpha }_1},\dots ,{\mathcal{H}}_{p,{\alpha }_p})\in \mathsf{\Lambda }$ and a nonempty subset $S\subset {\mathbb{N}}_p$.

By Theorem 2 there exists exactly one mean $G_S\left(\mathbf{H}\right):I^p\to I$ such that G is ${\mathbf{G}}_S\left(\mathbf{H}\right)$-invariant, where ${\mathbf{G}}_S\left(\mathbf{H}\right):I^p\to I^p$ is given by

$${\left[{\mathbf{G}}_S\left(\mathbf{H}\right)\right]}_i:=\left\{\begin{array}{cc}{\mathcal{H}}_{p,{\alpha }_i}\hfill & \mathrm{for}i\in {\mathbb{N}}_p\backslash S,\hfill \\ G_S\left(\mathbf{H}\right)\hfill & \mathrm{for}i\in S.\hfill \end{array}\right.$$

On the other hand, in view of Lemma 3 we obtain that G is invariant with respect to the mean-type mapping ${\mathbf{H}}_0:I^p\to I^p$ given by

$${\left[{\mathbf{H}}_0\right]}_i:=\left\{\begin{array}{cc}{\mathcal{H}}_{p,{\alpha }_i}\hfill & \mathrm{for}i\in {\mathbb{N}}_p\backslash S,\hfill \\ {\mathcal{H}}_{p,\beta }\hfill & \mathrm{for}i\in S,\hfill \end{array}\right.\mathrm{where}\beta =\frac{1}{\left|S\right|}\sum _{i\in S}{\alpha }_i.$$

As G is both ${\mathbf{G}}_S\left(\mathbf{H}\right)$-invariant and ${\mathbf{H}}_0$-invariant we obtain $G_S\left(\mathbf{H}\right)={\mathcal{H}}_{p,\beta }$, and consequently ${\mathbf{G}}_S\left(\mathbf{H}\right)={\mathbf{H}}_0$. Observe that ${\mathbf{H}}_0\in \mathsf{\Lambda }$ is a straightforward implication of the equality

$$\sum _{i\in {\mathbb{N}}_p\backslash S}{\alpha }_i+\left|S\right|\beta =\sum _{i\in {\mathbb{N}}_p}{\alpha }_i=0.$$

Now we show that $\beta \in \mathbb{Q}\cap [-\frac{1}{p-1},1]$, which would complete the proof. However, this is easy in view of the definition of $\beta$ and the analogous property ${\alpha }_i\in \mathbb{Q}\cap [-\frac{1}{p-1},1]$, which is valid for all $i\in S$. □

Remark 3.

Let us emphasize that inclusions in the above theorem are strict. More precisely, we can prove by simple induction that the denominator of α in irreducible form has no prime divisors greater than p.