Abstract
The main goal of this paper is to propose a Multiple-Criteria Decision-Making (MCDM) approach that will facilitate decision-making in the field of logistics—i.e., in the selection of the optimal equipment for performing a logistics activity. For defining the objective weights of the criteria, the correlation coefficient and the standard deviation (CCSD method) are applied. Furthermore, for determining the semi-objective weights of the considered criteria, the indifference threshold-based attribute ratio analysis method (ITARA) is used. In this way, by combining these two methods, the weights of the criteria are determined with a higher degree of reliability. For the final ranking of the alternatives, the measurement of alternatives and ranking according to the compromise solution method (MARCOS) is utilized. For demonstrating the applicability of the proposed approach, an illustrative case study pointing to the selection of the best manual stacker for a small warehouse is performed. The final results are compared with the ones obtained using the other proved MCDM methods that confirmed the reliability and stability of the proposed approach. The proposed integrated approach shows itself as a suitable technique for applying in the process of logistics equipment selection, because it defines the most influential criteria and the optimal choice with regard to all of them in a relatively easy and comprehensive way. Additionally, conceiving the determination of the criteria with the combination of objective and semi-objective methods enables defining the objective weights concerning the attitudes of the involved decision-makers, which finally leads to more reliable results.
1. Introduction
Logistics has long been considered a key factor in economic development, spatial integration, and market integration in the developed world [1]. During the 1960s, logistics as a concept of the integration of the process of the distribution of goods gained its place in the theory and practice of business management. Within the logistics sector, there are three basic approaches: physical distribution management, materials management, and business logistics. The important issue that logistics is faced with is certainly the question of the selection of adequate equipment for dealing with material resources.
The efficiency of the performance of logistics activities strongly depends on the use of optimal equipment in the warehouse or for the transportation of the goods. Bad choices could lead to the damage or contamination of goods, delays in delivery, and an increase in costs [2]. Furthermore, the selection of equipment directly influences the performance of the company, so this kind of decision could be considered as strategic and of great importance [3]. In the case of manufacturing equipment selection, the selection of the equipment needed for performing logistics activities requires defining the crucial features of the equipment, comparing them with the equipment offered on the market, and selecting the most suitable one [4]. The costs are considered as the most influential criterion in equipment selection, but they could not be treated as the only one.
Decisions regarding equipment purchasing affect various criteria that are often mutually opposing. Besides this, making a decision based on only one or a few criteria as well as making a decision based on previous experience and intuition will not lead to a reasonable decision. The use of techniques based on mathematics and statistics increases the reliability of the decision and contributes to the assurance of the selection that is made. The utilization of the Multiple-Criteria Decision-Making (MCDM) method could be a suitable means for the facilitation of a decision process regarding logistics equipment selection.
Recently, the field of Multi-Criteria Decision-Making (MCDM) has been rapidly evolving, thanks to the large number of scientific publications dealing with the adoption of individual decisions based on employed techniques and methods that belong to the specified domain [5]. MCDM is quite a suitable tool for solving complex decision-making problems because of its ability to evaluate different alternatives using a specific set of criteria [6].
The main aim of this paper is to develop a novel integrated MCDM-based approach for equipment selection in a logistics system. The correlation coefficients (CC) and standard deviations (SD)—i.e., the CCSD method [7]—will be applied for determining the objective weights of the criteria. Besides that, the indifference threshold-based attribute ratio analysis method (ITARA) [8], as a semi-objective method, will be also applied for determining the weights of the criteria. Therefore, the weights of the criteria will be determined by applying a combined CCSD-ITARA approach in order to make an objective determination of criteria significance where the subjectivity—i.e., perspective of the decision-makers—is included to a moderate degree. When it comes to the ranking of the alternatives, the measurement of alternatives and ranking according to the compromise solution method (MARCOS) [9] will be applied. The applicability of the proposed approach will be demonstrated through the illustrative case study, pointing to the selection of a suitable type of stacker for purchasing. The proposed approach enables the facilitation of the selection process regarding the purchasing of logistics equipment, which is a manual stacker in the considered case. Thus, the practitioners could observe all the involved criteria and, based on them, select the most appropriate alternative. Scientifically, the proposed combination of methods is completely new, and its possibilities have not been fully tested yet. In this case, it is used for the facilitation of decision and selection processes in the logistics field, but its potential could be further explored in other areas as well.
The rest of the paper is organized as follows: In Section 1, introductory considerations are given. A literature review is presented in Section 2. Section 3 demonstrates the methodology. An illustrative case study is described in Section 4. Finally, at the end of the manuscript the conclusions are given.
2. Literature Review
Decision-making is a process as old as humanity itself. Every day, each of us usually makes a large number of decisions. However, one of the problems that arise is to choose from the multitude of possible solutions the solution by which we will achieve the desired goal to the greatest degree, taking into account the objective limitations, which, to a greater or lesser extent, limit our freedom of judgment [10,11,12]. As could be inferred, the decision process involves the synergy of action of the human factor, mathematical methods, and IT tools [13]. In each study on the issue of decision-making, attention is focused on three general concepts—namely, the decision-making process, the decision-maker, and the decision itself—with the constant attempt to find a suitable way to make an appropriate decision. Intending to facilitate the decision process, scholars have proposed various methods that belong to the MCDM field.
MCDM has been developed as an integral part of operational research in order to create mathematical tools aimed at supporting the subjective evaluation of criteria by decision-makers [14,15]. MCDM is created in such a way that facilitates the selection of the most desirable alternative, the classification of the alternatives into a smaller number of categories, and the ranking of these alternatives following subjective requirements [16,17]. As already mentioned, there are a whole range of various MCDM techniques that have been applied to solving different types of complex problems. Each of the developed MCDM methods has its advantages, disadvantages, and limitations. Additionally, according to the problem that is being solved, it is necessary to consider an adequate technique [18,19,20].
Thus, MCDM considers situations in which the decision-maker must choose one of the alternatives from a set of available alternatives, which are judged based on several often-conflicting criteria [17,20]. The remarkably extensive development of the field of decision-making theory over the past few decades certainly has contributed to the presence of a multitude of MCDM methods. Perhaps the best-known and most widely applied MCDM methods are: simple additive weighting (SAW) [21]; the analytic hierarchy process (AHP) [22]; the analytic network process (ANP) [23]; elimination et choix traduisant la realité (ELECTRE) [24]; the preference ranking organization method for enrichment evaluation (PROMETHEE) [25]; the technique for order performance by similarity to ideal solution (TOPSIS) [26]; Višekriterijumska optimizacija i kompromisno rešenje (VIKOR) [27]; the complex proportional assessment of alternatives (COPRAS) [28]; and so forth.
In order to cope with a wider spectrum of problems, there is a new generation of newly developed MCDM methods and MCDM-based approaches, such as a new additive ratio assessment method (ARAS) [29]; multi-objective optimization on the basis of the ratio analysis method (MOORA) [30]; multi-objective optimization by ratio analysis plus full multiplicative form (MULTIMOORA) [31]; the step-wise weight assessment ratio analysis method (SWARA) [32]; the pivot pair-wise relative criteria importance assessment method (PIPRECIA) [33]; the multi-attributive ideal-real comparative analysis method (MAIRCA) [34]; the full consistency method (FUCOM) [35]; the evaluation based on distance from the average solution method (EDAS) [36]; a combined compromise solution method (CoCoSo) [37]; and so on. It is important to note that some of the aforementioned methods are used for weight determination and some of them for the ranking of alternatives.
Until now, MCDM methods have been used in the logistics field to contribute to and simplify the decision process regarding the various issues. A very popular theme that occupied scientific attention is certainly the question of reverse logistics [38,39,40]. Thence, the authors examined the problem of the selection of the logistics center or warehouse location [41,42]. The issue of humanitarian logistics is resolved by applying different MCDM techniques too [43,44]. The selection of the partners suitable for performing the logistics activities has been also performed by applying MCDM methods [45,46].
The topic connected to the equipment selection pointed to material handling is also present in the works of various authors. For example, Mathew and Sahu [47] used four methods for resolving the problem of equipment selection, and they are: CODAS, EDAS, MOORA, and WASPAS. The authors also based the selection of the equipment on the fuzzy axiomatic design principles [48]. Suitable equipment is selected in the fuzzy environment too [49]. Saputro and Rouyendegh [50] used the TOPSIS and MOMILP methods to find the best solution regarding the equipment for the warehouse. As can be concluded, there is enough space for observing the issue of the selection of the appropriate equipment for a logistics center. With that aim, in this paper an integrated approach based on the CCSD, ITARA, and MARCOS methods is proposed. The main reason for involving the CCSD and ITARA methods in the procedure of determining the criteria weights relies on the fact that they enable the definition of the criteria weights in an objective way but with incorporating a hint of the subjectivity of the decision-maker. In some cases, it is necessary to incorporate the requirements of the decision-maker to some suitable extent because the decision-maker knows what his/her possibilities and requests are. The MARCOS method, which is utilized for the final ranking of the considered alternatives, is a relatively recently proposed method whose possibilities have not been completely examined until now. The mentioned method enables the selection of a compromise solution that is optimal for the present conditions and fulfills all the given criteria to a satisfying degree.
3. Methodology
In this study, an integrated model including the CCSD, ITARA, and MARCOS methods is applied to determine the best stacker (Figure 1).
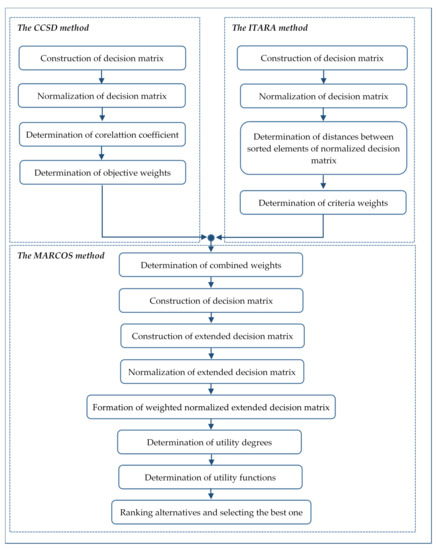
Figure 1.
The computational procedure of the integrated CCSD-ITARA-MARCOS approach.
The CCSD and ITARA methods are used to determine weights of the criteria, whereas the MARCOS method is used to rank the alternatives—i.e., in our case, stackers—and to select the best one.
3.1. The CCSD Method
The CCSD method was developed by Wang and Luo [7]. The CCSD method is an objective weighting method. However, so far the CCSD method has been used for solving a variety of problems, such as problems in the supply chain [51,52], technological forecasting [53], financial performance evaluation [54], environmental issues [55], and so forth.
The steps of this method are as follows [7,53]:
Step 1: A decision matrix () is constructed. This matrix includes alternatives, based on the criteria, .
In Equation (1), denotes the performance of the th alternative on the th criterion.
Step 2: This matrix is normalized using Equation (2) (for beneficial criteria) and Equation (3) (for cost criteria).
Step 3: The criterion is removed to take into account its impact on decision-making. With criterion , the performance value is computed using Equation (4) [56].
In Equation (4), denotes the weight of kth criterion calculated using some method for the subjective criteria weights determination, such as the AHP, SWARA, or PIPRECIA methods.
Step 4: The correlation coefficient () between criterion’s value and is computed using Equation (5).
where:
Step 5: In order to determine the objective weights () of criteria, a non-linear optimization model is written as:
In Equation (8), denotes criterion’s standard deviation, and it can be calculated using Equation (9).
The non-linear model indicated in Equation (8) is solved using MS Excel Solver (Microsoft corp., Redmond, WA, USA), Lingo 16 (Lindo Systems, Chicago, IL, USA), and MATLAB (The MathWorks, Inc., Natick, MA, USA).
3.2. The ITARA Method
The ITARA method was recently developed by Hatefi [8] and is a semi-objective method for determining the weights of criteria. The steps of the ITARA method are as follows [8]:
Step 1: A decision matrix () is constructed. This matrix was indicated in Equation (1).
Step 2: Normalized values and (Normalized Indifference Threshold) are obtained using Equations (10) and (11), respectively.
In Equation (11), denotes the Indifference Threshold of the th criterion.
Step 3: Normalized values are sorted in ascending order, then they are named in such a way that .
Step 4: The distance () between and is computed as follows.
Step 5: The difference () between and is calculated as follows.
Step 6: The weights of the criteria () are computed as follows.
where:
These weights are combined using Equation (16) [57].
3.3. The MARCOS Method
The MARCOS method is developed by Stević et al. [9]. Although the method is new, so far it has been applied for solving different decision-making problems, such as the assessment of project management software [58], supplier selection [59], the evaluation of human resources [60], road traffic analysis [61], and so on.
In our study, the MARCOS method is used to rank stackers and to determine the best one. The steps of this method are as follows [9]:
Step 1: The decision matrix is constructed. This matrix was indicated in Equation (1).
Step 2: An extended decision matrix () is formed.
While the ideal solution () is the best alternative, the anti-ideal solution () is the worst alternative. These values are computed as follows.
In Equations (18) and (19), denotes the beneficial criteria and presents the cost criteria.
Step 3: The extended decision matrix is normalized using Equations (20) and (21).
In Equations (20) and (21), is an element of the normalized matrix ().
Step 4: The normalized values are multiplied by the weights () of criteria by using Equation (22) to identify the weighted matrix ().
Step 5: The utility degrees () of the alternatives are computed concerning the anti-ideal and ideal solution, respectively.
where:
Step 6: The utility functions () of the alternatives are determined using Equation (26).
where:
In Equation (27), denotes the utility function concerning the anti-ideal solution. In Equation (28), presents the utility function concerning the ideal solution.
Step 7: The alternatives are ranked with respect to the final utility function. The alternative with the highest final utility function is determined as the best one.
4. An Illustrative Case Study
In this study, the best manual stacker will be selected for small warehouses. For this, two logistics experts were asked to identify suitable alternatives for small warehouses and evaluation criteria. The logistics experts identified eight alternatives and five criteria, which are the Price of Stacker (PS) (USD), Capacity (CPC) (kg), Lift Height (LH) (mm), Warranty Period (WRP) (Month), and Fork Length (FL) (mm). All the data are obtained from websites selling stackers. Table 1 indicates the decision matrix.

Table 1.
Decision matrix.
First of all, the CCSD method is applied to the above matrix to determine the objective weights of the criteria. The results of the CCSD are indicated in Table 2.

Table 2.
The results of the CCSD.
Then, the value of for each criterion is determined by the experts. These values are indicated in Table 3.

Table 3.
The value of
The steps of the ITARA method are applied to the decision matrix to achieve the weights of the criteria. The results of the ITARA method, the results of the CCSD, and the combined weights of criteria are indicated in Table 4.

Table 4.
The results of the ITARA, CCSD, and combined weights.
The combined weights are transferred to the MARCOS method. Then, the extended decision matrix is formed using step 2 of the MARCOS method. Table 5 indicates the extended decision matrix.

Table 5.
The extended decision matrix.
Then, the extended decision matrix is normalized using Equations (20) and (21). Table 6 presents the normalized matrix.

Table 6.
The normalized matrix.
Then, the normalized values are multiplied by weights () of the criteria using Equation (22) to determine the weighted matrix. Table 7 indicates the weighted matrix.

Table 7.
The weighted matrix.
Using Equations (23)–(28), the results of the MARCOS method are obtained. The results of the MARCOS method and the rankings of stackers are indicated in Table 8.

Table 8.
The results of the MARCOS method.
According to the results of the MARCOS method, the rankings of the stackers are as follows: Stc8, Stc3, Stc7, Stc4, Stc5, Stc1, Stc2, and Stc6. As can be seen from the input data presented in Table 1, the parameters connected to the Stc8 are always medium to high, which finally emphasizes this choice as a compromise and optimal.
In order to confirm the stability and reliability of the proposed model, the gained results are compared with the results obtained using the following MCDM methods: the weighted aggregated sum product assessment (WASPAS) method [62], additive ratio assessment (ARAS) [29], and grey relational analysis (GRA) [63]. The comparison of the gained ranking orders of the alternatives is shown in Figure 2.
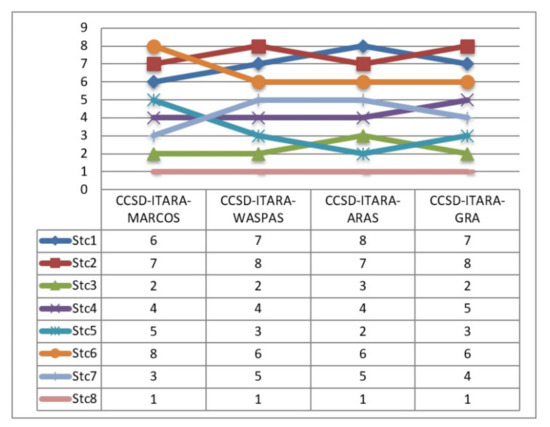
Figure 2.
Testing the stability of the proposed approach.
5. Discussion and Conclusions
The selection of equipment for dealing with materials during the logistics process is a very important task for decision-makers because this choice has a significant impact on the future operation of a logistics center. This kind of decision could be treated as strategic because the selected type of equipment could contribute to decreasing costs, shortening the time needed for performing an activity, and providing a higher security for goods and products. All of the points mentioned lead to the conclusion that these decisions require an analytical approach that involves all the criteria that are important for performing the evaluation process. For that matter, the MCDM methods could be a suitable and useful tool that facilitates the decision process and enables the making of a proper decision for the given conditions. For the facilitation of a decision-making process regarding equipment selection in the logistics field, in this paper we proposed the application of a novel integrated CCSD-ITARA-MARCOS MCDM model. The usefulness of this integrated model is demonstrated through the illustrative case study and pointed to the selection of the appropriate manual stacker. Additionally, two domain experts were involved in the evaluation process in regard to identifying suitable alternatives—i.e., manual stackers for small warehouses—according to the given set of evaluation criteria.
In the conducted case study, the weights of the evaluation criteria were determined by applying and combining the CCSD method and the ITARA method. When it comes to the process of determining weights, both the methods are convenient and easy to apply. The main difference between these methods is their orientation. The CCSD method is objective, whereas the ITARA method is semi-objective. Additionally, the CCSD method does not need a specific normalization method and can include more data on criteria weights [7], whereas the ITARA method belongs to a group of methods that are based on measuring data dispersion. The reason for employing objective and semi-objective methods when it comes to the determination of weights of criteria is that subjective methods often led to a decrease in the accuracy of evaluation with the increase in the number of criteria [8]. The main advantage of this combination relies on the fact that the standpoint of the decision-maker is appreciated to a certain degree. Namely, every decision-maker has a particular attitude regarding the criteria, meaning that for someone something is more important than to for another. If the significance of criteria is determined only on an objective basis then the individual dimension is lost. In this case, combining the objective and semi-objective methods for obtaining the criteria significance reflects the intention of the preservation of the objectiveness of evaluation together with acknowledging the preferences of decision-makers without disturbing the reliability of criteria significance determination.
The final ranking order is obtained by utilizing the newly developed MARCOS method. The MARCOS method primarily is based on testing the reference values of alternatives related to ideal values [9]. Thus, the given method emphasizes the alternative that represents some kind of compromise solution regarding the given requirements. The final evaluation and ranking order are strongly influenced by determining the criteria significance. In the present case, as was previously stated, the significance of the criteria is determined very thoughtfully and carefully, and all because of gaining the most reliable results. It is undeniable that the MARCOS method is easy to use and that it facilitates the decision process, but in combination with the CCSD and ITARA applied for determining the importance of the considered criteria, the reliability of the performed evaluation and the gained ranking order increased.
Following the results of the applied integrated model, the stacker designated as Stc8 is the best in terms of the evaluated criteria. With the aim of testing the proposed approach based on the mentioned MCDM methods, the obtained results are compared with the results determined using the WASPAS, ARAS, and GRA methods. In the computing procedures of all three methods, the same weights of the criteria are involved, which were obtained by applying the CCSD-ITARA. In all observations, the stacker Stc8 is in first place and represents the best choice for the given conditions. Besides this, the stacker Stc3 is in the second place, except in the case when is applied in ARAS, when it is in 3rd place. Thus, in this way the reliability and stability of the proposed approach are completely confirmed.
The proposed integrated CCSD-ITARA-MARCOS model proved to be extremely successful when it comes to solving problems in a logistics system—i.e., a stacker selection problem. The use of the CCSD-ITARA-MARCOS model is very beneficial because it is very comprehensive and empowers us to make confident judgments. However, the applicability of the proposed model should not be limited only to the logistics field. Its potential and possibilities should be examined in other fields, such as information technologies, strategy selection, personnel selection, etc. In that way, all the aspects of the proposed model will be observed and the potential shortages could be resolved.
The key advantage of the introduced integrated model is its simplicity, ease of use, and objectivity that appreciates the standpoint of decision-makers to an acceptable degree. However, the main limitation of the proposed model is that it deals with crisp numbers. The decision-making environment is characterized by uncertainty and vagueness, so it is very difficult to correctly express the evaluation criteria through crisp numbers. In other words, the reliability of the performed evaluation decreases because unexpected changes could cause a situation where, for example, the first ranked alternative is not acceptable because the conditions have changed. In order to better incorporate uncertainty into the evaluation process, an extension with fuzzy, grey, and neutrosophic numbers is proposed. In this way, the proposed model would be improved and the possibility of making impropriate decisions would be reduced. Furthermore, by involving a greater number of decision-makers, the subjective dimension could be incorporated to a greater extent and interesting results would be obtained.
Besides the mentioned shortages, the CCSD-ITARA-MARCOS model proved its applicability and ability to help in the process of decision-making. Overall, the proposed hybrid model is flexible, adaptable, and effective, and it can help decision-makers solve problems in other areas as well. Additionally, the model is quite simple and can be easily modified depending on the problem one wants to solve.
Author Contributions
Conceptualization, A.U., D.K., and G.P.; methodology, A.U., D.K., D.S., and Ç.K.; validation, P.T.N.; data curation, G.P.; writing—original draft preparation, D.S. and Ç.K.; writing—review and editing, A.U., and P.T.N.; supervision, D.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tadić, S.; Zečević, S.; Petrović-Vujačić, J. Global trends and logistics development. Ekon. Vidici 2013, 18, 519–532. [Google Scholar]
- Mohsen; Hassan, M.D. A framework for selection of material handling equipment in manufacturing and logistics facilities. J. Manuf. Technol. Manag. 2010, 21, 246–268. [Google Scholar] [CrossRef]
- Tuzkaya, G.; Gülsün, B.; Kahraman, C.; Özgen, D. An integrated fuzzy multi-criteria decision making methodology for material handling equipment selection problem and an application. Expert Syst. Appl. 2010, 37, 2853–2863. [Google Scholar] [CrossRef]
- Tabucanon, M.T.; Batanov, D.N.; Verma, D.K. Decision support system for multicriteria machine selection for flexible manufacturing systems. Comput. Ind. 1994, 25, 131–143. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Stević, Ž.; Mardani, A. Modelling procedure for the selection of steel pipes supplier by applying fuzzy AHP method. Oper. Res. Eng. Sci. Theory Appl. 2020, 39–53. [Google Scholar] [CrossRef]
- Đalić, I.; Stević, Ž.; Karamasa, C.; Puška, A. A novel integrated fuzzy PIPRECIA–interval rough SAW model: Green supplier selection. Decis. Mak. Appl. Manag. Eng. 2020, 3, 126–145. [Google Scholar] [CrossRef]
- Wang, Y.M.; Luo, Y. Integration of correlations with standard deviations for determining attribute weights in multiple attribute decision making. Math. Comput. Model. 2010, 51, 1–12. [Google Scholar] [CrossRef]
- Hatefi, M.A. Indifference threshold-based attribute ratio analysis: A method for assigning the weights to the attributes in multiple attribute decision making. Appl. Soft Comput. 2019, 74, 643–651. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Puška, A.; Chatterjee, P. Sustainable supplier selection in healthcare industries using a new MCDM method: Measurement of alternatives and ranking according to COmpromise solution (MARCOS). Comput. Ind. Eng. 2020, 140, 106231. [Google Scholar] [CrossRef]
- Popovic, G.; Stanujkic, D.; Brzakovic, M.; Karabasevic, D. A multiple-criteria decision-making model for the selection of a hotel location. Land Use Policy 2019, 84, 49–58. [Google Scholar] [CrossRef]
- Karabašević, D.; Zavadskas, E.K.; Stanujkic, D.; Popovic, G.; Brzakovic, M. An Approach to Personnel Selection in the IT Industry Based on the EDAS Method. Transform. Bus. Econ. 2018, 17, 54–65. [Google Scholar]
- Stanujkic, D.; Karabasevic, D.; Zavadskas, E.K. A New Approach for Selecting Alternatives Based on the Adapted Weighted Sum and the SWARA Methods: A Case of Personnel Selection. Econ. Comput. Econ. Cybern. Stud. Res. 2017, 51, 39–56. [Google Scholar]
- Hansson, S.O.; Hadorn, G.H. Argument-based decision support for risk analysis. J. Risk Res. 2018, 21, 1449–1464. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Kildienė, S. State of art surveys of overviews on MCDM/MADM methods. Technol. Econ. Dev. Econ. 2014, 20, 165–179. [Google Scholar] [CrossRef]
- Stanujkic, D.; Zavadskas, E.K.; Liu, S.; Karabasevic, D.; Popovic, G. Improved OCRA method based on the use of interval grey numbers. J. Grey Syst. 2017, 29, 49–60. [Google Scholar]
- Mardani, A.; Jusoh, A.; Nor, K.; Khalifah, Z.; Zakwan, N.; Valipour, A. Multiple criteria decision-making techniques and their applications–a review of the literature from 2000 to 2014. Econ. Res. Ekon. Istraživanja 2015, 28, 516–571. [Google Scholar] [CrossRef]
- Popovic, G.; Stanujkic, D.; Karabasevic, D. A framework for the evaluation of hotel property development projects. Int. J. Strat. Prop. Manag. 2019, 23, 96–107. [Google Scholar] [CrossRef]
- Bakir, M.; Akan, Ş.; Kiraci, K.; Karabasevic, D.; Stanujkic, D.; Popovic, G. Multiple-Criteria Approach of the Operational Performance Evaluation in the Airline Industry: Evidence from the Emerging Markets. Rom. J. Econ. Forecast. 2020, 23, 149. [Google Scholar]
- Stanujkic, D.; Karabasevic, D.; Zavadskas, E.K.; Smarandache, F.; Brauers, W.K. A bipolar fuzzy extension of the MULTIMOORA method. Informatica 2019, 30, 135–152. [Google Scholar] [CrossRef]
- Karabasevic, D.; Maksimovic, M.; Stanujkic, D.; Brzakovic, P.; Brzakovic, M. The evaluation of websites in the textile industry by applying ISO/IEC 9126-4 standard and the EDAS method. Ind. Text. 2018, 69, 489–494. [Google Scholar]
- Churchman, C.W.; Ackoff, R.L. An approximate measure of value. J. Oper. Res. Soc. Am. 1954, 2, 172–187. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Saaty, T.L. Decision Making with Dependence and Feedback: Analytic Networkprocess; RWS Publications: Pittsburgh, PA, USA, 1996. [Google Scholar]
- Roy, B. Multicriteria for Decision Aiding; Kluwer: London, UK, 1996. [Google Scholar]
- Brans, J.P.; Vincke, P. A preference ranking organization method: The PROMETHEE method for MCDM. Manag. Sci. 1985, 31, 647–656. [Google Scholar] [CrossRef]
- Yoon, K.P.; Hwang, C.L. Multiple Attribute Decision Making: An Introduction; Sage Publications: Thousand Oaks, CA, USA, 1995; Volume 104. [Google Scholar]
- Opricovic, S. Multicriteria Optimization of Civil Engineering Systems; Faculty of Civil Engineering: Belgrade, Serbia, 1998. (In Serbian) [Google Scholar]
- Zavadskas, E.K.; Kaklauskas, A.; Sarka, V. The new method of multi-criteria complex proportional assessment of projects. Techological Econ. Dev. Econ. 1994, 1, 131–139. [Google Scholar]
- Zavadskas, E.K.; Turskis, Z. A new additive ratio assessment (ARAS) method in multicriteria decision-making. Technol. Econ. Dev. Econ. 2010, 16, 159–172. [Google Scholar] [CrossRef]
- Brauers, W.K.; Zavadskas, E.K. The MOORA method and its application to privatization in a transition economy. Control Cybern. 2006, 35, 445–469. [Google Scholar]
- Brauers, W.K.M.; Zavadskas, E.K. Project management by MULTIMOORA as an instrument for transition economies. Technol. Econ. Dev. Econ. 2010, 16, 5–24. [Google Scholar] [CrossRef]
- Keršuliene, V.; Zavadskas, E.K.; Turskis, Z. Selection of rational dispute resolution method by applying new step-wise weight assessment ratio analysis (SWARA). J. Bus. Econ. Manag. 2010, 11, 243–258. [Google Scholar] [CrossRef]
- Stanujkic, D.; Zavadskas, E.K.; Karabasevic, D.; Smarandache, F.; Turskis, Z. The use of Pivot Pair-wise Relative Criteria Importance Assessment method for determining weights of criteria. Rom. J. Econ. Forecast. 2017, 20, 116–133. [Google Scholar]
- Gigović, L.; Pamučar, D.; Bajić, Z.; Milićević, M. The combination of expert judgment and GIS-MAIRCA analysis for the selection of sites for ammunition depots. Sustainability 2016, 8, 372. [Google Scholar] [CrossRef]
- Pamučar, D.; Stević, Ž.; Sremac, S. A new model for determining weight coefficients of criteria in mcdm models: Full consistency method (FUCOM). Symmetry 2018, 10, 393. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Olfat, L.; Turskis, Z. Multi-criteria inventory classification using a new method of evaluation based on distance from average solution (EDAS). Informatica 2015, 26, 435–451. [Google Scholar] [CrossRef]
- Yazdani, M.; Zarate, P.; Zavadskas, E.K.; Turskis, Z. A Combined Compromise Solution (CoCoSo) method for multi-criteria decision-making problems. Manag. Decis. 2019, 57, 2501–2519. [Google Scholar] [CrossRef]
- Wadhwa, S.; Madaan, J.; Chan, F.T.S. Flexible decision modeling of reverse logistics system: A value adding MCDM approach for alternative selection. Robot. Comput. Integr. Manuf. 2009, 25, 460–469. [Google Scholar] [CrossRef]
- Prakash, C.; Barua, M.K. A combined MCDM approach for evaluation and selection of third-party reverse logistics partner for Indian electronics industry. Sustain. Prod. Consum. 2016, 7, 66–78. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, Z.; Zhang, H.; Wang, Y.; Yang, Y.; Li, Y. An integrated MCDM approach considering demands-matching for reverse logistics. J. Clean. Prod. 2019, 208, 199–210. [Google Scholar] [CrossRef]
- Żak, J.; Węgliński, S. The selection of the logistics center location based on MCDM/A methodology. Transp. Res. Procedia 2014, 3, 555–564. [Google Scholar] [CrossRef]
- Mihajlović, J.; Rajković, P.; Petrović, G.; Ćirić, D. The selection of the logistics distribution center location based on MCDM methodology in southern and eastern region in Serbia. Oper. Res. Eng. Sci. Theory Appl. 2019, 2, 72–85. [Google Scholar] [CrossRef]
- Celik, E.; Gumus, A.T.; Alegoz, M. A trapezoidal type-2 fuzzy MCDM method to identify and evaluate critical success factors for humanitarian relief logistics management. J. Intell. Fuzzy Syst. 2014, 27, 2847–2855. [Google Scholar] [CrossRef]
- Budak, A.; Kaya, İ.; Karaşan, A.; Erdoğan, M. Real-time location systems selection by using a fuzzy MCDM approach: An application in humanitarian relief logistics. Appl. Soft Comput. 2020, 92. [Google Scholar] [CrossRef]
- Aguezzoul, A. Third-party logistics selection problem: A literature review on criteria and methods. Omega 2014, 49, 69–78. [Google Scholar] [CrossRef]
- Jamshidi, A.; Jamshidi, F.; Ait-Kadi, D.; Ramudhin, A. A review of priority criteria and decision-making methods applied in selection of sustainable city logistics initiatives and collaboration partners. Int. J. Prod. Res. 2019, 57, 5175–5193. [Google Scholar] [CrossRef]
- Mathew, M.; Sahu, S. Comparison of new multi-criteria decision making methods for material handling equipment selection. Manag. Sci. Lett. 2018, 8, 139–150. [Google Scholar] [CrossRef]
- Khandekar, A.V.; Chakraborty, S. Selection of material handling equipment using fuzzy axiomatic design principles. Informatica 2015, 26, 259–282. [Google Scholar] [CrossRef]
- Hadi-Vencheh, A.; Mohamadghasemi, A. A new hybrid fuzzy multi-criteria decision making model for solving the material handling equipment selection problem. Int. J. Comput. Integr. Manuf. 2015, 28, 534–550. [Google Scholar] [CrossRef]
- Eko Saputro, T.; Daneshvar Rouyendegh, B. A hybrid approach for selecting material handling equipment in a warehouse. Int. J. Manag. Sci. Eng. Manag. 2016, 11, 34–48. [Google Scholar] [CrossRef]
- Singh, R.K.; Benyoucef, L. A consensus based group decision making methodology for strategic selection problems of supply chain coordination. Eng. Appl. Artif. Intell. 2013, 26, 122–134. [Google Scholar] [CrossRef]
- Hanane, A.; Brahim, O.; Bouchra, F. CCSD and TOPSIS methodology for selecting supplier in a paper company. In Proceedings of the 2016 4th IEEE International Colloquium on Information Science and Technology (CiSt), Tangier, Morocco, 24–26 October 2016; pp. 275–280. [Google Scholar]
- Dahooie, J.H.; Zavadskas, E.K.; Firoozfar, H.R.; Vanaki, A.S.; Mohammadi, N.; Brauers, W.K.M. An improved fuzzy MULTIMOORA approach for multi-criteria decision making based on objective weighting method (CCSD) and its application to technological forecasting method selection. Eng. Appl. Artif. Intell. 2019, 79, 114–128. [Google Scholar] [CrossRef]
- Heidary Dahooie, J.; Zavadskas, E.K.; Vanaki, A.S.; Firoozfar, H.R.; Lari, M.; Turskis, Z. A new evaluation model for corporate financial performance using integrated CCSD and FCM-ARAS approach. Econ. Res. Ekon. Istraživanja 2019, 32, 1088–1113. [Google Scholar] [CrossRef]
- Kim, I.; Park, K.; Lee, K.; Park, M.; Lim, H.; Shin, H.; Kim, S.D. Application of various cytotoxic endpoints for the toxicity prioritization of fine dust (PM2.5) sources using a multi-criteria decision-making approach. Environ. Geochem. Health 2019, 42, 1775–1788. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Methods for multiple attribute decision making. In Multiple Attribute Decision Making; Springer: Berlin/Heidelberg, Germany, 1981; pp. 58–191. [Google Scholar]
- Zavadskas, E.K.; Podvezko, V. Integrated determination of objective criteria weights in MCDM. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 267–283. [Google Scholar] [CrossRef]
- Puška, A.; Stojanović, I.; Maksimović, A.; Osmanović, N. Evaluation software of project management used measurement of alternatives and ranking according to compromise solution (MARCOS) method. Oper. Res. Eng. Sci. Theory Appl. 2020, 3, 89–102. [Google Scholar]
- Badi, I.; Pamucar, D. Supplier selection for steelmaking company by using combined Grey-MARCOS methods. Decis. Mak. Appl. Manag. Eng. 2020, 3, 37–48. [Google Scholar] [CrossRef]
- Stević, Ž.; Brković, N. A Novel Integrated FUCOM-MARCOS Model for Evaluation of Human Resources in a Transport Company. Logistics 2020, 4, 4. [Google Scholar] [CrossRef]
- Stanković, M.; Stević, Ž.; Das, D.K.; Subotić, M.; Pamučar, D. A new fuzzy MARCOS method for road traffic risk analysis. Mathematics 2020, 8, 457. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J.; Zakarevicius, A. Optimization of weighted aggregated sum product assessment. Elektronika Ir Elektrotechnika 2012, 122, 3–6. [Google Scholar] [CrossRef]
- Deng, J. Control problems of grey systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).