Abstract
Currently, information and communication technology (ICT) has acquired an important role in education. The incorporation of ICT by mathematics teachers has been a challenge as it requires an improvement in their knowledge of the use of new technologies. We aimed to examine the most relevant items of the indicators related to teaching mathematics and ICT, to estimate the relationships between teachers individually and by clusters, and to analyze the incidence of age variables, teaching experience, and gender in this study. A total of 73 high school teachers were included in this cross-sectional study. A validated questionnaire was used to assess mathematics and teaching practice, use, resources, and domain of ICT. Principal component analysis (PCA) was applied to determine the associations among variables of the present study. The application of ICT to teaching was associated with the use of ICT resources in the classroom and indicated that teachers made more choice in selecting a variety of software than electing different hardware devices. Teachers combined technology with educational platforms to improve student learning in mathematics. The general perception of mathematics teachers about their digital competence does not match with models employed in the classroom. Gender was not an influencing factor.
1. Introduction
The benefits of using information and communication technology (ICT) for educational purposes have been supported by numerous studies in recent decades [1,2]. ICT provides tools for online training and scalable, student-adapted mobile teaching solutions [3]. In addition, integration of ICT into teaching has developed exponentially with the incorporation of methodologies and digital resources [4]. In this sense, the educational policies of developed countries consider digital competence in education to be essential, and therefore invest in training, technological resources for the classroom [5,6], and sustainable educational models with technologies [7].
The use of ICT by mathematics teachers implies a positive attitude toward technology and the use of compatible teaching methodologies for its implementation in and out of the classroom [8]. In addition, the proper use of technology significantly simplifies tasks, promotes collaborative work [9], and motivates the learning of students [10,11]. The positive effects of ICT are observed in students’ academic performance [12,13]. There are doubts surrounding its proper use by teachers as a result of initial reluctance and lack of specific training [14,15].
It is reasonable to evaluate how mathematics teachers perceive the training and use of ICT [16,17]. In this context, this study was performed to evaluate the relationships among some of the variables of the dimensions “mathematics and teaching practice”, “ICT in the teacher environment”, and “uses, resources, and ICT mastery”. We analyzed the variables of these dimensions to examine their relevance from different perspectives. We also estimated the profiles of teachers according to their perceptions, classified them into clusters, and evaluated their differences based on gender, age, and teaching experience.
1.1. The Teaching of Mathematics
In addition to its ability to strengthen abstract thinking, mathematics is important because it plays a role in the development of all areas of knowledge and the modernization of society. In fact, all children are educated to acquire mathematical competence because it is considered to be a discriminating element in their future academic paths [18]. The ability to transmit knowledge of formalisms and mathematical logic to students facilitates their ability to effectively learn such concepts [19]. In this sense, it is essential to provide initial and continuous training to teachers and also provide them with tools and resources related to the didactics of mathematics [20]. In studying the didactic of mathematics, Vergnaud et al. (2013) highlighted the importance of the conceptual component of schematics for mathematical learning and the resolution of a problem as a source and criterion of mathematical knowledge. According to Brousseau et al. (1986), real or imaginary situations could serve as active methods of learning for the teaching of mathematics.
The didactic of mathematics emerged in France in the 1970s as an approach to investigating the pedagogical aspects of mathematical problems in the educational environment. Didactic is defined by Chevallard “as the science of the dissemination of knowledge in any social group, such as a class of students, the society in general, etc.”, and it focuses on the elements of local or global praxeologies [21]. According to Chevallard, praxeology consists of several sets of tasks, techniques (to perform these tasks), technologies, and a theory that justifies these technologies [22]. In addition, schools articulate the didactic and the pedagogical, mediated by the teacher as a facilitator. In other words, through concrete transfer processes influenced by sociocultural factors, the teacher transforms the knowledge needed to teach into knowledge that has been taught [23]. This transposition shows the growing difference between mathematics developed by mathematicians and mathematics for teaching [23].
In the didactics of mathematics, there is a logical relationship among knowledge, subject, and situations [24]. Trouche showed differences between the main intellectual currents in the didactic of mathematics; Brousseau discussed what needs to be done, whereas Chevallard focused on institutional constraints. In terms of mathematical knowledge, Vergnaud highlighted the individual and social construct in progress, and Chevallard emphasized the social and historical construct [25].
1.2. ICT in the Teaching of Mathematics
The incorporation of ICT in education has evolved given the large amount of online educational resources, the widespread educational offerings, the exchange of knowledge, and the connections among learning communities [26,27,28]. Similarly, the application of technology in education, eliminates certain space-time barriers in the teaching-learning process and enables the implementation of active methodologies [29]. In addition, ICT facilitates collaboration among all agents of the educational community [30].
One of the more prominent points of math didactics is problem solving [25]. To do this, it is necessary to analyze, search, and discriminate against the relevant data to its resolution. The use of adequate technology, allows the discrimination of more relevant data [31]. Technology reinforces mathematical thought forms and their representation [32]. In addition, cognitive technology tools promote the learning of mathematical concepts by expanding the possibilities of representation and by amplifying and reorganizing students’ approaches to problem solving [1]. Virtual technology applications can even promote students’ creativity and experimentation, and allow one to create and manipulate their own representations [33]. In addition, virtual environments have a friendly and intuitive graphical interface that favors the motivation of the students and a dynamic feedback of the application, encouraging them to persist in problem solving [34,35].
For their part, dynamic geometry’s applications (Geogebra, Cinderella, etc.) help the student to visualize and easily experience the associated processes through interactive changes that favor the exploration of all possibilities [36,37]. Other ICT resources are programming environments that develop language and abstract mathematical thinking [38]. In addition, it allows one to interpret reality in mathematical terms and promotes the ability to solve problems [39,40,41]. The wide variety of available resources facilitate its use by the teacher [38]. In contrast, technological applications that guide students in a step by step way to default formulas or representations without allowing a free experimentation by the student, condition their significant learning of mathematics [42].
There are personal factors, such as perceptions or attitude toward ICT, that condition the use of technology [43,44]. To facilitate the integration of technology into classrooms, repositories of methodological resources and digital content that are accessible to mathematics teachers can be provided [45]. Despite the innovative advances of technology in mathematical education, its incorporation and development by teachers has been found to be lower than expected [46]. As a result, it is necessary to adequately train teachers to enable the effective use of technology in the classroom [47].
The general literature about the effect of ICT on teaching and learning mathematics focuses mainly on innovative uses or new tools and applications. In contrast, studies that consider the teaching dimension are scarce [25]. Therefore, it is necessary to determine the impact of digital resources and the professional development of mathematics teachers through technology [31] and establish constructs that measure their technological pedagogical knowledge [48].
1.3. ICT Training for Mathematics Teachers
It is desirable to provide ICT training to future teachers in the didactics of mathematics, which has a strong social orientation due to its transformative power [49]. The ICT training of mathematics teachers, in addition to providing training and professional development, should encourage the integration of new active methodologies in the classroom [50] and provide effective tools for learning mathematics [51]. Despite this, technological advances are a challenge for many teachers, due to the complexity of the continuously changing software [52,53]. In addition, there is the difficulty of training teachers to adapt new methodological strategies in their teaching style and to expand their ICT tool knowledge in both their personal and professional environment [54,55].
ICT training is also conditioned by attitudes toward technology [43]. Other factors that promote a positive perception of ICT training include its simplicity and usefulness as compared with traditional methods [56]. The flexibility of training programs and personalized training are also valued factors [57]. In this sense, if teachers are trained as agents of change, then technology will enable innovation and sustainable development in schools [58]. Furthermore, the proper training and technology effectively promotes an inclusive classroom for students with disabilities [59].
1.4. ICT Use by Mathematics Teachers
The use of technology by teachers is influenced by their perception and by the training they have received [17]. Following initial reluctance, teachers generally perceive ICT as a tool with great potential in the educational setting [16,60]. Numerous authors have emphasized that ICT is a useful tool to motivate students [61,62] and promote learning [8]. In addition, the quantity and quality of ICT resources held by schools influence the use of technologies by teachers [5], as well as the national investment in I+D of each country [63].
In Spain, the National Institute of Educational Technologies and Teacher Training (INTEF), following European guidelines, establishes the Common Framework for Digital Teaching Competence [64]. Despite the frequent use of the term “digital teaching competence”, different authors have argued that it was ambiguous and have proposed the existence of several interconnected competencies; therefore, the concept must be expanded by differentiating generic and specific professional skills [65,66]. Therefore, Touron recommended a validated instrument that measured digital teaching competence, taking into consideration the provisions of the INTEF Framework [67].
These technological skills are limited by the teacher’s perception about his knowledge in ICT, associated as second-order barriers [68]. In addition, Presby et al. (2017) concluded that teachers would be perpetual novices in this regard because of the constant innovations in educational technology. The influence of social and cultural aspects that could delay the integration of technology into classrooms must also be taken into account. In addition, another effect that slows teachers’ development of technological skills is the adaptation to emerging new pedagogies [69,70].
While technological innovation in classrooms is widespread, the impact on academic performance in high school has not been universal, so it is necessary to promote technological initiatives that are systemic, effective, and sustainable. The Organization for Economic Co-operation and Development (OECD) reported that technologies do not add extra value to education if they are not reinforced by cognitive, creative, communicative, teamwork, and perseverance skills [71]. In this context, Daniels et al. (2018) considered technology to be an instrument that must be selected and an appropriately used by the teacher, and they asserted that effective methodological strategies must also be applied to positively influence students’ learning and their academic performance.
The pedagogical use of mathematical software in secondary education promotes practice, establishes interactive environments for learning [72], facilitates the students’ interpretation of relationships among functions and graphs [73,74], and helps students to understand complex concepts of arithmetic and algebra [75]. Therefore, the use of pedagogical software in mathematics promotes meaningful learning, provided that it is designed with appropriate cognitive parameters and that the teacher applies it with an effective teaching method [76].
In contrast, despite the resources available, the use of educational software by mathematics teachers is lower than desirable [77]. In addition, the lack of training and low use could be due to the limited number of free software programs and the general limitations on the digital educational competence of students [78]. The use is also reduced if the software is not updated or has limitations [79]. The use of mathematical software by teachers could also be influenced by factors such as age, gender, and teaching experience [80].
Schools in Spain are adequately resourced for technology use in classrooms [6]. Its proper use favors and increases interactivity with students [81]. The use of digital interactive whiteboards (IWBs) to teach mathematics to lower-ability pupils in small groups significantly improved their command over mathematics as compared with teaching without them [82]. Despite the quantified positive effects of ICTs on students’ academic performance, it is necessary to evaluate these results through an in-depth analysis of the most effective methodological elements in the didactics of mathematics [83]. In this sense, a theoretical teaching basis is essential for proposing interactive mathematical tasks and for evaluating the achievements of students in their learning [84].
However, teachers do not necessarily properly use the available resources [2], for example, they do not take advantage of the interactive and innovative features of IWBs but use them only as a regular whiteboard or presentation tool [81]. This restricted use limits the students’ interaction and learning [85]. While technology-based classroom assessment can provide a wealth of information on learning, the teachers may not know how to collect or use such data effectively [86].
In line with the above, a recent study showed that teaching experience was negatively correlated with digital competence and its pedagogical use in the classroom [87]. Other authors have found it to be positively correlated with the experience of teachers but not with their age [88]. As for gender, some findings have shown that the relationship between perceived utility and intent to use IWBs was stronger for men than for women [14]. Other authors have shown that, as compared with women, men tended to receive more support from their peers and demonstrated higher levels of self-efficacy in the use of technology [89], and they experienced less anxiety and greater self-confidence [90].
1.5. Justification
Despite the importance of the use of ICT in the classroom and its benefits, the didactic of mathematics at secondary and higher education levels has remained stagnant, compartmentalized, and oriented to the exposure of the teacher [17,91]. In line with the above, we see limited use of educational software [78] and hardware [2,43]. In addition, the use of IWBs is reduced to traditional whiteboards or presentation tools without taking advantage of the innovative resources that they offer [92]. IWBs are rarely used to improve student learning, even for teachers who are experienced in their use [93]. Restrained by resistance to change, teachers often waste the teaching potential of mobile devices and underutilize them [17].
The autonomous city of Melilla has the highest rate of school failure and the ratio per class in Spain and throughout Europe [94]. For this reason, a comprehensive study was conducted to analyze the students and teachers. The study of teachers is justified because they are considered to be one of the factors that have a significant impact on the motivation of students and their academic performance [10,95]. It is considered to be necessary to deepen the relationship between mathematics teachers and ICT. This study analyzes the digital competence of teachers through their perceptions of ICT training, use, and mastery in general. This study focuses on the dimensions “mathematics and teaching practice”, “ICT in the teacher environment”, and “uses, resources and mastery of ICT”.
Given this background, this research aims to achieve the following three objectives: (1) to examine the most relevant items of the previously mentioned indicators, (2) to estimate the relationships between teachers individually and between clusters, and (3) to analyze the influence of age variables, teaching experience, and gender in this study sample. Thus, the following research questions were posed: (PI1) Do mathematics teachers continue to undergo training in ICT? (PI2) Do mathematics teachers use ICT to teach? (PI3) Do teachers use more software than hardware devices? (PI4) Does gender, age, and teaching experience have an influence on the use of ICT? (PI5) Is there a relationship among items in ICT training, use, and resource indicators?
2. Materials and Methods
To achieve the above set of objectives, we applied a descriptive quantitative cross-sectional study [96] to assess the training and use of ICT by mathematics teachers. The study population was selected with the following inclusion criteria: (1) resides in the AC of Melilla, (2) is a teacher of high school, and (3) teaches the subject of mathematics. To ensure the reliability of data collection, questionnaires were filled out online through Google forms during the third quarter of the 2018–2019 academic year. Mathematics teachers were asked to respond in general terms about teaching that occurred during that period.
With the established criteria, the population amounted to a total of 73 teachers, of which 34.25% were women. The sample was comprised of 61 teachers, covering the entire center of the city and representing 83.56% of the population, of which 34.42% were women. The sample consisted of a total of 40 men and 21 women. In this cohort, 5 were under the age of 30, 16 were between 31 and 40 years old, 25 were between 41 and 50 years old, 8 were between 51 and 60 years old, and 7 were more than 61 years old.
The quantitative instrument was designed ad hoc and included the following: (i) a literature review, (ii) establishment of the dimensions of the questionnaire, (iii) formulation of items, (iv) validation of content through expert judgement, (v) construct validation, and (vi) reliability analysis [97,98]. The questionnaire was set up ad hoc and contained Likert-scale closed items with four graduated levels (1, none; 2, a little; 3, enough; and 4, a lot). The instrument was validated by expert judgement to determine the values of reliability and validity. The internal consistency of the obtained data matrix was also verified. The results were optimal since the Tucker–Lewis Index factor of reliability was 0.965. In addition, for the validation of the instrument, the Kaiser–Guttman criterion and the “broken-stick” method were used.
The Kaiser–Guttman criterion (Figure 1a), is used to select those axes that represent interesting variation in the data; specifically, it calculates the average of all inherent values and retains those that are higher than the global mean. In addition, the broken-stick (Figure 1b) model was used, which randomly divided the length of one bar into the number of PCA axes and compared this result to its inherent values. In Figure 1, when the white bar exceeds or equals the red one, the number of axes is considered optimal. According to Figure 1, for the first criterion, 10 axes would be the optimal selection for the instrument, and for the second criterion, 8 would be ideal. Since the instrument was designed with eight axes, the results are optimal.
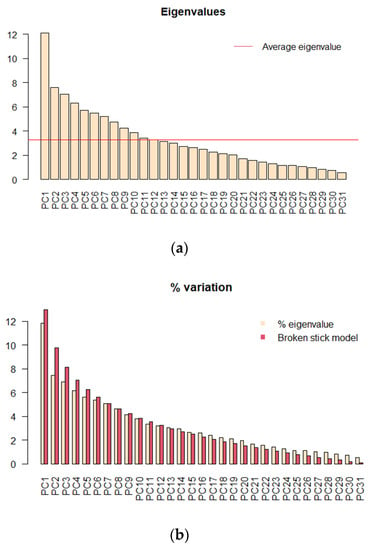
Figure 1.
Instrument validation. (a) Kaiser–Guttman criteria; (b) Broken-stick criteria.
2.1. Procedure
The items in this study were analyzed by R Studio 1.3.1073 and Python software and were related to the following dimensions: (A) “teacher data”; (B) “mathematics and teaching practice”; (C) “ICT in the teacher environment”; and (D) “uses, resources, and ICT mastery”. The encoding used is detailed in the following Table 1.

Table 1.
Relationships among items, indicators, dimensions, and coding used in the questionnaire. Information and communication technology (ICT).
2.2. Statistical Analyses
According to Figure 2, more than 30% of the variables had a high or very high correlation. For this reason, a principal component analysis (PCA) was carried out to analyze these correlations more thoroughly. To ensure that the PCA was optimal, the following process was performed:
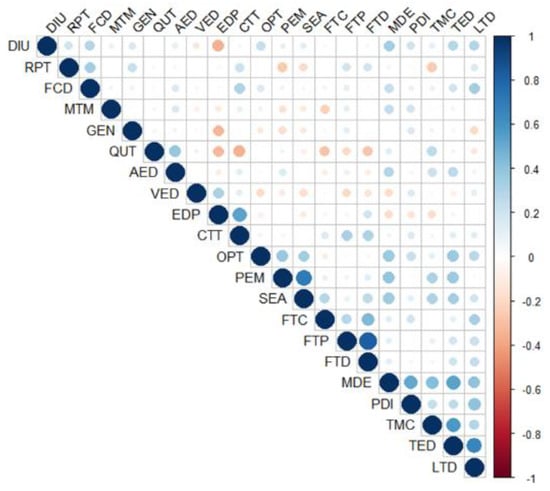
Figure 2.
Correlogram chart. Linear correlations among study variables.
- The inflated value of the variance was analyzed. Since no vif was greater than 0.8, no variables needed to be removed.
- The data were standardized for the PCA.
PCA was used to reduce dimensionality and avoid collinearity problems. Therefore, the objectives of its application can be summarized as follows:
- To optimally represent a set of variables and individuals (or cases);
- To transform original variables that are generally correlated into new uncorrelated variables, facilitating the interpretation of the data (reducing the dimensionality of the data);
- To define which variables contribute the most as a source of variability;
- To determine which variables are related to each other and which ones are not;
- To identify if the set of variables describes an important structure or is only random noise.
A PCA reduces the dimensionality of multivariate data to two or three main components, which can be viewed graphically, with a minimal loss of information. This assumes that the greatest variations are the most relevant.
3. Results
Of the set of variables, only 84 values were missing. Therefore, to proceed with subsequent statistical analyses, these values were omitted rather than imputed by the mean or mode.
The first analysis, shown in Figure 1, shows positive and very significant correlations between continuous training and the selection of effective teaching approaches to guide students’ thinking and learning in mathematics (CTT with EDP); the use of platforms and specific software to teach mathematics (PEM with SEA); ICT training for personal and professional uses (FTP with FTD); and the selection of technologies that improve student learning in a lessons and the selection of contents and methodologies, the use of material and combined strategies, and the perception of self-sufficiency in digital competence (TED with TMC, MDE, and LTD). The results reveal negative correlations between the selection of effective teaching approaches to guide the thinking and learning of mathematics students and technical English learning (EDP with DIU).
Positive but very weak correlations are observed among teaching experience and the use of resources that combine contents, ITC, and pedagogical approaches (AED with MDE, TMC, and TED). Furthermore, age is positively and very weakly correlated with TMC. Conversely, age is negatively correlated with the selection of efficient teaching approaches to guide the thinking and learning of mathematics students and also with the knowledge required to use technologies (QUT with EDP and CTT). Furthermore, a negative and very weak correlation exists with the perception of training for professional and personal use (FTP and FTD).
Gender is positively and weakly correlated with the resolution of technical problems (RPT), and negatively correlated with the selection of efficient teaching approaches to guide the ideas and learning of mathematics students (EDP). Moreover, negative and very weak correlations are observed with the use of hardware, software, and educative platforms in the classrooms, as well as with the perception of combining technologies and approaches to teaching mathematics (PEM, SEA, and LTD).
Figure 3 shows information on the two main components, PC1 (first and third quadrants) and PC2 (second and fourth quadrants). As there is a strong linear correlation among the study variables (see the third and fourth quadrants), the implementation of PCA is ideal. In PCA, square cosine (cos2) allows us to identify the variables that contribute most to each of these dimensions (the quality of representation). This information is also represented by the modulus of each vector (the length of the arrows), i.e., the larger its modulus, the greater its influence. To determine whether or not the selected variables are optimal, the data in the PCA chart were analyzed using cos2. We concluded that the variables in blue GEN, VED, MTM, and UTA could be removed because they had a lower rendering quality in the factor map.
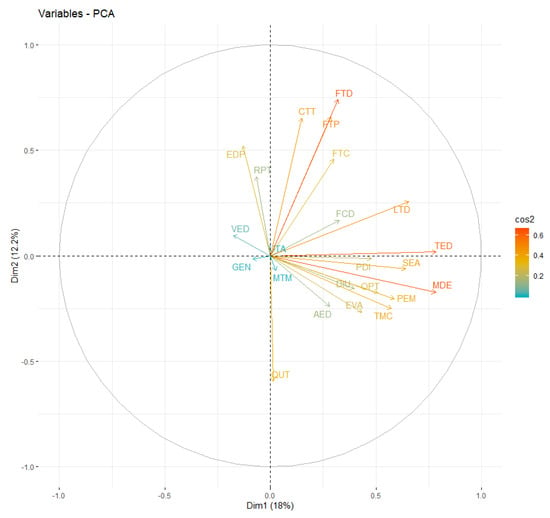
Figure 3.
Principal component analysis (PCA) for the research variables.
Items that are correlated with PC1 (Dim.1) and PC2 (Dim.2) are the most important in explaining the variability in the dataset. In Figure 2, we observe how positively correlated items tend to be grouped, as in the case of the technical knowledge needed to use technology (CTT); ICT training for teaching practice, personal use, and improving the curriculum (FTD, FTP, and FTC, respectively); continuous training in emerging technologies (FCD); the pedagogical use of technology (LTD); and the appropriate selection of technologies that improve approaches to teaching lessons (TED). Conversely, the teaching experience item (AED), which is negatively correlated with the previous ones, is located in opposite quadrants of the graph.
In contrast, there is a positive correlation between teaching experience (AED) and age (QUT); gender (GEN); the perception that methodological techniques are improvable (MTM); the use of virtual learning environments to teach mathematics classes (EVA); the selection of technologies in the classroom that improve the presentation of content (TMC); the mastery of English for the proper use of technology (DIU); the use of computers, laptops, tablets, etc., to learn or review mathematics (OPT); the use of educational platforms to teach math classes (PEM); the use of tools or software in the interactive digital whiteboard PDI; the use of educational software to teach mathematics classes (SEA); and the use of strategies that combine contents, technologies, and teaching approaches on which teachers have been trained (MDE).
The modulus of each vector measures the quality of these variables on the factor map. Variables with large moduli are clearly represented, such as ICT training for teaching practice (FTD); the selection of technologies that improve approaches to teaching lessons (TED); the pedagogical use of technology (LTD); and the use of strategies that combine contents, technologies, and teaching approaches on which teachers have been trained (MDE). The remaining variables that do not correlate with either PC1 or PC2, or that correlate with the other dimensions have a slight association. These factors include the use of a wide variety of teaching approaches in the classroom environment (VED); genre (GEN); the use of ICT resources (projectors, digital interactive whiteboards, etc.) to teach classes (UTA); and the perception that methodological techniques are improvable (MTM).
To obtain the results with greater robustness, non-metric multidimensional scaling (NMDS) analysis was carried out using the following steps:
- If there were no dependent variables, the metaMDS package was used, which is applicable to unsupervised regressions.
- The NMDS goodness of fit was multiplied by 200 for graphical representation.
The large dispersion around the red line (Figure 4a) suggests that the original differences are not well preserved in the small number of dimensions. In our case, the adjustment seems to be quite good, which is also indicated by the goodness-of-fit measures (Figure 4b).
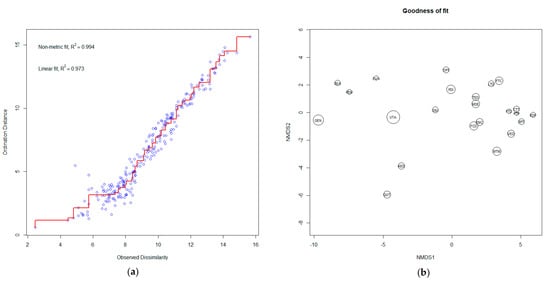
Figure 4.
Non-metric multidimensional scaling analysis (NMDS). (a) Linear fit; (b) Goodness-of-fit.
Figure 4 shows the NMDS analysis, which was executed with Python and compared with the PCA results (Figure 2). The results reveal that the R2 of the unsupervised regression model with this algorithm is high (99.4%). In turn, the variables that have the greatest weight in this study are FTD, TED, and MED. Similar findings were obtained with respect to the PCA.
Figure 5 shows PCA combined with a cluster analysis to determine which groups of variables form these clusters. As can be seen in this diagram, the groups are quite condensed. In this figure, we observe that all variables can be grouped into three clusters, i.e., the scores of the individuals can be segmented into three groups, each of which has a similar impact on the participants.
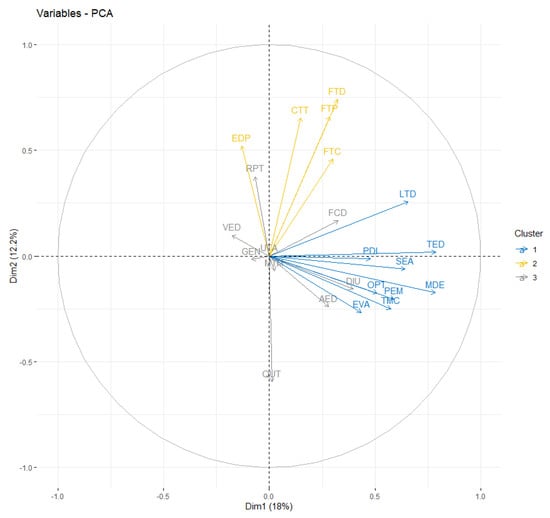
Figure 5.
Cluster classification (by color) of study items using PCA.
The first cluster contains most of the indicators of “C.2 ICT and teaching” and “C.3 ICT resources”. The results indicate that the application of ICT to teaching is in line with the use of ICT resources in the classroom. They also suggest that teachers used more software or applications (SEA, PEM, and EVA), than hardware or devices (UTA, OPT, and PDI). Teachers who combine technology with content generally use educational software (TMC), with educational platforms and technology that improve student learning. To a lesser extent, this is correlated with the use of computers in the classroom with virtual Moodle mathematics learning environments (EVA). We highlight the LTD position in different quadrants as compared with other elements in the same cluster.
In the second cluster, there is a significant correlation among the indicators “B.2 teaching practice”, “C.1 training”, and “D.5 ICT domain”. There is also an overall correlation between training for teaching and personal use (FTP and FTD), with a higher score in ICT training for teaching use. In addition, there is a significant correlation between these factors and training for curriculum improvement (FTC), although to a lesser extent. EDP is in the second quadrant, while the other items in the same cluster are grouped in the first quadrant.
The third cluster, which includes gender, age, and teaching experience, is more heterogeneous, encompassing several items of all the above indicators, and the relationships among them are of low significance. In addition, mathematics teachers did not link English learning to technologies (DIU) and declared that they barely used ICT resources in the classroom (e.g., the projector or digital interactive whiteboard) (UTA).
Figure 6 shows that gender is not grouped into clusters since it has a large dispersion in the four quadrants. In other words, gender has a low contribution to explaining the variability of the scores. For the purpose of comparison, an individual case analysis was applied to identify the scoring patterns (Figure 5). These show low redundancy, that is, a high dispersion of points, which does not show a clear differentiation between men (GEN-0) and women (GEN-1). Gender differences are observed in the first quadrant with 87.50% of men versus 12.50% of women. If the total sample is used, this result is not significant.
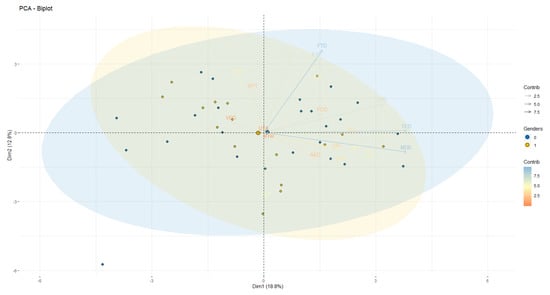
Figure 6.
PCA biplot. Score per individual, differentiated by gender.
4. Discussion
From the analysis of the linear correlations (Figure 2), very significant associations are observed among variables used in the indicator “ICT and teaching”. There are also correlations between training for personal and professional use, as well as a relationship between the use of platforms and educative software for the teaching of mathematics. Moreover, quite significant associations are evident between the mastery of ITC and its use to explore strategies for guiding students towards in learning mathematics. Accordingly, Avila et al. (2019) pointed out the importance of including methodological elements of mathematics didactics in the digital training of teachers.
From the analysis of PCA (Figure 3), the most representative variables are ICT training for the teaching function (FTD), the selection of teaching technologies (TED), and the use of materials and strategies that combine content and technologies (MDE). The results are in line with previous studies that claimed teachers used ICT to teach mathematics [53] and incorporated new methodological strategies [55]. In addition, ICTs make it possible to develop content more effectively as didactic support [93] and to distribute and share these resources online, thereby facilitating collaborative work [26,27,28].
The findings of this study show that most of the items of the indicators “ICT training”, “ICT and teaching”, and “ICT domain” are positively correlated. The relationships among these indicators shows us that mathematics teachers affirm that ICT training is indispensable for personal use (FTP), teaching practice (FTD), and the enrichment of their curriculum (FTC). In addition, they have the necessary technical knowledge to use ICT (CTT), which is manifested as digital competence (FCD), and the combination of technologies and teaching approaches for use in the classroom (TED and LTD).
In line with these results, the scientific literature posits that teachers, once the initial reservations have passed, emphasize the importance of expanding their knowledge of ICT tools for both personal and professional use and implementing methodological strategies in the classroom [55]. Similarly, Daniels et al. (2013) highlighted the relevance of methodological elements associated with the didactic of mathematics, considering technology to be a tool to optimize them but incapable of influencing the learning of students. Teachers who are trained in ICT also see improvements in self-efficiency and confidence with the use of technology [95], resulting in their interest in technology. ICT training also promotes and stimulates collaborative work amongst teachers [99].
In this study, we observe that a positive perception of the teacher toward ICT results in continuous training in technology and its use to explore new methodological strategies in the didactics of mathematics. In contrast, Melilla’s mathematics teachers generally present high digital competences, but they have a weak use of ICT in the classroom, with a conservative pedagogical attitude. This apparent contradiction in our results might be due to what teachers know by “digital competence” and its teaching applications in the classroom.
In the same line, Gudmundsdottir et al. (2018) and Pettersson et al. (2018) highlighted the ambiguity of the term “digital competence” proposing the existence of several digital competences and recommended differentiating among general and professional digital competence [65,66]. These authors argued that the professional teacher who was also digitally able must internalize ICTs, must be able to adapt them to the pedagogical environment and integrate them into a sociocultural context. For this purpose, a specific training is necessary, taking into consideration the level of competence according to a validated instrument [67].
Linear correlations are weakly significant between teaching experience and the use of resources that combine contents, ICT, and pedagogical approaches. In terms of age, there are negative, slightly significant correlations among age, the selection of effective teaching approaches to guide the thinking and learning of mathematics students, the knowledge needed to use technology, and training for personal and professional use.
PCA shows that teaching experience is negatively correlated with the selection of comprehensive and effective approaches to mathematics teaching and technical problem-solving (RPT).
Along the same line of argument, researchers have observed that teaching experience is negatively correlated with digital competence and extensive pedagogical use [87]. Other authors have argued that the constant evolution of technology and innovative pedagogies has caused teachers to remain perpetual apprentices, regardless of their experience [69,70]. However, Cardelli et al. (2004) asserted that sociocultural factors were conditions of teaching mathematics, while Chevalard et al. (1991) reported that institutional factors were influential.
Other noteworthy results are the positive correlation among teaching experience (AED) and teachers’ perception of the improvement of their methodological techniques (MTM), the selection of technologies (TMC), learning English for the proper use of ICT (DIU), and the use of virtual learning environments (EVA). In line with the above items, AED is associated with the use of classroom computers (OPT), educational platforms (PEM), educational software (SEA), and digital interactive whiteboards with the use of classroom materials that combine content and technologies (MDE). In addition, the mathematics teachers declared that they barely use ICT resources in the classroom, such as the projector or digital interactive whiteboards (UTA). When initially focusing on the relationships among UTA, PDI, and RPT, they appear to be contradictory.
A possible explanation of the low rating of PDI (the use of digital interactive whiteboards and specific software for the teaching of mathematics), could be the high ratio of classrooms in Melilla in secondary and post-16 education [94]. Along the same line, the findings of Cabus et al. (2017) suggested that when the ratio was low, significant improvements could be observed in mathematics students’ academic performance with the use of IWBs. In addition, Botuzova (2020) reported that the lack of use could be caused by the low digital competence of the students.
A deeper analysis of these results indicates that teachers with more experience have had limited ICT training, which conditions the use of digital resources in the classroom. They use platforms and educational software for content preparation, whereas they use hardware, typically PPs, for the presentation of such content [81]. The limited use of hardware is explained by the difficulty in resolving technical issues. Similarly, it is evident that the teaching experience is negatively correlated with digital competence, its integration and pedagogical use in the classroom, and motivation [87]. In contrast, a recent study noted that this was positively related to a teacher’s experience but not to their age [88]. This limited use has a negative impact on the interconnection and evaluation of student learning [86].
The comparative analysis between linear correlations and PCA shows that they produce similar results and both suggest that correlations with gender are weak. Individually, the two genders scored inversely in “I use a wide variety of teaching approaches in the classroom environment” (VED), “I consider my methodological techniques to be improved” (MTM), “I use educational platforms (Tutor Factory, Wepack, etc.) to teach mathematics” (PEM), and “I train and upgrade in digital competence (I keep up with important new technologies)” (FCD), that is, if men’s scores increased, women’s scores decreased. In the results of the study, no significant differences were observed among teachers with respect to the variables analyzed.
These findings are not in line with some previous research that reported a difference in perception between genders [89,90,91,92,93,94,95,96,97,98,99,100], which has been explained by the gender roles assumed and previous learning experiences [14]. Regarding the use of digital resources in the classroom, a recent study concluded that the relationship between perceived utility and the intention to use hardware was stronger for men than for women [14]. For this reason, it is necessary to implement training actions that reduce this perceived difference between men and women [4]. In addition, teacher training and training programs should be kept up-to-date and incorporate active methodological strategies in the classroom, such as gamification [50].
Finally, math teachers, according to the variables analyzed, can be grouped into three distinct clusters. The first relates mainly to technological resources, and it can be concluded that the use of technology in the teaching of mathematics is influenced by ICT resources in the classroom [5]. Along the same line, other authors have maintained that country investments on I+D were also factors to take into consideration [63].
The second cluster is largely associated with ICT training and shows a significant relation among digital competences, ICT training, and efficient pedagogical approaches to the teaching of mathematics. Similarly, Nousiainen et al. (2018), maintained that a teacher´s training in ICT was conducive to the skill and practice of new active methodologies. However, other authors have claimed that both a continuous training in specific software for teaching mathematics [53] and pedagogical strategies with ICT condition the use of technology by the mathematics teachers [54,55].
The third cluster is a heterogeneous mixture of variables with different weights in this study. Items with low weights are gender, the use of hardware in the classroom, and teaching practice self-evaluation. In contrast, the teachers´ marks in this group are high in their capacity to resolve technical problems, continuous training in ICT, and English learning. This provides relevant information on teacher classification in relation to their ICT knowledge and uses, which is necessary to design effective training programs [101].
5. Conclusions
The general perception of Melilla´s mathematics teachers about their own digital competence does not match with traditional pedagogical models employed in the classroom. Consequently, this difference negatively influences their training in digital skills. Therefore, it would be recommendable to assess the digital competence of mathematics teachers using a validated instrument.
Less experienced teachers were better trained in ICT and employed it in a broad sense. Among these teachers, no general differences were observed based on gender. Grouping the study items into three clusters allowed us to identify profiles of mathematics teachers and design specific ad hoc actions to improve their professional competences.
The limitations of the study were associated with the cross-sectional design that was employed, i.e., data from participants were collected at a specific place and time, but the scores of the analyzed variables could vary over time. Similarly, another limitation of this study was that the items in the questionnaire affected only the “use” of technology and did not address questions about “how” that technology was used. The strengths lie in the statistical approach used to determine the relationships among the different items in this study.
On the basis of these results, several lines of future research are proposed in relation to teaching practices in an aim to clarify which variables are influential, and then to quantify their effect. We also recommend expanding the items of teachers’ perceptions regarding their training and the evaluation of the teaching function. A broader and more in-depth study that captures functional differentiation is necessary to establish a comprehensive instrument that evaluates the teaching function with the contribution of all the agents of the educational community involved (teachers, students, parents, etc.). Other possible lines of research include quantifying the impact of ICTs on the teaching function and the performance of students.
Author Contributions
Conceptualization, H.H.-M. (Hossein Hossein-Mohand) and M.G.-G.; methodology, H.H.-M. (Hossein Hossein-Mohand) and J.M.T.-T.; software, H.H.-M. (Hassan Hossein-Mohand); validation, H.H.-M. (Hassan Hossein-Mohand), M.G.-G., and J.M.T.-T.; formal analysis, M.G.-G. investigation, H.H.-M. (Hossein Hossein-Mohand); resources, H.H.-M. (Hossein Hossein-Mohand); data curation, H.H.-M. (Hossein Hossein-Mohand); writing—original draft preparation, H.H.-M. (Hossein Hossein-Mohand); writing—review and editing, H.H.-M. (Hossein Hossein-Mohand) and J.M.T.-T.; visualization, M.G.-G.; supervision, M.G.-G., J.M.T.-T. and H.H.-M. (Hassan Hossein-Mohand). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alonso-Garcia, S.; Aznar-Diaz, I.; Caceres-Reche, M.P.; Trujillo-Torres, J.M.; Romero-Rodriguez, J.M. Systematic Review of Good Teaching Practices with ICT in Spanish Higher Education. Trends and Challenges for Sustainability. Sustainability 2019, 11, 7150. [Google Scholar] [CrossRef]
- Fernandes, G.W.R.; Rodrigues, A.M.; Ferreira, C.A. Professional development and use of digital technologies by science teachers: A review of theoretical frameworks. Res. Sci. Educ. 2018, 50, 1–36. [Google Scholar] [CrossRef]
- Ahmad, N.; Hoda, N.; Alahmari, F. Developing a Cloud-Based Mobile Learning Adoption Model to Promote Sustainable Education. Sustainability 2020, 12, 3126. [Google Scholar] [CrossRef]
- Prendes-Espinosa, M.-P.; Garcia-Tudela, P.-A.; Solano-Fernandez, I.-M. Gender equality and ICT in the context of formal education: A systematic review. Comunicar 2020, 28, 9–20. [Google Scholar] [CrossRef]
- Gui, M.; Parma, A.; Comi, S. Does Public Investment in ICTs Improve Learning Performance? Evidence from Italy. Policy Internet 2018, 10, 141–163. [Google Scholar] [CrossRef]
- INE. Estadística de la Sociedad de la Información y la Comunicación en los Centros Educativos no Universitarios. Curso 2018–2019; Instituto Nacional de Estadística: Madrid, Spain, 2020.
- Nevado Pena, D.; Lopez Ruiz, V.R.; Alfaro Navarro, J.L. An analysis of the key role of human and technological development in the smart specialization of smart European regions. Inf. Technol. Dev. 2019. [Google Scholar] [CrossRef]
- Griffith, S.F.; Hagan, M.B.; Heymann, P.; Heflin, B.H.; Bagner, D.M. Apps as Learning Tools: A Systematic Review. Pediatrics 2020, 145. [Google Scholar] [CrossRef]
- Dalby, D. Professional learning through collaborative research in mathematics. Prof. Dev. Educ. 2019, 15. [Google Scholar] [CrossRef]
- Andersen, S.C.; Beuchert, L.; Nielsen, H.S.; Thomsen, M.K. The Effect of Teacher’s Aides in the Classroom: Evidence from a Randomized Trial. J. Eur. Econ. Assoc. 2020, 18, 469–505. [Google Scholar] [CrossRef]
- Mikropoulos, T.A. Research on E-Learning and ICT in Education: Technological, Pedagogical and Instructional Perspectives; Springer: Berlin, Germany, 2018. [Google Scholar]
- Alemayehu, G.; Natarajan, M. Impact of ICT facility on student’s academic performance in Jimma University, Ethiopia. Int. J. Inf. Dissem. Technol. 2018, 8, 136–142. [Google Scholar] [CrossRef][Green Version]
- Guillén-Gámez, F.D.; Mayorga-Fernández, M.J. Identification of Variables that Predict Teachers’ Attitudes toward ICT in Higher Education for Teaching and Research: A Study with Regression. Sustainability 2020, 12, 1312. [Google Scholar] [CrossRef]
- Chen, I.H.; Gamble, J.H.; Lee, Z.-H.; Fu, Q.-L. Formative assessment with interactive whiteboards: A one-year longitudinal study of primary students’ mathematical performance. Comp. Educ. 2020, 150. [Google Scholar] [CrossRef]
- Mercader, C. Explanatory model of barriers to integration of digital technologies in higher education institutions. Educ. Inf. Technol. 2020. [Google Scholar] [CrossRef]
- Podolsky, A.; Kini, T.; Darling-Hammond, L. Does teaching experience increase teacher effectiveness? A review of US research. J. Prof. Cap. Community 2019, 4, 286–308. [Google Scholar] [CrossRef]
- Sánchez-Prieto, J.C.; Huang, F.; Olmos-Miguelanez, S.; Garcia-Penalvo, F.J.; Teo, T. Exploring the unknown: The effect of resistance to change and attachment on mobile adoption among secondary pre-service teachers. Br. J. Educ. Technol. 2019, 50, 2433–2449. [Google Scholar] [CrossRef]
- Gispert, H. Mathematics education in France: 1800–1980. In Handbook on the History of Mathematics Education; Springer: Berlin, Germany, 2014; pp. 229–240. [Google Scholar]
- Flegas, K.; Charalampos, L. Exploring Logical Reasoning and Mathematical Proof in Grade 6 Elementary School Students. Can. J. Sci. Math. Technol. Educ. 2013, 13, 70–89. [Google Scholar] [CrossRef]
- Butlen, D.; Masselot, P. Challenges and modalities of formation for the teachers of the schools in didactics of mathematics. Can. J. Sci. Math. Technol. Educ. 2019, 19, 91–106. [Google Scholar] [CrossRef]
- Chevallard, Y. La Transposición Didáctica, 2ª Reimp; Aique Grupo Editor: Buenos Aires, Argentina, 2005. [Google Scholar]
- Chevallard, Y. La Transposición Didáctica, Del Saber Sabio al Saber Enseñado; Aique Grupo Editor: Buenos Aires, Argentina, 1991; Volume 3. [Google Scholar]
- Cardelli, J. Reflexiones críticas sobre el concepto de Transposición Didáctica de Chevallard. Cuad. Antropol. Soc. 2004. [Google Scholar] [CrossRef]
- Brousseau, G. The Study of the Didactical Conditions of School Learning in Mathematics. In Activity Sign; Springer: Boston, MA, USA, 2005; pp. 159–168. [Google Scholar] [CrossRef]
- Trouche, L.; Monaghan, J.; Borwein, J.M. Didactics of Mathematics: Concepts, Roots, Interactions and Dynamics from France; Springer: Berlin, Germany, 2016; Volume 110, pp. 219–256. [Google Scholar]
- Ferraro, S. Is information and communication technology satisfying educational needs at school? Comp. Educ. 2018, 122, 194–204. [Google Scholar] [CrossRef]
- Konnova, L.; Lipagina, L.; Postovalova, G.; Rylov, A.; Stepanyan, I. Designing Adaptive Online Mathematics Course Based on Individualization Learning. Educ. Sci. 2019, 9, 182. [Google Scholar] [CrossRef]
- Mora, H.; Signes-Pont, M.T.; Fuster-Guillo, A.; Pertegal-Felices, M.L. A collaborative working model for enhancing the learning process of science & engineering students. Comp. Human Behav. 2020, 103, 140–150. [Google Scholar] [CrossRef]
- Sánchez-Prieto, J.; Trujillo-Torres, J.M.; Gómez-García, M.; Gómez-García, G. Gender and Digital Teaching Competence in Dual Vocational Education and Training. Educ. Sci. 2020, 10, 84. [Google Scholar] [CrossRef]
- Hershkovitz, A.; Baruch, A.F. La relación profesor-alumno y la comunicación en Facebook: Percepciones de los alumnos. Comunicar: Rev. Cient. Iberoam. Comun. Educ. 2017, 53, 91–101. [Google Scholar]
- Trouche, L.; Rocha, K.; Gueudet, G.; Pepin, B. Transition to digital resources as a critical process in teachers’ trajectories: The case of Anna’s documentation work. Zdm-Math. Educ. 2020. [Google Scholar] [CrossRef]
- Moreno-Armella, L.; Hegedus, S. From static to dynamic mathematics: Historical and representational perspectives. In The SimCalc Vision and Contributions; Springer: Berlin, Germany, 2013; pp. 27–45. [Google Scholar]
- Moyer-Packenham, P.S.; Westenskow, A. Effects of virtual manipulatives on student achievement and mathematics learning. Int. J. Virtual Pers. Learn. Environ. 2013, 4, 35–50. [Google Scholar] [CrossRef]
- Fiorella, L.; Kuhlmann, S.; Vogel-Walcutt, J.E.J. Effects of Playing an Educational Math Game That Incorporates Learning by Teaching. J. Educ. Comp. Res. 2019, 57, 1495–1512. [Google Scholar] [CrossRef]
- Gomez, T.; Moron, C.; Ferrandez, D.; Saiz, P.; Garrido, R. Gamification in the Education: The Benefits of Learning through Play. In Proceedings of the Inted2017: 11th International Technology, Education and Development Conference, Valencia, Spain, 6–8 March 2017; pp. 1051–1060. [Google Scholar]
- Sinclair, N. Generations of research on new technologies in mathematics education. Teach. Math. Appl.: Int. J. IMA 2014, 33, 166–178. [Google Scholar] [CrossRef]
- Birgin, O.; Acar, H. The effect of computer-supported collaborative learning using GeoGebra software on 11th grade students’ mathematics achievement in exponential and logarithmic functions. Int. J. Math. Educ. Sci. Technol. 2020. [Google Scholar] [CrossRef]
- Angeli, C.; Giannakos, M. Computational thinking education: Issues and challenges. Comp. Human Behav. 2020, 105. [Google Scholar] [CrossRef]
- DeJarnette, A.F. Students’ challenges with symbols and diagrams when using a programming environment in mathematics. Digit. Exp. Math. Educ. 2019, 5, 36–58. [Google Scholar] [CrossRef]
- Korkmaz, Ö. The effect of scratch-and lego mindstorms Ev3-Based programming activities on academic achievement, problem-solving skills and logical-mathematical thinking skills of students. Malays. Online J. Educ. Sci. 2018, 4, 73–88. [Google Scholar]
- Smith, C.P.; Neumann, M.D. Scratch it out! Enhancing geometrical understanding. Teach. Child. Math. 2014, 21, 185–188. [Google Scholar] [CrossRef]
- Anderson-Pence, K.L. Examining the Impact of DIfferent Virtual Manipulative Types on the Nature of Students’ SMall-Group Discussions: An Exploratory Mixed-Methods Case Study of Techno-Mathematical Discourse. Ph.D. Thesis, Utah State University, Logan, UT, USA, 2014. [Google Scholar]
- Liu, Q.; Geertshuis, S.; Grainger, R. Understanding academics’ adoption of learning technologies: A systematic review. Comp. Educ. 2020, 151. [Google Scholar] [CrossRef]
- Semerci, A.; Aydin, M.K. Examining High School Teachers’ Attitudes towards ICT Use in Education. Int. J. Prog. Educ. 2018, 14, 93–105. [Google Scholar] [CrossRef]
- Silva, J.B.; Silva, I.N.; Bilessimo, S. Technological Structure for Technology Integration in the Classroom, Inspired by the Maker Culture. J. Inf. Technol. Educ.-Res. 2020, 19, 167–204. [Google Scholar] [CrossRef]
- Lavicza, Z.; Prodromou, T.; Fenyvesi, K.; Hohenwarter, M.; Juhos, I.; Koren, B.; Diego-Mantecon, J.M. Integrating STEM-related Technologies into Mathematics Education at a Large Scale. Int. J. Technol. Math. Educ. 2020, 27, 3–11. [Google Scholar] [CrossRef]
- Baya’a, N.; Daher, W.; Anabousy, A. The Development of In-Service Mathematics Teachers’ Integration of ICT in a Community of Practice: Teaching-in-Context Theory. Int. J. Emerg. Technol. Learn. 2019, 14, 125–139. [Google Scholar] [CrossRef]
- Hsu, L.W.; Chen, Y.J. Examining teachers’ technological pedagogical and content knowledge in the era of cloud pedagogy. S. Afr. J. Educ. 2019, 39. [Google Scholar] [CrossRef]
- Avila, C.M.V.; Borges, A.L.A. The Process of Teaching-Learning of the Didactics of the Mathematics from the Science, Technology and Society Approach. Rev. Conrado 2019, 15, 259–262. [Google Scholar]
- Nousiainen, T.; Kangas, M.; Rikala, J.; Vesisenaho, M. Teacher competencies in game-based pedagogy. Teach. Teacher Educ. 2018, 74, 85–97. [Google Scholar] [CrossRef]
- McCulloch, A.W.; Hollebrands, K.; Lee, H.; Harrison, T.; Mutlu, A. Factors that influence secondary mathematics teachers’ integration of technology in mathematics lessons. Comp. Educ. 2018, 123, 26–40. [Google Scholar] [CrossRef]
- Gómez-García, M.; Soto-Varela, R.; Morón-Marchena, J.A.; del Pino-Espejo, M.J. Using Mobile Devices for Educational Purposes in Compulsory Secondary Education to Improve Student’s Learning Achievements. Sustainability 2020, 12, 3724. [Google Scholar]
- Zbiek, R.M. Contemporary Framing of Technology in Mathematics Teaching. In Educating Prospective Secondary Mathematics Teachers: Knowledge, Identity, and Pedagogical Practices; Strutchens, M.E., Huang, R., Potari, D., Losano, L., Eds.; Springer International Publishing Ag: Cham, Switzerland, 2018; pp. 109–124. [Google Scholar]
- Hinojo Lucena, F.J.; López Belmonte, J.; Fuentes Cabrera, A.; Trujillo Torres, J.M.; Pozo Sánchez, S. Academic effects of the use of flipped learning in physical education. Int. J. Environ. Res. Public Health 2020, 17, 276. [Google Scholar] [CrossRef] [PubMed]
- Zahorec, J.; Nagyova, A.; Haskova, A. Teachers’ Attitudes to Incorporation Digital Means in Teaching Process in Relation to the Subjects They Teach. Int. J. Eng. Pedag. 2019, 9, 101–120. [Google Scholar] [CrossRef]
- Ozudogru, M. The Factors Predicting Pre-Service Teachers’ Achievement in Teacher Training Classrooms. Eurasian J. Educ. Res. 2020, 87, 157–178. [Google Scholar] [CrossRef]
- Galimullina, E.; Ljubimova, E.; Ibatullin, R. SMART education technologies in mathematics teacher education—Ways to integrate and progress that follows integration. Open Learn. 2020, 35, 4–23. [Google Scholar] [CrossRef]
- Holdsworth, S.; Maynes, N. “But What If I Fail?” A Meta-Synthetic Study of the Conditions Supporting Teacher Innovation. Can. J. Educ./Revue Can. L’Éduc. 2017, 40, 665–703. [Google Scholar]
- Fernández Batanero, J.M.; López Meneses, E.; Cabero Almenara, J. Knowledge and degree of training of primary education teachers in relation to ICT taught to disabled students. Br. J. Educ. Technol. 2019, 50, 1961–1978. [Google Scholar] [CrossRef]
- Burke, P.F.; Schuck, S.; Aubusson, P.; Kearney, M.; Frischknecht, B. Exploring teacher pedagogy, stages of concern and accessibility as determinants of technology adoption. Technol. Pedag. Educ. 2018, 27, 149–163. [Google Scholar] [CrossRef]
- Gordon, A.; Young-Jones, A.; Hayden, S.; Fursa, S.; Hart, B. Dispositional mindfulness, perceived social support, and academic motivation: Exploring differences between Dutch and American students. New Ideas Psychol. 2020, 56. [Google Scholar] [CrossRef]
- Lazarides, R.; Gaspard, H.; Dicke, A.-L. Dynamics of classroom motivation: Teacher enthusiasm and the development of math interest and teacher support. Learn. Instr. 2019, 60, 126–137. [Google Scholar] [CrossRef]
- Ma, J.K.H.; Vachon, T.E.; Cheng, S. National Income, Political Freedom, and Investments in R&D and Education: A Comparative Analysis of the Second Digital Divide Among 15-Year-Old Students. Soc. Indic. Res. 2019, 144, 133–166. [Google Scholar] [CrossRef]
- INTEF. Competencia Digital Docente Septiembre 2017; INTEF: Madrid, Spain, 2017. [Google Scholar]
- Gudmundsdottir, G.B.; Hatlevik, O.E. Newly qualified teachers’ professional digital competence: Implications for teacher education. Eur. J. Teacher Educ. 2018, 41, 214–231. [Google Scholar] [CrossRef]
- Pettersson, F. On the issues of digital competence in educational contexts—A review of literature. Educ. Inf. Technol. 2018, 23, 1005–1021. [Google Scholar] [CrossRef]
- Touron, J.; Martin, D.R.; Navarro Asencio, E.; Pradas, S.; Inigo, V. Construct validation of a questionnaire to measure teachers’ digital competence (TDC). Rev. Esp. Pedag. 2018, 76, 25–54. [Google Scholar] [CrossRef]
- Presby, R.E. Barriers to Reducing the Digital-Use Divide as Perceived by Middle School Principals. Ph.D. Thesis, Brandmane University, Irvine, CA, USA, 2017. [Google Scholar]
- Engen, B.K. Understanding social and cultural aspects of teachers’ digital competencies. Comunicar 2019, 27, 9–19. [Google Scholar] [CrossRef]
- Daniels, J.; Jacobsen, M.; Varnhagen, S.; Friesen, S. Barriers to systemic, effective, and sustainable technology use in high school classrooms. Can. J. Learn. Technol./Revue Can. L’Apprentissage Technol. 2013, 39. [Google Scholar] [CrossRef]
- OECD. Panorama de la Educación 2015: Indicadores de la OCDE; Organisation for Economic Co-Operation and Development: Paris, France, 2016. [Google Scholar]
- Çekmez, E. Using dynamic mathematics software to model a real-world phenomenon in the classroom. Interact. Learn. Environ. 2019, 28, 526–538. [Google Scholar] [CrossRef]
- Acikgul, K.; Aslaner, R. Effects of Geogebra supported micro teaching applications and technological pedagogical content knowledge (TPACK) game practices on the TPACK levels of prospective teachers. Educ. Inf. Technol. 2020, 25, 2023–2047. [Google Scholar] [CrossRef]
- Donnelly-Hermosillo, D.F.; Gerard, L.F.; Linn, M.C. Impact of graph technologies in K-12 science and mathematics education. Comp. Educ. 2020, 146. [Google Scholar] [CrossRef]
- Verschaffel, L.; Depaepe, F.; Mevarech, Z. Learning Mathematics in Metacognitively Oriented ICT-Based Learning Environments: A Systematic Review of the Literature. Educ. Res. Int. 2019, 2019. [Google Scholar] [CrossRef]
- Garcia, F.Y.H.; Rangel, E.G.H.; Mera, N.A.G. Gamification in mathematics education: A systematic review. Telos-Rev. Interdiscip. Cienc. Soc. 2020, 22, 62–75. [Google Scholar] [CrossRef]
- Esfijani, A.; Zamani, B.E. Factors influencing teachers’ utilisation of ICT: The role of in-service training courses and access. Res. Learn. Technol. 2020, 28. [Google Scholar] [CrossRef]
- Botuzova, Y.V. Experience of Using ICT Tools for Teaching Mathematical Analysis to Future Teachers of Mathematics. Inf. Technol. Learn. Tools 2020, 75, 153–169. [Google Scholar]
- Roanes-Lozano, E.; Galan-Garcia, J.L.; Solano-Macias, C. Some Reflections About the Success and Impact of the Computer Algebra System DERIVE with a 10-Year Time Perspective. Math. Comp. Sci. 2019, 13, 417–431. [Google Scholar] [CrossRef]
- Nunes, P.S.; Nascimento, M.M.; Catarino, P.; Martins, P. Factors that Influence the Use of Educational Software in Mathematics Teaching. Rev. Iberoam. Sobre Calid. Efic. Cambio Educ. 2020, 18, 113–129. [Google Scholar] [CrossRef]
- Kearney, M.; Schuck, S.; Aubusson, P.; Burke, P.F. Teachers’ technology adoption and practices: Lessons learned from the IWB phenomenon. Teacher Dev. 2018, 22, 481–496. [Google Scholar] [CrossRef]
- Cabus, S.J.; Haelermans, C.; Franken, S. SMART in Mathematics? Exploring the effects of in-class-level differentiation using SMART board on math proficiency. Br. J. Educ. Technol. 2017, 48, 145–161. [Google Scholar] [CrossRef]
- Drijvers, P. Empirical Evidence for Benefit? Reviewing Quantitative Research on the Use of Digital Tools in Mathematics Education. In Uses of Technology in Primary and Secondary Mathematics Education—Tools, Topics and Trends; Ball, L., Ladel, S., Tabach, M., Drijvers, P., Siller, H.S., Vale, C., Eds.; Springer: Berlin, Germany, 2018; pp. 161–175. [Google Scholar]
- Salles, F.; Dos Santos, R.; Keskpaik, S. When didactics meet data science: Process data analysis in large-scale mathematics assessment in France. Large-Scale Assess. Educ. 2020, 8. [Google Scholar] [CrossRef]
- Aflalo, E.; Zana, L.; Huri, T. The interactive whiteboard in primary school science and interaction. Interact. Learn. Environ. 2018, 26, 525–538. [Google Scholar] [CrossRef]
- Li, Y.; Yang, H.H.; MacLeod, J. Preferences toward the constructivist smart classroom learning environment: Examining pre-service teachers’ connectedness. Interact. Learn. Environ. 2019, 27, 349–362. [Google Scholar] [CrossRef]
- Hsu, C.-Y.; Tsai, M.-J.; Chang, Y.-H.; Liang, J.-C. Surveying in-service teachers’ beliefs about game-based learning and perceptions of technological pedagogical and content knowledge of games. J. Educ. Technol. Soc. 2017, 20, 134–143. [Google Scholar]
- Spiteri, M.; Rundgren, S.-N.C. Literature Review on the Factors Affecting Primary Teachers’ Use of Digital Technology. Technol. Knowl. Learn. 2020, 25, 115–128. [Google Scholar] [CrossRef]
- Hatlevik, O.E.; Throndsen, I.; Loi, M.; Gudmundsdottir, G.B. Students’ ICT self-efficacy and computer and information literacy: Determinants and relationships. Comp. Educ. 2018, 118, 107–119. [Google Scholar] [CrossRef]
- Cussó-Calabuig, R.; Farran, X.C.; Bosch-Capblanch, X. Effects of intensive use of computers in secondary school on gender differences in attitudes towards ICT: A systematic review. Educ. Inf. Technol. 2018, 23, 2111–2139. [Google Scholar] [CrossRef]
- Bosch, H.E.; Bergero, M.S.; Nasso, C.; Pérez, M.M.; Rampazzi, M.C. Innovaciones didácticas para ciencias y matemática asistida por TIC. TE ET 2017, 19, 60–64. [Google Scholar]
- De Vita, M.; Verschaffel, L.; Elen, J. Towards a better understanding of the potential of interactive whiteboards in stimulating mathematics learning. Learn. Environ. Res. 2018, 21, 81–107. [Google Scholar] [CrossRef]
- Loong, E.Y.-K.; Herbert, S. Primary school teachers’ use of digital technology in mathematics: The complexities. Math. Educ. Res. J. 2018, 30, 475–498. [Google Scholar] [CrossRef]
- Consejo Escolar del Estado. Informe 2019 Sobre el Estado del Sistema Educativo; Ministerio de Educación y Formación Profesional: Madrid, Spain, 2019.
- Kim, H.-K. Meta analysis on the improvement of academic performance by the teaching method for underachievers of learning mathematics. Math. Educ. 2020, 59, 31–45. [Google Scholar]
- Vallés Martínez, M.S.; D’Ancona, C.; Angeles, M.; Izquierdo Escribano, A. Las Encuestas Sobre Inmigración en España y en Europa. Tópicos, Medios de Comunicación y Política Migratoria; Informe sobre els gitanos romanesos a Barcelona Inédito; Ministerio de Trabajo y Asuntos Sociales, Observatorio Permanente de la Inmigración: Madrid, Spain; Vincle: Barcelona, Spain, 1999.
- Cisneros-Cohernour, E.J.; Jorquera Jaramillo, M.C.; Aguilar Pereyra, Á.M. Validación de instrumentos de evaluación docente en el contexto de una universidad española. Voces Silenc. Rev. Latinoam. Educ. 2012, 3, 41–55. [Google Scholar] [CrossRef]
- Rosenbluth, A.; Cruzat-Mandich, C.; Ugarte, M.L. Methodology to Validate a Competencies Assessment Tool for Psychology Students. Univ. Psychol. 2016, 15, 303–314. [Google Scholar]
- Dalby, D.; Swan, M. Using digital technology to enhance formative assessment in mathematics classrooms. Br. J. Educ. Technol. 2019, 50, 832–845. [Google Scholar] [CrossRef]
- Park, J.-H.; Kim, C.; Ham, J. High-school students’ understanding and use of mathematics textbooks. Math. Educ. 2019, 58, 589–607. [Google Scholar]
- Wyss, C.; Rosenberger, K.; Buehrer, W. Student Teachers’ and Teacher Educators’ Professional Vision: Findings from an Eye Tracking Study. Educ. Psychol. Rev. 2020. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).