Semi-Local Analysis and Real Life Applications of Higher-Order Iterative Schemes for Nonlinear Systems
Abstract
1. Introduction
2. Semi-Local Convergence
- (H1)
- Let be a continuous operator that is Fréchet differentiable at some with .
- (H2)
- There exists a divided difference of order one .
- (H3)
- There exist and such that for each
- (H4)
- There exist functions , continuous and nondecreasing with
3. Numerical Results
- A processor Intel(R) Core (TM) i5-3210M (Intel, Santa Clara, CA, USA)
- CPU @ 2.50 GHz (64-bit machine) (Intel, Santa Clara, CA, USA)
- Microsoft Windows 8 (Microsoft Corporation, Albuquerque, NM, USA).
4. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ezquerro, J.A.; Grau-Sánchez, M.; Hernández-veron, M.A.; Noguera, M. A family of iterative methods that uses divided differences of first and second orders. Numer. Algor. 2015, 70, 571–589. [Google Scholar] [CrossRef]
- Grau-Sánchez, M.; Noguera, M. Frozen divided difference scheme for solving system of nonlinear equations. J. Comput. Appl. Math. 2011, 235, 1739–1743. [Google Scholar] [CrossRef]
- Ortega, J.M.; Rheinboldt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Ostrowski, A.M. Solutions of Equations and System of Equations; Academic Press: New York, NY, USA, 1960. [Google Scholar]
- Petković, M.S. Remarks on On a general class of multipoint root finding methods of high computational efficiency. SIAM J. Numer. Anal. 2011, 49, 1317–1319. [Google Scholar] [CrossRef]
- Potra, F.A.; Pták, V. Nondiscrete Introduction and Iterative Process; (Research Notes in Mathematics); Pitman Advanced Pub. Program: Roma, Italy, 1984. [Google Scholar]
- Amat, S.; Busquier, S.; Plaza, S. Dynamics of the King and Jarratt iterations. Aequationes Math. 2005, 69, 212–223. [Google Scholar] [CrossRef]
- Amat, S.; Busquier, S.; Plaza, S. Chaotic dynamics of a third-order Newton-type method. J. Math. Anal. Appl. 2010, 366, 24–32. [Google Scholar] [CrossRef]
- Amat, S.; Hernández, M.A.; Romero, N. A modified Chebyshev’s iterative method with at least sixth order of convergence. Appl. Math. Comput. 2008, 206, 164–174. [Google Scholar] [CrossRef]
- Argyros, I.K. Convergence and Application of Newton-Type Iterations; Springer: New York, NY, USA, 2008. [Google Scholar]
- Argyros, I.K.; Hilout, S. Computational Methods in Nonlinear Analysis; World Scientific Publishing Company: Hackensack, NJ, USA, 2013. [Google Scholar]
- Argyros, I.K.; George, S.; Magrenan, A.A. Local convergence for multi-point-parametric Chebyshev-Halley-type methods of high convergence order. J. Comput. Appl. Math. 2015, 282, 215–224. [Google Scholar] [CrossRef]
- Behl, R.; Kanwar, V.; Sharma, K.K. Optimal equi-scaled families of Jarratt’s method. Int. J. Comput. Math. 2013, 290, 408–422. [Google Scholar] [CrossRef]
- Ezquerro, J.A.; Hernández, M.A. New iterations of R-order four with reduced computational cost. BIT Numer. Math. 2009, 49, 325–342. [Google Scholar] [CrossRef]
- Kelley, C.T. Solving Nonlinear Equations with Newton’s Method; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar]
- Wang, X.; Zhang, T.; Qian, W.; Teng, M. Seventh-order derivative-free iterative method for solving nonlinear systems. Numer. Algor. 2015, 70, 545–558. [Google Scholar] [CrossRef]
- Traub, J.F. Iterative Method for the Solution of Equations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1964. [Google Scholar]
- Grau-Sánchez, M.; Noguera, M.; Amat, S. On the approximation of derivatives using divided difference operators preserving the local convergence order of iterative methods. J. Comput. Appl. Math. 2013, 237, 363–372. [Google Scholar] [CrossRef]
- Grau-Sánchez, M.; Noguera, M.; Diaz-Barrero, J.L. On the local convergence of a family of two-step iterative methods for solving nonlinear equations. J. Comput. Appl. Math. 2014, 255, 753–764. [Google Scholar] [CrossRef]
- Steffensen, J.F. Remarks on iteration. Skand. Aktuar. Tidskr 1933, 16, 64–72. [Google Scholar] [CrossRef]
- Bhalla, S.; Kumar, S.; Argyros, I.K.; Behl, R. A family of higher order derivative free methods for nonlinear systems with local convergence analysis. Comput. Appl. Math. 2018, 37, 5807–5827. [Google Scholar] [CrossRef]
- Aizenshtein, M.; Bartoň, M.; Elber, G. Global solutions of well-constrained transcendental systems using expression trees and a single solution test. Comput. Aided Geom. Des. 2012, 29, 265–279. [Google Scholar] [CrossRef]
- Van Sosin, B.; Elber, G. Solving piecewise polynomial constraint systems with decomposition and a subdivision-based solver. Comput. Aided Des. 2017, 90, 37–47. [Google Scholar] [CrossRef]
- Bartoň, M. Solving polynomial systems using no-root elimination blending schemes. Comput. Aided Des. 2011, 43, 1870–1878. [Google Scholar] [CrossRef]
- Sharma, J.R.; Arora, H. An efficient derivative free iterative method for solving systems of nonlinear equations. Appl. Anal. Discrete Math. 2013, 7, 390–403. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, T. A family of Steffensen-type methods with seventh-order convergence. Numer. Algor. 2013, 62, 429–444. [Google Scholar] [CrossRef]
- Wolfram, S. The Mathematica Book, 5th ed.; Wolfram Media: Champaign, IL, USA, 2003. [Google Scholar]
- Gelfand, I.M. Some problems in the theory of quasi-linear equations. Trans. Amer. Math. Soc. Ser. 1963, 2, 295–381. [Google Scholar]
- Jacobsen, J.; Schmitt, K. The Liouville Bratu Gelfand problem for radial operators. J. Differ. Equ. 2002, 184, 283–298. [Google Scholar] [CrossRef]
- Jalilian, R. Non-polynomial spline method for solving Bratu’s problem. Comput. Phys. Commun. 2010, 181, 1868–1872. [Google Scholar] [CrossRef]
- Wan, Y.Q.; Guo, Q.; Pan, N. Thermo-electro-hydrodynamic model for electrospinning process. Int. J. Nonlinear Sci. Numer. Simul. 2004, 5, 5–8. [Google Scholar] [CrossRef]
- Kapania, R.K. A pseudo-spectral solution of 2-parameter Bratu’s equation. Comput. Mech. 1990, 6, 55–63. [Google Scholar] [CrossRef]
- Simpson, R.B. A method for the numerical determination of bifurcation states of nonlinear systems of equations. SIAM J. Numer. Anal. 1975, 12, 439–451. [Google Scholar] [CrossRef]
- Sauer, T. Numerical Analysis, 2nd ed.; Pearson: London, UK, 2012. [Google Scholar]
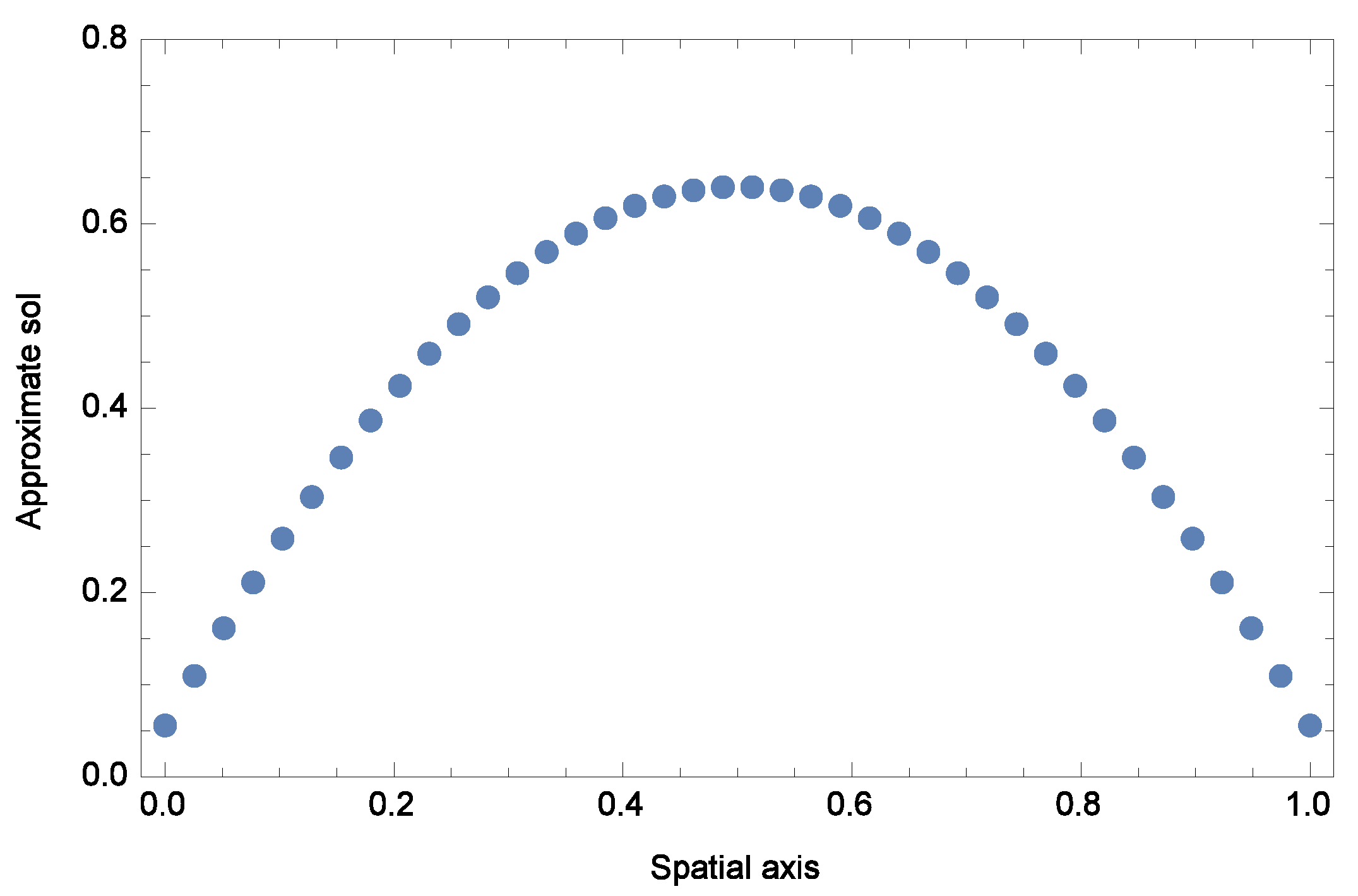
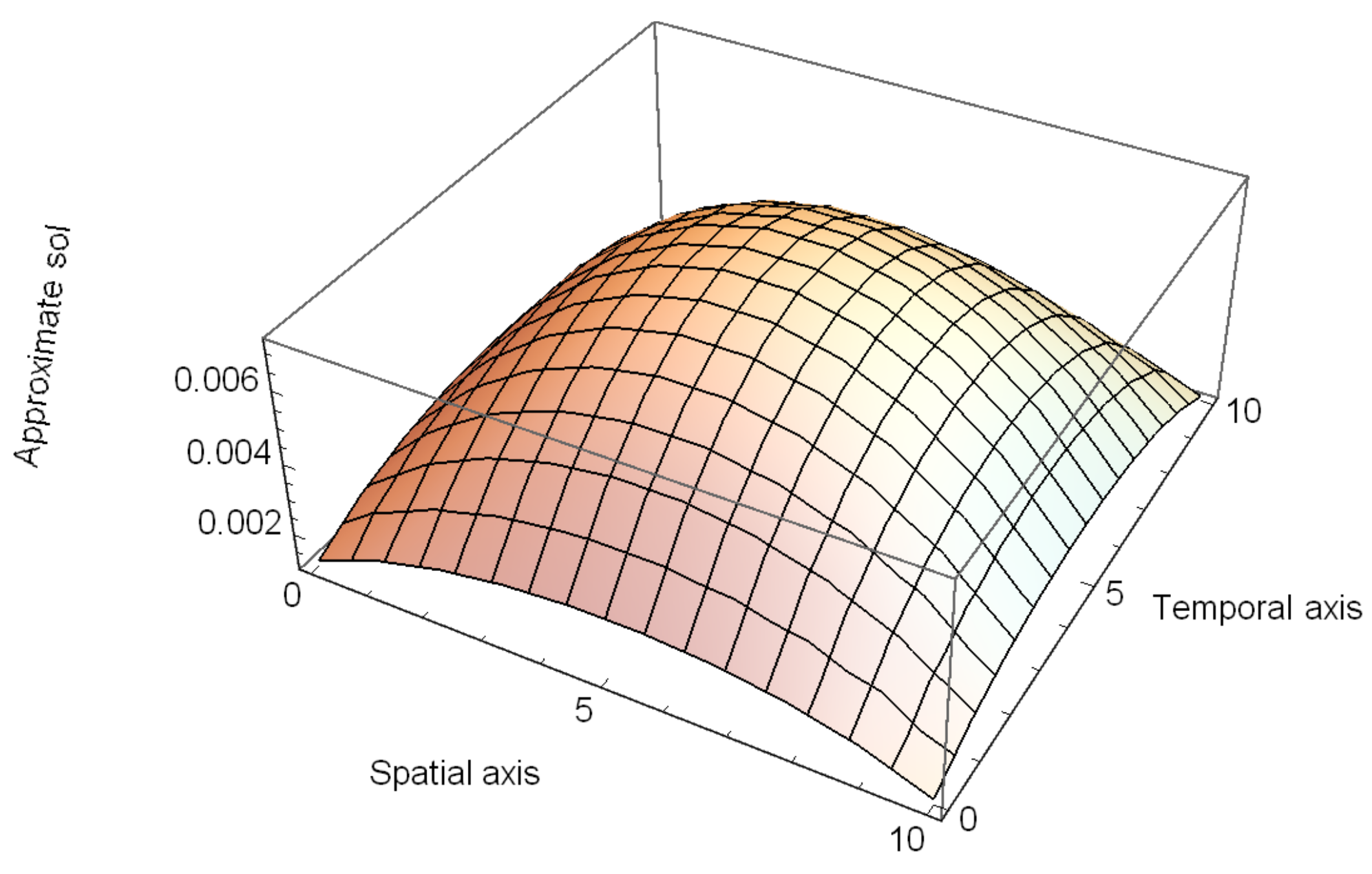

| Scheme | CPU Time (s) | ||||
|---|---|---|---|---|---|
| Scheme | CPU Time (s) | ||||
|---|---|---|---|---|---|
| Scheme | CPU Time (s) | ||||
|---|---|---|---|---|---|
| − | − | ||||
| − | − | ||||
| − | − | ||||
| − | − | ||||
| Scheme | CPU Time (s) | ||||
|---|---|---|---|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behl, R.; Bhalla, S.; Argyros, I.K.; Kumar, S. Semi-Local Analysis and Real Life Applications of Higher-Order Iterative Schemes for Nonlinear Systems. Mathematics 2020, 8, 92. https://doi.org/10.3390/math8010092
Behl R, Bhalla S, Argyros IK, Kumar S. Semi-Local Analysis and Real Life Applications of Higher-Order Iterative Schemes for Nonlinear Systems. Mathematics. 2020; 8(1):92. https://doi.org/10.3390/math8010092
Chicago/Turabian StyleBehl, Ramandeep, Sonia Bhalla, Ioannis K. Argyros, and Sanjeev Kumar. 2020. "Semi-Local Analysis and Real Life Applications of Higher-Order Iterative Schemes for Nonlinear Systems" Mathematics 8, no. 1: 92. https://doi.org/10.3390/math8010092
APA StyleBehl, R., Bhalla, S., Argyros, I. K., & Kumar, S. (2020). Semi-Local Analysis and Real Life Applications of Higher-Order Iterative Schemes for Nonlinear Systems. Mathematics, 8(1), 92. https://doi.org/10.3390/math8010092





