Numerical Analysis of an Osseointegration Model
Abstract
1. Introduction
2. Biological Problem and Its Variational Formulation
3. Fully Discrete Approximations and an a Priori Error Analysis
4. Numerical Results
4.1. Numerical Scheme
4.2. Numerical Convergence
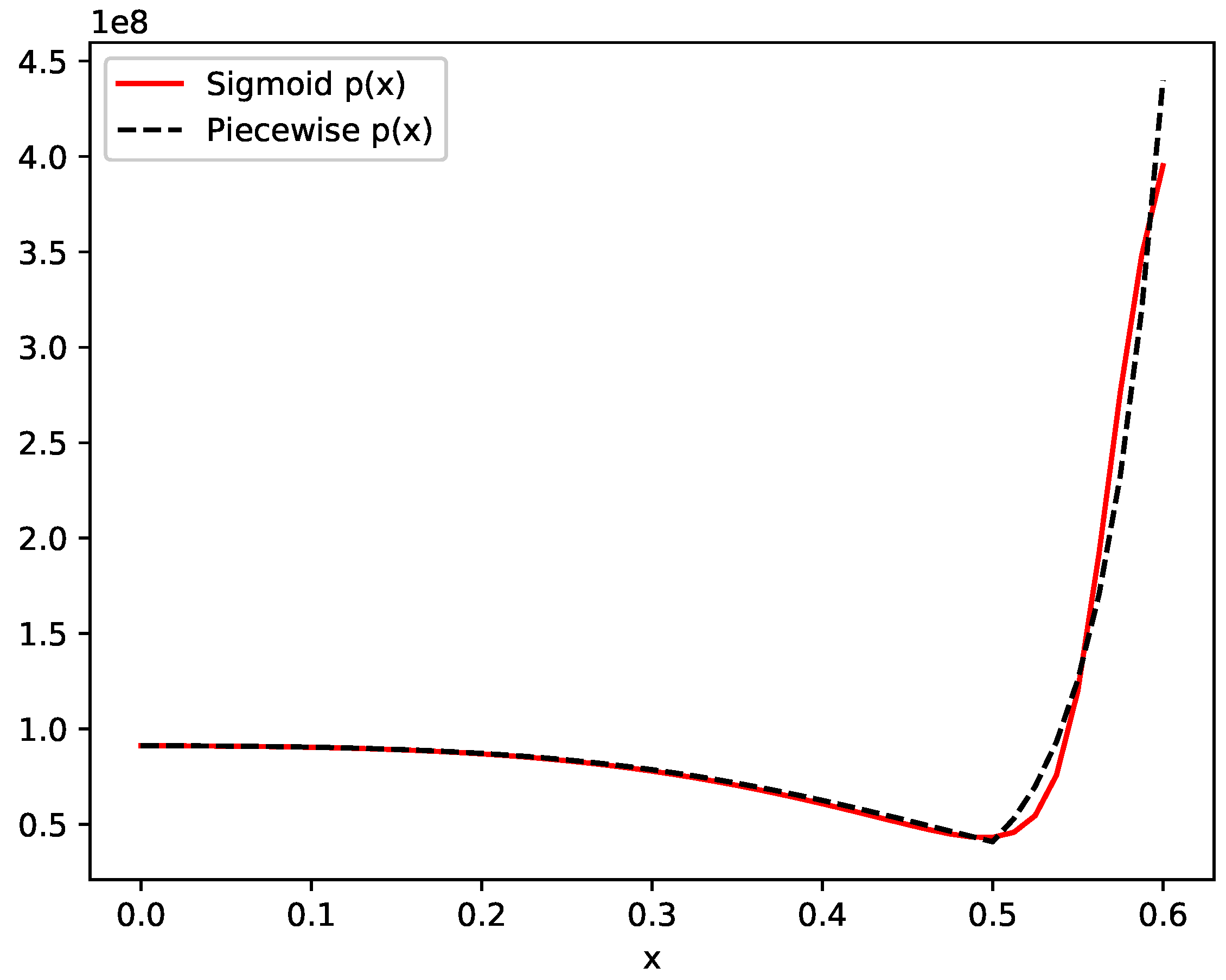
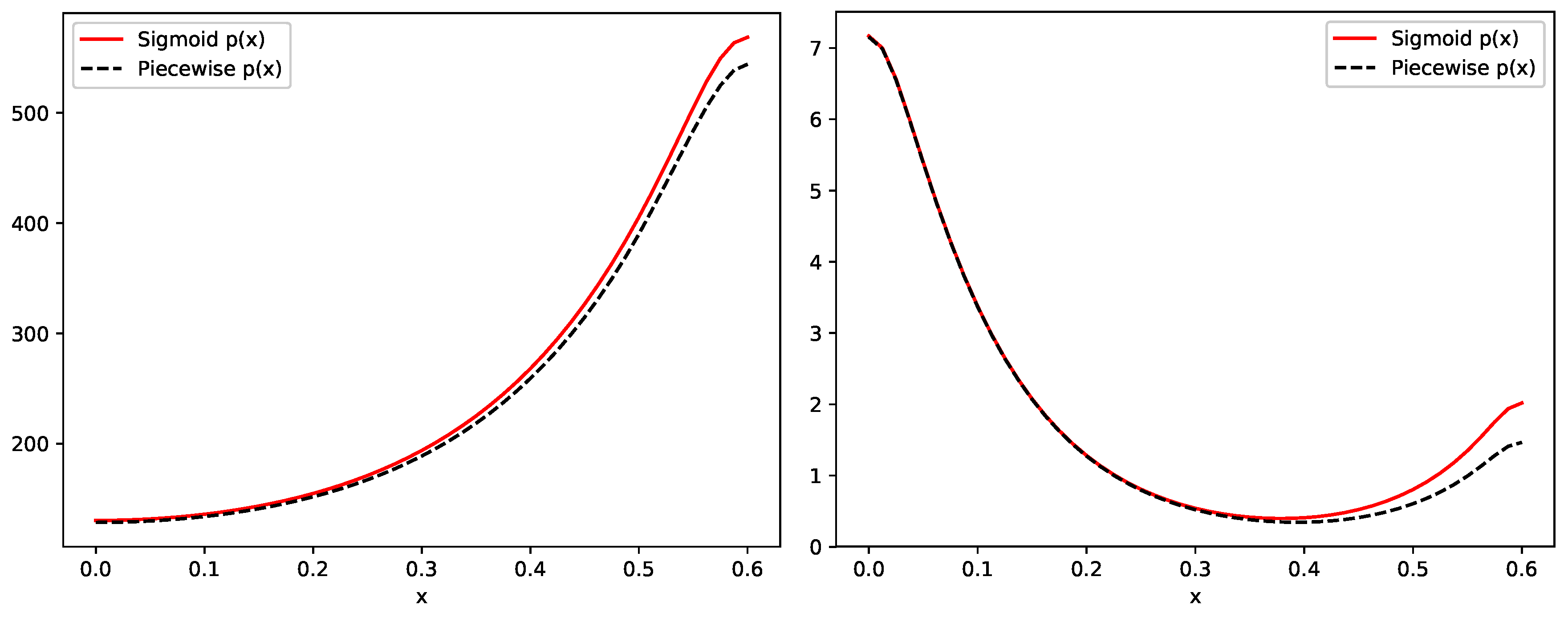
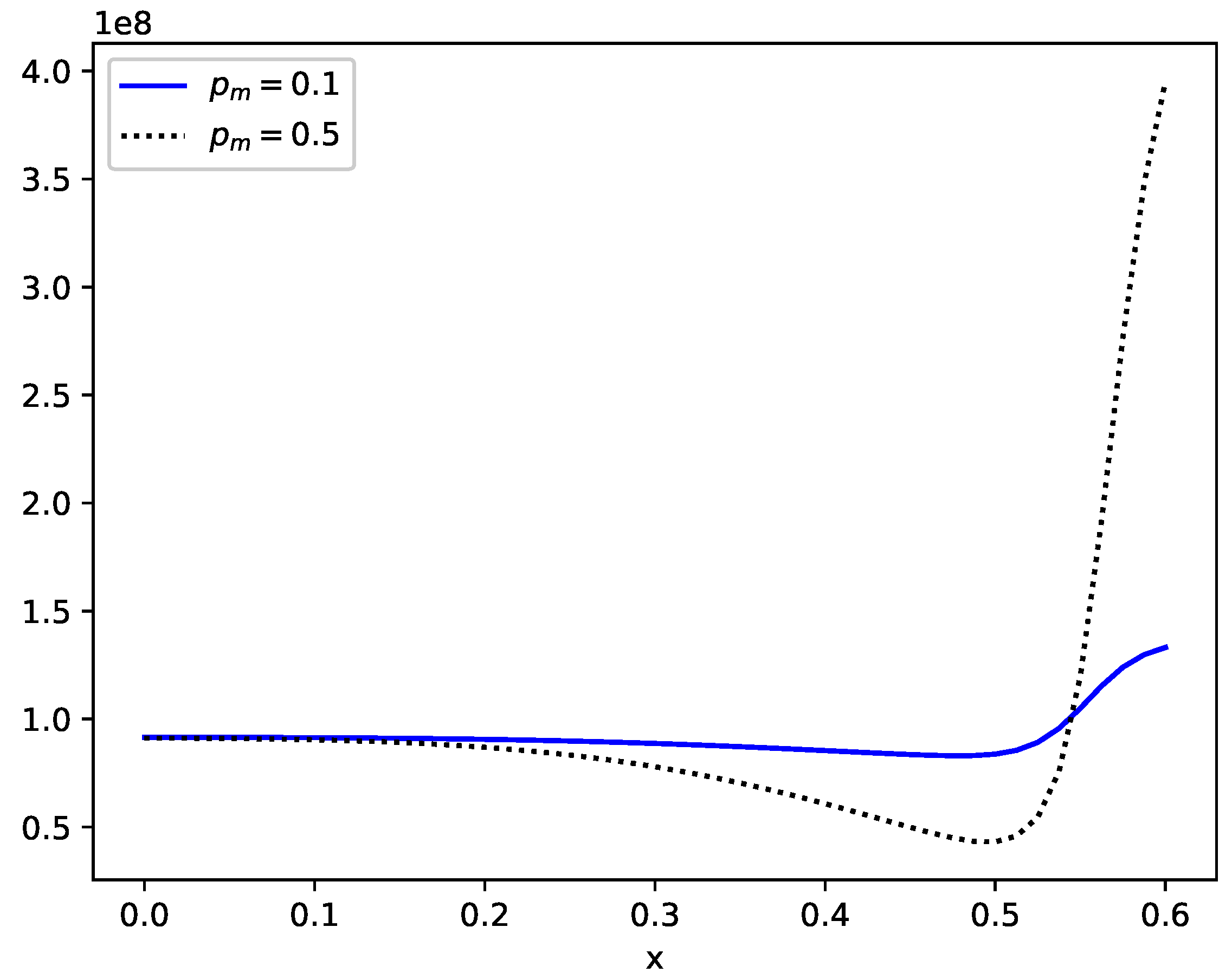
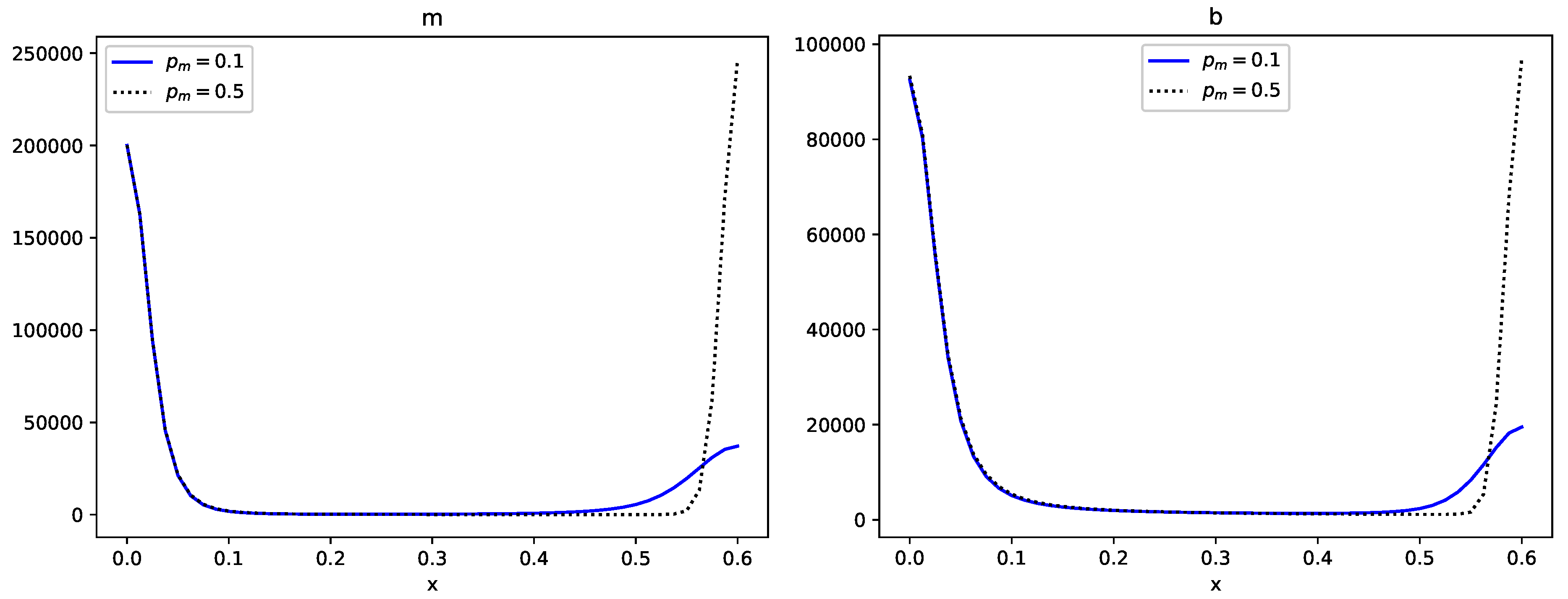
4.3. One-Dimensional Examples
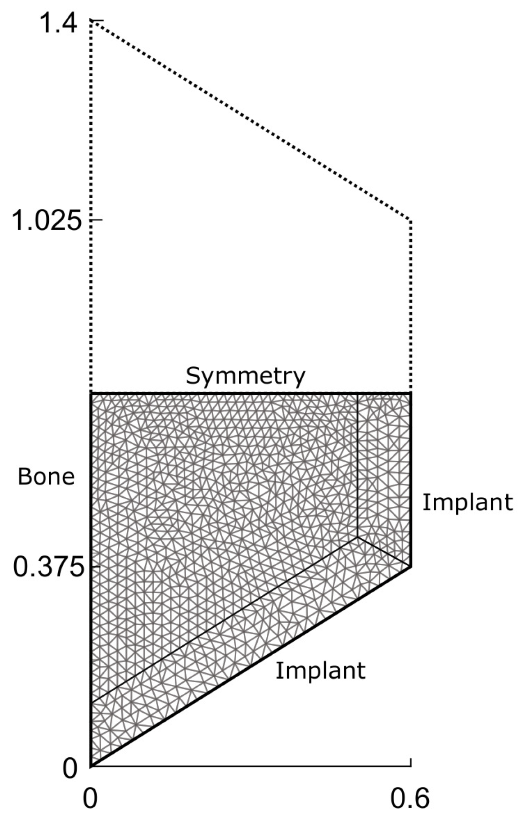
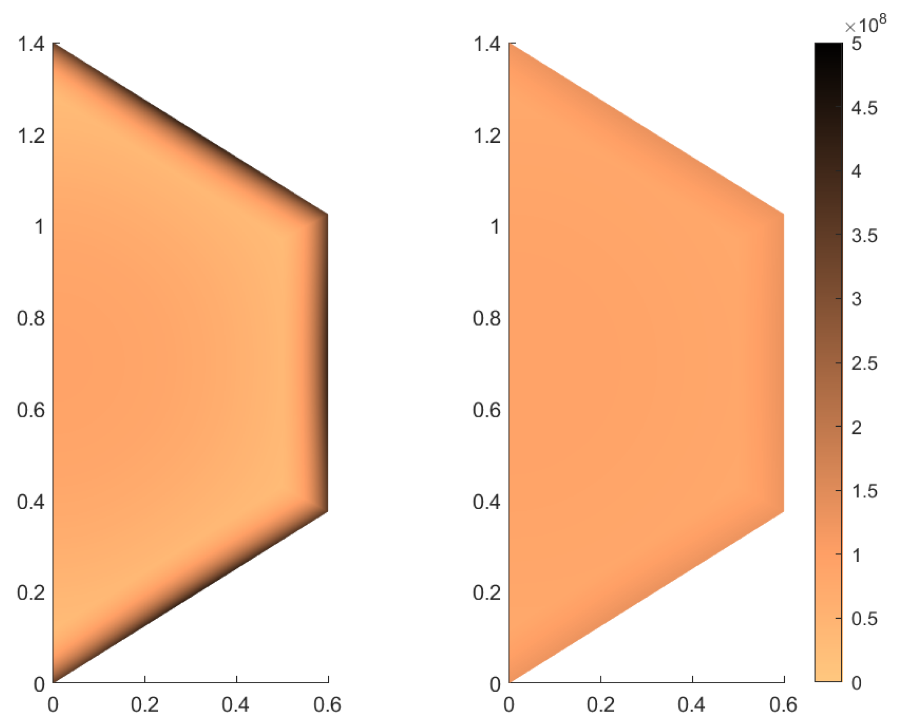
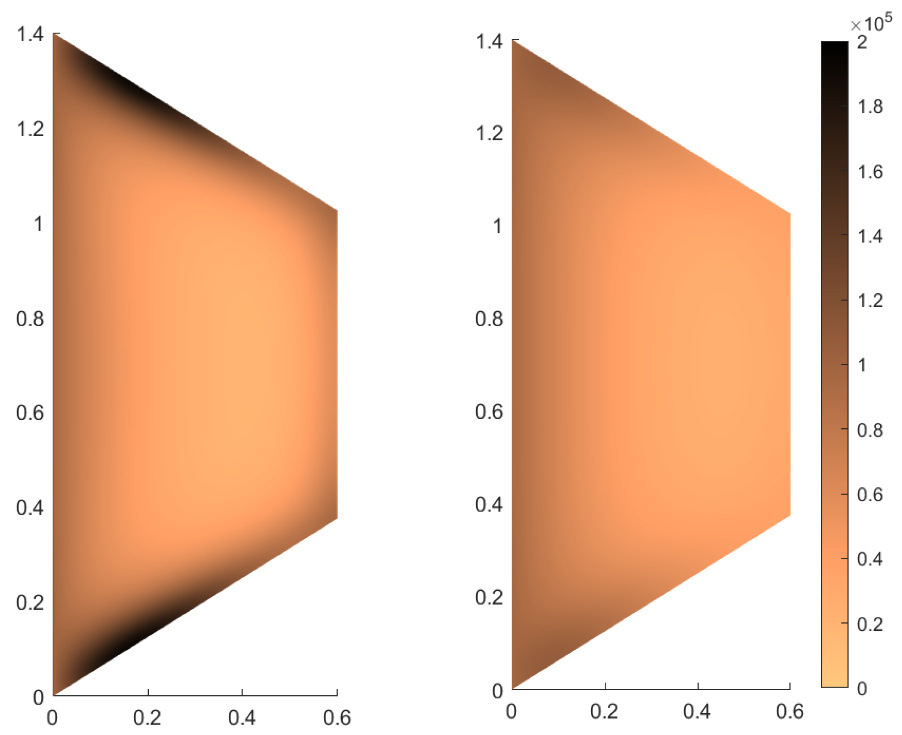
4.4. Two-Dimensional Example
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Haas, R.; Polak, C.; Fürhauser, R.; Mailath-Pokorny, G.; Dörtbudak, O.; Watzek, G. A long-term follow-op of 76 Bränemark single-tooth implants. Clin. Oral Implants Res. 2002, 13, 38–43. [Google Scholar] [CrossRef] [PubMed]
- Soncini, M.; Pietrabissa, R.; Rodriguez y Baena, R. Computational approach for the mechanical reliability of a dental implant. In Computer Methods in Biomechanics and Biomedical Engineering; Middleton, J., Pande, G.N., Jones, M.L., Eds.; Gordon and Breach Science Publishers: London, UK, 2001. [Google Scholar]
- Azcarate-Velázquez, F.; Castillo-Oyagüe, R.; Oliveros-López, L.G.; Torres-Lagares, D.; Martínez-González, Á.J.; Pérez-Velasco, A.; Lynch, C.D.; Gutiérrez-Pérez, J.L.; Serrera-Figallo, M.Á. Influence of bone quality on the mechanical interaction between implant and bone: A finite element analysis. J. Dent. 2019, 88, 103–161. [Google Scholar] [CrossRef] [PubMed]
- Baggi, L.; Cappelloni, I.; Di Girolamo, M.; Maceri, F.; Vairo, G. The influence of implant diameter and length on stress distribution of osseointegrated implants related to crestal bone geometry: A three-dimensional finite element analysis. J. Prosthet. Dent. 2008, 100, 422–431. [Google Scholar] [CrossRef]
- Cos Juez, F.J.; Sánchez Lasheras, F.; García Nieto, P.G.; Álvarez-Arenal, A. Non-linear numerical analysis of a double-threaded titanium alloy dental implant by FEM. Appl. Math. Comput. 2008, 2008, 952–967. [Google Scholar] [CrossRef]
- Dorogoy, A.; Haïat, G.; Shemtov-Yona, K.; Rittel, D. Modeling ultrasonic wave propagation in a dental implant—Bone system. J. Mech. Behav. Biomed. Mater. 2019, 20, 103. [Google Scholar] [CrossRef]
- Farronato, D.; Manfredini, M.; Stevanello, A.; Campana, V.; Azzi, L.; Farronato, M. A Comparative 3D Finite Element Computational Study of Three Connections. Materials 2019, 12, 3135. [Google Scholar] [CrossRef]
- Fernandez, J.W.; Das, R.; Cleary, P.W.; Hunter, P.J.; Thomas, C.D.L.; Clement, J.G. Using smooth particle hydrodynamics to investigate femoral cortical bone remodeling at the Haversian level. Int. J. Numer. Methods Biomed. Eng. 2013, 29, 129–143. [Google Scholar] [CrossRef]
- Giorgio, I.; Andreaus, U.; Scerrato, D.; Braidotti, P. Modeling of a non-local stimulus for bone remodeling process under cyclic load: Application to a dental implant using a bioresorbable porous material. Math. Mech. Solids 2017, 22, 1790–1805. [Google Scholar] [CrossRef]
- Guan, H.; van Staden, R.C.; Johnson, N.; Loo, Y.-C. Dynamic modeling and simulation of dental implant insertion process—A finite element study. Finite Elem. Anal. Des. 2011, 47, 886–897. [Google Scholar] [CrossRef]
- Hasan, I.; Rahimi, A.; Keilig, L.; Brinkmann, K.T.; Bourauel, C. Computational simulation of internal bone remodeling around dental implants: A sensitivity analysis. Comput. Methods Biomech. Biomed. Eng. 2012, 15, 807–814. [Google Scholar] [CrossRef]
- He, Y.; Hasan, I.; Keilig, L.; Fischer, D.; Ziegler, L.; Abboud, M.; Wahl, G.; Bourauel, C. Biomechanical characteristics of immediately loaded and osseointegration dental implants inserted into Sika deer antler. Med. Eng. Phys. 2018, 59, 8–14. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Hasan, I.; Keilig, L.; Fischer, D.; Ziegler, L.; Abboud, M.; Wahl, G.; Bourauel, C. Numerical investigation of bone remodeling around immediately loaded dental implants using sika deer (Cervus nippon) antlers as implant bed. Comput. Methods Biomech. Biomed. Eng. 2018, 21, 359–369. [Google Scholar] [CrossRef] [PubMed]
- Hoang, K.C.; Khoo, B.C.; Liu, G.R.; Nguyen, N.C.; Patera, A.T. Rapid identification of material properties of the interface tissue in dental implant systems using reduced basis method. Inverse Probl. Sci. Eng. 2013, 21, 1310–1334. [Google Scholar] [CrossRef]
- Hou, P.J.; Ou, K.L.; Wang, C.C.; Huang, C.F.; Ruslin, M.; Sugiatno, E.; Yang, T.S.; Chou, H.H. Hybrid micro/nanostructural surface offering improved stress distribution and enhanced osseointegration properties of the biomedical titanium implant. J. Mech. Behav. Biomed. Mater. 2018, 79, 173–180. [Google Scholar] [CrossRef]
- Joshi, S.; Kumar, S.; Jain, S.; Aggarwal, R.; Choudhary, S.; Reddy, N.K. 3D Finite Element Analysis to Assess the Stress Distribution Pattern in Mandibular Implant-supported Overdenture with Different Bar Heights. J. Contemp. Dent. Pract. 2019, 20, 794–800. [Google Scholar] [CrossRef] [PubMed]
- Kurniawan, D.; Nor, F.M.; Lee, H.Y.; Lim, J.Y. Finite element analysis of bone-implant biomechanics: Refinement through featuring various osseointegration conditions. Int. J. Oral Maxillofac. Surg. 2012, 41, 1090–1196. [Google Scholar] [CrossRef] [PubMed]
- Lencioni, K.A.; Noritomi, P.Y.; Macedo, A.P.; Ribeiro, R.F.; Almeida, R.P. Influence of different implants on the biomechanical behavior of tooth-implant fixed partial dentures: A three-dimensional finite element analysis. J. Oral Implantol. 2019. [Google Scholar] [CrossRef]
- Lima de Andrade, C.; Carvalho, M.A.; Bordin, D.; da Silva, W.J.; del Bel Cury, A.A.; Sotto-Maior, B.S. Biomechanical Behavior of the Dental Implant Macrodesign. Int. J. Oral Maxillofac. Implant. 2017, 32, 264–270. [Google Scholar] [CrossRef]
- Lin, D.; Li, Q.; Li, W.; Duckmanton, N.; Swain, M. Mandibular bone remodeling induced by dental implant. J. Biomech. 2010, 43, 287–293. [Google Scholar] [CrossRef]
- Murase, K.; Stenlund, P.; Thomsen, P.; Lausmaa, J.; Palmquist, A. Three-dimensional modeling of removal torque and fracture progression around implants. J. Mater. Sci. Mater. Med. 2018, 29, 104. [Google Scholar] [CrossRef]
- Rittel, D.; Dorogoy, A.; Shemtov-Yona, K. Modeling the effect of osseointegration on dental implant pullout and torque removal tests. Clin. Implant Dent. Relat. Res. 2018, 20, 683–691. [Google Scholar] [CrossRef] [PubMed]
- Sayyedi, A.; Rashidpour, M.; Fayyaz, A.; Ahmadian, N.; Dehghan, M.; Faghani, F.; Fasihg, P.J. Comparison of Stress Distribution in Alveolar Bone with Different Implant Diameters and Vertical Cantilever Length via the Finite Element Method. Long Term Eff. Med. Implant. 2019, 29, 37–43. [Google Scholar] [CrossRef]
- Sotto-Maior, B.S.; Mercuri, E.G.; Senna, P.M.; Assis, N.M.; Francischone, C.E.; del Bel Cury, A.A. Evaluation of bone remodeling around single dental implants of different lengths: A mechanobiological numerical simulation and validation using clinical data. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 699–706. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Li, Q.; McClean, C.; Fan, Y. Numerical simulation of dental bone remodeling induced by implant- supported fixed partial denture with or without cantilever extension. Int. J. Numer. Method Biomed. Eng. 2013, 29, 1134–1147. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L.; Yang, J.; Hu, X.; Luo, J. Three dimensional finite element analysis of a novel osteointegrated dental implant designed to reduce stress peak of cortical bone. Acta Bioeng. Biomech. 2014, 16, 21–28. [Google Scholar] [PubMed]
- Moreo, P.; García-Aznar, J.M.; Doblaré, M. Bone ingrowth on the surface of endosseous implants. Part 1: Mathematical model. J. Theor. Biol. 2009, 260, 1–12. [Google Scholar] [CrossRef]
- Moreo, P.; García-Aznar, J.M.; Doblaré, M. Bone ingrowth on the surface of endosseous implants. Part 2: Theoretical and numerical analysis. J. Theor. Biol. 2009, 260, 13–26. [Google Scholar] [CrossRef]
- Fernández, J.R.; García-Aznar, J.M.; Masid, M. Numerical analysis of an osteoconduction model arising in bone-implant integration. ZAMM Z. Angew. Math. Mech. 2017, 97, 1050–1063. [Google Scholar]
- Fernández, J.R.; Masid, M. Analysis of a model for the propagation of the ossification front. J. Comput. Appl. Math. 2017, 318, 624–633. [Google Scholar]
- Lekszycki, T.; dell’Isola, F. A mixture model with evolving mass densities for describing synthesis and resorption phenomena in bones reconstructed with bio-resorbable materials. Zeit. Ang. Math. Mech. 2012, 92, 426–444. [Google Scholar] [CrossRef]
- Lu, Y.; Lekszycki, T. New description of gradual substitution of graft by bone tissue including biomechanical and structural effects, nutrients supply and consumption. Cont. Mech. Thermod. 2018, 30, 995–1009. [Google Scholar] [CrossRef]
- George, D.; Allena, R.; Rémond, Y. Integrating molecular and cellular kinetics into a coupled continuum mechanobiological stimulus for bone reconstruction. Cont. Mech. Thermod. 2019, 31, 725–740. [Google Scholar] [CrossRef]
- Barbu, V. Optimal Control of Variational Inequalities; Pitman: Boston, MA, USA, 1984. [Google Scholar]
- Brezis, H. Equations et inéquations non linéaires dans les espaces vectoriels en dualité. Ann. Inst. Fourier 1968, 18, 115–175. [Google Scholar] [CrossRef]
- Chau, O.; Fernández, J.R.; Shillor, M.; Sofonea, M. Variational and numerical analysis of a quasistatic viscoelastic contact problem with adhesion. J. Comput. Appl. Math. 2003, 159, 431–465. [Google Scholar] [CrossRef]
- Ciarlet, P.G. Basic error estimates for elliptic problems. In Handbook of Numerical Analysis; Ciarlet, P.G., Lions, J.L., Eds.; 1993; Volume II, pp. 17–351. [Google Scholar]
- Barboteu, M.; Fernández, J.R.; Hoarau-Mantel, T.V. A class of evolutionary variational inequalities with applications in viscoelasticity. Math. Model. Methods Appl. Sci. 2005, 15, 1595–1617. [Google Scholar] [CrossRef]
- Campo, M.; Fernández, J.R.; Kuttler, K.L.; Shillor, M.; Viaño, J.M. Numerical analysis and simulations of a dynamic frictionless contact problem with damage. Comput. Methods Appl. Mech. Eng. 2006, 196, 476–488. [Google Scholar] [CrossRef]
- Alnaes, S.; Blechta, J.; Hake, J.; Johansson, A.; Kehlet, B.; Logg, A.; Richardson, C.; Ring, J.; Rognes, M.E.; Wells, G.N. The FEniCS Project Version 1.5 M. Arch. Numer. Softw. 2005, 3. [Google Scholar] [CrossRef]
- Logg, A.; Mardal, K.-A.; Wells, G.N. (Eds.) Automated Solution of Differential Equations by the Finite Element Method; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hecht, F. New development in FreeFem++. J. Numer. Math. 2012, 20, 251–265. [Google Scholar] [CrossRef]
- Conconi, M.; Parenti-Castelli, V. A sound and efficient measure of joint congruence. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2014, 228, 935–941. [Google Scholar] [CrossRef]
- Valigi, M.C.; Logozzo, S. Do Exostoses Correlate with Contact Disfunctions? A Case Study of a Maxillary Exostosis. Lubricants 2019, 7, 15. [Google Scholar] [CrossRef]



| h↓ | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 8.440 | 4.712 | 2.845 | 1.925 | 1.477 | 1.276 | 1.202 | 1.167 | 1.151 | |
| 7.919 | 4.199 | 2.322 | 1.387 | 0.927 | 0.719 | 0.644 | 0.610 | 0.593 | |
| 7.768 | 4.052 | 2.175 | 1.236 | 0.771 | 0.553 | 0.474 | 0.437 | 0.420 | |
| 7.707 | 3.992 | 2.114 | 1.175 | 0.708 | 0.482 | 0.400 | 0.362 | 0.343 | |
| 7.668 | 3.953 | 2.075 | 1.135 | 0.667 | 0.438 | 0.348 | 0.309 | 0.290 | |
| 7.634 | 3.919 | 2.041 | 1.100 | 0.631 | 0.400 | 0.301 | 0.262 | 0.243 | |
| 7.602 | 3.887 | 2.008 | 1.067 | 0.597 | 0.364 | 0.256 | 0.216 | 0.197 | |
| 7.570 | 3.855 | 1.976 | 1.034 | 0.563 | 0.329 | 0.214 | 0.170 | 0.151 | |
| 7.539 | 3.823 | 1.944 | 1.001 | 0.530 | 0.295 | 0.178 | 0.125 | 0.105 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baldonedo, J.; Fernández, J.R.; Segade, A. Numerical Analysis of an Osseointegration Model. Mathematics 2020, 8, 87. https://doi.org/10.3390/math8010087
Baldonedo J, Fernández JR, Segade A. Numerical Analysis of an Osseointegration Model. Mathematics. 2020; 8(1):87. https://doi.org/10.3390/math8010087
Chicago/Turabian StyleBaldonedo, Jacobo, José R. Fernández, and Abraham Segade. 2020. "Numerical Analysis of an Osseointegration Model" Mathematics 8, no. 1: 87. https://doi.org/10.3390/math8010087
APA StyleBaldonedo, J., Fernández, J. R., & Segade, A. (2020). Numerical Analysis of an Osseointegration Model. Mathematics, 8(1), 87. https://doi.org/10.3390/math8010087






