Structure Functions of Pseudo Null Curves in Minkowski 3-Space

Abstract

In this work, the embankment surfaces with pseudo null base curves are investigated in Minkowski 3-space. The representation formula of pseudo null curves is obtained via the defined structure functions and the k-type pseudo null helices are discussed completely. Based on the theories of pseudo null curves, a class of embankment surfaces are constructed and characterized by the structure functions of the pseudo null base curves.

1. Introduction

With the development of the theory of relativity, geometers and researchers often extend some topics in classical differential geometry of Riemannian manifolds to those of semi-Riemannian manifolds, especially to Lorentz–Minkowski manifolds. However, due to the causal character of vectors in Lorentz–Minkowski space, some problems become a little strange and different, especially the ones related to lightlike (null) vectors, such as null curves, pseudo null curves, B-scrolls and the marginally trapped surfaces and so on.

It is well known that a space curve is called a helix if its tangent vector makes a constant angle with a fixed direction and it is called a slant helix if its principal normal vector makes a constant angle with a fixed direction [1]. The helix and the slant helix play important roles in the curve theory, and they can be applied into the science of biology and physics etc., such as analyzing the structure of DNA and characterizing the motion of particles in a magnetic field [2]. Due to these fascinating applications, the helix and the slant helix have been discussed widely, not only in the Euclidean space, but also in the Lorentz–Minkowski space [3,4]. Recently, one of the authors investigated the representation formula of null curves via the defined structure functions [5,6] and the null helix and k-type null slant helices in Minkowski four-space were discussed in [6]. Motivated by those ideas, in the second part of this paper, the pseudo null curves are represented by the new defined structure functions, at the same time, the k-type pseudo null helices are defined and characterized by the structure functions in the third part.

Naturally, the surface theory can also be generalized into the Lorentz–Minkowski space. In surface theory, there exists an important class of surfaces, called ruled surfaces, which can be applied in computer aided geometric designs (CAGD), surface approximations and tool path planning, etc. The embankment surfaces as the envelope of cones are just formed by two ruled surfaces with the same base curves [7]. Combining the theories of pseudo null curves, a kind of embankment surface, with pseudo null base curves, are discussed in the fourth part of this work.

Throughout this paper, all the geometric objects under consideration are smooth and all surfaces are connected unless otherwise stated.

2. Representation Formula of Pseudo Null Curves

A Minkowski three-space ${\mathbb{E}}_1^3$ is provided with the standard flat metric given by

$$\langle ·,·\rangle =-d{x}_1^2+d{x}_2^2+d{x}_3^2$$

in terms of the natural coordinate system $(x_1,x_2,x_3)$. Recall that a vector v is spacelike, timelike and lightlike (null), if $\langle v,v\rangle >0$ or $v=0$, $\langle v,v\rangle <0$ and $\langle v,v\rangle =0$, $(v\ne 0)$, respectively. The norm of v is defined by $\parallel v\parallel =\sqrt{|\langle v,v\rangle |}$. For any two vectors $x=(x_1,x_2,x_3)$, $y=(y_1,y_2,y_3)\in {\mathbb{E}}_1^3$, their exterior product is given by

$$x\times y=\left|\begin{array}{ccc}{e}_1& e_2& e_3\\ x_1& x_2& x_3\\ y_1& y_2& y_3\end{array}\right|=\left(-\left|\begin{array}{cc}{x}_2& x_3\\ y_2& y_3\end{array}\right|,\left|\begin{array}{cc}{x}_3& x_1\\ y_3& y_1\end{array}\right|,\left|\begin{array}{cc}{x}_1& x_2\\ y_1& y_2\end{array}\right|\right),$$

where $\{e_1,e_2,e_3\}$ is an orthogonal basis in ${\mathbb{E}}_1^3$. An arbitrary curve $r\left(t\right)$ is spacelike, timelike or lightlike if all of its velocity vectors are spacelike, timelike or lightlike. At the same time, a surface is said to be timelike, spacelike or lightlike if all of its normal vectors are spacelike, timelike or lightlike, respectively [8]. Furthermore, the spacelike curves in ${\mathbb{E}}_1^3$ can be classified into the first and the second kind of spacelike curves and the pseudo null curves according to their principal normal vectors are spacelike, timelike and lightlike, respectively. Among of them, the pseudo null curves are defined as following.

Definition 1

([9]). A spacelike curve $r\left(t\right)$ framed by Frenet frame $\{\alpha ,\beta ,\gamma \}$ in ${\mathbb{E}}_1^3$ is called a pseudo null curve, if its principal normal vector β and binormal vector γ are linearly independent null vectors.

Remark 1.

The pseudo null lines are excluded from consideration throughout this paper.

Proposition 1

([9]). Let $r\left(s\right):\mathbf{I}\to {\mathbb{E}}_1^3$ be a pseudo null curve parameterized by arc-length s, i.e., $\parallel r^{\prime }\left(s\right)\parallel =1$. Then there exists a unique Frenet frame $\{r^{\prime }\left(s\right)=\alpha ,\beta ,\gamma \}$, such that

$$\begin{array}{c}\left(\begin{array}{c}{\alpha }^{\prime }\left(s\right)\\ {\beta }^{\prime }\left(s\right)\\ {\gamma }^{\prime }\left(s\right)\end{array}\right)=\left(\begin{array}{ccc}0& 1& 0\\ 0& \kappa \left(s\right)& 0\\ -1& 0& -\kappa \left(s\right)\end{array}\right)\left(\begin{array}{c}\alpha \left(s\right)\\ \beta \left(s\right)\\ \gamma \left(s\right)\end{array}\right),\end{array}$$

(1)

where $\langle \alpha ,\alpha \rangle =\langle \beta ,\gamma \rangle =1,$ $\langle \beta ,\beta \rangle =\langle \gamma ,\gamma \rangle =\langle \alpha ,\beta \rangle =\langle \alpha ,\gamma \rangle =0$ and $\alpha \times \beta =\beta ,$ $\beta \times \gamma =\alpha ,$ $\gamma \times \alpha =\gamma .$ In sequence, $\alpha ,\beta ,\gamma$ is called the tangent, principal normal and binormal vector field of $r\left(s\right)$, respectively. The function $\kappa \left(s\right)$ is called the curvature function.

Remark 2.

In some research papers for pseudo null curves such as [9], the function $\kappa \left(s\right)$ is also called torsion function. Throughout the paper, the pseudo null curves are parameterized by arc-length s.

The cone curves on ${\mathbb{Q}}^2$ and null curves in ${\mathbb{E}}_1^3$ are described by the defined structure functions in [5,10], respectively. Motivated by them, the pseudo null curves in ${\mathbb{E}}_1^3$ can also be characterized.

First, we write $r^{\prime }\left(s\right)=({\xi }_1\left(s\right),{\xi }_2\left(s\right),{\xi }_3\left(s\right))$, since $r^{\prime }\left(s\right)$ is a unit spacelike vector, then $-{\xi }_1^2+{\xi }_2^2+{\xi }_3^2=1.$ Without loss of generality, we can assume

$$\frac{{\xi }_3+{\xi }_1}{1+{\xi }_2}=\frac{1-{\xi }_2}{{\xi }_3-{\xi }_1}=f,{\xi }_2=g,$$

where $f=f\left(s\right)$ and $g=g\left(s\right)$ are non-constant functions of arc-length s. Then

$${\xi }_1=\frac{f(1+g)-f^{-1}(1-g)}{2},{\xi }_2=g,{\xi }_3=\frac{f(1+g)+f^{-1}(1-g)}{2}.$$

(2)

Therefore, the pseudo null curve $r\left(s\right)$ can be written as

$$r\left(s\right)=\int ({\xi }_1,{\xi }_2,{\xi }_3)ds=\frac{1}{2}\int \left(f(1+g)-f^{-1}(1-g),2g,f(1+g)+f^{-1}(1-g)\right)ds.$$

Furthermore, through direct calculations, we have

$$r^{″}\left(s\right)=\frac{1}{2}\left(f^{\prime }(1+g)+f{g}^{\prime }+f^{\prime }{f}^{-2}(1-g)+f^{-1}{g}^{\prime },2g^{\prime },f^{\prime }(1+g)+f{g}^{\prime }-f^{\prime }{f}^{-2}(1-g)-f^{-1}{g}^{\prime }\right).$$

(3)

Due to $\langle r^{″}\left(s\right),r^{″}\left(s\right)\rangle =0$, we get

$$\frac{f^{\prime }}{f}=\frac{2g^{\prime }}{g^2-1}.$$

(4)

Solving the above differential Equation (4), we get

$$cf=\frac{g-1}{g+1},(0\ne c\in \mathbb{R}).$$

(5)

Proposition 2.

Let $r\left(s\right)$ be a pseudo null curve in ${\mathbb{E}}_1^3$. Then $r\left(s\right)$ can be written as

$$r\left(s\right)=\frac{1}{2}\int \left(f(1+g)-f^{-1}(1-g),2g,f(1+g)+f^{-1}(1-g)\right)ds,$$

where $f\left(s\right),g\left(s\right)$ are non-constant functions and they satisfy

$$cf=\frac{g-1}{g+1},(0\ne c\in \mathbb{R}).$$

Definition 2.

The functions $f\left(s\right)$ and $g\left(s\right)$ in Proposition 2 are called structure functions of the pseudo null curve $r\left(s\right)$.

Proposition 3.

Let $r\left(s\right)$ be a pseudo null curve in ${\mathbb{E}}_1^3$. Then the curvature function $\kappa \left(s\right)$ of $r\left(s\right)$ and its structure function $g\left(s\right)$ are related by

$$\kappa \left(s\right)=\frac{g^{″}\left(s\right)}{g^{\prime }\left(s\right)}.$$

(6)

Proof of Proposition 3.

According to Equation (3), through some calculations, we have

$$r^{‴}\left(s\right)=\frac{1}{2}\left({(f^{\prime }(1+g)+f{g}^{\prime }+f^{\prime }{f}^{-2}(1-g)+f^{-1}{g}^{\prime })}^{\prime },2g^{″},{(f^{\prime }(1+g)+f{g}^{\prime }-f^{\prime }{f}^{-2}(1-g)-f^{-1}{g}^{\prime })}^{\prime }\right).$$

From the Frenet formula in Equation (1), we know $r^{‴}\left(s\right)=\kappa \left(s\right)r^{″}\left(s\right)$. Comparing the above equation to Equation (3), we can obtain the result easily. □

Meanwhile, from the Frenet formula in Equations (1) and (2), through direct calculations, we can get the representations of $\alpha$ and $\beta$. Then, according to Proposition 3, by solving a differential equation system derived by ${\gamma }^{\prime }=-\alpha -\kappa \gamma$, it is not difficult to get the representation of $\gamma$. Thus, we have the following conclusion.

Proposition 4.

Let $r\left(s\right)$ be a pseudo null curve in ${\mathbb{E}}_1^3$. Then the Frenet frame $\{\alpha ,\beta ,\gamma \}$ of $r\left(s\right)$ can be represented by the structure functions $f\left(s\right),g\left(s\right)$ as

$$\left\{\begin{array}{cc}\hfill \alpha & =\frac{1}{2}\left(f(1+g)-f^{-1}(1-g),2g,f(1+g)+f^{-1}(1-g)\right),\hfill \\ \hfill \beta & =\frac{1}{2}\left(f^{\prime }(1+g)+f{g}^{\prime }+f^{\prime }{f}^{-2}(1-g)+f^{-1}{g}^{\prime },2g^{\prime },f^{\prime }(1+g)+f{g}^{\prime }-f^{\prime }{f}^{-2}(1-g)-f^{-1}{g}^{\prime }\right),\hfill \\ \hfill \gamma & =\frac{1}{2g^{\prime }}\left(c_1+\int [f^{-1}(1-g)-f(1+g)]dg,2\left(c_2-\int gdg\right),c_3-\int [f(1+g)+f^{-1}(1-g)]dg\right),\hfill \end{array}\right.$$

where $c_i(i=1,2,3)\in \mathbb{R}$ and they are related by $\langle \alpha ,\gamma \rangle =0$, $\langle \beta ,\gamma \rangle =1$ and $\langle \gamma ,\gamma \rangle =0$.

In what follows, we will be concerned with the pseudo null curves with constant curvatures.

Theorem 1.

Let $r\left(s\right)$ be a pseudo null curve in ${\mathbb{E}}_1^3$. If the curvature function $\kappa \left(s\right)$ is constant, then the structure functions $f\left(s\right),g\left(s\right)$ can be written as

1. 

when $\kappa \left(s\right)=0,$ $f\left(s\right)=\frac{as-1}{as+1},g\left(s\right)=as,(0\ne a\in \mathbb{R});$

2. 

when $\kappa \left(s\right)=c,$ $f\left(s\right)=\frac{e^{cs}-1}{e^{cs}+1},g\left(s\right)=e^{cs},(0\ne c\in \mathbb{R}).$

Proof of Theorem 1.

Let the curvature function $\kappa \left(s\right)$ is constant c, from Equation (6), we have $g^{″}\left(s\right)=c{g}^{\prime }\left(s\right).$

Case 1: $\kappa \left(s\right)=c=0$. It is easy to get $g^{\prime }\left(s\right)=a,g\left(s\right)=as+c_1,(0\ne a\in \mathbb{R},c_1\in \mathbb{R})$. By the parameter transformation $s\to s+s_0$, where $s_0$ is a constant, we can omit the integration constant $c_1$ here, then $g\left(s\right)=as$. Furthermore, from Equation (5) we have

$$c_{2}f\left(s\right)=\frac{as-1}{as+1},(0\ne c_2\in \mathbb{R}).$$

By an appropriate transformation, we can let $c_2=1$. Thus, we have $f\left(s\right)=\frac{as-1}{as+1}.$

Case 2: $\kappa \left(s\right)=c\ne 0$. Similar to the proving procedure in Case 1, we can get $g\left(s\right)=e^{cs}$ and $f\left(s\right)=\frac{e^{cs}-1}{e^{cs}+1}.$ This completes the proof. □

From Proposition 2 and Theorem 1, the following conclusion can be achieved easily through simple integrations [11].

Theorem 2.

Let $r\left(s\right)$ be a pseudo null curve with constant curvature $\kappa \left(s\right)$ in ${\mathbb{E}}_1^3$. Then $r\left(s\right)$ can be written as

1. 

when $\kappa \left(s\right)=0,$ $r\left(s\right)=\frac{1}{2}\left(a{s}^2,a{s}^2,-2s\right),(0\ne a\in \mathbb{R});$

2. 

when $\kappa \left(s\right)=c,$ $r\left(s\right)=\frac{1}{c}\left(e^{cs},e^{cs},-cs\right),(0\ne c\in \mathbb{R}).$

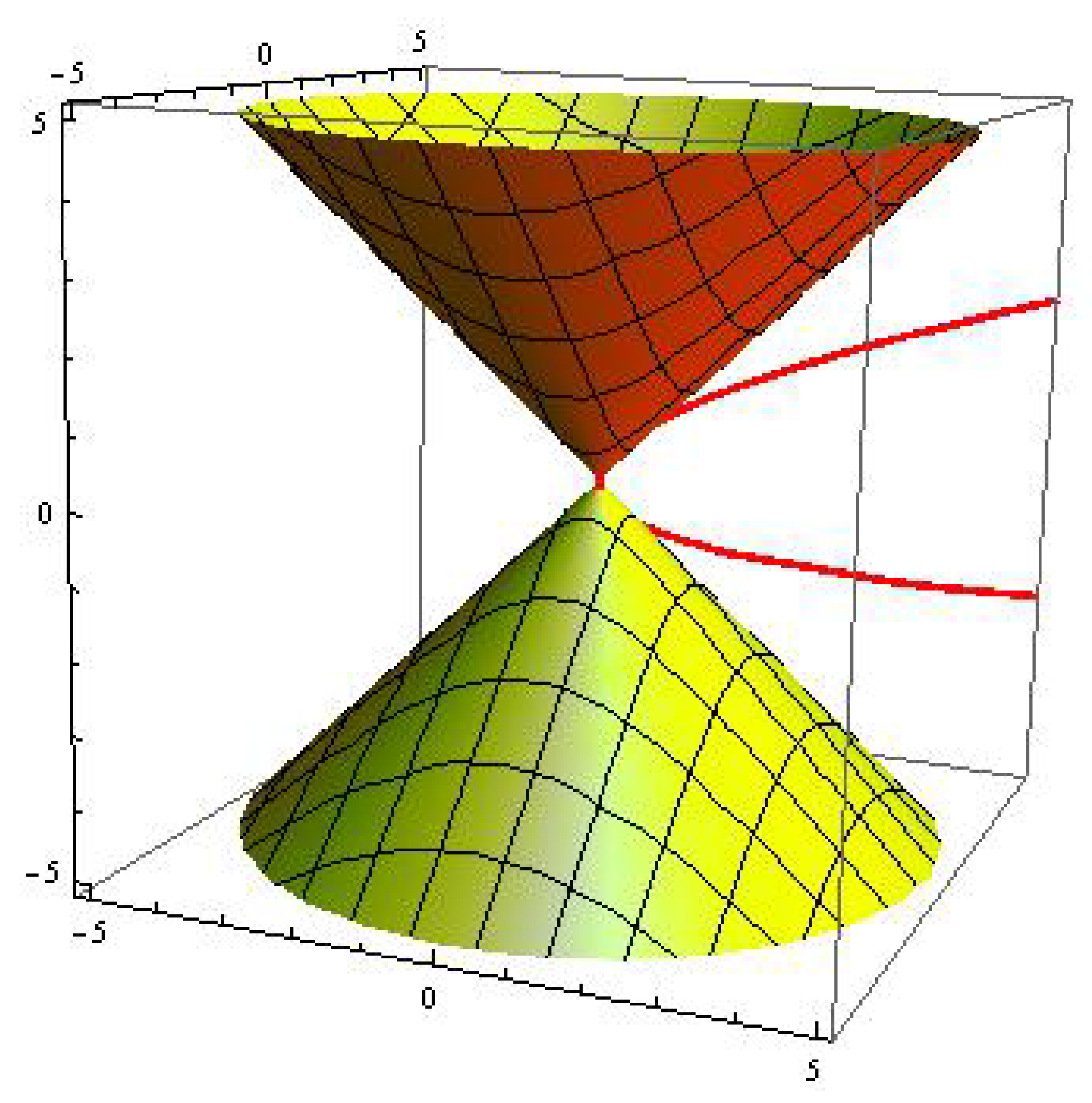
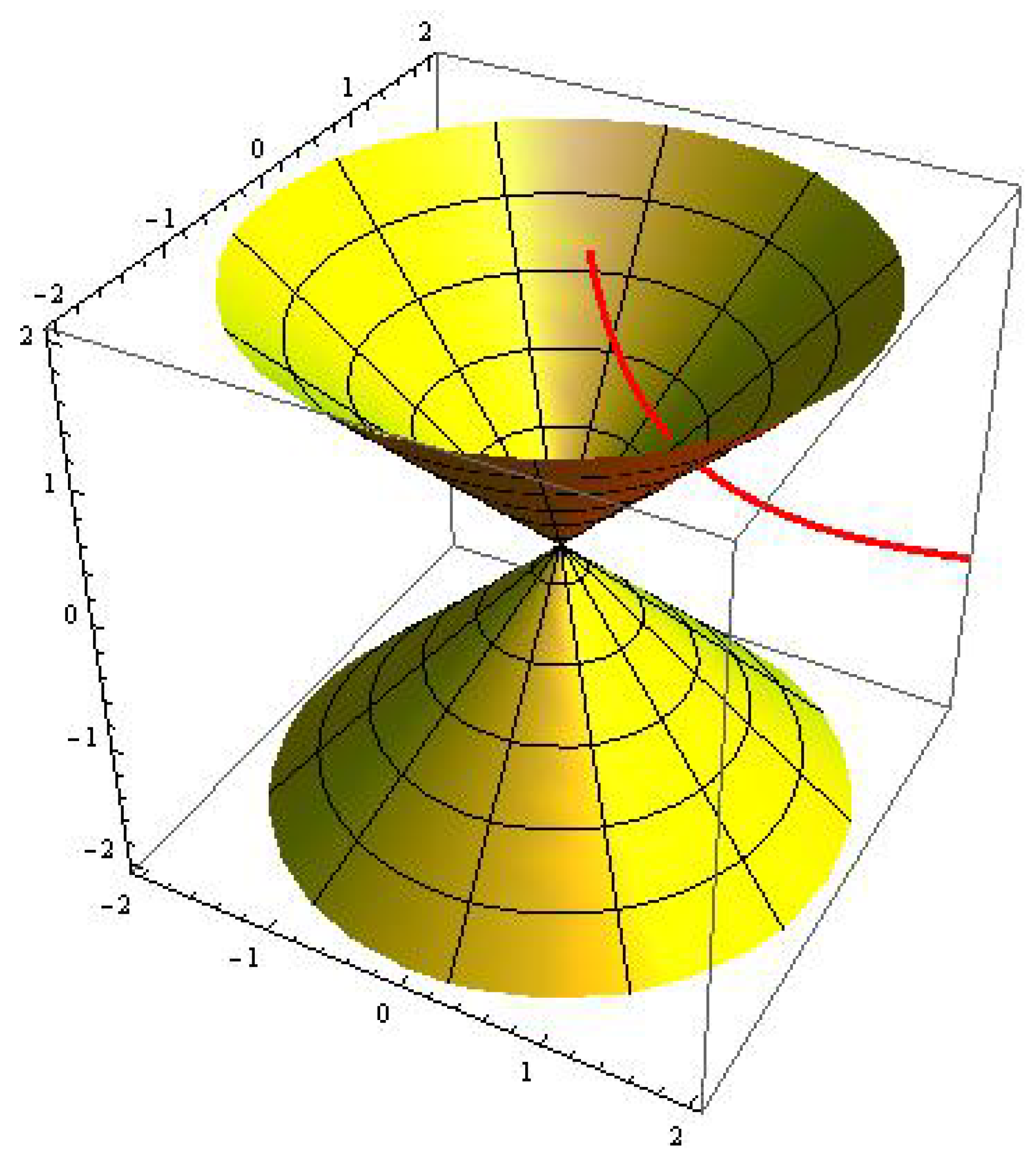
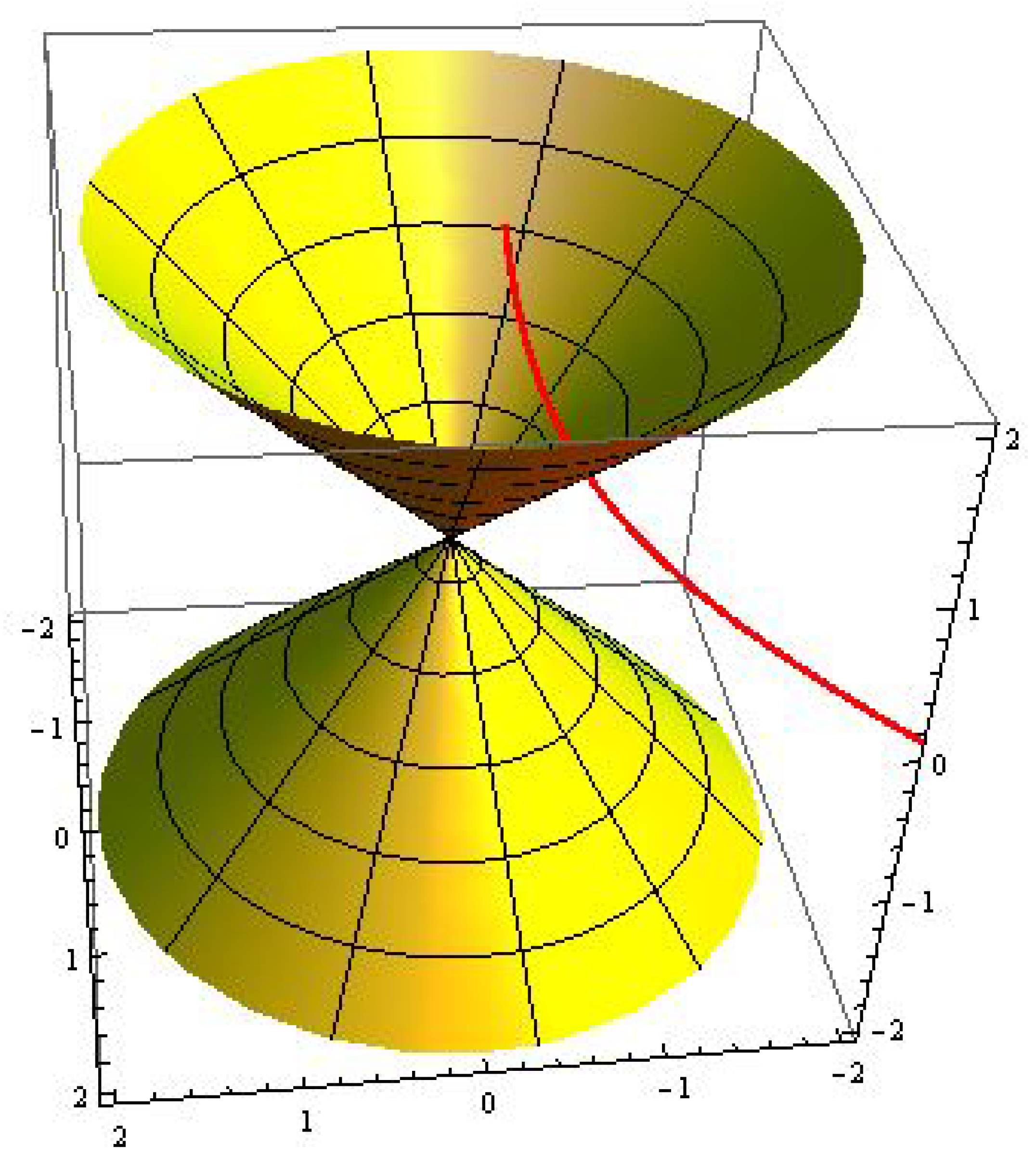
Example 1.

Consider pseudo null curves with constant curvatures.

1. 

$r_1\left(s\right)=(s^2,s^2,-s)$ with $\kappa \left(s\right)=0$ (See Figure 1);

2. 

$r_2\left(s\right)=(e^s,e^s,-s)$ with $\kappa \left(s\right)=1$ (See Figure 2).

3. k-Type Pseudo Null Helices

In this section, we define the k-type pseudo null helices and investigate their properties.

Definition 3

([6]). Let $r\left(s\right):\mathbf{I}\to {\mathbb{E}}_1^3$ be a pseudo null curve with Frenet frame $\{\alpha ,\beta ,\gamma \}$. If there exists a non-zero constant vector field V such that $\langle \alpha ,V\rangle \ne 0$ (respectively, $\langle \beta ,V\rangle \ne 0,\langle \gamma ,V\rangle \ne 0)$ is a constant for all $s\in \mathbf{I}$, then $r\left(s\right)$ is said to be a k-type (k=1,2,3) pseudo null helix and V is called the axis of $r\left(s\right)$.

Remark 3.

If the tangent vector α, principal normal vector β or the binormal vector γ of $r\left(s\right)$ is a constant vector, then every fixed direction V satisfies the above definition. Throughout this paper, we assume this situation never happens.

Let V be the axis of a k-type pseudo null helix $r\left(s\right)$. Then V can be decomposed by

$$V=v_1\alpha \left(s\right)+v_2\beta \left(s\right)+v_3\gamma \left(s\right),$$

(7)

where $v_i=v_i\left(s\right)(i=1,2,3)$ are differentiable functions of arc-length s. Thus

$$v_1=\langle \alpha ,V\rangle ,v_2=\langle \gamma ,V\rangle ,v_3=\langle \beta ,V\rangle .$$

By taking the derivative with respect to s on the both sides of Equation (7), we get

$$(v_1^{\prime }-v_3)\alpha +(v_1+v_2^{\prime }+v_2\kappa )\beta +(v_3^{\prime }-v_3\kappa )\gamma =0,$$

which implies

$$\left\{\begin{array}{c}{v}_1^{\prime }-v_3=0,\hfill \\ v_1+v_2^{\prime }+v_2\kappa =0,\hfill \\ v_3^{\prime }-v_3\kappa =0.\hfill \end{array}\right.$$

(8)

3.1. One-Type Pseudo Null Helix

Theorem 3.

Any pseudo null curve is a one-type pseudo null helix in ${\mathbb{E}}_1^3$.

Proof of Theorem 3.

Based on the definition of one-type pseudo null helix, we have

$$\langle \alpha ,V\rangle =v_1=C_0,$$

(9)

where $C_0$ is a non-zero constant. Differentiating Equation (9) with respect to s, we get

$$\langle \beta ,V\rangle =v_3=0.$$

(10)

From Equation (8), the curvature $\kappa \left(s\right)$ is an arbitrary function of arc-length s, together with Equations (9) and (10), we get

$$v_1=C_0,v_2=e^{-\int \kappa ds}(c_1-C_0\int e^{\int \kappa ds}ds),v_3=0,$$

where $c_1\in \mathbb{R}.$

Conversely, if $\kappa \left(s\right)$ is an arbitrary function, we can define a vector field V as

$$V=c\alpha +e^{-\int \kappa ds}(c_1-c\int e^{\int \kappa ds}ds)\beta ,(c_1,c\in \mathbb{R}andc\ne 0).$$

Then, we have $V^{\prime }=0$ and $\langle \alpha ,V\rangle =c$. This completes the proof. □

As a consequence of Theorem 3, we have

Corollary 1.

Let $r\left(s\right)$ be a one-type pseudo null helix. Then the axis V is spacelike and it can be read as

$$V=c\alpha +e^{-\int \kappa ds}(c_1-c\int e^{\int \kappa ds}ds)\beta$$

(11)

or it can be represented by the structure function as

$$V=c\alpha +\frac{1}{g^{\prime }}(c_1-cg)\beta ,$$

(12)

where $c_1,c\in \mathbb{R}$ and $c\ne 0$.

Proof of Corollary 1.

From Theorem 3, the axis V in Equation (11) can be obtained and it is spacelike from $\langle V,V\rangle =c^2>0$. Substituting Equation (6) to Equation (11), we can get Equation (12) easily. □

3.2. Two-Type Pseudo Null Helix

Theorem 4.

There does not exist two-type pseudo null helix in ${\mathbb{E}}_1^3$.

Proof of Theorem 4.

Based on the definition of two-type pseudo null helix, we have $\langle \beta ,V\rangle =v_3=C_0$, where $C_0$ is a non-zero constant. Substituting $v_3=C_0$ into Equation (8), we have $\kappa C_0=0$. Due to $C_0\ne 0$, we know $\kappa \left(s\right)\equiv 0$. At the same time, from Theorem 2 and the Frenet formula of Equation (1), we know $\beta =(a,a,0),(0\ne a\in \mathbb{R})$ is a constant vector. This contradicts Remark 3. □

3.3. Three-Type Pseudo Null Helix

Theorem 5.

Let $r\left(s\right)$ be a pseudo null curve in ${\mathbb{E}}_1^3$. Then $r\left(s\right)$ is a three-type pseudo null helix if and only if its curvature $\kappa \left(s\right)$ satisfies

$${\kappa }^{″}\left(s\right)={\kappa }^{\prime }\left(s\right)\kappa \left(s\right).$$

Explicitly, the curvature function $\kappa \left(s\right)$ can be written as

1. 

$\kappa \left(s\right)=-2{(s+c_1)}^{-1};$

2. 

$\kappa \left(s\right)=2atana(s+c_2);$

3. 

$\kappa \left(s\right)=\frac{a+a{e}^{a(s+c_3)}}{1-e^{a(s+c_3)}},$

where $a>0$ and $c_i(i=1,2,3)\in \mathbb{R}$.

Proof of Theorem 5.

Based on the definition of three-type pseudo null helix, we have

$$\langle \gamma ,V\rangle =v_2=C_0,$$

(13)

where $C_0$ is a non-zero constant. Then, by taking derivative on both sides of Equation (13), we get

$$\langle \alpha ,V\rangle +\kappa \langle \gamma ,V\rangle =0.$$

(14)

Due to Equation (14) together with Equation (8), we obtain

$$v_1=-\kappa C_0,v_2=C_0,v_3=-{\kappa }^{\prime }{C}_0.$$

(15)

Substituting $v_3$ into the third equation of Equation (8), we know

$${\kappa }^{″}\left(s\right)={\kappa }^{\prime }\left(s\right)\kappa \left(s\right).$$

(16)

Let ${\kappa }^{\prime }\left(s\right)=p\left(\kappa \right)$, then Equation (16) can be rewritten by

$$\frac{dp}{d\kappa }p=\kappa p.$$

Since the curve $r\left(s\right)$ is a planar curve when $\kappa \left(s\right)$ is a constant [11], then $p\ne 0$ for a three-type pseudo null helix. Solving the following differential equation

$$\frac{dp}{dk}=\kappa ,$$

we have

$$2{\kappa }^{\prime }={\kappa }^2+c_0,(c_0\in \mathbb{R}).$$

(17)

Solving the differential Equation (17), we get three cases as follows.

Case 1: $c_0=0$. It is easy to get

$$\kappa \left(s\right)=-\frac{2}{s+c_1},(c_1\in \mathbb{R}).$$

Taking it into Equation (15), we have

$$v_1=\frac{2C_0}{s+c_1},v_2=C_0,v_3=-\frac{2C_0}{{(s+c_1)}^2}.$$

Case 2: $c_0=4a^2>0,(a>0)$. By direct calculations, we obtain

$$\kappa \left(s\right)=2atana(s+c_2),(c_2\in \mathbb{R}).$$

Substituting it into Equation (15), we get

$$v_1=-2a{C}_{0}tana(s+c_2),v_2=C_0,v_3=-2a^2{C}_0{sec}^{2}a(s+c_2).$$

Case 3: $c_0=-a^2<0,(a>0)$. After direct calculations, we obtain

$$\kappa \left(s\right)=\frac{a+a{e}^{a(s+c_3)}}{1-e^{a(s+c_3)}},(c_3\in \mathbb{R}).$$

Taking it into Equation (15), we have

$$v_1=\frac{a{C}_0+a{C}_0{e}^{a(s+c_3)}}{e^{a(s+c_3)}-1},v_2=C_0,v_3=-\frac{2a^2{C}_0{e}^{a(s+c_3)}}{{(1-e^{a(s+c_3)})}^2}.$$

Conversely, when $\kappa \left(s\right)$ satisfies one of the following conditions, we can choose an appropriate constant vector V as

• $V=\frac{2c}{s+c_1}\alpha +c\beta -\frac{2c}{{(s+c_1)}^2}\gamma$ for $\kappa \left(s\right)=-\frac{2}{s+c_1};$
• $V=-2catana(s+c_2)\alpha +c\beta -2c{a}^2{sec}^{2}a(s+c_2)\gamma$ for $\kappa \left(s\right)=2atana(s+c_2);$
• $V=\frac{ca+ca{e}^{a(s+c_3)}}{e^{a(s+c_3)}-1}\alpha +c\beta -\frac{2c{a}^2{e}^{a(s+c_3)}}{{(1-e^{a(s+c_3)})}^2}\gamma$ for $\kappa \left(s\right)=\frac{a+a{e}^{a(s+c_3)}}{1-e^{a(s+c_3)}}.$

Obviously, for each case, we have $V^{\prime }=0$ and $\langle \gamma ,V\rangle =c,(0\ne c\in \mathbb{R})$. □

As a consequence of Theorem 5, we have

Corollary 2.

Let $r\left(s\right)$ be a three-type pseudo null helix. Then the axis V can be read as

1. 

when $\kappa \left(s\right)=-\frac{2}{s+c_1}$, the axis V is lightlike. And

$$V=\frac{2c}{s+c_1}\alpha +c\beta -\frac{2c}{{(s+c_1)}^2}\gamma ;$$

2. 

when $\kappa \left(s\right)=2atana(s+c_2)$, the axis V is timelike. And

$$V=-2catana(s+c_2)\alpha +c\beta -2c{a}^2{sec}^{2}a(s+c_2)\gamma ;$$

3. 

when $\kappa \left(s\right)=\frac{a+a{e}^{a(s+c_3)}}{1-e^{a(s+c_3)}}$, the axis V is spacelike. And

$$V=\frac{ca+ca{e}^{a(s+c_3)}}{e^{a(s+c_3)}-1}\alpha +c\beta -\frac{2c{a}^2{e}^{a(s+c_3)}}{{(1-e^{a(s+c_3)})}^2}\gamma ,$$

where $0<a,0\ne c,c_i(i=1,2,3)\in \mathbb{R}$.

From Theorem 5 and Proposition 3, we have

Corollary 3.

Let $r\left(s\right)$ be a three-type pseudo null helix. Then the structure functions $f\left(s\right),g\left(s\right)$ of $r\left(s\right)$ can be written as

1. 

when $\kappa \left(s\right)=-\frac{2}{s+c},$ $f\left(s\right)=\frac{s+1}{s-1},g\left(s\right)=-\frac{1}{s}$;

2. 

when $\kappa \left(s\right)=2atana(s+c),$ $f\left(s\right)=\frac{-a+tanas}{a+tanas},g\left(s\right)=\frac{tanas}{a}$;

3. 

when $\kappa \left(s\right)=\frac{a+a{e}^{a(s+c)}}{1-e^{a(s+c)}},$ $f\left(s\right)=\frac{1-a(1-e^{as})}{1+a(1-e^{as})},g\left(s\right)=\frac{1}{a(1-e^{as})}$,

where $0<a,c\in \mathbb{R}$.

Proof of Corollary 3.

When $\kappa \left(s\right)=-\frac{2}{s+c}$, by the parameter transformation $s\to s+s_0$, ($s_0\in \mathbb{R}$), we can let $c=0$, i.e., $\kappa \left(s\right)=-\frac{2}{s}$. From Equation (6), we know $\frac{g^{″}}{g^{\prime }}=-\frac{2}{s},$ then $g\left(s\right)=-\frac{1}{s}+c_1,(c_1\in \mathbb{R})$. Without loss of generality, we can put $c_1=0$, then $g\left(s\right)=-\frac{1}{s}.$ Furthermore, from Equation (5), we have

$$c_{2}f\left(s\right)=\frac{s+1}{s-1},(0\ne c_2\in \mathbb{R}).$$

By an appropriate transformation, we can let $c_2=1$. Thus, $f\left(s\right)=\frac{s+1}{s-1}.$

Similarly, when $\kappa \left(s\right)=2atana(s+c)$ and $\kappa \left(s\right)=\frac{a+a{e}^{a(s+c)}}{1-e^{a(s+c)}}$, by the parameter transformation, we can get

$$\frac{g^{″}}{g^{\prime }}=2atanasand\frac{g^{″}}{g^{\prime }}=\frac{a+a{e}^{as}}{1-e^{as}}.$$

Solving the above two differential equations analogous to the first case, i.e., $\kappa \left(s\right)=-\frac{2}{s+c}$, we can get the other two conclusions easily. □

Substituting the conclusions obtained in Corollary 3 to the representation formula shown by Proposition 2, after direct integrations, we have

Corollary 4.

Let $r\left(s\right)$ be a three-type pseudo null helix. Then $r\left(s\right)$ can be written as

1. 

$r\left(s\right)=(ln|s|,-ln|s|,s)$ for $\kappa \left(s\right)=-\frac{2}{s+c}$;

2. 

$r\left(s\right)=-\frac{1}{a^2}\left(ln|cosas|,ln|cosas|,a^{2}s\right)$ for $\kappa \left(s\right)=2atana(s+c)$;

3. 

$r\left(s\right)=\frac{1}{a^2}\left(ln|1-e^{-as}|,-ln|1-e^{-as}|,a^{2}s\right)$ for $\kappa \left(s\right)=\frac{a+a{e}^{a(s+c)}}{1-e^{a(s+c)}}$,

where $0<a,c\in \mathbb{R}$.

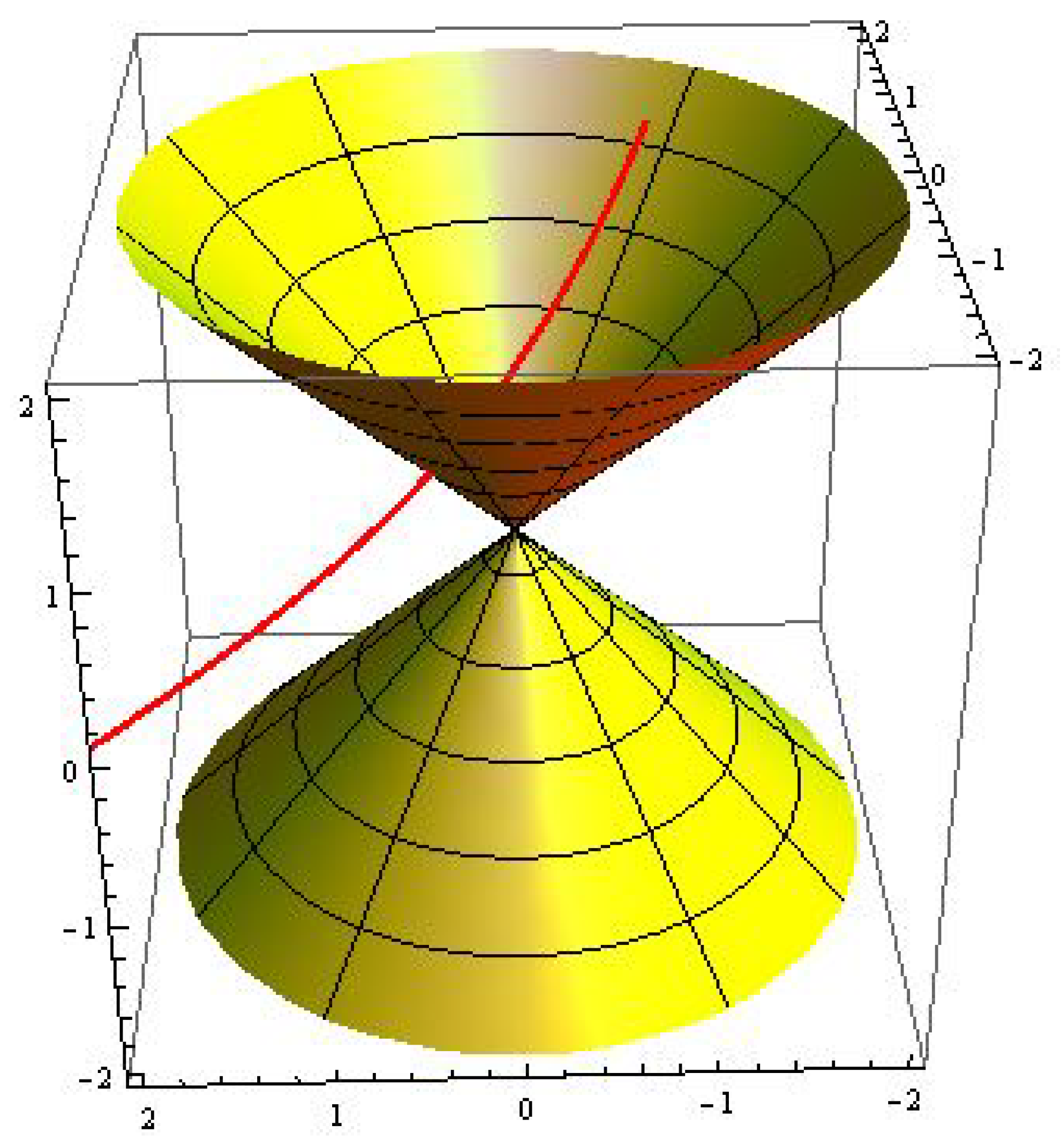
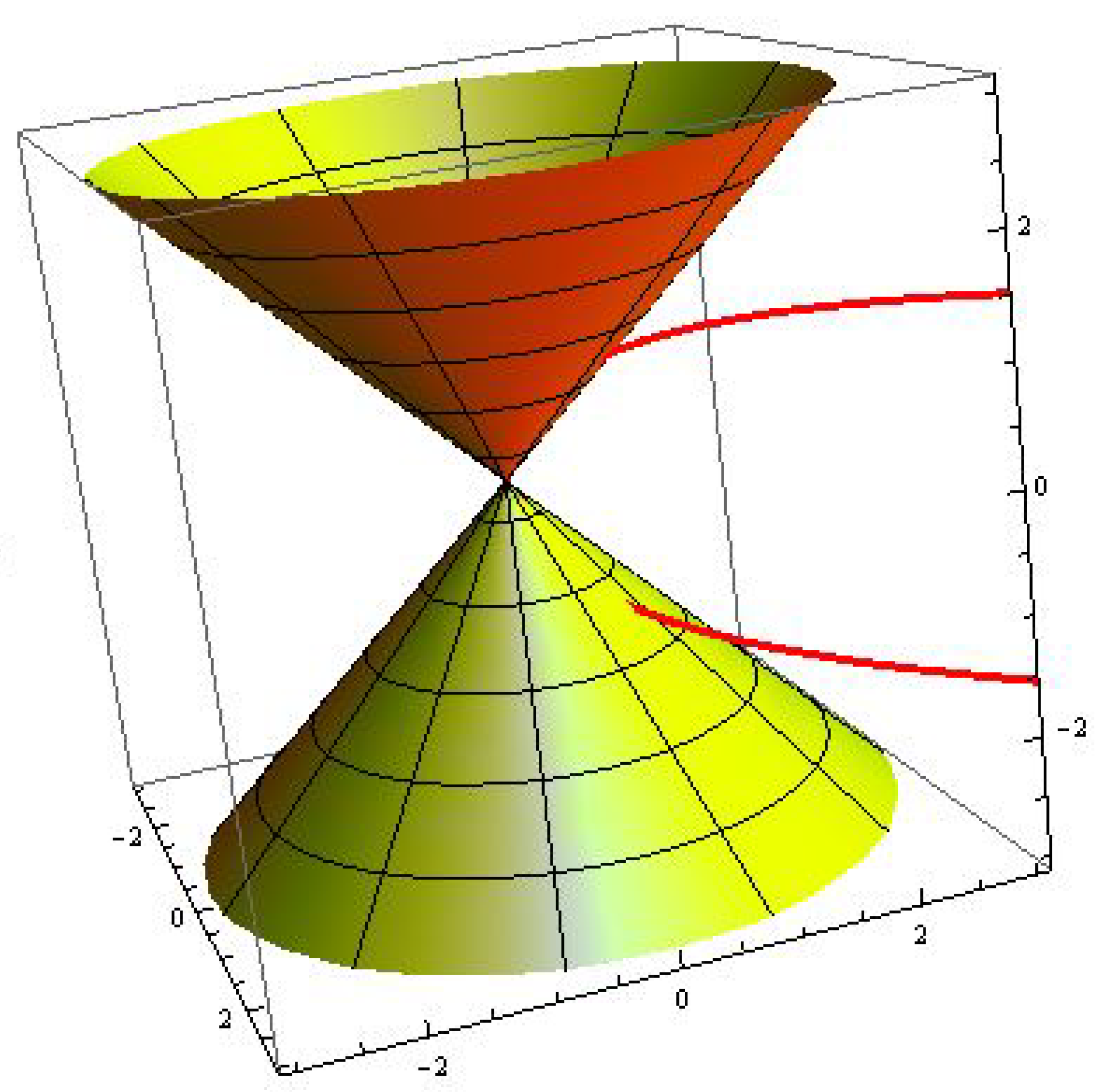
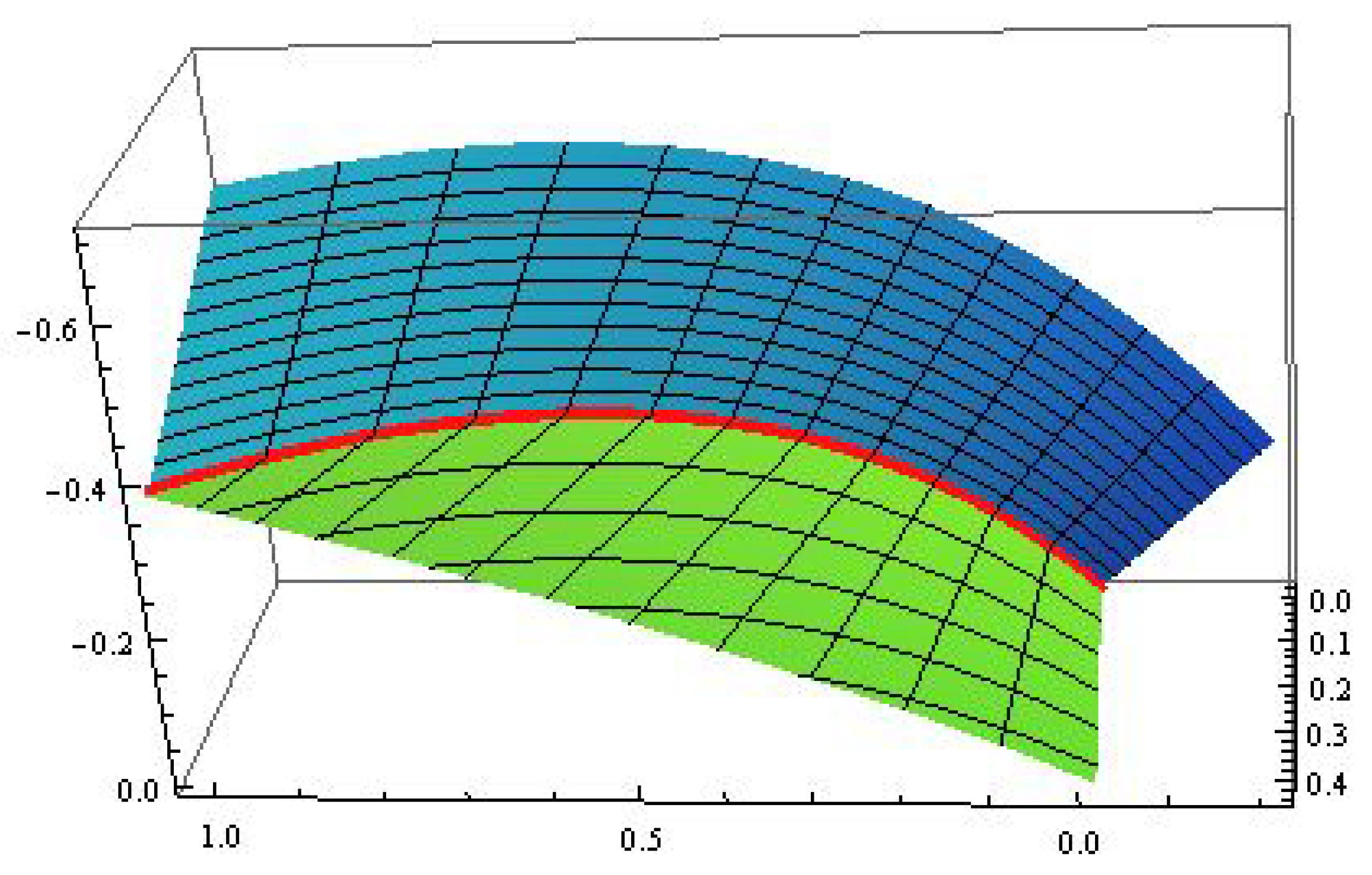
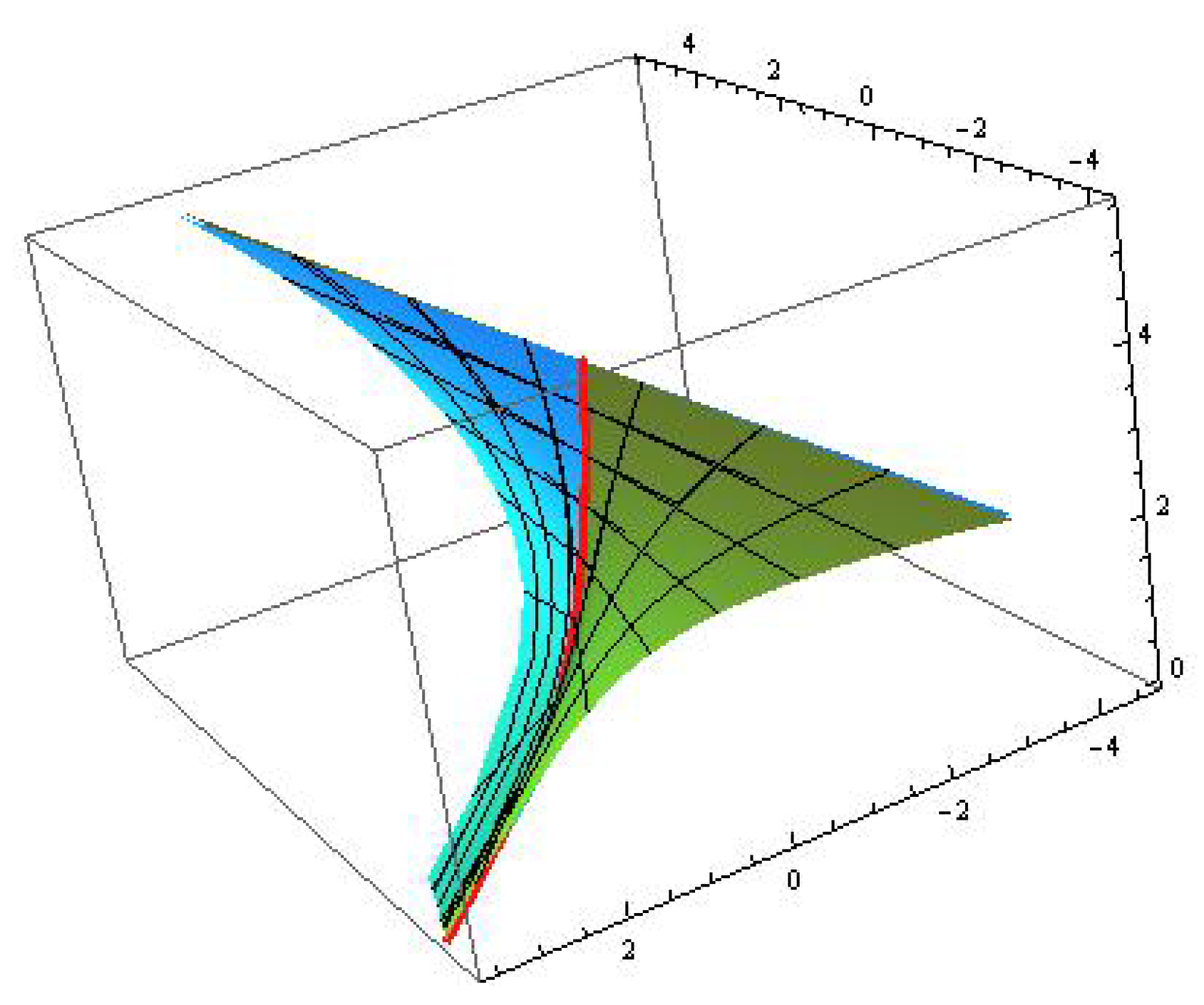
Example 2.

Consider three-type pseudo null helices:

1. 

$r_1\left(s\right)=(lns,-lns,s),(s>0)$ (see Figure 3);

2. 

$r_2\left(s\right)=-\left(lncoss,lncoss,s\right),(-\frac{\pi }{2}+2n\pi <s<\frac{\pi }{2}+2n\pi ,n\in \mathbb{Z})$ (see Figure 4);

3. 

$r_3\left(s\right)=\left(ln(1-e^{-s}),-ln(1-e^{-s}),s\right),(s>0)$ (see Figure 5).

4. Embankment Surfaces with Pseudo Null Base Curves

Given a one parameter family of regular implicit surfaces ${\Phi }_c:f(X,c)=0,c\in [c_1,c_2].$ The intersection curve of two neighbored surfaces ${\Phi }_c$ and ${\Phi }_{c+\Delta c}$ fulfills the two equations $f(X,c)=0$ and $f(X,c+\Delta c)=0.$ We consider the limit for $\Delta c\to 0$ and get

$$f_c(X,c)=\underset{\Delta c\to 0}{lim}\frac{f(X,c)-f(X,c+\Delta c)}{\Delta c}=0,$$

which motivates the following definition.

Definition 4

([7]). Let ${\Phi }_c:f(X,c)=0,c\in [c_1,c_2]$ be a one parameter family of regular implicit ${\mathbf{C}}^2$-surfaces. The surface defined by the two equations

$$f(X,c)=0,f_c(X,c)=0$$

is called an envelope of the given family of surfaces.

Definition 5

([7]). Let $\Gamma :X=\mathbf{c}\left(s\right)=\left(a\right(s),b(s),c(s\left)\right)$ be a regular space curve and $0<m\in \mathbb{R}$ with $|m{c}^{\prime }|<\sqrt{{a^{\prime }}^2+{b^{\prime }}^2}.$ The envelope of the one parameter family of cones

$$f(X;s)={(x-a\left(s\right))}^2+{(y-b\left(s\right))}^2-m^2{(z-c\left(s\right))}^2=0$$

is called an embankment surface and Γ its base curve.

Remark 4

([7]). In fact, the embankment surface in above definition is consisted by two ruled surfaces which can be represented as follows

$$X=X(s,t)=\mathbf{c}\left(s\right)+t{b}_{1,2}\left(s\right)$$

with $b_1\left(s\right)=({\xi }_1\left(s\right),{\eta }_1\left(s\right),1),b_2\left(s\right)=({\xi }_2\left(s\right),{\eta }_2\left(s\right),1)$ and $({\xi }_1\left(s\right),{\eta }_1\left(s\right)),({\xi }_2\left(s\right),{\eta }_2\left(s\right))$ are intersection points of the circle ${\xi }^2+{\eta }^2-m^2=0$ and the line $\xi a^{\prime }+\eta b^{\prime }-m^2{c}^{\prime }=0.$

Motivated by the generating process of embankment surfaces, we can construct a kind of embankment surface in ${\mathbb{E}}_1^3$ based on a pseudo null curve as follows.

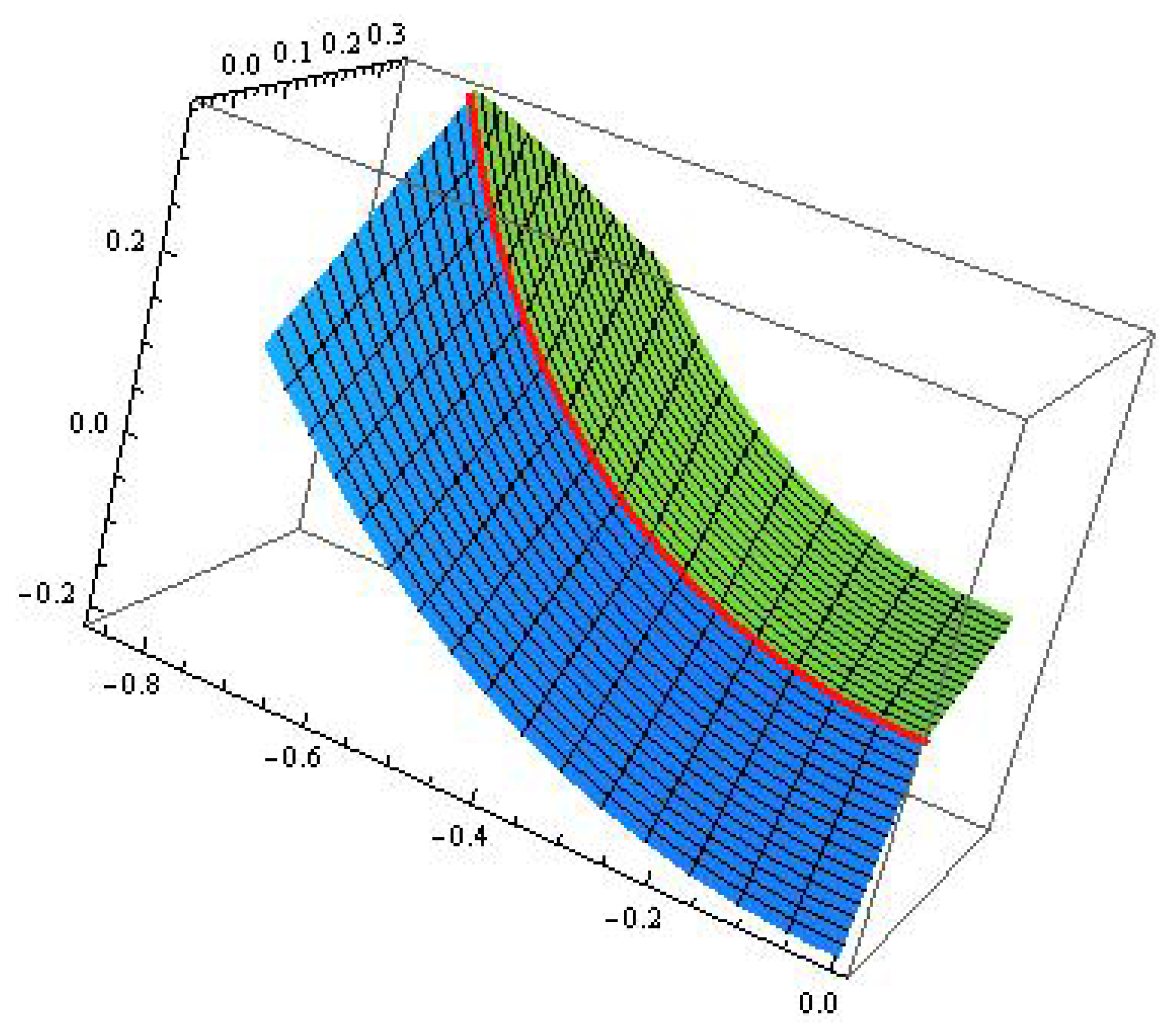
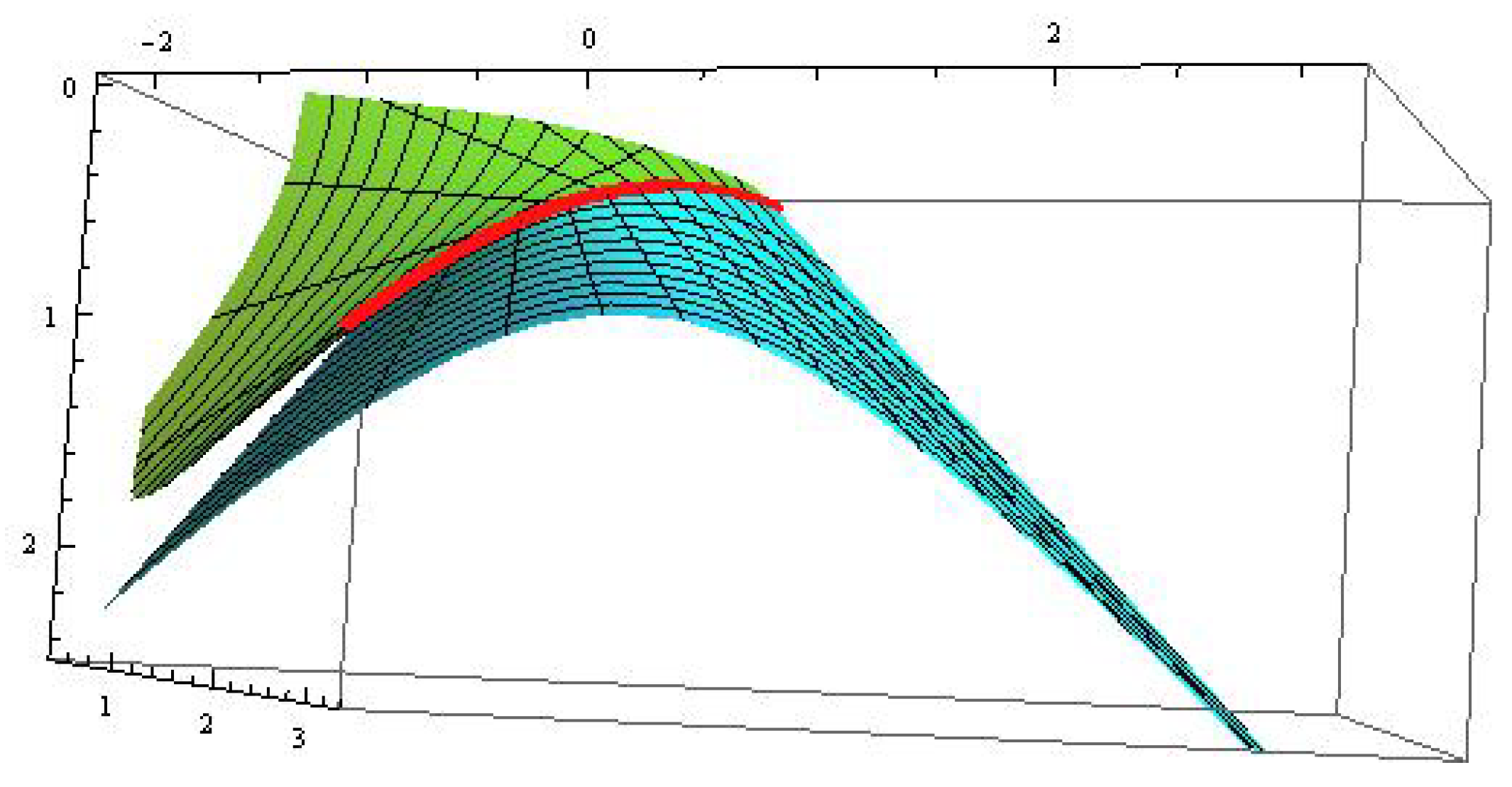
Definition 6.

Let $r\left(s\right)$ be a pseudo null curve framed by $\{\alpha ,\beta ,\gamma \}$ in ${\mathbb{E}}_1^3$ and $b_{1,2}\left(s\right)=\frac{1}{\sqrt{2}}(\beta \pm \gamma )$. Then the surface partner

$$X_{1,2}(s,t)=r\left(s\right)+\frac{t}{\sqrt{2}}(\beta \pm \gamma )$$

is called an embankment surface and $r\left(s\right)$ its base curve.

Example 3.

Consider an embankment surface $X_{1,2}(s,t)=r\left(s\right)+\frac{t}{\sqrt{2}}(\beta \pm \gamma )$ with a pseudo null base curve $r\left(s\right)$ of curvature $\kappa \left(s\right)=\frac{1}{s+1}$ (see Figure 6).

From Proposition 3, the structure functions of $r\left(s\right)$ are

$$f\left(s\right)=\frac{s^2+2s-2}{s^2+2s+2},g\left(s\right)=\frac{s^2+2s}{2}.$$

Then, by Proposition 2, we know

$$r\left(s\right)=\frac{\sqrt{2}}{18}(\sqrt{2}{s}^3+3\sqrt{2}{s}^2,s^3+3s^2+9s,s^3+3s^2-9s).$$

From Proposition 4, the principal normal vector β and binormal vector γ of $r\left(s\right)$ are $\beta =\frac{\sqrt{2}(s+1)}{3}(\sqrt{2},1,1)$ and

$$\gamma =-\frac{1}{12(s+1)}\left(s^4+4s^3+4s^2+9,\frac{s^4+4s^3+10s^2+12s-9}{\sqrt{2}},\frac{s^4+4s^3-2s^2-12s-9}{\sqrt{2}}\right).$$

Combining the conclusions obtained in Section 3, when the base curve of an embankment surface is a three-type pseudo null helix, we have

Theorem 6.

Let $X_{1,2}(s,t)$ be an embankment surface with three-type pseudo null helix $r\left(s\right)$ as its base curve. Then $X_{1,2}(s,t)$ can be classified as

1. 

when $\kappa \left(s\right)=-\frac{2}{s+c}$, $X_{1,2}(s,t)=(ln|s|,-ln\left|s\right|,s)+\frac{t}{\sqrt{2}}(\beta \pm \gamma ),$ where

$$\beta =\frac{1}{s^2}(-1,1,0),\gamma =\frac{1}{2}(s^2+1,s^2-1,2s);$$

2. 

when $\kappa \left(s\right)=2atana(s+c)$, $X_{1,2}(s,t)=-\frac{1}{a^2}\left(ln|cosas|,ln|cosas|,a^{2}s\right)+\frac{t}{\sqrt{2}}(\beta \pm \gamma ),$ where

$$\beta ={sec}^{2}as(1,1,0),\gamma =-\frac{1}{2a^2}\left({sin}^{2}as+a^2{cos}^{2}as,{sin}^{2}as-a^2{cos}^{2}as,asin2as\right);$$

3. 

when $\kappa \left(s\right)={\displaystyle \frac{a+a{e}^{a(s+c)}}{1-e^{a(s+c)}}}$, $X_{1,2}(s,t)=\frac{1}{a^2}\left(ln|1-e^{-as}|,-ln|1-e^{-as}|,a^{2}s\right)+\frac{t}{\sqrt{2}}(\beta \pm \gamma ),$ where

$$\beta =\frac{e^{as}}{{(1-e^{as})}^2}\left(-1,1,0\right),\gamma =\frac{1}{2a^2{e}^{as}}\left(a^2{(e^{as}-1)}^2+1,a^2{(e^{as}-1)}^2-1,2a(e^{as}-1)\right),$$

where $0<a$, $c\in \mathbb{R}.$

Proof of Theorem 6.

From Corollary 4, when $\kappa \left(s\right)=-\frac{2}{s+c}$ $(c\in \mathbb{R})$, the pseudo null curve $r\left(s\right)=(ln|s|,-ln|s|,s)$. According to Equation (1), we obtain

$$\alpha =r^{\prime }\left(s\right)=\frac{1}{s}(1,-1,s),\beta ={\alpha }^{\prime }=\frac{1}{s^2}(-1,1,0),\gamma =(\frac{1}{2}+c_1{s}^2,-\frac{1}{2}+c_2{s}^2,s+c_3{s}^2),$$

where $c_1,c_2,c_3$ are constants and related by $\langle \alpha ,\gamma \rangle =0,\langle \beta ,\gamma \rangle =1,\langle \gamma ,\gamma \rangle =0.$ Through some direct calculations, we obtain $c_1=c_2=\frac{1}{2},c_3=0.$ Therefore

$$\gamma =\frac{1}{2}(s^2+1,s^2-1,2s).$$

Similar to the first case, we can get the other two results, their explicit proofs are omitted here. □

Example 4.

Consider the embankment surfaces $X_{1,2}(s,t)$ with a three-type pseudo null helix stated in Example 2 as its base curve.

1. 

The embankment surface with base curve $r\left(s\right)=(lns,-lns,s),(s>0)$ are read as (see Figure 7)

$$X_{1,2}(s,t)=(lns,-lns,s)+\frac{t}{\sqrt{2}}(-\frac{1}{s^2}\pm \frac{1}{2}(1+s^2),\frac{1}{s^2}\pm \frac{1}{2}(s^2-1),\pm s);$$

2. 

The embankment surface with base curve $r\left(s\right)=-\left(lncoss,lncoss,s\right),(-\frac{\pi }{2}+2n\pi <s<\frac{\pi }{2}+2n\pi ,n\in \mathbb{Z})$ are read as (see Figure 8)

$$X_{1,2}(s,t)=-\left(lncoss,lncoss,s\right)+\frac{t}{\sqrt{2}}({sec}^{2}s\mp \frac{1}{2},{sec}^{2}s\pm \frac{cos2s}{2},\pm \frac{sin2s}{2});$$

3. 

The embankment surface with base curve $r\left(s\right)=\left(ln(1-e^{-s}),-ln(1-e^{-s}),s\right),(s>0)$ are written as (see Figure 9)

$X_{1,2}(s,t)=\left(ln(1-e^{-s}),-ln(1-e^{-s}),s\right)+\frac{t}{\sqrt{2}}\left(\pm \frac{{(1-e^s)}^2+1}{2e^s}-\frac{e^s}{{(1-e^s)}^2},\frac{e^s}{{(1-e^s)}^2}\pm \frac{{(1-e^s)}^2-1}{2e^s},\pm \frac{e^s-1}{e^s}\right)$.

Remark 5.

The idea to study pseudo null curves by constructing structure functions can be extended into other space–times and space forms, such as the hyperbolic space–time and de-Sitter space–time. At the same time, the structure functions of pseudo null curves defined in this work can also be applied to some other submanifolds, such as the canal (tube) submanifold, translation submanifold, product submanifold and rotation submanifold, which play important roles in CAD (CAGD).