Second-Order Parabolic Equation to Model, Analyze, and Forecast Thermal-Stress Distribution in Aircraft Plate Attack Wing–Fuselage
Abstract
1. Problem Introduction
2. Technical Characteristics of the P64 OSCAR B Aircraft
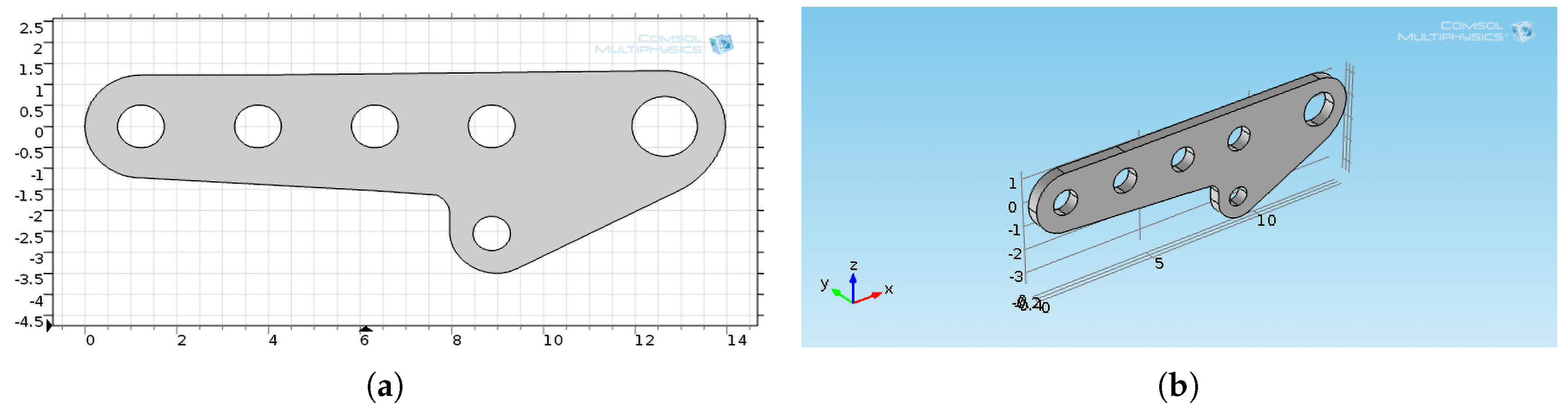
Plate-Attack Wing–Fuselage: Geometrical and Physical Characteristics
3. Proposed Model
3.1. Physical–Mathematical Modeling: Background
3.1.1. Heat Equation
3.1.2. Constitutive Laws
3.2. Initial and Boundary Conditions
3.3. Steady-State Case
4. Preliminary Lemmas
- 1.
- if on and in , then in ;
- 2.
- the following estimation of stability holds:
5. Model Realization in COMSOL-Multiphysics®
5.1. Model Physics
5.2. Model Geometry
5.3. Parameter Setting
5.4. Fixed-Constraint Setting
5.5. Plate Heat Transmission
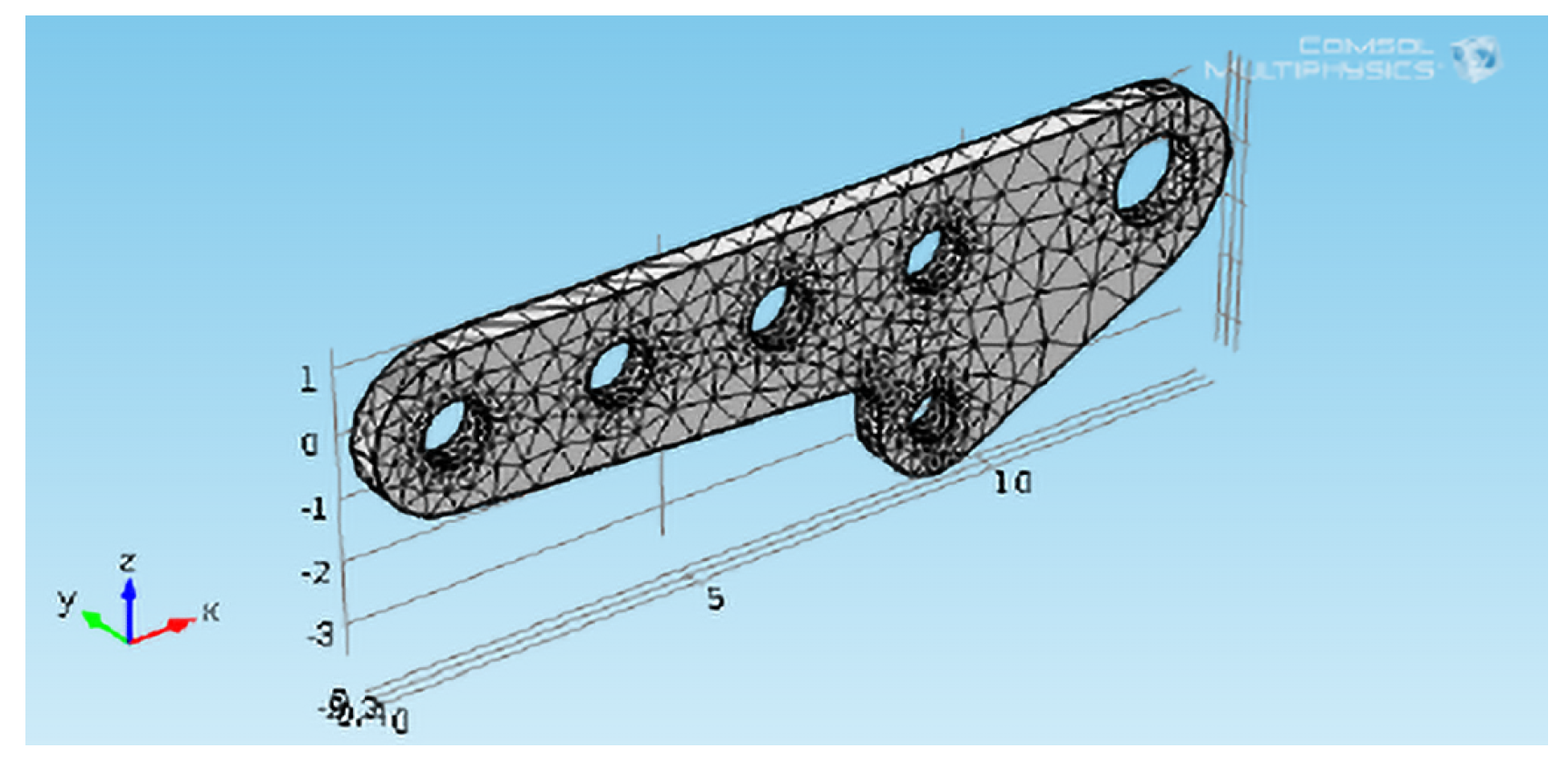
5.6. Mesh Creation
5.7. Choice of Significant Temperatures
5.8. Boundary-Condition Setting
5.9. Determination of Heat-Transfer Coefficients h
6. Relevant Results
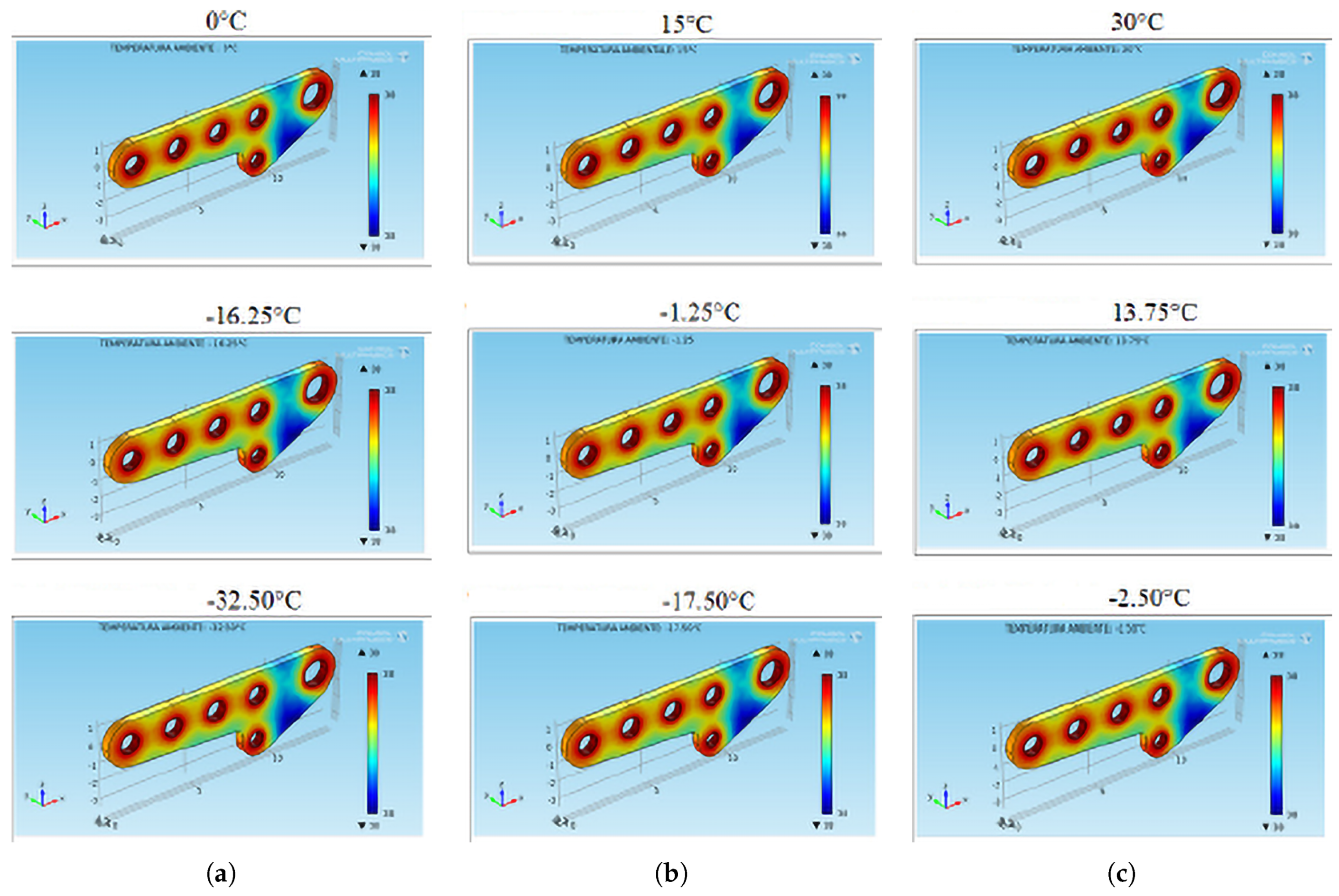
6.1. Simulations in Steady-State Conditions
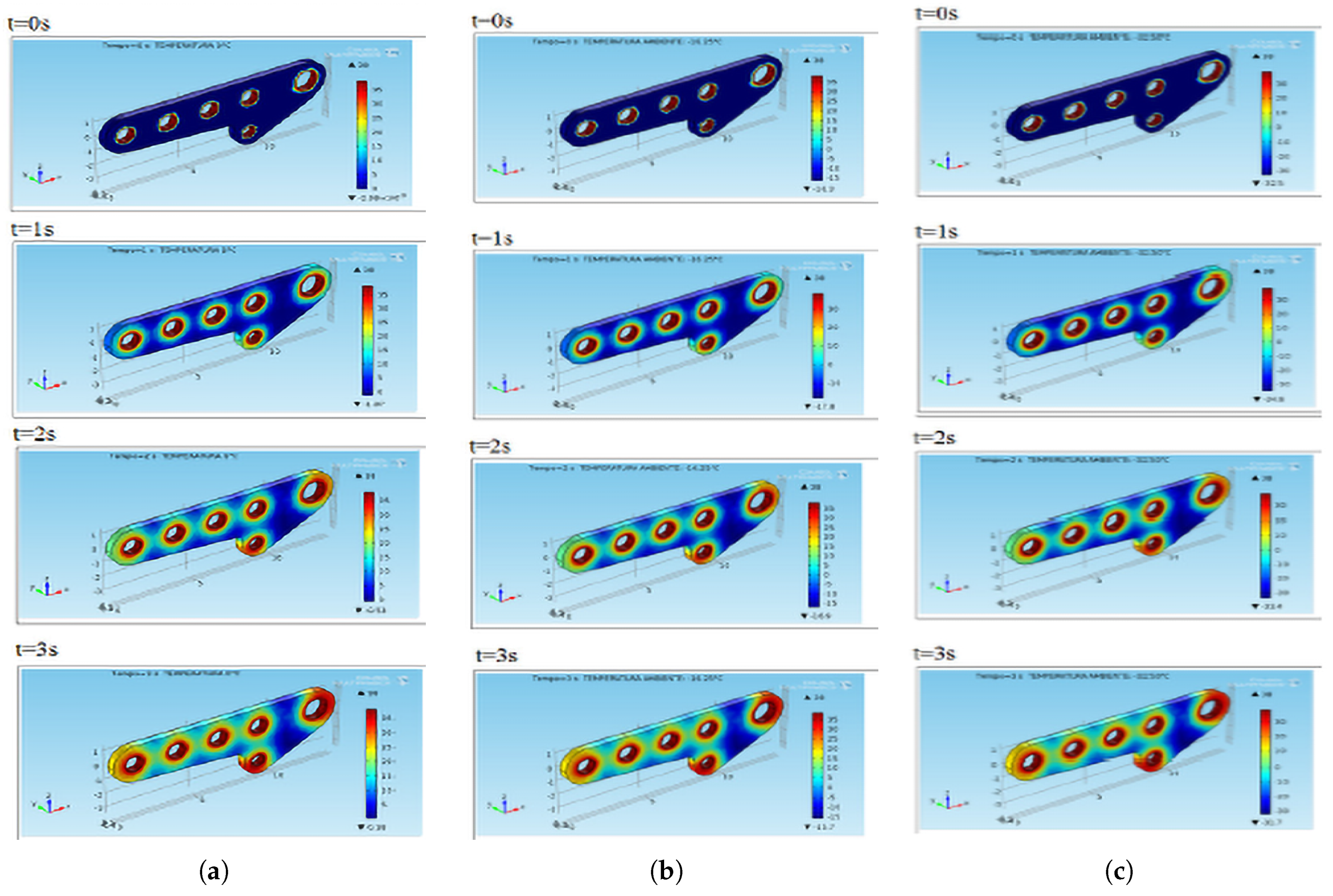
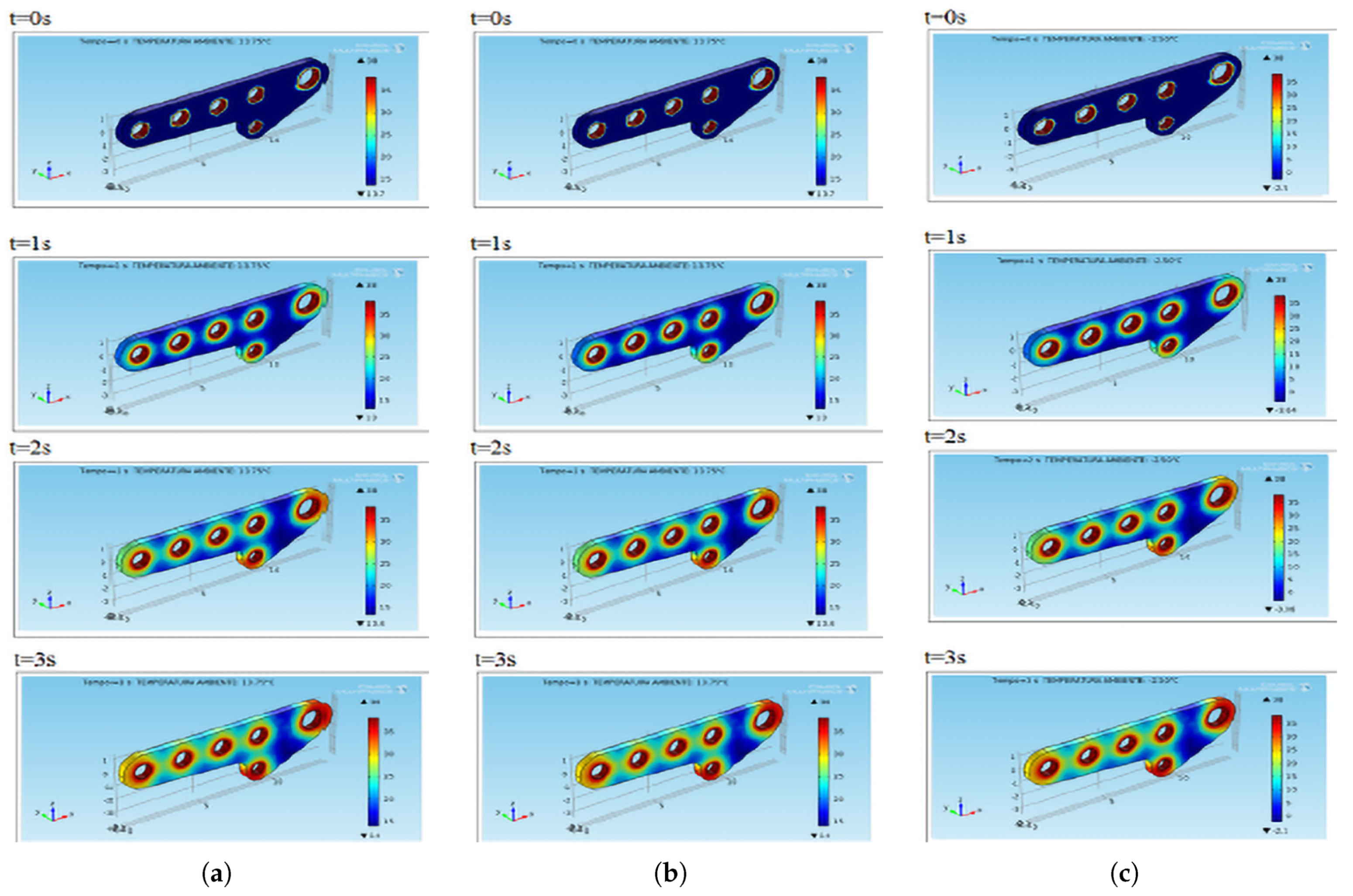
6.2. Simulations in Dynamic Conditions
7. Experimental Investigations by IR Thermal Imaging and Result Comparison
7.1. Pretreatment with Penetrating Liquids
7.2. IR Thermography: Brief Overview
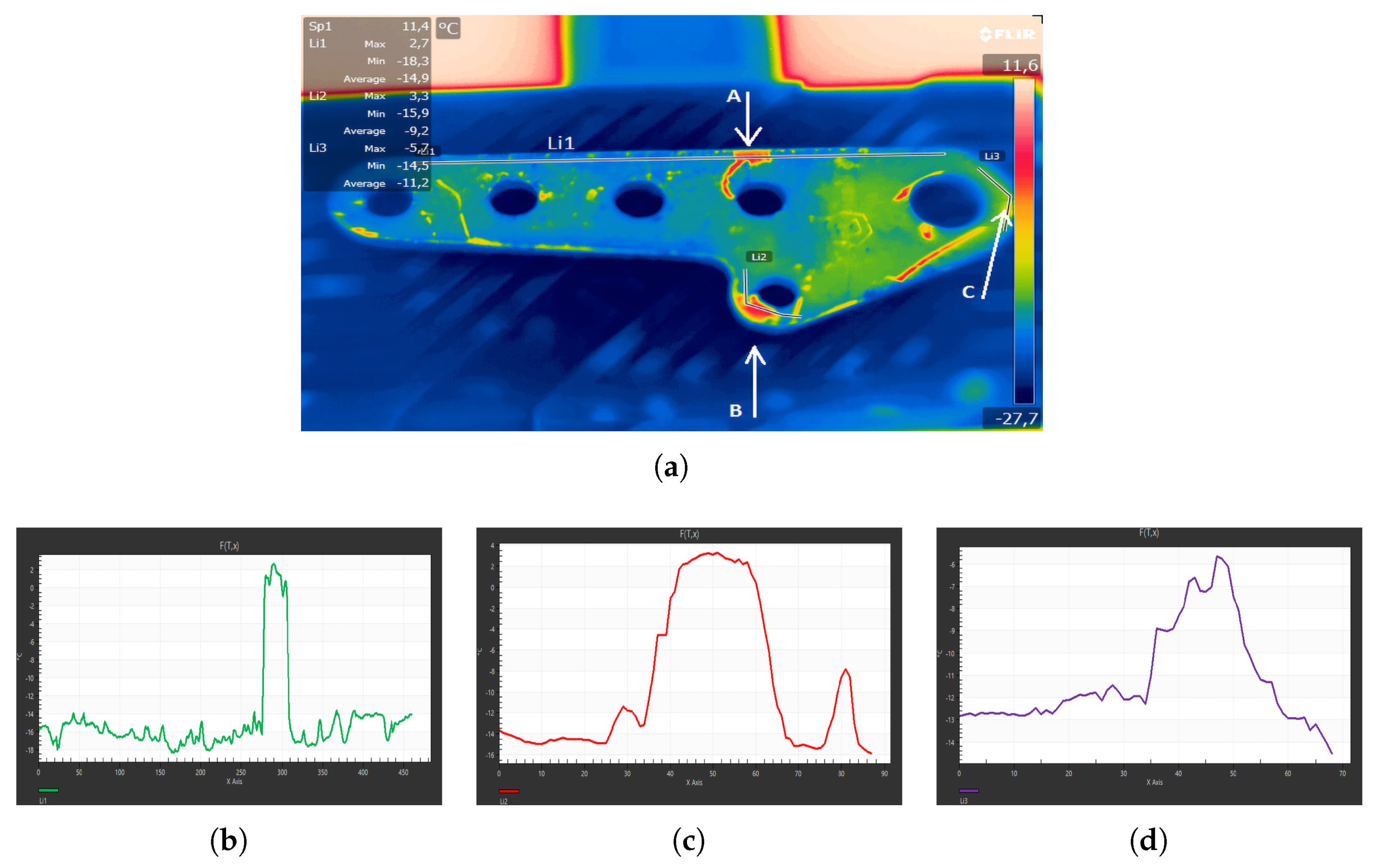
7.3. Thermographic Investigation at −18 (°C)
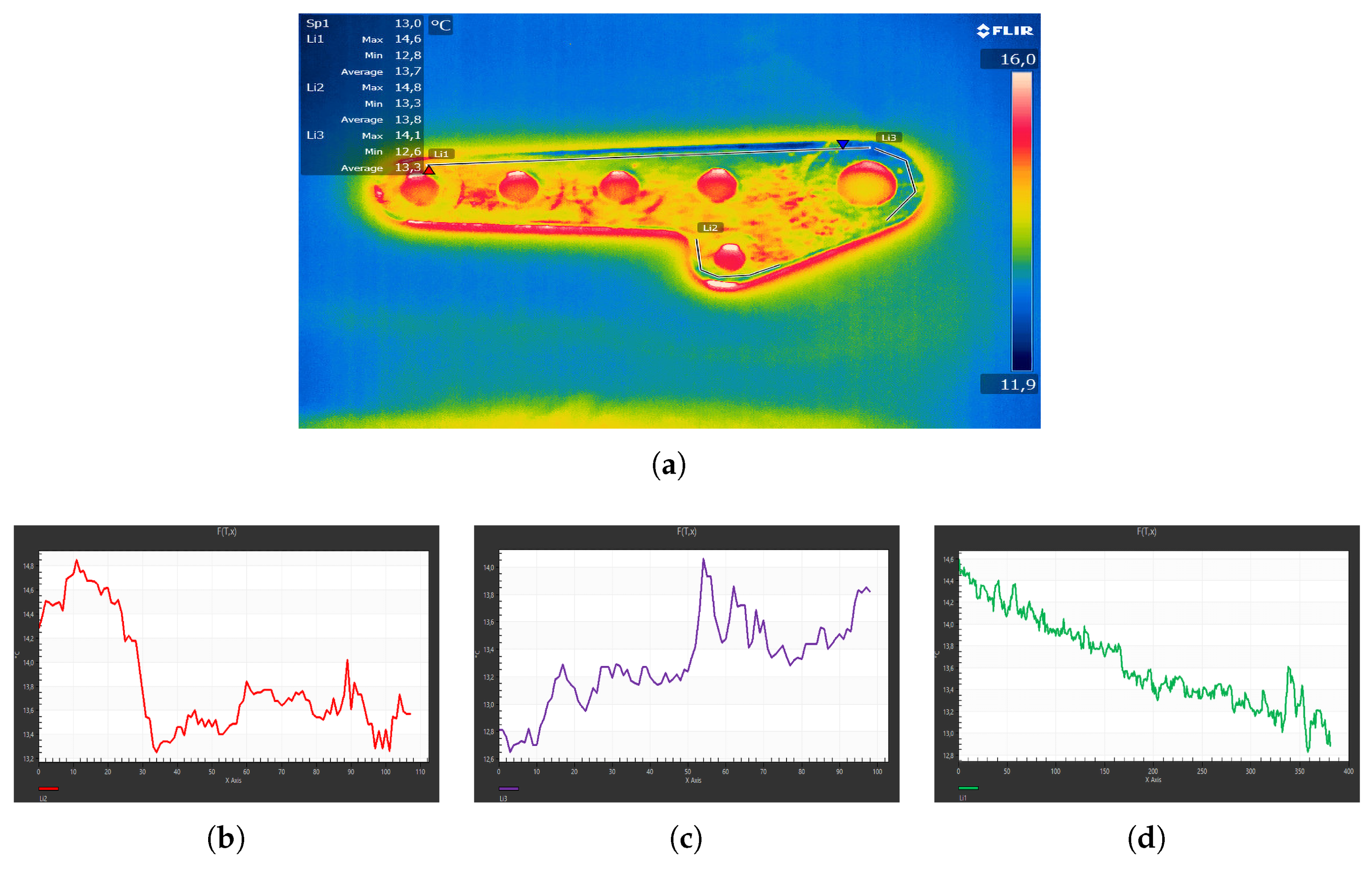
7.4. Thermographic Investigation at 15 (°C)
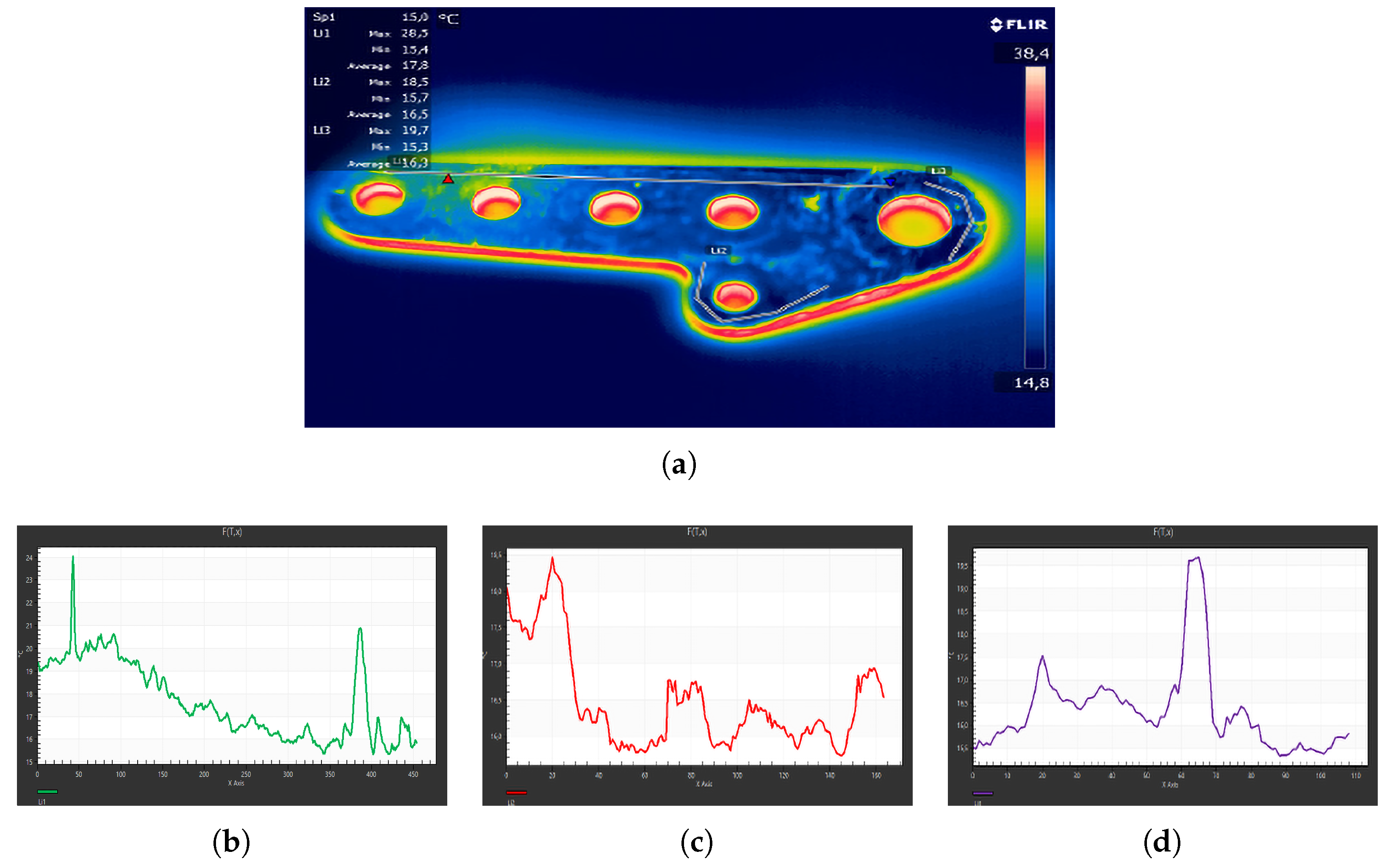
7.5. Thermographic Investigation at 30 (°C)
8. Conclusions and Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| NDT and E | Nondestructive Testing and Evaluation |
| UT | Ultrasound Technique |
| ECs | Eddy Currents |
| P64 OSCAR | The aircraft under study |
| IR | Infrared Thermography |
| PDE | Partial Differential Equation |
| FEM | Finite Element Method |
| UV | Ultraviolet Radiation |
| FLIR SC660 | A type of thermal camera |
| alloy 2024, 3630N | Special aluminum-copper alloy and special steel, respectively |
| C | Carbon |
| Chromium | |
| Molybdenum | |
| Manganese | |
| Silicon | |
| S | Sulfur |
| P | Phosphorus |
| Euclidean n-dimensional space | |
| t | Temporal variable |
| T | Absolute temperature |
| D | Diffusion coefficient |
| f | External heat source |
| Density | |
| r | Rate of heat per unit of mass |
| V | Volume |
| e | Internal energy |
| Heat flux vector | |
| External normal vector | |
| k | Thermal conductivity |
| Specific heat at constant pressure | |
| Boundary of V | |
| Stefan–Boltzmann constant | |
| Surface emissivity | |
| External absolute temperature | |
| h | Heat-transfer coefficient |
| Cylinder | |
| Parabolic frontier | |
| Lateral part of | |
| Diffusive term | |
| Convective term | |
| Reactive term | |
| , | Bounded functions in |
| Plate attack wing–fuselage temperature | |
| , , | Markers |
References
- Yillikci, Y.K.; Findik, F. Survey of Aircraft Materials: Design for Airworthiness and Sustainability. Period. Eng. Nat. Sci. 2013, 1, 8–33. [Google Scholar]
- Fleischer, R.L. High-Strength, High-Temperature Intermetallic Compounds. J. Mater. Sci. 1987, 22, 2281–2288. [Google Scholar] [CrossRef]
- Gladkov, O. To the theory of internal thermal equilibrium in heterogeneous structures. Tech. Phys. Lett. 1998, 24, 29–36. [Google Scholar] [CrossRef]
- Gladkov, O. On the theory of nonlinear thermal conductivity. Tech. Phys. Lett. 2016, 61, 157–164. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, K.; Dixit, A.R. A Review of the Mechanical and Thermal Properties of Graphene and ints Hybrid Polymer Nanocomposites for Strctural Applications. J. Mater. Sci. 2018, 54, 5992–6026. [Google Scholar] [CrossRef]
- Axtman, S.J.; Wilck, J.H. A Review of Aviation Manufacturing and Supply Chain Processes. Int. J. Supply Chain Manag. 2007, 4, 22–27. [Google Scholar]
- Villa dos Santos, C.; Leiva, D.R.; Rodrigues Costa, F.; Rodrigues Gregolin, J.A. Materials Selection for Sustainable Executive Aircraft Interiors. Mater. Res. 2016, 19, 339–352. [Google Scholar] [CrossRef]
- Smurov, M.Y.; Gubenki, A.V.; Ksenofontova, T.Y.; Staroselets, V.S. Comparative Analysis of Innovative Materials Application in Aircraft Building of Different Countries. Int. J. Appl. Eng. Res. 2017, 12, 394–401. [Google Scholar]
- Job, M.; Tesh, M. Air Distasters; Australian Aviation: Brookwell, Australia, 2018. [Google Scholar]
- Kalanchiam, M.; Chinnasamy, M. Advantages of Composite Materials in Aicraft Structures. World Acad. Sci. Eng. Technol. Int. J. Aerosp. Mech. Eng. 2012, 6, 2428–2432. [Google Scholar]
- Sun, J.; Guan, Q.; Liu, Y.; Leng, J. Morphing Aircraft Based on Smart Materials and Structures: A State-of-the-Art Review. J. Intell. Syst. Struct. 2016, 1, 1–24. [Google Scholar] [CrossRef]
- Burrascano, P.; Callegari, S.; Montisci, A.; Ricci, M.; Versaci, M. Ultrasonic Nondestructive Evaluation Systems: Industrial Application Issues.; Springer International Publishing: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Zolfaghari, A. Reliability and sensitivity of visible liquid penetrant NDT for inspection of welded components. Prod. Orient. Test./Nondestruct. Test. 2017, 59, 290–294. [Google Scholar] [CrossRef]
- Versaci, M. Fuzzy Approach and Eddy Currents NDT/NDE Devices in Industrial Applications. Electron. Lett. 2016, 52, 943–945. [Google Scholar] [CrossRef]
- Versaci, M.; La Foresta, F.; Morabito, F.C.; Angiulli, G. A Fuzzy Divergence for Solving Electrostatic Identification Problems for NDT Applications. Int. J. Appl. Electromagn. Mech. 2018, 57, 133–146. [Google Scholar] [CrossRef]
- Angiulli, G.; Versaci, M. A Neuro-Fuzzy Network for the Design of Circular and Triangular Equilateral Microstrip Antennas. Int. J. Infrared Millimeter Waves 2002, 23, 1513–1520. [Google Scholar] [CrossRef]
- Morabito, F.C.; Versaci, M. A Fuzzy Neural Approach to Localizing Holes in Conducting Plates. IEEE Trans. Magn. 2001, 37, 3534–3537. [Google Scholar] [CrossRef]
- Rai, M. Thermal Imaging System and Its Real Time Applications: A Survey. J. Eng. Technol. 2017, 6, 290–303. [Google Scholar]
- Salsa, S. Partial Differential Equation in Action; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Bathe, K.J. Finite Element Procedures; Prentice Hall, Pearson Edication, Inc.: Upper Saddle River, NJ, USA, 2014. [Google Scholar]
- Abali, B.E. An Accurate Finite Element Method for the Numerical Solution of Isothermal and Incompressible Flow of Viscous Fluid. Energies 2019, 4, 5. [Google Scholar] [CrossRef]
- Li, J.; Chen, Y.-T. Computational Partial Differential Equations Using MatLab; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 2019. [Google Scholar]
- Quarteroni, A. Numerical Models For Differential Problems; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Fox, W.P.; Bauldry, W.C. Advanced Problem Solving with Maple: A First Course; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 2019. [Google Scholar]
- Singh, R.; Sadeghi, S.; Shabani, B. Thermal Conductivity Enhancement of Phase Change Materials for Low-Temperature Thermal Energy Storage Applications. Fluids 2019, 12, 75. [Google Scholar] [CrossRef]
- Lienhard, J.H., IV; Lienhard, J.H., V. A Heat Transfer Textbook; Philogiston Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Cacciola, M.; Pellicanó, D.; Megali, G.; Lay-Ekuakille, A.; Versaci, M.; Morabito, F.C. Aspects about air pollution prediction on urban environment. In Proceedings of the 4th IMEKO TC19 Symposium on Environmental Instrumentation and Measurement 2013: Protection Environment, Climate and Pollution Control, Lecce, Italy, 3–4 June 2013; pp. 15–20. [Google Scholar]



| Length | 7.24 (m) | Wingspan | 10 (m) |
| Weight | 600 (kg) | Maximum take-off weight | 1100 (kg) |
| Engine | Lycoming 0-360 180 (HP) | Cruise speed | 250 (km/h) |
| Autonomy | 4, 5 (h) | Maximum cruising altitude | 5000 (m a.s.l.) |
| Symbol | Standard Values | Symbol | Standard Values |
|---|---|---|---|
| 477 (J/(kg K)) | k (thermal conductivity) | 42.7 (W/(m K) | |
| Thermal expansion coefficient | 12.3 (1/K) | (density) | 7850 (kg/mq) |
| Young’s module | 200 (Pa) | Poisson’s coefficient | 0.28 (dimensionless) |
| (°C) | Flight Altitude (m) | (°C) | Flight Altitude (m) | (°C) | Flight Altitude (m) |
|---|---|---|---|---|---|
| −3.25 | 500 | 11.75 | 500 | 31.75 | 500 |
| −6.50 | 1000 | 8.50 | 1000 | 28.50 | 1000 |
| −9.75 | 1500 | 5.25 | 1500 | 25.25 | 1500 |
| −13.00 | 2000 | 2.00 | 2000 | 22.00 | 2000 |
| −19.50 | 3000 | −4.50 | 3000 | 15.50 | 3000 |
| −22.75 | 3500 | −775 | 3500 | 12.25 | 3500 |
| −26.00 | 4000 | −11.00 | 4000 | 9.00 | 4000 |
| −29.25 | 4500 | −14.25 | 4500 | 5.75 | 4500 |
| h | h | h | |||
|---|---|---|---|---|---|
| 0 | 0.3671 | 15 | 0.4235 | 35 | 0.4482 |
| −16.25 | 0.3681 | −1.25 | 0.3631 | 13.75 | 0.4269 |
| −32.5 | 0.3371 | −17.50 | 0.3658 | −2.5 | 0.3628 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Angiulli, G.; Calcagno, S.; De Carlo, D.; Laganá, F.; Versaci, M. Second-Order Parabolic Equation to Model, Analyze, and Forecast Thermal-Stress Distribution in Aircraft Plate Attack Wing–Fuselage. Mathematics 2020, 8, 6. https://doi.org/10.3390/math8010006
Angiulli G, Calcagno S, De Carlo D, Laganá F, Versaci M. Second-Order Parabolic Equation to Model, Analyze, and Forecast Thermal-Stress Distribution in Aircraft Plate Attack Wing–Fuselage. Mathematics. 2020; 8(1):6. https://doi.org/10.3390/math8010006
Chicago/Turabian StyleAngiulli, Giovanni, Salvatore Calcagno, Domenico De Carlo, Filippo Laganá, and Mario Versaci. 2020. "Second-Order Parabolic Equation to Model, Analyze, and Forecast Thermal-Stress Distribution in Aircraft Plate Attack Wing–Fuselage" Mathematics 8, no. 1: 6. https://doi.org/10.3390/math8010006
APA StyleAngiulli, G., Calcagno, S., De Carlo, D., Laganá, F., & Versaci, M. (2020). Second-Order Parabolic Equation to Model, Analyze, and Forecast Thermal-Stress Distribution in Aircraft Plate Attack Wing–Fuselage. Mathematics, 8(1), 6. https://doi.org/10.3390/math8010006









