A Novel Forward-Backward Algorithm for Solving Convex Minimization Problem in Hilbert Spaces

Abstract

In this work, we aim to investigate the convex minimization problem of the sum of two objective functions. This optimization problem includes, in particular, image reconstruction and signal recovery. We then propose a new modified forward-backward splitting method without the assumption of the Lipschitz continuity of the gradient of functions by using the line search procedures. It is shown that the sequence generated by the proposed algorithm weakly converges to minimizers of the sum of two convex functions. We also provide some applications of the proposed method to compressed sensing in the frequency domain. The numerical reports show that our method has a better convergence behavior than other methods in terms of the number of iterations and CPU time. Moreover, the numerical results of the comparative analysis are also discussed to show the optimal choice of parameters in the line search.

1. Introduction

Let H be a real Hilbert space, and let $f,g:H\to \mathbb{R}\cup \{+\infty \}$ be proper, lower-semicontinuous, and convex functions. The convex minimization problem is modeled as follows:

$$\begin{array}{c}\hfill {\displaystyle \underset{x\in H}{min}(f\left(x\right)+g\left(x\right)).}\end{array}$$

(1)

Throughout this paper, assume that Problem (1) is nonempty, and the solution set is denoted by $S_{*}$. We know that Problem (1) can be described by the fixed point equation, that is,

$$\begin{array}{c}\hfill x={\mathrm{prox}}_{\alpha g}(x-\alpha \nabla f\left(x\right))\end{array}$$

(2)

where $\alpha >0$ and ${\mathrm{prox}}_g$ is the proximal operator of g defined by ${\mathrm{prox}}_g={(Id+\partial g)}^{-1}$ where $Id$ denotes the identity operator in H and $\partial g$ is the classical convex subdifferential of g. Using this fixed point equation, one can define the following iteration process:

$$\begin{array}{c}\hfill {\displaystyle x^{k+1}=\underset{\mathrm{backward}\mathrm{step}}{\underbrace{{\mathrm{prox}}_{{\alpha }_{k}g}}}\underset{\mathrm{forward}\mathrm{step}}{\underbrace{(x^k-{\alpha }_k\nabla f\left(x^k\right))}},}\end{array}$$

(3)

where ${\alpha }_k$ is a suitable stepsize. This algorithm is known as the forward-backward algorithm, and it includes, as special cases, the gradient method [1,2,3] and the proximal algorithm [4,5,6,7]. Recently, the construction of algorithms has become a crucial technique for solving some nonlinear and optimization problems (see also [8,9,10,11,12,13,14,15]).

In 2005, Combettes and Wajs [16] proposed the following algorithm, which is based on iteration (3) as follows:

Algorithm 1 ([16]). Given $ϵ\in (0,min\{1,\frac{1}{\alpha }\})$ and letting $x^0\in {\mathbb{R}}^N,$ for $k\ge 1$: $$\begin{array}{ccc}\hfill y^k& =& x^k-{\alpha }_k\nabla f\left(x^k\right),\hfill \\ \hfill x^{k+1}& =& x^k+{\lambda }_k({\mathrm{prox}}_{{\alpha }_{k}g}{y}^k-x^k),\hfill \end{array}$$ (4) where ${\alpha }_k\in [ϵ,\frac{2}{\alpha }-ϵ]$, ${\lambda }_k\in [ϵ,1]$ and $\alpha$ is the Lipschitz constant of the gradient of $f.$

It was proven that the sequence generated by (4) converges to minimizers of $f+g$. However, we note that the convergence of Algorithm 1 depends on the Lipschitz continuity of the gradient of f, which is not an easy task to find in general.

The Douglas–Rachford algorithm is another method that can be used to solve the problem (1). It is defined in the following manner:

Algorithm 2 ([16]). Fix $ϵ\in (0,1),\gamma >0$ and let $x^0\in {\mathbb{R}}^N.$ For $k\ge 1$, calculate $$\begin{array}{ccc}\hfill y^k& =& {\mathrm{prox}}_{\gamma g}{x}^k,\hfill \\ \hfill x^{k+1}& =& x^k+{\lambda }_k({\mathrm{prox}}_{\gamma f}(2y^k-x^k)-y^k),\hfill \end{array}$$ (5) where ${\lambda }_k\in [ϵ,2-ϵ]$.

It was shown that the sequence $\left(x^k\right)$ defined by (5) converges to minimizers of $f+g$. In this case, we see that the main drawback of Algorithm 2 is that it requires two proximity operators of convex functions f and g per iteration. This leads to a slow convergence speed of algorithms based on Algorithm 2. Please see Section 4 for its convergence.

Very recently, Cruz and Nghia [17] introduced the forward-backward algorithm by using the line search technique in the framework of Hilbert spaces. Assume that the following conditions are satisfied:

$\left(\mathrm{A}1\right)$$f,g:H\to \mathbb{R}\cup \{+\infty \}$ are two proper, $l.s.c$, convex functions where $\mathrm{dom}g\subseteq \mathrm{dom}f$ and $\mathrm{dom}g$ is nonempty, closed, and convex.

$\left(\mathrm{A}2\right)$f is Fréchet differentiable on an open set that contains $\mathrm{dom}g$. The gradient $\nabla f$ is uniformly continuous on bounded subsets of $\mathrm{dom}g$. Moreover, it maps any bounded subset of $\mathrm{dom}g$ to a bounded set in H.

Linesearch 1.

Let$\sigma >0,\theta \in (0,1)$and$\delta \in (0,\frac{1}{2})$.

Input. Given$\alpha =\sigma$and$J(x,\alpha ):={\mathrm{prox}}_{\alpha g}(x-\alpha \nabla f\left(x\right))$with$x\in \mathrm{dom}g$

  While $\alpha \parallel \nabla f\left(J\right(x,\alpha \left)\right)-\nabla f\left(x\right)\parallel >\delta \parallel J(x,\alpha )-x\parallel$

do$\alpha =\theta \alpha .$

  End While

Output.$\alpha$.

It was proven that Line Search 1 is well defined, i.e., this line search stops after finitely many steps. By this fact, Cruz and Nghia [17] also considered the following algorithm:

Algorithm 3.Fix$\sigma >0,\theta \in (0,1)$and$\delta \in (0,\frac{1}{2})$, and let$x^0\in \mathrm{dom}g$. For$k\ge 1$, calculate: $$x^{k+1}={\mathrm{prox}}_{{\alpha }_{k}g}(x^k-{\alpha }_k\nabla f\left(x^k\right)),$$ with${\alpha }_k:=$Line Search 1$(x^k,\sigma ,\theta ,\delta )$.

They showed that the sequence $\left(x^k\right)$ generated by Algorithm 3 involving the line search technique that eliminates the Lipschitz assumption on the gradient of f converges weakly to minimizers of $f+g$. It is observed that, to obtain its convergence, one has to find the stepsize $\alpha$ in each iteration. This can be costly and time consuming in computation.

Recently, there have been many works on modifying the forward-backward method for solving convex optimization problems (see, for example, [18,19,20,21,22,23]).

In variational theory, Tseng [24] introduced the following method for solving the variational inequality problem (VIP):

$$\begin{array}{ccc}\hfill y^k& =& P_C(x^k-\lambda F{x}^k),\hfill \\ \hfill x^{k+1}& =& y^k+\lambda (F{y}^k-F{x}^k),\hfill \end{array}$$

(6)

where $P_C$ is a metric projection from a Hilbert space onto the set C, F is a monotone and L-Lipschitz continuous mapping, and $\lambda \in (0,1/L)$. Then, the sequence generated by (6) weakly converges to a solution of VIP. This method is often called Tseng’s extragradient method and has received great attention by researchers due to its convergence speed (see, for example, [25,26,27,28]). Following this research direction, the main challenge is to design novel algorithms that can speed up the convergence rate compared to Algorithms 1–3.

In this paper, inspired by Cruz and Nghia [17], we suggest a new forward-backward algorithm to solve the convex minimization problem. We then prove weak convergence theorems of the proposed algorithm. Finally, some numerical experiments in signal recovery are given to show its efficiency. Numerical experiments show that our new algorithms have a better convergence behavior than other methods in comparison. The main advantage of this work is that our schemes do not require the computation of the Lipschitz constant as assumed in Algorithm 1.

The content is organized as follows: In Section 2, we recall the useful concepts that will be used in the sequel. In Section 3, we establish the main theorem of our algorithms. In Section 4, we give numerical experiments to validate the convergence theorems, and finally, in Section 5, we give the conclusions of this paper.

2. Preliminaries

In this section, we give some definitions and lemmas that play an essential role in our analysis. The strong and weak convergence of ${\displaystyle {\left(x^k\right)}_{k\in \mathbb{N}}}$ to x will be denoted by $x^k\to x$ and $x^k\rightharpoonup x,$ respectively. The subdifferential of h at z is defined by:

$$\partial h\left(z\right)=\{u\in H:⟨u,x-z⟩\le h(x)-h(z),z\in H\}.$$

It is known that $\partial h$ is maximal monotone [29].

The proximal operator of g is defined by ${\mathrm{prox}}_g:H\to \mathrm{dom}g$ with ${\mathrm{prox}}_g\left(z\right)={(Id+\partial g)}^{-1}\left(z\right),z\in H$. We know that the ${\mathrm{prox}}_g$ is single valued with full domain. Moreover, we have:

$$\begin{array}{c}\hfill \frac{z-{\mathrm{prox}}_{\alpha g}\left(z\right)}{\alpha }\in \partial g\left({\mathrm{prox}}_{\alpha g}\left(z\right)\right)\mathrm{for}\mathrm{all}z\in H,\alpha >0.\end{array}$$

(7)

The following lemma is crucial in convergence analysis.

Lemma 1

([29]). Let H be a Hilbert space. Let S be a nonempty, closed, and convex set of H, and let $\left(x^k\right)$ be a sequence in H that satisfies:

(i) ${\displaystyle \underset{k\to \infty }{lim}\parallel x^k-x\parallel }$ exists for each $x\in S$;

(ii) ${\omega }_w\left(x^k\right)\subset S$.

Then, $\left(x^k\right)$ weakly converges to an element of S.

3. Main Results

In this section, we suggest a new forward-backward algorithm and prove the weak convergence. Next, we assume that Conditions (A1)–(A2) hold.

Algorithm 4.Step 0.Given$\sigma >0,\theta \in (0,1),\gamma \in (0,2)$, and$\delta \in (0,\frac{1}{2}).$Let$x^0\in \mathrm{dom}g$. Step 1.Calculate: $$\begin{array}{c}\hfill y^k={\mathrm{prox}}_{{\alpha }_{k}g}(x^k-{\alpha }_k\nabla f\left(x^k\right))\end{array}$$ where${\alpha }_k=\sigma {\theta }^{m_k}$and$m_k$is the smallest nonnegative integer such that: $$\begin{array}{c}\hfill {\alpha }_k\parallel \nabla f\left(x^k\right)-\nabla f\left(y^k\right)\parallel \le \delta \parallel x^k-y^k\parallel .\end{array}$$ (8) If$x^k=y^k$, then stop, and$y^k$is a solution of$S_{*}$. Else, go to Step 2. Step 2.Calculate: $$\begin{array}{c}\hfill x^{k+1}=x^k-\gamma {\eta }_k{d}_k\end{array}$$ where: $$\begin{array}{c}\hfill d_k=x^k-y^k-{\alpha }_k(\nabla f\left(x^k\right)-\nabla f\left(y^k\right))\hspace{1em}\mathrm{and}\hspace{1em}{\eta }_k=(1-\delta )\frac{\parallel x^k-y^k{\parallel }^2}{\parallel d_k{\parallel }^2}.\end{array}$$ Set$k:=k+1$, and go toStep 1.

We next summarize the methods for solving the convex minimization problem (CMP) in Figure 1.

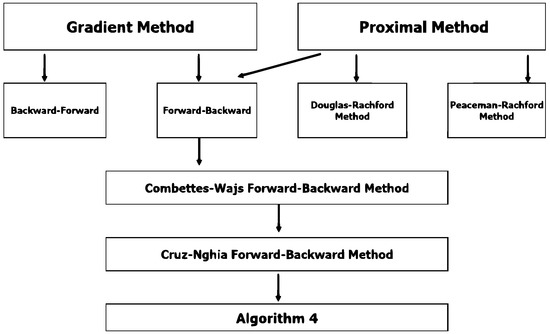
Figure 1. The flowchart of the method for the convex minimization problem (CMP).

Theorem 1.

Let ${\left(x^k\right)}_{k\in \mathbb{N}}$ and ${\left({\alpha }_k\right)}_{k\in \mathbb{N}}$ be generated by Algorithm 4. If there is $\alpha >0$ such that ${\alpha }_k\ge \alpha >0$ for all $k\in \mathbb{N}$, then ${\left(x^k\right)}_{k\in \mathbb{N}}$ weakly converges to an element of $S_{*}$.

Proof. 

Let $x_{*}$ be a solution in $S_{*}$. Then, we obtain:

$$\begin{array}{lll}\parallel x^{k+1}-x_{*}{\parallel }^2& =& \parallel x^k-\gamma {\eta }_k{d}_k-x_{*}{\parallel }^2\\ & =& \parallel x^k-x_{*}{\parallel }^2-2\gamma {\eta }_k⟨x^k-x_{*},d_k⟩+{\gamma }^2{\eta }_k^2{\parallel d_k\parallel }^2.\end{array}$$

(9)

Using the definition of $d_k$ and the line search (8), we have:

$$\begin{array}{cc}\hfill & ⟨x^k-x_{*},d_k⟩\hfill \\ =& ⟨x^k-y^k,d_k⟩+⟨y^k-x_{*},d_k⟩\hfill \\ =& ⟨x^k-y^k,x^k-y^k-{\alpha }_k(\nabla f\left(x^k\right)-\nabla f\left(y^k\right))⟩+⟨y^k-x_{*},x^k-y^k-{\alpha }_k(\nabla f\left(x^k\right)-\nabla f\left(y^k\right))⟩\hfill \\ =& \parallel x^k-y^k{\parallel }^2-⟨x^k-y^k,{\alpha }_k(\nabla f\left(x^k\right)-\nabla f\left(y^k\right))⟩+⟨y^k-x_{*},x^k-y^k-{\alpha }_k(\nabla f\left(x^k\right)-\nabla f\left(y^k\right))⟩\hfill \\ \ge & \parallel x^k-y^k{\parallel }^2-{\alpha }_k\parallel x^k-y^k\parallel \parallel \nabla f\left(x^k\right)-\nabla f\left(y^k\right)\parallel +⟨y^k-x_{*},x^k-y^k-{\alpha }_k(\nabla f\left(x^k\right)-\nabla f\left(y^k\right))⟩\hfill \\ \ge & \parallel x^k-y^k{\parallel }^2-\delta {\parallel x^k-y^k\parallel }^2+⟨y^k-x_{*},x^k-y^k-{\alpha }_k(\nabla f\left(x^k\right)-\nabla f\left(y^k\right))⟩.\hfill \end{array}$$

(10)

Since $y^k={\mathrm{prox}}_{{\alpha }_{k}g}(x^k-{\alpha }_k\nabla f\left(x^k\right))$, it follows that $(I-{\alpha }_k\nabla f)x^k\in (I-{\alpha }_k\partial g)y^k$. Moreover, since $\partial g$ is maximal monotone, there is $v^k\in \partial g\left(y^k\right)$ such that:

$$\begin{array}{c}\hfill (I-{\alpha }_k\nabla f)x^k=y^k-{\alpha }_k{v}^k.\end{array}$$

This shows that:

$$\begin{array}{c}\hfill v^k=\frac{1}{{\alpha }_k}(x^k-y^k-{\alpha }_k\nabla f\left(x^k\right)).\end{array}$$

(11)

On the other hand, $0\in \nabla f\left(x_{*}\right)+\partial g\left(x_{*}\right)\subseteq \partial (f+g)\left(x_{*}\right)$ and $\nabla f\left(y^k\right)+v^k\in \partial (f+g)y^k$. Therefore, we see that:

$$\begin{array}{c}\hfill ⟨\nabla f\left(y^k\right)+v^k,y^k-x_{*}⟩\ge 0.\end{array}$$

(12)

Substituting (11) into (12), we get that:

$$\begin{array}{c}\hfill \frac{1}{{\alpha }_k}⟨x^k-y^k-{\alpha }_k\nabla f\left(x^k\right)+{\alpha }_k\nabla f\left(y^k\right),y^k-x_{*}⟩\ge 0.\end{array}$$

(13)

This gives:

$$\begin{array}{c}\hfill ⟨x^k-y^k-{\alpha }_k\nabla f\left(x^k\right)+{\alpha }_k\nabla f\left(y^k\right),y^k-x_{*}⟩\ge 0.\end{array}$$

(14)

Combining (10) and (14), we obtain:

$$\begin{array}{c}\hfill ⟨x^k-x_{*},d_k⟩\ge (1-\delta ){\parallel x^k-y^k\parallel }^2.\end{array}$$

(15)

Since ${\eta }_k=(1-\delta )\frac{\parallel x^k-y^k{\parallel }^2}{\parallel d_k{\parallel }^2}$, we have ${\eta }_k\parallel d_k{\parallel }^2=(1-\delta ){\parallel x^k-y^k\parallel }^2$. This shows that:

$$\begin{array}{c}\hfill -2\gamma {\eta }_k(1-\delta )\parallel x^k-y^k{\parallel }^2=-2\gamma {\eta }_k^2{\parallel d_k\parallel }^2.\end{array}$$

(16)

By (15) and (16), we see that:

$$\begin{array}{lll}-2\gamma {\eta }_k⟨x^k-x_{*},d_k⟩& \le & -2\gamma {\eta }_k(1-\delta ){\parallel x^k-y^k\parallel }^2\\ & =& -2\gamma {\eta }_k^2{\parallel d_k\parallel }^2.\end{array}$$

Therefore, from (9) and the above, we have:

$$\begin{array}{lll}\parallel x^{k+1}-x_{*}{\parallel }^2& \le & \parallel x^k-x_{*}{\parallel }^2-2\gamma {\eta }_k^2\parallel d_k{\parallel }^2+{\gamma }^2{\eta }_k^2{\parallel d_k\parallel }^2\\ & =& \parallel x^k-x_{*}{\parallel }^2-\frac{2}{\gamma }\parallel \gamma {\eta }_k{d}_k{\parallel }^2+{\parallel \gamma {\eta }_k{d}_k\parallel }^2\\ & =& \parallel x^k-x_{*}{\parallel }^2-\frac{2-\gamma }{\gamma }{\parallel \gamma {\eta }_k{d}_k\parallel }^2.\hfill \end{array}$$

(17)

Since $x^{k+1}=x^k-\gamma {\eta }_k{d}_k$, it follows that $\gamma {\eta }_k{d}_k=x^k-x^{k+1}$. This implies:

$$\begin{array}{ccc}\hfill \parallel x^{k+1}-x_{*}{\parallel }^2& \le & \parallel x^k-x_{*}{\parallel }^2-\frac{2-\gamma }{\gamma }{\parallel x^k-x^{k+1}\parallel }^2.\hfill \end{array}$$

(18)

Thus, ${\displaystyle \underset{k\to \infty }{lim}\parallel x^k-x_{*}\parallel }$ exists, and hence, $\left(x^k\right)$ is bounded. This yields ${\displaystyle \underset{k\to \infty }{lim}\parallel x^k-x^{k+1}\parallel =0.}$ We note, by (18), that:

$$\frac{2-\gamma }{\gamma }\parallel x^k-x^{k+1}{\parallel }^2\le \parallel x^k-x_{*}{\parallel }^2-{\parallel x^{k+1}-x_{*}\parallel }^2.$$

By the monotonicity of $\nabla f$, we see that:

$$\begin{array}{lll}\parallel d_k{\parallel }^2& =& \parallel x^k-y^k-{\alpha }_k(\nabla f\left(x^k\right)-\nabla f\left(y^k\right)){\parallel }^2\\ & =& \parallel x^k-y^k{\parallel }^2+{\alpha }_k^2{\parallel \nabla f\left(x^k\right)-\nabla f\left(y^k\right)\parallel }^2-2{\alpha }_k⟨x^k-y^k,\nabla f\left(x^k\right)-\nabla f\left(y^k\right)⟩\\ & \le & (1+{\delta }^2){\parallel x^k-y^k\parallel }^2,\end{array}$$

equivalently:

$$\frac{1}{\parallel d_k{\parallel }^2}\ge \frac{1}{(1+{\delta }^2){\parallel x^k-y^k\parallel }^2}.$$

Therefore, we have:

$$\begin{array}{c}\hfill {\eta }_k=(1-\delta )\frac{\parallel x^k-y^k{\parallel }^2}{\parallel d_k{\parallel }^2}\ge \frac{1-\delta }{1+{\delta }^2}.\end{array}$$

(19)

On the other hand, we have:

$$\begin{array}{c}\hfill {\eta }_k\parallel d_k{\parallel }^2=(1-\delta ){\parallel x^k-y^k\parallel }^2.\end{array}$$

(20)

Therefore, it follows that:

$$\begin{array}{lll}\parallel x^k-y^k{\parallel }^2& =& \frac{1}{1-\delta }({\eta }_k\parallel d_k{\parallel }^2)\\ & =& \frac{1}{(1-\delta )\left({\gamma }^2{\eta }_k\right)}(\parallel \gamma {\eta }_k{d}_k{\parallel }^2)\\ & =& \frac{1}{(1-\delta )\left({\gamma }^2{\eta }_k\right)}{\parallel x^{k+1}-x^k\parallel }^2.\end{array}$$

(21)

Combining (20) and (21), we obtain:

$${\parallel x^k-y^k\parallel }^2\le \frac{1+{\delta }^2}{{\left[(1-\delta )\gamma \right]}^2}{\parallel x^{k+1}-x^k\parallel }^2.$$

Since $\parallel x^{k+1}-x^k\parallel \to 0$ as $k\to \infty$, $\parallel x^k-y^k\parallel \to 0$ as $k\to \infty$. By the boundedness of ${\left(x^k\right)}_{k\in \mathbb{N}}$, we know that the set of its weak accumulation points is nonempty. Let $x^{\infty }$ be a weak accumulation point of ${\left(x^k\right)}_{k\in \mathbb{N}}$. Therefore, there is a subsequence ${\left(x^{n_k}\right)}_{k\in \mathbb{N}}$ of ${\left(x^k\right)}_{k\in \mathbb{N}}$. Next, we show that $x^{\infty }\in S_{*}.$ Let $(v,u)\in \mathrm{Graph}(\nabla (f)+\partial (g\left)\right)$, that is $u-\nabla f\left(v\right)\in \partial g\left(v\right)$. Since $y^{k_n}={(I+{\alpha }_{k_n}\partial g)}^{-1}(I-{\alpha }_{k_n}\nabla f)x^{k_n},$ we obtain:

$$\begin{array}{c}\hfill (I-{\alpha }_{k_n}\nabla f)x^{k_n}\in (I+{\alpha }_{k_n}\partial g)y^{k_n},\end{array}$$

which yields:

$$\begin{array}{c}\hfill \frac{1}{{\alpha }_{k_n}}(x^{k_n}-y^{k_n}-{\alpha }_{k_n}\nabla f\left(x^{k_n}\right))\in \partial g\left(y^{k_n}\right).\end{array}$$

Since $\partial g$ is maximal, we have:

$$⟨v-y^{k_n},u-\nabla f\left(v\right)-\frac{1}{{\alpha }_{k_n}}(x^{k_n}-y^{k_n}-{\alpha }_{k_n}\nabla f\left(x^{k_n}\right))⟩\ge 0.$$

This shows that

$$\begin{array}{lll}⟨v-y^{k_n},u⟩& \ge & ⟨v-y^{k_n},\nabla f\left(v\right)+\frac{1}{{\alpha }_{k_n}}(x^{k_n}-y^{k_n}-{\alpha }_{k_n}\nabla f\left(x^{k_n}\right))⟩\\ & =& ⟨v-y^{k_n},\nabla f\left(v\right)-\nabla f\left(x^{k_n}\right)⟩+⟨v-y^{k_n},\frac{1}{{\alpha }_{k_n}}(x^{k_n}-y^{k_n})⟩\\ & =& ⟨v-y^{k_n},\nabla f\left(v\right)-\nabla f\left(y^{k_n}\right)⟩+⟨v-y^{k_n},\nabla f\left(y^{k_n}\right)-\nabla f\left(x^{k_n}\right)⟩\\ & & +⟨v-y^{k_n},\frac{1}{{\alpha }_{k_n}}(x^{k_n}-y^{k_n})⟩\\ & \ge & ⟨v-y^{k_n},\nabla f\left(y^{k_n}\right)-\nabla f\left(x^{k_n}\right)⟩+⟨v-y^{k_n},\frac{1}{{\alpha }_{k_n}}(x^{k_n}-y^{k_n})⟩.\end{array}$$

Since ${\displaystyle \underset{k\to \infty }{lim}\parallel x^k-y^k\parallel =0}$ and by (A2), we have ${\displaystyle \underset{k\to \infty }{lim}\parallel \nabla f\left(x^k\right)-\nabla f\left(y^k\right)\parallel =0}$. Hence, we obtain:

$$\begin{array}{c}\hfill {\displaystyle ⟨v-x^{\infty },u⟩=\underset{n\to \infty }{lim}⟨v-y^{k_n},u⟩\ge 0.}\end{array}$$

(22)

Hence, we obtain $0\in (\nabla f+\partial g)x^{\infty }$, and consequently, $x^{\infty }\in S_{*}$. This shows that $\left(x^k\right)$ converges weakly to an element of $S_{*}$ by applying Lemma 1. We thus complete the proof. □

4. Numerical Experiments

Next, we apply our result to the signal recovery in compressive sensing. We show the performance of our proposed Algorithm 4, Algorithm 1 of Combettes and Wajs [16], Algorithm 2 of Douglas–Rachford [22], and Algorithm 3 of Cruz and Nghia [17]. This problem can be modeled as:

$$\begin{array}{c}\hfill y=Ax+ϵ,\end{array}$$

(23)

where $y\in {\mathbb{R}}^M$ is the observed data, $ϵ$ is the noise, $A:{\mathbb{R}}^N\to {\mathbb{R}}^M(M<N)$ is a bounded and linear operator, and $x\in {\mathbb{R}}^N$ is a recovered vector containing m nonzero components. It is known that (23) can be modeled as the LASSO problem:

$$\begin{array}{c}\hfill {\displaystyle \underset{x\in {\mathbb{R}}^N}{min}(\frac{1}{2}{\parallel Ax-y\parallel }_2^2+{\lambda \parallel x\parallel }_1),}\end{array}$$

(24)

where $\lambda >0$. Therefore, we can apply the proposed method to solve (1) when $f\left(x\right)=\frac{1}{2}{\parallel y-Ax\parallel }_2^2$ and $g\left(x\right)={\lambda \parallel x\parallel }_1.$

In experiment, y is generated by the Gaussian noise with SNR = 40, A is generated by the normal distribution with mean zero and variance one, and $x\in {\mathbb{R}}^N$ is generated by a uniform distribution in [−2, 2]. We use the stopping criterion by:

$$\mathrm{MSE}=\frac{1}{N}{\parallel x^k-x^{*}\parallel }^2<{10}^{-3},$$

where $x^k$ is an estimated signal of $x_{*}$.

In the following, the initial point $x^0$ is chosen randomly, and ${\alpha }_k$ in Algorithm 1 is $\frac{1}{{\parallel A\parallel }^2}$ and ${\lambda }_k=0.5$. In Algorithm 2, ${\lambda }_k=0.02$ and $\gamma =0.02$. Let $\sigma =100,\theta =0.1,\mathrm{and}\delta =0.1$ in Algorithm 3 and Algorithm 4, and let $\gamma =1.9$ in Algorithm 4. We denote by CPU the time of CPU and by iter the number of iterations. In Table 1, we test the experiment five times and then calculate the averages of CPU and iter. All numerical experiments presented were obtained from MATLAB R2010a running on the same laptop computer. The numerical results are shown as follows:

Table 1. Computational results for compressed sensing.

m-Sparse Signal	Method	N = 512, M = 256
		CPU	Iter
m = 10	Algorithm 1	2.4095	1150
	Algorithm 2	22.1068	608
	Algorithm 3	0.9103	399
	Algorithm 4	0.7775	326
m = 20	Algorithm 1	7.2877	2073
	Algorithm 2	41.1487	1106
	Algorithm 3	1.5127	589
	Algorithm 4	1.3803	516
m = 25	Algorithm 1	10.2686	2463
	Algorithm 2	50.6234	1310
	Algorithm 3	1.9321	706
	Algorithm 4	1.7597	611
m = 30	Algorithm 1	13.4585	2825
	Algorithm 2	57.5277	1477
	Algorithm 3	2.1781	751
	Algorithm 4	2.0341	669

From Table 1, we see that the experiment result of Algorithm 4 was better than those of Algorithms 1 and 2 in terms of CPU time and number of iterations in each cases.

Next, we provide Figure 2 to show signal recovery in compressed sensing for one example and Figure 3 to show the convergence of each algorithm for all cases via the graph of the MSE value and number of iterations when $N=512$, $M=256$, and $m=20$.

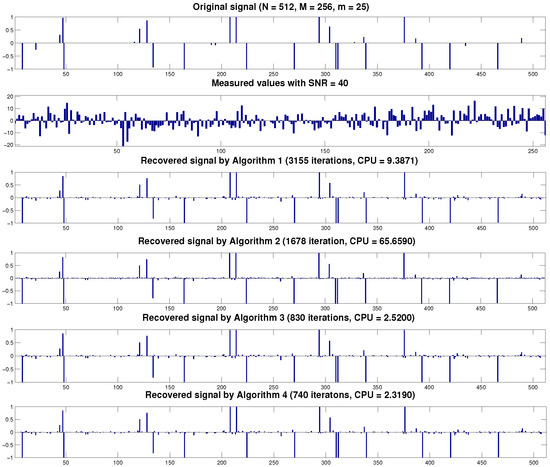
Figure 2. Original signal, observed data, and recovered signal by Algorithm 1, Algorithm 2, Algorithm 3, and Algorithm 4 when $N=512$ and $M=256$.

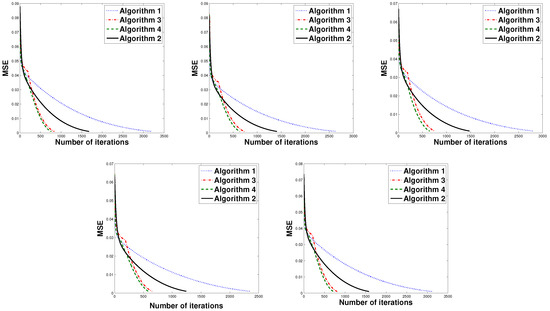
Figure 3. The MSE value and number of iterations for all cases when $N=512$ and $M=256$.

From Figure 2 and Figure 3, it is revealed that the convergence speed of Algorithm 4 was better than the other algorithm. To be more precise, Algorithm 2 had the highest CPU time since it required two proximity operators in computation per iteration. Moreover, Algorithm 1 that had the stepsize that was bounded above by the Lipschitz constant had the highest number of iterations. In our experiments, it was observed that the initial guess did not have any significant effect on the convergence behavior.

Next, we analyze the convergence and the effects of the stepsizes, which depended on parameters $\delta ,\theta ,\gamma$, and $\sigma$ in Algorithm 4.

We next study the effect of the parameter $\delta$ in the proposed algorithm for each value of $\delta$.

From Table 2, we observe that the CPU time and the number of iterations of Algorithm 4 became larger when the parameter $\delta$ approached $0.5$ when $N=512,M=265$ and $N=1024,M=512$. Figure 4 shows the numerical results for each $\delta$.

Table 2. The convergence of Algorithm 4 with each $\delta$.

Given: σ = 100, θ = 0.1, γ = 1.9
δ	N = 512, M = 256 m = 20		N = 1024, M = 512 m = 20
	CPU	Iter	CPU	Iter
0.20	3.2934	495	12.6411	487
0.28	3.4913	550	14.9438	533
0.36	3.4361	635	16.5947	605
0.44	4.4041	743	20.6721	703

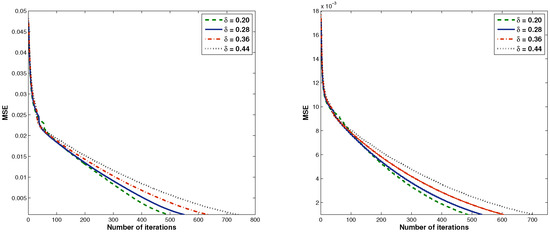
Figure 4. Graph of number of iterations versus MSE when $N=512,M=265$ and $N=1024,M=512$, respectively.

From Figure 4, we see that our algorithm worked effectively when the value of $\delta$ was taken close to zero.

Next, we investigate the effect of the parameter $\theta$ in the proposed algorithm. We intend to vary this parameter and study its convergence behavior. The numerical results are shown in Table 3.

Table 3. The convergence of Algorithm 4 with each $\theta$.

Given: σ = 100, δ = 0.1, γ = 1.9
θ	N = 512, M = 256 m = 20		N = 1024, M = 512 m = 20
	CPU	Iter	CPU	Iter
0.3	4.0185	382	13.4732	354
0.5	4.2358	312	22.2328	342
0.7	7.5081	298	27.8198	320
0.9	21.7847	290	85.3605	311

From Table 3, we observe that the CPU time of Algorithm 4 became larger and the number of iterations had a small reduction when the parameter $\theta$ approached one when $N=512,M=265$ and $N=1024,M=512$. Figure 5 shows the numerical results for each $\theta$.

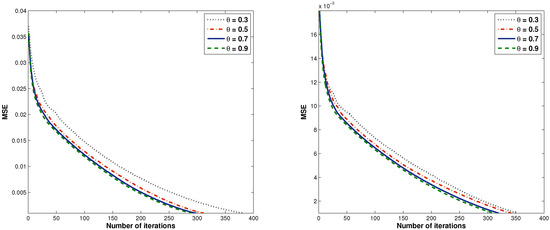
Figure 5. Graph of the number of iterations versus MSE where $N=512,M=265$ and $N=1024,M=512$, respectively.

From Figure 5, it is shown that Algorithm 4 worked effectively when the value of $\theta$ was chosen close to one.

Next, we study the effect of the parameter $\gamma$ in the proposed algorithm. The numerical results are shown in Table 4.

Table 4. The convergence of Algorithm 4 with each $\gamma$.

Given: σ = 100, θ = 0.1, δ = 0.1
γ	N = 512, M = 256 m = 20		N = 1024, M = 512 m = 20
	CPU	Iter	CPU	Iter
0.8	13.9690	1450	38.2790	1624
1.1	7.8978	988	23.3411	1124
1.4	5.1804	724	17.6275	866
1.7	3.8323	554	13.6241	700

From Table 4, we see that the CPU time and the number of iterations of Algorithm 4 became smaller when the parameter $\gamma$ approached two when $N=512,M=265$ and $N=1024,M=512$. We show numerical results for each cases of $\gamma$ in Figure 6.

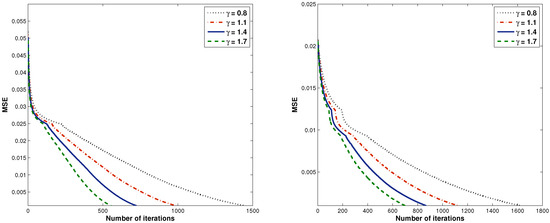
Figure 6. Graph of the number of iterations versus MSE where $N=512,M=265$ and $N=1024,M=512$, respectively.

From Figure 6, it is shown that Algorithm 4 worked effectively when the value of $\gamma$ was chosen close to two.

Next, we study the effect of the parameter $\sigma$ in the proposed algorithm. The numerical results are given in Table 5.

Table 5. The convergence of Algorithm 4 with each $\sigma$.

Given: δ = 0.1, θ = 0.1, γ = 1.9
σ	N = 512, M = 256 m = 20		N = 1024, M = 512 m = 20
	CPU	Iter	CPU	Iter
5	4.7055	680	11.7794	496
30	6.2280	843	11.3827	453
55	4.4271	634	14.2537	532
80	3.9635	606	16.5507	596

From Table 5, we see that the parameter $\sigma$ had no effect in terms of the number of iterations and CPU time when $N=512,M=265$ and $N=1024,M=512$.

5. Conclusions

In this work, we studied the modified forward-backward splitting method using line searches to solve convex minimization problems. We proved the weak convergence theorem under some weakened assumptions on the stepsize. It was found that the proposed algorithm had a better convergence behavior than other methods through experiments. Our algorithms did not require the Lipschitz condition on the gradient of functions. We also presented numerical experiments in signal recovery and provided a comparison to other algorithms. Moreover, the effects of all parameters were shown in Section 4. This main advantage was very useful and convenient in practice for solving some optimization problems.