Characteristic Function and Time Consistency for Two-Stage Games with Network Externalities

Abstract

Time consistency is a property of the solution to a cooperative dynamic game which guarantees that this solution remains stable with respect to its revision by players over time. The fulfillment of this property is directly related to the characteristic function and its behavior with the course of the game as any solution is based on this function. In this paper, we will examine the characteristic functions for two economic models with network externalities represented by a two-stage network game using the theory developed for this class of games. For a network game with positive externalities represented by a public goods provision model, we demonstrate a sufficient condition for time consistency. For a network game with negative externalities represented by a market competition model, we show that the cooperative solution is always time consistent.

1. Introduction

One of the main features of the solution to a cooperative dynamic game is its stability with respect to its revision by players over time. Failure to meet this property may eventually lead to a refusal of cooperation and an inability to implement the cooperative agreement. In the literature, this property of the solution is called time consistency. The time consistency problem for the first time was addressed in [1] for a class of differential games. Later on, this issue was also studied for other classes of cooperative dynamic games. It is important to note that the time consistency of the solution applies only to dynamic games, and it has no special meaning for static games. The fulfillment of the time consistency property is directly related to the characteristic function and its behavior with the course of the game. This function is defined for each coalition of players and reflects how the worth or strength of that coalition changes over time. Moreover, any cooperative solution to the game is based on the characteristic function and, therefore, a change in this function may lead to a change in the cooperative solution itself resulting in time inconsistency.

In this paper, we will examine the time consistency problem for two models with network externalities represented by a two-stage network game. The theoretical fundamentals of cooperative two-stage network games including time consistency were introduced in [2,3,4]. Is it supposed that players create a network at the first game stage by announcing potential partners they wish to be connected with, and at the second stage players choose actions. Thus, having made their choices, players are rewarded according to given payoff functions. Under this setting, the sufficient condition for the cooperative solution to be time consistent is that the worth of any coalition is constant over time. Put differently, the characteristic functions in the two-stage game and its one-stage subgame under the cooperative agreement must coincide. For this reason, we study the characteristic functions in the game. We will do it for two economic models. First, we start with an asymmetric cooperative model of public goods provision in a network based on [5,6,7,8]. We will show that in this model players benefit from adding more links as links create positive externalities, and provide conditions guaranteeing the time consistency of a cooperative solution. Second, we examine an asymmetric cooperative model of market competition. There we will demonstrate that, under the cooperative agreement, players are not interested in establishing links between each other, thus forming the empty network as links create negative externalities. However, any cooperative solution is time consistent in the latter model.

When players cooperate, they maximize the sum of their payoffs in the game. So, assuming a revenue-minus-cost structure of a player’s payoff function, the total costs of the grand coalition amount to the sum of its members’ costs. This is a so-called model without transferable technologies (see, for example [9,10] with respect to market competition), which is in line with the classical idea of maximizing the sum of players’ payoffs. We will also draw on it in our analysis. As for determining the characteristic function, we will use the maximin approach [11], although there are other approaches [10,12,13,14,15,16] in the same context of the model under consideration. Since the characteristic function is key in sustaining the cooperative agreement during its implementation, we study when this function does not change over time under the two economic models as cooperative two-stage games with network externalities.

The paper is organized as follows. The next section briefly summarizes the basic concepts of the theory of cooperative two-stage network games and provides definitions of characteristic functions during the implementation of the cooperative agreement. Then, Section 3 analyzes the behavior of these functions within the framework of a network model of public goods provision with positive externalities. Section 4 provides an analysis of the characteristic functions in a network model of market competition with negative externalities. Finally, Section 5 concludes.

2. Preliminaries

Let $N=\{1,\dots ,n\}$ be a finite set of players with $n⩾3$. Players may be connected in a network $(N,g)$ where N is the set of its nodes coinciding with the player set and $g\subseteq \left\{\right(i,j):i,j\in N,i\ne j\}$ is a collection of undirected pairs of players called links. For brevity, we associate network $(N,g)$ with the set g. Neighbors of a player $i\in N$ in g are players from $N_i\left(g\right)=\{j\in N:(i,j)\in g\}$. Following [4], we consider a two-stage model. At its first stage, players by binary profiles of actions $g_i=(g_{i1},\dots ,g_{in})$, $i\in N$, simultaneously choose partners they wish to establish connections with from specified set $L_i\subset N\backslash \left\{i\right\}$, $i\in N$, being also limited in the number of offers ${\ell }_i$, $i\in N$. If both players wish to establish a connection between themselves, a link is formed. Thus, a network g is created. Next, at the second stage once the network is formed each player $i\in N$ may revise it by deleting some of the established links, i.e., by choosing a binary profile $d_i\left(g\right)=(d_{i1}\left(g\right),\dots ,d_{in}\left(g\right))$, and also she chooses an action from a given set $U_i$. A player $i\in N$ is rewarded by a real-valued payoff function $h_i(u_i,u_{N_i\left(g^d\right)})$, which depends on her action $u_i\in U_i$ and the profile of actions $u_{N_i\left(g^d\right)}=\{u_j:j\in N_i\left(g^d\right)\}$ of her neighbors in the network $g^d\subseteq g$, which appears after the revision of links. An example of network g of eight nodes and ten links is shown in Figure 1 (left), whereas a possible network $g^d$ is shown in the same figure (right).

Figure 1. An example of networks g (left) and $g^d$ (right).

In a cooperative scenario, players wish to maximize their total payoff, i.e., to maximize ${\sum }_{i\in N}{h}_i(u_i,u_{N_i\left(g^d\right)})$ by choosing actions jointly at both stages followed by allocation of the maximum value among them. The profile of actions that maximizes the aforementioned sum is called a cooperative strategy profile. The corresponding players’ actions at both stages will be denoted by ${\overline{g}}_i$, $i\in N$, at the first stage (resulting in network $\overline{g}$), and $({\overline{d}}_i\left(\overline{g}\right),{\overline{u}}_i)$, $i\in N$, at the second stage of the game. To determine an allocation, we require the characteristic function, which is a real-valued function defined over all subsets of the player set. For any subset $S\subseteq N$, a coalition, characteristic function $v_1\left(S\right)$ measures its worth in the two-stage game. Following [11], it is the maximum payoff that this coalition can guarantee for itself (the maximin value) in a two-stage zero-sum game between two players: coalition S maximizing the sum of the payoffs of its members and its complement $N\backslash S$ minimizing the payoff to S. Having determined $v_1$, we can allocate the maximum total payoff, $v_1\left(N\right)$, among the players according to an appropriate cooperative solution, which is a rule specifying how this value is allocated. When implementing the cooperative agreement and creating feasible network $\overline{g}$ at the first game stage, it is important that no player decides to abandon the agreement at the second stage of the game after (possible) re-evaluation of the worths of coalitions and the cooperative solution itself. This leads us to a characteristic function $v_2(\overline{g},S)$ in the one-stage subgame resulting to this solution. In the subgame, the value $v_2(\overline{g},S)$ amounts to the maximin value in a one-stage zero-sum game between coalition S maximizing the sum of the payoffs of its members and its complement $N\backslash S$ minimizing the payoff to S given that network $\overline{g}$ has been formed. Finding characteristic functions $v_1$ and $v_2$ has been reduced to solving associated maximization problems when meeting the next property (P): for any two feasible networks g, $\tilde{g}$, such that $\tilde{g}\subset g$, and a player $i\in N$ the inequality $h_i(u_i,u_{N_i\left(g\right)})⩾h_i(u_i,u_{N_i\left(\tilde{g}\right)})$ holds true for any profiles $(u_i,u_{N_i\left(g\right)})\in U_i\times {\prod }_{j\in N_i\left(g\right)}{U}_j$ and $(u_i,u_{N_i\left(\tilde{g}\right)})\in U_i\times {\prod }_{j\in N_i\left(\tilde{g}\right)}{U}_j$ (see [4] for details). If the aforementioned property is met, then characteristic function $v_1$ is given by:

$$v_1\left(S\right)=\left\{\begin{array}{cc}{\displaystyle \sum _{i\in N}}{h}_i({\overline{u}}_i,{\overline{u}}_{N_i\left(\overline{g}\right)}),\hfill & S=N,\hfill \\ \underset{g_i,i\in S}{max}\underset{u_i\in U_i,i\in S}{max}{\displaystyle \sum _{i\in S}}{h}_i(u_i,u_{N_i\left(g\right)\cap S}),\hfill & S\subset N,\hfill \\ 0,\hfill & S=⌀,\hfill \end{array}\right.$$

whereas if network $\overline{g}$ is formed at the first game stage by the actions from the cooperative strategy profile, characteristic function $v_2$ is of the form:

$$v_2(\overline{g},S)=\left\{\begin{array}{cc}{\displaystyle \sum _{i\in N}}{h}_i({\overline{u}}_i,{\overline{u}}_{N_i\left(\overline{g}\right)}),\hfill & S=N,\hfill \\ \underset{u_i\in U_i,i\in S}{max}{\displaystyle \sum _{i\in S}}{h}_i(u_i,u_{N_i\left(\overline{g}\right)\cap S}),\hfill & S\subset N,\hfill \\ 0,\hfill & S=⌀.\hfill \end{array}\right.$$

These functions are key in sustaining the cooperative agreement during its implementation, i.e., the time consistency of a cooperative solution (a rule prescribing the way in which the total cooperative payoff is allocated). When these functions coincide, the cooperative solution is time consistent, and players will not need to review it at the second stage of the game, thus continuing to adhere to the cooperative agreement. It is worth noting that certain cooperative solutions are time consistent even if the values of the characteristic functions differ for some (but not all) coalitions. Since we do not stipulate the choice of the cooperative solution, we will examine the coincidence of these functions. We will do this for two important economic applications of the two-stage network game theory.

3. Positive Externalities: Public Goods Provision

First, we examine a model of public goods provision. Let an action $u_i$ of player i expressing her level of effort belong to set $U_i=[0,\infty )$. Following [6,7], we assume that a player’s payoff function is defined as the difference between benefits from her own and neighbors’ effort and her costs associated with the choice:

$$h_i(u_i,u_{N_i\left(g\right)})=f\left(u_i+\sum _{j\in N_i\left(g\right)}{u}_j\right)-c_i{u}_i,c_i>0,i\in N.$$

Function f is twice-differentiable, strictly concave with $f\left(0\right)=0$, $f^{\prime }>0$, and $f^{″}<0$. The addition of new links creates positive externalities, i.e., $h_i(u_i,u_{N_i\left(g\right)})⩾h_i(u_i,u_{N_i\left(\tilde{g}\right)})$ for any profile $(u_1,\dots ,u_n)$, feasible networks g, $\tilde{g}$ and a player i such that such that $\tilde{g}\subset g$ and $|N_i\left(g\right)|>|N_i\left(\tilde{g}\right)|$. That is, property (P) holds. Indeed, owing the monotonicity of function f, we have

$$h_i(u_i,u_{N_i\left(g\right)})-h_i(u_i,u_{N_i\left(\tilde{g}\right)})=f\left(u_i+\sum _{j\in N_i\left(g\right)}{u}_j\right)-f\left(u_i+\sum _{j\in N_i\left(\tilde{g}\right)}{u}_j\right)⩾0.$$

The common objective of players is to maximize

$$\sum _{i\in N}{h}_i(u_i,u_{N_i\left(g\right)})=\sum _{i\in N}\left[f\left(u_i+\sum _{j\in N_i\left(g\right)}{u}_j\right)-c_i{u}_i\right].$$

(1)

Following [4], when players follow their cooperative strategies, they choose actions ${\overline{g}}_i$, $i\in N$, at the first stage of the game, thus creating a network $\overline{g}$ and not changing the network at the second stage. In addition, at the second stage, players choose actions ${\overline{u}}_i$, $i\in N$, maximizing the sum in (1). We write a corresponding optimization problem. First, $g_{ij}$ is a binary variable, so $g_{ij}(1-g_{ij})=0$ for any $i,j\in N$, $i\ne j$. Second, the link is formed only if both players agree to form it, so $g_{ij}=g_{ji}$. Third, players can offer links only to players from $L_i\subseteq N\backslash \left\{i\right\}$, $i\in N$; thus, $g_{ij}=0$ for any $j\notin L_i$. Next, the number of offers is limited, so ${\sum }_{j\in L_i:i\in L_j}{g}_{ij}⩽{\ell }_i$, $i\in N$, recalling that both players must agree on the link between them. Finally, $u_i⩾0$ for any $i\in N$. Therefore, to maximize (1) given the above constraints, we use the Karush–Kuhn–Tucker theorem. We write the Lagrangian function:

$$\begin{array}{cc}\hfill \sum _{i\in N}[f\left(u_i+\sum _{j\in L_i:i\in L_j}{g}_{ij}{u}_j\right)& -c_i{u}_i+{\lambda }_i{u}_i+{\mu }_i\left({\ell }_i-\sum _{j\in L_i:i\in L_j}{g}_{ij}\right)\hfill \\ & +\sum _{j\in L_i:i\in L_j}({\nu }_{ij}(g_{ij}-g_{ji})+{\sigma }_{ij}{g}_{ij}(1-g_{ij}))],\hfill \end{array}$$

where $\left\{{\lambda }_i\right\}$, $\left\{{\mu }_i\right\}$, $\left\{{\nu }_{ij}\right\}$, and $\left\{{\sigma }_{ij}\right\}$ are some constants. We arrive at the following result.

Proposition 1.

If $\left\{{\overline{g}}_{ij}\right\}$ and $\overline{u}$ compose a cooperative strategy profile, then there exist constants $\left\{{\lambda }_i\right\}⩾0$, $\left\{{\mu }_i\right\}⩾0$, $\left\{{\nu }_{ij}\right\}$, and $\left\{{\sigma }_{ij}\right\}$ such that $\left\{{\overline{g}}_{ij}\right\}$ and $\overline{u}$ are feasible, and

$$\begin{array}{cc}\hfill & \frac{\partial f\left({\overline{u}}_i+{\sum }_{j\in L_i:i\in L_j}{\overline{g}}_{ij}{\overline{u}}_j\right)}{\partial u_i}+\sum _{j\in L_i:i\in L_j}\frac{\partial f\left({\overline{u}}_j+{\sum }_{k\in L_j:j\in L_k}{\overline{g}}_{jk}{\overline{u}}_k\right)}{\partial u_i}{\overline{g}}_{ji}-c_i+{\lambda }_i=0,i\in N,\hfill \\ \hfill & \frac{\partial f\left({\overline{u}}_i+{\sum }_{k\in L_i:i\in L_k}{\overline{g}}_{ik}{\overline{u}}_k\right)}{\partial g_{ij}}{\overline{u}}_j-{\mu }_i+{\nu }_{ij}-{\nu }_{ji}+{\sigma }_{ij}(1-2{\overline{g}}_{ij})=0,i,j\in N:i\in L_j,j\in L_i,\hfill \\ \hfill & {\lambda }_i{\overline{u}}_i=0,i\in N,\hfill \\ \hfill & {\mu }_i\left({\ell }_i-\sum _{j\in L_i:i\in L_j}{\overline{g}}_{ij}\right)=0,i\in N.\hfill \end{array}$$

Hence, $v_1\left(N\right)={\sum }_{i\in N}\left[f\left({\overline{u}}_i+{\sum }_{j\in L_i:i\in L_j}{\overline{g}}_{ij}{\overline{u}}_j\right)-c_i{\overline{u}}_i\right]$.

Proof. 

The proof immediately follows from the Karush–Kuhn–Tucker theorem adapted for the optimization problem under consideration. If we substitute the cooperative strategy profile into (1), we get $v_1\left(N\right)$. □

We can rewrite $v_1\left(N\right)$ in a more convenient way in terms of network $\overline{g}$ formed at the first game stage as $v_1\left(N\right)={\sum }_{i\in N}\left[f\left({\overline{u}}_i+{\sum }_{j\in L_i:i\in L_j}{\overline{g}}_{ij}{\overline{u}}_j\right)-c_i{\overline{u}}_i\right]={\sum }_{i\in N}\left[f\left({\overline{u}}_i+{\sum }_{j\in N_i\left(\overline{g}\right)}{\overline{u}}_j\right)-c_i{\overline{u}}_i\right]$. To find the value $v_1\left(S\right)$ for a nonempty coalition $S\subset N$, we use the following reasoning. The complement $N\backslash S$ acts against S; thus, it does not establish links with players from S as links create positive externalities. Therefore, players from S being disconnected from $N\backslash S$ maximize the sum of their payoffs. Hence, we get the result similar to Proposition 1, which also draws on the Karush–Kuhn–Tucker theorem.

Proposition 2.

If $\left\{g_{ij}^S\right\}$ and $u^S$ compose a profile maximizing the total payoff to coalition $S\subset N$, then there exist constants $\left\{{\lambda }_i\right\}⩾0$, $\left\{{\mu }_i\right\}⩾0$, $\left\{{\nu }_{ij}\right\}$, and $\left\{{\sigma }_{ij}\right\}$ such that ${\left\{g_{ij}^S\right\}}_{i,j\in S}$ and ${\left\{u_i^S\right\}}_{i\in S}$ are feasible, and

$$\begin{array}{cc}\hfill & \frac{\partial f\left(u_i^S+{\sum }_{j\in L_i\cap S:i\in L_j}{g}_{ij}^S{u}_j^S\right)}{\partial u_i^S}+\sum _{j\in L_i\cap S:i\in L_j}\frac{\partial f\left(u_j^S+{\sum }_{k\in L_j\cap S:j\in L_k}{g}_{jk}^S{u}_k^S\right)}{\partial u_i^S}{g}_{ji}^S-c_i+{\lambda }_i=0,i\in S,\hfill \\ \hfill & \frac{\partial f\left(u_i^S+{\sum }_{k\in L_i\cap S:i\in L_k}{g}_{ik}^S{u}_k^S\right)}{\partial g_{ij}^S}{u}_j^S-{\mu }_i+{\nu }_{ij}-{\nu }_{ji}+{\sigma }_{ij}(1-2g_{ij}^S)=0,i,j\in S:i\in L_j,j\in L_i,\hfill \\ \hfill & {\lambda }_i{u}_i^S=0,i\in S,\hfill \\ \hfill & {\mu }_i\left({\ell }_i-\sum _{j\in L_i\cap S:i\in L_j}{g}_{ij}^S\right)=0,i\in S.\hfill \end{array}$$

Hence, $v_1\left(S\right)={\sum }_{i\in S}\left[f\left(u_i^S+{\sum }_{j\in L_i\cap S:i\in L_j}{g}_{ij}^S{u}_j^S\right)-c_i{u}_i^S\right]$.

Now, we can determine characteristic function $v_2$. For the coalition N, equality $v_2(\overline{g},N)=v_1\left(N\right)$ holds true by the Bellman optimality principle. To get $v_2(\overline{g},S)$, $S\subset N$, we note that players from S cannot establish new links at the second stage. Players from S will also not delete any links between them as links create positive externalities. As for the players from $N\backslash S$, they will delete all links connecting them with players from S. Therefore, given feasible network $\overline{g}$ formed at the first game stage, S will maximize

$$\sum _{i\in S}{h}_i(u_i,u_{N_i\left(\overline{g}\right)\cap S})=\sum _{i\in S}\left[f\left(u_i+\sum _{j\in N_i\left(\overline{g}\right)\cap S}{u}_j\right)-c_i{u}_i\right],$$

(2)

over actions $u_i\in U_i$, $i\in S$. The next result characterizes the optimal solution of the above problem.

Proposition 3.

If ${\widehat{u}}^S$ compose a profile maximizing (2) when network $\overline{g}$ is formed at the first game stage, then there exist constants $\left\{{\lambda }_i\right\}⩾0$, such that ${\left\{{\widehat{u}}_i^S\right\}}_{i\in S}$ are feasible, and

$$\begin{array}{cc}\hfill & \frac{\partial f\left({\widehat{u}}_i^S+{\sum }_{j\in N_i\left(\overline{g}\right)\cap S}{\widehat{u}}_j^S\right)}{\partial u_i^S}+\sum _{j\in N_i\left(\overline{g}\right)\cap S}\frac{\partial f\left({\widehat{u}}_j^S+{\sum }_{k\in N_j\left(\overline{g}\right)\cap S}{\widehat{u}}_k^S\right)}{\partial u_i^S}-c_i+{\lambda }_i=0,i\in S,\hfill \\ \hfill & {\lambda }_i{\widehat{u}}_i^S=0,i\in S.\hfill \end{array}$$

Hence, $v_2(\overline{g},S)={\sum }_{i\in S}\left[f\left({\widehat{u}}_i^S+{\sum }_{j\in N_i\left(\overline{g}\right)\cap S}{\widehat{u}}_j^S\right)-c_i{\widehat{u}}_i^S\right]$.

From Propositions 2 and 3, we conclude that characteristic functions $v_1\left(S\right)$ and $v_2(\overline{g},S)$ may not coincide, which implies that a cooperative solution may not be time consistent (see [1,4,17] for more details). However, in some instances, these functions coincide. We provide a sufficient condition when it is the case.

Proposition 4.

When ${\ell }_i=n-1$ for any $i\in N$, that is, each player can offer any number of links (but not necessarily to all players), it holds that $v_1\left(S\right)=v_2(\overline{g},S)$ for any $S\subset N$.

Proof. 

Since a link addition creates positive externalities, when forming network $\overline{g}$ at the first game stage in a cooperative manner, any link $(i,j)$ such that $i\in L_j$ and $j\in L_i$ will be established as players are not restricted in the number of offers. Next, when determining $v_1\left(S\right)$ for $S\subset N$, players from S will establish links $(i,j)$ such that $i\in L_j\cap S$ and $j\in L_i\cap S$. So, $g_{ij}^S={\overline{g}}_{ij}$ for any pair of players from S. Hence, $v_1\left(S\right)=v_2(\overline{g},S)$ for any $S\subset N$ by Propositions 2 and 3, and the equality of characteristic functions implies the time consistency of any cooperative solution. □

Example 1.

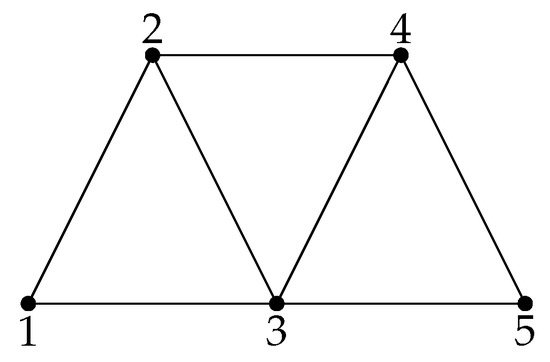
Consider a five-person game with $N=\{1,2,3,4,5\}$, function $f\left(x\right)=ln(1+x)$, and the following parameters: $c_1=0.1$, $c_2=0.5$, $c_3=c_5=0.3$, $c_4=0.2$. Further, let $L_i=N\backslash \left\{i\right\}$ for all $i\in N$ and ${\ell }_1={\ell }_5=2$, ${\ell }_2={\ell }_4=3$, ${\ell }_3=4$. By Proposition 1–3, we conclude that under cooperation players form network $\overline{g}=\{(1,2),(1,3),(2,3),(2,4),(3,4),(3,5),(4,5)\}$ demonstrated in Figure 2 and choose actions from the profile $\overline{u}=(21.7679,0,0,12.8965,0)$, and hence $v_1\left(N\right)=v_2(\overline{g},N)=10.7808$. To demonstrate the difference in characteristic functions, we take coalition $\{1,2,5\}$ and obtain $v_1\left(\{1,2,5\}\right)=7.3036$, but $v_2(\overline{g},\{1,2,5\})=4.5954$. For coalition, say, $\{1,2,3\}$, the values of characteristic functions coincide: $v_1\left(\{1,2,3\}\right)=v_2(\overline{g},\{1,2,3\})=7.3036$.

Figure 2. Network $\overline{g}$.

4. Negative Externalities: Market Competition

We now examine a model of market competition. Consider an industry of firms (players) producing homogeneous goods with outputs $u_i\in U_i=[0,q_i]$, $i\in N$, for some $q_i>0$. The payoff to player $i\in N$ (firm’s profit) is given by:

$$h_i(u_i,u_{N_i\left(g\right)})=p\left(u_i+\sum _{j\in N_i\left(g\right)}{u}_j\right)u_i-c_i{u}_i,c_i>0,$$

where p is the inverse demand function, and it is twice-differentiable, non-negative, nonincreasing, and convex; $c_i$ is unit cost. The inverse demand function depends on the outputs of a player and her neighbors, which becomes natural when customers account for the location of players. Here, the network is incorporated into the inverse demand function and not the player’s costs, as opposed to [18,19]. We note that new links create negative externalities for players, i.e., $h_i(u_i,u_{N_i\left(g\right)})⩽h_i(u_i,u_{N_i\left(\tilde{g}\right)})$ for any profile $(u_1,\dots ,u_n)$, feasible networks g, $\tilde{g}$, and a player i such that $\tilde{g}\subset g$ and $|N_i\left(g\right)|>|N_i\left(\tilde{g}\right)|$, and property (P) does not hold. Indeed,

$$h_i(u_i,u_{N_i\left(g\right)})-h_i(u_i,u_{N_i\left(\tilde{g}\right)})=\left[p\left(u_i+\sum _{j\in N_i\left(g\right)}{u}_j\right)-p\left(u_i+\sum _{j\in N_i\left(\tilde{g}\right)}{u}_j\right)\right]u_i⩽0.$$

This fact does not allow us directly to use the theory developed in [4] so as propositions from the previous section for determining the cooperative strategy profile $\overline{u}$ and the characteristic functions $v_1\left(S\right)$ and $v_2(g,S)$ for $S\subseteq N$. However, since the addition of links creates negative externalities, players never agree on establishing them, thus forming the empty network under cooperation. To prove this claim, we consider two feasible profiles: a profile at which players form the empty network $g^{*}=⌀$ and choose $u^{*}$, in which i’s component maximizes $h_i\left(u_i\right)$, $i\in N$, (thus, $u^{*}$ maximizes the sum ${\sum }_{i\in N}{h}_i\left(u_i\right)$), and a profile at which players form a feasible network g, do not revise it at the second stage, and choose u. Consider the difference in player i’s payoffs:

$$\begin{array}{cc}\hfill h_i\left(u_i^{*}\right)-h_i(u_i,u_{N_i\left(g\right)})& =p\left(u_i^{*}\right)u_i^{*}-c_i{u}_i^{*}-p\left(u_i+\sum _{j\in N_i\left(g\right)}{u}_j\right)u_i+c_i{u}_i\hfill \\ \hfill & ⩾p\left(u_i^{*}\right)u_i^{*}-c_i{u}_i^{*}-p\left(u_i\right)u_i+c_i{u}_i=h_i\left(u_i^{*}\right)-h_i\left(u_i\right),\hfill \end{array}$$

which is non-negative as $u_i^{*}$ maximizes $h_i\left(u_i\right)$ for all $i\in N$. Therefore, ${\sum }_{i\in N}{h}_i\left(u_i^{*}\right)⩾{\sum }_{i\in N}{h}_i(u_i,u_{N_i\left(g\right)})$ for any g and u. This means that the profile at which players form the empty network and choose $u^{*}$ is the cooperative strategy profile. To find the maximum total payoff to players from N, that is, $v_1\left(N\right)$, we write the Lagrangian function: ${\sum }_{i\in N}[(p\left(u_i\right)-c_i)u_i+{\lambda }_i{u}_i+{\mu }_i(q_i-u_i)]$, where $\left\{{\lambda }_i\right\}$ and $\left\{{\mu }_i\right\}$ are some constants.

Proposition 5.

If $\overline{u}$ is a part of a cooperative strategy profile, then there exist constants $\left\{{\lambda }_i\right\}⩾0$, $\left\{{\mu }_i\right\}⩾0$ such that $\overline{u}$ is feasible, and

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}p\left({\overline{u}}_i\right)}{\mathrm{d}{u}_i}{\overline{u}}_i+p\left({\overline{u}}_i\right)-c_i+{\lambda }_i-{\mu }_i=0,{\lambda }_i{\overline{u}}_i=0,{\mu }_i(q_i-{\overline{u}}_i)=0,i\in N.\hfill \end{array}$$

Hence, $v_1\left(N\right)=v_2(\overline{g},N)={\sum }_{i\in N}[p\left({\overline{u}}_i\right)-c_i]{\overline{u}}_i$.

Proof. 

The statement follows from the Karush–Kuhn–Tucker theorem adapted for the optimization problem under consideration. □

To find values $v_1\left(S\right)$ and $v_2(g,S)$ for $S\subset N$, we have to solve optimization problems similar to the problem from Proposition 5, but for $\left|S\right|$ players, noting that players do not establish links under cooperation. Thus, we arrive at the result.

Proposition 6.

If $u^S$ is a part of a profile maximizing the total payoff to coalition $S\subset N$, then there exist constants $\left\{{\lambda }_i\right\}⩾0$, $\left\{{\mu }_i\right\}⩾0$ such that $u^S$ is feasible, and

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}p\left(u_i^S\right)}{\mathrm{d}{u}_i}{u}_i^S+p\left(u_i^S\right)-c_i+{\lambda }_i-{\mu }_i=0,{\lambda }_i{u}_i^S=0,{\mu }_i(q_i-u_i^S)=0,i\in S.\hfill \end{array}$$

Hence, $u_i^S={\overline{u}}_i$ for any player $i\in S$, and $v_1\left(S\right)=v_2(\overline{g},S)={\sum }_{i\in S}[p\left({\overline{u}}_i\right)-c_i]{\overline{u}}_i$.

Proof. 

Since players from S do not form links in the two-stage game under cooperation, $\overline{g}=⌀$ and $v_1\left(S\right)=v_2(\overline{g},S)$. The remaining part of the proof follows from the Karush–Kuhn–Tucker theorem. □

Noting that the characteristic functions $v_1$ and $v_2$ coincide, any cooperative solution to the two-stage game (within the context of the market competition model) is time consistent.

Example 2.

Consider the player set N and function $p\left(x\right)=a-x$ with $c_i<a$, $q_i⩽a$ for all $i\in N$. We have demonstrated that players do not create links when cooperating, so the values ${\ell }_i$ and sets $L_i$, $i\in N$ do not influence the cooperative behavior. For this reason, we do not specify them. Assuming a non-negative value of the inverse demand function at the cooperative strategy profile, by Proposition 5, we conclude that players form the empty network $\overline{g}=⌀$ and choose actions from $\overline{u}$, where

$${\overline{u}}_i=\left\{\begin{array}{cc}{q}_i,\hfill & {\displaystyle q_i⩽\frac{a-c_i}{2},}\hfill \\ {\displaystyle \frac{a-c_i}{2},}\hfill & {\displaystyle q_i>\frac{a-c_i}{2}.}\hfill \end{array}\right.$$

So, $v_1\left(N\right)=v_2(\overline{g},N)={\sum }_{i\in N}(a-c_i-{\overline{u}}_i){\overline{u}}_i$. Similarly, Proposition 6 implies that $v_1\left(S\right)=v_2(\overline{g},S)={\sum }_{i\in S}(a-c_i-{\overline{u}}_i){\overline{u}}_i$ for any coalition $S\subset N$. Additionally, if $q_i=a$ for all $i\in N$ (see, for example, [15]), then ${\overline{u}}_i=(a-c_i)/2$, which implies that $v_1\left(S\right)=v_2(\overline{g},S)={\sum }_{i\in S}{(a-c_i)}^2/4$ for any coalition $S\subseteq N$.

5. Conclusions

In the models under consideration (so-called models without transferable technologies), we supposed that the costs of a coalition amount to the sum of its members’ costs. However, in case of transferable technologies, the unit costs for each player in the coalition becomes the minimum unit costs among the players from it (assuming linearity). Clearly, a more general type of costs may be introduced, but even in this case, the models under consideration will retain their positive and negative externalities, respectively. This will only require adapting the corresponding optimality conditions. The possibility of calculating the characteristic functions allows us to find a variety of cooperative solutions and perform their comparative analysis. For example, when it comes to the issue of the time consistency of a cooperative solution, we can definitely conclude that the solution will meet this property in the examined model with negative externalities. At the same time, depending on the chosen cooperative solution, the (possible) difference in characteristic functions in the model with positive externalities can, nevertheless, lead to its time consistency; but, even if it is not the case, there are known methods of game regularization in the literature.