Bijective, Non-Bijective and Semi-Bijective Translations on the Triangular Plane †
Abstract
:1. Introduction
2. Preliminaries
2.1. Discrete Translations
- surjective if in the target, there is at least one element in the domain, such that .
- injective if in the domain, whenever then a = b. Formally:
- bijective if it is both injective and surjective.
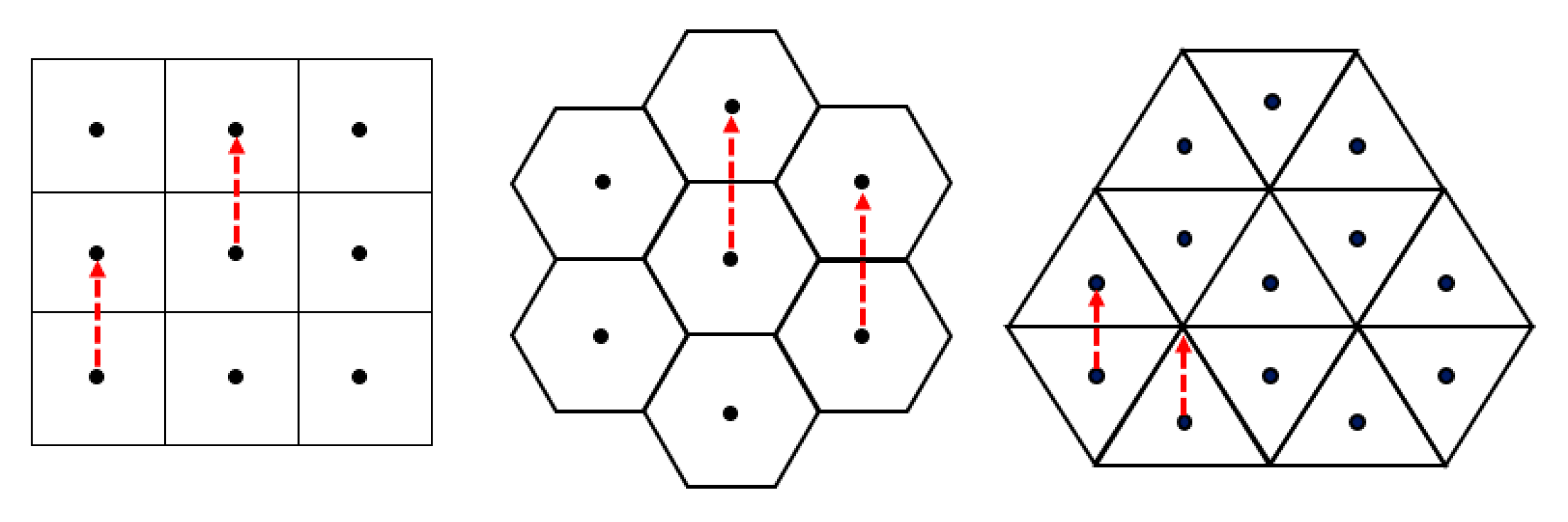
Translations on the Traditional Grid
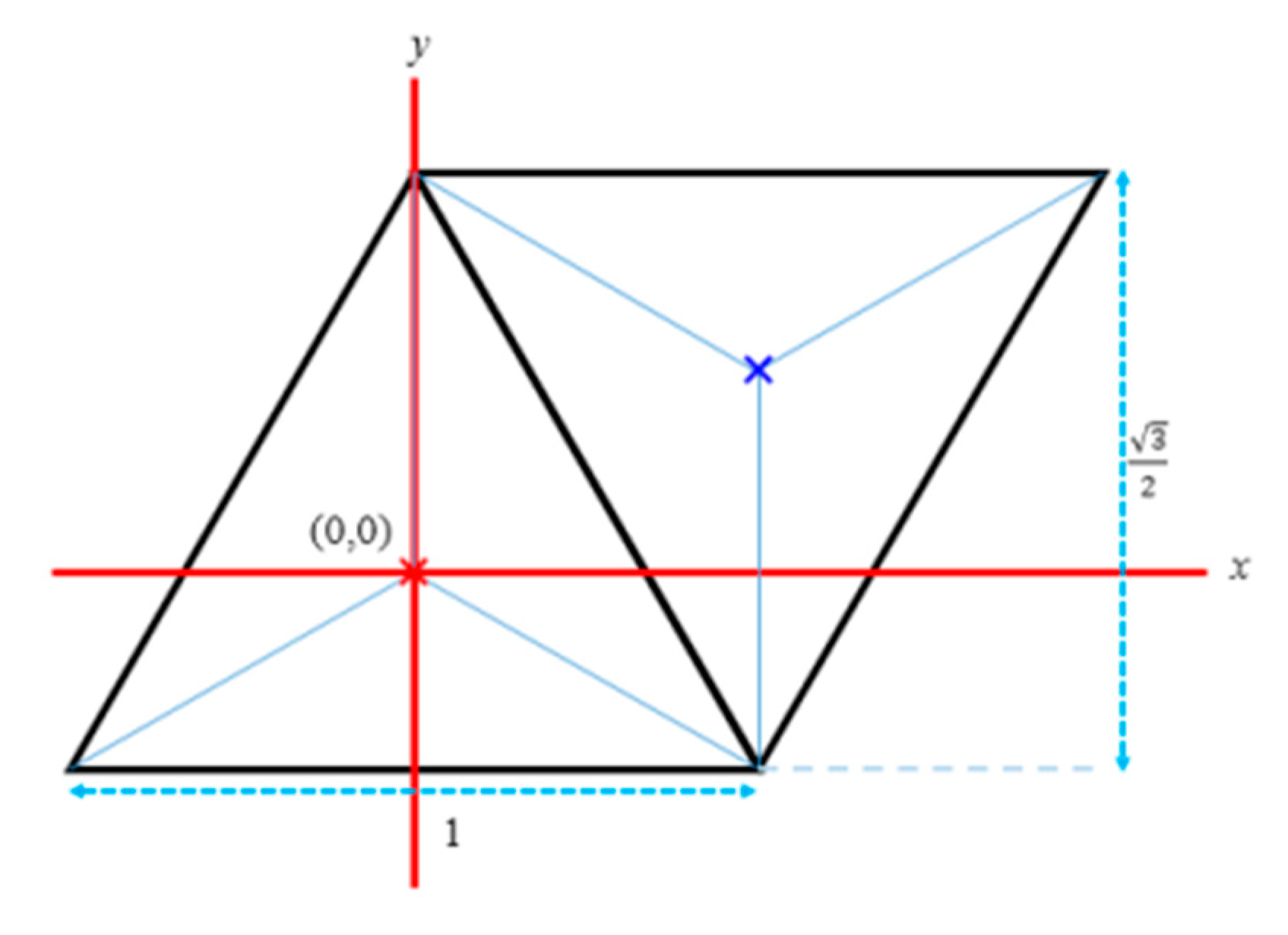
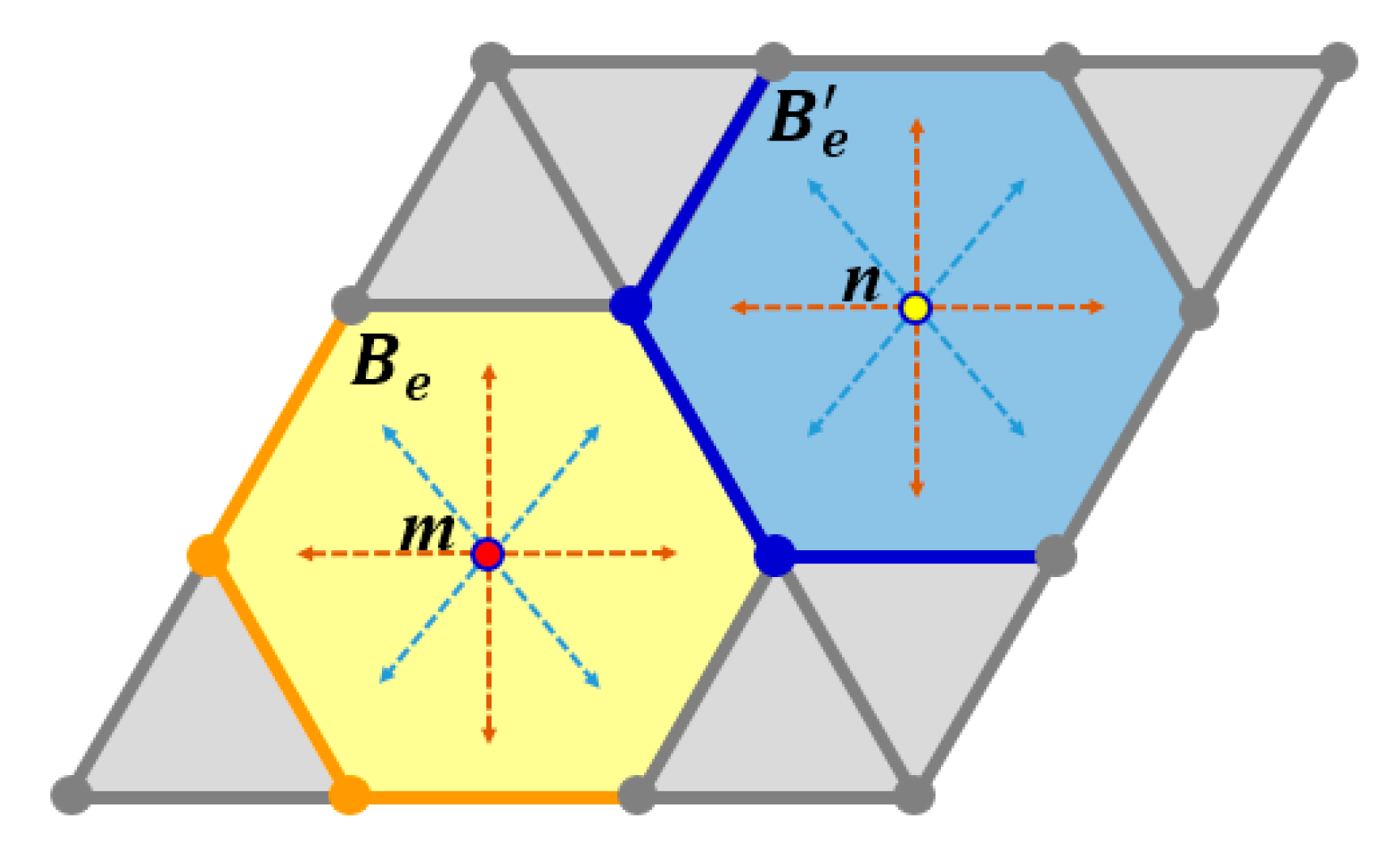
2.2. Notions and Notations on the Triangular Grid
3. Translations on the Triangular Grid
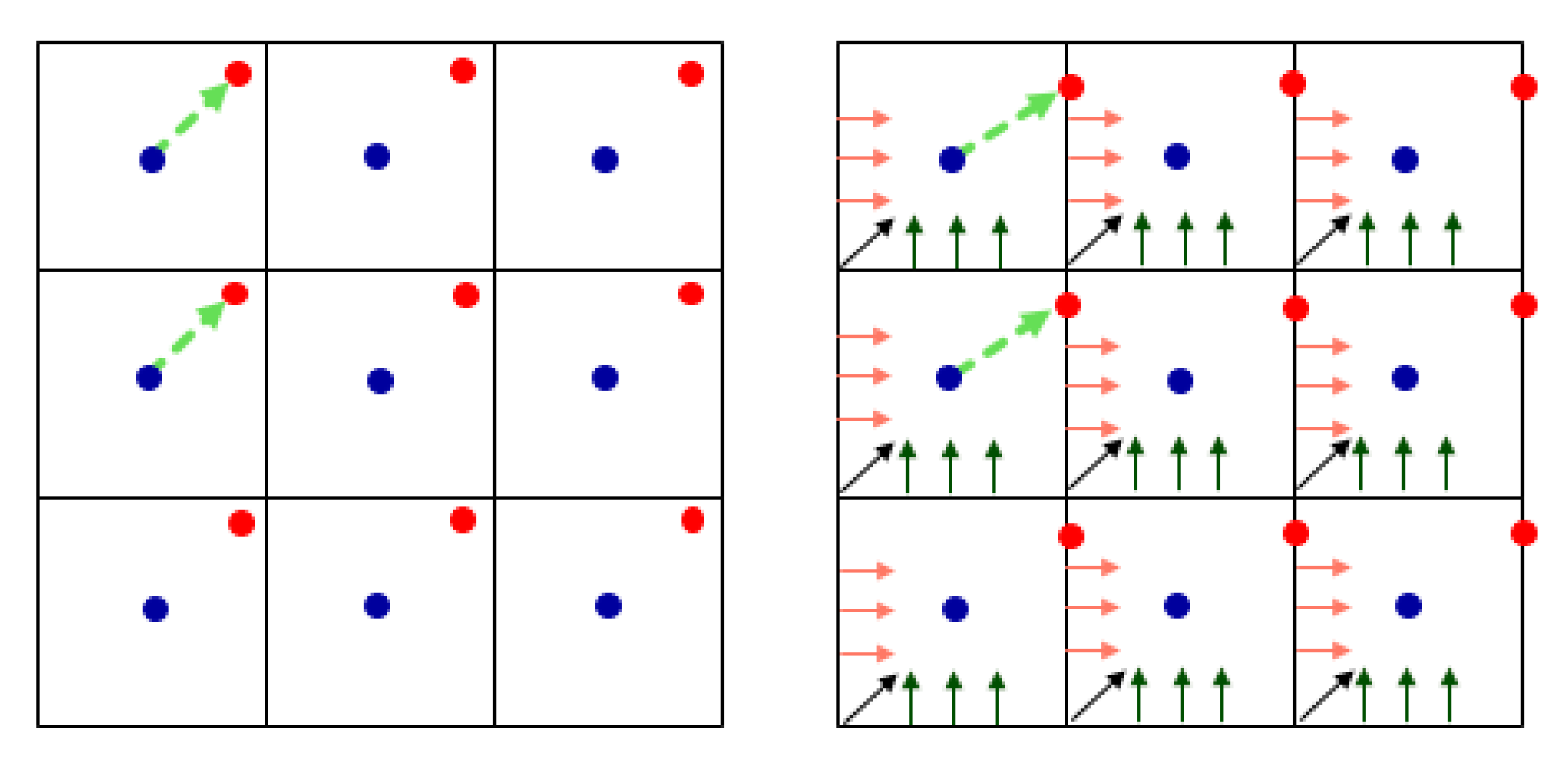
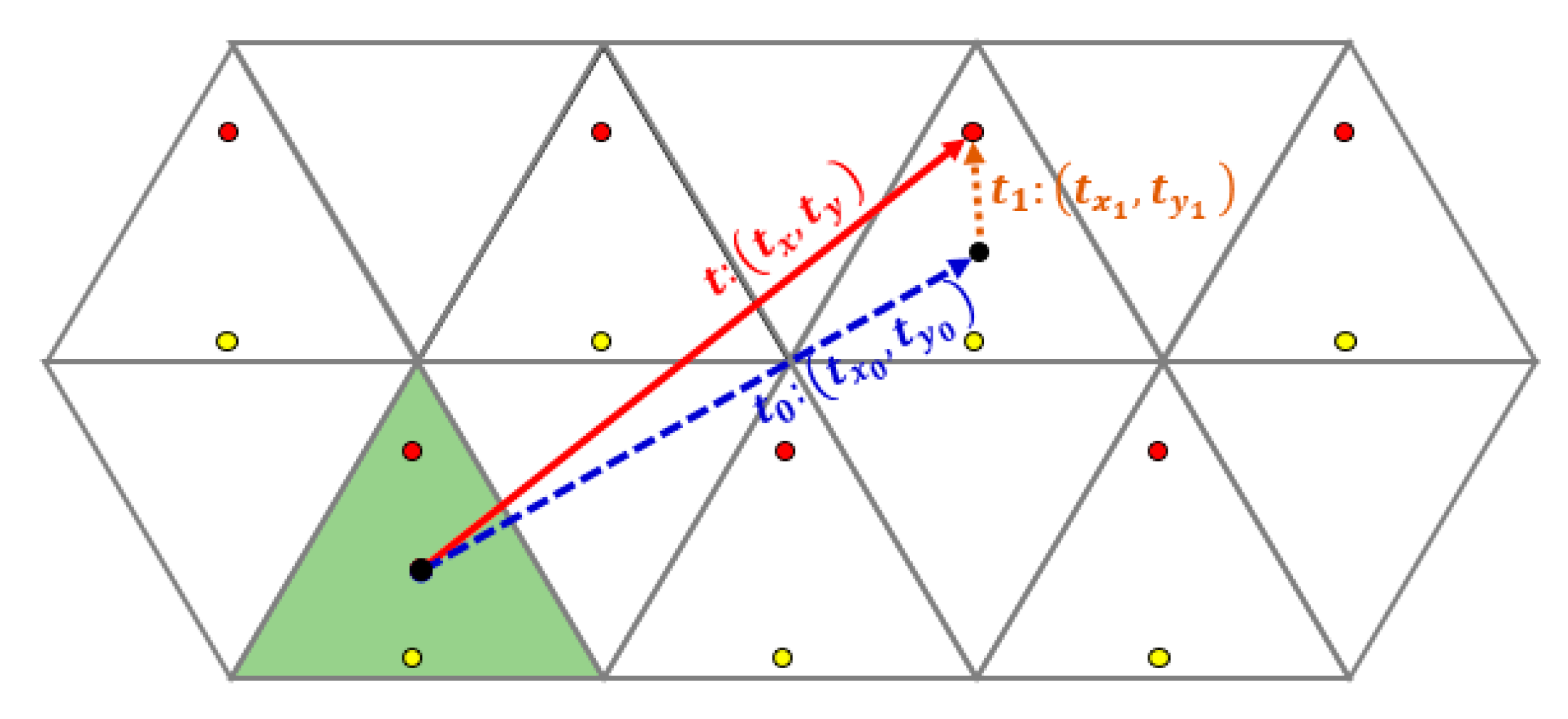
3.1. “Integer” + “Fractional” Vectors
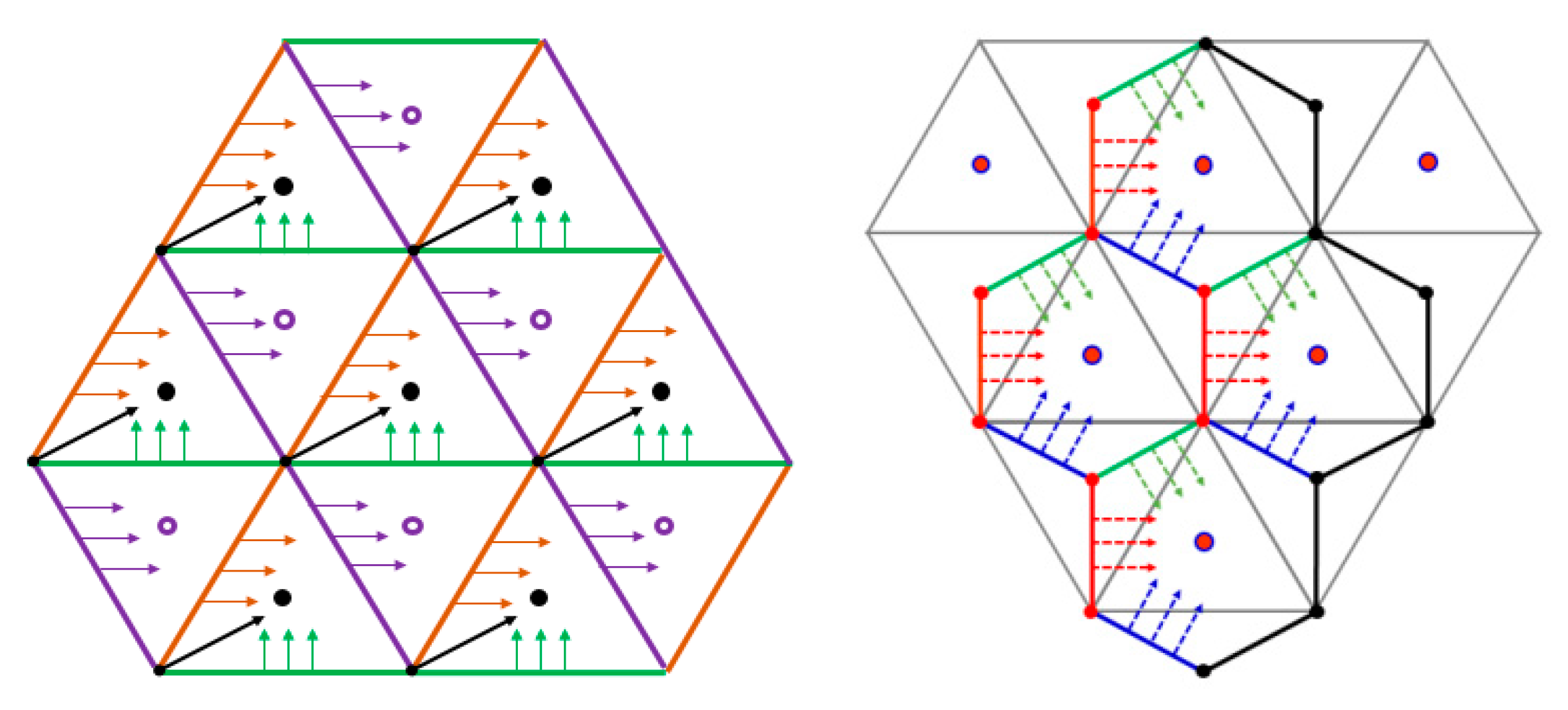
3.2. Rounding the Border Points
- (1)
- Every corner point is mapped to the nearest even midpoint which has the maximal x coordinate value among the pixels sharing this corner point.
- (2)
- For points which are not corner points, we have the following strategy:
- (3)
- Every non-corner point on the ‘/’ direction (brown) border lines is mapped to the nearest even midpoint.
- (4)
- Every non-corner point on the ‘\’ direction (purple) border lines is mapped to the nearest odd midpoint.
- (5)
- Every point on the horizontal (green) border lines that is not a corner is mapped to the nearest even midpoint.
- (6)
- For the sake of completeness, we also give the assignment for all other points:
- (7)
- Finally, every point (x, y) which is not on the borders should be mapped to its nearest midpoint based on their distances.
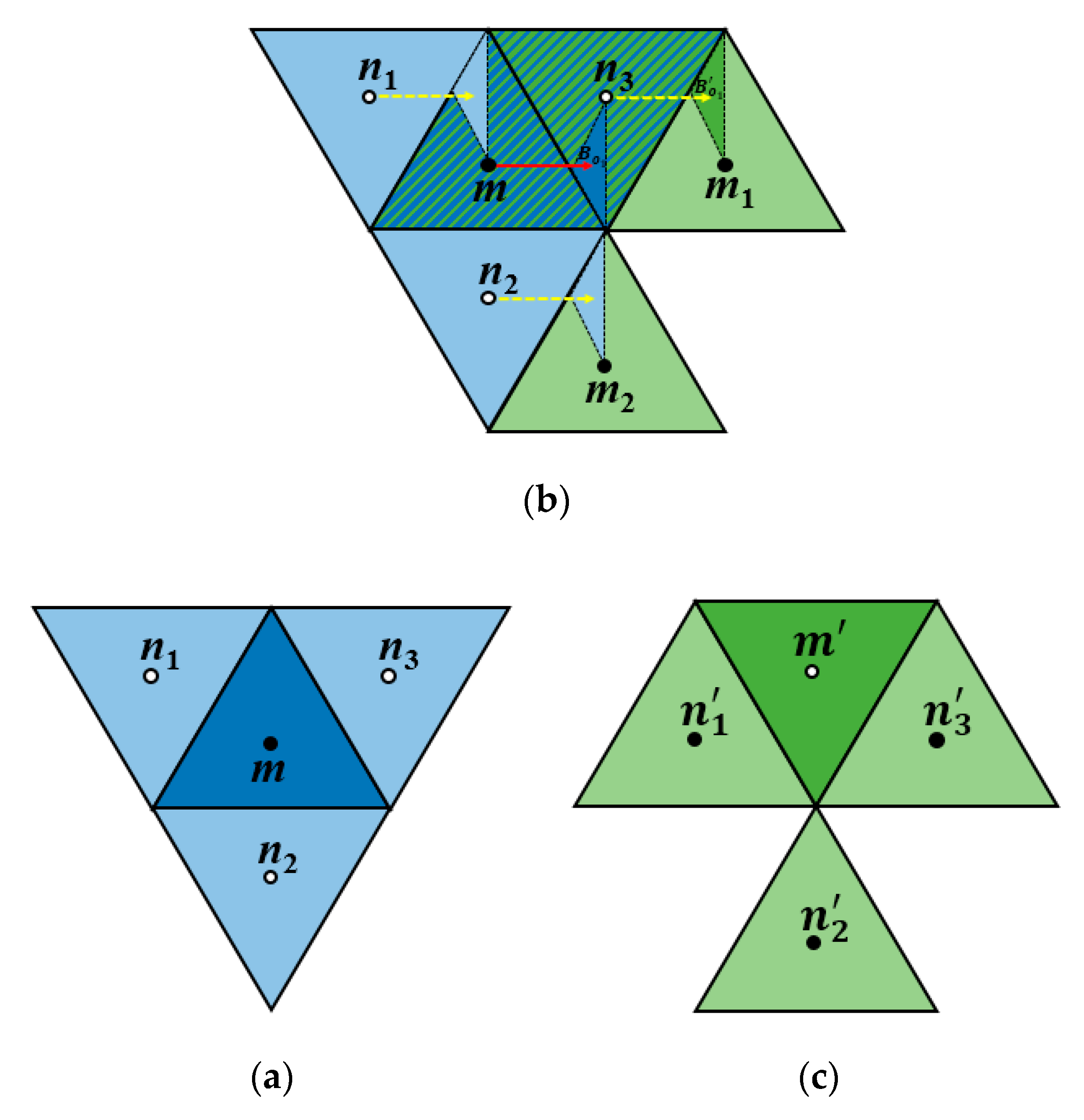
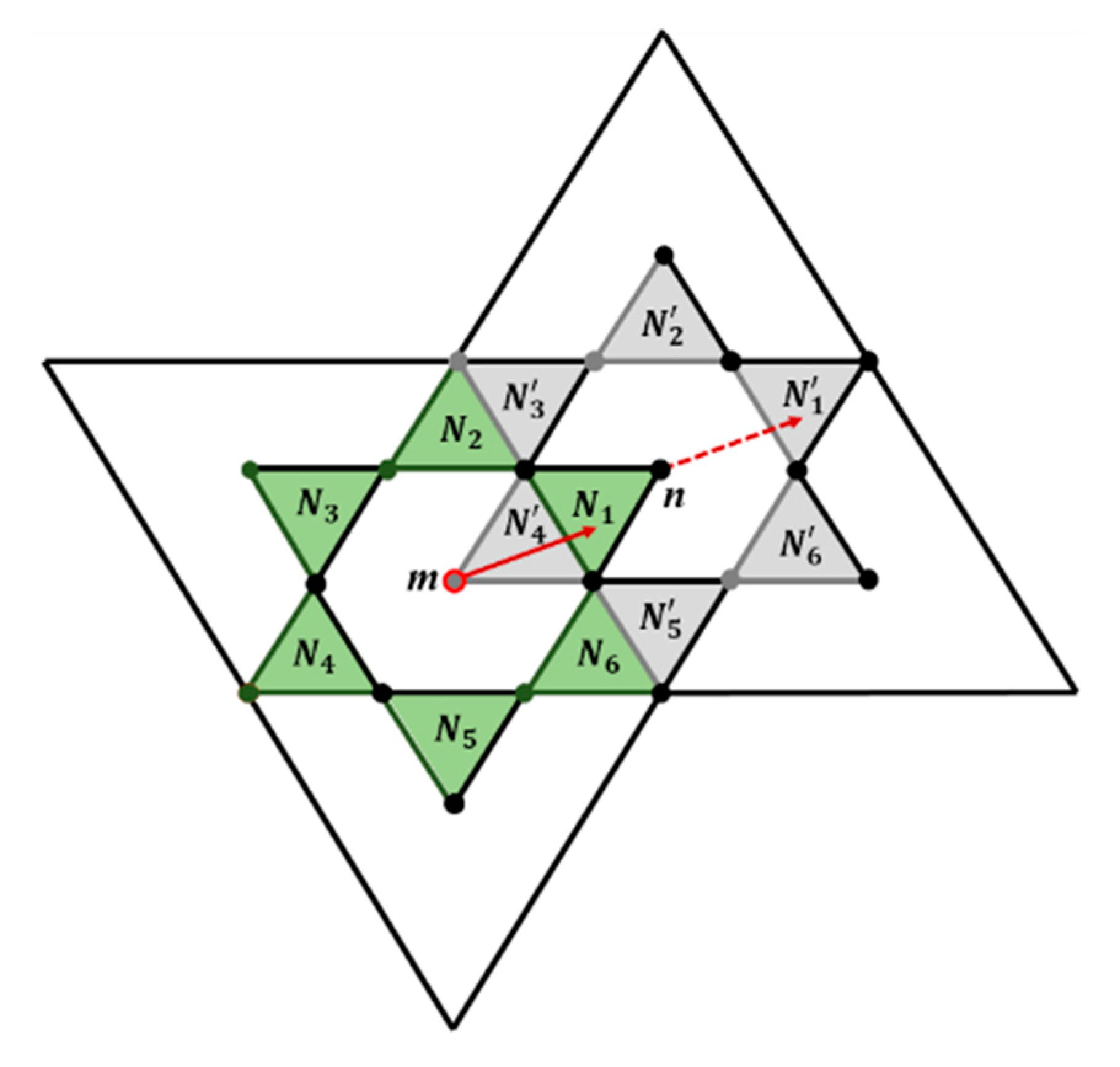
4. Main Results: Characterizing Strongly Bijective, Semi-Bijective, and Non-Bijective Translation Vectors
4.1. Vectors of Bijective Translations
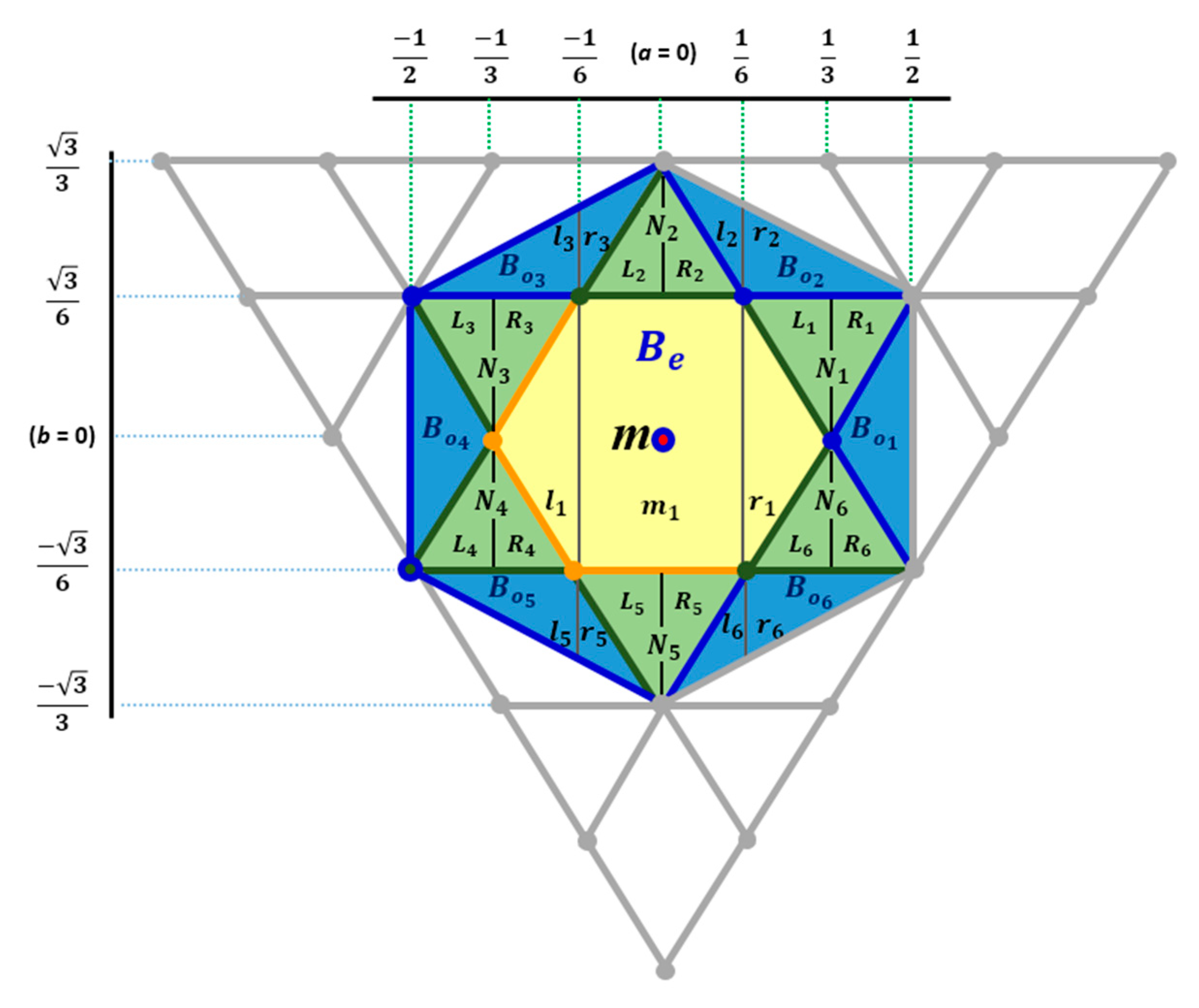
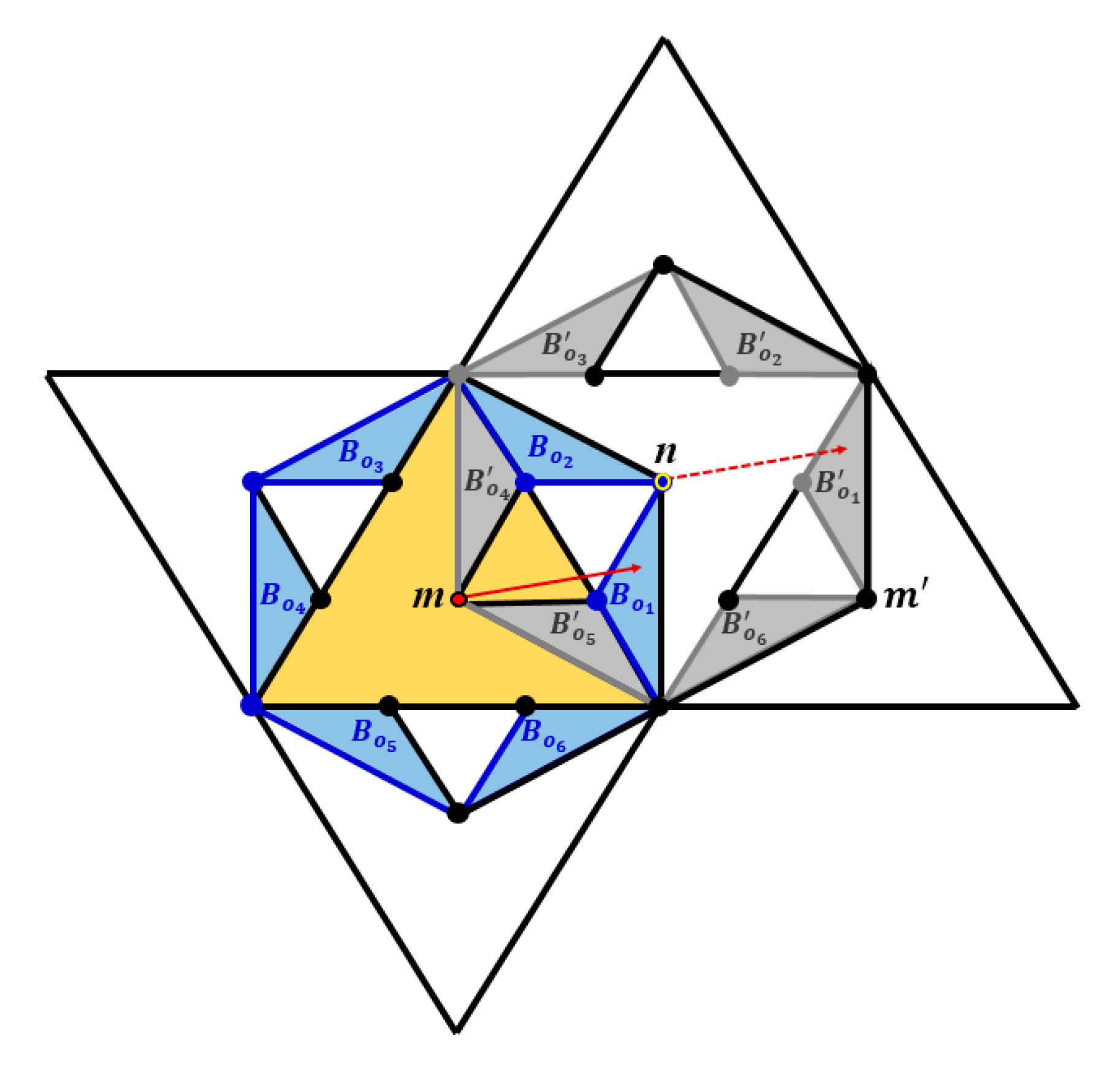
4.1.1. Characterizing Strongly Bijective Translations
4.1.2. Characterizing Semi-Bijective Translations
4.2. Characterizing the Non-Bijective Translation Vectors
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Klette, R.; Rosenfeld, A. Digital geometry: Geometric methods for digital picture analysis. In Morgan Kaufmann; Elsevier: San Francisco, CA, USA, 2004; Volume I-XVIII, pp. 1–656. ISBN 978-1-55860-861-0. [Google Scholar]
- Kaufman, A. Voxels as a computational representation of geometry. Presented at the SIGGRAPH’99—Course 29, Los Angeles Convention Center, Los Angeles, CA, USA, 8–13 August 1999; pp. 14–58. [Google Scholar]
- Pluta, K.; Romon, P.; Kenmochi, Y.; Passat, N. Bijective Digitized Rigid Motions on Subsets of the Plane. J. Math. Imaging Vis. 2017, 59, 84–105. [Google Scholar] [CrossRef]
- Nagy, B. Isometric transformations of the dual of the hexagonal lattice. In Proceedings of the 6th IEEE International Symposium on Image and Signal Processing and Analysis, ISPA, Salzburg, Austria, 16–18 September 2009; pp. 432–437. [Google Scholar]
- Pluta, K.; Romon, P.; Kenmochi, Y.; Passat, N. Bijective rigid motions of the 2D Cartesian grid. In DGCI 2016: Discrete Geometry for Computer Imagery; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; Volume 9647, pp. 359–371. [Google Scholar]
- Rosenfeld, A. Continuous functions on digital pictures. Pattern Recognit. Lett. 1986, 4, 177–184. [Google Scholar] [CrossRef]
- Nagy, B. Characterization of digital circles in triangular grid. Pattern Recognit. Lett. 2004, 25, 1231–1242. [Google Scholar] [CrossRef]
- Nagy, B.; Moisi, E.V. Memetic algorithms for reconstruction of binary images on triangular grids with 3 and 6 projections. Appl. Soft Comput. 2017, 52, 549–565. [Google Scholar] [CrossRef]
- Kardos, P.; Palágyi, K. Topology preservation on the triangular grid. Ann. Math. Artif. Intell. 2015, 75, 53–68. [Google Scholar] [CrossRef]
- Kardos, P.; Palágyi, K. Unified Characterization of P-Simple Points in Triangular, Square, and Hexagonal Grids. In Computational Modeling of Objects Presented in Images. Fundamentals, Methods, and Applications, Proceedings of the International Symposium Computational Modeling of Objects Represented in Images, Niagara Falls, NY, USA, 21–23 September 2016; Springer: Cham, Switzerland, 2017; Volume 10149, pp. 79–88. [Google Scholar]
- Abuhmaidan, K.; Nagy, B. Non-bijective translations on the triangular plane. In Proceedings of the IEEE 16th World Symposium on Applied Machine Intelligence and Informatics (SAMI 2018), Kosice, Slovakia, 7–10 February 2018; pp. 183–188. [Google Scholar]
- Mazo, L.; Baudrier, É. Object digitization up to a translation. J. Comput. Syst. Sci. 2018, 95, 193–203. [Google Scholar] [CrossRef] [Green Version]
- Nagy, B. An algorithm to find the number of the digitizations of discs with a fixed radius. Electron. Notes Discret. Math. 2005, 20, 607–622. [Google Scholar] [CrossRef]
- Avkan, A.; Nagy, B.; Saadetoglu, M. Digitized Rotations of Closest Neighborhood on the Triangular Grid. In Combinatorial Image Analysis, Proceedings of the 19th International Workshop, (IWCIA 2018), Porto, Portugal, 22–24 November 2018; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 11255, pp. 53–67. [Google Scholar]
- Avkan, A.; Nagy, B.; Saadetoglu, M. Digitized Rotations of 12 Neighbors on the Triangular Grid. Ann. Math. Artif. Intell. 2019. accepted. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abuhmaidan, K.; Nagy, B. Bijective, Non-Bijective and Semi-Bijective Translations on the Triangular Plane. Mathematics 2020, 8, 29. https://doi.org/10.3390/math8010029
Abuhmaidan K, Nagy B. Bijective, Non-Bijective and Semi-Bijective Translations on the Triangular Plane. Mathematics. 2020; 8(1):29. https://doi.org/10.3390/math8010029
Chicago/Turabian StyleAbuhmaidan, Khaled, and Benedek Nagy. 2020. "Bijective, Non-Bijective and Semi-Bijective Translations on the Triangular Plane" Mathematics 8, no. 1: 29. https://doi.org/10.3390/math8010029
APA StyleAbuhmaidan, K., & Nagy, B. (2020). Bijective, Non-Bijective and Semi-Bijective Translations on the Triangular Plane. Mathematics, 8(1), 29. https://doi.org/10.3390/math8010029





