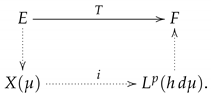Banach Lattice Structures and Concavifications in Banach Spaces

Abstract

Let $(\mathsf{\Omega },\mathsf{\Sigma },\mu )$ be a finite measure space and consider a Banach function space $Y(\mu )$. We say that a Banach space E is representable by $Y(\mu )$ if there is a continuous bijection $I:Y(\mu )\to E$. In this case, it is possible to define an order and, consequently, a lattice structure for E in such a way that we can identify it as a Banach function space, at least regarding some local properties. General and concrete applications are shown, including the study of the notion of the pth power of a Banach space, the characterization of spaces of operators that are isomorphic to Banach lattices of multiplication operators, and the representation of certain spaces of homogeneous polynomials on Banach spaces as operators acting in function spaces.

1. Introduction

The theory of Banach lattices, and in particular the theory of Banach function spaces, provides powerful specific tools in mathematical analysis. These tools can be added to those of the Banach space theory when the spaces considered have this supplementary structure. In this paper, we are interested in constructing a technique to transfer some of these techniques from the Banach lattices to the Banach space setting by means of some local identification of subspaces. Using Banach-space-type isomorphisms among substructures of the spaces involved (one of them a Banach function space, the other just a Banach space) we can identify lattice-type properties and constructions in Banach spaces.

The main notion that we develop is the pth power of a Banach space. The concept of the pth power of a Banach function space, sometimes called p-concavification, is a useful construction both in the context of the study of the structure of the classical Banach spaces and that of the theory of operators on these spaces. It must be said that the notion of p-concavification can be extended to abstract Banach lattices; the way of doing it is nowadays classical—see [1,2]. Some recent papers have extended it to some typical Banach space constructions (for example, tensor products, see [3,4,5]), but always in a Banach lattice framework (Fremlin tensor products). As far as we know, the present paper is the first attempt of translating this notion to the Banach space setting.

This transfer makes it possible to find some new results of the factorization of operators between Banach spaces. Indeed, our main goal is to understand some factorization arguments that are performed for Banach function spaces—the so-called Maurey–Rosenthal theorems (see, for example, [6,7])—in the Banach space framework in order to show concrete representations of subspaces of Banach spaces as weighted $L^p$-spaces. The lattice geometric structure of the Banach function spaces regarding p-convexity and p-concavity inherited by the Banach spaces by means of our representation allows us to do this. The link between the factorization of operators and the concrete representation of Banach function spaces and operators is a classical tool in Banach lattice theory (see, for example, [8,9] and ([10], Chapter III.H )). In our case, the arguments involve factorization of operators $T:E\to F$ (E and F Banach spaces) through inclusion maps $X(\mu )\to L^p(hd\mu )$ as

Note that for the cases $X(\mu )=L^{q^{\prime }}(\mu )$, $1\le q^{\prime }\le \infty$, this scheme can be understood as a strong version of the one that holds for maps that belong to some classical operator ideals (as, for instance, the ideal of p-integral operators). Finally, some applications in the representation of spaces of multiplication operators and spaces of polynomials are given.

From a technical point of view, we systematically use the identification provided by the integration with respect to vector measures. It is well known that order-continuous Banach function spaces are deeply related to spaces of integrable functions with respect to a vector measure. In fact, there is a representation theorem that allows the relation of both classes of spaces (see ([11], Theorem 8), ([12], Proposition 3.9). In particular, this provides a first representation result, using a linear isomorphism in this case: A Banach space is representable as an order-continuous Banach function space with a weak unit if and only if it is the range of an integration map of a (countably additive) vector measure which is an isomorphism. This technique has been widely used for the identification of the optimal domain of some relevant operators; the reader can find some examples and applications in [12,13,14,15,16] and the references therein.

2. Standard Definitions and Basic Concepts

Our notation is standard. As usual, if E and F are Banach spaces, we will write $L(E,F)$ for the space of (linear and continuous) operators endowed with its natural norm and $B_E$ for the closed unit ball of E.

2.1. Banach Function Spaces, pth Powers, and Vector Measures

Consider a finite measure space $(\mathsf{\Omega },\mathsf{\Sigma },\mu )$ and the space $L^0(\mu )$ of all measurable real functions on $\mathsf{\Omega }$, where functions which are equal $\mu$-a.e. are identified. The usual $\mu$-a.e. pointwise order can be considered in this space. Following ([2], p. 28), we say that a Banach function space over $\mu$ is a Banach space $X(\mu )$ of integrable functions in $L^0(\mu )$ satisfying that if $|f|\le |g|$ with $f\in L^0(\mu )$ and $g\in X(\mu )$, then $f\in X(\mu )$ and $\parallel f\parallel \le \parallel g\parallel$. The reader is referred to [2,12,17,18,19] for general facts on Banach function spaces. We say that $X(\mu )$ is order continuous if for every sequence ${(f_n)}_n\in X(\mu )$ such that $f_n\downarrow 0$ satisfies that $\parallel f_n{\parallel }_{X(\mu )}\to 0$. For the case of the finite measure, the set of all simple functions is dense in any order-continuous Banach function space. The Köthe dual $X{(\mu )}^{\prime }$ of $X(\mu )$ is the Banach function space over $\mu$ of all functions $\{g\in L^0(\mu ):fg\in L^1(\mu )\}$ endowed with the norm

$${\parallel g\parallel }_{X{(\mu )}^{\prime }}:=\underset{f\in B_{X(\mu )}}{sup}\int fgd\mu .$$

This is a particular case of a space of multiplication operators. If $X(\mu )$ and $Y(\mu )$ are Banach function spaces over the same measure $\mu$, we write $M(X(\mu ),Y(\mu ))$ for the Banach function space of the ($\mu$-a.e. equal classes of) functions g that define operators from $X(\mu )$ to $Y(\mu )$ by means of the formula $M_g(f):=f·g\in Y(\mu )$, $f\in X(\mu )$. The norm ${\parallel g\parallel }_{M(X(\mu ),Y(\mu ))}$ for a function g in this space if given by the operator norm of $M_g$. Many papers have been written on spaces of multiplication operators; for a current review see, for example, [20]; also see [21] for an extension of this notion to the setting of non-commutative spaces.

Recall that an operator $T\in L(E,F)$ between two Banach lattices E and F is said to be p-convex if there is a constant $k>0$ such that for every finite family of vectors $x_1,\dots ,x_n\in E$,

$$\parallel {(\sum _{i=1}^n{|T(x_i)|}^p)}^{1/p}\parallel \le k{(\sum _{i=1}^n{\parallel x_i\parallel }^p)}^{1/p}.$$

(1)

The operator T is said to be p-concave if there exists a constant $k>0$ such that for every finite collection $x_1,\dots ,x_n\in E$,

$${(\sum _{i=1}^n{\parallel T(x_i)\parallel }^p)}^{1/p}\le k\parallel {(\sum _{i=1}^n{|x_i|}^p)}^{1/p}\parallel .$$

(2)

The best constants $k>0$ in the Inequalities (1) and (2) are denoted by $M^{(q)}(T)$ and $M_{(q)}(T)$, respectively. When the identity map defined on a Banach lattice E is p-convex (resp. p-concave), E is said to be p-convex (resp. p-concave). In such cases, the best constants are denoted by $M^{(q)}(E)$ and $M_{(q)}(E)$, respectively.

For $0<p<\infty$, the pth power of $X(\mu )$ is defined as the set of functions

$$X{(\mu )}_{\left[p\right]}:=\{f\in L^0{(\mu ):|f|}^{1/p}\in X(\mu )\}.$$

It is a Banach function space over $\mu$ with the norm

$${\parallel f\parallel }_{X{(\mu )}_{\left[p\right]}}:=\parallel {|f|}^{1/p}{\parallel }_{X(\mu )}^{p}f\in X{(\mu )}_{\left[p\right]},$$

whenever $X(\mu )$ is p-convex (with the p-convexity constant $M^{(p)}(X(\mu ))$ equal to 1). It is order continuous if and only if $X(\mu )$ is so (see ([12], Chapter 2)).

Consider the measurable space $(\mathsf{\Omega },\mathsf{\Sigma })$ and a Banach space valued set function $m:\mathsf{\Sigma }\to E$. We say that m is a (countably additive) vector measure if $m({\cup }_{n=1}^{\infty }{A}_n)={\sum }_{n=1}^{\infty }m(A_n)$ in the norm topology of E for all sequences ${\left\{A_n\right\}}_n$ of pairwise disjoint sets of $\mathsf{\Sigma }$. Let $E^{\prime }$ be the dual space of the Banach space E. If $x^{\prime }\in E^{\prime }$ the formula $⟨m,x^{\prime }⟩(A):=⟨m(A),x^{\prime }⟩$, $A\in \mathsf{\Sigma }$ defines a countably additive scalar measure. We write $|⟨m,x^{\prime }⟩|$ for its variation, which is given by $|⟨m,x^{\prime }⟩|(A):=sup{\sum }_{B\in \mathsf{\Pi }}|⟨m(B),x^{\prime }⟩|$ for $A\in \mathsf{\Sigma }$, where the supremum is computed over all finite measurable partitions $\mathsf{\Pi }$ of A. The non-negative function $\parallel m\parallel$ whose value on a set $A\in \mathsf{\Sigma }$ is given by $\parallel m\parallel (A)=sup\{|⟨m,x^{\prime }⟩|(A):x^{\prime }\in E^{\prime },\parallel x^{\prime }\parallel \le 1\}$ is called the semivariation of m. We say that $A\in \mathsf{\Sigma }$ is null if $\parallel m\parallel (A)=0$. It is well known that there is always a measure $\mu$ that is defined as $⟨m,x^{\prime }⟩$ for an element $x^{\prime }\in E^{\prime }$ which is equivalent to m, that is, the set of null sets coincides for both measures. Such a measure is called a Rybakov measure (see Chapter IX in [22]).

Integration with respect to vector measures was first considered in [23] as a tool for studying the extension of the Riesz representation theorem for linear forms in the dual of a $C(K)$ space to Banach space valued functions. The space of integrable functions with respect to a vector measure m is denoted by $L^1(m)$, and it is a Banach function space over any Rybakov measure $\mu$. The elements of this space are classes of the $\mu$-a.e. measurable functions f that are integrable with respect to each scalar measure $⟨m,x^{\prime }⟩$, and for every $A\in \mathsf{\Sigma }$, there is an element ${\int }_{A}fdm\in E$ such that $⟨{\int }_{A}fdm,x^{\prime }⟩={\int }_{A}fd⟨m,x^{\prime }⟩$ for every $x^{\prime }\in E^{\prime }$. The space $L^1(m)$ of m-a.e. equal m-integrable functions is an orde- continuous Banach lattice endowed with the norm

$${\parallel f\parallel }_{L^1(m)}:=\underset{x^{\prime }\in B_{E^{\prime }}}{sup}\int |f|d|⟨m,x^{\prime }⟩|,$$

and the m-a.e. order; recall that the set of m-null sets coincides with the set of null sets of any Rybakov measure for m, and so the notion of an “m-a.e. property“ is well-defined. Some information on the isomorphic structure of the spaces $L^1(m)$ can be found in [12,24]. Moreover, the expression

$${\parallel f\parallel }_{L^1(m)}:=\underset{A\in \mathsf{\Sigma }}{sup}\parallel {\int }_{A}fdm{\parallel }_E$$

gives a norm for $L^1(m)$, since we always have (for the case of real Banach spaces) that ${|||f|||}_{L^1(m)}\le {|||f|||}_{L^1(m)}\le 2{\parallel f\parallel }_{L^1(m)},$$f\in L^1(m)$ (see, for example, [12], Lem. 3.11, Prop. 3.12). For $1\le p<\infty$, the spaces $L^p(m)$ can be defined—as in the classical case—as the spaces of classes of measurable functions f that satisfy that ${|f|}^p\in L^1(m)$. They are also order-continuous Banach function spaces over any Rybakov measure for m with a weak unit ${\chi }_{\mathsf{\Omega }}$, with the usual order, and endowed with the norm ${\parallel f\parallel }_{L^p(m)}=\parallel {|f|}^p{\parallel }_{L^1(m)}^{1/p}$, $f\in L^p(m)$. Finally, the space $L^{\infty }(m)$ is defined as $L^{\infty }(\eta )$ for any Rybakov measure $\eta$ for m. With this notation, the formula

$$\underset{g\in B_{L^{\infty }(m)}}{sup}\parallel \int fgdm{\parallel }_E,f\in L^1(m)$$

also gives the norm ${\parallel ·\parallel }_{L^1(m)}$. As usual, we will write $I_m:L^1(m)\to E$ for the integration map

$$I_m(f):=\int fdm,f\in L^1(m).$$

The definition of the norm in $L^1(m)$ makes clear that $\parallel I_m\parallel =1$.

Let $T:X(\mu )\to E$ be an operator, where $X(\mu )$ is a Banach function space over a finite measure space $(\mathsf{\Omega },\mathsf{\Sigma },\mu )$. We will say that T is order-to-norm continuous if $\parallel T({\chi }_{A_n})\parallel {\to }_{n}0$ if $A_n\downarrow \varnothing$. If $X(\mu )$ is order continuous, we have that all continuous operators are order-to-norm continuous. In this case, an operator T defines a vector measure $m_T:\mathsf{\Sigma }\to E$ by the formula $m_T(A):=T({\chi }_A)$, $A\in \mathsf{\Sigma }$; we will use this associated measure throughout the paper. The operator T is $\mu$-determined if the semivariation $\parallel m_T\parallel$ of this measure is equivalent to $\mu$, i.e., $\mu$-null sets and $\parallel m_T\parallel$-null sets coincide. It is well known that such an operator can be extended with continuity to the space $L^1(m_T)$ of integrable functions with respect to the vector measure $m_T$. This extension is given by the integration map $I_{m_T}$, and satisfies that it is optimal, that is, $L^1(m_T)$ is the bigger order-continuous Banach function space to which T can be extended (see ([12], Chapter 4)).

2.2. The Basic Construction

Let $(\mathsf{\Omega },\mathsf{\Sigma },\mu )$ be a finite measure space and let $Y(\mu )$ be a Banach function space over $\mu$.

Definition 1.

We say that a Banach space $(E,\parallel ·{\parallel }_E)$ is representable over a Banach function space $(Y(\mu ),\parallel ·{\parallel }_{Y(\mu )})$ if there is a continuous bijection $I:Y(\mu )\to E$.

This implies that I is an isomorphism, and so the lattice structure of $Y(\mu )$ is inherited by E. This means that an order relation for E can be provided by the relation:

$$x\le y\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}{I}^{-1}(x)\le I^{-1}(y)$$

for all $x,y\in E$. It is obviously compatible when the equivalent norm $x⇝\parallel I^{-1}{(x)\parallel }_{Y(\mu )}$ is considered for E, and we can define the lattice elements in a natural manner, that is,

$$x\vee y=I(I^{-1}(x)\vee I^{-1}(y)),x\wedge y=I(I^{-1}(x)\wedge I^{-1}(y)),$$

and so $|x|=I(|I^{-1}(x)|)$. Indeed,

$$|x|=x\vee 0-x\wedge 0=I(I^{-1}(x)\vee 0)-I(I^{-1}(x)\wedge 0)=I(|I^{-1}(x)|),$$

and so we also have that $I^{-1}(|x|)=|I^{-1}(x)|$.

Remark 1.

The notion of a cyclic Banach space ([2], 1.a, pp. 12–14) gives an interesting example of a representable Banach space. A Banach space E with respect to a σ-complete Boolean algebra of projections is cyclic if there exists a vector $x\in E$ such that E equals the closure of the linear span of the projections of x (Definition 1.a.12 in [2]). Those spaces can be endowed with an order and an equivalent norm in such a way that it is isomorphic to an order-continuous Banach lattice with a weak unit (Theorem 1.b.14 [2]), which can always be represented as a Banach function space. The proof of this result by Bade can be found, for example, in ([25], Section V.3).

Let us write the following basic fact as a lemma, since it will be used several times through the paper.

Lemma 1.

Suppose that the Banach space $(E,\parallel ·{\parallel }_E)$ is representable over a Banach function space $(Y(\mu ),\parallel ·{\parallel }_{Y(\mu )})$. Then, the expression

$${|||x|||}_E:=sup\left\{{\parallel y\parallel }_E:y\in E,|y|\le |x|\right\},x\in E$$

gives a lattice norm for this space that is equivalent to the original one.

Proof. 

The function $x⇝{|||x|||}_E$ is clearly sub-additive and positively homogeneous. Note first that, if $x,y\in E$, $|y|\le |x|$ means that $I^{-1}(|y|)\le I^{-1}(|x|)$, and so

$$|I^{-1}(y)|=I^{-1}(I(|I^{-1}(y)|))\le I^{-1}(I(|I^{-1}(x)|))=|I^{-1}(x)|.$$

Now, if $x\in E$ and $\epsilon >0$, we clearly have that there is an element $y\in E$ such that $|y|\le |x|$ and

$$\begin{array}{ccc}\hfill {\parallel x\parallel }_E\le {|||x|||}_E& \le & {\parallel y\parallel }_E+\epsilon \le \parallel I\parallel \parallel I^{-1}{(y)\parallel }_{Y(\mu )}+\epsilon \hfill \\ & \le & \parallel I\parallel \parallel I^{-1}{(x)\parallel }_{Y(\mu )}+\epsilon \le \parallel I\parallel \parallel I^{-1}{\parallel \parallel x\parallel }_E+\epsilon ,\hfill \end{array}$$

where we have used the fact that ${\parallel ·\parallel }_{Y(\mu )}$ is a lattice norm. This proves the equivalence of $|||·{|||}_E$ and ${\parallel ·\parallel }_E$. □

Example 1.

(i)

Consider a pair of Banach function spaces $X(\mu )$ and $Y(\mu )$ over a finite measure space $(\mathsf{\Omega },\mathsf{\Sigma },\mu )$. Take the space

$$M(X(\mu ),Y(\mu ))=\left\{g\in L^0(\mu ):fg\in Y(\mu ),f\in X(\mu )\right\}$$

of all functions defining multiplication operators by means of the identification $g⇝M_g:X(\mu )\to Y(\mu ),$ $M_g(f):=fg$. As we said in the introduction, it is a Banach function space over μ (see for instance [26,27]) when the operator norm and the natural μ-a.e. order are considered. Obviously, the space of all linear operators as $T:=M_g$ for $g\in M(X(\mu ),Y(\mu ))$ is a subspace of the Banach space $L(X(\mu ),Y(\mu ))$ which is representable over $M(X(\mu ),Y(\mu ))$.

(ii)

Consider a finite measure space $(\mathsf{\Omega },\mathsf{\Sigma },\mu )$ and a Banach space F. Take an order-to-norm continuous operator $T:L^{\infty }(\mu )\to F$ and consider the canonical vector measure $m_T:\mathsf{\Sigma }\to F$ given by $m_T(A)=T({\chi }_A)$, $A\in \mathsf{\Sigma }$. Assume also that T is μ-determined, i.e., $\parallel m_T\parallel (A)=0$ if and only if $\mu (A)=0$. Using the information about the computation of the norm in $L^1(m_T)$ given in Section 2.1, we find that

$$I_{m_T}\circ M_g(f):=I_{m_T}(gf)$$

defines an operator from $L^{\infty }$ into F for every $g\in L^1(m_T)$ and

$$\parallel I_{m_T}\circ M_g{\parallel }_{L(L^{\infty }(\mu ),F)}={\parallel g\parallel }_{L^1(m_T)}.$$

Then, the space

$$E:=\left\{I_{m_T}\circ M_g\in L(L^{\infty }(\mu ),F):g\in L^1(m_T)\right\},$$

which is a subspace of $L(L^{\infty }(\mu ),F)$, is representable over $L^1(m_T)$, which is a Banach function space over each Rybakov measure η for $m_T$.

For technical reasons, in this paper, we will need to distinguish between the fact that a subspace S of a Banach space E is representable as a Banach function space and the fact that a linear subspace S of E that is complete with its own topology can be continuously embedded in E. Thus, we will say that a Banach space $S\subseteq E$ is a subspace of the Banach space E if the inclusion $\iota :S\to E$ is continuous; that is, with the word “subspace", we do not assume that the topology of S and the one inherited from E are the same, and so S is not necessarily closed in E. We are thinking, for example, in $L^{\infty }[0,1]$ as a subspace of $L^2[0,1]$. This allows the understanding of the following definition in the adequate way.

Definition 2.

Let E be a Banach space. We say that a (not necessarily closed) linear subspace S of E is a Banach function subspace of E if there is a Banach function space $Y(\mu )$ such that there is a bijection $I:Y(\mu )\to S$ such that

$${\parallel x\parallel }_E\le \parallel I^{-1}{(x)\parallel }_{Y(\mu )}=:{\parallel x\parallel }_{I(Y(\mu ))}$$

for all $x\in S$.

Note that in this case, $(S,\parallel ·{\parallel }_{I(Y(\mu ))})$ is representable over $Y(\mu )$ by means of I. Thus, all of the Banach lattice definitions for the Banach function subspace $S=I(Y(\mu ))$ of the Banach space E can be constructed by means of the ones of $Y(\mu )$, as has been explained in this section.

Example 2.

For example, let us consider the Banach function space $Y(\mu )=L^{\infty }[0,1]$ and the Banach space $E={\ell }^2$. Taking into account the representation of ${\ell }^2$ as $L^2[0,1]$ given by the Fourier transform $I=\mathcal{F}:L^2[0,1]\to {\ell }^2$ and the inclusion $L^{\infty }[0,1]\subseteq L^2[0,1]$, we can consider

$$S=\mathcal{F}(L^{\infty }[0,1]).$$

Then, in our terms, S is a Banach function subspace of ${\ell }^2$ via $\mathcal{F}$, although this map does not respect the Banach lattice structure of $L^{\infty }[0,1]$ since it is not a lattice homomorphism.

3. Order-Continuous Banach Function Subspaces and $\mathit{p}$th Powers of Banach Spaces

Let us start by providing some technical tools that give the link between the structure of the Banach function spaces $Y(\mu )$ over which the Banach spaces E are represented and the vector measures associated to the identification map of $Y(\mu )$ and E. Recall that we are assuming that the measure $\mu$ is finite. First, we show a characterization of these representations in terms of vector measures over $\sigma$-algebras, which is in fact the main tool of the paper. For a vector measure $m:\mathsf{\Sigma }\to E$ we denote by $\mathrm{rg}(m)$ the range of the measure $\mathrm{rg}(m)=\{m(A):A\in \mathsf{\Sigma }\}$.

Theorem 1.

Let E be a Banach space. The following assertions are equivalent.

(1)

There is a finite measure μ and an order-continuous Banach function space $Y(\mu )$ such that E is representable on $Y(\mu )$.

(2)

There is a measurable space $(\mathsf{\Omega },\mathsf{\Sigma })$ and a vector measure $m:\mathsf{\Sigma }\to E$ such that

(i)

$span\{\mathrm{rg}(m)\}$ is dense in E, and

(ii)

for every sequence $(f_n)$ of simple functions, if ${(I_m(f_n))}_n$ is Cauchy in E, then ${(f_n)}_n$ is a Cauchy sequence in $L^1(m)$ too.

Proof. 

(2) ⇒ (1) Assume that there is a vector measure m as in (2). Consider the space $L^1(m)$ of integrable functions. The integration map $I_m:L^1(m)\to E$ is continuous, so it is enough to prove that it defines a bijection. Take $x\in E$. Then, by hypothesis, it is the limit of a sequence ${(x_n)}_n$ of elements of $span\{\mathrm{rg}(m)\}$. For each n, $x_n$ can be written as a finite sum $x_n={\sum }_{i=1}^k{\lambda }_i^{n}m(A_i^n)$, and so it can be identified with the integral $\int f_{n}dm$ of the simple function $f_n:={\sum }_{i=1}^k{\lambda }_i^n{\chi }_{A_i^n}$, and so $x={lim}_n\int f_{n}dm$. Consequently, it is a Cauchy sequence of E and then, by hypothesis, ${(f_n)}_n$ is a Cauchy sequence in $L^1(m)$ with limit $f\in L^1(m)$. Clearly, $\int fdm=x$, and this proves that the integration map $I_m$ is surjective.

Suppose that it is not injective. Then, there is a non-null element $f\in L^1(m)$ such that $I_m(f)=0$. Take a sequence ${(f_n)}_n$ of simple functions converging to f in $L^1(m)$ and consider the sequence ${(g_n)}_n$ defined for $n\in \mathbb{N}$ as $g_{2n}:=f_n$ and $g_{2n-1}=0$ for all $n\in \mathbb{N}$. Then, by the continuity of $I_m$, ${(I_m(g_n))}_n$ is a Cauchy sequence, since it converges to 0. However, ${(g_n)}_n$ is not Cauchy in $L^1(m)$.

(1) ⇒ (2) Since E is representable over $Y(\mu )$, there is a continuous bijection $I:Y(\mu )\to E$. The Open Mapping Theorem gives that it is in fact an isomorphism. Define the vector measure m by $m(A):=I({\chi }_A)$, $A\in \mathsf{\Sigma }$, and note that the fact that I is bijective implies that $\parallel m\parallel$ is equivalent to $\mu$, that is, both have the same null sets. The Optimal Domain Theorem (see ([12], Theorem 4.14)) asserts that I can be extended to $L^1(m)$ with continuity, and so $Y(\mu )\subseteq L^1(m)$. This gives that the isomorphism I can be factored as $I=I_m\circ i$, where $i:Y(\mu )\to L^1(m)$ is the inclusion map. Now, take a simple function f. Taking into account that $\parallel I_m\parallel \le 1$, we have that

$${\parallel f\parallel }_{Y(\mu )}\le \parallel I^{-1}{\parallel \parallel I(f)\parallel }_E=\parallel I^{-1}\parallel \parallel I_m{(i(f))\parallel }_E\le \parallel I^{-1}{\parallel \parallel i(f)\parallel }_{L^1(m)}\le \parallel I^{-1}{\parallel \parallel i\parallel \parallel f\parallel }_{Y(\mu )}.$$

This and the order continuity of $Y(\mu )$ and $L^1(m)$ give that $span\{\mathrm{rg}(m)\}$ is dense in E, since the order continuity implies that simple functions are dense. In addition, the representation $I=I_m\circ i$ implies that a sequence of functions ${(f_n)}_n$ is Cauchy in $L^1(m)$ if and only if ${(I_m(f_n))}_n$ is so in E. This gives (1) ⇒ (2) and finishes the proof. □

Example 3.

Let $1<p<\infty$ and let $\nu :\mathsf{\Sigma }\to F$ be a (Banach space valued) vector measure. Consider the space $L(L^p(\nu ),F)$ and the integration operator $I_{\nu }:L^p(\nu )\to F$. The Banach function space $L^{p^{\prime }}(\nu )$, where $p^{\prime }$ is the conjugate exponent of p given by $1/p+1/p^{\prime }=1$, can be isometrically identified with the space of operators $S:=\{I_{{\nu }_g}:g\in L^{p^{\prime }}(\nu )\}$. The identification (see ([12], Chapter 3)) is given by $I_{{\nu }_g}:L^p(\nu )\to F$ defined by

$$I_{{\nu }_g}(f):=I_{\nu }(fg)=\int fgd\nu$$

for each $g\in L^{p^{\prime }}(\nu )$. Let us define the vector measure $m:\mathsf{\Sigma }\to L(L^p(\nu ),F)$ by $m(A):=I_{{\nu }_{{\chi }_A}}$. It can easily be seen that $L^1(m)=L^{p^{\prime }}(\nu )$ isometrically, and so (2) of Theorem 1 is satisfied by m.

Let us now analyze when a particular subspace S of a Banach space E that satisfies that it is the range of an injective continuous linear map from a Banach function space $Y(\mu )$ can itself be identified with the Banach function space $Y(\mu )$. In other words, let us see when the existence of a continuous inclusion from a Banach function space on a subspace S of Banach space E assures that $\overline{S}$ is a (copy of a) Banach function subspace in E.

Proposition 1.

Suppose that there is an order-continuous Banach function space $Y(\mu )$ such that there is a continuous injective map ι in a Banach space E, i.e., $\iota :Y(\mu )\hookrightarrow E$. Then, the following statements are equivalent.

(1)

$\overline{\iota (Y(\mu ))}$ is a Banach subspace of E that can be represented over a Banach function space $Z(\mu )$ containing $Y(\mu )$.

(2)

There is a constant $K>0$ such that for every simple function $f\in Y(\mu )$,

$$\underset{h\in B_{L^{\infty }(\mu )}}{sup}{\parallel \iota (fh)\parallel }_E\le K{\parallel \iota (f)\parallel }_E.$$

Proof. 

(2) ⇒ (1) By the same arguments that were used in the proof of (1) ⇒ (2) of Theorem 1, the inclusion map $\iota$ can be extended to $L^1(m_{\iota })$, where $m_{\iota }$ is the vector measure given by $m_{\iota }(A):=\iota ({\chi }_A)$, $A\in \mathsf{\Sigma }$. Since ${sup}_{h\in B_{L^{\infty }(\mu )}}{\parallel \iota (fh)\parallel }_E$ gives another expression for the norm of $L^1(m_{\iota })$ when $f\in Y(\mu )$ is a simple function (in this case we have that $\iota (fh)=\int fhd{m}_{\iota }$), we have that the inequality in (2) gives

$${\parallel \iota (f)\parallel }_E\le {\parallel f\parallel }_{L^1(m_{\iota })}\le K{\parallel \iota (f)\parallel }_E,f\in Y(\mu ).$$

Since simple functions are dense in $Y(\mu )$, these inequalities can be extended to the whole space $L^1(m_{\iota })$, which gives the desired isomorphism among $L^1(m_{\iota })$ and $\overline{\iota (Y(\mu ))}$. Note that the fact that $\iota$ is injective gives that $\iota$ is $\mu$-determined, and so $\mu$ is equivalent to $\parallel m_{\iota }\parallel$ and to any Rybakov measure for $m_{\iota }$. The identification of $Z(\mu )$ with $L^1(m_{\iota })$ gives the result.

(1) ⇒ (2) By hypothesis, we have that $\iota$ can be extended to an isomorphism from $Z(\mu )$. This gives that there are constants $Q>0$ and $k>0$ such that for every simple function $f\in Y(\mu )$,

$$\underset{h\in B_{L^{\infty }(\mu )}}{sup}{\parallel \iota (fh)\parallel }_E\le Q\underset{h\in B_{L^{\infty }(\mu )}}{sup}{\parallel fh\parallel }_{Z(\mu )}={Q\parallel f\parallel }_{Z(\mu )}\le Qk{\parallel \iota (f)\parallel }_E.$$

This gives the result for $K=Qk$. □

Example 4.

Let us consider again Example 3. If η is a Rybakov measure for m and $1\le q<\infty$, the space $L^q(m)$ is a Banach function space over η included in $L^1(m)$. We have that $L^1(m)$ is isometric to $L^{p^{\prime }}(\nu )$, which is also isometric to a subspace of $L(L^p(\nu ),F)$. Clearly, for every $f\in L^q(m)$,

$$\underset{h\in B_{L^{\infty }(\eta )}}{sup}{\parallel \int fhdm\parallel }_F={\parallel f\parallel }_{L^1(m)}={\parallel f\parallel }_{L^{p^{\prime }}(\nu )},$$

and so (2) in Proposition 1 holds. Thus, $\overline{L^q(m)}=L^{p^{\prime }}(m)$.

Note that the same argument also gives that $L^{\infty }(\eta )$ is a Banach function subspace of $L(L^p(m),F)$, although it is not order continuous.

After the previous results, we are ready for defining structures that are naturally given for Banach function spaces, but which do not have a Banach space counterpart. In this paper, we will consider the construction of pth powers of Banach spaces. We start by showing that, as a direct consequence of Theorem 1, we can assure the existence and give a concrete description of the pth powers of representable Banach spaces. Recall that we are considering finite measures $\mu$.

By definition of representability, there is a one-to-one identification $I:Y(\mu )\to E$ that relates the elements of $Y(\mu )$ and the elements of E. For a Banach function space containing ${\chi }_{\mathsf{\Omega }}$, the inclusion $Y{(\mu )}_{\left[p\right]}\subseteq Y(\mu )$ holds if $0<p\le 1$, but the converse inclusion does not hold in general. This implies that we have to consider the cases $0<p\le 1$ and $1\le p<\infty$ separately.

First consider the case $0<p\le 1$. We define the pth power $E_{\left[p\right]}$ of the Banach space E as

$$E_{\left[p\right]}:=\left\{e\in E:I^{-1}(e)\in Y{(\mu )}_{\left[p\right]}\right\}.$$

A natural candidate for quasi-norm of the space is given by the expression

$${\parallel e\parallel }_{E_{\left[p\right]}}:=\parallel I(|I^{-1}(e){|}^{1/p}){\parallel }_E^p,e\in E_{\left[p\right]}.$$

Note that this is well defined, since for each $e\in E$, $I^{-1}(e)\in Y(\mu )$ that contains $Y{(\mu )}_{\left[p\right]}$. Moreover, for the elements $e\in E_{\left[p\right]}$, we have

$$|I^{-1}{(e)|}^{1/p}\in {(Y{(\mu )}_{\left[p\right]})}_{[1/p]}=Y(\mu ),$$

and so $I(|I^{-1}(e){|}^{1/p})$ makes sense and gives again an element of E.

However, for $p>1$, the pth power of a Banach space defined as above does not necessarily exist as a Banach subspace of E. For example, for $p=2$, the 2nd power of $L^2[0,1]$ is $L^1[0,1]$, which is not a subspace continuously included in $L^2[0,1]$: The inclusion $L^2[0,1]\subset L^1[0,1]$ is proper. Therefore, by definition, if we take $E=L^2[0,1]$, we have that $E_{\left[2\right]}=L^2[0,1]\cap L^1[0,1]=L^2[0,1]$, and so $E_{\left[2\right]}$ is the normed space $(L^2[0,1],\parallel ·{\parallel }_{L^1[0,1]})$. Actually, the pth power is not necessarily normed, but only quasi-normed: Consider, for example, $p=3$ instead of $p=2$ in the example.

This forces us to define the pth power of a Banach space for $p>1$ in a different way; in fact, it must be a “super" space $E_{\left[p\right]}$ such that $E\subseteq E_{\left[p\right]}$.

Let $p\ge 1$ and suppose that E is representable over a Banach function space $Y(\mu )$ containing ${\chi }_{\mathsf{\Omega }}$. Define on E the quasi-norm $|||·{|||}_{E_{\left[p\right]}}$ by

$${|||e|||}_{E_{\left[p\right]}}=\parallel I^{-1}(e){\parallel }_{Y{(\mu )}_{\left[p\right]}},e\in E.$$

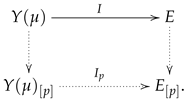
It is a quasi-norm, since ${\parallel ·\parallel }_{Y{(\mu )}_{\left[p\right]}}$ is so and $I^{-1}$ is linear. Note that this formula only makes sense for elements of E, and an extension argument is needed for defining $E_{\left[p\right]}$. We can define the pth power $E_{\left[p\right]}$ of E for $p>1$ as the completion of E with the quasi-norm $|||·{|||}_{E_{\left[p\right]}}$, with the usual definitions. The map I can be extended to $Y{(\mu )}_{\left[p\right]}$ as a linear and continuous operator $I_p$ by continuity, since the following diagram commutes, where the vertical arrows are inclusions:

Consequently, the natural way of defining the quasi-norm for $E_{\left[p\right]}$ is by means of the formula

$${\parallel e\parallel }_{E_{\left[p\right]}}:=\parallel I(|I_p^{-1}(e){|}^{1/p}){\parallel }_E^p,e\in E_{\left[p\right]},$$

which makes sense since $|I_p^{-1}{(e)|}^{1/p}\in Y(\mu )$. The better way of understanding what this formula means is just to take into account that I is a bijection, and so there is a dense set in E for which the formula can be explicitly computed, since simple functions are dense both in $Y(\mu )$ and in $Y{(\mu )}_{\left[p\right]}$ and satisfy that ${|f|}^{1/p}\in Y(\mu )$. Moreover, for the elements e of E that satisfy that $I_p^{-1}(e)$ are simple functions, we have that

$$\begin{array}{ccc}\hfill {|||e|||}_{E_{\left[p\right]}}& =& \parallel I^{-1}{(e)\parallel }_{Y{(\mu )}_{\left[p\right]}}=\parallel {|I^{-1}(e)|}^{1/p}{\parallel }_{Y(\mu )}^p\hfill \\ & \le & \parallel I^{-1}{\parallel }^p\parallel I(|I_p^{-1}{(e)|}^{1/p}){\parallel }_E^p=\parallel I^{-1}{\parallel }^p{\parallel e\parallel }_{E_{\left[p\right]}},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\parallel e\parallel }_{E_{\left[p\right]}}& =& \parallel I(|I_p^{-1}{(e)|}^{1/p}){\parallel }_E^p\le {\parallel I\parallel }^p\parallel {|I^{-1}(e)|}^{1/p}{\parallel }_{Y(\mu )}^p\hfill \\ & =& {\parallel I\parallel }^p\parallel I^{-1}(e){\parallel }_{Y{(\mu )}_{\left[p\right]}}={\parallel I\parallel }^p{|||e|||}_{E_{\left[p\right]}}.\hfill \end{array}$$

Consequently, we have that the extension by continuity of this formula for simple functions to the whole space $E_{\left[p\right]}$ works, since it is equivalent on a dense subset to the quasi-norm $|||·{|||}_{E_{\left[p\right]}}$.

Summing up all the elements of this construction, we can formulate the following general definition for all cases $0<p<\infty$.

Definition 3.

Let $0<p<\infty$. Let E be a Banach space that is representable over an order-continuous Banach function space $Y(\mu )$ that contains ${\chi }_{\mathsf{\Omega }}$. We define the pth power $E_{\left[p\right]}$ of the Banach space E as the quasi-normed space $(E_{\left[p\right]},\parallel ·{\parallel }_{E_{\left[p\right]}})$ given by the completion of

$$E_{\left[p\right]}:=\left\{e\in E:I^{-1}(e)\in Y{(\mu )}_{\left[p\right]}\right\},$$

with the quasi-norm defined by the formula

$${\parallel e\parallel }_{E_{\left[p\right]}}:=\parallel I(|I^{-1}(e){|}^{1/p}){\parallel }_E^p,$$

for the elements $e\in E_{\left[p\right]}$ such that $|I^{-1}{(e)|}^{1/p}$ is a simple function, and by continuity for the rest of the elements of the space.

Proposition 2.

Let $0<p<\infty$ and let E be a Banach space that is representable over a p-convex order-continuous Banach function space $Y(\mu )$. Then, the quasi-norm ${\parallel ·\parallel }_{E_{\left[p\right]}}$ is equivalent to a norm, and so $E_{\left[p\right]}$ is normable.

Proof. 

By the arguments given just above, we know that ${\parallel ·\parallel }_{E_{\left[p\right]}}$ is a quasi-norm, so we only need to prove that it is equivalent to a norm. The candidate for comparing with ${\parallel ·\parallel }_{E_{\left[p\right]}}$ is given by the expression

$$inf\left\{\sum _{i=1}^n\parallel I_p^{-1}(e_i){\parallel }_{Y{(\mu )}_{\left[p\right]}}:e_1,\dots ,e_n\in E_{\left[p\right]}\mathrm{with}|I_p^{-1}(e)|\le \sum _{i=1}^n|I_p^{-1}(e_i)|\right\}.$$

It is clearly a semi-norm. Let us show that it is in fact a norm that is equivalent to ${\parallel ·\parallel }_{E_{\left[p\right]}}$. Since by hypothesis, the space $Y(\mu )$ is order continuous, we have that simple functions are dense, and so we can consider only elements of $E_{\left[p\right]}\cap E$ in the computation and change $I_p$ by I. The result is a consequence of the following inequalities:

$$\begin{array}{ccc}\hfill \frac{{\parallel e\parallel }_{E_{\left[p\right]}}}{{\parallel I\parallel }^p}& \ge & \parallel I^{-1}{(e)\parallel }_{Y{(\mu )}_{\left[p\right]}}\hfill \\ & \ge & inf\left\{\sum _{i=1}^n\parallel I(e_i){\parallel }_{Y{(\mu )}_{\left[p\right]}}:|I^{-1}(e)|\le \sum _{i=1}^n|I^{-1}(e_i)|\right\}\hfill \\ & =& inf\left\{\sum _{i=1}^n\parallel |I(e_i){|}^{1/p}{\parallel }_{Y(\mu )}^p:|I^{-1}(e)|\le \sum _{i=1}^n|I^{-1}(e_i)|\right\}\hfill \\ & \ge & \frac{1}{M^{(p)}{(Y(\mu ))}^p}inf\left\{\parallel {\left(\sum _{i=1}^n{|I^{-1}(e_i)|}^{p·(1/p)}\right)}^{1/p}{\parallel }_{Y(\mu )}^p:|I^{-1}(e)|\le \sum _{i=1}^n|I^{-1}(e_i)|\right\}\hfill \\ & \ge & \frac{\parallel I^{-1}{(e)\parallel }_{Y{(\mu )}_{\left[p\right]}}}{M^{(p)}{(Y(\mu ))}^p}=\frac{\parallel |I^{-1}{(e)|}^{1/p}{\parallel }_{Y(\mu )}^p}{M^{(p)}{(Y(\mu ))}^p}\hfill \\ & \ge & \frac{\parallel I(|I^{-1}(e){|}^{1/p}){\parallel }_E^p}{M^{(p)}{(Y(\mu ))}^p·{\parallel I\parallel }^p}=\frac{{\parallel e\parallel }_{E_{\left[p\right]}}}{M^{(p)}{(Y(\mu ))}^p·{\parallel I\parallel }^p}.\hfill \end{array}$$

 □

Corollary 1.

Let $0<p\le 1$ and let E be a Banach space that is representable over an order-continuous Banach function space $Y(\mu )$ by means of the map $I:Y(\mu )\to E$. Then, $E_{\left[p\right]}$ is a Banach space when endowed with the quasi-norm ${\parallel ·\parallel }_{E_{\left[p\right]}}$, which is equivalent to a norm which is continuously included in E. Moreover, $(E_{\left[p\right]}{,\parallel ·\parallel }_{E_{\left[p\right]}}{)=(Y(\mu )}_{\left[p\right]}{,\parallel ·\parallel }_{Y{(\mu )}_{\left[p\right]}})$ isomorphically and if, in addition, I is an isometry, then

(i)

The function ${\parallel ·\parallel }_{E_{\left[p\right]}}$ is in fact a norm, and

(ii)

$(E_{\left[p\right]}{,\parallel ·\parallel }_{E_{\left[p\right]}}{)=(Y(\mu )}_{\left[p\right]}{,\parallel ·\parallel }_{Y{(\mu )}_{\left[p\right]}})$ isometrically.

Proof. 

It is well known that the pth power of $Y(\mu )$ satisfies that $Y{(\mu )}_{\left[p\right]}\subseteq Y(\mu )$ whenever $0<p\le 1$ and $\mu$ is finite; of course, there is a genuine inclusion, that is, the inclusion is injective since the equivalence classes are defined by the same measure. If $e\in E_{\left[p\right]}$, we have that $|I^{-1}{(e)|\in Y(\mu )}_{\left[p\right]}$, and so $|I^{-1}{(e)|}^{1/p}\in Y(\mu )$. Therefore,

$$\frac{{\parallel e\parallel }_E}{\parallel I\parallel }\le \parallel I^{-1}{(e)\parallel }_{Y(\mu )}\le \parallel I^{-1}{(e)\parallel }_{Y{(\mu )}_{\left[p\right]}}=\parallel |I^{-1}{(e)|}^{1/p}{\parallel }_{Y(\mu )}^p\le \parallel I^{-1}{\parallel }^p{\parallel e\parallel }_{E_{\left[p\right]}}.$$

The same arguments (that is, the identification of $E_{\left[p\right]}$ with $Y{(\mu )}_{\left[p\right]}$) allow us to prove that the space $E_{\left[p\right]}$ is linear and that it is in fact a Banach space, since $Y{(\mu )}_{\left[p\right]}$ is (see [12], Chapter 2). Note that for $0<p\le 1$, every Banach function space $Y(\mu )$ is p-convex, and its p-convexity constant $M^{(p)}(Y(\mu ))$ equals one. Clearly, by the definition of $E_{\left[p\right]}$, we get that $(E_{\left[p\right]}{,\parallel ·\parallel }_{E_{\left[p\right]}}{)=(Y(\mu )}_{\left[p\right]}{,\parallel ·\parallel }_{Y{(\mu )}_{\left[p\right]}})$ isomorphically. Finally, if I is an isometry, then $\parallel I\parallel =1=\parallel I^{-1}\parallel$. Therefore, the computations at the end of the proof of Proposition 2 show that ${\parallel ·\parallel }_{E_{\left[p\right]}}$ equals the norm appearing in this proof. Again, the quoted computations provide the isometry. □

Corollary 2.

Let E be a Banach space that is representable on an order-continuous Banach function space $Y(\mu )$ containing ${\chi }_{\mathsf{\Omega }}$ and $0<p\le 1$. Then, $E_{\left[p\right]}$ is a $1/p$-convex Banach function subspace of E that is isomorphic to $L^{1/p}(m)$ for a certain vector measure m that is equivalent to μ.

Proof. 

Since $p\le 1$, we have that $Y{(\mu )}_{\left[p\right]}\subseteq Y(\mu )$ and, by using Corollary 1, $Y{(\mu )}_{\left[p\right]}$ is isometric to $E_{\left[p\right]}$, with the isometry given by the restriction of I to $Y{(\mu )}_{\left[p\right]}$. On the other hand, for the representing vector measure $m:\mathsf{\Sigma }\to E$ given by $m(A):=I({\chi }_A)$, $A\in \mathsf{\Sigma }$, we have that $L^1(m)=Y(\mu )$, and so $L^{1/p}(m)=Y{(\mu )}_{\left[p\right]}$. It is well known that this space is $1/p$-convex (see ([12], Chapter 3)). □

For $p>1$, a similar proof based on Proposition 2 gives the following result.

Corollary 3.

Let $1\le p$. Let E be a Banach space that is representable over a p-convex Banach function space $Y(\mu )$ (with a p-convex constant equal to 1) by means of the map $I:Y(\mu )\to E$. Then, $E_{\left[p\right]}$ is a Banach space when endowed with the quasi-norm

$${\parallel e\parallel }_{E_{\left[p\right]}}:=\parallel I(|I^{-1}(e){|}^{1/p}){\parallel }_E^p,e\in E_{\left[p\right]},$$

which contains E continuously. Moreover, $(E_{\left[p\right]}{,\parallel ·\parallel }_{E_{\left[p\right]}}{)=(Y(\mu )}_{\left[p\right]}{,\parallel ·\parallel }_{Y{(\mu )}_{\left[p\right]}})$ isomorphically as well as isometrically if I is an isomorphism.

The last part of this section is devoted to showing some fundamental applications of the pth powers of Banach spaces. As the reader will see, this construction gives, for example, a systematic way for providing new canonical decompositions of a Banach space E as products of elements of some selected subspaces of E, as well as new interpolation formulae. To simplify, note that after Proposition 2, we can assume (and we do) without loss of generality that I is an isometry.

(a) Decomposition Theorem (Product Theorem for Banach Spaces)

Let us introduce the notion of a pointwise product of Banach spaces. Recall that given a pair of Banach function spaces $X(\mu )$ and $Y(\mu )$ over the same measure $\mu$, the product $X(\mu )\pi Y(\mu )$ is defined as follows. Consider the space of all the functions in $L^0(\mu )$ for which the function

$$\pi (f):=inf\left\{\sum _{i=1}^n\parallel g_i{\parallel }_{X(\mu )}\parallel h_i{\parallel }_{Y(\mu )}:g_i\in X(\mu ),h_i\in Y(\mu ),1\le i\le n,|f|\le \sum _{i=1}^n|g_i||h_i|\right\}$$

is finite. Under some requirements, this is a normed space of classes of $\mu$-a.e. equal measurable functions, and its completion is what is called the product space $X(\mu )\pi Y(\mu )$. It is a Banach function space over the same measure $\mu$. If the spaces $X(\mu )$ and $Y(\mu )$ satisfy adequate p-convexity requirements, the norm can be computed just by using single product decompositions instead of sums of such products. The reader can find all the information that is needed in ([28], §2) and [26] (see also ([29], §2) for a slightly different definition and main properties, and in [30] for a general setting for the pointwise-type products of Banach spaces).

Let us show that our construction allows us to define the (pointwise) product of Banach spaces. Let E be a Banach space that is representable by the Banach function space $Z(\mu )$ with a representation given by $I:Z(\mu )\to E$. Consider $E_0$ and $E_1$ two Banach function subspaces of E (with different norms that of E) such that $I^{-1}(E_0)\pi I^{-1}(E_1)\subset Z(\mu )$. We define the product $E_0\pi E_1$ as

$$E_0\pi E_1:=\left\{e\in E:\mathrm{there}\mathrm{is}f\in I^{-1}(E_0)\pi I^{-1}(E_1)\mathrm{such}\mathrm{that}I(f)=e\right\},$$

with the norm ${\parallel e\parallel }_{E_0\pi E_1}:=\pi (I^{-1}(e))$ given by:

$$inf\left\{\sum _{j=1}^n\parallel f_j{\parallel }_{X(\mu )}{\parallel g_j\parallel }_{Y(\mu )}:\sum _{j=1}^n{f}_j·g_j=I^{-1}(e),f_j\in I^{-1}(E_0),g_j\in I^{-1}(E_1)\right\}.$$

We can say that an element e of E is a pointwise product of two elements $e_0\in E_0$ and $e_1\in E_1$ if $I^{-1}(e)=I^{-1}(e_0)·I^{-1}(e_1)$.

Using the product decomposition of the elements of a Banach function space and Corollary 2, we directly obtain the following canonical decomposition of Banach spaces that can be represented as Banach function spaces.

Corollary 4.

Let E be a Banach space that is representable isometrically as an order-continuous Banach function space $Z(\mu )$ over a finite measure μ and $0<p<1$. Then,

$$E=E_{\left[p\right]}\pi E_{[1-p]}$$

isometrically. Consequently, each element of E can be decomposed as a pointwise product of an element of $E_{\left[p\right]}$ and an element of $E_{[1-p]}$.

Proof. 

Take $X(\mu )=Z{(\mu )}_{\left[p\right]}$ and $Y(\mu )=Z{(\mu )}_{[1-p]}$. It can be easily seen that

$$Z(\mu )=X(\mu )\pi Y(\mu )=Z{(\mu )}_{\left[p\right]}\pi Z{(\mu )}_{[1-p]}$$

isometrically just by using Hölder’s inequality for Banach lattices (see [2], Proposition 1.d.2). If $e\in E$, we have that $I^{-1}(e)\in Z(\mu )$, and then $|I^{-1}(e)|$ can be written as

$$|I^{-1}(e)|=|I^{-1}{(e)|}^p{|I^{-1}(e)|}^{1-p}.$$

Since $I(|I^{-1}(e){|}^p)\in I(X(\mu ))=E_{\left[p\right]}$ and $I(|I^{-1}(e){|}^{1-p})\in I(Y(\mu ))=E_{[1-p]}$, $X(\mu )$ and $Y(\mu )$ are Banach function spaces with the corresponding pth power and $(1-p)$th power quasi-norms being norms, and I is an isometry, we get the result. □

A similar result should be obtained by considering the construction for different spaces F and H as being representable as Banach function spaces $X(\mu )$ and $Y(\mu )$ by using the transference of the lattice structure on these spaces provided by isometry I; the results in ([28], §2), [26,29,31,32] may be used for this aim.

(b) Lozanovskii Theorem for Banach Spaces

The representation technique presented in this section can also be applied for obtaining a Banach space version of the well-known Lozanovskii Decomposition Theorem, which establishes that $L^1(\mu )$ for a finite measure $\mu$ can be written as the pointwise product of every order-continuous Banach function space $X(\mu )\subseteq L^1(\mu )$ and its Köthe dual.

Corollary 5.

Let E be a Banach space that is representable as $L^1(\mu )$ for a certain finite measure μ and with I being an isometry. Suppose that $E_0$ is the range by I of an order-continuous Banach function subspace $X(\mu )$ of $L^1(\mu )$ with the Fatou property. Then, $E_0^{*}$ is also isometric to a Banach function subspace of $L^1(\mu )$, and

$$E=E_0\pi E_0^{*}$$

isometrically.

Proof. 

Recall that $X(\mu )$ is assumed to have the Fatou property. Since we have that $I^{-1}(E_0)=X(\mu )$ is an order-continuous Banach function space included in $L^1(\mu )$, we have that

$${(I^{-1}(E_0))}^{*}={(I^{-1}(E_0))}^{\prime }=X{(\mu )}^{\prime }$$

isometrically, and also ${(I^{-1}(E_0))}^{\prime }\subseteq L^1(\mu )$. Moreover, since I is an isomorphism, we have that ${(I^{-1})}^{*}$ is so, and ${\left(I^{-1}(E_0)\right)}^{*}={(I^{-1})}^{*}(E_0^{*}).$ Thus, $I({\left(I^{-1}(E_0)\right)}^{*})$ is isomorphic to $E_0^{*}$. Define $E_1:=I\left(I^{-1}{(E_0)}^{\prime }\right)$. Then, the fact that I is an isometry provides that

$$E_0\pi E_0^{*}=E_0\pi E_1$$

is isometric to $I^{-1}(E_0)\pi {(I^{-1}(E_0))}^{\prime }=X(\mu )\pi X{(\mu )}^{\prime }$, and by using the Lozanovskii Theorem (see ([32], Theorem 6)), we get that this is equal to $L^1(\mu )$, which is isometric to E. This gives the result. □

(c) Interpolation Theorem

A particular case of product space combined with $\theta$ and $(1-\theta )$th powers of the involved spaces $X(\mu )$ and $Y(\mu )$ provides the so-called Calderón–Lozanovskii interpolation of Banach function spaces. Indeed, it is well known that for an interpolation couple of Banach function spaces $X_0(\mu )$ and $X_1(\mu )$, the Calderón–Lozanovskii interpolation space $X_0{(\mu )}^{1-\theta }{X}_1{(\mu )}^{\theta }$ of index $0<\theta <1$ is defined as

$$X_0{(\mu )}^{1-\theta }{X}_1{(\mu )}^{\theta }=\left\{f\in L^0(\mu ):|f|={|g|}^{1-\theta }{|h|}^{\theta },g\in X_0(\mu ),h\in X_1(\mu )\right\},$$

with the norm

$$\parallel f\parallel =inf\left\{{\parallel g\parallel }_{X_0(\mu )}^{1-\theta }{\parallel h\parallel }_{X_1(\mu )}^{\theta }:|f|={|g|}^{1-\theta }{|h|}^{\theta },g\in X_0(\mu ),h\in X_1(\mu )\right\}.$$

It is well known that, under some requirements, this space coincides with the complex interpolation space of $X_0(\mu )$ and $X_1(\mu )$ with index $\theta$ (see [33]).

Using the main interpolation theorem for operators applied to the present context, we obtain the following results.

Corollary 6.

Let $0<\theta <1$. Suppose that the Banach space E is representable as the Banach function space $Z(\mu )$ by means of an isometry I, and $E_0$ and $E_1$ are Banach function subspaces of E that are represented by the Banach function subspaces $X_0(\mu )$ and $X_1(\mu )$ of $Z(\mu )$, respectively by means of I, which also defines isometries from $X_i(\mu )$ into $E_i$, $i=0,1$. Then, the complex interpolation space ${[E_0,E_1]}_{\theta }$ can be represented as the Calderón–Lozanovskii space $X_0{(\mu )}^{1-\theta }{X}_1{(\mu )}^{\theta }$ by means of I.

Proof. 

Just consider the isometric equalities

$${[E_0,E_1]}_{\theta }={[X_0(\mu ),X_1(\mu )]}_{\theta }=X_0{(\mu )}^{1-\theta }{X}_1{(\mu )}^{\theta }.$$

 □

Corollary 7.

Let $0<p,\theta ,q<1$. Suppose that the Banach space E is representable as the Banach function space $Y(\mu )$. Then, the complex interpolation space ${[E_{\left[p\right]},E_{\left[q\right]}]}_{\theta }$ can be described as

$${[E_{\left[p\right]},E_{\left[q\right]}]}_{\theta }=E_{[p(1-\theta )+q\theta ]}.$$

Proof. 

This is a consequence of the isometries

$${[E_{\left[p\right]},E_{\left[q\right]}]}_{\theta }={[Y_{\left[p\right]}(\mu ),Y_{\left[q\right]}(\mu )]}_{\theta }=Y{(\mu )}_{\left[p\right]}^{1-\theta }Y{(\mu )}_{\left[q\right]}^{\theta }=Y{(\mu )}_{[p(1-\theta )+q\theta ]}=E_{[p(1-\theta )+q\theta ]}.$$

 □

4. Applications: Banach Lattice Structures in Banach Spaces

4.1. p-Concave Order-Continuous Banach Spaces

Through this section, we take $1\le p<\infty$. Let us show first some direct applications of our results to the case of Banach spaces that are representable as order-continuous Banach function spaces with non-trivial convexity or concavity. For example, it is easy to prove that under certain extra requirements, if E is representable on a q-convex space, then E is representable as an $L^q$-space.

Corollary 8.

Let E be a Banach space. The following assertions are equivalent.

(1)

There is a finite measure μ and an order-continuous p-concave Banach function space $Y(\mu )$ such that E is representable on $Y(\mu )$.

(2)

There is a measurable space $(\mathsf{\Omega },\mathsf{\Sigma })$, a constant $K>0$, and a vector measure $m:\mathsf{\Sigma }\to E$ such that

(i)

for every simple function f and $A\in \mathsf{\Sigma }$, $\parallel I_m(f{\chi }_A)\parallel \le \parallel I_m(f)\parallel$, and

(ii)

for every finite set $f_1,\dots ,f_N$ of simple functions,

$${(\sum _{n=1}^N{\parallel f_n\parallel }_{L^1(m)}^p)}^{1/p}\le K\parallel I_m((\sum _{n=1}^N|f_n{{|}^p)}^{1/p}){\parallel }_E.$$

Proof. 

(2) ⇒ (1) By using (2)(i), we have:

$${\parallel f\parallel }_{L^1(m)}\le 2\underset{A}{sup}\parallel {\int }_{A}fdm\parallel \le 2\parallel I_m(f)\parallel \le 2\parallel f{\chi }_A{\parallel }_{L^1(m)}.$$

For every simple function f, we have that $I_m$ is an isomorphism, and so E is representable as $L^1(m)$. Thus, (ii) gives that the space $L^1(m)$ is also q-concave, since it is enough that the required inequality is satisfied for simple functions (see [12], Lemma 2.52).

(1) ⇒ (2) Since E is representable on $Y(\mu )$, there is an isomorphism $I:Y(\mu )\to E$, and so we can define the vector measure $m_I$ by $m_I(A)=I({\chi }_A)$, $A\in \mathsf{\Sigma }$, and $L^1(m_I)=Y(\mu )$. That is, the integration map $I_{m_I}$ is an isomorphism, and so (ii) is obvious. □

Corollary 9.

Suppose that there is a finite positive measure μ and an order-continuous q-convex Banach function space $Y(\mu )$ such that E is representable on $Y(\mu )$ by means of a q-concave operator $I:Y(\mu )\to E$. Then, E is representable as $L^q(\eta )$ for a certain finite measure that is equivalent to μ.

Proof. 

This is a direct application of the Maurey–Rosenthal theorem (see, for example, [6,7]). Indeed, a q-concave operator from a q-convex order-continuous Banach function space factors by means of a multiplication operator through a space $L^q(hd\mu )$. Since I is an isomorphism, it can easily be seen that $h>0$ and that E is isomorphic to $L^q(\eta )$ (for $d\eta =hd\mu$) and to $Y(\mu )$. This gives the result. □

Corollary 10.

Let $1\le q<\infty$. Suppose that there is a finite measure μ and an order-continuous q-concave Banach function space $Y(\mu )$ such that E is representable on $Y(\mu )$. Then, E has a Banach function subspace (with continuous inclusion) that is isomorphic to $L^q(\eta )$, where η and μ are equivalent.

Proof. 

If $Y(\mu )$ is a Banach function space, then $Y{(\mu )}_{[1/q]}$ is q-convex and $Y{(\mu )}_{[1/q]}\subseteq Y(\mu )$. Consider the inclusion map $\iota :Y{(\mu )}_{[1/q]}\to Y$ and its composition $I\circ \iota :Y{(\mu )}_{[1/q]}\to E$. Then, we have that $I\circ \iota$ is q-concave too, since

$$\begin{array}{ccc}\hfill {\left(\sum _{i=1}^n{\parallel I\circ \iota (f_i)\parallel }_E^q\right)}^{\frac{1}{q}}& \le & \parallel I\parallel {\left(\sum _{i=1}^n{\parallel \iota (f_i)\parallel }_{Y(\mu )}^q\right)}^{\frac{1}{q}}\hfill \\ & \le & \parallel I\parallel \parallel M_{(q)}(Y(\mu ))\parallel {\left(\sum _{i=1}^n{|\iota (f_i)|}^q\right)}^{\frac{1}{q}}{\parallel }_{Y(\mu )}\hfill \\ & \le & \parallel I\parallel \parallel M_{(q)}(Y(\mu ))\parallel \iota \parallel \parallel {\left(\sum _{i=1}^n{|f_i|}^q\right)}^{\frac{1}{q}}{\parallel }_{Y{(\mu )}_{[1/q]}}.\hfill \end{array}$$

The same Maurey–Rosenthal theorem quoted in the proof of Corollary 9 gives that there is a function $h>0$ such that $Y{(\mu )}_{[1/q]}\subseteq L^q(hd\mu )$ and there is an injective map $I_0:L^q(hd\mu )\to E$ such that $I\circ \iota =I_0\circ i_0$, where $i_0:Y{(\mu )}_{[1/q]}\to L^q(hd\mu )$ is the inclusion map. This gives the result. □

4.2. Banach Function Subspaces of Multiplication Operators between Banach Spaces

In this section, we apply the previous results to compute the set of all Banach function subspaces of spaces of operators defined from a given Banach function space. In order to do that, we will use some well-known results of vector measures and multiplication operators that can be found in [34,35]. Consider an order-continuous Banach function space $X(\mu )$, a Banach space F, and the space of continuous operators $L(X(\mu ),F)$.

Every operator $T\in L(X(\mu ),F)$ defines a vector measure $m_T:\mathsf{\Sigma }\to F$ by $m_T(A):=T({\chi }_A)$. Assume in what follows that T is $\mu$-determined. Take the space $L^1(m_T)$ and notice that for every $g\in L^{\infty }(m_T)$, the expression $T_g(f):=T(fg)$, $f\in X(\mu )$ defines a continuous operator from $X(\mu )$ to F.

The space of all the operators defined in this way (i.e., as compositions of a multiplication by an $L^{\infty }$-function and T) can be extended to a bigger space that is isometrically isomorphic to a subspace of $L(X(\mu ),F)$ by means of vector measures. One of the Radon–Nikodým theorems for vector measures establishes that for a Rybakov measure $\eta$ for $m_T$, $L^{\infty }(\eta )$ can be identified with the space of vector measures that are scalarly dominated by $m_T$ (see [35,36]).

Let E be a Banach space, and let n and m be two vector measures, $n,m:\mathsf{\Sigma }\to E$. We say that n is scalarly dominated by m if and only if there exists a constant $M>0$ such that $|⟨n,x^{*}⟩|(A)\le M|⟨m,x^{*}⟩|(A)$, for all measurable sets $A\in \mathsf{\Sigma }$ and for all $x^{*}\in X^{*}$. In this case, the Radon–Nikodým Theorem for vector valued measures gives a function $h\in L^{\infty }(m_T)$ such that $n(A)=\int hd{m}_T$ for all $A\in \mathsf{\Sigma }$ (see [36], Theorem 1). This implies that the continuity of T provides a continuous map $L^{\infty }(\mu )\to L(X(\mu ),F)$.

This construction can be extended to all the functions of the space of multiplication operators $M(X(\mu ),L^1(m_T))$. Indeed, T can be extended to $L^1(m_T)$, which contains $X(\mu )$, by means of the integration map $I_{m_T}$. Thus, it can easily be seen that the space of continuous operators $R:X(\mu )\to F$ defined as the composition of a measurable function $g\in L^0(\eta )$ and T, i.e., $R(f)=I_{m_T}(gf)\in F$, $f\in X(\mu )$, is exactly defined by the functions g belonging to the space of multiplication operators $M(X(\mu ),L^1(m_T))$. Notice that this space is well defined, since T is $\mu$-determined, and so $\mu$-null sets and $m_T$-null sets coincide. Moreover, if $\iota$ is the inclusion $\iota :M(X(\mu ),L^1(m_T))\to L(X(\mu ),F)$, $\iota (g)(·):=\int g(·)d{m}_T$, we have that for every $g\in M(X(\mu ),L^1(m_T))$,

$${\parallel \iota (g)\parallel }_{L(X,F)}=\underset{f\in B_{X(\mu )}}{sup}\parallel \int gfd{m}_T\parallel ={\parallel g\parallel }_{M(X(\mu ),L^1(m_T))}.$$

This identification allows us to prove the following Representation Theorem for Banach function spaces of operators as spaces of multiplication operators.

Theorem 2.

Let $X(\mu )$ be an order-continuous Banach function space and let F be a Banach space. The following statements are equivalent for a Banach function space $Y(\mu )$ such that the simple functions are dense.

(1)

There is a subspace E of $L(X(\mu ),F)$ that is isomorphic to $Y(\mu )$, and the isomorphism $\iota :Y(\eta )\to E$ satisfies that $\iota ({\chi }_A)(·)=\iota ({\chi }_{\mathsf{\Omega }})({\chi }_A(·))$.

(2)

There is a μ-determined operator $T\in L(X(\mu ),F)$ such that

$$Y(\mu )=M_0(X(\mu ),L^1(m_T)),$$

with $M_0(X(\mu ),L^1(m_T))$ being the closure of the simple functions in $M(X(\mu ),L^1(m_T))$.

Proof. 

The above discussion gives (2) ⇒ (1). For the converse, take the operator $T:X(\mu )\to E$ defined as $T:=\iota ({\chi }_{\mathsf{\Omega }})$. Then, for every $A\in \mathsf{\Sigma }$, the operator $\iota ({\chi }_A):X(\mu )\to F$ belongs to $\iota (Y(\mu ))$ and satisfies $\iota ({\chi }_A)(f)=T({\chi }_{A}f)$ for every $f\in X(\mu )$ as a consequence of the assumption on $\iota$ and the fact that simple functions are dense in $Y(\mu )$. Then, the operator T provides the vector measure $m_T:\mathsf{\Sigma }\to F$. Let us show that $Y(\mu )=M(X(\mu ),L^1(m_T))$. If $h\in Y(\mu )$ is a simple function, then we have that $\iota (h)(f):=\int hfd{m}_T$ for all $f\in X(\mu )$. The isomorphism between E and $Y(\mu )$, together with the fact that simple functions are dense in $Y(\mu )$, implies that this formula works for every function h in $Y(\mu )$, and so for each $f\in X(\mu )$, $hf\in L^1(m_T)$ which implies $h\in M(X(\mu ),L^1(m_T)).$ Conversely, if $h\in M(X(\mu ),L^1(m_T))$ and is a simple function $h={\sum }_{i=1}^n{\lambda }_i{\chi }_{A_i}$, we have that it defines an operator $T_h:X(\mu )\to L^1(m_T)$ which can be represented as

$$T_h(f)=\sum _{i=1}^n{\lambda }_i\iota ({\chi }_{A_i})=T(\sum _{i=1}^n{\lambda }_i{\chi }_{A_i}f)=T(hf).$$

Therefore, $T_h\in E=Y(\mu )$, and the density of the simple functions in both spaces gives the result. □

4.3. Orthogonal Polynomials on Banach Spaces

In this section, we use the results in [37] to provide a description of certain spaces of polynomials. Let $n\in \mathbb{N}$. Recall that an n-homogeneous polynomial $P:X(\mu )\to F$ from the Banach function space $X(\mu )$ on the Banach space F is called orthogonally additive if $P(f+g)=P(f)+P(g)$ whenever $f,g\in X(\mu )$ and $|f|\wedge |g|=0$. Following Bu and Buskes (see [37]), we write $P_o{(}^{n}X(\mu ),F)$ for the space of all continuous n-homogeneous orthogonally additive polynomials from $X(\mu )$ to F. This notion can be translated directly to representable Banach spaces.

Suppose that E is a Banach space that is representable over the space $X(\mu )$ by means of the isomorphism $I:X(\mu )\to E$. Then, we say that an n-homogeneous polynomial $P:E\to F$ is orthogonally additive if $P(x+y)=P(x)+P(y)$ whenever $|I^{-1}(x)|\wedge |I^{-1}(y)|=0.$ We will use the same notation for the space of orthogonally additive n-homogeneous polynomials in $P_o{(}^{n}E,F)$ acting in the representable Banach space E.

In [37], it is proven that $P_o{(}^{n}X(\mu ),F)$ coincides isometrically with the space of all linear and continuous operators $L(X{(\mu )}_{\left[n\right]},F)$ ([37], Corollary 7.6). In order to do that, the authors identify the nth power of $X(\mu )$ with a certain quotient of the positive (sometimes called Fremlin) symmetric tensor product ([37], Proposition 7.5). Using our results, we can establish the following corollaries, which are direct consequences of Corollary 7.6 in [37].

Corollary 11.

Let E be a Banach space that is representable over an n-convex Banach function space. Then, $P_o{(}^{n}E,F)$ coincides isomorphically with the space of all linear and continuous operators $L(E_{\left[n\right]},F)$.

Proof. 

Since E is representable, we have that there is a Banach function space over a finite measure $X(\mu )$ and an isomorphism $I:X(\mu )\to E$. Notice that the identification of E and $X(\mu )$ directly provides the isomorphic equality $P_o{(}^{n}E,F)=P_o{(}^{n}X(\mu ),F)$. To see this, just define the map ${\iota }_n:P_o{(}^{n}X(\mu ),F)\to P_o{(}^{n}E,F)$ by ${\iota }_n(P)(x):=I(P(I^{-1}(x)))$ for $P\in P_o{(}^{n}X(\mu ),F)$ and $x\in E$. It is clear that P is orthogonally additive if and only if ${\iota }_n(P)$ is. Indeed, if $x,y\in E$ are orthogonal, we have

$$\begin{array}{ccc}\hfill I(P(I^{-1}(x)))+I(P(I^{-1}(y)))& =& I\left(P(I^{-1}(x))+P(I^{-1}(y))\right)\hfill \\ & =& I\left(P(I^{-1}(x)+I^{-1}(y))\right)=I\left(P(I^{-1}(x+y))\right).\hfill \end{array}$$

Thus, we obtain the identification. The norm

$$|||{\iota }_n{(P)|||}_{P{(}^{n}E,F)}=\underset{x\in B_E}{sup}\parallel P(I(I^{-1}(x)))\parallel ,$$

given for $P\in P_o{(}^{n}X(\mu ),F)$, is clearly equivalent to

$${|||P|||}_{P_o{(}^{n}X(\mu ),F)}=\underset{f\in B_{X(\mu )}}{sup}\parallel P(I(f))\parallel .$$

Now, it is enough to apply Corollary 7.6 in [37] and Corollary 3 to obtain the isomorphic equalities

$$P_o{(}^{n}E,F)=P_o{(}^{n}X(\mu ),F)=L(X{(\mu )}_{\left[n\right]},F)=L(E_{\left[n\right]},F).$$

 □

Corollary 12.

Let E be a Banach space. Suppose that there is a measurable space $(\mathsf{\Omega },\mathsf{\Sigma })$ and a vector measure $m:\mathsf{\Sigma }\to E$ satisfying that $span\{\mathrm{rg}(m)\}$ is dense in E, $L^1(m)$ is n-convex, and such that a sequence ${(f_n)}_n\subseteq L^1(m)$ is Cauchy if and only if ${(I_m(f_n))}_n$ is so in E. Then,

$$P_o{(}^{n}E,F)=L(L^{1/n}(m),F)=L(E_{\left[n\right]},F).$$

Proof. 

Let us consider the integration map associated to $I_m$. An application of Theorem 1 gives that E can be represented as the Banach function space $L^1(m)$. Since it is n-convex, we have that by Corollary 3, the nth power $L^{1/n}(m)$ is a Banach function space, and so the same argument given in the proof of Corollary 11 works. □

Corollary 13.

Let E be a Banach space. Suppose that there is a measurable space $(\mathsf{\Omega },\mathsf{\Sigma })$ and a vector measure $m:\mathsf{\Sigma }\to E$ such that $span\{rg(m)\}$ is dense in E, and there is a constant $Q>0$ such that for each $f_1,\dots ,f_N\in L^1(m)$,

$$\parallel {(\sum _{i=1}^N{|f_i|}^n)}^{1/n}{\parallel }_{L^1(m)}\le Q{(\sum _{i=1}^N\parallel I_m(f_i){\parallel }_E^n)}^{1/n}.$$

Then,

$$P_o{(}^{n}E,F)=L(L^{1/n}(m),F)=L(E_{\left[n\right]},F).$$

Proof. 

Let us consider the integration map associated to $I_m$. The inequality in the statement gives that, in particular, for each function $f\in L^1(m)$,

$$\parallel I_m{(f)\parallel }_E\le {\parallel f\parallel }_{L^1(m)}\le Q{\parallel I_m(f)\parallel }_E,$$

and so $I_m$ is an isomorphism. The inequality in the statement and the continuity of $I_m$ imply that $L^1(m)$ is n-convex. After renorming if necessary, we have that the n-convexity constant of $L^1(m)$ can be assumed to be 1 ([2], Proposition 1.d.8). Corollary 12 gives the result. □

Let us finish with a concrete application in the case where we can represent the space as an $L^q$-space.

Corollary 14.

Let $n\in \mathbb{N}$ and $q\in \mathbb{R}$ such that $n\le q$. Let E be a Banach space and suppose that there is a finite measure μ and an order-continuous q-convex Banach function space $Y(\mu )$ such that E is representable on $Y(\mu )$ by means of a q-concave operator $I:Y(\mu )\to E$. Then, there is a measure η equivalent to μ such that

$$P_o{(}^{n}E,F)=L(L^{q/n}(\eta ),F).$$

Proof. 

By Corollary 9, we have that E is representable as $L^q(\eta )$ for a certain finite measure that is equivalent to $\mu$. Then, by Corollary 11, and taking into account that $q\ge n$ and $L^q{(\eta )}_{\left[n\right]}=L^{q/n}(\eta )$, we have that

$$P_o{(}^{n}E,F)=P_o{(}^n{L}^q(\eta ),F)=L(L^{q/n}(\eta ),F).$$

This proves the corollary. □

Remark 2.

An extension of the results presented in this section and some interesting applications could be obtained by considering the general framework of the homogeneous functional calculus explained in [2], which allows the identification of the elements of a Banach lattice with the corresponding ones of its p-concavification. This is the point of view used in [38] to study the lattice geometric properties ($(p,q)$-concavity and $(p,q)$-convexity) of the polynomials. The interested reader can find a full explanation of this technique in Section 4 of the above-mentioned paper (see also Definition 3.5 and Proposition 3.6 in it).