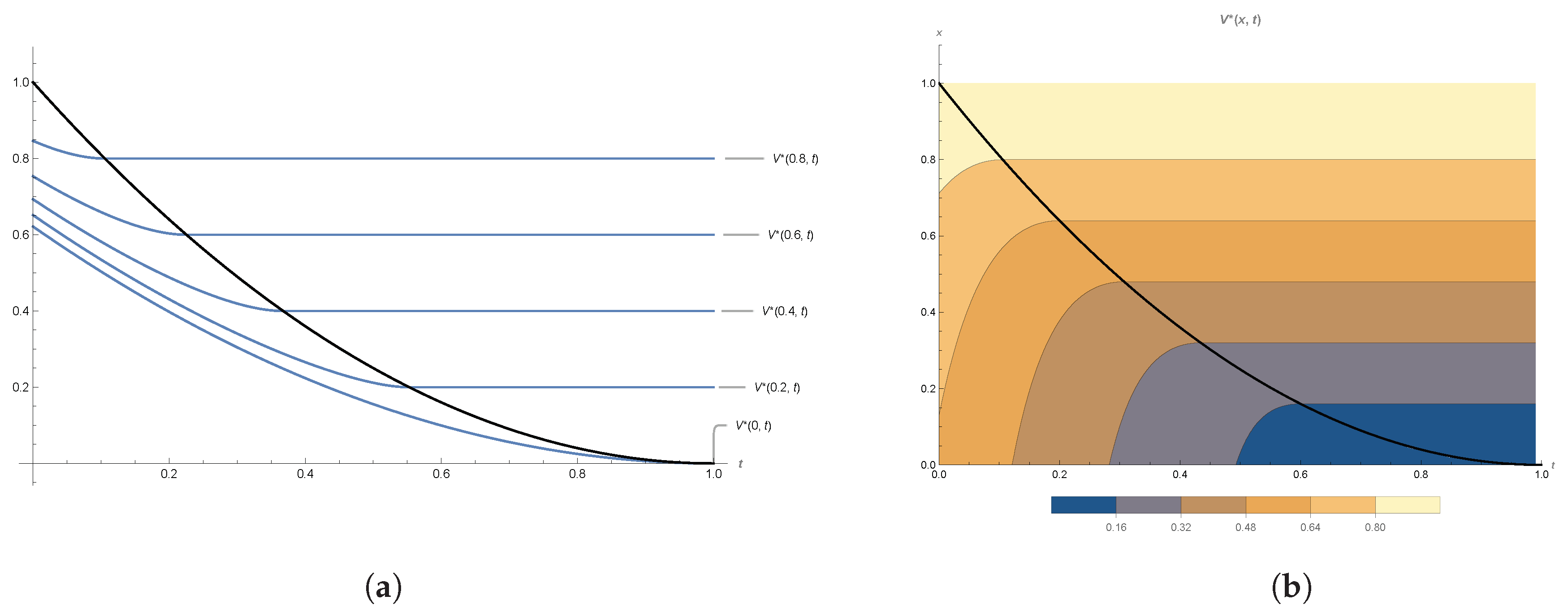A Class of Itô Diffusions with Known Terminal Value and Specified Optimal Barrier

Abstract

In this paper, we study the optimal stopping-time problems related to a class of Itô diffusions, modeling for example an investment gain, for which the terminal value is a priori known. This could be the case of an insider trading or of the pinning at expiration of stock options. We give the explicit solution to these optimization problems and in particular we provide a class of processes whose optimal barrier has the same form as the one of the Brownian bridge. These processes may be a possible alternative to the Brownian bridge in practice as they could better model real applications. Moreover, we discuss the existence of a process with a prescribed curve as optimal barrier, for any given (decreasing) curve. This gives a modeling approach for the optimal liquidation time, i.e., the optimal time at which the investor should liquidate a position to maximize the gain.

1. Introduction

In this paper, we study the optimal stopping-time problems related to an Itô diffusion, $\{X_s\}$, for time s in $[t,1]$, modeling for example an investment gain, for which the terminal value, say at time $s=1$, is a priori known. This could be the case of an insider trading [1,2,3] or of the pinning at expiration of stock options [4,5,6,7].

Roughly speaking, the class of stochastic processes subject of our study is defined by bringing the infinite horizon mean-reverting Ornstein–Uhlenbeck process with constant parameters to a finite horizon. We solve and provide explicit solutions to the optimal stopping-time problems associated with this class, which contains as particular case but it is not limited to, the optimal stopping time associated with the Brownian bridge

$$d{X}_s=-\frac{X_s}{1-s}ds+d{B}_s,\hspace{1em}s\in [t,1],\hspace{1em}\mathrm{with} X_t=x.$$

In this case, it is known (see [8,9]) that the optimal stopping time of

$$sup\{\mathbb{E}\left[X_{\tau }\right|X_t=x]:\tau \mathrm{stopping} \mathrm{time} \mathrm{in}[t,1]\}=:V(x,t)$$

is the one given by

$${\tau }_{*}:=inf\{s\in [t,1]:X_s\ge {\beta }_{*}\sqrt{1-s}\},$$

for an appropriate constant ${\beta }_{*}\approx 0.84$. In other words, if the stock price is equal to the optimal barrier ${\beta }_{*}\sqrt{1-t}$ at time t then $X_t=V(X_t,t)$ and thus the stock price is equal to the maximum gain in expectation.

We also present different processes whose optimal barrier has the same form as the optimal barrier of the Brownian bridge. They represent a catalogue of possible alternatives to the Brownian bridge which in practice could offer a better fitting to real applications.

Moreover, we discuss the existence of a process with a prescribed curve as optimal barrier, for any given (decreasing) curve. This gives a modeling approach for the optimal liquidation time, i.e., the optimal time at which the investor should liquidate a position to maximize the gain. More precisely, an investor takes short/long positions in the financial market based on her view about the future economy; for example, the real estate price is believed to increase in the long term, the inflation is believed to increase in the short term, the value of a certain company is believed to reduce in the medium term, etc. If $X_s$ is the market price at a time s of a product of the market which is the object of the investor’s view, the investor’s view can be modeled as a deterministic function $\gamma (s)$ which represents the “right” expected value at time s, assigned by the investor to the product at the time $t<s$ when the position needs to be taken. One may think of $\gamma$ as the short/medium/long period view. Of course, if the evolution of the economy induces the investor to distrust her initial view, the position is liquidated. Otherwise, if the investor maintains her view over time, we are interested in answering the following question: what is the optimal time at which the investor should liquidate her position to maximize the gain?

Similar problems have been studied in the recent literature. As mentioned at the beginning, the optimal stopping time associated with the case in which $\{X_s\}$ evolves like a Brownian bridge (finite horizon, i.e., $s\in [0,1]$) was originally investigated in [8] and later with a different approach in [9], and its optimal barrier is equal to ${\beta }_{*}\sqrt{1-s}$. In [10], the authors study the double optimal stopping-time problem, i.e., a pair of stopping times ${\tau }_1<{\tau }_2$ such that the expected spread between the payoffs at ${\tau }_1$ and ${\tau }_2$ is maximized, still associated with the case in which $\{X_s\}$ evolves like a Brownian bridge. The two optimal barriers which define the two optimal stopping times are found to have the same shape as in [9], i.e., ${\beta }_1\sqrt{1-s}$, ${\beta }_1\approx -0.56$, and ${\beta }_2\sqrt{1-s}$, ${\beta }_2={\beta }_{*}$. In [11], the authors study the optimal stopping problem when $\{X_s\}$ evolves like a mean-reverting Ornstein–Uhlenbeck process (infinite horizon, i.e., $s\in [0,\infty )$), but in the presence of a stop-loss barrier, i.e., a level $B<0$ such that the position is liquidated as $X_s\le B$. Furthermore, they study the dependency of the optimal barrier (which is a level $b>0$ in this case) to the parameters of the Ornstein–Uhlenbeck process and to the stop-loss level B.

The contribution of this paper consists of giving solutions for optimal stopping problems related to a class of non-homogeneous diffusion processes. Generally, such solutions are not easy to obtain in explicit form, and having them is useful in modeling procedures.

The paper is organized as follows. In Section 2, we introduce the class of processes studied in our work. In Section 3 and Section 4, we find the optimal barrier by using the Hamilton–Jacobi–Bellman equations and prove the optimality. In Section 5, we give a simple application and, in Section 6, we discuss the results contained in the paper.

2. The Formulation of the Problem

Our problem can be formulated as follows. Let us consider a mean-reverting Ornstein–Uhlenbeck process with constant coefficients $\theta \ge 0$, $\sigma >0$:

$$d{Z}_t=-\theta Z_{t}dt+\sigma d{B}_t,\hspace{1em}t>0,$$

where $\{B_t\}$ is the standard Brownian motion. The mean of $Z_t$ converges to 0 and its variance converges to ${\sigma }^2/(2\theta )$, as t goes to ∞, which is infinite if $\theta =0$.

We want to adapt this model, which has infinite time horizon, to a finite time horizon. Without loss of generality, we assume the final time to be $t=1$. We define the function

$$b(s):=\gamma (s)-\gamma (1),\hspace{1em}s\in [0,1],$$

(1)

that will be used below to make the time-change, where $\gamma$ is the function that carries the view of the future in the model. The function b is assumed to be a non-negative decreasing continuous function, therefore differentiable almost everywhere. We map s in $[0,1]$ to t in $[0,\infty ]$ by $t=-ln[b(s)/b(0)]$, we define $X_s:=b(s)Z_{-ln[b(s)/b(0)]}+\gamma (1)$ and we rewrite the Ornstein–Uhlenbeck process as

$$d\left[\frac{X_s-\gamma (1)}{b(s)}\right]=-\theta \frac{X_s-\gamma (1)}{b(s)}d[-lnb(s)]+\sigma d\left[B_{-lnb(s)}\right],\hspace{1em}s\in (0,1].$$

Indeed, one can verify that

$$\begin{array}{cc}d\left[\frac{X_s-\gamma (1)}{b(s)}\right]=d\left[Z_{-ln[b(s)/b(0)]}\right]\hfill & =-\theta Z_{-ln[b(s)/b(0)]}d[-ln[b(s)/b(0)]]+\sigma d\left[B_{-ln[b(s)/b(0)]}\right]\hfill \\ & {\displaystyle =-\theta \frac{X_s-\gamma (1)}{b(s)}d[-lnb(s)+lnb(0)]+\sigma d[B_{-lnb(s)}-B_{-lnb(0)}]}\hfill \\ & {\displaystyle =-\theta \frac{X_s-\gamma (1)}{b(s)}d[-lnb(s)]+\sigma d\left[B_{-lnb(s)}\right].}\hfill \end{array}$$

As, by Lemma 1, $X_1=\gamma (1)$, the quantity $Z_{-ln[b(s)/b(0)]}=[X_s-\gamma (1)]/b(s)$ represents the deviation of the market price to the final value in proportion to the deviation of the “right” value to the final value, at time s. As

$$d\left[\frac{X_s-\gamma (1)}{b(s)}\right]=\frac{d{X}_s}{b(s)}-(X_s-\gamma (1))\frac{b^{\prime }(s)}{b^2(s)}$$

and $d\left[B_{-lnb(s)}\right]=\sqrt{{[-lnb(s)]}^{\prime }}d{B}_s$, if we relabel the parameters by $\theta :={\alpha }^2$ and $\sigma :=\sqrt{2/{\beta }^2}$, we have that

$$\begin{array}{c}{\displaystyle \frac{d{X}_s}{b(s)}-(X_s-\gamma (1))\frac{b^{\prime }(s)}{b^2(s)}={\alpha }^2\frac{X_s-\gamma (1)}{b(s)}\frac{b^{\prime }(s)}{b(s)}ds+\sqrt{\frac{2}{{\beta }^2}}\sqrt{\frac{-b^{\prime }(s)}{b(s)}}d{B}_s.}\hfill \end{array}$$

By multiplying by $b(s)$ the two terms, we then obtain the equation for $\{X_s\}$:

$$d{X}_s=(1+{\alpha }^2)(X_s-\gamma (1))\frac{b^{\prime }(s)}{b(s)}ds+\sqrt{\frac{-2b^{\prime }(s)b(s)}{{\beta }^2}}d{B}_s,\hspace{1em}s\in (t,1),\hspace{1em}{X}_t=x,$$

(2)

starting at any time t in $(0,1)$.

Please note that despite there are different ways to map $[0,1]$ to $[0,\infty ]$ making use of the function b, the chosen map is the most natural one. Indeed, with this choice we have the following equation for the expected value of $X_s-\gamma (1)$:

$$\begin{array}{cc}d[ln\mathbb{E}[X_s-\gamma (1)]]=\frac{d\mathbb{E}[X_s-\gamma (1)]}{\mathbb{E}[X_s-\gamma (1)]}\hfill & =\frac{\mathbb{E}\left[d{X}_s\right]}{\mathbb{E}[X_s-\gamma (1)]}\hfill \\ & {\displaystyle =\frac{(1+{\alpha }^2)\mathbb{E}[X_s-\gamma (1)]}{\mathbb{E}[X_s-\gamma (1)]}\frac{b^{\prime }(s)}{b(s)}ds=(1+{\alpha }^2)d[lnb(s)],}\hfill \end{array}$$

i.e., the rate of change in logarithmic scale of $\mathbb{E}[X_s-\gamma (1)]$ is proportional to the same rate of $b(s)$.

We are interested in the optimization problem

$$V(x,t):=\underset{\tau }{sup}\mathbb{E}\left[X_{\tau }\right|X_t=x],$$

(3)

where $\tau \in [t,1]$ is a stopping time. Here we assume that at the final time, which without loss of generality is normalized to $s=1$, the market price coincides with the “right” value, i.e., $X_1=\gamma (1)$, as proved in Lemma 1.

Remark 1.

If $\alpha =1$, $\beta ={\beta }_{*}$, $\gamma (s)={\beta }_{*}\sqrt{1-s}$, Equation (2) becomes:

$$d{X}_s=-\frac{X_s}{1-s}ds+d{B}_s,$$

which is the SDE of a Brownian bridge already treated in [9].

Lemma 1.

The process $\{X_s\}$ defined by (2) is equal to

$$X_s=b^{1+{\alpha }^2}(s)\left[\frac{x-\gamma (1)}{b^{1+{\alpha }^2}(t)}+{\int }_t^s\sqrt{\frac{-2b^{\prime }(r)}{{\beta }^2{b}^{1+2{\alpha }^2}(r)}}d{B}_r\right]+\gamma (1),\hspace{1em}s\in [t,1].$$

(4)

Hence, $X_1=\gamma (1)$ and for $s\in [t,1]$,

$$\begin{array}{cc}\hfill \mathbb{E}\left[X_s\right]& =\gamma (1)+(x-\gamma (1)){\left[b(s)/b(t)\right]}^{1+{\alpha }^2},\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill Var\left[X_s\right]& ={(b(s)/\beta )}^2\left\{\begin{array}{cc}{\displaystyle \frac{1-{\left[b(s)/b(t)\right]}^{2{\alpha }^2}}{{\alpha }^2},}\hfill & \alpha \ne 0\hfill \\ {\displaystyle -ln{\left[b(s)/b(t)\right]}^2,\hspace{1em}}\hfill & \alpha =0\hfill \end{array}\right..\hfill \end{array}$$

(6)

Remark 2.

Please note that by (5), the function γ uniquely determines the average value of the process $\{X_s\}$ which is generally known as the growth curve of the diffusion process.

Proof. 

By multiplying the two terms of Equation (2) by ${[b(t)/b(s)]}^{1+{\alpha }^2}$, which is not identically zero, this can be rewritten as

$${\left[\frac{b(t)}{b(s)}\right]}^{1+{\alpha }^2}[d{X}_s-(1+{\alpha }^2)(X_s-\gamma (1))\frac{b^{\prime }(s)}{b(s)}ds]={\left[\frac{b(t)}{b(s)}\right]}^{1+{\alpha }^2}\sqrt{\frac{-2b^{\prime }(s)b(s)}{{\beta }^2}}d{B}_s.$$

Since the Itô derivative of $(X_s-\gamma (1)){[b(t)/b(s)]}^{1+{\alpha }^2}$ is equal to

$$d\left[(X_s-\gamma (1)){\left[\frac{b(t)}{b(s)}\right]}^{1+{\alpha }^2}\right]={\left[\frac{b(t)}{b(s)}\right]}^{1+{\alpha }^2}[d{X}_s-(1+{\alpha }^2)(X_s-\gamma (1))\frac{b^{\prime }(s)}{b(s)}ds],$$

we have that

$$(X_s-\gamma (1)){\left[\frac{b(t)}{b(s)}\right]}^{1+{\alpha }^2}=X_t-\gamma (1)+{\int }_t^s{\left[\frac{b(t)}{b(r)}\right]}^{1+{\alpha }^2}\sqrt{\frac{-2b^{\prime }(r)b(r)}{{\beta }^2}}d{B}_r.$$

This implies the expression for $X_s$ in (4). Moreover, the formulas for the mean and the variance of $X_s$ can be directly derived from this expression and the Itô isometry.

Lastly, as the $\mathrm{Var}\left[X_s\right]\to 0$ when s converges to 1, and since $\{X_s\}$ is continuous, we obtain $X_1=\gamma (1)$. This completes the proof. □

Remark 3.

The statements of the Lemma 1 on the mean and variance of $\{X_s\}$ are consistent with the corresponding quantities for the Ornstein–Uhlenbeck process $\{Z_t\}$ introduced at the beginning of the section, i.e., $\mathbb{E}[(X_s-\gamma (1))/b(s)]\to 0$ and $Var[(X_s-\gamma (1))/b(s)]\to 1/{(\alpha \beta )}^2={\sigma }^2/(2\theta )$ as $s\to 1$.

Moreover, observe that $Var\left[X_s\right]$ depends continuously on α also when $\alpha =0$ since $(1-{\left[b(s)/b(t)\right]}^{2{\alpha }^2})/{\alpha }^2$ converges to $-ln{\left[b(s)/b(t)\right]}^2$ as $\alpha \to 0$.

3. The HJB Equation

In this section, we derive the Hamilton–Jacobi–Bellman (HJB) that allows discovery of a candidate solution for the optimal stopping problem given in (3).

Defining the bivariate Markov process $\{Y_s\}:=\{(s,X_s)\}$, we have that its generator is given by the operator

$$\mathcal{L}f(s,x)={\partial }_{s}f(s,x)+(1+{\alpha }^2)(x-\gamma (1))\frac{b^{\prime }(s)}{b(s)}{\partial }_{x}f(s,x)-\frac{b^{\prime }(s)b(s)}{{\beta }^2}{\partial }_{xx}f(s,x)$$

(7)

acting on any function $f\in {\mathcal{C}}_0^2$. The first differential operator comes from the first component of the process $\{Y_s\}$, while the remaining two differential operators come from the Itô representation of the $\{X_s\}$ process given in (2). The introduction of the process $\{Y_s\}$ is required just to convert a non-homogeneous Markov process to a bivariate homogeneous one.

The HJB equation for the function V defined in (3) is given by $max\{\mathcal{L}V(t,x),0\}=0$. Following [12], we can find a continuation set, $\{(x,t):x<a(t)+\gamma (1)\}$ for an unknown function a, where the function V is harmonic. The complement of this set is the stopping set, where trivially $V(x,t)=x$. Therefore, we have the following PDE system

$$\left\{\begin{array}{cc}{\displaystyle V_t(x,t)+(1+{\alpha }^2)(x-\gamma (1))\frac{b^{\prime }(t)}{b(t)}{V}_x(x,t)-\frac{b^{\prime }(t)b(t)}{{\beta }^2}{V}_{xx}(x,t)=0,}\hfill & x<a(t)+\gamma (1)\hfill \\ V(x,t)=x,\hfill & x\ge a(t)+\gamma (1)\hfill \\ V_x(x,t)=1,\hfill & x=a(t)+\gamma (1)\hfill \\ V(x,t)\to \gamma (1),\hfill & x\to -\infty \hfill \end{array}\right.$$

(8)

with $t\in [0,1]$ and where $a:[t,1]\to \mathbb{R}$ is the free boundary such that the stopping time

$${\tau }^{*}:=inf\{s\in [t,1):X_s\ge a(s)+\gamma (1)\}$$

is the optimal stopping time for the problem (3), i.e., $V(x,t)=\mathbb{E}\left[X_{{\tau }^{*}}\right|X_t=x]$.

The three boundary conditions in (8) are necessary, but not sufficient, conditions for V to be a candidate solution of the optimal stopping problem. Indeed, the first and second conditions are the HJB expressions in the continuation and stopping sets, respectively. The third equation is the smooth fit condition and the last one expresses the fact that minimum possible gain is $\gamma (1)$, since the process $\{X_s\}$ will end up there almost surely when $s=1$.

If we assume that given $y\in \mathbb{R}$, $V(ya(t)+\gamma (1),t)-\gamma (1)$ has a value proportional to $a(t)$ independently on t, and $a(t)=b(t)$, i.e.,

$$V(x,t)-\gamma (1)=f\left(\frac{x-\gamma (1)}{b(t)}\right)b(t)$$

(9)

for an appropriate function f, then (8) can be rewritten as

$$\left\{\begin{array}{cc}{\displaystyle f(y)+{\alpha }^{2}y{f}^{\prime }(y)-\frac{1}{{\beta }^2}{f}^{″}(y)=0,}\hfill & y<1\hfill \\ f(y)=y,\hfill & y\ge 1\hfill \\ f^{\prime }(1)=1,\hfill \\ f(y)\to 0,\hfill & y\to -\infty \hfill \end{array}\right.$$

(10)

where $y=(x-\gamma (1))/b(t)$. Indeed, from (9), it follows that

$$\begin{array}{c}{\displaystyle V_t(x,t)=f\left(\frac{x-\gamma (1)}{b(t)}\right)b^{\prime }(t)-f^{\prime }\left(\frac{x-\gamma (1)}{b(t)}\right)\frac{x-\gamma (1)}{b(t)}{b}^{\prime }(t),}\hfill \\ {\displaystyle V_x(x,t)=f^{\prime }\left(\frac{x-\gamma (1)}{b(t)}\right),}\hfill \\ {\displaystyle V_{xx}(x,t)=f^{″}\left(\frac{x-\gamma (1)}{b(t)}\right)\frac{1}{b(t)}.}\hfill \end{array}$$

Therefore, Equation in (8) becomes

$$b^{\prime }(t)f(y)-y{b}^{\prime }(t)f^{\prime }(y)+(1+{\alpha }^2)y{b}^{\prime }(t)f^{\prime }(y)-\frac{b^{\prime }(t)}{{\beta }^2}{f}^{″}(y)=0,$$

which, after simplifying the term in $f^{\prime }(y)$ and dividing by $b^{\prime }(t)$, yields the equation in (10). The conditions in (10) come directly from the conditions in (8) and from (9).

Lemma 2.

Equation (10) admits a unique solution, the function $F_{\alpha }$, for any $\alpha \ge 0$ and for a unique $\beta =\beta (\alpha )$ which depends on α. The function $F_{\alpha }$ is given by

$$F_{\alpha }(y):=\left\{\begin{array}{cc}{e}^{y-1},\hfill & \alpha =0\hfill \\ h_1(-\alpha \beta (\alpha )y)/h_1(-\alpha \beta (\alpha )),\hfill & \alpha >0\hfill \end{array}\right.,$$

(11)

where the function $h_1$ is defined below in (17a).

Proof. 

If $\alpha =0$, the differential equation in (10) becomes

$$f(y)-\frac{1}{{\beta }^2}{f}^{″}(y)=0,$$

which admits as general solution $f(y)=c_1{e}^{\beta y}+c_2{e}^{-\beta y}$, with $c_1,c_2\in \mathbb{R}$. The boundary conditions in (10) give constraints on the parameters. Indeed, we have that

$$\begin{array}{cc}\hfill \underset{y\to -\infty }{lim}f(y)=0& \Rightarrow c_2=0,\hfill \\ \hfill f(1)=1& \Rightarrow c_1=e^{-\beta }.\hfill \end{array}$$

Therefore, the solution assumes the form $f(y)=e^{\beta (y-1)}$. Finally, the boundary condition $f^{\prime }(1)=1$ implies that $\beta =1$ and the solution is

$$f(y)=e^{y-1}.$$

Therefore, when $\alpha =0$ the equation with boundary conditions (10) admits solution if and only if $\beta =\beta (0):=1$.

Assume now $\alpha >0$. By substituting $f(y)=:h(-\beta y)$, with $\beta >0$, and using $x=-\beta y$, we can rewrite the differential equation in (10) without boundary conditions by

$$h(x)+{\alpha }^{2}x{h}^{\prime }(x)=h^{″}(x),\hspace{1em}x>-\beta .$$

(12)

This can be rewritten as

$$\frac{d}{dx}\left[e^{-{(\alpha x)}^2/2}{h}^{\prime }(x)\right]=e^{-{(\alpha x)}^2/2}h(x).$$

Finally, with a further substitution $h(x)=:u(\alpha x)exp[{(\alpha x)}^2/4]$ and $z=\alpha x$, we obtain the so-called parabolic cylinder differential equation

$$u^{″}(z)=\left(\frac{z^2}{4}+\frac{1}{{\alpha }^2}-\frac{1}{2}\right)u(z),\hspace{1em}z>-\alpha \beta .$$

(13)

Two linear independent solutions of the parabolic cylinder differential equation are

$$\begin{array}{cc}\hfill {\widehat{u}}_1(z)& =exp\left(-\frac{1}{4}{z}^2\right)M\left(\frac{1}{2{\alpha }^2},\frac{1}{2},\frac{1}{2}{z}^2\right),\hfill \end{array}$$

(14a)

$$\begin{array}{cc}\hfill {\widehat{u}}_2(z)& =zexp\left(-\frac{1}{4}{z}^2\right)M\left(\frac{1}{2{\alpha }^2}+\frac{1}{2},\frac{1}{2}+1,\frac{1}{2}{z}^2\right),\hfill \end{array}$$

(14b)

where $M(a,b,z)$ is the Kummer’s function, see [13] [Chapter 13]. The functions ${\widehat{u}}_1$ and ${\widehat{u}}_2$ are respectively an even and an odd function. They depend on the parameter $\alpha >0$; however, to keep notation as simple as possible, the dependence on the parameter will be dropped.

For convenience, let us introduce other two independent solutions $u_1$ and $u_2$ defined by the following linear combinations of ${\widehat{u}}_1$ and ${\widehat{u}}_2$:

$$\begin{array}{cc}{u}_1(z)\hfill & =\frac{1}{\sqrt[2{\alpha }^2]{2}}\left[\frac{\sqrt{\pi }}{\Gamma \left(1+1/(2{\alpha }^2)\right)}{\widehat{u}}_1(z)-\frac{\sqrt{2\pi }}{\Gamma \left(1/(2{\alpha }^2)\right)}{\widehat{u}}_2(z)\right],\hfill \end{array}$$

(15a)

$$\begin{array}{cc}{u}_2(z)\hfill & =\sqrt[2{\alpha }^2]{2}\left[\frac{sin(\pi /(2{\alpha }^2))}{\Gamma \left(1-1/(2{\alpha }^2)\right)}{\widehat{u}}_1(z)+\frac{\sqrt{2}cos(\pi /(2{\alpha }^2))}{\Gamma \left(1/2-1/(2{\alpha }^2)\right)}{\widehat{u}}_2(z)\right],\hfill \end{array}$$

(15b)

where $\Gamma$ denotes the gamma function. The expressions above are well defined for all $\alpha >0$. Please note that the function $u_1$ converges to 0 and $u_2$ diverges as $\left|z\right|$ goes to ∞. Moreover,

$$\begin{array}{cc}\hfill \underset{\left|z\right|\to \infty }{lim}{e}^{z^2/4}{z}^{1/{\alpha }^2}{u}_1(z)& =1,\hfill \end{array}$$

(16a)

$$\begin{array}{cc}\hfill \underset{\left|z\right|\to \infty }{lim}{e}^{-z^2/4}{z}^{1-1/{\alpha }^2}{u}_2(z)& =\sqrt{\pi /2}.\hfill \end{array}$$

(16b)

Using the relation between u and h, we have that

$$\begin{array}{cc}{h}_1(z)\hfill & :=u_1(z)exp(z^2/4)\hfill \\ & =\frac{1}{\sqrt[2{\alpha }^2]{2}}\left[\frac{\sqrt{\pi }}{\Gamma \left(1/2+1/(2{\alpha }^2)\right)}M\left(\frac{1}{2{\alpha }^2},\frac{1}{2},\frac{z^2}{2}\right)-\frac{z\sqrt{2\pi }}{\Gamma \left(1/(2{\alpha }^2)\right)}M\left(\frac{1}{2{\alpha }^2}+\frac{1}{2},\frac{3}{2},\frac{z^2}{2}\right)\right],\hfill \end{array}$$

(17a)

$$\begin{array}{cc}{h}_2(z)\hfill & :=u_2(z)exp(z^2/4)\hfill \\ & =\sqrt[2{\alpha }^2]{2}\left[\frac{sin(\pi /(2{\alpha }^2))}{\Gamma (1-1/(2{\alpha }^2))}M\left(\frac{1}{2{\alpha }^2},\frac{1}{2},\frac{z^2}{2}\right)+\frac{z\sqrt{2}cos(\pi /(2{\alpha }^2))}{\Gamma \left(1/2-1/(2{\alpha }^2)\right)}M\left(\frac{1}{2{\alpha }^2}+\frac{1}{2},\frac{3}{2},\frac{z^2}{2}\right)\right],\hfill \end{array}$$

(17b)

and, by (16), it follows that for $\left|z\right|\to \infty$

$$\begin{array}{cc}{h}_1(z)\hfill & \sim z^{-1/{\alpha }^2},\hfill \end{array}$$

(18a)

$$\begin{array}{cc}{h}_2(z)\hfill & \sim \sqrt{\pi /2}{e}^{z^2/2}{z}^{1/{\alpha }^2-1}.\hfill \end{array}$$

(18b)

Going back to the differential equation in (10) without boundary conditions, we can write all its solutions by

$$\begin{array}{c}\hfill f(y)=c_1{h}_1(-\alpha \beta y)+c_2{h}_2(-\alpha \beta y),\end{array}$$

(19)

with $c_1,c_2\in \mathbb{R}$. Applying the boundary conditions in (10), we have that

$$\begin{array}{cc}\hfill \underset{y\to -\infty }{lim}f(y)=0& \Rightarrow c_2=0,\hfill \\ \hfill f(1)=1& \Rightarrow c_1=1/h_1(-\alpha \beta ).\hfill \end{array}$$

Therefore, the solution assumes the form

$$\begin{array}{cc}\hfill f(y)& =\frac{h_1(-\alpha \beta y)}{h_1(-\alpha \beta )}.\hfill \end{array}$$

(20)

Finally, the boundary condition $f^{\prime }(1)=1$ implies

$$-\alpha \beta \frac{h_1^{\prime }(-\alpha \beta )}{h_1(-\alpha \beta )}=1.$$

(21)

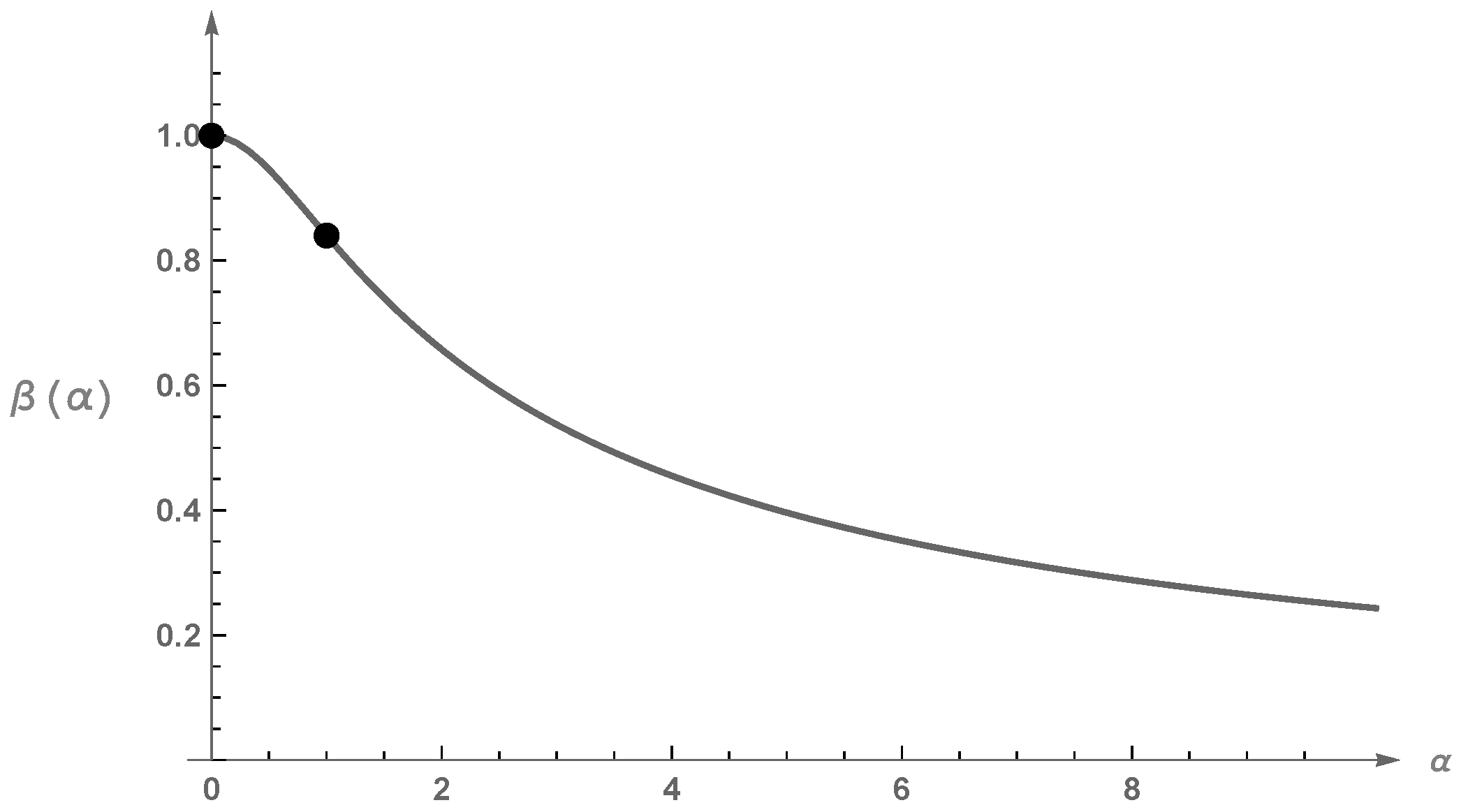
For every given $\alpha >0$, by Lemma A1 proved in the Appendix A, the equation $x_{\alpha }{h}_1^{\prime }(x_{\alpha })=h_1(x_{\alpha })$ admits a unique negative solution $x_{\alpha }$. Therefore, if $\beta (\alpha ):=-x_{\alpha }/\alpha$ (see Figure 1), then the differential equation with boundary conditions (10) admits the unique solution given by (20) with $\beta =\beta (\alpha )$. This completes the proof.  □

Remark 4.

Considering again the case of the Brownian bridge treated in [9], i.e., $\alpha =1$, we have that

$$\begin{array}{cc}\hfill h_1(z)& =\frac{1-\Phi (z)}{\varphi (z)}\hfill \end{array}$$

where $\Phi (z)=\mathbb{P}[Z\le z]$ with Z a standard Normal distributed and $\varphi (z)={\Phi }^{\prime }(z)$. Equation (21) becomes

$$\frac{\varphi (\beta (1))}{\Phi (\beta (1))}=\frac{1-{\beta }^2(1)}{\beta (1)}$$

and it admits the unique solution $\beta (1)\approx 0.84$ as already shown in [8,9].

4. The Solution

In this section, we verify that the solution V to the HJB equation found in Section 3 is indeed solution to the optimal stopping problem (3). This is a needed verification as we remind that the HJB equation represents only a necessary condition for the solution to the optimal stopping-time problem, but it is not a sufficient condition.

Theorem 1.

The function

$$V^{*}(x,t):=\left\{\begin{array}{cc}{\displaystyle \gamma (1)+F_{\alpha }\left(\frac{x-\gamma (1)}{\gamma (t)-\gamma (1)}\right)(\gamma (t)-\gamma (1)),}\hfill & x<\gamma (t)\hfill \\ x,\hfill & x\ge \gamma (t)\hfill \end{array}\right.,$$

(22)

with $F_{\alpha }$ defined in (11), is equal to the value function $V(x,t)$ in (3) and ${\tau }^{*}=inf\{s\in [t,1]:X_s\ge \gamma (t)\}$ is the optimal stopping time.

Proof. 

Consider the process $\{V^{*}(X_s,s)\}$. By the Itô formula and the definition of $V^{*}$, it follows that

$$\begin{array}{cc}d{V}^{*}(X_s,s)\hfill & =V_t^{*}(X_s,s)ds+V_x^{*}(X_s,s)d{X}_t-\frac{b^{\prime }(s)b(s)}{{\beta }^2}{V}_{xx}^{*}(X_s,s)ds\hfill \\ & {\displaystyle =(1+{\alpha }^2)(X_s-\gamma (1))\frac{b^{\prime }(s)}{b(s)}{\mathrm{𝟙}}_{[b(s),\infty )}(X_s)ds+V_x^{*}(X_s,s)\sqrt{\frac{-2b^{\prime }(s)b(s)}{{\beta }^2}}d{B}_s.}\hfill \end{array}$$

Please note that $\{{\int }_t^s{V}_x^{*}(X_r,r)\sqrt{-2b^{\prime }(r)b(r)/{\beta }^2}d{B}_r\}$ is a martingale as

$$\begin{array}{cc}\hfill V_x^{*}(X_r,r)\sqrt{-2b^{\prime }(r)b(r)/{\beta }^2}=& V_x^{*}(X_r,r)\sqrt{-2b^{\prime }(r)b(r)/{\beta }^2}{\mathrm{𝟙}}_{(-\infty ,b(r))}(X_r)\hfill \\ \hfill \hspace{1em}& +\sqrt{-2b^{\prime }(r)b(r)/{\beta }^2}{\mathrm{𝟙}}_{[b(r),\infty )}(X_r)\hfill \end{array}$$

is bounded.

Let $\tau \in [t,1]$ be a stopping time. Since $V^{*}(x,t)\ge x$, as shown in Lemma A2 proved in Appendix A, and the variable $(1+{\alpha }^2)(X_s-\gamma (1))[b^{\prime }(s)/b(s)]{\mathrm{𝟙}}_{[b(s),\infty )}(X_s)$ is non-positive, as the function b is non-negative and decreasing, and since $\{{\int }_t^s{V}_x^{*}(X_r,r)\sqrt{-2b^{\prime }(r)b(r)/{\beta }^2}d{B}_r\}$ is a martingale, then, by the Optional Sampling theorem,

$$\begin{array}{cc}\hfill \mathbb{E}\left[X_{\tau }\right]\le \mathbb{E}\left[V^{*}(X_{\tau },\tau )\right]=& V^{*}(x,t)+\mathbb{E}\left[{\int }_t^{\tau }(1+{\alpha }^2)(X_r-\gamma (1))\frac{b^{\prime }(r)}{b(r)}{\mathrm{𝟙}}_{[b(r),\infty )}(X_r)dr\right]\hfill \\ \hfill \hspace{1em}& +\mathbb{E}\left[{\int }_t^{\tau }{V}_x^{*}(X_r,r)\sqrt{-2b^{\prime }(r)b(r)/{\beta }^2}d{B}_s\right]\hfill \\ \hfill =& V^{*}(x,t)+\mathbb{E}\left[{\int }_t^{\tau }(1+{\alpha }^2)(X_r-\gamma (1))\frac{b^{\prime }(r)}{b(r)}{\mathrm{𝟙}}_{[b(r),\infty )}(X_r)dr\right]\le V^{*}(x,t).\hfill \end{array}$$

Hence, since this is true for any stopping time $\tau$, we have that $V(x,t)\le V^{*}(x,t)$.

On the other hand, since $V^{*}(X_{{\tau }^{*}},{\tau }^{*})=X_{{\tau }^{*}}$, then $(1+{\alpha }^2)(X_s-\gamma (1))[b^{\prime }(s)/b(s)]{\mathrm{𝟙}}_{[b(s),\infty )}(X_s)=0$, for every s in $[t,{\tau }^{*})$, and thus

$$V(x,t)\ge \mathbb{E}\left[V^{*}(X_{{\tau }^{*}},{\tau }^{*})\right]=V^{*}(x,t)+\mathbb{E}\left[{\int }_t^{{\tau }^{*}}{V}_x^{*}(X_r,r)\sqrt{-2b^{\prime }(r)b(r)/{\beta }^2}d{B}_s\right]=V^{*}(x,t).$$

This completes the proof.  □

5. Application

In this section, we show a brief application of the results of the previous sections. The process $\{X_s\}$ can model a pair trading process; see [14] for a survey or [15,16] for applications using the Ornstein–Uhlenbeck process. For our purposes we assume that we have a predicting model for the process trend that is given by

$$b(s)={(1-s)}^d,\hspace{1em}s\in [0,1],$$

(23)

with $d>0$, which ensures that the function b is non-increasing for $s\in [0,1]$. For fitting purposes one could choose a general function b of type $b(s)={\sum }_i{c}_i{(1-s)}^{d_i}$, with restrictions on the coefficients to ensure the decreasing property. We use (23) to simplify the calculations. In addition, we assume $\gamma (1)=0$ such that $\gamma (s)=b(s)$. $X_1=0$ may represent the fact that at time $s=1$ some information is publicly disclosed, such as the earning reports of the underlining stocks, that eliminates the pair difference.

As $b^{\prime }(s)/b(s)=-d/(1-s)$ and $b^{\prime }(s)b(s)=-d{(1-s)}^{2d-1}$, by substituting in (2), we obtain that

$$d{X}_s=-\frac{d(1+\theta )}{{(1-d)}^d}{(1-s)}^{1-d}{X}_{s}ds+\sqrt{\frac{2d}{{\beta }^2}{(1-s)}^{2d-1}}d{B}_s,\hspace{1em}s\in [0,1],\hspace{1em}{X}_0=x.$$

(24)

Figure 2 shows the value function $V^{*}(x,t)=max\left\{x, F_{\alpha }\left(x{(1-t)}^{-d}\right){(1-t)}^d\right\}$ obtained by (22).

It can be interpreted as both the time to sell the underlying pair trading and the price of an American call option with null strike price derived on the underlying pair trading process.

6. Discussion

The relevance of Theorem 1 is in that it proves the existence of a class of Itô diffusion processes for any specified (decreasing) optimal stopping boundary function b and gives the explicit expression of the corresponding value function (3). This provides a flexible model for the optimal liquidation time, i.e., the optimal time at which the investor should liquidate a position to maximize the gain, when the investor owns, or decides to include, additional information on the future trend of the underlining stock.

As an example, we can find the class of processes that have the same optimal stopping barrier of the standard Brownian bridge, i.e., with $\gamma (t):=\beta (\alpha )\sqrt{1-t}$. By choosing $d=1/2$ in (23) we get the following Itô representation, for $\alpha \ge 0$,

$$d{X}_s=-\frac{(1+{\alpha }^2)}{2}\frac{X_s}{1-s}ds+d{B}_s,\hspace{1em}s\in [t,1],\hspace{1em}{X}_t=x.$$

(25)

It follows that multiplying by a constant factor $(1+{\alpha }^2)/2$ the drift in the Itô representation of the Brownian bridge the optimal barrier has the same shape as the barrier of the Brownian bridge up to a factor equal to $\beta (\alpha )/\beta (1)$. For $\alpha \ge 0$, $\alpha \ne 1$, the process $\{X_s\}$ in (25) is not a Brownian bridge as, by Lemma 1, it is equal to

$$X_s=x+{\int }_t^s{\left[\frac{1-s}{1-r}\right]}^{(1+{\alpha }^2)/2}d{B}_r,\hspace{1em}s\in [t,1].$$

(26)

This class of processes is already known in the literature under the name of α-Wiener bridges, see for example [17], even if technically they are not bridges. Indeed, they cannot be generated, for $\alpha \ne 1$, by conditioning a gaussian Itô diffusion to be equal to 0 at time 1.

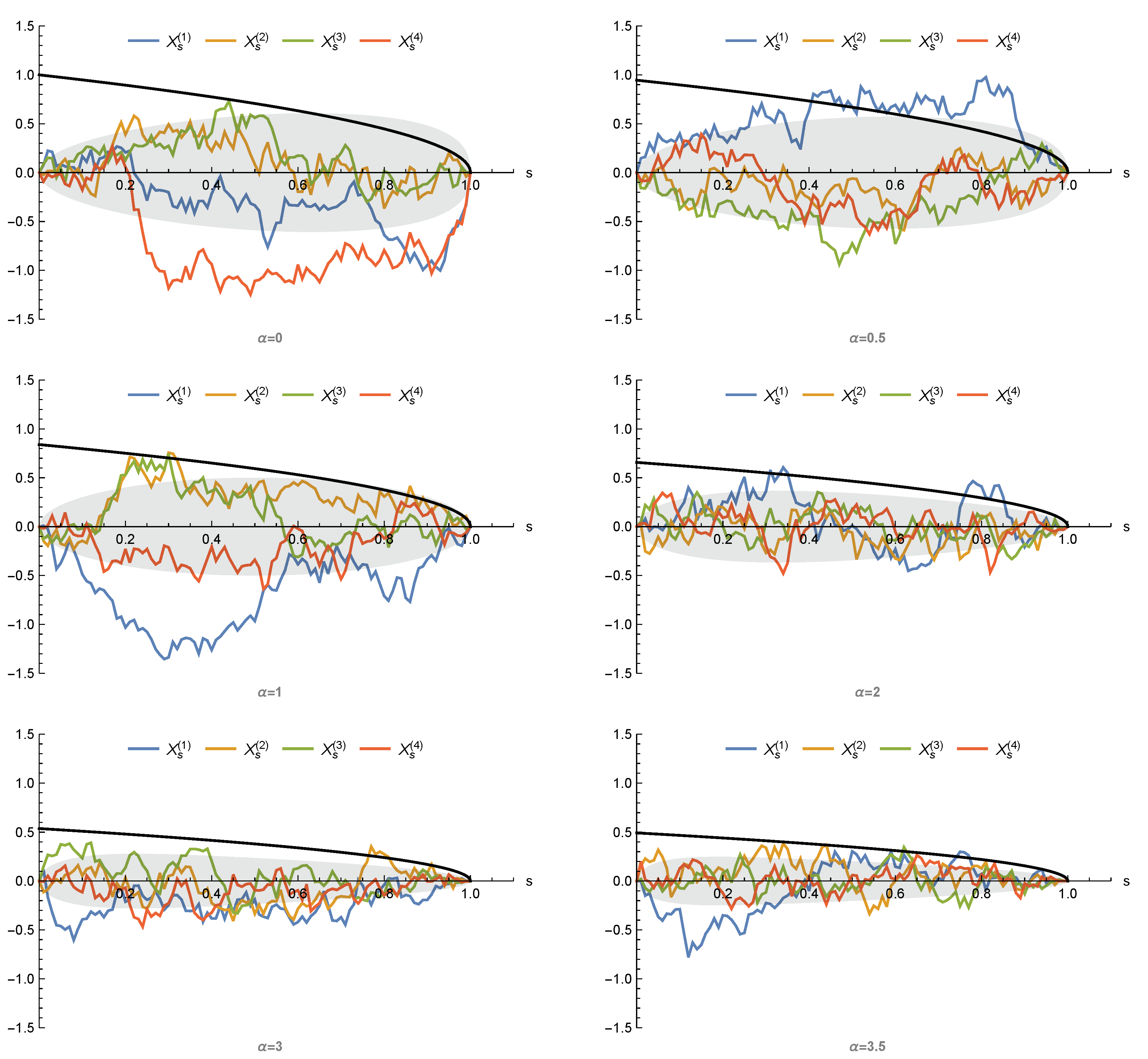
By the result above, they can be characterized by the fact that the associated optimal barrier is identical, modulo a factor, to the one of the Brownian bridge. Figure 3 gives a sample of simulations for different values of $\alpha \ge 0$. This class provides a catalogue of alternative diffusion processes to the Brownian bridge which in practice could offer a better fitting to the data.

In the literature, the $\alpha$-Wiener bridges have already been used in economic settings. They appeared from the first time in [18] to model the arbitrage profit associated with some future contracts in absence of transaction costs. Then in [19,20] they were used to describe the fundamental component of an exchange rate process. For more information we refer the reader to [21] and references therein.