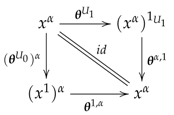
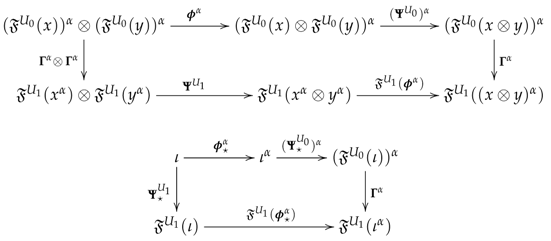
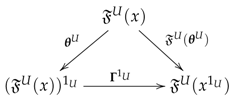
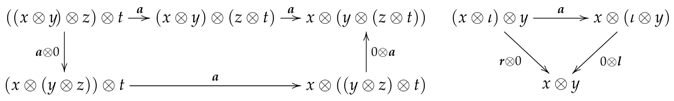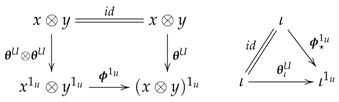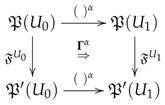Cohomology of Presheaves of Monoids
Abstract
1. Introduction and Summary
1.1. Outline of Results
- (a)
- , the category defined by the partially ordered set of open subsets of a topological space X. That is, in the cohomology of presheaves of monoids (and presheaves of groups, then) on a topological space.
- (b)
- , the category defined by the ordered set . That is, in the cohomology of pairs of monoids.
- (c)
- , the simplicial category of finite ordered sets , with non-decreasing maps between them as its morphisms. That is, in the cohomology of simplicial monoids.
- (d)
- , where X is a topological space. That is, in the cohomology of presheaves of simplicial monoids on a topological space (or, equivalently, of simplicial presheaves of monoids on a topological space).
- (e)
- , where is the orbit category of a group G, whose objects are the transitive left G-sets , for any subgroup , and whose morphisms are the G-equivariant maps between them. That is, in the (Borel) equivariant cohomology of simplicial monoids endowed with a left G-action by automorphisms. Here, one regards such a simplicial monoid as the presheaf of monoids on such that .
- (i)
- If is a presheaf of monoids on and A is -module, every simple 3-cocycle gives rise to a prestack .
- (ii)
- For any prestack on , there exist a presheaf of monoids , a -module A, a simple 3-cocycle , and an equivalence .
- (iii)
- If and are simple 3-cocycles, where and are presheaves of monoids, A is a -module, and is a -module, then there is an equivalence if and only if there are isomorphisms and such that in .
1.2. Organization of The Paper
2. Preliminaries on the Cohomology of Small Categories
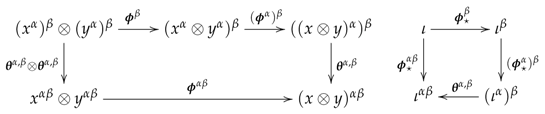
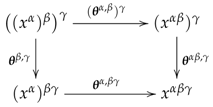
3. Coefficients for the Cohomology of Presheaves of Monoids
- -
- for each , with multiplication ,
- -
- for each arrow in , the homomorphism is given by ,
- -
- for any , the homomorphism is the projection ,
- -
- for any object , the internal group operation is defined by .
4. Derivations of Presheaves of Monoids
5. Cohomologies for Presheaves of Monoids
6. Cochains, Cocycles, Coboundaries
7. Low Dimensional Simple Cochains, Cocycles and Coboundaries
- ⧫
- A 1-cochain is a map assigning an element
- ⧫
- A 2-cochain is a function assigning elements
- ⧫
- The coboundary acts on an 1-cochain f by
- ⧫
- A 3-cochain is a function assigning elements
- ⧫
- The coboundary acts on a 2-cochain g by
- ⧫
- A 4-cochain is a function assigning elements
- ⧫
- The coboundary acts on a 3-cochain h by
8. Extensions of Presheaves of Monoids
- (i)
- for any object U of , , , , and ,
- (ii)
- for any arrow of , , and ,
- (i)
- Any -extension of with abelian kernel is an extension of by a -module.
- (ii)
- If, for any object U of , the monoid is regular, then every extension of by a -module is an -extension of with abelian kernel.
- -
- for any object U of and , let be the element of determined by the equation
- -
- for each arrow of and , let be the element of determined by the equation
9. Prestacks of Monoidal Abelian Monoids
- (PD1)
- a monoidal abelian groupoid , for each object U of ; that is, an abelian groupoid enriched with a tensor product , a unit object , and natural morphismssatisfying the commutativity of the diagrams
- (PD2)
- a monoidal functor , for each arrow of ; that is, a functor between the underlying groupoids endowed with natural morphisms and a morphism , satisfying the commutativities
- (PD3)
- a monoidal transformation , for each two arrows of ; that is, a family of natural morphisms , making commutative the diagrams
- (PD4)
- a monoidal transformation , for each object U of ; that is, a family of natural morphisms making commutative the diagrams
- (PA1)
- for any three composable arrows of and , the squarecommutes, that is,
- (PA2)
- for each in and , both inner triangles in the squarecommute, that is,
- (EPD1)
- a monoidal equivalence , for each object U of ; that is, an equivalence between the underlying groupoids enriched with natural morphisms and a morphism , satisfying
- (EPD2)
- a monoidal transformationfor each morphism of ; that is, a family of natural morphismsmaking commutative the diagrams
- (EPA1)
- for any two composable arrows of and , the diagramcommutes, that is,
- (EPA2)
- for any objects U of and x of , the triangle below commutes.
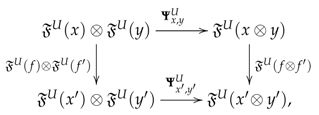
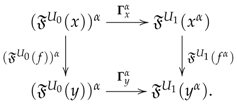
- ⧫
- The presheaf of monoids : For any object U of , let be the set of objects of the monoidal abelian groupoid . The effect on objects of tensor functor gives a multiplication on , simply by putting , which is associative and unitary, with identity , the unit object of , since being skeletal the existence of the structure constraints , , and forces the equalities and . Thus, is a monoid. For each arrow of , the function on objects of the monoidal functor in (PD2) gives a homomorphism of monoids , . The equalities and follow from the presence of the structure morphisms and , since is skeletal. Furthermore, if is any other arrow , the equality , that is for any , holds due to is skeletal and we have the structure morphisms in (PD3). Similarly, we see that because we have the morphisms as data in (PD4). Thus, is a presheaf of monoids.
- ⧫
- The -module A: For any object U of and each , let the abelian group of automorphisms of x in . For any other , the homomorphisms (26), , and (27), , are respectively defined by the functors and ; that is, for every , and . If is an arrow in , the homomorphism (28), , , is defined by the monoidal functor . For and , the equality holds since the naturality of associativity constraint of tell us that, in the abelian group , we have . Similarly, the equality follows from the naturality of the unit constraints and , which imply the equalities and , and the abelianity of the group . If is an arrow in , the naturality of the structure morphisms and , in (PD2), gives the equalities and . Then, as the group is abelian, we conclude that and . If is any other arrow , the equalities are consequence of being the group abelian and the naturality of the structure morphisms in (PD3), which tell us that . Similarly, the equality follows from the naturality of the morphisms , which says that , and the abelianity of the group . Thus, all the requirements in (30) are verified and we conclude that A is actually a -module.
- ⧫
- ⧫
- The equivalence : Previously to show such an equivalence, it is worth analyzing in relation to :
10. The Particular Case Where the Monoids Are Groups
10.1. the Coefficients for the Cohomology of a Presheaf of Groups
10.2. Derivations of Presheaves of Groups
10.3. Singular Extensions of Presheaves of Groups
10.4. Prestacks of Categorical Groups
Author Contributions
Funding
Conflicts of Interest
References
- Kashiwara, M.; Schapira, P. Categories and Sheaves; Grundlehren der Mathematischen Wissenschaften, 332; Springer: Berlin, Germany, 2006; 497p. [Google Scholar]
- Calvo, M.; Cegarra, A.M.; Heredia, B.A. Structure and classification of monoidal groupoids. Semigroup Forum 2008, 87, 35–79. [Google Scholar] [CrossRef]
- Leech, J. -coextensions of monoids. Mem. Am. Math. Soc. 1975, 1, 1–66. [Google Scholar]
- Leech, J. The cohomology of monoids. Unpublished lecture notes. 1976. [Google Scholar]
- Sinh, H.K. Gr-catégories. Ph.D. Thesis, Université Paris VII, Paris, France, 1975. [Google Scholar]
- Gerstenhaber, M.; Schack, S.D. On the deformation of algebra morphisms and diagrams. Trans. Am. Math. Soc. 1983, 279, 1–50. [Google Scholar] [CrossRef]
- Gerstenhaber, M.; Schack, S.D. The cohomology of presheaves of algebras. I. Presheaves over a partially ordered set. Trans. Am. Math. Soc. 1988, 310, 135–165. [Google Scholar]
- Gerstenhaber, M.; Giaquinto, A.; Schack, S.D. Diagrams of Lie algebras. J. Pure Appl. Algebra 2005, 196, 169–184. [Google Scholar] [CrossRef][Green Version]
- Dwyer, W.G.; Kan, D.M. An obstruction theory for diagrams of simplicial sets. Ned. Akad. Wet. Indag. Math. 1984, 46, 139–146. [Google Scholar] [CrossRef]
- Dwyer, W.G.; Kan, D.M. Hochschild-Mitchell cohomology of simplicial categories and the cohomology of simplicial diagrams of simplicial sets. Ned. Akad. Wet. Indag. Math. 1988, 50, 111–120. [Google Scholar]
- Moerdijk, I.; Svensson, J.-A. The equivariant Serre spectral sequence. Proc. Am. Math. Soc. 1993, 118, 263–278. [Google Scholar] [CrossRef]
- Moerdijk, I.; Svensson, J.-A. A Shapiro lemma for diagrams of spaces with applications to equivariant topology. Compositio Math. 1995, 96, 249–282. [Google Scholar]
- Blanc, D.; Johnson, M.W.; Turner, J.M. Local-to-global spectral sequences for the cohomology of diagrams. J. Pure Appl. Algebra 2009, 213, 34–53. [Google Scholar] [CrossRef][Green Version]
- Bousfield, A.K.; Kan, D.M. Homotopy Limits, Completions and Localizations; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1972; Volume 304, 348p. [Google Scholar]
- Gabriel, P.; Zisman, M. Calculus of Fractions and Homotopy Theory; Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 35; Springer: New York, NY, UYA, 1967; 168p. [Google Scholar]
- McDuff, D. On the classifying spaces of discrete monoids. Topology 1979, 18, 313–320. [Google Scholar] [CrossRef][Green Version]
- Whitehead, J.H.C. On group extensions with operators. Q. J. Math. Oxf. Ser. 1950, 1, 219–228. [Google Scholar] [CrossRef]
- Grillet, P.-A. Left coset extensions. Semigrpup Forum 1974, 7, 200–263. [Google Scholar] [CrossRef]
- Mac Lane, S. Categories for the Working Mathematician, 2nd ed.; Graduate Texts in Mathematics, 5; Springer: New York, NY, USA, 1998; 314p. [Google Scholar]
- Roos, J.-E. Sur les foncteurs dérivś de . Applications. C. R. Acad. Sci. Paris 1961, 252, 3702–3704. [Google Scholar]
- Watts, C.E. A homology theory for small categories. In Proc. Conf. Categorical Algebra (La Jolla, Calif., 1965); Springer: New York, NY, USA, 1966; pp. 331–335. [Google Scholar]
- Wells, C. Extension theories for monoids. Semigroup Forum 1978, 16, 13–35. [Google Scholar] [CrossRef]
- Cegarra, A.M. Cohomology of monoids with operators. Semigroup Forum 2019, 99, 67–105. [Google Scholar] [CrossRef]
- Goerss, P.G.; Jardine, J.F. Simplicial Homotopy Theory; Modern Birkhäuser Classics; Birkhäuser Verlag: Basel, Switzerland, 2009; 510p. [Google Scholar]
- Joyal, A.; Street, R. Braided tensor categories. Adv. Math. 1993, 102, 20–78. [Google Scholar] [CrossRef]
- Cegarra, A.M. Cohomology of diagrams of groups. The classification of (co)fibred categorical groups. Int. Math. J. 2003, 3, 643–680. [Google Scholar]
- Breen, L. Théorie de Schreier supŕieure. Ann. Sci. Éc. Norm. Super. 1992, 25, 465–514. [Google Scholar] [CrossRef]
- Saavedra, R.N. Catégories Tannakiennes; Lecture Notes in Mathematics; Springer: New York, NY, USA, 1972; Volume 265, 418p. [Google Scholar]
- Eckmann, B.; Hilton, P.J. Group-like structures in general categories. I. Multiplications and comultiplications. Math. Ann. 1961, 145, 227–255. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrasco, P.; Cegarra, A.M. Cohomology of Presheaves of Monoids. Mathematics 2020, 8, 116. https://doi.org/10.3390/math8010116
Carrasco P, Cegarra AM. Cohomology of Presheaves of Monoids. Mathematics. 2020; 8(1):116. https://doi.org/10.3390/math8010116
Chicago/Turabian StyleCarrasco, Pilar, and Antonio M. Cegarra. 2020. "Cohomology of Presheaves of Monoids" Mathematics 8, no. 1: 116. https://doi.org/10.3390/math8010116
APA StyleCarrasco, P., & Cegarra, A. M. (2020). Cohomology of Presheaves of Monoids. Mathematics, 8(1), 116. https://doi.org/10.3390/math8010116