Cohomology of Presheaves of Monoids

Abstract

The purpose of this work is to extend Leech cohomology for monoids (and so Eilenberg-Mac Lane cohomology of groups) to presheaves of monoids on an arbitrary small category. The main result states and proves a cohomological classification of monoidal prestacks on a category with values in groupoids with abelian isotropy groups. The paper also includes a cohomological classification for extensions of presheaves of monoids, which is useful to the study of $\mathcal{H}$-extensions of presheaves of regular monoids. The results apply directly in several settings such as presheaves of monoids on a topological space, simplicial monoids, presheaves of simplicial monoids on a topological space, monoids or simplicial monoids on which a fixed monoid or group acts, and so forth.

1. Introduction and Summary

This work grew out of the problem of stating a precise classification theorem for prestacks [1] on a small category $\mathrm{C}$ with values in the 2-category of monoidal abelian groupoids, that is, of tensor groupoids whose isotropy groups are abelian. The non-fibered case, that is, when $\mathrm{C}$ is the final category, was treated recently in [2], where it is shown how monoidal abelian groupoids are classified by elements of Leech third cohomology groups of monoids $H^3(M,A)$ [3,4]. In that classification process, for each monoidal abelian groupoid, M is its monoid of connected components, with multiplication induced by the tensor product, the coefficients A are provided by its automorphism groups, and the classifying datum $c\in H^3(M,A)$ is the cohomology class of a certain 3-cocycle canonically constructed from its structure associativity constraint. For categorical groups (also known as Gr-categories), that is, monoidal groupoids where the objects are quasi-invertible, that cohomological classification goes back to that given by Sinh in [5], where she proved that categorical groups are classified by the elements of the third Eilenberg-Mac Lane cohomology groups. When $\mathrm{C}$ is an arbitrary small category, every prestack on $\mathrm{C}$ valued in monoidal abelian groupoids produces, by taking connected components, not a monoid as in the punctual case but rather a presheaf on $\mathrm{C}$ with values in the category $\mathbf{Mon}$ of monoids. Then, we were naturally led to a research for an adequate cohomology theory for presheaves of monoids $\mathcal{M}:{\mathrm{C}}^{\mathrm{op}}\to \mathbf{Mon}$. Here, we provide a proposal for such a cohomology theory, which enjoys desirable properties whose study the paper is dedicated to.

Presheaves on small categories are rather familiar objects and arise in many situations. The cohomology of presheaves of several algebraic structures (groups, rings, etc.) has been object of study with interest along the last decades. Particularly, we should refer here to the seminal work by Gerstenhaber-Shack (in deformation theory) on cohomology of presheaves of algebras (e.g., associative or Lie) [6,7,8], which greatly inspires part of this paper on cohomology of presheaves of monoids. Also, our exposition is strongly influenced by several papers on cohomology of diagrams of simplicial sets (in equivariant homotopy theory). Particularly we should refer those by Dwayer-Kan [9,10], Moerdijk-Svensson [11,12], and Blanc-Johnson-Turner [13]. Notice that, when each monoid is replaced by its nerve (i.e., its simplicial classifying space), every presheaf of monoids $\mathcal{M}$ on a small category produces a presheaf of simplicial sets, $\mathbf{N}\mathcal{M}$, whose homotopy type is represented by its homotopy colimit [14]. Thus, Gabriel-Zisman cohomology groups [15] of the simplicial set $\mathrm{hocolim}\mathbf{N}\mathcal{M}$ naturally arise from a presheaf of monoids $\mathcal{M}$. In this setting, it is worth to recall that every path-connected CW-complex has the same homotopy type as the classifying space of a monoid [16].

1.1. Outline of Results

In this paper we actually present two cohomology theories for presheaves of monoids. For both theories, we start by associating to each presheaf of monoids $\mathcal{M}:{\mathrm{C}}^{\mathrm{op}}\to \mathbf{Mon}$ a small category, denoted by $\mathrm{D}\left(\mathcal{M}\right)$, whose left modules, that is, the abelian group valued functors on it, provide the coefficients. This is justified because of the existence of an equivalence

$$\mathbf{Ab}\left(\mathrm{Psh}(\mathrm{C},\mathbf{Mon}){\downarrow }_{\mathcal{M}}\right)\simeq \mathrm{D}\left(\mathcal{M}\right)\text{-}\mathrm{Mod}$$

(1)

between the category of abelian group objects in the slice category of presheaves of monoids on $\mathrm{C}$ over $\mathcal{M}$ and the category of abelian group valued functors on $\mathrm{D}\left(\mathcal{M}\right)$. The first cohomology theory of a presheaf of monoids $\mathcal{M}$ is then defined as the cohomology of the category $\mathrm{D}\left(\mathcal{M}\right)$, that is, by the right derived functors

$$H^n(\mathcal{M},-)=R^n{\mathrm{Hom}}_{\mathrm{D}\left(\mathcal{M}\right)}(\mathbb{Z},-)={\mathrm{Ext}}_{\mathrm{D}\left(\mathcal{M}\right)}^n(\mathbb{Z},-)(n\ge 0),$$

(2)

where $\mathbb{Z}$ is the constant $\mathrm{D}\left(\mathcal{M}\right)$-module given by the abelian group of integers. For the second one, which following to Gerstenhaber and Shack [7] we call the simple cohomology theory, we previously introduce the left exact functor of derivations, $\mathrm{Der}(\mathcal{M},-):\mathrm{D}\left(\mathcal{M}\right)$-Mod → Ab, and prove its representability by showing that it is naturally isomorphic to the hom functor ${\mathrm{Hom}}_{\mathrm{D}\left(\mathcal{M}\right)}(I\mathcal{M},-)$ provided by the (suitably defined) ideal augmentation $I\mathcal{M}$ of the presheaf $\mathcal{M}$. Then, we define the simple cohomology theory of $\mathcal{M}$ by the right derived functors

$$H_s^n(\mathcal{M},-)=R^{n-1}\mathrm{Der}(\mathcal{M},-)={\mathrm{Ext}}_{\mathrm{D}\left(\mathcal{M}\right)}^{n-1}(I\mathcal{M},-)(n\ge 1).$$

(3)

When $\mathrm{C}$ is the final category, then a presheaf of monoids $\mathcal{M}$ on $\mathrm{C}$ is simply a monoid and the $H^n(\mathcal{M},-)$ above are just the cohomology functors of the monoid $\mathcal{M}$ by Leech [3,4]. Furthermore, in this case, there are natural isomorphisms $H^n(\mathcal{M},-)\cong H_s^n(\mathcal{M},-)$ for all $n\ge 2$, so that both cohomology theories are essentially the same. However, in general the $H^n(\mathcal{M},-)$ are different of the simples ones $H_s^n(\mathcal{M},-)$. For instance, when $\mathrm{C}=G$ is a group (regarded as an one-object category) and $\mathcal{M}=H$ is a right G-group, then $\mathrm{D}\left(\mathcal{M}\right)=H⋊G$, the semidirect product group, and the cohomology functors $H^n(\mathcal{M},-)$ agree with the ordinary Eilenberg-Mac Lane cohomology functors $H^n(H⋊G,-)$, whereas the functors $H_s^n(\mathcal{M},-)$ agree with the vector cohomology groups $H_{n-1}^n(G,H;-)$ by Whitehead [17]. A main result in this paper states that, for any presheaf of monoids $\mathcal{M}$ on a small category $\mathrm{C}$, there is a natural long exact sequence

$$\cdots \to H^n(\mathcal{M},A)\to H^n({\mathrm{C}}^{\mathrm{op}},A)\to H_s^{n+1}(\mathcal{M},A)\to H^{n+1}(\mathcal{M},A)\to H^{n+1}({\mathrm{C}}^{\mathrm{op}},A)\to \cdots ,$$

(4)

for any $\mathrm{D}\left(\mathcal{M}\right)$-module A, connecting the cohomology groups of $\mathcal{M}$ in both theories with those of the category $\mathrm{C}$ with coefficients in the right module obtained by restricting the coefficients A to ${\mathrm{C}}^{\mathrm{op}}$ through its natural inclusion into $\mathrm{D}\left(M\right)$.

Following general methods by Gerstenhaber-Schack and Gabriel-Zisman, we define, for every presheaf $\mathcal{M}$ and any $\mathrm{D}\left(\mathcal{M}\right)$-module A, cochain complexes of abelian groups $C^{•}(\mathcal{M},A)$ and ${\mathrm{C}}_s^{•}(\mathcal{M},A)$ such that there are natural isomorphisms

$$\begin{array}{cc}\hfill & H_s^n(\mathcal{M},A)\cong H^n{C}_s^{•}(\mathcal{M},A),(n\ge 1),\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & H^n(\mathcal{M},A)\cong H^n{C}^{•}(\mathcal{M},A)\cong H^n(\mathrm{hocolim}\mathbf{N}\mathcal{M},A),(n\ge 0).\hfill \end{array}$$

(6)

When the category ${\mathrm{C}}^{\mathrm{op}}$ is cohomologically trivial, for instance whenever $\mathrm{C}$ has a final object, we deduce the existence of natural isomorphisms

$$H_s^n(\mathcal{M},A)\cong H^n(\mathcal{M},A)\cong H^n(\mathrm{hocolim}\mathbf{N}\mathcal{M},A),(n\ge 2).$$

(7)

These isomorphisms hold then in several relevant cases we have in mind, as for example when

(a)

$\mathrm{C}=O\left(X\right)$, the category defined by the partially ordered set of open subsets of a topological space X. That is, in the cohomology of presheaves of monoids (and presheaves of groups, then) on a topological space.

(b)

$\mathrm{C}=\left[1\right]$, the category defined by the ordered set $\{0<1\}$. That is, in the cohomology of pairs of monoids.

(c)

$\mathrm{C}=\Delta$, the simplicial category of finite ordered sets $\left[p\right]=\{0<1<\cdots <p\}$, with non-decreasing maps between them as its morphisms. That is, in the cohomology of simplicial monoids.

(d)

$\mathrm{C}=O\left(X\right)\times \Delta$, where X is a topological space. That is, in the cohomology of presheaves of simplicial monoids on a topological space (or, equivalently, of simplicial presheaves of monoids on a topological space).

(e)

$\mathrm{C}=Or\left(G\right)\times \Delta$, where $Or\left(G\right)$ is the orbit category of a group G, whose objects are the transitive left G-sets $G/H$, for any subgroup $H\subseteq G$, and whose morphisms are the G-equivariant maps between them. That is, in the (Borel) equivariant cohomology of simplicial monoids endowed with a left G-action by automorphisms. Here, one regards such a simplicial monoid $\mathcal{M}$ as the presheaf of monoids on $Or\left(G\right)\times \Delta$ such that $(G/H,\left[p\right])\mapsto {\mathrm{Hom}}_G(G/H,{\mathcal{M}}_p)\cong {\mathcal{M}}_p^H$.

We dedicate much of the paper to show natural realizations for the cohomology classes in $H_s^2(\mathcal{M},A)$ and $H_s^3(\mathcal{M},A)$. For any presheaf of monoids $\mathcal{M}$ on a small category $\mathrm{C}$ and any $\mathrm{D}\left(M\right)$-module A, we prove the existence of a natural bijection

$$\mathrm{Ext}(\mathcal{M},A)\cong H_s^2(\mathcal{M},A),$$

(8)

between the set of equivalence classes of extensions (aka coextensions) of $\mathcal{M}$ by A and the second simple cohomology group of $\mathcal{M}$ with coefficients in A. This classification result is showed to be useful in the study of the structure of $\mathcal{H}$-extensions of $\mathcal{M}$ with abelian kernel, that is, locally surjective morphisms of presheaves of monoids $\mathfrak{f}:\mathcal{E}\to \mathcal{M}$ such that, for any objet U of $\mathrm{C}$, the congruence kernel of ${\mathfrak{f}}_U:\mathcal{E}\left(U\right)\to \mathcal{M}\left(U\right)$ is contained in the Green’s relation $\mathcal{H}$ of $\mathcal{E}\left(U\right)$ and the Shützenberger groups of the kernel classes are abelian. Following to Grillet [18] and Leech [3], we introduce a certain full subcategory of $\mathrm{D}\left(\mathcal{M}\right)$-Mod, which we call the category of $\mathcal{D}\left(M\right)$-modules, and we prove that when the presheaf of monoids $\mathcal{M}$ is locally regular then equivalence classes of $\mathcal{H}$-extensions of $\mathcal{M}$ with abelian kernel correspond bijectively to the elements of $H_s^2(\mathcal{M},A)$.

Our results on the classification of prestacks on a small category $\mathrm{C}$, that is, of contravariant pseudo-functors from $\mathrm{C}$ to the 2-category of monoidal abelian groupoids, by the third simple cohomology groups of presheaves of monoids on $\mathrm{C}$, can be summarized as follows:

(i)

If $\mathcal{M}$ is a presheaf of monoids on $\mathrm{C}$ and A is $\mathrm{D}\left(\mathcal{M}\right)$-module, every simple 3-cocycle $h\in Z_s^3(\mathcal{M},A)$ gives rise to a prestack $\mathfrak{P}(\mathcal{M},A,h)$.

(ii)

For any prestack $\mathfrak{P}$ on $\mathrm{C}$, there exist a presheaf of monoids $\mathcal{M}$, a $\mathrm{D}\left(\mathcal{M}\right)$-module A, a simple 3-cocycle $h\in Z_s^3(\mathcal{M},A)$, and an equivalence $\mathfrak{P}(\mathcal{M},A,h)\simeq \mathfrak{P}$.

(iii)

If $h\in Z_s^3(\mathcal{M},A)$ and $h^{\prime }\in Z_s^3({\mathcal{M}}^{\prime },A^{\prime })$ are simple 3-cocycles, where $\mathcal{M}$ and ${\mathcal{M}}^{\prime }$ are presheaves of monoids, A is a $\mathrm{D}\left(\mathcal{M}\right)$-module, and $A^{\prime }$ is a $\mathrm{D}\left({\mathcal{M}}^{\prime }\right)$-module, then there is an equivalence $\mathfrak{P}(\mathcal{M},A,h)\simeq \mathfrak{P}({\mathcal{M}}^{\prime },A^{\prime },h^{\prime })$ if and only if there are isomorphisms $\mathfrak{f}:{\mathcal{M}}^{\prime }\cong \mathcal{M}$ and $F:A^{\prime }\cong {\mathfrak{f}}^{*}A$ such that $\left[h^{\prime }\right]=F_{*}^{-1}{\mathfrak{f}}^{*}\left(\left[h\right]\right)$ in $H_s^3({\mathcal{M}}^{\prime },A^{\prime })$.

Thus, prestacks on $\mathrm{C}$ are classified by triples $(\mathcal{M},A,c)$ where $\mathcal{M}$ is a presheaf of monoids on $\mathrm{C}$, A is a $\mathrm{D}\left(\mathcal{M}\right)$-module, and $c\in H_s^3(\mathcal{M},A)$.

1.2. Organization of The Paper

The plan of the paper is, briefly, as follows. After the first introductory and summary section, the rest is organized in nine sections. Section 2 is preparatory and comprises some notations and a review on cohomology of small categories. In Section 3 we analyze the coefficients we use for the cohomology of presheaves of monoids. Section 4 is dedicated to the notion of derivation of presheaves of monoids. The main Section 5 includes the definition of the cohomology groups $H^n(\mathcal{M},A)$ and $H_s^n(\mathcal{M},A)$ and a first study of their properties. In particular, we state here the above mentioned linking long exact sequences. The following Section 6 and Section 7 are dedicated to cochains, cocycles, and coboundaries. We provide in Section 6 of suitable cochain complexes $C^{•}(\mathcal{M},A)$ and $C_s^{•}(\mathcal{M},A)$ for computing the cohomology groups $H^n(\mathcal{M},A)$ and $H_s^n(\mathcal{M},A)$, and in the brief Section 7 we specify, for future reference, what low dimensional simple cochains, cocycles, and coboundaries are. Section 8 is mainly devoted to state the classification of extensions of presheaves of monoids by means of the groups $H_s^2(\mathcal{M},A)$, while the long Section 9 is entirely dedicated to show the classification of prestacks by means of the cohomology groups $H_s^3(\mathcal{M},A)$. In the last Section 10, we analyze how our previous results specialize when we focus on presheaves of groups.

2. Preliminaries on the Cohomology of Small Categories

Let $\mathrm{K}$ be a small category. A (left) $\mathrm{K}$-module is a functor $A:\mathrm{K}\to \mathbf{Ab}$. The category of $\mathrm{K}$-modules, with morphisms the natural transformations, is denoted by $\mathrm{K}$-Mod. We make reference to [19] (Chapter VIII, §3) for formalities but point out that this is an abelian category with sufficiently many projective and injective objects. For any two $\mathrm{K}$-modules A and $A^{\prime }$, the abelian group structure of ${\mathrm{Hom}}_{\mathrm{K}}(A,A^{\prime })$ is given by pointwise addition. The zero $\mathrm{K}$-module is the constant functor given by the abelian group 0, and a sequence $A\to A^{\prime }\to A^{″}$ is exact if and only if it is locally exact, that is, every sequence of abelian groups $A\left(U\right)\to A^{\prime }\left(U\right)\to A^{″}\left(U\right)$, $U\in \mathrm{ObK}$, is exact. There is a free $\mathrm{K}$-module functor,

$$\mathcal{F}:\mathbf{Set}{\downarrow }_{\mathrm{ObK}}\to \mathrm{K}\text{-}\mathrm{Mod},$$

(9)

from the slice category of sets over the set of objects of $\mathrm{K}$ to the category of $\mathrm{K}$-modules. For every $S=(S,\pi :S\mapsto \mathrm{ObK})$, the free $\mathrm{K}$-module $\mathcal{F}S$ assigns to each $U\in \mathrm{ObK}$ the free abelian group on the pairs $(s,\alpha )$ where $s\in S$ and $\alpha \in {\mathrm{Hom}}_{\mathrm{K}}(\pi s,U)$. The homomorphism $\mathcal{F}\left(\beta \right):\mathcal{F}\left(U\right)\to \mathcal{F}\left(V\right)$, induced by a morphism $\beta :U\to V$ in $\mathrm{K}$, is defined on generators by $\mathcal{F}S\left(\beta \right)(s,\alpha )=(s,\beta \alpha )$.

Proposition 1.

For $S=(S,\pi :S\to \mathrm{ObK})$ any set over $\mathrm{ObK}$ and any $\mathrm{K}$-module A, there is a natural isomorphism of abelian groups

$${\mathrm{Hom}}_{\mathrm{K}}(\mathcal{F}S,A)\cong \prod _{s\in S}A\left(\pi s\right),f\mapsto {\left(f_{\pi s}(s,1_{\pi s})\right)}_{s\in S}.$$

(10)

Proof. 

This is a straightforward consequence of Yoneda Lemma. □

From the above, it is plainly seen that every free $\mathrm{K}$-module is projective.

The cohomology groups of $\mathrm{K}$ with coefficients in a $\mathrm{K}$-module A [20,21], denoted $H^n(\mathrm{K},A)$, are defined by

$$H^n(\mathrm{K},A)={\mathrm{Ext}}_{\mathrm{K}}^n(\mathbb{Z},A).$$

(11)

Above $\mathbb{Z}:\mathrm{K}\to \mathbf{Ab}$ denotes the constant functor defined by the group of integers.

To exhibit an explicit cochain complex that computes the cohomology groups $H^n(\mathrm{K},A)$, let $\mathbf{N}\mathrm{K}$ be the nerve of $\mathrm{K}$. That is, the simplicial set whose p-simplices are sequences

$$\beta =(\beta 0\stackrel{{\beta }_1}{\to }\cdots \stackrel{{\beta }_p}{\to }\beta p)$$

of p composable morphisms in $\mathrm{K}$ (objects $\beta 0$ of $\mathrm{K}$ if $p=0$), and whose face and degeneracy operators

$${\mathbf{N}}_{p+1}\mathrm{K}\stackrel{d_i}{\to }{\mathbf{N}}_p\mathrm{K}\stackrel{s_j}{\to }{\mathbf{N}}_{p+1}\mathrm{K}$$

are defined by $d_0\beta =\beta 1$, $d_1\beta =\beta 0$, and $s_0\beta =1_{\beta 0}$ if $p=0$, and for $p\ge 1$ by

$$\begin{array}{cc}{d}_i\beta \hfill & =\left\{\begin{array}{ccc}({\beta }_2,\dots ,{\beta }_p)\hfill & \mathrm{if}\hfill & i=0,\hfill \\ ({\beta }_1,\dots ,{\beta }_{i+1}{\beta }_i,\dots ,{\beta }_p)\hfill & \mathrm{if}\hfill & 0<i<p,\hfill \\ ({\beta }_1,\dots ,{\beta }_{p-1})\hfill & \mathrm{if}\hfill & i=p.\hfill \end{array}\right.\hfill \\ s_j\beta \hfill & =({\beta }_1,\dots ,{\beta }_j,1_{\beta j},{\beta }_{j+1},\dots ,{\beta }_p).\hfill \end{array}$$

(12)

There is a canonical “last object” functor from the category of simplices of $\mathbf{N}\mathrm{K}$ to K, $\Delta \mathbf{N}\mathrm{K}\to K$, $\beta \mapsto \beta p$. Then, by composing with it, every $\mathrm{K}$-module A defines a system of coefficients on $\mathbf{N}\mathrm{K}$ [15]) and produces a cosimplicial abelian group, denoted ${\mathrm{C}}^{•}(\mathrm{K},A)$, in which each $C^p(\mathrm{K},A)$ is the abelian group of those maps $\phi$ that assign to each p-simplex $\beta \in {\mathbf{N}}_p\mathrm{K}$ an element $\phi \left(\beta \right)\in A\left(\beta p\right)$. The coface homomorphisms

$$d^i:C^{p-1}(\mathrm{K},A)\to C^p(\mathrm{K},A)$$

are given by

$$d^i\phi \left(\beta \right)=\left\{\begin{array}{ccc}\phi \left(d_i\beta \right)\hfill & \mathrm{if}\hfill & 0\le i<p,\hfill \\ A\left({\beta }_p\right)\phi \left(d_p\beta \right)\hfill & \mathrm{if}\hfill & i=p.\hfill \end{array}\right.d^i\phi \left(\beta \right)=\left\{\begin{array}{ccc}\phi \left(d_i\beta \right)\hfill & \mathrm{if}\hfill & 0\le i<p,\hfill \\ A\left({\beta }_p\right)\phi \left(d_p\beta \right)\hfill & \mathrm{if}\hfill & i=p.\hfill \end{array}\right.$$

(13)

The so-called standard cochain complex of $\mathrm{K}$ with coefficients in A, also written as $C^{•}(\mathrm{K},A)$, is its alternating sum faces cochain complex, whose coboundaries are

$$\partial ={\displaystyle \sum _{i=0}^p}{(-1)}^i{d}^i:C^{p-1}(\mathrm{K},A)\to C^p(\mathrm{K},A).$$

(14)

We have the following (well-known) relevant fact.

Proposition 2.

There are natural isomorphisms

$$H^n(\mathrm{K},A)\cong H^n{C}^{•}(\mathrm{K},A),n=0,1,\cdots .$$

(15)

Proof. 

For each integer $p\ge 0$, let $\pi :{\mathbf{N}}_p\mathrm{K}\to \mathrm{ObK}$ be the map given by $\pi \left(\beta \right)=\beta p$, and let $Q_p$ be the free $\mathrm{K}$-module on $({\mathbf{N}}_p\mathrm{K},\pi )$. Thus, for each $U\in \mathrm{ObK}$, $Q_p\left(U\right)$ is the free abelian group with generators those $\beta =({\beta }_1,\dots ,{\beta }_{p+1})\in {\mathbf{N}}_{p+1}\mathrm{K}$ such that $\beta (p+1)=U$, and for each arrow $\alpha :U\to V$ in $\mathrm{K}$, the induced $Q_p\left(\alpha \right):Q_p\left(U\right)\to Q_p\left(V\right)$ is given on generators by $Q_p\left(\alpha \right)\left(\beta \right)=({\beta }_1,\dots ,{\beta }_p,\alpha {\beta }_{p+1})$. These $Q_p$ define an augmented chain complex of projective $\mathrm{K}$-modules,

$$Q_{•}=Q_{•}\left(\mathrm{K}\right)\stackrel{\mu }{\to }\mathbb{Z},$$

(16)

whose differential, at any object U of $\mathrm{K}$, $\partial :Q_p\left(U\right)\to Q_{p-1}\left(U\right)$ is given on generators by the usual boundary formula $\partial \left(\beta \right)={\sum }_{i=0}^p{(-1)}^i{d}_i\left(\beta \right)$, and whose augmentation $\mu :Q_0\left(U\right)\to \mathbb{Z}$ by $\mu \left(\beta \right)=1$. Indeed, (16) is a projective resolution of $\mathbb{Z}$ since, at any object U of $\mathrm{K}$, the augmented chain complex

$$Q_{•}\left(U\right)\stackrel{\mu }{\to }\mathbb{Z}:\cdots \to Q_2\left(U\right)\stackrel{\partial }{⟶}{Q}_1\left(U\right)\stackrel{\partial }{⟶}{Q}_0\left(U\right)\stackrel{\mu }{⟶}\mathbb{Z}\to 0$$

(17)

has a contracting homotopy $\mathsf{\Phi }$, which is given on generators by ${\mathsf{\Phi }}_{-1}\left(1\right)=1_U$, and ${\mathsf{\Phi }}_p\left(\beta \right)={(-1)}^{p+1}({\beta }_1,\dots ,{\beta }_{p+1},1_U)$.

Therefore, for any $\mathrm{K}$-module A, the cohomology groups $H^n(\mathrm{K},A)$ can be computed as those of the cochain complex ${\mathrm{Hom}}_{\mathrm{K}}(Q_{•}\left(\mathrm{K}\right),A)$. As the isomorphisms (10) provide an isomorphism of cochain complexes ${\mathrm{Hom}}_{\mathrm{K}}(Q_{•}\left(\mathrm{K}\right),A)\cong C^{•}(\mathrm{K},A)$, the result follows. □

We will use later the following (also well-known) consequence.

Proposition 3.

Assume $\mathrm{K}$ has an initial object ∅. Then, for any $\mathrm{K}$-module A,

$$H^n(\mathrm{K},A)=\left\{\begin{array}{ccc}0& if\hfill & n>0,\hfill \\ A(\varnothing )& if\hfill & n=0.\hfill \end{array}\right.$$

(18)

Proof. 

Let ${\varnothing }_U:\varnothing \to U$ denote the arrow from ∅ to an object U of $\mathrm{K}$. For any $\mathrm{K}$-module A, the augmented cochain complex

$$0\to A(\varnothing )\stackrel{ϵ}{\to }{C}^0(\mathrm{K},A)\stackrel{\partial }{\to }{C}^1(\mathrm{K},A)\stackrel{\partial }{\to }{C}^2(\mathrm{K},A)\to \cdots ,$$

(19)

where the coaugmentation is defined by $ϵ\left(a\right)\left(U\right)=A\left({\varnothing }_U\right)\left(a\right)$, has a contracting homotopy $\mathsf{\Phi }$, which is defined by ${\mathsf{\Phi }}_{-1}\left(\phi \right)=\phi (\varnothing )$ and, for $p\ge 0$, ${\mathsf{\Phi }}_p\left(\phi \right)(\beta 0\to \cdots \to \beta p)=\phi (\varnothing \to \beta 0\to \cdots \to \beta p)$. □

3. Coefficients for the Cohomology of Presheaves of Monoids

Let $\mathrm{C}$ be a fixed small category. A presheaf of monoids on $\mathrm{C}$ is a contravariant functor

$$\mathcal{M}:{\mathrm{C}}^{\mathrm{op}}\to \mathbf{Mon}$$

(20)

from $\mathrm{C}$ into the category of monoids. Thus, $\mathcal{M}$ provides a monoid $\mathcal{M}\left(U\right)$ to each object U of $\mathrm{C}$, and a homomorphism

$$\mathcal{M}\left(\sigma \right):\mathcal{M}\left(U\right)\to \mathcal{M}\left(V\right),\mathrm{denoted}\mathrm{by}x\mapsto x^{\sigma },$$

(21)

to each arrow $\sigma :V\to U$ in $\mathrm{C}$. If $\mathcal{M}$ and ${\mathcal{M}}^{\prime }$ are presheaves of monoids on $\mathrm{C}$, a morphism $\mathfrak{f}:\mathcal{M}\to {\mathcal{M}}^{\prime }$ is a natural transformation, so it consists of homomorphisms of monoids $\mathfrak{f}={\mathfrak{f}}_U:\mathcal{M}\left(U\right)\to {\mathcal{M}}^{\prime }\left(U\right)$, one for each object U of $\mathrm{C}$, such that

$$\mathfrak{f}(x^{\sigma })=\mathfrak{f}{(x)}^{\sigma }$$

(22)

for any $\sigma :V\to U$ in $\mathrm{C}$ and $x\in \mathcal{M}\left(U\right)$. This defines the category $\mathrm{Psh}(\mathrm{C},\mathbf{Mon})$ of presheaves of monoids on $\mathrm{C}$.

The Leech category of factorizations of a monoid M, denoted by $\mathrm{D}\left(M\right)$, has objects the elements $x\in M$ and morphisms $(u_0,u_1):x\to y$ pairs of elements $u_0,u_1\in M$ satisfying $u_{0}x{u}_1=y$. Composition of morphisms in $\mathrm{D}\left(M\right)$ is given by the formula $(u_0^{\prime },u_1^{\prime })(u_0,u_1)=(u_0^{\prime }{u}_0,u_1{u}_1^{\prime })$, and the identity of an object x is the morphism $(e,e):x\to x$, where e is the identity of the monoid. The construction $M\mapsto \mathrm{D}\left(M\right)$ defines a functor

$$\mathrm{D}:\mathbf{Mon}\to \mathbf{Cat}$$

(23)

from the category of monoids to the category of small categories, which acts on monoid homomorphisms in the natural way. By composing with $\mathrm{D}$, every presheaf of monoids $\mathcal{M}$ defines a presheaf of categories $\mathrm{D}\mathcal{M}:{\mathrm{C}}^{\mathrm{op}}\to \mathbf{Cat}$. Let

$$\mathrm{D}\left(\mathcal{M}\right)$$

(24)

be the category obtained by applying the Grothendieck construction on $\mathrm{D}\mathcal{M}$. Its objects are then pairs $(U,x)$ where $U\in \mathrm{ObC}$ and $x\in \mathcal{M}\left(U\right)$, and an arrow $(\sigma ,v_0,v_1):(U,x)\to (V,y)$, between two such objects of $\mathrm{D}\left(\mathcal{M}\right)$, consists of an arrow $\sigma :V\to U$ in $\mathrm{C}$ together with a pair of elements $v_0,v_1\in \mathcal{M}\left(V\right)$ such that $v_0{x}^{\sigma }{v}_1=y$. The composition in $\mathrm{D}\left(\mathcal{M}\right)$ of two morphisms $(\sigma ,v_0,v_1):(U,x)\to (V,y)$ and $(\tau ,w_0,w_1):(V,y)\to (W,z)$ is defined in the evident way

$$(\tau ,w_0,w_1)(\sigma ,v_0,v_1)=(\sigma \tau ,w_0{v}_0^{\tau },v_1^{\tau }{w}_1),$$

(25)

and the identities are $(1,e,e):(U,x)\to (U,x)$, where 1 is the identity arrow of U in $\mathrm{C}$ and e is the identity of the monoid $\mathcal{M}\left(U\right)$.

Notation 1.

Let $A:\mathrm{D}\left(\mathcal{M}\right)\to \mathbf{Ab}$ be a $\mathrm{D}\left(\mathcal{M}\right)$-module. For any $U\in \mathrm{ObC}$ and $u,x\in \mathcal{M}\left(U\right)$, the effect of the homomorphism

$$A(1,u,e):A(U,x)\to A(U,ux)isdenotedbya\mapsto ua,$$

(26)

and the effect of the homomorphism

$$A(1,e,u):A(U,x)\to A(U,xu)isdenotedbya\mapsto au.$$

(27)

For any morphism $\sigma :V\to U$ in $\mathrm{C}$ and any $x\in \mathcal{M}\left(U\right)$, the effect of the homomorphism

$$A(\sigma ,e,e):A(U,x)\to A(V,x^{\sigma })isdenotedbya\mapsto a^{\sigma }.$$

(28)

Thus, for any morphism $(\sigma ,v_0,v_1):(U,x)\to (V,y)$ in $\mathrm{D}\left(\mathcal{M}\right)$, the image of an $a\in A(U,x)$ by $A(\sigma ,v_0,v_1):A(U,x)\to A(V,y)$ writes $\left(v_0{a}^{\sigma }\right)v_1=v_0\left(a^{\sigma }{v}_1\right)$, so that we can omit the parenthesis and write

$$A(\sigma ,v_0,v_1)\left(a\right)=v_0{a}^{\sigma }{v}_1.$$

(29)

In these terms, we can say that a $\mathrm{D}\left(\mathcal{M}\right)$-module A consists of the family of abelian groups $A(U,x)$, $U\in \mathrm{ObC}$, $x\in \mathcal{M}\left(U\right)$, together with maps (26), (27) and (28) satisfying the equalities below, whenever they make sense.

$$\left\{\begin{array}{c}u(a+a^{\prime })=ua+u{a}^{\prime },(a+a^{\prime })u=au+a^{\prime }u,{(a+a^{\prime })}^{\sigma }=a^{\sigma }+a^{\prime \sigma },\hfill \\ u^{\prime }\left(ua\right)=\left(u^{\prime }u\right)a,\left(ua\right)u^{\prime }=u\left(a{u}^{\prime }\right),\left(au\right)u^{\prime }=a\left(u{u}^{\prime }\right),ea=a=ae,\hfill \\ {\left(ua{u}^{\prime }\right)}^{\sigma }=u^{\sigma }{a}^{\sigma }{u}^{\prime \sigma },{\left(a^{\sigma }\right)}^{\tau }=a^{\sigma \tau },a^1=a.\hfill \end{array}\right.$$

(30)

Furthermore, a morphism of $\mathrm{D}\left(\mathcal{M}\right)$-modules $F:A\to A^{\prime }$ is a family of homomorphisms $F=F_{(U,x)}:A(U,x)\to A^{\prime }(U,x)$, $U\in \mathrm{ObC}$, $x\in \mathcal{M}\left(U\right)$, such that

$$F\left(ua\right)=uF\left(a\right),F\left(au\right)=F\left(a\right)u,F\left(a^{\sigma }\right)=F{\left(a\right)}^{\sigma }.$$

(31)

The following proposition justifies why the $\mathrm{D}\left(\mathcal{M}\right)$-modules naturally arise as coefficients for the cohomology of a presheaf of monoids on $\mathrm{C}$.

Proposition 4.

There is an equivalence

$$\mathbf{Ab}\left(\mathrm{Psh}(\mathrm{C},\mathbf{Mon})\downarrow {}_{\mathcal{M}}\right)\simeq \mathrm{D}\left(\mathcal{M}\right)\text{-}\mathrm{Mod}$$

(32)

between the category of abelian group objects in the slice category of presheaves of monoids on $\mathrm{C}$ over $\mathcal{M}$ and the category of $\mathrm{D}\left(\mathcal{M}\right)$-modules.

Proof. 

This can be given paralleling the proof of Theorem 6 in [22] and we omit the details here but briefly let us stress that the abelian group object corresponding to a $\mathrm{D}\left(\mathcal{M}\right)$-module A can be written as $\mathcal{E}\to \mathcal{M}$, where

-

for each $U\in \mathrm{ObC}$, $\mathcal{E}\left(U\right)=\left\{\right(x,a)\mid x\in \mathcal{M}(U),a\in A(U,x\left)\right\}$ with multiplication $(x,a)(y,b)=(xy,xb+ay)$,

-

for each arrow $\sigma :V\to U$ in $\mathrm{C}$, the homomorphism ${\left(\right)}^{\sigma }:\mathcal{E}\left(U\right)\to \mathcal{E}\left(V\right)$ is given by ${(x,a)}^{\sigma }=(x^{\sigma },a^{\sigma })$,

-

for any $U\in \mathrm{ObC}$, the homomorphism $\mathcal{E}\left(U\right)\to \mathcal{M}\left(U\right)$ is the projection $(x,a)\mapsto x$,

-

for any object $U\in \mathrm{ObC}$, the internal group operation $\mathcal{E}\left(U\right){\times }_{\mathcal{M}\left(U\right)}\mathcal{E}\left(U\right)\stackrel{+}{\to }\mathcal{E}\left(U\right)$ is defined by $(x,a)+(x,b)=(x,a+b)$.

 □

4. Derivations of Presheaves of Monoids

Let $\mathcal{M}$ be a presheaf of monoids on $\mathrm{C}$. If A is a $\mathrm{D}\left(\mathcal{M}\right)$-module, a derivation of $\mathcal{M}$ in A, $d:\mathcal{M}\to A$, is a function that assigns to each pair $(U,x)$, where $U\in \mathrm{ObC}$ and $x\in \mathcal{M}\left(U\right)$, an element $d(U,x)\in A(U,x)$ satisfying

$$\begin{array}{c}\hfill d(U,xy)=xd(U,y)+d(U,x)y,\mathrm{for}\mathrm{any}\mathrm{object}U\mathrm{of}\mathrm{C}\mathrm{and}x,y\in \mathcal{M}\left(U\right),\end{array}$$

(33)

$$\begin{array}{c}\hfill d{(U,x)}^{\sigma }=d(V,x^{\sigma }),\mathrm{for}\mathrm{any}\mathrm{morphism}\sigma :V\to U\mathrm{of}\mathrm{C}\mathrm{and}x\in \mathcal{M}\left(U\right).\end{array}$$

(34)

Under pointwise addition, the set of all derivations $d:\mathcal{M}\to A$ may be given an abelian group structure. We denote this abelian group by $\mathrm{Der}(\mathcal{M},A)$. Note that for a $\mathrm{D}\left(\mathcal{M}\right)$-module morphism $F:A\to A^{\prime }$ and a derivation $d:\mathcal{M}\to A$ the “composition” $Fd:\mathcal{M}\to A^{\prime }$, $(U,x)\mapsto F\left(d\right(U,x\left)\right)$, again is a derivation. With this

$$\mathrm{Der}(\mathcal{M},-):\mathrm{D}\left(\mathcal{M}\right)\text{-}\mathrm{Mod}\to \mathbf{Ab},$$

(35)

becomes a functor. Next we prove that this functor is representable. Let

$$\mathbb{Z}\mathcal{M}$$

(36)

be the $\mathrm{D}\left(\mathcal{M}\right)$-module which assigns to each object $(U,x)$ of $\mathrm{D}\left(\mathcal{M}\right)$ the abelian group $\mathbb{Z}\mathcal{M}(U,x)$ which is free on the set of pairs $(x_0,x_1)$ of elements $x_0,x_1\in \mathcal{M}\left(U\right)$ such that $x_0{x}_1=x$, and, for each arrow $\sigma :V\to U$ and $v_0,v_1\in \mathcal{M}\left(V\right)$,

$$v_0{(x_0,x_1)}^{\sigma }{v}_1=(v_0{x}_0^{\sigma },x_1^{\sigma }{v}_1).$$

(37)

There is an augmentation morphism over the constant $\mathrm{D}\left(\mathcal{M}\right)$-module $\mathbb{Z}$

$$ϵ:\mathbb{Z}\mathcal{M}\to \mathbb{Z}$$

(38)

which, at each object $(U,x)$ of $\mathrm{D}\left(\mathcal{M}\right)$, is the homomorphism $ϵ:\mathbb{Z}\mathcal{M}(U,x)\to \mathbb{Z}$ given on generators by $ϵ(x_0,x_1)=1$. We call the kernel of $\mu$, denoted by $I\mathcal{M}$, the augmentation ideal of $\mathcal{M}$. Thus, we have the short exact sequence of $\mathrm{D}\left(\mathcal{M}\right)$-modules

$$0\to I\mathcal{M}\to \mathbb{Z}\mathcal{M}\to \mathbb{Z}\to 0.$$

(39)

Notice that each $I\mathcal{M}(U,x)$ is the free abelian group on the set of generators

$$\left\{(x_0,x_1)-(x,e)\mid x_0,x_1\in \mathcal{M}\left(U\right),x_0{x}_1=x,(x_0,x_1)\ne (x,e)\right\},$$

(40)

and for each arrow $\sigma :V\to U$ and $v_0,v_1\in \mathcal{M}\left(V\right)$,

$$\begin{array}{cc}\hfill v_0{\left((x_0,x_1)-(x,e)\right)}^{\sigma }{v}_1& =\left((v_0{x}_0^{\sigma },x_1^{\sigma }{v}_1)-(v_0{x}^{\sigma },v_1)\right)\hfill \\ & =\left((v_0{x}_0^{\sigma },x_1^{\sigma }{v}_1)-(v_0{x}^{\sigma }{v}_1,e)\right)-\left((v_0{x}^{\sigma },v_1)-(v_0{x}^{\sigma }{v}_1,e)\right).\hfill \end{array}$$

(41)

Proposition 5.

Let $\mathcal{M}$ be a presheaf of monoids on $\mathrm{C}$. For any $\mathrm{D}\left(\mathcal{M}\right)$-module A, there is a natural isomorphism

$$\mathrm{Der}(\mathcal{M},A)\cong {\mathrm{Hom}}_{\mathrm{D}\left(\mathcal{M}\right)}(I\mathcal{M},A).$$

(42)

Proof. 

There is a derivation $\delta :\mathcal{M}\to I\mathcal{M}$ given, at each $U\in \mathrm{ObC}$ and $x\in \mathcal{M}\left(U\right)$, by

$$\delta (U,x)=(e,x)-(x,e)$$

(43)

and then a homomorphism ${\mathrm{Hom}}_{\mathrm{D}\left(\mathcal{M}\right)}(I\mathcal{M},A)\to \mathrm{Der}(\mathcal{M},A)$, $F\mapsto F\delta$. In the other direction, if $d:\mathcal{M}\to A$ is any derivation, there is a morphism of $\mathrm{D}\left(\mathcal{M}\right)$-modules $F_d:I\mathcal{M}\to A$ defined by the homomorphisms

$$F_d:I\mathcal{M}(U,x)\to A(U,x)(U\in \mathrm{ObC},x\in \mathcal{M}\left(U\right))$$

(44)

which act on generators by

$$F_d\left((x_0,x_1)-(x,e)\right)=x_{0}d(U,x_1).$$

(45)

So defined, $F_d$ is actually a morphism of $\mathrm{D}\left(\mathcal{M}\right)$-modules. In effect, for any arrow $\sigma :V\to U$ in $\mathrm{C}$, $v_0,v_1\in \mathcal{M}\left(V\right)$, and $x_0,x_1\in \mathcal{M}\left(U\right)$, we have

$$\begin{array}{cc}\hfill F_d\left(v_0{\left((x_0,x_1)-(x_0{x}_1,e)\right)}^{\sigma }{v}_1\right)& \stackrel{\left(41\right)}{=}{v}_0{x}_0^{\sigma }d(V,x_1^{\sigma }{v}_1)-v_0{\left(x_0{x}_1\right)}^{\sigma }d(V,v_1)\hfill \\ & =v_0{x}_0^{\sigma }{x}_1^{\sigma }d(V,v_1)+v_0{x}_0^{\sigma }d(V,x_1^{\sigma })v_1-v_0{x}_0^{\sigma }{x}_1^{\sigma }d(V,v_1)\hfill \\ & =v_0{x}_0^{\sigma }d{(V,x_1)}^{\sigma }{v}_1=v_0{\left(F_d\left((x_0,x_1)-(x,e)\right)\right)}^{\sigma }{v}_1.\hfill \end{array}$$

A quite straightforward verification shows that both maps $F\mapsto F\delta$ and $d\mapsto F_d$ are mutually inverse. For instance, $F_{F\delta }=F$ since, for any $U\in \mathrm{ObC}$ and $x_0,x_1\in \mathcal{M}\left(U\right)$,

$$\begin{array}{cc}\hfill F_{F\delta }\left((x_0,x_1)-(x_0{x}_1,e)\right)& =x_{0}F\delta (U,x_1)=x_{0}F\left((e,x_1)-(x_1,e)\right)=F\left(x_0(e,x_1)-x_0(x_1,e)\right)\hfill \\ & =F\left((x_0,x_1)-(x_0{x}_1,e)\right).\hfill \end{array}$$

 □

5. Cohomologies for Presheaves of Monoids

Let $\mathcal{M}$ be a presheaf of monoids on $\mathrm{C}$. For any $\mathrm{D}\left(\mathcal{M}\right)$-module A and each integer $n\ge 0$, we define the n-th cohomology group of $\mathcal{M}$ with coefficients in A by $H^n(\mathcal{M},A)=H^n(\mathrm{D}\left(\mathcal{M}\right),A)$, that is,

$$H^n(\mathcal{M},A)={\mathrm{Ext}}_{\mathrm{D}\left(\mathcal{M}\right)}^n(\mathbb{Z},A).$$

(46)

Also, for each $n\ge 1$, we define the n-th simple cohomology group of $\mathcal{M}$ with coefficients in a A by

$$H_s^n(\mathcal{M},A)=R^{n-1}\mathrm{Der}(\mathcal{M},-)\left(A\right),$$

(47)

where $R^{n-1}\mathrm{Der}(\mathcal{M}.-)$ is the $(n-1)$-th right derived functor of the left-exact functor of derivations (35) or, equivalently, by Proposition 5, as

$$H_s^n(\mathcal{M},A)={\mathrm{Ext}}_{\mathrm{D}\left(\mathcal{M}\right)}^{n-1}(I\mathcal{M},A)$$

(48)

(we refer the reader to Section 6, to justify the above terminology of “simple,” which is taken from Gersterhaber and Schack [7]).

Example 1.

Let Γ be a monoid, regarded as a small category with only one object, say ∗, in which the arrows are the elements of Γ and the composition of two of them $\ast \stackrel{x}{\to }\ast \stackrel{y}{\to }\ast$ is given by the monoid multiplication $\ast \stackrel{xy}{\to }\ast$, and the identity is $e:\ast \to \ast$. Then, a presheaf of monoids $\mathcal{M}$ on Γ is the same thing as a monoid enriched with a left Γ-action by endomorphisms, and the corresponding simple cohomology groups $H_s^n(\mathcal{M},A)$ above are just the equivariant cohomology groups of the Γ-monoid $\mathcal{M}$ introduced and studied recently in [23]. When both Γ and $\mathcal{M}$ are groups, the cohomology groups $H_s^n(\mathcal{M},A)$ agree with those $H_{n-1}^n(\mathsf{\Gamma },\mathcal{M};A)$ introduced by Whitehead in [17] on the cohomology of groups with operators, while the cohomology groups $H^n(\mathcal{M},A)$ above agree with the ordinary Eilenberg-Mac Lane cohomology groups $H^n(\mathcal{M}⋊\mathsf{\Gamma },A)$ of the semidirect product group.

Example 2.

If $\mathrm{C}=\ast$, the final category, then a presheaf of monoids $\mathcal{M}$ on $\mathrm{C}$ is simply a monoid and the $H^n(\mathcal{M},A)$ above are just the cohomology groups of the monoid by Leech [3,4]. Furthermore, in this case, $\mathbb{Z}\mathcal{M}$ is a projective $\mathrm{D}\left(\mathcal{M}\right)$-module, as it is free on the inclusion map $e=\left\{e\right\}\to \mathcal{M}=\mathrm{ObD}\left(\mathcal{M}\right)$, whence there are natural isomorphisms

$$H^n(\mathcal{M},A)={\mathrm{Ext}}_{\mathrm{D}\left(\mathcal{M}\right)}^n(\mathbb{Z},A)\cong {\mathrm{Ext}}_{\mathrm{D}\left(\mathcal{M}\right)}^{n-1}(I\mathcal{M},A)=H_s^n(\mathcal{M},A)$$

(49)

for all $n\ge 2$.

But notice that in general the cohomology groups $H^n$ are different of the simple ones $H_s^n$, as the following example shows.

Example 3.

let e be the constant presheaf on a small category $\mathrm{C}$ defined by the trivial monoid. Then, $\mathrm{D}\left(e\right)\cong {\mathrm{C}}^{\mathrm{op}}$ and, for any ${\mathrm{C}}^{\mathrm{op}}$-module A, we have $H^n(e,A)=H^n({\mathrm{C}}^{\mathrm{op}},A)$, whereas $H_s^n(e,A)=0$ as $\mathrm{Der}(e,-)=0$. Let, for instance, $\mathrm{C}=C_k$ be the finite cyclic group of order k (regarded as a category with only one object). Then $\mathrm{D}\left(e\right)=C_k$ and, for the trivial $C_k$-module $\mathbb{Z}$, we have $H^2(e,\mathbb{Z})=H^2(C_k,\mathbb{Z})=\mathbb{Z}/k\mathbb{Z}$, while $H_s^2(e,\mathbb{Z})=0$.

The following property is naturally expected for the simple cohomology groups $H_s^n(\mathcal{M},A)$ but it is not satisfied by the cohomology groups $H^n(\mathcal{M},A)$. Recall that the free presheaf of monoids on a set S endowed with a map $\pi :S\to \mathrm{ObC}$ is defined to be

$${\displaystyle \coprod _{s\in S}}F{\mathrm{Hom}}_{\mathrm{C}}(-,\pi s):{\mathrm{C}}^{\mathrm{op}}\to \mathbf{Mon},$$

(50)

where, for any set X, $FX$ denotes the free monoid on X. For instance, the free presheaf on the empty set is e, the constant presheaf on $\mathrm{C}$ defined by the trivial monoid e. As we showed in Example 3 above, the cohomology groups of the free presheaf e are the same as the cohomology groups of the category ${\mathrm{C}}^{\mathrm{op}}$ which, obviously, do not vanish in general. However, for the simple cohomology groups, we have the following.

Proposition 6.

If $\mathcal{M}$ is a free presheaf of monoids on $\mathrm{C}$, then $H_s^n(\mathcal{M},-)=0$ for $n\ge 2$.

Proof. 

If $\mathcal{M}$ is free on $(S,\pi )$, for every $\mathrm{D}\left(\mathcal{M}\right)$-module A, we have an isomorphism

$$\mathrm{Der}(\mathcal{M},A)\cong {\displaystyle \prod _{s\in S}}A\left(\pi s,(s,1_{\pi s})\right),d\mapsto {\left(d\left(\pi s,(s,1_{\pi s})\right)\right)}_{s\in S}.$$

(51)

From this observation, it is easy to see that the functor $\mathrm{Der}(\mathcal{M},-):\mathrm{D}\left(\mathcal{M}\right)$-Mod → Ab is right exact, whence its right derived functors $H_s^{n+1}(\mathcal{M},-)=R^n\mathrm{Der}(\mathcal{M},-)$ vanish for all $n\ge 1$. □

If $\mathcal{M}$ is a presheaf of monoids on $\mathrm{C}$, for any $\mathrm{D}\left(\mathcal{M}\right)$-module A let

$$A\left(e\right):{\mathrm{C}}^{\mathrm{op}}\to \mathbf{Ab}$$

(52)

denote the presheaf of abelian groups on $\mathrm{C}$ (= ${\mathrm{C}}^{\mathrm{op}}$-module) which assigns to any $U\in \mathrm{ObC}$ the abelian group $A(U,e)$, and to any morphism $\sigma :V\to U$ of $\mathrm{C}$ the homomorphism (28)

$$A(U,e)\to A(V,e),a\mapsto a^{\sigma }.$$

(53)

As we shall establish below, in Theorem 1, there is a natural long exact sequence linking the cohomology groups $H_s^n(\mathcal{M},A)$, $H^n(\mathcal{M},A)$, and $H^n({\mathrm{C}}^{\mathrm{op}},A)$. The proof is based on the following auxiliary result. Recall the $\mathrm{D}\left(\mathcal{M}\right)$-module $\mathbb{Z}\mathcal{M}$ constructed in Section 4.

Lemma 1.

Let $\mathcal{M}$ be a presheaf of monoids on $\mathrm{C}$. For any $\mathrm{D}\left(\mathcal{M}\right)$-module A, there are natural isomorphisms

$${\mathrm{Ext}}_{\mathrm{D}\left(\mathcal{M}\right)}^n(\mathbb{Z}\mathcal{M},A)\cong H^n({\mathrm{C}}^{\mathrm{op}},A\left(e\right))(n\ge 0).$$

(54)

Proof. 

Below, we represent the p-simplices $\beta$ of $\mathbf{N}{\mathrm{C}}^{\mathrm{op}}$ as sequences $\beta =(\beta 0\stackrel{{\beta }_1}{\leftarrow }\cdots \stackrel{{\beta }_p}{\leftarrow }\beta p)$ of p composable arrows in $\mathrm{C}$.

For each integer $p\ge 0$, let the set ${\mathbf{N}}_p{\mathrm{C}}^{\mathrm{op}}$ of p-simplices of the nerve of the category ${\mathrm{C}}^{\mathrm{op}}$ be endowed with the map $\pi :{\mathbf{N}}_p\left({\mathrm{C}}^{\mathrm{op}}\right)\to \mathrm{ObD}\left(\mathcal{M}\right)$ given by $\pi \left(\beta \right)=(\beta p,e)$, and let $Q_p$ denote the free $\mathrm{D}\left(\mathcal{M}\right)$-module on $({\mathbf{N}}_p\left({\mathrm{C}}^{\mathrm{op}}\right),\pi )$. Then, for each $(U,x)\in \mathrm{ObD}\left(\mathcal{M}\right)$, $Q_p(U,x)$ is the free abelian group with generators the triples $(\beta ;x_0,x_1)$ where $\beta \in {\mathbf{N}}_{p+1}{\mathrm{C}}^{\mathrm{op}}$ and $x_0,x_1\in \mathcal{M}\left(U\right)$ satisfy that $\beta (p+1)=U$ and $x_0{x}_1=x$. If $(\sigma ,v_0,v_1):(U,x)\to (V,y)$ is an arrow in $\mathrm{D}\left(\mathcal{M}\right)$, the induced homomorphism $Q_p(U,x)\to Q_p(V,y)$ acts on generators by (recall notation (29))

$$v_0{(\beta ;x_0,x_1)}^{\sigma }{v}_1=({\beta }_1,\dots ,{\beta }_p,{\beta }_{p+1}\sigma ;v_0{x}_0^{\sigma },x_1^{\sigma }{v}_1).$$

(55)

These $Q_p$ form an augmented complex of $\mathrm{D}\left(\mathcal{M}\right)$-modules

$$Q_{•}\to \mathbb{Z}\mathcal{M}:\cdots \to Q_2\stackrel{\partial }{\to }{Q}_1\stackrel{\partial }{\to }{Q}_0\stackrel{\mu }{\to }\mathbb{Z}\mathcal{M},$$

(56)

whose differential operators, at an object $(U,x)$ of $\mathrm{D}\left(\mathcal{M}\right)$, $\partial :Q_p(U,x)\to Q_{p-1}(U,x)$, are defined on generators by $\partial (\beta ;x_0,x_1)={\sum }_{i=0}^p{(-1)}^i(d_i\beta ;x_0,x_1)$, and the augmentation $\mu :Q_0(U,x)\to \mathbb{Z}\mathcal{M}(U,x)$ by $\mu (\beta ;x_0,x_1)=(x_0,x_1)$.

Every $Q_p$ is free, and therefore projective. Furthermore, $Q_{•}\to \mathbb{Z}\mathcal{M}\to 0$ is exact owing to, at any object $(U,x)$ of $\mathrm{D}\left(\mathcal{M}\right)$, the augmented chain complex $Q_{•}(U,x)\to \mathbb{Z}\mathcal{M}(U,x)$ has a contracting homotopy $\mathsf{\Phi }$, which is given by the homomorphisms defined on generators by ${\mathsf{\Phi }}_{-1}(x_0,x_1)=(1_U,x_0,x_1)$ and, for $p\ge 0$, ${\mathsf{\Phi }}_p({\beta }_1,\dots ,{\beta }_{p+1};x_0,x_1)=({\beta }_1,\dots ,{\beta }_{p+1},1_U;x_0,x_1)$. It follows that, for any $\mathrm{D}\left(\mathcal{M}\right)$-module A, there are natural isomorphisms ${\mathrm{Ext}}_{\mathrm{D}\left(\mathcal{M}\right)}^n(\mathbb{Z}\mathcal{M},A)\cong H^n{\mathrm{Hom}}_{\mathrm{D}\left(\mathcal{M}\right)}(Q_{•},A)$. Now, we have the isomorphisms of abelian groups

$${\mathrm{Hom}}_{\mathrm{D}\left(\mathcal{M}\right)}(Q_p,A)\stackrel{\left(10\right)}{\cong }{\displaystyle \prod _{\beta \in {\mathbf{N}}_p{\mathrm{C}}^{\mathrm{op}}}}A(\beta p,e)=C^p({\mathrm{C}}^{\mathrm{op}},A\left(e\right))$$

(57)

which provide an isomorphism ${\mathrm{Hom}}_{\mathrm{D}\left(\mathcal{M}\right)}(Q_{•},A)\cong C^{•}({\mathrm{C}}^{\mathrm{op}},A\left(e\right))$, whence the result follows from Proposition 2. □

Theorem 1

(The linking long exact sequences). Let $\mathcal{M}$ be a presheaf of monoids on $\mathrm{C}$. For any $\mathrm{D}\left(\mathcal{M}\right)$-module A, there is a natural long exact sequence

$$\begin{array}{c}0\to H^0(\mathcal{M},A)\to H^0({\mathrm{C}}^{\mathrm{op}},A\left(e\right))\to H_s^1(\mathcal{M},A)\to H^1(\mathcal{M},A)\to H^1({\mathrm{C}}^{\mathrm{op}},A\left(e\right))\to \cdots \hfill \\ \cdots \to H^n(\mathcal{M},A)\to H^n({\mathrm{C}}^{\mathrm{op}},A\left(e\right))\to H_s^{n+1}(\mathcal{M},A)\to H^{n+1}(\mathcal{M},A)\to \cdots \hfill \end{array}$$

Proof. 

The short exact sequence of $\mathrm{D}\left(\mathcal{M}\right)$-modules $I\mathcal{M}\hookrightarrow \mathbb{Z}\mathcal{M}\twoheadrightarrow \mathbb{Z}$, see (39), induces the long exact sequence

$$\cdots \to {\mathrm{Ext}}_{\mathrm{D}\left(\mathcal{M}\right)}^n(\mathbb{Z},A)\to {\mathrm{Ext}}_{\mathrm{D}\left(\mathcal{M}\right)}^n(\mathbb{Z}\mathcal{M},A)\to {\mathrm{Ext}}_{\mathrm{D}\left(\mathcal{M}\right)}^n(I\mathcal{M},A)\to {\mathrm{Ext}}_{\mathrm{D}\left(\mathcal{M}\right)}^{n+1}(\mathbb{Z},A)\to \cdots$$

(58)

Since ${\mathrm{Ext}}_{\mathrm{D}\left(\mathcal{M}\right)}^n(\mathbb{Z},A)=H^n(\mathcal{M},A)$, by (46), ${\mathrm{Ext}}_{\mathrm{D}\left(\mathcal{M}\right)}^n(\mathbb{Z}\mathcal{M},A)\cong H^n({\mathrm{C}}^{\mathrm{op}},A\left(e\right))$, by Lemma 1, and ${\mathrm{Ext}}_{\mathrm{D}\left(\mathcal{M}\right)}^n(I\mathcal{M},A)=H_s^{n+1}(\mathcal{M},A)$, by (48), the claimed exact sequence follows. □

Corollary 1.

If $\mathrm{C}$ has a final object, then for any a presheaf of monoids $\mathcal{M}$ on $\mathrm{C}$ and any $\mathrm{D}\left(\mathcal{M}\right)$-module A there are natural isomorphisms

$$H_s^n(\mathcal{M},A)\cong H^n(\mathcal{M},A)(n\ge 2).$$

(59)

Proof. 

This follows from the long exact sequence in Theorem 1 and Proposition 3. □

6. Cochains, Cocycles, Coboundaries

In this section we provide suitable cochain complexes for computing the cohomologies of presheaves of monoids.

Below we regard each monoid $\mathsf{\Gamma }$ as a small category with only one object, as in Example 1. Then, the simplicial set $\mathbf{N}\mathsf{\Gamma }$ is just its classifying space, that is, the reduced simplicial set whose p-simplices $\tau =(\ast \stackrel{{\tau }_1}{\to }\cdots \stackrel{{\tau }_p}{\to }\ast )=({\tau }_1,\dots ,{\tau }_p)$ are the elements of ${\mathsf{\Gamma }}^p$.

Let $\mathcal{M}$ be a presheaf of monoids on $\mathrm{C}$. By composing with the nerve functor, it gives rise to a presheaf of simplicial sets $\mathbf{N}\mathcal{M}:{\mathrm{C}}^{\mathrm{op}}\to \mathbf{SSet}$. Let $\mathsf{\Psi }\left(\mathcal{M}\right)$ denote the simplicial replacement construction by Bousfield-Kan [14] on $\mathbf{N}\mathcal{M}$; that is, the bisimplicial set whose set of $(p,q)$-bisimplices is

$${\mathsf{\Psi }}_{p,q}\left(\mathcal{M}\right)={\displaystyle \coprod _{\beta \in {\mathbf{N}}_p{\mathrm{C}}^{\mathrm{op}}}}{\mathbf{N}}_q\mathcal{M}\left(\beta 0\right).$$

(60)

Here, we represent the p-simplices $\beta$ of $\mathbf{N}{\mathrm{C}}^{\mathrm{op}}$ as sequences

$$\beta =(\beta 0\stackrel{{\beta }_1}{\leftarrow }\cdots \stackrel{{\beta }_p}{\leftarrow }\beta p)$$

of p composable arrows in $\mathrm{C}$ (objects $\beta 0$ of $\mathrm{C}$ if $p=0$). The vertical face and degeneracy operators are defined by those of the simplicial sets $\mathbf{N}\mathcal{M}\left(\beta 0\right)$, and the horizontal face operators by those of $\mathbf{N}{\mathrm{C}}^{\mathrm{op}}$, except that $d_0^h:{\mathsf{\Psi }}_{p,q}\left(\mathcal{M}\right)\to {\mathsf{\Psi }}_{p-1,q}\left(\mathcal{M}\right)$ is defined by $d_0^h(\beta ;\tau )=(d_0\beta ,{\tau }^{{\beta }_1})$.

There is a canonical functor ${\Delta }^2\mathsf{\Psi }\left(\mathcal{M}\right)\to \mathrm{D}\left(\mathcal{M}\right)$, from the category of bisimplices of $\mathsf{\Psi }\left(\mathcal{M}\right)$ to $\mathrm{D}\left(\mathcal{M}\right)$, $(\beta ,\tau )\mapsto (\beta p,{({\tau }_1\cdots {\tau }_q)}^{{\beta }_1\cdots {\beta }_p})$. Then, by composition with it, every $\mathrm{D}\left(\mathcal{M}\right)$-module A defines a system of coefficients on $\mathsf{\Psi }\left(\mathcal{M}\right)$ and gives rise to a bicosimplicial abelian group, denoted

$$C^{•,•}(\mathcal{M},A),$$

(61)

in which each $C^{p,q}(\mathcal{M},A)$ is the abelian group of all functions $\phi$ that assign to each $(p,q)$-bisimplex $(\beta ,\tau )\in {\mathsf{\Psi }}_{p,q}\left(\mathcal{M}\right)$ an element

$$\phi (\beta ,\tau )\in A(\beta p,{({\tau }_1\cdots {\tau }_q)}^{{\beta }_1\cdots {\beta }_p})(\in A(\beta p,e)\mathrm{if}q=0).$$

(62)

The horizontal and vertical coface homomorphisms

$$C^{p-1,q}(\mathcal{M},A)\stackrel{d_h^i}{\to }{C}^{p,q}(\mathcal{M},A)\stackrel{d_v^j}{\leftarrow }{C}^{p,q-1}(\mathcal{M},A)$$

(63)

are respectively given by

$$\begin{array}{cc}\hfill d_h^i\phi (\beta ,\tau )& =\left\{\begin{array}{ccc}\phi (d_0\beta ,{\tau }^{{\beta }_1})\hfill & \mathrm{if}\hfill & i=0,\hfill \\ \phi (d_i\beta ,\tau )\hfill & \mathrm{if}\hfill & 0<i<p,\hfill \\ \phi {(d_p\beta ,\tau )}^{{\beta }_p}\hfill & \mathrm{if}\hfill & i=p,\hfill \end{array}\right.\hfill \end{array}$$

(64)

$$\begin{array}{cc}\hfill d_v^j\phi (\beta ,\tau )& =\left\{\begin{array}{ccc}{\tau }_1^{{\beta }_1\cdots {\beta }_p}\phi (\beta ,d_0\tau )\hfill & \mathrm{if}\hfill & j=0,\hfill \\ \phi (\beta ,d_j\tau )\hfill & \mathrm{if}\hfill & 0<j<q,\hfill \\ \phi (\beta ,d_q\tau ){\tau }_q^{{\beta }_1\cdots {\beta }_p}\hfill & \mathrm{if}\hfill & j=q.\hfill \end{array}\right.\hfill \end{array}$$

(65)

Let also write $C^{•,•}(\mathcal{M},A)$ for its alternating faces sum cochain bicomplex, whose horizontal and vertical coboundaries are

$$\begin{array}{cc}\hfill {\partial }_h& ={\displaystyle \sum _{i=0}^p}{(-1)}^i{d}_h^i:C^{p-1,q}(\mathcal{M},A)\to C^{p,q}(\mathcal{M},A),\hfill \end{array}$$

(66)

$$\begin{array}{cc}\hfill {\partial }_v& ={(-1)}^p{\displaystyle \sum _{j=0}^q}{(-1)}^j{d}_v^j:C^{p,q-1}(\mathcal{M},A)\to C^{p,q}(\mathcal{M},A).\hfill \end{array}$$

(67)

Definition 1.

Let $\mathcal{M}$ be a presheaf of monoids on $\mathrm{C}$. We define the complex of cochains of $\mathcal{M}$ with coefficients in a $\mathrm{D}\left(\mathcal{M}\right)$-module A as $C^{•}(\mathcal{M},A)=\mathrm{Tot}{C}^{•,•}(\mathcal{M},A)$, the total cochain complex of the bicomplex $C^{•,•}(\mathcal{M},A)$. That is, $C^{•}(\mathcal{M},A)$ is given by

$$C^n(\mathcal{M},A)={\displaystyle \underset{p+q=n}{⨁}}{C}^{p,q}(\mathcal{M},A),\partial ={\partial }_h+{\partial }_v:C^{n-1}(\mathcal{M},A)\to C^n(\mathcal{M},A).$$

(68)

Notice that the homotopy colimit of $\mathbf{N}\mathcal{M}$ is the simplicial set diagonal of $\mathsf{\Psi }\left(\mathcal{M}\right)$:

$$\mathrm{hocolim}\mathbf{N}\mathcal{M}=\mathrm{diag}\mathsf{\Psi }\left(\mathcal{M}\right).$$

(69)

Then, every $\mathrm{D}\left(\mathcal{M}\right)$-module A defines a coefficient system on $\mathrm{hocolim}\mathbf{N}\mathcal{M}$ and the corresponding cohomology groups are justly calculated as

$$H^n(\mathrm{hocolim}\mathbf{N}\mathcal{M},A)=H^n{C}^{•}(\mathrm{hocolim}\mathbf{N}\mathcal{M},A),$$

(70)

where $C^{•}(\mathrm{hocolim}\mathbf{N}\mathcal{M},A)$ is the alternating faces sum cochain complex of the diagonal cosimplicial abelian group $\mathrm{diag}{C}^{•,•}(\mathcal{M},A)$; that is,

$$C^n(\mathrm{hocolim}\mathbf{N}\mathcal{M},A)=C^{n,n}(\mathcal{M},A),\partial ={\displaystyle \sum _{i=0}^n}{(-1)}^i{d}_h^i{d}_v^i:C^{n-1,n-1}(\mathcal{M},A)\to C^{n,n}(\mathcal{M},A).$$

(71)

Proposition 7.

Let $\mathcal{M}$ be a presheaf of monoids on $\mathrm{C}$. For any $\mathrm{D}\left(\mathcal{M}\right)$-module A, there are natural isomorphisms

$$H^n{C}^{•}(\mathcal{M},A)\cong H^n(\mathrm{hocolim}\mathbf{N}\mathcal{M},A).$$

(72)

Proof. 

This is a direct application of the generalized Eilenberg-Zilber theorem of Dold-Puppe (see, e.g., Reference [24] (Chapter IV, Theorem 2.4), which shows that both cochain complexes $C^{•}(\mathcal{M},A)$ and $C^{•}(\mathrm{hocolim}\mathbf{N}\mathcal{M},A)$ are cohomology equivalent in a natural way. □

A subcomplex of $C^{•}(\mathcal{M},A)$ plays an important role in our development. Following Gerstenhaber-Schack [7], we establish the following

Definition 2.

Let $\mathcal{M}$ be a presheaf of monoids. If A is a $\mathrm{D}\left(\mathcal{M}\right)$-module, we say that a n-cochain $\phi \in C^n(\mathcal{M},A)$ is simple if $\phi (\beta ,\ast )=0$ for every $\beta \in {\mathbf{N}}_n{\mathrm{C}}^{\mathrm{op}}$, that is, if $\phi {\mid }_{{}_{{\mathsf{\Psi }}_{n,0}}}=0$. We denote the subcomplex of simple cochains of $C^{•}(\mathcal{M},A)$ by

$$C_s^{•}(\mathcal{M},A),$$

(73)

so that $C_s^0(\mathcal{M},A)=0$ and, for $n\ge 1$,

$$C_s^n(\mathcal{M},A)={\displaystyle \underset{\begin{array}{c}p+q=n\hfill \\ q\ge 1\hfill \end{array}}{⨁}}{C}^{p,q}(\mathcal{M},A)={\displaystyle \underset{p+q=n-1}{⨁}}{C}^{p,q+1}(\mathcal{M},A).$$

(74)

Theorem 2.

Let $\mathcal{M}$ be a presheaf of monoids on $\mathrm{C}$. For any $\mathrm{D}\left(\mathcal{M}\right)$-module A there are natural isomorphisms

$$\begin{array}{c}{H}_s^n(\mathcal{M},A)\cong H^n{C}_s^{•}(\mathcal{M},A),n\ge 1,\hfill \end{array}$$

(75)

$$\begin{array}{c}{H}^n(\mathcal{M},A)\cong H^n{C}^{•}(\mathcal{M},A),n\ge 0.\hfill \end{array}$$

(76)

Proof. 

To start, we construct a bisimplicial $\mathrm{D}\left(\mathcal{M}\right)$-module $Q_{•,•}$ and a simplicial $\mathrm{D}\left(\mathcal{M}\right)$-module $B_{•}$, as follows.

In $Q_{•,•}$, each $Q_{p,q}$ is the free $\mathrm{D}\left(\mathcal{M}\right)$-module on the set ${\mathsf{\Psi }}_{p,q}\left(\mathcal{M}\right)$, endowed with the map $\pi :{\mathsf{\Psi }}_{p,q}\left(\mathcal{M}\right)\to \mathrm{ObD}\left(\mathcal{M}\right)$ given by

$$\pi (\beta ,\tau )=(\beta p,{({\tau }_1\cdots {\tau }_q)}^{{\beta }_1\cdots {\beta }_p})((\beta p,e)\mathrm{if}q=0).$$

(77)

Thus, for each object $(U,x)$ of $\mathrm{D}\left(\mathcal{M}\right)$, $Q_{p,q}(U,x)$ is the free abelian group with generators the quadruplets $(\beta ;\tau ;u_0,u_1)$ with $\beta \in {\mathbf{N}}_{p+1}{C}^{\mathrm{op}}$, $\tau \in {\mathbf{N}}_q\mathcal{M}\left(\beta 0\right)$, and $u_0,u_1\in \mathcal{M}\left(U\right)$, such that $\beta (p+1)=U$ and

$$u_0{({\tau }_1\cdots {\tau }_q)}^{{\beta }_1\cdots {\beta }_{p+1}}{u}_1=x.$$

(78)

If $(\alpha ,v_0,v_1):(U,x)\to (V,y)$ is an arrow in $\mathrm{D}\left(\mathcal{M}\right)$, the induced homomorphism $Q_{p,q}(U,x)\to Q_{p,q}(V,y)$ acts on generators by (recall notation (29))

$$v_0{(\beta ;\tau ;u_0,u_1)}^{\alpha }{v}_1=({\beta }_1,\dots ,{\beta }_p,{\beta }_{p+1}\alpha ;\tau ;v_0{u}_0^{\alpha },u_1^{\alpha }{v}_1).$$

(79)

The horizontal and vertical face morphisms at an object $(U,x)$ of $\mathrm{D}\left(\mathcal{M}\right)$,

$$Q_{p-1,q}\left(U\right)\stackrel{d_i^h}{\leftarrow }{Q}_{p,q}\left(U\right)\stackrel{d_j^v}{\to }{Q}_{p,q-1}\left(U\right),$$

(80)

are defined on generators by

$$\begin{array}{cc}{d}_i^h(\beta ;\tau ;u_0,u_1)=\hfill & \left\{\begin{array}{ccc}(d_0\beta ,{\tau }^{{\beta }_1};u_0,u_1)\hfill & \mathrm{if}\hfill & i=0,\hfill \\ (d_i\beta ,\tau ;u_0,u_1)\hfill & \mathrm{if}\hfill & 0<i\le p,\hfill \end{array}\right.\hfill \\ d_j^v(\beta ;\tau ;u_0,u_1)=\hfill & \left\{\begin{array}{ccc}(\beta ;d_0\tau ;u_0{\tau }_1^{{\beta }_1\cdots {\beta }_{p+1}},u_1)\hfill & \mathrm{if}\hfill & j=0,\hfill \\ (\beta ;d_j\tau ;u_0,u_1)\hfill & \mathrm{if}\hfill & 0<j<q,\hfill \\ (\beta ;d_q\tau ;u_0,{\tau }_q^{{\beta }_1\dots {\beta }_{p+1}}{u}_1)\hfill & \mathrm{if}\hfill & j=q.\hfill \end{array}\right.\hfill \end{array}$$

(81)

In $B_{•}$, each $\mathrm{D}\left(\mathcal{M}\right)$-module $B_q$ assigns to an object $(U,x)$ of $\mathrm{D}\left(\mathcal{M}\right)$ the free abelian group $B_q(U,x)$ whose generators are those $\tau \in {\mathbf{N}}_{q+2}\mathcal{M}\left(U\right)$ such that ${\tau }_1\cdots {\tau }_{q+2}=x$. If $(\alpha ,v_0,v_1):(U,x)\to (V,y)$ is an arrow in $\mathrm{D}\left(\mathcal{M}\right)$, then

$$v_0{\tau }^{\alpha }{v}_1=(v_0{\tau }_1^{\alpha },{\tau }_2^{\alpha },\dots ,{\tau }_{q+1}^{\alpha },{\tau }_{q+2}^{\alpha }{v}_1).$$

(82)

At any $(U,x)$, the face homomorphisms $d_j:B_q(U,x)\to B_{q-1}(U,x)$, $0\le j\le q$, are induced by the face maps $d_{j+1}:{\mathbf{N}}_{q+2}\mathcal{M}\left(U\right)\to {\mathbf{N}}_{q+1}\mathcal{M}\left(U\right)$; that is, on generators,

$$d_j\left(\tau \right)=({\tau }_1,\dots ,{\tau }_{j+1}{\tau }_{j+2},\dots ,{\tau }_{q+2}).$$

(83)

Let us point out that, regarding $B_{•}$ as a constant in the horizontal direction bisimplicial $\mathrm{D}\left(\mathcal{M}\right)$-module, a bisimplicial augmentation

$$\mu :Q_{•,•}\to B_{•}$$

(84)

is determined by the morphisms $\mu :Q_{0,q}\to B_q$ which, at each object $(U,x)$ of $\mathrm{D}\left(\mathcal{M}\right)$, consist of the homomorphisms $\mu :Q_{0,q}(U,x)\to B_q(U,x)$ defined on generators by

$$\mu (\beta ;\tau ;u_0,u_1)=(u_0,{\tau }_1^{{\beta }_1},\dots ,{\tau }_q^{{\beta }_1},u_1).$$

(85)

Now, let also write $Q_{•,•}$ for its associated alternating faces sum chain bicomplex, in which the horizontal and vertical boundaries are

$${\partial }_{p,q}^h={\displaystyle \sum _{i=0}^p}{(-1)}^i{d}_i^h:Q_{p,q}\to Q_{p-1,q},{\partial }_{p,q}^v={(-1)}^p{\displaystyle \sum _{j=0}^q}{(-1)}^j{d}_j^v:Q_{p,q}\to Q_{p,q-1},$$

(86)

and let $\mathrm{Tot}{Q}_{•,•}$ be its total complex. Thus,

$${\mathrm{Tot}}_n{Q}_{•,•}={\displaystyle \underset{p+q=n}{⨁}}{Q}_{p,q},\partial ={\partial }^h+{\partial }^v:{\mathrm{Tot}}_n{Q}_{•,•}\to {\mathrm{Tot}}_{n-1}{Q}_{•,•}.$$

(87)

Hence, if we denote also by $B_{•}$ to its associated alternating faces sum chain complex, in which the boundaries are ${\partial }_q={\sum }_{j=0}^q{(-1)}^j{d}_j:B_q\to B_{q-1}$, we have an augmented morphism of chain bicomplexes of $\mathrm{D}\left(\mathcal{M}\right)$-modules $\mu :Q_{•,•}\to B_{•}$, were $B_{•}$ is here view as bicomplex concentrated in degree zero in the horizontal direction, which, we claim, induces a homology equivalence between the associated total complexes $\mathrm{Tot}{Q}_{•,•}\to \mathrm{Tot}{B}_{•}=B_{•}$, and therefore natural isomorphisms

$$H_n\mathrm{Tot}{Q}_{•,•}\cong H_n{B}_{•},n\ge 0.$$

(88)

In effect, it suffices to prove that, for any $q\ge 0$, the augmented chain complex of $\mathrm{D}\left(\mathcal{M}\right)$-modules $Q_{•,q}\stackrel{\mu }{\to }{B}_q\to 0$ is exact. But this holds since, at any object $(U,x)$ of $\mathrm{D}\left(\mathcal{M}\right)$, the augmented chain complex of abelian groups

$$\cdots \stackrel{{\partial }^h}{\to }{Q}_{2,q}(U,x)\stackrel{{\partial }^h}{\to }{Q}_{1,q}(U,x)\stackrel{{\partial }^h}{\to }{Q}_{0,q}(U,x)\stackrel{\mu }{\to }{B}_q(U,x)\to 0$$

(89)

admits a contraction Φ, which is given by the homomorphisms defined on generators by

$$\left\{\begin{array}{c}{\mathsf{\Phi }}_{-1}\left(\tau \right)=(1_U;{\tau }_2,\dots ,{\tau }_{q+1};{\tau }_1,{\tau }_{q+2}),\hfill \\ {\mathsf{\Phi }}_p(\beta ;\tau ;u_0,u_1)={(-1)}^{p+1}({\beta }_1,\dots ,{\beta }_{p+1},1_U;\tau ;u_0,u_1),p\ge 0.\hfill \end{array}\right.$$

(90)

Let us now compute the homology of the complex $B_{•}$: There is an augmentation over the constant $\mathrm{D}\left(\mathcal{M}\right)$-module $\mathbb{Z}$, $ϵ:B_{•}\to \mathbb{Z}$, given by the morphism of $\mathrm{D}\left(\mathcal{M}\right)$-modules $ϵ:B_0\to \mathbb{Z}$ which, at any object $(U,x)$ of $\mathrm{D}\left(\mathcal{M}\right)$, consists of the homomorphism $ϵ:B_0(U,x)\to \mathbb{Z}$ defined on generators by $ϵ\left(\tau \right)=1$. The resulting augmented complex $B_{•}\to \mathbb{Z}\to 0$ is exact due to, for any object $(U,x)\in \mathrm{D}\left(\mathcal{M}\right)$, the augmented chain complex

$$\cdots \stackrel{\partial }{\to }{B}_2(U,x)\stackrel{\partial }{\to }{B}_1(U,x)\stackrel{\partial }{\to }{B}_0(U,x)\stackrel{ϵ}{\to }\mathbb{Z}\to 0$$

(91)

has a contracting homotopy defined by the homomorphisms ${\mathsf{\Psi }}_q$, which act on generators by

$$\left\{\begin{array}{c}{\mathsf{\Psi }}_{-1}\left(1\right)=(x,e),\hfill \\ {\mathsf{\Psi }}_q\left(\tau \right)=({\tau }_1,\dots ,{\tau }_{q+2},e),q\ge 0.\hfill \end{array}\right.$$

(92)

Therefore, $H_0{B}_{•}\cong \mathbb{Z}$ and $H_q{B}_{•}=0$ for all $q\ge 1$.

It follows that $H_0\mathrm{Tot}{Q}_{•,•}\cong \mathbb{Z}$ and $H_n\mathrm{Tot}{Q}_{•,•}=0$ for all $n\ge 1$. Since, at every degree $n\ge 0$, ${\mathrm{Tot}}_n{Q}_{•,•}={⨁}_{p+q=n}{Q}_{p,q}$ is a projective $\mathrm{D}\left(\mathcal{M}\right)$-module, we conclude that $\mathrm{Tot}{Q}_{•,•}$ is actually a projective resolution of the constant $\mathrm{D}\left(\mathcal{M}\right)$-module $\mathbb{Z}$. Therefore, for any $\mathrm{D}\left(\mathcal{M}\right)$-module A, there are natural isomorphisms

$$H^n(\mathcal{M},A)={\mathrm{Ext}}_{\mathrm{D}\left(\mathcal{M}\right)}^n(\mathbb{Z},A)\cong H^n{\mathrm{Hom}}_{\mathrm{D}\left(\mathcal{M}\right)}\left(\mathrm{Tot}{Q}_{•,•},A\right).$$

(93)

Now, there are isomorphisms

$${\mathrm{Hom}}_{\mathrm{D}\left(\mathcal{M}\right)}(Q_{p,q},A)\stackrel{\left(10\right)}{\cong }{C}^{p,q}(\mathcal{M},A)$$

(94)

which, as a direct and straightforward verification shows, provide a natural isomorphism of cochain complexes ${\mathrm{Hom}}_{\mathrm{D}\left(\mathcal{M}\right)}\left(\mathrm{Tot}{Q}_{•,•},A\right)\cong \mathrm{Tot}{C}^{•,•}(\mathcal{M},A)=C^{•}(\mathcal{M},A)$. Thus, we conclude the claimed isomorphisms (76), namely

$$H^n(\mathcal{M},A)\cong H^n{C}^{•}(\mathcal{M},A).$$

(95)

To show the remaining isomorphisms (75), let ${\widehat{Q}}_{•,•}$ be the chain bicomplex of $\mathrm{D}\left(\mathcal{M}\right)$-modules obtained from $Q_{•,•}$ by taking ${\widehat{Q}}_{p,q}=Q_{p,q+1}$, with coboundaries ${\widehat{\partial }}_{p,q}^h={\partial }_{p,q+1}^h$ and ${\widehat{\partial }}_{p,q}^v={\partial }_{p,q+1}^v$, let also ${\widehat{B}}_{•}$ be the chain complex constructed from $B_{•}$ by taking ${\widehat{B}}_q=B_{q+1}$ and coboundary ${\widehat{\partial }}_q={\partial }_{q+1}$, and let $\widehat{\mu }:{\widehat{Q}}_{•,•}\to {\widehat{B}}_{•}$ be the augmentation obtained from $\mu$ by taking ${\widehat{\mu }}_q={\mu }_{q+1}$. Then, as every augmented chain complex $\widehat{\mu }:{\widehat{Q}}_{•,q}\to {\widehat{B}}_q\to 0$ is exact, there are induced natural isomorphisms $H_n\mathrm{Tot}{\widehat{Q}}_{•,•}\cong H_n{\widehat{B}}_{•}$. Now, for $q\ge 1$, we have $H_q({\widehat{B}}_{•})=H_{q+1}\left(B_{•}\right)=0$. To compute $H_0({\widehat{B}}_{•})$, notice that $B_0=\mathbb{Z}\mathcal{M}$ and that the morphism $ϵ:B_0\to \mathbb{Z}$ above is just the augmentation $ϵ:\mathbb{Z}\mathcal{M}\to \mathbb{Z}$ in (38). Then, as $B_{•}\stackrel{ϵ}{\to }\mathbb{Z}\to 0$ is exact,

$$H_0({\widehat{B}}_{•})=\mathrm{Coker}(B_2\stackrel{\partial }{\to }{B}_1)=\mathrm{Ker}(B_0\stackrel{ϵ}{\to }\mathbb{Z})\stackrel{\left(39\right)}{=}I\mathcal{M},$$

(96)

the augmentation ideal of $\mathcal{M}$. It follows that $H_0\mathrm{Tot}{\widehat{Q}}_{•,•}\cong I\mathcal{M}$ and, for $n\ge 1$, $H_n\mathrm{Tot}{\widehat{Q}}_{•,•}=0$, whence we can conclude that $\mathrm{Tot}{\widehat{Q}}_{•,•}$ is a projective resolution of $I\mathcal{M}$. Therefore, for any $\mathrm{D}\left(\mathcal{M}\right)$-module A and $n\ge 1$, there are natural isomorphisms

$$H_s^n(\mathcal{M},A)={\mathrm{Ext}}_{\mathrm{D}\left(\mathcal{M}\right)}^{n-1}(I\mathcal{M},A)\cong H^{n-1}{\mathrm{Hom}}_{\mathrm{D}\left(\mathcal{M}\right)}(\mathrm{Tot}{\widehat{Q}}_{•,•},A).$$

(97)

Finally, as we have the isomorphisms

$$\begin{array}{cc}\hfill {\mathrm{Hom}}_{\mathrm{D}\left(\mathcal{M}\right)}({\mathrm{Tot}}_{n-1}{\widehat{Q}}_{•,•},A)& ={\displaystyle \underset{p+q=n-1}{⨁}}{\mathrm{Hom}}_{\mathrm{D}\left(\mathcal{M}\right)}({\widehat{Q}}_{p,q},A)={\displaystyle \underset{p+q=n-1}{⨁}}{\mathrm{Hom}}_{\mathrm{D}\left(\mathcal{M}\right)}(Q_{p,q+1},A)\hfill \\ & \stackrel{\left(94\right)}{\cong }{\displaystyle \underset{p+q=n-1}{⨁}}{C}^{p,q+1}(\mathcal{M},A)\stackrel{\left(74\right)}{=}{C}_s^n(\mathcal{M},A),\hfill \end{array}$$

which are compatible with the coboundaries (recall that $C_s^0(\mathcal{M},A)=0$), we conclude the claimed isomorphisms $H_s^n(\mathcal{M},A)\cong H^n{C}_s^{•}(\mathcal{M},A)$. □

Corollary 2.

If $\mathrm{C}$ has a final object, for any presheaf of monoids $\mathcal{M}$ on $\mathrm{C}$ and any $\mathrm{D}\left(\mathcal{M}\right)$-module A, there are natural isomorphisms

$$H_s^n(\mathcal{M},A)\cong H^n(\mathrm{hocolim}\mathbf{N}\mathcal{M},A)(n\ge 2).$$

(98)

7. Low Dimensional Simple Cochains, Cocycles and Coboundaries

In the rest of the paper we will only use the simple cohomology groups $H_s^n(\mathcal{M},A)$ for $n\le 3$. Therefore, for future reference we specify below the relevant truncated subcomplex of the complex $C_s^{•}(\mathcal{M},A)$, namely

$$0\to C_s^1(\mathcal{M},A)\stackrel{\partial }{\to }{C}_s^2(\mathcal{M},A)\stackrel{\partial }{\to }{C}_s^3(\mathcal{M},A)\stackrel{\partial }{\to }{C}_s^4(\mathcal{M},A)$$

(99)

where:

⧫

A 1-cochain $f\in C_s^1(\mathcal{M},A)$ is a map assigning an element

$$f(U;x)\in A(U,x),\mathrm{to}\mathrm{every}U\in \mathrm{ObC}\mathrm{and}x\in \mathcal{M}\left(U\right).$$

(100)

⧫

A 2-cochain $g\in C_s^2(\mathcal{M},A)$ is a function assigning elements

$$\left\{\begin{array}{cc}g(U;x,y)\in A(U,xy),\hfill & \mathrm{to}\mathrm{each}U\in \mathrm{ObC}\mathrm{and}x,y\in \mathcal{M}\left(U\right),\hfill \\ g(\alpha ;x)\in A(U_1,x^{\alpha }),\hfill & \mathrm{to}\mathrm{every}\mathrm{arrow}{U}_0\stackrel{\alpha }{\leftarrow }{U}_1\mathrm{of}\mathrm{C}\mathrm{and}x\in \mathcal{M}\left(U_0\right).\hfill \end{array}\right.$$

(101)

⧫

The coboundary $\partial :C_s^1(\mathcal{M},A)\to C_s^2(\mathcal{M},A)$ acts on an 1-cochain f by

$$\begin{array}{c}(\partial f)(U;x,y)=xf(U;y)-f(U;xy)+f(U;x)y,\hfill \end{array}$$

(102)

$$\begin{array}{c}(\partial f)(\alpha ;x)=f(U_1;x^{\alpha })-f{(U_0;x)}^{\alpha }.\hfill \end{array}$$

(103)

⧫

A 3-cochain $h\in C_s^3(\mathcal{M},A)$ is a function assigning elements

$$\left\{\begin{array}{cc}h(U;x,y,z)\in A(U,xyz),\hfill & \mathrm{to}\mathrm{every}U\in \mathrm{ObC}\mathrm{and}x,y,z\in \mathcal{M}\left(U\right),\hfill \\ h(\alpha ;x,y)\in A(U_1,x^{\alpha }{y}^{\alpha }),\hfill & \mathrm{to}\mathrm{every}\mathrm{arrow}{U}_0\stackrel{\alpha }{\leftarrow }{U}_1\mathrm{of}\mathrm{C}\mathrm{and}x,y\in \mathcal{M}\left(U_0\right),\hfill \\ h(\alpha ,\beta ;x)\in A(U_2,x^{\alpha \beta }),\hfill & \mathrm{to}\mathrm{each}\mathrm{arrows}{U}_0\stackrel{\alpha }{\leftarrow }{U}_1\stackrel{\beta }{\leftarrow }{U}_2\mathrm{of}\mathrm{C}\mathrm{and}x\in \mathcal{M}\left(U_0\right).\hfill \end{array}\right.$$

(104)

⧫

The coboundary $\partial :C_s^2(\mathcal{M},A)\to C_s^3(\mathcal{M},A)$ acts on a 2-cochain g by

$$\begin{array}{c}(\partial g)(U;x,y,z)=xg(U;y,z)-g(U;xy,z)+g(U;x,yz)-g(U;x,y)z,\hfill \end{array}$$

(105)

$$\begin{array}{c}(\partial g)(\alpha ;x,y)=g(U_1;x^{\alpha },y^{\alpha })-g{(U_0;x,y)}^{\alpha }-x^{\alpha }g(\alpha ;y)+g(\alpha ;xy)-g(\alpha ;x)y^{\alpha },\hfill \end{array}$$

(106)

$$\begin{array}{c}(\partial g)(\alpha ,\beta ;x)=g(\beta ;x^{\alpha })-g(\alpha \beta ;x)+g{(\alpha ;x)}^{\beta }.\hfill \end{array}$$

(107)

⧫

A 4-cochain $\phi \in C_s^4(\mathcal{M},A)$ is a function assigning elements

$$\left\{\begin{array}{c}\phi (U;x,y,z,t)\in A(U,xyzt),\mathrm{to}\mathrm{each}U\in \mathrm{ObC}\mathrm{and}x,y,z,t\in \mathcal{M}\left(U\right),\hfill \\ \phi (\alpha ;x,y,z)\in A(U_1,x^{\alpha }{y}^{\alpha }{z}^{\alpha }),\mathrm{to}\mathrm{every}\mathrm{arrow}{U}_0\stackrel{\alpha }{\leftarrow }{U}_1\mathrm{of}\mathrm{C}\mathrm{and}x,y,z\in \mathcal{M}\left(U_0\right),\hfill \\ \phi (\alpha ,\beta ;x,y)\in A(U_2,x^{\alpha \beta }{y}^{\alpha \beta }),\mathrm{to}\mathrm{each}\mathrm{arrows}{U}_0\stackrel{\alpha }{\leftarrow }{U}_1\stackrel{\beta }{\leftarrow }{U}_2\mathrm{of}\mathrm{C}\mathrm{and}x,y\in \mathcal{M}\left(U_0\right).\hfill \\ \phi (\alpha ,\beta ,\gamma ;x)\in A(U_3,x^{\alpha \beta \gamma }),\mathrm{to}\mathrm{each}\mathrm{arrows}{U}_0\stackrel{\alpha }{\leftarrow }{U}_1\stackrel{\beta }{\leftarrow }{U}_2\stackrel{\gamma }{\leftarrow }{U}_3\mathrm{of}\mathrm{C}\mathrm{and}x\in \mathcal{M}\left(U_0\right).\hfill \end{array}\right.$$

(108)

⧫

The coboundary $\partial :C_s^3(\mathcal{M},A)\to C_s^4(\mathcal{M},A)$ acts on a 3-cochain h by

$$\begin{array}{cc}\hfill (\partial h)(U;x,y,z,t)=& xh(U;y,z,t)-h(U;xy,z,t)+h(U;x,yz,t)-h(U;x,y,zt)\hfill \\ \hfill & +h(U;x,y,z)t,\hfill \end{array}$$

(109)

$$\begin{array}{cc}\hfill (\partial h)(\alpha ;x,y,z)=& h(U_1;x^{\alpha },y^{\alpha },z^{\alpha })-h{(U_0;x,y,z)}^{\alpha }-x^{\alpha }h(\alpha ;y,z)+h(\alpha ;xy,z)\hfill \\ \hfill & -h(\alpha ;x,yz)+h(\alpha ;x,y)z^{\alpha },\hfill \end{array}$$

(110)

$$\begin{array}{cc}\hfill (\partial h)(\alpha ,\beta ;x,y)=& h(\beta ;x^{\alpha },y^{\alpha })-h(\alpha \beta ;x,y)+h{(\alpha ;x,y)}^{\beta }+x^{\alpha \beta }h(\alpha ,\beta ;y)\hfill \\ \hfill & -h(\alpha ,\beta ;xy)+h(\alpha ,\beta ;x)y^{\alpha \beta },\hfill \end{array}$$

(111)

$$\begin{array}{cc}\hfill (\partial h)(\alpha ,\beta ,\gamma ;x)=h(\beta ,\gamma ;x^{\alpha })& -h(\alpha \beta ,\gamma ;x)+h(\alpha ,\beta \gamma ;x)-h{(\alpha ,\beta ;x)}^{\gamma }.\hfill \end{array}$$

(112)

As usually, we write $Z_s^n(\mathcal{M},A)$ and $B_s^n(\mathcal{M},A)$ for the respective groups of n-cocycles and n-coboundaries of the cochain complex $C_s^{•}(\mathcal{M},A)$, and refer to them as the abelian groups of simple n-cocycles and simple n-coboundaries of the presheaf of monoids $\mathcal{M}$ with coefficients in the $\mathrm{D}\left(\mathcal{M}\right)$-module A, respectively.

A direct comparison shows that simple 1-cocycles are the same as derivations, that is

$$Z_s^1(\mathcal{M},A)=\mathrm{Der}(\mathcal{M},A).$$

(113)

In the next sections we give natural interpretations to simple 2- and 3-cocycles.

8. Extensions of Presheaves of Monoids

If $\mathcal{M}$ is a presheaf of monoids on $\mathrm{C}$, by an extension (or coextension) of $\mathcal{M}$ we shall mean a morphism of presheaves of monoids $\mathfrak{f}:\mathcal{E}\to \mathcal{M}$ which is locally surjective, that is, for any $U\in \mathrm{ObC}$, the homomorphism ${\mathfrak{f}}_U:\mathcal{E}\left(U\right)\to \mathcal{M}\left(U\right)$ is surjective. If A is a $\mathrm{D}\left(\mathcal{M}\right)$-module, an extension $\overline{\mathcal{E}}=(\mathcal{E},\mathfrak{f},+)$ of $\mathcal{M}$ by A is an extension $\mathfrak{f}:\mathcal{E}\to \mathcal{M}$ of $\mathcal{M}$ endowed, for each $U\in \mathrm{ObC}$ and $x\in \mathcal{M}\left(U\right)$, with a simply-transitive action

$$+:A(U,x)\times {\mathfrak{f}}_U^{-1}\left(x\right)\to {\mathfrak{f}}_U^{-1}\left(x\right),(a,w)\mapsto a+w,$$

(114)

of the group $A(U,x)$ on the fibre ${\mathfrak{f}}_U^{-1}\left(x\right)\subseteq \mathcal{E}\left(U\right)$ of ${\mathfrak{f}}_U:\mathcal{E}\left(U\right)\to \mathcal{M}\left(U\right)$ at x, such that the following two conditions hold:

(i)

for any object U of $\mathrm{C}$, $\omega \in {\mathfrak{f}}_U^{-1}\left(x\right)$, ${\omega }^{\prime }\in {\mathfrak{f}}_U^{-1}\left(x^{\prime }\right)$, $a\in A(U,x)$, and $a^{\prime }\in A(U,x^{\prime })$,

$$(a+w)(a^{\prime }+w^{\prime })=a{x}^{\prime }+x{a}^{\prime }+w{w}^{\prime },$$

(115)

(ii)

for any arrow $\sigma :V\to U$ of $\mathrm{C}$, $\omega \in {\mathfrak{f}}_U^{-1}\left(x\right)$, and $a\in A(U,x)$,

$${(a+w)}^{\sigma }=a^{\sigma }+w^{\sigma }.$$

(116)

Two such extensions of $\mathcal{M}$ by A, say $\overline{\mathcal{E}}$ and ${\overline{\mathcal{E}}}^{\prime }$, are equivalent if there is an isomorphism of presheaves of monoids $\mathfrak{g}:\mathcal{E}\cong {\mathcal{E}}^{\prime }$ such that ${\mathfrak{f}}^{\prime }\mathfrak{g}=\mathfrak{f}$ and ${\mathfrak{g}}_U(a+w)=a+{\mathfrak{g}}_U\left(w\right)$, for any $U\in \mathrm{ObC}$, $w\in \mathcal{E}\left(U\right)$ and $a\in A(U,{\mathfrak{f}}_U\left(w\right))$. Let

$$\mathrm{Ext}(\mathcal{M},A)$$

(117)

denote the set of equivalence classes [$\overline{\mathcal{E}}$] of extensions $\overline{\mathcal{E}}$ of $\mathcal{M}$ by A.

The classification result we show in Theorem 3 below, for extensions of a presheaf of monoids $\mathcal{M}$ by $\mathrm{D}\left(\mathcal{M}\right)$-modules, is useful to analyze the structure of $\mathcal{H}$-extensions of $\mathcal{M}$ with abelian kernel, that is, extensions $\mathfrak{f}:\mathcal{E}\to \mathcal{M}$ such that, for every object U of $\mathrm{C}$, the congruence kernel of the surjective homomorphism ${\mathfrak{f}}_U:\mathcal{E}\left(U\right)\to \mathcal{M}\left(U\right)$ is included in the Green’s relation $\mathcal{H}$ of $\mathcal{E}\left(U\right)$ and, for any element $x\in \mathcal{M}\left(U\right)$, the (left) Schützenberger group of the kernel class ${\mathfrak{f}}_U^{-1}\left(x\right)$ is abelian. The results by Grillet in [18] and, mainly, by Leech in References [3,4] on group extensions of monoids lie behind the content of the next proposition, where by a $\mathcal{D}\left(\mathcal{M}\right)$-module we mean a $\mathrm{D}\left(\mathcal{M}\right)$-module A which restricts to a $\mathcal{D}\left(\mathcal{M}\right(U\left)\right)$-module [3] for every object U of $\mathrm{C}$, that is, such that for any $x,u_0,u_1,u_0^{\prime },u_1^{\prime }\in \mathcal{M}\left(U\right)$ with $u_{0}x=u_0^{\prime }x$ and $x{u}_1=x{u}_1^{\prime }$, the equality $u_{0}a{u}_1=u_0^{\prime }a{u}_1^{\prime }$ holds for all $a\in A(U,x)$.

Proposition 8.

Let $\mathcal{M}$ be a presheaf of monoids on $\mathrm{C}$.

(i) 

Any $\mathcal{H}$-extension of $\mathcal{M}$ with abelian kernel is an extension of $\mathcal{M}$ by a $\mathcal{D}\left(\mathcal{M}\right)$-module.

(ii) 

If, for any object U of $\mathrm{C}$, the monoid $\mathcal{M}\left(U\right)$ is regular, then every extension of $\mathcal{M}$ by a $\mathcal{D}\left(\mathcal{M}\right)$-module is an $\mathcal{H}$-extension of $\mathcal{M}$ with abelian kernel.

Proof. 

(i) Suppose $\mathfrak{f}:\mathcal{E}\to \mathcal{M}$ is an $\mathcal{H}$-extension of $\mathcal{M}$ with abelian kernel. Let us recall that, for each $U\in \mathrm{ObC}$ and $x\in \mathcal{M}\left(U\right)$, the kernel group $\Sigma (U,x)$ of ${\mathfrak{f}}_U$ at x, is the quotient of the submonoid $\{a\in \mathcal{E}(U)\mid {\mathfrak{f}}_U(a)x=x\}\subseteq \mathcal{E}\left(U\right)$ by the congruence in which $a\equiv a^{\prime }$ if $a{\omega }_x=a^{\prime }{\omega }_x$ for some (then, for any) ${\omega }_x\in {\mathfrak{f}}_U^{-1}\left(x\right)$. By [3] (Lemma 2.4) or [4] (Chapter V, Lemma 1.7), there is a canonical simply-transitive left action

$$+:\Sigma (U,x)\times {\mathfrak{f}}_U^{-1}\left(x\right)\to {\mathfrak{f}}_U^{-1}\left(x\right),(\left[a\right],{\omega }_x)\mapsto \left[a\right]+{\omega }_x=a{\omega }_x.$$

(118)

By [3] (Lemma 2.28) or [4] (Chapter V, Theorem 1.15), the assignment $(U,x)\mapsto \Sigma (U,x)$, for each $U\in \mathrm{ObC}$ and $x\in \mathcal{M}\left(U\right)$, is the correspondence on objects of a $\mathcal{D}\left(\mathcal{M}\right)$-module $\Sigma$ (the kernel of $\mathfrak{f}$), which applies a morphism $(\sigma ,v,v^{\prime }):(U,x)\to (V,y)$ in $\mathrm{D}\left(\mathcal{M}\right)$ to the homomorphism $\Sigma (U,x)\to \Sigma (V,y)$ that carries each $\left[a\right]\in \Sigma (U,x)$ to the element $v{\left[a\right]}^{\sigma }{v}^{\prime }\in \Sigma (V,y)$ satisfying

$$v{\left[a\right]}^{\sigma }{v}^{\prime }+{\omega }_v{\omega }_x^{\sigma }{\omega }_{v^{\prime }}={\omega }_v{a}^{\sigma }{\omega }_x^{\sigma }{\omega }_{v^{\prime }}$$

(119)

for some (and then by any) ${\omega }_x\in {\mathfrak{f}}_U^{-1}\left(x\right)$, ${\omega }_v\in {\mathfrak{f}}_V^{-1}\left(v\right)$, and ${\omega }_x\in {\mathfrak{f}}_U^{-1}\left(x\right)$.

The extension $\mathfrak{f}:\mathcal{E}\to \mathcal{M}$ is recognized to be an extension of $\mathcal{M}$ by the its $\mathcal{D}\left(\mathcal{M}\right)$-module kernel Σ thanks to the simply-transitive actions (118).

(ii) At any object U of $\mathrm{C}$, every extension of $\mathcal{M}$ by a $\mathcal{D}\left(\mathcal{M}\right)$-module is an extension of the regular monoid $\mathcal{M}\left(U\right)$ by an $\mathcal{D}\left(\mathcal{M}\right(U\left)\right)$-module. Hence, the result follows from Leech’s Theorems 3.9 and 5.18 in Reference [3]. □

Theorem 3.

Let $\mathcal{M}$ be a presheaf of monoids on $\mathrm{C}$. For any $\mathrm{D}\left(\mathcal{M}\right)$-module A there is a natural bijection

$$\mathrm{Ext}(\mathcal{M},A)\cong H_s^2(\mathcal{M},A).$$

(120)

Proof. 

This falls naturally into three parts.

1. The natural a map $\mathrm{F}:\mathrm{Ext}(\mathcal{M},A)\to H^2(\mathcal{M},A)$. Let $\overline{\mathcal{E}}=(\mathcal{E},\mathfrak{f},+)$ be an extension of $\mathcal{M}$ by A. For each object U of $\mathrm{C}$, the homomorphism ${\mathfrak{f}}_U:\mathcal{E}\left(U\right)\twoheadrightarrow \mathcal{M}\left(U\right)$ is surjective, so we can choose a family of section maps $S=(S_U:\mathcal{M}\left(U\right)\to \mathcal{E}\left(U\right))$, one for each $U\in \mathrm{ObC}$, such that ${\mathfrak{f}}_U{S}_U=i{d}_{\mathcal{M}\left(U\right)}$. Then, a 2-cocycle

$$g=g_{\overline{\mathcal{E}},S}\in Z_s^2(\mathcal{M},A)$$

(121)

is defined as follows:

-

for any object U of $\mathrm{C}$ and $x,y\in \mathcal{M}\left(U\right)$, let $g(U;x,y)$ be the element of $A(U,xy)$ determined by the equation

$$S_U\left(xy\right)=g(U;x,y)+S_U\left(x\right)S_U\left(y\right).$$

(122)

-

for each arrow $U_0\stackrel{\alpha }{\leftarrow }{U}_1$ of $\mathrm{C}$ and $x\in \mathcal{M}\left(U_0\right)$, let $g(\alpha ;x)$ be the element of $A(U_1,x^{\alpha })$ determined by the equation

$${\left(S_{U_0}\left(x\right)\right)}^{\alpha }=g(\alpha ;x)+S_{U_1}\left(x^{\alpha }\right).$$

(123)

To verify the cocycle condition $(\partial g)(U;x,y,z)=0$, see (105), we see that

$$\begin{array}{ccc}{S}_U\left(\left(xy\right)z\right)\hfill & \stackrel{\left(122\right)}{=}\hfill & g(U;xy,z)+S_U\left(xy\right)S_U\left(z\right)\stackrel{\left(122\right)}{=}g(U;xy,z)+\left(g(U;x,y)+S_U\left(x\right)S_U\left(y\right)\right)S_U\left(z\right)\hfill \\ & \stackrel{\left(115\right)}{=}\hfill & g(U;xy,z)+g(U;x,y)z+S_U\left(x\right)S_U\left(y\right)S_U\left(z\right),\hfill \\ S_U\left(x\left(yz\right)\right)\hfill & \stackrel{\left(122\right)}{=}\hfill & g(U;x,yz)+S_U\left(x\right)S_U\left(yz\right)\stackrel{\left(122\right)}{=}g(U;x,yz)+S_U\left(x\right)\left(g(U;y,z)+S_U\left(y\right)S_U\left(z\right)\right)\hfill \\ & \stackrel{\left(115\right)}{=}\hfill & g(U;x,yz)+xg(U;y,z)+S_U\left(x\right)S_U\left(y\right)S_U\left(z\right),\hfill \end{array}$$

and by comparison the result follows. Analogously, the cocycle condition $(\partial g)(\alpha ;x,y)=0$, see (106), follows from the equality $x^{\alpha }{y}^{\alpha }={\left(xy\right)}^{\alpha }$, since

$$\begin{array}{ccc}{S}_{U_1}\left({\left(xy\right)}^{\alpha }\right)\hfill & \stackrel{\left(123\right)}{=}\hfill & -g(\alpha ;xy)+{\left(S_{U_0}\left(xy\right)\right)}^{\alpha }\stackrel{\left(123\right)}{=}-g(\alpha ;xy)+{\left(g(U_0;x,y)+S_{U_0}\left(x\right)S_{U_0}\left(y\right)\right)}^{\alpha }\hfill \\ & \stackrel{\left(116\right)}{=}\hfill & -g(\alpha ;xy)+g{(U_0;x,y)}^{\alpha }+{\left(S_{U_0}\left(x\right)\right)}^{\alpha }{\left(S_{U_0}\left(y\right)\right)}^{\alpha }\hfill \\ & \stackrel{\left(123\right)}{=}\hfill & -g(\alpha ;xy)+g{(U_0;x,y)}^{\alpha }+\left(g(\alpha ;x)+S_{U_1}\left(x^{\alpha }\right)\right)\left(g(\alpha ;y)+S_{U_1}\left(y^{\alpha }\right)\right)\hfill \\ & \stackrel{\left(115\right)}{=}\hfill & -g(\alpha ;xy)+g{(U_0;x,y)}^{\alpha }+g(\alpha ;x)y^{\alpha }+x^{\alpha }g(\alpha :y)+S_{U_1}\left(x^{\alpha }\right)S_{U_1}\left(y^{\alpha }\right),\hfill \\ S_{U_1}\left(x^{\alpha }{y}^{\alpha }\right)\hfill & \stackrel{\left(122\right)}{=}\hfill & g(U_1;x^{\alpha },y^{\alpha })+S_{U_1}\left(x^{\alpha }\right)S_{U_1}\left(y^{\alpha }\right),\hfill \end{array}$$

while the cocycle condition $(\partial g)(\alpha ,\beta ;x)=0$, see (107), follows from the equality $x^{\alpha \beta }={\left(x^{\alpha }\right)}^{\beta }$:

$$\begin{array}{ccc}{S}_{U_2}({(x^{\alpha })}^{\beta })\hfill & \stackrel{\left(123\right)}{=}\hfill & -g(\beta ;x^{\alpha })+{\left(S_{U_1}\left(x^{\alpha }\right)\right)}^{\beta }\stackrel{\left(123\right)}{=}-g(\beta ;x^{\alpha })+{\left(-g(\alpha ;x)+{\left(S_{U_0}\left(x\right)\right)}^{\alpha }\right)}^{\beta }\hfill \\ & \stackrel{\left(116\right)}{=}\hfill & -g(\beta ;x^{\alpha })-g{(\alpha ;x)}^{\beta }+{\left(S_{U_0}\left(x\right)\right)}^{\alpha \beta },\hfill \\ S_{U_2}\left(x^{\alpha \beta }\right)\hfill & \stackrel{\left(123\right)}{=}\hfill & -g(\alpha \beta ;x)+{\left(S_{U_0}\left(x\right)\right)}^{\alpha \beta }.\hfill \end{array}$$

The cohomology class $[g_{\overline{\mathcal{E}},S}]\in H^2(\mathcal{M},A)$ does not depend on the choice of the sections maps $S_U:\mathcal{M}\left(U\right)\to \mathcal{E}\left(U\right)$: Suppose maps $S_U^{\prime }:\mathcal{M}\left(U\right)\to \mathcal{E}\left(U\right)$, one for each $U\in \mathrm{Ob}\left(\mathrm{C}\right)$, with ${\mathfrak{f}}_U{S}_U^{\prime }=i{d}_{\mathcal{M}\left(U\right)}$. Then, let $f\in C^1(\mathcal{M},A)$ be the 1-cochain where, for any $U\in \mathrm{ObC}$ and any $x\in \mathcal{M}\left(U\right)$, the element $f(U;x)\in A(U,x)$ is determined by the equation $f(U;x)+S_U^{\prime }\left(x\right)=S_U\left(x\right)$. For any $x,y\in \mathcal{M}\left(U\right)$, if we compute $S_U\left(xy\right)\in \mathcal{E}\left(U\right)$ in the following two ways

$$\begin{array}{ccc}{S}_U\left(xy\right)\hfill & \stackrel{\left(122\right)}{=}\hfill & g_{\overline{\mathcal{E}},S}(U;x,y)+S_U\left(x\right)S_U\left(y\right)\hfill \\ & =\hfill & g_{\overline{\mathcal{E}},S}(U;x,y)+\left(f(U;x)+S_U^{\prime }\left(x\right)\right)\left(f(U;y)+S_U^{\prime }\left(y\right)\right)\hfill \\ & \stackrel{\left(115\right)}{=}\hfill & g_{\overline{\mathcal{E}},S}(U;x,y)+f(U;x)y+xf(U;y)+S_U^{\prime }\left(x\right)S_U^{\prime }\left(y\right),\hfill \\ S_U\left(xy\right)\hfill & =\hfill & f(U;xy)+S_U^{\prime }\left(xy\right)\stackrel{\left(122\right)}{=}f(U;xy)+g_{\overline{\mathcal{E}},S^{\prime }}(U;x,y)+S_U^{\prime }\left(x\right)S_U^{\prime }\left(y\right),\hfill \end{array}$$

it follows, by comparison, that $g_{\overline{\mathcal{E}},S^{\prime }}(U;x,y)=(g_{\overline{\mathcal{E}},S}+\partial f)(U;x,y)$, see (102). Similarly, for any arrow $\alpha :U_1\to U_0$ in $\mathrm{C}$ and any $x\in \mathcal{M}\left(U_0\right)$, we can compute ${\left(S_{U_0}\left(x\right)\right)}^{\alpha }\in \mathcal{E}\left(U_1\right)$ in two ways

$$\begin{array}{ccc}{\left(S_{U_0}\left(x\right)\right)}^{\alpha }\hfill & \stackrel{\left(116\right)}{=}\hfill & g_{\overline{\mathcal{E}},S}(\alpha ;x)+S_{U_1}\left(x^{\alpha }\right)=g_{\overline{\mathcal{E}},S}(\alpha ;x)+f(U_1;x^{\alpha })+S_{U_1}^{\prime }\left(x^{\alpha }\right),\hfill \\ {\left(S_{U_0}\left(x\right)\right)}^{\alpha }\hfill & =\hfill & {(f(U_0;x)+S_{U_0}^{\prime }\left(x\right))}^{\alpha }\stackrel{\left(116\right)}{=}f{(U_0;x)}^{\alpha }+{(S_{U_0}^{\prime }\left(x\right))}^{\alpha }\hfill \\ & \stackrel{\left(123\right)}{=}\hfill & f{(U_0;x)}^{\alpha }+g_{\overline{\mathcal{E}},S^{\prime }}(\alpha ;x)+S_{U_1}^{\prime }\left(x^{\alpha }\right),\hfill \end{array}$$

whence it follows that $g_{\overline{\mathcal{E}},S^{\prime }}(\alpha ;x)=(g_{\overline{\mathcal{E}},S}+\partial f)(\alpha ;x)$, see (103). Thus, $g_{\overline{\mathcal{E}},S^{\prime }}=g_{\overline{\mathcal{E}},S}+\partial f$ and $[g_{\overline{\mathcal{E}},S}]=[g_{\overline{\mathcal{E}},S^{\prime }}]$.

Furthermore, for an equivalence $\mathfrak{g}:\mathcal{E}\cong {\mathcal{E}}^{\prime }$ of extensions $\overline{\mathcal{E}}$ and ${\overline{\mathcal{E}}}^{\prime }$ of $\mathcal{M}$ by A we easily see that $g_{{\overline{\mathcal{E}}}^{\prime },\mathfrak{g}S}=g_{\overline{\mathcal{E}},S}$, and therefore we have a map

$$\mathrm{F}:\mathrm{Ext}(\mathcal{M},A)\to H_s^2(\mathcal{M},A),\left[\overline{\mathcal{E}}\right]\mapsto [g_{\overline{\mathcal{E}},S}].$$

(124)

2. The map F is surjective: For every $g\in Z^2(\mathcal{M},A)$, an extension ${\overline{\mathcal{E}}}_g=({\mathcal{E}}_g,\mathfrak{f},+)$ of $\mathcal{M}$ by A can be constructed as follows. For each object U of $\mathrm{C}$, we define

$${\mathcal{E}}_g\left(U\right)=\left\{(x,a)\mid x\in \mathcal{M}\left(U\right),a\in A(U,x)\right\}$$

(125)

with multiplication

$$(x,a)(y,b)=(xy,-g(U;x,y)+xb+ay).$$

(126)

A straightforward verification shows that this multiplication (126) is associative thanks to the cocycle condition $(\partial g)(U;x,y,z)=0$ in (105). Moreover, from equations $(\partial g)(U;x,e,e)=0$ and $(\partial g)(U;e,e,x)=0$ we get $xg(U;e,e)=g(U;x,e)$ and $g(U;e,e)x=g(U;e,x)$, whence it is easy to see that the multiplication (126) is unitary, with identity $(e,g(U;e,e\left)\right)$. Hence, ${\mathcal{E}}_g\left(U\right)$ is actually a monoid. For any arrow $\alpha :U_1\to U_0$ of $\mathrm{C}$, the homomorphism ${\left(\right)}^{\alpha }:{\mathcal{E}}_g\left(U_0\right)\to {\mathcal{E}}_g\left(U_1\right)$ is given by

$${(x,a)}^{\alpha }=(x^{\alpha },g(\alpha ,x)+a^{\alpha }).$$

(127)

This is actually a homomorphism of monoids, since, for any $(x,a),(y,b)\in {\mathcal{E}}_g\left(U_0\right)$, the equality ${\left((x,a)(y,b)\right)}^{\alpha }={(x,a)}^{\alpha }{(y,b)}^{\alpha }$ follows from the 2-cocycle condition $(\partial g)(\alpha ;x,y)=0$ in (106); while the requirement ${(e,g(U_0,e,e))}^{\alpha }=(e,g(U_1;e,e))$ holds owing to the 2-cocycle condition $(\partial g)(\alpha ;e,e)=0$. If $U_2\stackrel{\beta }{\to }{U}_1\stackrel{\alpha }{\to }{U}_0$ are any two composable arrows in $\mathrm{C}$, the equality ${\left({(x,a)}^{\alpha }\right)}^{\beta }={(x,a)}^{\alpha \beta }$, for any $(x,a)\in {\mathcal{E}}_g\left(U_0\right)$, follows from the 2-cocycle condition $(\partial g)(\alpha ,\beta ;x)=0$ in (107), whereas the condition $(\partial g)(1_{U_0},1_{U_0};x)=0$ gives the equality ${(x,a)}^{1_{U_0}}=(x,a)$. Thus, ${\mathcal{E}}_g$ is a presheaf of monoids on $\mathrm{C}$.

The locally surjective morphism $\mathfrak{f}:{\mathcal{E}}_g\to \mathcal{M}$ is defined, at each $U\in \mathrm{ObC}$, by the projection homomorphism ${\mathfrak{f}}_U:{\mathcal{E}}_g\left(U\right)\to \mathcal{M}\left(U\right)$, ${\mathfrak{f}}_U(x,a)=x$. For any $x\in \mathcal{M}\left(U\right)$, the simply transitive action $+:A(U,x)\times {\mathfrak{f}}_U^{-1}\left(x\right)\to {\mathfrak{f}}_U^{-1}\left(x\right)$ is given by $b+(x,a)=(x,b+a)$. Conditions (115) and (116) are easily verified, so that ${\overline{\mathcal{E}}}_g=({\mathcal{E}}_g,\mathfrak{f},+)$ is actually an extension of $\mathcal{M}$ by A.

Now, for each $U\in \mathrm{ObC}$, let $S_U:\mathcal{M}\left(U\right)\to {\mathcal{E}}_g\left(U\right)$ be the obvious section map with $S_U\left(x\right)=(x,0)$. Then, the equalities, for any $x,y\in \mathcal{M}\left(U\right)$ and $\alpha :U_1\to U_0$,

$$(xy,0)=g(U;x,y)+(x,0)(y,0),{(x,0)}^{\alpha }=g(\alpha ;x)+(x^{\alpha },0),$$

(128)

show that $g_{{\overline{\mathcal{E}}}_g,S}=g$, and therefore $F\left[{\overline{\mathcal{E}}}_g\right]=\left[g\right]$.

3. The map F is injective: For any extension $\overline{\mathcal{E}}=(\mathcal{E},\mathfrak{f},+)$ of $\mathcal{M}$ by A and any family of section maps $S={(S_U:\mathcal{M}\left(U\right)\to \mathcal{E}\left(U\right))}_{U\in \mathrm{ObC}}$, there is an isomorphism of extensions ${\overline{\mathcal{E}}}_{g_{\overline{\mathcal{E}},S}}\cong \overline{\mathcal{E}}$ which is locally defined by the isomorphisms of monoids

$${\mathcal{E}}_{g_{\overline{\mathcal{E}},S}}\left(U\right)\cong \mathcal{E}\left(U\right),(x,a)\mapsto a+S_U\left(x\right).$$

(129)

Furthermore, if $g,g^{\prime }\in Z^2(\mathcal{M},A)$ are cohomologous, say $g^{\prime }=g+\partial f$ for some $f\in C^1(\mathcal{M},A)$, then there is an isomorphism of extensions ${\overline{\mathcal{E}}}_g\cong {\overline{\mathcal{E}}}_{g^{\prime }}$ which is defined by the isomorphisms of monoids

$${\mathcal{E}}_g\left(U\right)\cong {\mathcal{E}}_{g^{\prime }}\left(U\right),(x,a)\mapsto (x,f(U;x)+a).$$

(130)

Hence, the injectivity of F follows. □

9. Prestacks of Monoidal Abelian Monoids

To start, we fix some notation. Recall that a groupoid $\mathrm{G}$ is termed abelian whenever its automorphism groups ${\mathrm{Aut}}_{\mathrm{G}}\left(x\right)$, $x\in \mathrm{ObG}$, are abelian. We shall use additive notation for them. Thus, if $a:x\to y$, $b:y\to z$ are morphisms an abelian groupoid $\mathrm{G}$, their composite is written as $b+a:x\to z$, the identity morphism of an object x is denoted by $0_x$, and the inverse of $a:x\to y$ is $-a:y\to x$.

If $\mathrm{C}$ is any fixed small category, by a prestack of monoidal abelian groupoids on $\mathrm{C}$ we mean a contravariant pseudo-functor from $\mathrm{C}$ to the 2-category of monoidal abelian groupoids, see Reference [1] for instance. Thus, such a prestack $\mathfrak{P}$ consists of the data (PDi) and axioms (PAj) that follow.

(PD1)

a monoidal abelian groupoid $\mathfrak{P}\left(U\right)=\left(\mathfrak{P}\right(U),\otimes ,\iota ,\mathit{a},\mathit{l},\mathit{r})$, for each object U of $\mathrm{C}$; that is, an abelian groupoid $\mathfrak{P}\left(U\right)$ enriched with a tensor product $\otimes :\mathfrak{P}\left(U\right)\times \mathfrak{P}\left(U\right)\to \mathfrak{P}\left(U\right)$, a unit object $\iota$, and natural morphisms

$${\mathit{a}}_{x,y,z}:(x\otimes y)\otimes z\to x\otimes (y\otimes z),{\mathit{l}}_x:\iota \otimes x\to x,{\mathit{r}}_x:x\otimes \iota \to x,$$

(131)

satisfying the commutativity of the diagrams

$$\begin{array}{cc}\hfill {\mathit{a}}_{x,y,z\otimes t}+{\mathit{a}}_{x\otimes y,z,t}& =(0_x\otimes {\mathit{a}}_{y,z,t})+{\mathit{a}}_{x,y\otimes z,t}+({\mathit{a}}_{x,y,z}\otimes 0_t),\hfill \end{array}$$

(132)

$$\begin{array}{cc}\hfill (0_x\otimes {\mathit{l}}_y)+{\mathit{a}}_{x,\iota ,y}& ={\mathit{r}}_x\otimes 0_y.\hfill \end{array}$$

(133)

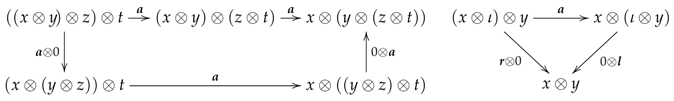
(PD2)

a monoidal functor ${\left(\right)}^{\alpha }=({()}^{\alpha },{\mathit{\varphi }}^{\alpha },{\mathit{\varphi }}_{★}^{\alpha }):\mathfrak{P}\left(U_0\right)\to \mathfrak{P}\left(U_1\right)$, for each arrow $U_0\stackrel{\alpha }{\leftarrow }{U}_1$ of $\mathrm{C}$; that is, a functor between the underlying groupoids endowed with natural morphisms ${\mathit{\varphi }}_{x,y}^{\alpha }:x^{\alpha }\otimes y^{\alpha }\to {(x\otimes y)}^{\alpha }$ and a morphism ${\mathit{\varphi }}_{★}^{\alpha }:\iota \to {\iota }^{\alpha }$, satisfying the commutativities

$$\begin{array}{c}{\mathit{\varphi }}_{x,y\otimes z}^{\alpha }+(0_{x^{\alpha }}\otimes {\mathit{\varphi }}_{y,z}^{\alpha })+{\mathit{a}}_{x^{\alpha },y^{\alpha },z^{\alpha }}={\left({\mathit{a}}_{x,y,z}\right)}^{\alpha }+{\mathit{\varphi }}_{x\otimes y,z}^{\alpha }+({\mathit{\varphi }}_{x,y}^{\alpha }\otimes 0_{z^{\alpha }}),\hfill \end{array}$$

(134)

$$\begin{array}{c}{\left({\mathit{r}}_x\right)}^{\alpha }+{\mathit{\varphi }}_{x,\iota }^{\alpha }+(0_{x^{\alpha }}\otimes {\mathit{\varphi }}_{★}^{\alpha })={\mathit{r}}_{x^{\alpha }},{\left({\mathit{l}}_x\right)}^{\alpha }+{\mathit{\varphi }}_{\iota ,x}^{\alpha }+({\mathit{\varphi }}_{★}^{\alpha }\otimes 0_{x^{\alpha }})={\mathit{l}}_{x^{\alpha }},\hfill \end{array}$$

(135)

(PD3)

a monoidal transformation ${\mathit{\theta }}^{\alpha ,\beta }:{\left({\left(\right)}^{\alpha }\right)}^{\beta }\Rightarrow {\left(\right)}^{\alpha \beta }$, for each two arrows $U_0\stackrel{\alpha }{\leftarrow }{U}_1\stackrel{\beta }{\leftarrow }{U}_2$ of $\mathrm{C}$; that is, a family of natural morphisms ${\mathit{\theta }}_x^{\alpha ,\beta }:{\left(x^{\alpha }\right)}^{\beta }\to x^{\alpha \beta }$, making commutative the diagrams

$$\begin{array}{cc}\hfill {\mathit{\varphi }}_{x,y}^{\alpha \beta }+({\mathit{\theta }}_x^{\alpha ,\beta }\otimes {\mathit{\theta }}_y^{\alpha ,\beta })& ={\mathit{\theta }}_{x\otimes y}^{\alpha ,\beta }+{\left({\mathit{\varphi }}_{x,y}^{\alpha }\right)}^{\beta }+{\mathit{\varphi }}_{x^{\alpha },y^{\alpha }}^{\beta },\hfill \end{array}$$

(136)

$$\begin{array}{cc}\hfill {\mathit{\theta }}_{\iota }^{\alpha ,\beta }+{\left({\mathit{\varphi }}_{★}^{\alpha }\right)}^{\beta }+{\mathit{\varphi }}_{★}^{\beta }& ={\mathit{\varphi }}_{★}^{\alpha \beta }.\hfill \end{array}$$

(137)

(PD4)

a monoidal transformation ${\mathit{\theta }}^U:i{d}_{\mathfrak{P}\left(U\right)}\Rightarrow {\left(\right)}^{1_U}$, for each object U of $\mathrm{C}$; that is, a family of natural morphisms ${\mathit{\theta }}_x^U:x\to x^{1_u}$ making commutative the diagrams

$$\begin{array}{cc}\hfill {\mathit{\theta }}_{x\otimes y}^U& ={\mathit{\varphi }}_{x,y}^{1_u}+({\mathit{\theta }}_x^U\otimes {\mathit{\theta }}_y^U),\hfill \end{array}$$

(138)

$$\begin{array}{cc}\hfill {\mathit{\theta }}_{\iota }^U& ={\mathit{\varphi }}_{★}^{1_u}.\hfill \end{array}$$

(139)

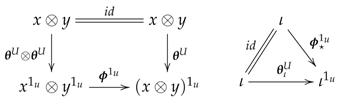
All these data are subject to the following two coherence conditions:

(PA1)

for any three composable arrows $U_0\stackrel{\alpha }{\leftarrow }{U}_1\stackrel{\beta }{\leftarrow }{U}_2\stackrel{\gamma }{\leftarrow }{U}_3$ of $\mathrm{C}$ and $x\in \mathrm{Ob}\mathfrak{P}\left(U_0\right)$, the square

commutes, that is,

$${\mathit{\theta }}_x^{\alpha ,\beta \gamma }+{\mathit{\theta }}_{x^{\alpha }}^{\beta ,\gamma }={\mathit{\theta }}_x^{\alpha \beta ,\gamma }+{({\mathit{\theta }}_x^{\alpha ,\beta })}^{\gamma }.$$

(140)

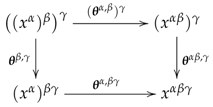
(PA2)

for each $U_0\stackrel{\alpha }{\leftarrow }{U}_1$ in $\mathrm{C}$ and $x\in \mathrm{Ob}\mathfrak{P}\left(U_0\right)$, both inner triangles in the square

commute, that is,

$${\mathit{\theta }}_x^{1_{U_0},\alpha }=-{({\mathit{\theta }}_x^{U_0})}^{\alpha },{\mathit{\theta }}_x^{\alpha ,1_{U_1}}=-{\mathit{\theta }}_{x^{\alpha }}^{U_1}.$$

(141)

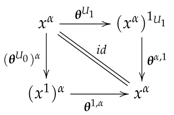
If $\mathfrak{P}$ and ${\mathfrak{P}}^{\prime }$ are two such prestacks on $\mathrm{C}$, then an equivalence $\mathfrak{F}:\mathfrak{P}\to {\mathfrak{P}}^{\prime }$ is a pseudo-natural equivalence, in other words it consists of the following data

(EPD1)

a monoidal equivalence ${\mathfrak{F}}^U=({\mathfrak{F}}^U,{\mathsf{\Psi }}^U,{\mathsf{\Psi }}_{★}^U):\mathfrak{P}\left(U\right)\to {\mathfrak{P}}^{\prime }\left(U\right)$, for each object U of $\mathrm{C}$; that is, an equivalence between the underlying groupoids ${\mathfrak{F}}^U:\mathfrak{P}\left(U\right)\to {\mathfrak{P}}^{\prime }\left(U\right)$ enriched with natural morphisms ${\mathsf{\Psi }}_{x,y}^U:{\mathfrak{F}}^U\left(x\right)\otimes {\mathfrak{F}}^U\left(y\right)\to {\mathfrak{F}}^U(x\otimes y)$ and a morphism ${\mathsf{\Psi }}_{★}^U:\iota \to {\mathfrak{F}}^U\left(\iota \right)$, satisfying

$$\begin{array}{c}{\mathsf{\Psi }}_{x,y\otimes z}^U+(0_{{\mathfrak{F}}^U\left(x\right)}\otimes {\mathsf{\Psi }}_{y,z}^U)+{\mathit{a}}_{{\mathfrak{F}}^U\left(x\right),{\mathfrak{F}}^U\left(y\right),{\mathfrak{F}}^U\left(z\right)}={\mathfrak{F}}^U\left({\mathit{a}}_{x,y,z}\right)+{\mathsf{\Psi }}_{x\otimes y,z}^U+({\mathsf{\Psi }}_{x,y}^U\otimes 0_{{\mathfrak{F}}^U\left(z\right)}),\hfill \end{array}$$

(142)

$$\begin{array}{c}{\mathfrak{F}}^U\left({\mathit{r}}_x\right)+{\mathsf{\Psi }}_{x,\iota }^U+(0_{{\mathfrak{F}}^U\left(x\right)}\otimes {\mathsf{\Psi }}_{★}^U)={\mathit{r}}_{{\mathfrak{F}}^U\left(x\right)},{\mathfrak{F}}^U\left({\mathit{l}}_x\right)+{\mathsf{\Psi }}_{\iota ,x}^U+({\mathsf{\Psi }}_{★}^U\otimes 0_{{\mathfrak{F}}^U\left(x\right)})={\mathit{l}}_{{\mathfrak{F}}^U\left(x\right)}.\hfill \end{array}$$

(143)

(EPD2)

a monoidal transformation

for each morphism $U_0\stackrel{\alpha }{\leftarrow }{U}_1$ of $\mathrm{C}$; that is, a family of natural morphisms

$${\mathsf{\Gamma }}_x^{\alpha }:{\left({\mathfrak{F}}^{U_0}\left(x\right)\right)}^{\alpha }\to {\mathfrak{F}}^{U_1}\left(x^{\alpha }\right)$$

(144)

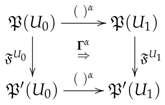making commutative the diagrams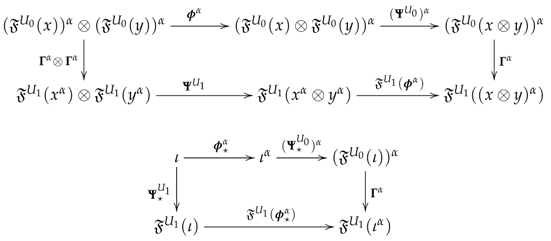

$$\begin{array}{c}\hfill {\mathfrak{F}}^{U_1}\left({\mathit{\varphi }}_{x,y}^{\alpha }\right)+{\mathsf{\Psi }}_{x^{\alpha },y^{\alpha }}^{U_1}+({\mathsf{\Gamma }}_x^{\alpha }\otimes {\mathsf{\Gamma }}_y^{\alpha })={\mathsf{\Gamma }}_{x\otimes y}^{\alpha }+{({\mathsf{\Psi }}_{x,y}^{U_0})}^{\alpha }+{\mathit{\varphi }}_{{\mathfrak{F}}^{U_0}\left(x\right),{\mathfrak{F}}^{U_0}\left(y\right)}^{\alpha },\end{array}$$

(145)

$$\begin{array}{c}\hfill {\mathsf{\Gamma }}_{\iota }^{\alpha }+{({\mathsf{\Psi }}_{★}^{U_0})}^{\alpha }+{\mathit{\varphi }}_{★}^{\alpha }={\mathfrak{F}}^{U_1}\left({\mathit{\varphi }}_{★}^{\alpha }\right)+{\mathsf{\Psi }}_{★}^{U_1}.\end{array}$$

(146)

All subject to the following two axioms:

(EPA1)

for any two composable arrows $U_0\stackrel{\alpha }{\leftarrow }{U}_1\stackrel{\beta }{\leftarrow }{U}_2$ of $\mathrm{C}$ and $x\in \mathrm{Ob}\mathfrak{P}\left(U_0\right)$, the diagram

commutes, that is,

$${\mathsf{\Gamma }}_x^{\alpha \beta }+{\mathit{\theta }}_{{\mathfrak{F}}^{U_0}\left(x\right)}^{\alpha ,\beta }={\mathfrak{F}}^{U_2}({\mathit{\theta }}_x^{\alpha ,\beta })+{\mathsf{\Gamma }}_{x^{\alpha }}^{\beta }+{\left({\mathsf{\Gamma }}_x^{\alpha }\right)}^{\beta }.$$

(147)

(EPA2)

for any objects U of $\mathrm{C}$ and x of $\mathfrak{P}\left(U\right)$, the triangle below commutes.

$${\mathsf{\Gamma }}_x^{1_U}+{\mathit{\theta }}_{{\mathfrak{F}}^U\left(x\right)}^U={\mathfrak{F}}^U\left({\mathit{\theta }}_x^U\right).$$

(148)

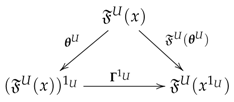
The following is an useful result about transporting prestack structure.

Lemma 2.

Suppose ${\mathfrak{P}}^{\prime }$ is a prestack of monoidal abelian groupoids on $\mathrm{C}$, and ${\mathfrak{F}}^U:\mathfrak{P}\left(U\right)\to {\mathfrak{P}}^{\prime }\left(U\right)$ is a $\mathrm{ObC}$-indexed family of equivalences of groupoids. Then, there is a prestack of monoidal abelian groupoids $\mathfrak{P}$ and an equivalence $\mathfrak{F}:\mathfrak{P}\to {\mathfrak{P}}^{\prime }$ which agrees on the underlying groupoids with the given functors ${\mathfrak{F}}^U$.

Proof. 

Notice that to provide the datum (PD1) in the construction of our prestack $\mathfrak{P}$, we can simultaneously provide the datum (EPD1) for the construction of $\mathfrak{F}$, since ${\mathfrak{F}}^U$ and ${\mathfrak{F}}^U\times {\mathfrak{F}}^U$ are equivalences: For each object U of $\mathrm{C}$, let us select objects $x\otimes y$ and $\iota$ in $\mathfrak{P}\left(U\right)$ together with morphisms ${\mathsf{\Psi }}_{x,y}^U:{\mathfrak{F}}^U\left(x\right)\otimes {\mathfrak{F}}^U\left(y\right)\to {\mathfrak{F}}^U(x\otimes y)$ and ${\mathsf{\Psi }}_{★}^U:\iota \to {\mathfrak{F}}^U\left(\iota \right)$ in ${\mathfrak{P}}^{\prime }\left(U\right)$. Then, there is a unique monoidal structure on $\mathfrak{P}\left(U\right)$ such that ${\mathfrak{F}}^U$ together with the morphisms ${\mathsf{\Psi }}_{x,y}^U$ and ${\mathsf{\Psi }}_{★}^U$ turns to be a monoidal equivalence. The tensor product $f\otimes f^{\prime }:x\otimes y\to x^{\prime }\otimes y^{\prime }$ of morphisms $f:x\to y$ and $f^{\prime }:x^{\prime }\to x^{\prime }$ in $\mathfrak{P}\left(U\right)$ is determined by the commutativity of the diagram

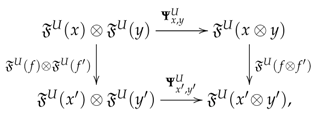the unit object is $\iota$, and the structure constraints $\mathit{a}$, $\mathit{l}$ and $\mathit{r}$ are uniquely determined by Equations (142) and (143). Similarly, (EPD2) tell us how to satisfy (PD2): For each arrow $\alpha :U_1\to U_0$ in $\mathrm{C}$, let us choose objects $x^{\alpha }$ in $\mathfrak{P}\left(U_1\right)$ together with morphisms ${\mathsf{\Gamma }}_x^{\alpha }:{\left({\mathfrak{F}}^{U_0}\left(x\right)\right)}^{\alpha }\to {\mathfrak{F}}^{U_1}\left(x^{\alpha }\right)$. Then, the assignment $x\mapsto x^{\alpha }$ is the function on objects of the functor ${\left(\right)}^{\alpha }:\mathfrak{P}\left(U_0\right)\to \mathfrak{P}\left(U_1\right)$, whose effect on a morphism $f:x\to y$ of $\mathfrak{P}\left(U_0\right)$ is the morphism $f^{\alpha }:x^{\alpha }\to y^{\alpha }$ determined by the commutative square

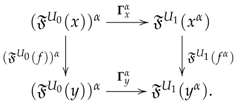This functor ${\left(\right)}^{\alpha }$ becomes a monoidal functor in a unique way such that ${\mathsf{\Gamma }}^{\alpha }$ turns to be a monoidal transformation, since its structure constraints ${\varphi }^{\alpha }$ and ${\varphi }_{★}^{\alpha }$ are uniquely determined by the Equations (145) and (146). Finally, axiom (EPA1) uniquely determines the datum (PD3) for $\mathfrak{P}$, while (EPA2) do the same with the datum (PD4). All the requirements (132)–(141) for $\mathfrak{P}$ are consequence of the corresponding ones for ${\mathfrak{P}}^{\prime }$ since the ${\mathfrak{F}}^U$ are faithful. In getting $\mathfrak{P}$ we have also got the equivalence $\mathfrak{F}:\mathfrak{P}\to {\mathfrak{P}}^{\prime }$. □

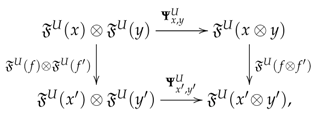
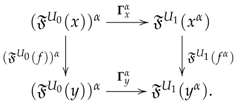
Theorem 4 below shows a classification for equivalence classes of prestacks of monoidal abelian groupoids on $\mathrm{C}$ by means of triads $(\mathcal{M},A,c)$, where $\mathcal{M}$ is a presheaf of monoids on $\mathrm{C}$, A is a $\mathrm{D}\left(\mathcal{M}\right)$-module, and c is a cohomology class $c\in H_s^3(\mathcal{M},A)$. Previously, we show how every 3-cocycle $h\in Z_s^3(\mathcal{M},A)$ gives rise to a prestack of monoidal abelian groupoids on $\mathrm{C}$

$$\mathfrak{P}(\mathcal{M},A,h)$$

(149)

which, for abbreviation, we also denote by ${\mathfrak{P}}_h$. Its data are as follows:

(PD1) For each object U of $\mathrm{C}$, the underlying groupoid ${\mathfrak{P}}_h\left(U\right)$ has as set of objects the elements of the monoid $\mathcal{M}\left(U\right)$. If $x\ne y$ are different elements of $\mathcal{M}\left(U\right)$, then ${\mathrm{Hom}}_{{\mathfrak{P}}_h\left(U\right)}(x,y)=\varnothing$, whereas its isotropy group at an x is ${\mathrm{Aut}}_{{\mathfrak{P}}_h\left(U\right)}\left(x\right)=A(U,x)$, the abelian group that A attaches to the object $(U,x)$ of $\mathrm{D}\left(\mathcal{M}\right)$. Its tensor product is given by

$$(x\stackrel{a}{⟶}x)\otimes (y\stackrel{b}{⟶}y)=(xy\stackrel{xb+ay}{⟶}xy).$$

(150)

The identity of the monoid $\mathcal{M}\left(U\right)$ provides the unit object, that is, $\iota =e$, and the associativity and unit constraints are

$$\begin{array}{cc}\hfill {\mathit{a}}_{x,y,z}=& h(U;x,y,z):\left(xy\right)z\to x\left(yz\right),\hfill \end{array}$$

(151)

$$\begin{array}{c}\hfill {\mathit{l}}_x=-h(U;e,e,x):ex\to x,{\mathit{r}}_x=h(U;x,e,e):xe\to x,\end{array}$$

(152)

which are easily seen to be natural since the $A(U,x)$ are abelian groups. Equation (132) hold thanks to the 3-cocycle condition $\partial h=0$ in (109). Besides, if we take $y=e=z$ and replace t with y in (109), we get

$$h(U;x,e,e)y=h(U;x,e,y)-xh(U;e,e,y)$$

(153)

which just is (133).

(PD2) For each arrow $U_0\stackrel{\alpha }{\leftarrow }{U}_1$ of $\mathrm{C}$, the functor ${\left(\right)}^{\alpha }:{\mathfrak{P}}_h\left(U_0\right)\to {\mathfrak{P}}_h\left(U_1\right)$ acts by

$${(x\stackrel{a}{⟶}x)}^{\alpha }=(x^{\alpha }\stackrel{a^{\alpha }}{⟶}{x}^{\alpha }),$$

(154)

and its monoidal structure constraints are defined by

$$\begin{array}{cc}\hfill {\mathit{\varphi }}_{x,y}^{\alpha }=& -h(\alpha ;x,y):x^{\alpha }{y}^{\alpha }\to {\left(xy\right)}^{\alpha }\hfill \end{array}$$

(155)

$$\begin{array}{c}\hfill {\mathit{\varphi }}_{★}^{\alpha }=h(\alpha ;e,e):e\to e^{\alpha }.\end{array}$$

(156)

The 3-cocycle condition $\partial h=0$ in (110) directly provides the verification of (134). If, firstly, we take $y=e=z$ in (110) and, secondly, we take $x=e=y$ and then we replace z with x also in (110), we get the equalities

$$\begin{array}{c}h(U_1;x^{\alpha },e,e)=h{(U_0;x,e,e)}^{\alpha }-h(\alpha ;x,e)+x^{\alpha }h(\alpha ,e,e),\hfill \end{array}$$

(157)

$$\begin{array}{c}-h(U_1;e,e,x^{\alpha })=-h{(U_0;e,e,x)}^{\alpha }-h(\alpha ;e,x)+h(\alpha ,e,e)x^{\alpha },\hfill \end{array}$$

(158)

which tell us that the requirements in (135) hold.

(PD3) For each $U_0\stackrel{\alpha }{\leftarrow }{U}_1\stackrel{\beta }{\leftarrow }{U}_2$ in $\mathrm{C}$, the monoidal transformation ${\mathit{\theta }}^{\alpha ,\beta }:{\left({\left(\right)}^{\alpha }\right)}^{\beta }\Rightarrow {\left(\right)}^{\alpha \beta }$ is defined, at each object x of $\mathcal{M}\left(U_0\right)$, by

$${\mathit{\theta }}_x^{\alpha ,\beta }=h(\alpha ,\beta ;x):{\left(x^{\alpha }\right)}^{\beta }\to x^{\alpha \beta }.$$

(159)

The coherence condition (136) holds owing to the cocycle condition $\partial h=0$ in (111). Furthermore, taking $x=y=e$ in (111) we obtain

$$h(\alpha \beta ;e,e)=h(\alpha ,\beta ;e)+h(\alpha ;e,e)+h(\beta ;e,e)$$

(160)

which just reads the requirement (137).

(PD4) For each object U of $\mathrm{C}$, the monoidal transformation ${\mathit{\theta }}^U:i{d}_{{\mathfrak{P}}_h\left(U\right)}\Rightarrow {\left(\right)}^{1_U}$ is given, at each object x, by

$${\mathit{\theta }}_x^U=-h(1_U,1_U;x):x\to x^{1_U}.$$

(161)

Taking $\alpha =1_U=\beta$ in (111) we obtain

$$h(1_U,1_U;xy)=h(1_U;x,y)+xh(1_U,1_U;y)+h(1_U,1_U;x)y$$

(162)

which, taking opposites, says that (138) holds. Even more, taking $x=e=y$ in the above equation, we obtain

$$h(1_U;e,e)=-h(1_U,1_U;e),$$

(163)

that is, (139) is satisfied.

Finally, we verify axioms (PA1) and (PA2) for ${\mathfrak{P}}_h$: Here (140) reads

$$h(\alpha ,\beta \gamma )+h(\beta ,\gamma ;x^{\alpha })=h(\alpha \beta ,\gamma ;x)+h{(\alpha ,\beta ;x)}^{\gamma },$$

(164)

which follows directly from the cocycle condition $\partial h=0$ in (112). But we have even more, since if we take $\beta =1_{U_1}=\gamma$ in the above equality we get

$$h(\alpha ,1_{U_1},x)=h(1_{U_1},1_{U_1};x^{\alpha }),$$

(165)

while taking $\alpha =1_{U_0}=\beta$ and then replacing $\gamma$ by $\alpha$ we obtain

$$h(1_{U_0},\alpha ;x)=h{(1_{U_0},1_{U_0},x)}^{\alpha },$$

(166)

and these last two equalities just mean that (141) holds.

In the theorem below, we will use that the cohomology groups of presheaves of monoids $H_s^n(\mathcal{M},A)$ are functorial in the usual way, contravariant in $\mathcal{M}$ and covariant in A.

Theorem 4.

$\left(i\right)$ For any prestack of monoidal abelian groupoids $\mathfrak{P}$, there exist presheaf of monoids $\mathcal{M}$, a $\mathrm{D}\left(M\right)$-module A, a 3-cocycle $h\in Z_s^3(\mathcal{M},A)$, and an equivalence

$$\mathfrak{P}(\mathcal{M},A,h)\simeq \mathfrak{P}.$$

$\left(ii\right)$ Let $h\in Z_s^3(\mathcal{M},A)$ and $h^{\prime }\in {\mathbb{Z}}_s^3({\mathcal{M}}^{\prime },A^{\prime })$ be 3-cocycles, where $\mathcal{M}$ and ${\mathcal{M}}^{\prime }$ are presheaves of monoids, A is a $\mathrm{D}\left(\mathcal{M}\right)$-module, and $A^{\prime }$ is a $\mathrm{D}\left(M^{\prime }\right)$-module. There is an equivalence

$$\mathfrak{P}(\mathcal{M},A,h)\simeq \mathfrak{P}({\mathcal{M}}^{\prime },A^{\prime },h^{\prime })$$

if and only if there are isomorphisms $\mathfrak{f}:{\mathcal{M}}^{\prime }\cong \mathcal{M}$ and $F:A^{\prime }\cong {\mathfrak{f}}^{\ast }A$ such that

$$\left[h^{\prime }\right]=F_{\ast }^{-1}{\mathfrak{f}}^{\ast }\left(\left[h\right]\right),$$

in $H_s^3({\mathcal{M}}^{\prime },A^{\prime })$.

Proof. 

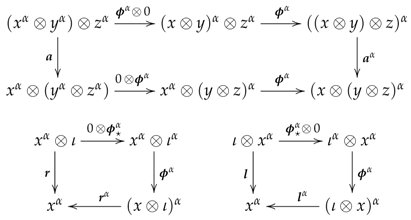
(i) Let $\mathfrak{P}$ be a prestack of monoidal abelian groupoids on $\mathrm{C}$. By Lemma 2, we can assume that for any object U of $\mathrm{C}$ the groupoid $\mathfrak{P}\left(U\right)$ is skeletal, that is, there is no morphisms between different objects. Then, we can construct a presheaf of monoids $\mathcal{M}$, a $\mathrm{D}\left(\mathcal{M}\right)$-module A, a 3-cocycle $h\in Z_s^3(\mathcal{M},A)$, and an equivalence $\mathfrak{P}(\mathcal{M},A,h)={\mathfrak{P}}_h\simeq \mathfrak{P}$ as follows:

⧫

The presheaf of monoids $\mathcal{M}$: For any object U of $\mathrm{C}$, let $\mathcal{M}\left(U\right)=\mathrm{Ob}\mathfrak{P}\left(U\right)$ be the set of objects of the monoidal abelian groupoid $\mathfrak{P}\left(U\right)$. The effect on objects of tensor functor $\otimes :\mathfrak{P}\left(U\right)\times \mathfrak{P}\left(U\right)\to \mathfrak{P}\left(U\right)$ gives a multiplication on $\mathcal{M}\left(U\right)$, simply by putting $xy=x\otimes y$, which is associative and unitary, with identity $e=\iota$, the unit object of $\mathfrak{P}\left(U\right)$, since being $\mathfrak{P}\left(U\right)$ skeletal the existence of the structure constraints ${\mathit{a}}_{x,y,z}$, ${\mathit{l}}_x$, and ${\mathit{r}}_x$ forces the equalities $\left(xy\right)z=x\left(yz\right)$ and $ex=x=xe$. Thus, $\mathcal{M}\left(U\right)$ is a monoid. For each arrow $\alpha :V\to U$ of $\mathrm{C}$, the function on objects of the monoidal functor ${\left(\right)}^{\alpha }:\mathfrak{P}\left(U\right)\to \mathfrak{P}\left(V\right)$ in (PD2) gives a homomorphism of monoids $\mathcal{M}\left(\alpha \right):\mathcal{M}\left(U\right)\to \mathcal{M}\left(V\right)$, $x\mapsto x^{\alpha }$. The equalities $e=e^{\alpha }$ and ${\left(xy\right)}^{\alpha }=x^{\alpha }{y}^{\alpha }$ follow from the presence of the structure morphisms ${\mathit{\varphi }}_{x,y}^{\alpha }$ and ${\mathit{\varphi }}_{★}^{\alpha }$, since $\mathfrak{P}\left(V\right)$ is skeletal. Furthermore, if $\beta :W\to V$ is any other arrow $\mathrm{C}$, the equality $\mathcal{M}\left(\alpha \beta \right)=\mathcal{M}\left(\beta \right)\mathcal{M}\left(\alpha \right)$, that is $x^{\alpha \beta }={\left(x^{\alpha }\right)}^{\beta }$ for any $x\in \mathcal{M}\left(U\right)$, holds due to $\mathcal{M}\left(W\right)$ is skeletal and we have the structure morphisms ${\mathit{\theta }}_x^{\alpha ,\beta }$ in (PD3). Similarly, we see that $\mathcal{M}\left(1_U\right)=i{d}_{\mathcal{M}\left(U\right)}$ because we have the morphisms ${\mathit{\theta }}_x^U:x\to x^{1_U}$ as data in (PD4). Thus, $\mathcal{M}$ is a presheaf of monoids.

⧫

The $\mathrm{D}\left(\mathcal{M}\right)$-module A: For any object U of $\mathrm{C}$ and each $x\in \mathcal{M}\left(U\right)$, let $A(U,x)={\mathrm{Aut}}_{\mathfrak{P}\left(U\right)}\left(x\right)$ the abelian group of automorphisms of x in $\mathfrak{P}\left(U\right)$. For any other $u\in \mathcal{M}\left(U\right)$, the homomorphisms (26), $A(U,x)\to A(U,ux)$, and (27), $A(U,x)\to A(U,xu)$, are respectively defined by the functors $u\otimes -:\mathfrak{P}\left(U\right)\to \mathfrak{P}\left(U\right)$ and $-\otimes u:\mathfrak{P}\left(U\right)\to \mathfrak{P}\left(U\right)$; that is, for every $a\in A(U,x)$, $ua=0_u\otimes a$ and $au=a\otimes 0_u$. If $\alpha :V\to U$ is an arrow in $\mathrm{C}$, the homomorphism (28), $A(U,x)\to A(V,x^{\alpha })$, $a\mapsto a^{\alpha }$, is defined by the monoidal functor ${\left(\right)}^{\alpha }:\mathfrak{P}\left(U\right)\to \mathfrak{P}\left(V\right)$. For $u,x,u^{\prime }\in \mathcal{M}\left(U\right)$ and $a\in A(U,x)$, the equality $\left(ua\right)u^{\prime }=u\left(a{u}^{\prime }\right)$ holds since the naturality of associativity constraint ${\mathit{a}}_{u,x,u^{\prime }}$ of $\mathfrak{P}\left(U\right)$ tell us that, in the abelian group $A(U,ux{u}^{\prime })$, we have $u\left(a{u}^{\prime }\right)+{\mathit{a}}_{u,x,u^{\prime }}={\mathit{a}}_{u,x,u^{\prime }}+\left(ua\right)u^{\prime }$. Similarly, the equality $ea=a=ae$ follows from the naturality of the unit constraints ${\mathit{l}}_x$ and ${\mathit{r}}_x$, which imply the equalities ${\mathit{l}}_x+ea=a+{\mathit{l}}_x$ and ${\mathit{r}}_x+ae=a+{\mathit{r}}_x$, and the abelianity of the group $A(U,x)$. If $\alpha :V\to U$ is an arrow in $\mathrm{C}$, the naturality of the structure morphisms ${\mathit{\varphi }}_{u,x}^{\alpha }$ and ${\mathit{\varphi }}_{x,u}^{\alpha }$, in (PD2), gives the equalities ${\left(ua\right)}^{\sigma }+{\mathit{\varphi }}_{u,x}^{\alpha }={\mathit{\varphi }}_{u,x}^{\alpha }+u^{\sigma }{a}^{\sigma }$ and ${\left(au\right)}^{\sigma }+{\mathit{\varphi }}_{x,u}^{\alpha }={\mathit{\varphi }}_{x,u}^{\alpha }+a^{\sigma }{u}^{\sigma }$. Then, as the group $A(U,x^{\alpha })$ is abelian, we conclude that ${\left(ua\right)}^{\alpha }=u^{\alpha }{a}^{\alpha }$ and ${\left(au\right)}^{\alpha }=a^{\alpha }{u}^{\alpha }$. If $\beta :W\to V$ is any other arrow $\mathrm{C}$, the equalities ${\left(a^{\alpha }\right)}^{\beta }=a^{\alpha \beta }$ are consequence of being the group $A(U,x^{\alpha \beta })$ abelian and the naturality of the structure morphisms ${\mathit{\theta }}_x^{\alpha ,\beta }$ in (PD3), which tell us that ${\left(a^{\alpha }\right)}^{\beta }+{\mathit{\theta }}_x^{\alpha ,\beta }={\mathit{\theta }}_x^{\alpha ,\beta }+a^{\alpha \beta }$. Similarly, the equality $a^{1_u}=a$ follows from the naturality of the morphisms ${\mathit{\theta }}_x^U$, which says that ${\mathit{\theta }}_x^U+a^{1_U}=a+{\mathit{\theta }}_x^U$, and the abelianity of the group $A(U,x)$. Thus, all the requirements in (30) are verified and we conclude that A is actually a $\mathrm{D}\left(\mathcal{M}\right)$-module.

⧫

The 3-cocycle $h\in Z_s^3(\mathcal{M},A)$: This is defined by

$$\left\{\begin{array}{cc}h(U;x,y,z)={\mathit{a}}_{x,y,z},\hfill & \mathrm{for}\mathrm{each}\mathrm{object}U\mathrm{of}\mathrm{C}\mathrm{and}x,y,z\in \mathcal{M}\left(U\right),\hfill \\ h(\alpha ;x,y)=-{\mathit{\varphi }}_{x,y}^{\alpha },\hfill & \mathrm{for}\mathrm{each}\mathrm{arrow}{U}_0\stackrel{\alpha }{\leftarrow }{U}_1\mathrm{of}\mathrm{C}\mathrm{and}x,y\in \mathcal{M}\left(U_0\right),\hfill \\ h(\alpha ,\beta ;x)={\mathit{\theta }}_x^{\alpha ,\beta },\hfill & \mathrm{each}\mathrm{each}\mathrm{arrows}{U}_0\stackrel{\alpha }{\leftarrow }{U}_1\stackrel{\beta }{\leftarrow }{U}_2\mathrm{of}\mathrm{C}\mathrm{and}x\in \mathcal{M}\left(U_0\right).\hfill \end{array}\right.$$

(167)

The 3-cocycle conditions $\partial h=0$ in (109), (110), (111), and (112) follow directly from the coherence Equations (132), (134), (136), and (140), respectively.

⧫

The equivalence ${\mathfrak{P}}_h\simeq \mathfrak{P}$: Previously to show such an equivalence, it is worth analyzing ${\mathfrak{P}}_h$ in relation to $\mathfrak{P}$:

Concerning the data in (PD1), a direct comparison shows that, for each object U of $\mathrm{C}$, both monoidal groupoids ${\mathfrak{P}}_h\left(U\right)$ and $\mathfrak{P}\left(U\right)$ have the same underlying groupoid and the same tensor product, as for any $a\in {\mathrm{Aut}}_{\mathfrak{P}\left(U\right)}\left(x\right)$ and $b\in {\mathrm{Aut}}_{\mathfrak{P}\left(U\right)}\left(y\right)$, $x\otimes y=xy$ and

$$a\otimes b=(a+0_x)\otimes (0_y+b)=(a\otimes 0_y)+(0_x\otimes b)=ay+xb,$$

(168)

as well as the same associativity constraint $\mathit{a}$ and the same unit object $\iota$. However, they have different left and right unit constraints, since in the original $\mathfrak{P}\left(U\right)$ they are ${\mathit{l}}_x:\iota \otimes x=x\to x$ and ${\mathit{r}}_x:x\otimes \iota =x\to x$, whereas in ${\mathfrak{P}}_h\left(U\right)$ they are respectively defined as

$$\left\{\begin{array}{c}-{\mathit{a}}_{\iota ,\iota ,x}:\iota \otimes x=(\iota \otimes \iota )\otimes x=x\to \iota \otimes (\iota \otimes x)=x,\hfill \\ {\mathit{a}}_{x,\iota ,\iota }:x\otimes \iota =(x\otimes \iota )\otimes \iota =x\to x\otimes (\iota \otimes \iota )=x,\hfill \end{array}\right.$$

(169)

With regards to the data in (PDA2), a direct comparison shows that, for any arrow $\alpha :U_1\to U_0$ in $\mathrm{C}$, both monoidal functors ${\left(\right)}^{\alpha }:{\mathfrak{P}}_h\left(U_0\right)\to {\mathfrak{P}}_h\left(U_1\right)$ and ${\left(\right)}^{\alpha }:\mathfrak{P}\left(U_1\right)\to \mathfrak{P}\left(U_0\right)$ coincide on objects and on morphisms, as well as they have the same structure morphisms ${\mathit{\varphi }}_{x,y}^{\alpha }:x^{\alpha }\otimes y^{\alpha }\to {(x\otimes y)}^{\alpha }$. But they have different unit structure morphism since, while in the original $\mathfrak{P}$ it is ${\mathit{\varphi }}_{\ast }^{\alpha }:\iota \to {\iota }^{\alpha }=\iota$, in ${\mathfrak{P}}_h$ it is $-{\mathit{\varphi }}_{\iota ,\iota }^{\alpha }:\iota ={\iota }^{\alpha }\otimes {\iota }^{\alpha }\to {(\iota \otimes \iota )}^{\alpha }=\iota$. Similarly, we see that the data in (PDA3) and in (PDA4) for both ${\mathfrak{P}}_h$ and $\mathfrak{P}$ are given by the same monoidal transformations ${\mathit{\theta }}^{\alpha ,\beta }$ and the same morphisms ${\mathit{\theta }}_x^U:x\to x^{1_U}=x$ (for these last, note that the equalities ${\mathit{\theta }}_x^U=-{\mathit{\theta }}_x^{1_U,1_U}$ follow from (141) by taking $\alpha =1_U$ therein).

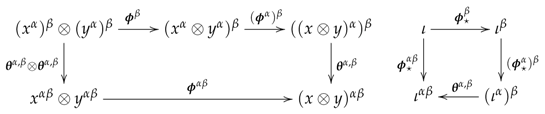
Then, an equivalence ${\mathfrak{F}}^U:{\mathfrak{P}}_h\to \mathfrak{P}$ is defined by the following data:

(EPD1) For each object U of $\mathrm{C}$, the monoidal functor ${\mathfrak{F}}^U:{\mathfrak{P}}_h\left(U\right)\to \mathfrak{P}\left(U\right)$ acts between the underlying groupoids as the identity, that is, ${\mathfrak{F}}^U(x\stackrel{a}{\to }x)=(x\stackrel{a}{\to }x)$. Its structure morphisms ${\mathsf{\Psi }}_{x,y}^U:x\otimes y\to x\otimes y$ are all identities, that is, ${\mathsf{\Psi }}_{x,y}^U=0_{x\otimes y}$, and the structure morphism ${\mathsf{\Psi }}_{★}^U:\iota \to \iota$ is defined by ${\mathsf{\Psi }}_{★}^U={\mathit{l}}_{\iota }:\iota \otimes \iota =\iota \to \iota$ ($={\mathit{r}}_{\iota }$, see Proposition 1.1 in Reference [25]), the unit constraint of $\mathfrak{P}\left(U\right)$ at the unit object $\iota$.

(EPD2) For any arrow $\alpha :U_1\to U_0$, the monoidal transformation ${\mathsf{\Gamma }}^{\alpha }$ is the identity transformation on the functor ${\left(\right)}^{\alpha }:\mathfrak{P}\left(U_0\right)\to \mathfrak{P}\left(U_1\right)$, that is, ${\mathsf{\Gamma }}_x^{\alpha }=0_{x^{\alpha }}$ for any object x of $\mathfrak{P}\left(U_0\right)$.

Notice that, for any object U of $\mathrm{C}$, the naturality of the morphisms ${\mathsf{\Psi }}_{x,y}^U=0_{x\otimes y}$ simply means that the tensor product ⊗ is the same in both ${\mathfrak{P}}_h\left(U\right)$ and $\mathfrak{P}\left(U\right)$, which is true as we commented before, and the coherence condition (142) is obviously satisfied, since the associativity constraints also agree in both monoidal groupoids. Here, the requirements in (143) read

$${\mathit{a}}_{x,\iota ,\iota }+(0_x\otimes {\mathit{l}}_{\iota })={\mathit{r}}_x,-{\mathit{a}}_{\iota ,\iota ,x}+({\mathit{r}}_{\iota }\otimes 0_x)={\mathit{l}}_x.$$

(170)

To verify them, first observe that, by naturality, we have the equalities ${\mathit{r}}_x+({\mathit{r}}_x\otimes 0_{\iota })={\mathit{r}}_x+{\mathit{r}}_{x\otimes \iota }$ and ${\mathit{l}}_x+(0_{\iota }\otimes {\mathit{l}}_x)={\mathit{l}}_x+{\mathit{l}}_{\iota \otimes x}$, whence ${\mathit{r}}_x\otimes 0_{\iota }={\mathit{r}}_{x\otimes \iota }={\mathit{r}}_x$ and $0_{\iota }\otimes {\mathit{l}}_x={\mathit{l}}_{\iota \otimes x}={\mathit{l}}_x$. Then, taking $y=\iota$ in (133) we obtain the equality $(0_x\otimes {\mathit{l}}_{\iota })+{\mathit{a}}_{x,\iota ,\iota }={\mathit{r}}_x\otimes 0_{\iota }={\mathit{r}}_x$, while taking $x=\iota$ and replacing y with x in (133) we obtain $({\mathit{r}}_{\iota }\otimes 0_x)-{\mathit{a}}_{\iota ,\iota ,x}=0_{\iota }\otimes {\mathit{l}}_x={\mathit{l}}_x$. Hence, Equation (170) hold since the group ${\mathrm{Aut}}_{\mathfrak{P}\left(U\right)}\left(x\right)$ is abelian.

Checking the remaining requirements, we see that Equations (145), (147) and (148) obviously hold, while (146) reads ${\left({\mathit{r}}_{\iota }\right)}^{\alpha }+{\mathit{\varphi }}_{★}^{\alpha }=-{\mathit{\varphi }}_{\iota ,\iota }^{\alpha }+{\mathit{r}}_{\iota }$. To its verification, note that, by naturality, we have the equality ${\mathit{r}}_{\iota }+(0_{\iota }\otimes {\mathit{\varphi }}_{★}^{\alpha })={\mathit{\varphi }}_{★}^{\alpha }+{\mathit{r}}_{\iota }$. Hence, $0_{\iota }\otimes {\mathit{\varphi }}_{★}^{\alpha }={\mathit{\varphi }}_{★}^{\alpha }$ since the group ${\mathrm{Aut}}_{\mathfrak{P}\left(U\right)}\left(\iota \right)$ is abelian. Then, taking $x=\iota$ in (135), we obtain the required equality in the equivalent form ${\left({\mathit{r}}_{\iota }\right)}^{\alpha }+{\mathit{\varphi }}_{\iota ,\iota }^{\alpha }+{\mathit{\varphi }}_{★}^{\alpha }={\mathit{r}}_{\iota }$.

(ii) Notice that ${\mathfrak{P}}_h=\mathfrak{P}(\mathcal{M},A,h)$ and ${\mathfrak{P}}_{h^{\prime }}=\mathfrak{P}(\mathcal{M},A,h^{\prime })$ are equivalent if and only if they are isomorphic since, for any object U of $\mathrm{C}$, both groupoids ${\mathfrak{P}}_h\left(U\right)$ and ${\mathfrak{P}}_{h^{\prime }}\left(U\right)$ are skeletal.

Suppose first that $\mathfrak{f}:{\mathcal{M}}^{\prime }\cong \mathcal{M}$ an isomorphism of presheaves and $F:A^{\prime }\cong {\mathfrak{f}}^{\ast }A$ an isomorphism of $\mathrm{D}\left({\mathcal{M}}^{\prime }\right)$-modules such that ${\mathfrak{f}}^{\ast }\left(\left[h\right]\right)=F_{\ast }\left(\left[h^{\prime }\right]\right)$. This means that there is a 2-cochain $g\in C^2({\mathcal{M}}^{\prime },{\mathfrak{f}}^{\ast }A)$ such that the equations below hold.

$$\begin{array}{cc}\hfill F\left(h^{\prime }(U;x,y,z)\right)=& h(U;\mathfrak{f}(x),\mathfrak{f}(y),\mathfrak{f}(z\left)\right)+\mathfrak{f}\left(x\right)g(U;y,z)-g(U;xy,z)+g(U;x,yz)\hfill \\ & -g(U;x,y)\mathfrak{f}(z),\hfill \end{array}$$

(171)

$$\begin{array}{cc}\hfill F\left(h^{\prime }(\alpha ;x,y)\right)=& h(\alpha ;\mathfrak{f}(x),\mathfrak{f}(y))+g(U_1;x^{\alpha },y^{\alpha })-g{(U_0;x,y)}^{\alpha }-{\mathfrak{f}\left(x\right)}^{\alpha }g(\alpha ;y)\hfill \\ & +g(\alpha ;xy)-g(\alpha ;x)\mathfrak{f}{\left(y\right)}^{\alpha },\hfill \end{array}$$

(172)

$$\begin{array}{c}\hfill F\left(h^{\prime }(\alpha ,\beta ;x\right)=h(\alpha ,\beta ;\mathfrak{f}(x))+g(\beta ;x^{\alpha })-g(\alpha \beta ;x)+g{(\alpha ,x)}^{\beta }.\end{array}$$

(173)

Then, we can define an isomorphism $\mathfrak{F}:{\mathfrak{P}}_{h^{\prime }}\cong {\mathfrak{P}}_h$ by the following data:

(EPD1) For each object U of $\mathrm{C}$, the monoidal isomorphism ${\mathfrak{F}}^U:{\mathfrak{P}}_{h^{\prime }}\left(U\right)\to {\mathfrak{P}}_h\left(U\right)$ acts, at the level of the underlying groupoids, by ${\mathfrak{F}}^U(a:x\to x)=(F\left(a\right):\mathfrak{f}\left(x\right)\to \mathfrak{f}\left(x\right))$, and its structure constrains are respectively defined by ${\mathsf{\Psi }}_{x,y}^U=g(U;x,y):\mathfrak{f}\left(x\right)\mathfrak{f}\left(y\right)=\mathfrak{f}\left(xy\right)\to \mathfrak{f}\left(xy\right)$ and ${\mathsf{\Psi }}_{\ast }^U=-g(U,e,e):e\to \mathfrak{f}\left(e\right)=e$.

(EPD2) For each arrow $\alpha :U_1\to U_0$ of $\mathrm{C}$, the monoidal transformation ${\mathsf{\Gamma }}^{\alpha }$ is given by

$${\mathsf{\Gamma }}_x^{\alpha }=-g(\alpha ;x):\mathfrak{f}{\left(x\right)}^{\alpha }=\mathfrak{f}\left(x^{\alpha }\right)\to \mathfrak{f}\left(x^{\alpha }\right).$$

(174)

So defined, it is plain to see that every ${\mathfrak{F}}^U$ is an isomorphism of groupoids. The naturality of the isomorphisms ${\mathsf{\Psi }}_{x,y}^U$ holds since F is a morphism of $\mathrm{D}\left(\mathcal{M}\right)$-modules and the groups $A(U,\mathfrak{f}(xy))$ are abelian. Equation (171) directly provides the verification of the coherence condition (142), as well as that of (143) just by taking $y=e=z$ therein. Similarly, the naturality of the morphisms ${\mathsf{\Gamma }}_x^{\alpha }$ follows from being F a morphism of $\mathrm{D}\left(\mathcal{M}\right)$-modules and the groups $A(U,\mathfrak{f}(x))$ abelian, whereas Equation (172) implies conditions (145) and (146), taking $x=e=y$ for the last one. Finally, say that (147) holds thanks to (173), from which one verifies also (148) by taking $\alpha =1_U=\beta$ therein.

Finally, we can prove the converse simply by retracting our above steps: Suppose we have an isomorphism $\mathfrak{F}:{\mathfrak{P}}_{h^{\prime }}\cong {\mathfrak{P}}_h$. Then, for each U of $\mathrm{C}$, let $\mathfrak{f}={\mathfrak{F}}^U:{\mathcal{M}}^{\prime }\left(U\right)\to \mathcal{M}\left(U\right)$ be the function on objects of the monoidal isomorphism ${\mathfrak{F}}^U:{\mathfrak{P}}_{h^{\prime }}\left(U\right)\to {\mathfrak{P}}_h\left(U\right)$. Since ${\mathfrak{P}}_h\left(U\right)$ is skeletal, the existence of the morphisms data ${\mathsf{\Psi }}_{x,y}^U$ and ${\mathsf{\Psi }}_{\ast }^U$ in (EPD1) forces the equalities $\mathfrak{f}\left(xy\right)=\mathfrak{f}\left(x\right)\mathfrak{f}\left(y\right)$ and $\mathfrak{f}\left(e\right)=e$. Similarly, for each $\alpha :U_1\to U_0$ in $\mathrm{C}$, the presence of the morphisms ${\mathsf{\Gamma }}_x^{\alpha }$ in the data (EPD2) implies the equalities $\mathfrak{f}\left(x^{\alpha }\right)=\mathfrak{f}{\left(x\right)}^{\alpha }$. Thus $\mathfrak{f}:{\mathcal{M}}^{\prime }\to \mathcal{M}$ is an isomorphism of presheaves of monoids. Now, if for each object U of $\mathrm{C}$ and $x\in {\mathcal{M}}^{\prime }\left(U\right)$, we define the isomorphism $F:A^{\prime }(U,x)\to A(U,\mathfrak{f}(x))$ by $F\left(a\right)={\mathfrak{F}}^U\left(a\right)$, the naturality of the morphisms ${\mathsf{\Psi }}_{x,y}^U$ and ${\mathsf{\Gamma }}_x^{\alpha }$ just tell us that $F:A^{\prime }\to {\mathfrak{f}}^{\ast }A$ is an isomorphism of $\mathrm{D}\left({\mathcal{M}}^{\prime }\right)$-modules. Finally, if we take the 2-cochain $g\in C^2({\mathcal{M}}^{\prime },{\mathfrak{f}}^{\ast }A)$ defined by $g(U;x,y)={\mathsf{\Psi }}_{x,y}^U$ and $g(\alpha ;x)={\mathsf{\Gamma }}_x^{\alpha }$, we easily see that that the coherence conditions (142), (145) and (147) imply the equalities in (171), (172), and (173), respectively. Thus, we have $F_{\ast }\left(h^{\prime }\right)={\mathfrak{f}}^{\ast }\left(h\right)+\partial g$, whence $F_{\ast }\left(\left[h^{\prime }\right]\right)={\mathfrak{f}}^{\ast }\left(\left[h\right]\right)$ in $H_s^3({\mathcal{M}}^{\prime },{\mathfrak{f}}^{\ast }A)$, and therefore $\left[h^{\prime }\right]=F_{\ast }^{-1}{\mathfrak{f}}^{\ast }\left(\left[h\right]\right)$ in $H_s^3({\mathcal{M}}^{\prime },A^{\prime })$. □

10. The Particular Case Where the Monoids Are Groups

In this section, we review how our results above specialize when we limit our attention to presheaves of groups $\mathcal{G}:{\mathrm{C}}^{\mathrm{op}}\to \mathbf{Gp}$.

10.1. the Coefficients for the Cohomology of a Presheaf of Groups

The coefficients for the cohomology of a presheaf of groups admit an easier description than that given in Section 3 for the coefficients for the cohomology of a presheaf of monoids. This is as follows.

Definition 3.

Let $\mathcal{G}$ be a presheaf of groups on $\mathrm{C}$. A$\mathcal{G}$-module is a presheaf of abelian groups on $\mathrm{C}$ (= ${\mathrm{C}}^{\mathrm{op}}$-module) A such that for each object U of $\mathrm{C}$ the abelian group $A\left(U\right)$ is a left $\mathcal{G}\left(U\right)$-module and for each arrow $\sigma :V\to U$ of $\mathrm{C}$ the induced homomorphism ${\left(\right)}^{\sigma }:A\left(U\right)\to A\left(V\right)$ is compatible with the modules structures via the group homomorphism ${\left(\right)}^{\sigma }:\mathcal{G}\left(U\right)\to \mathcal{G}\left(V\right)$; that is, for $x\in \mathcal{G}\left(U\right)$ and $a\in A\left(U\right)$

$${(x·a)}^{\sigma }=x^{\sigma }·a^{\sigma }.$$

(175)

In other words, such that the action maps $\mathcal{G}\left(U\right)\times A\left(U\right)\to A\left(U\right)$, $(x,a)\mapsto x·a$, define a natural transformation $\mathcal{G}\times A\to A$. A morphism $A\to A^{\prime }$ of $\mathcal{G}$-modules is a morphism of presheaves of abelian groups such that, for each object U of $\mathrm{C}$, the homomorphism $A\left(U\right)\to A^{\prime }\left(U\right)$ is of $\mathcal{G}\left(U\right)$-modules.

Let $\mathcal{G}$-Mod denote the category of $\mathcal{G}$-modules. There is a full and faithful embedding

$$\mathcal{G}\text{-}\mathrm{Mod}\hookrightarrow \mathrm{D}\left(\mathcal{G}\right)\text{-}\mathrm{Mod}$$

(176)

which identifies each $\mathcal{G}$-module A to the $\mathrm{D}\left(\mathcal{G}\right)$-module, equally denoted by A, such that $A(U,x)=A\left(U\right)$ for each object U of $\mathrm{C}$ and $x\in \mathcal{G}\left(U\right)$, and $v_0{a}^{\sigma }{v}_1=v_0·a^{\sigma }$, for each $\sigma :V\to U$ in $\mathrm{C}$ and $v_0,v_1\in \mathcal{G}\left(V\right)$.

Proposition 9.

For any presheaf of groups $\mathcal{G}$, the embedding (176) above is an equivalence of categories.

Proof. 

Let A be a $\mathrm{D}\left(\mathcal{G}\right)$-module. Define $A\left(e\right)$ to be the $\mathcal{G}$-module whose underlying presheaf $A\left(e\right):{\mathrm{C}}^{\mathrm{op}}\to \mathbf{Ab}$ assigns to each $U\in \mathrm{ObC}$ the abelian group $A(U,e)$ and to each morphism $\sigma :V\to U$ of $\mathrm{C}$ the homomorphism ${\left(\right)}^{\sigma }:A(U,e)\to A(V,e^{\sigma }=e)$. For each object U of $\mathrm{C}$, the $\mathcal{G}\left(U\right)$-action on $A(U,e)$ is given by $u·a=ua{u}^{-1}$. Then, an isomorphism of $\mathrm{D}\left(\mathcal{G}\right)$-modules $A\left(e\right)\cong A$ is given by the isomorphisms $F:A(U,e)\cong A(U,x)$ defined by $F\left(a\right)=ax$, for any $U\in \mathrm{ObC}$ and $x\in \mathcal{G}\left(U\right)$. □

It follows that there is no loss of generality in assuming that the coefficients for the cohomology groups of a presheaf of groups $\mathcal{G}$ are $\mathcal{G}$-modules. For these, all our constructions and results rewrite more simply and revisit those established in Reference [26]. Notice that, when we plug an $\mathcal{G}$-module A into the complex of cochains $C_s^{•}(\mathcal{G},A)$ of Section 6, we just obtain (up to normalization) the cochain complex shown in Reference [26] to compute the cohomology groups of $\mathcal{G}$ with coefficients in A.

10.2. Derivations of Presheaves of Groups

Let $\mathcal{G}$ be a presheaf of groups on $\mathrm{C}$. By definition,

$$H_s^n(\mathcal{G},-)=R^{n-1}\mathrm{Der}(\mathcal{G},-):\mathcal{G}\text{-}\mathrm{Mod}\to \mathbf{Ab}.$$

(177)

Here, a derivation of $\mathcal{G}$ in a $\mathcal{G}$-module A, say $d:\mathcal{G}\to A$, simply consists of a natural family of ordinary derivations $d_U:\mathcal{G}\left(U\right)\to A\left(U\right)$, one for each $U\in \mathrm{ObC}$. That is, the maps $d_U$ satisfy $d_U\left(xy\right)=x·d_U\left(y\right)+d_U\left(y\right)$ and, for any $\sigma :V\to U$ in $\mathrm{C}$, the equalities $d_U{\left(x\right)}^{\sigma }=d_V\left(x^{\sigma }\right)$ hold.

The $\mathcal{G}$-module $\mathbb{Z}\mathcal{G}$ in (36) assigns to each object U of $\mathrm{C}$ the underlying group of the ordinary integral group ring $\mathbb{Z}\mathcal{G}\left(U\right)=\mathbb{Z}\{x\mid x\in \mathcal{G}(U\left)\right\}$ turned into an $\mathcal{G}\left(U\right)$-module in the obvious way and, if $\sigma :V\to U$ is a morphism of $\mathrm{C}$, the corresponding homomorphism ${\left(\right)}^{\sigma }:\mathbb{Z}\mathcal{G}\left(U\right)\to \mathbb{Z}\mathcal{G}\left(V\right)$ is just the induced by ${\left(\right)}^{\sigma }:\mathcal{G}\left(U\right)\to \mathcal{G}\left(V\right)$. Then, the isomorphism in Proposition 5 reads

$$\mathrm{Der}(\mathcal{G},A)\cong {\mathrm{Hom}}_{\mathcal{G}}(I\mathcal{G},A),$$

(178)

where $I\mathcal{G}=\mathrm{Ker}(\mathbb{Z}\mathcal{G}\to \mathbb{Z})$ is the $\mathcal{G}$-module assigning to each object U of $\mathrm{C}$ the ordinary ideal augmentation $I\mathcal{G}\left(U\right)$ of the group $\mathcal{G}\left(U\right)$.

10.3. Singular Extensions of Presheaves of Groups

The main result in Section 8 particularizes here by giving the cohomological classification of short exact sequences of presheaves of groups on $\mathrm{C}$

$$0\to A\stackrel{\mathfrak{i}}{\to }\mathcal{E}\stackrel{\mathfrak{f}}{\to }\mathcal{G}\to 1$$

(179)

in which A is of abelian groups. Such a short exact sequence determines a $\mathcal{G}$-module structure on A in which, for each object U of $\mathrm{C}$, the action of the group $\mathcal{G}\left(U\right)$ on the abelian group $A\left(U\right)$ is determined by the formula ${\mathfrak{i}}_U(x·a)=w{\mathfrak{i}}_U\left(a\right)w^{-1}$, where $w\in {\mathfrak{f}}_U^{-1}\left(x\right)$ is an (any) element of the fibre of the epimorphism ${\mathfrak{f}}_U:\mathcal{E}\left(U\right)\to \mathcal{G}\left(U\right)$ at x. If A is a $\mathcal{G}$-module, we define a singular extension of $\mathcal{G}$ by A as a short exact sequence (179) such that the induced $\mathcal{G}$-module structure on A is the given one.

Proposition 10.

A singular extension of a presheaf of groups $\mathcal{G}$ by a $\mathcal{G}$-module A is the same thing as an extension of $\mathcal{G}$ by A (as defined in Section 8).

Proof. 

Suppose first that $(\mathcal{E},\mathfrak{f},+)$ is an extension of $\mathcal{G}$ by A. Then, we claim, every monoid $\mathcal{E}\left(U\right)$, $U\in \mathrm{ObC}$, is a group. In effect, let $w\in \mathcal{E}\left(U\right)$ and suppose that ${\mathfrak{f}}_U\left(w\right)=x$. Let us choose any $w^{\prime }\in f_U^{-1}\left(x^{-1}\right)$. Since $w{w}^{\prime }\in {\mathfrak{f}}_U^{-1}\left(e\right)$, we can write $w{w}^{\prime }=a+e$ for some $a\in A\left(U\right)$. Then,

$$w(-x^{-1}·a+w^{\prime })\stackrel{\left(115\right)}{=}-\left(x{x}^{-1}\right)·a+w{w}^{\prime }=-a+a+e=e,$$

so that $w^{-1}=-x^{-1}a+w^{\prime }$ is an inverse of w in $\mathcal{E}\left(U\right)$. Now, the bijections $\mathfrak{i}:A\left(U\right)\cong {\mathfrak{f}}_U^{-1}\left(e\right)=\mathrm{Ker}\left({\mathfrak{f}}_U\right)$, $\mathfrak{i}\left(a\right)=a+e$, define an isomorphism of presheaves of groups $\mathfrak{i}:A\cong \mathrm{Ker}\left(\mathfrak{f}\right)$ since, for any $U\in \mathrm{ObC}$,

$${\mathfrak{i}}_U\left(a\right){\mathfrak{i}}_U\left(a^{\prime }\right)=(a+e)(a^{\prime }+e)\stackrel{\left(115\right)}{=}(a+a^{\prime }+e)={\mathfrak{i}}_U(a+a^{\prime }),$$

and, for any $\sigma :V\to U$ in $\mathrm{C}$,

$${\mathfrak{i}}_V\left(a^{\sigma }\right)=a^{\sigma }+e=a^{\sigma }+e^{\sigma }\stackrel{\left(116\right)}{=}{(a+e)}^{\sigma }={\mathfrak{i}}_U{\left(a\right)}^{\sigma }.$$

Thus, $0\to A\stackrel{\mathfrak{i}}{\to }\mathcal{E}\stackrel{\mathfrak{f}}{\to }\mathcal{G}\to 1$ is an extension, which is singular since, for any $U\in \mathrm{ObC}$, $a\in A\left(U\right)$ and $w\in {\mathfrak{f}}_U^{-1}\left(x\right)$,

$$w{\mathfrak{i}}_u\left(a\right)w^{-1}=w(a+e)w^{-1}\stackrel{\left(115\right)}{=}(x·a+w)w^{-1}\stackrel{\left(115\right)}{=}x·a+e={\mathfrak{i}}_U(x·a).$$

Conversely, any singular extension $0\to A\stackrel{\mathfrak{i}}{\to }\mathcal{E}\stackrel{\mathfrak{f}}{\to }\mathcal{G}\to 1$ can be regarded as an extension, where the simply-transitive actions $+:A\left(U\right)\times {\mathfrak{f}}_U^{-1}\left(x\right)\to {\mathfrak{f}}_U^{-1}\left(x\right)$ are given by $a+w={\mathfrak{i}}_U\left(a\right)w$. The requirements in (115) and (116) are satisfied, since

$$\begin{array}{cc}\hfill (a+w)(a^{\prime }+w^{\prime })=& {\mathfrak{i}}_U\left(a\right)w{\mathfrak{i}}_U\left(a^{\prime }\right)w^{\prime }={\mathfrak{i}}_U\left(a\right)w{\mathfrak{i}}_U\left(a^{\prime }\right)w^{-1}w{w}^{\prime }={\mathfrak{i}}_U\left(a\right){\mathfrak{i}}_U(x·a^{\prime })w{w}^{\prime }\hfill \\ & ={\mathfrak{i}}_U(a+x·a^{\prime })w{w}^{\prime }=a+x·a^{\prime }+w{w}^{\prime },\hfill \\ \hfill {(a+w)}^{\sigma }=& {\left({\mathfrak{i}}_U\left(a\right)w\right)}^{\sigma }={\mathfrak{i}}_U{\left(a\right)}^{\sigma }{w}^{\sigma }={\mathfrak{i}}_V\left(a^{\sigma }\right)w^{\sigma }=a^{\sigma }+w^{\sigma }.\hfill \end{array}$$

 □

When two singular extensions $0\to A\stackrel{\mathfrak{i}}{\to }\mathcal{E}\stackrel{\mathfrak{f}}{\to }\mathcal{G}\to 1$ and $0\to A\stackrel{{\mathfrak{i}}^{\prime }}{\to }{\mathcal{E}}^{\prime }\stackrel{{\mathfrak{f}}^{\prime }}{\to }\mathcal{G}\to 1$ are viewed as extensions, they are isomorphic if and only if there is an isomorphism of presheaves of groups $\mathfrak{g}:\mathcal{E}\cong {\mathcal{E}}^{\prime }$ such that ${\mathfrak{f}}^{\prime }\mathfrak{g}=\mathfrak{f}$ and $\mathfrak{g}\mathfrak{i}={\mathfrak{i}}^{\prime }$. Then, Theorem 3 rewrites as follows (cf. Theorem 7.2 in Reference [26]).

Theorem 5.

The isomorphism classes of singular extensions of a presheaf of groups $\mathcal{G}$ by a $\mathcal{G}$-module A correspond bijectively to the elements of $H_s^2(\mathcal{G},A)$.

10.4. Prestacks of Categorical Groups

The results in Section 9 specialize here by giving the cohomological classification of prestacks of categorical groups. Let us recall that a categorical group (aka Gr-category or 2-group) is a monoidal groupoid $\mathrm{G}=(\mathrm{G},\otimes ,\iota ,\mathit{a},\mathit{l},\mathit{r})$ such that, for any object x, the endofunctor $x\otimes -:\mathrm{G}\to \mathrm{G}$ is an autoequivalence [5,25,27,28].

Lemma 3.

In any categorical group, the underlaying groupoid is abelian.

Proof. 

Let $\mathrm{G}$ be a categorical group. The group ${\mathrm{Aut}}_{\mathrm{G}}\left(\iota \right)$ is abelian since the multiplication

$${\mathrm{Aut}}_{\mathrm{G}}\left(\iota \right)\times {\mathrm{Aut}}_{\mathrm{G}}\left(\iota \right)\to {\mathrm{Aut}}_{\mathrm{G}}\left(\iota \right),(a,b)\mapsto {\mathit{r}}_{\iota }(a\otimes b){\mathit{r}}_{\iota }^{-1},$$

(180)

is a group homomorphisms [29]. For any object x, the group ${\mathrm{Aut}}_{\mathrm{G}}\left(x\right)$ is also abelian, since we have the group isomorphism ${\mathrm{Aut}}_{\mathrm{G}}\left(\iota \right)\cong {\mathrm{Aut}}_{\mathrm{G}}\left(x\right),a\mapsto {\mathit{r}}_x(i{d}_x\otimes a){\mathit{r}}_x^{-1}$. □

The 2-category of categorical groups is then a full 2-subcategory of the 2-category of monoidal abelian groupoids and therefore, for any small category $\mathrm{C}$, the 2-category of prestacks of categorical groups on $\mathrm{C}$ is a full 2-subcategory of the 2-category of prestacks of monoidal abelian groupoids on $\mathrm{C}$. In particular, two prestacks of categorical groups are equivalent if and only if they are equivalent as prestacks of monoidal abelian groupoids. In order to their classification, recall that a monoidal groupoid $(\mathrm{G},\otimes ,\iota ,\mathit{a},\mathit{l},\mathit{r})$ is a categorical group if and only if every object x has a quasi-inverse with respect to the tensor product, that is, there is an object $x^{\prime }$ with an arrow $x\otimes x^{\prime }\to \iota$. Then, for any presheaf of groups $\mathcal{G}$, any $\mathcal{G}$-module A and any 3-cocycle $h\in Z^3(\mathcal{G},A)$, the prestack of monoidal abelian groupoids $\mathfrak{P}(\mathcal{G},A,h)$ built as in (149) is easily recognized to be a prestack of categorical groups. Then, Theorem 4 particularizes as follows (cf. Theorem 8.5 in Reference [26]).

Theorem 5.

$\left(i\right)$ For any prestack of categorical groups $\mathfrak{P}$, there exist presheaf of groups $\mathcal{G}$, a $\mathcal{G}$-module A, a 3-cocycle $h\in Z_s^3(\mathcal{G},A)$ and an equivalence

$$\mathfrak{P}(\mathcal{G},A,h)\simeq \mathfrak{P}.$$

$\left(ii\right)$ Let $h\in Z_s^3(\mathcal{G},A)$ and $h^{\prime }\in {\mathbb{Z}}_s^3({\mathcal{G}}^{\prime },A^{\prime })$ be 3-cocycles, where $\mathcal{G}$ and ${\mathcal{G}}^{\prime }$ are presheaves of groups, A is a $\mathcal{G}$-module and $A^{\prime }$ is a ${\mathcal{G}}^{\prime }$-module. There is an equivalence

$$\mathfrak{P}(\mathcal{G},A,h)\simeq \mathfrak{P}({\mathcal{G}}^{\prime },A^{\prime },h^{\prime })$$

if and only if there is an isomorphism of presheaves of groups $\mathfrak{f}:{\mathcal{G}}^{\prime }\cong \mathcal{G}$ and a isomorphism of ${\mathcal{G}}^{\prime }$-modules $F:A^{\prime }\cong {\mathfrak{f}}^{\ast }A$ such that the equality of cohomology classes in $H_s^3({\mathcal{G}}^{\prime },A^{\prime })$ below holds.

$$\left[h^{\prime }\right]=F_{\ast }^{-1}{\mathfrak{f}}^{\ast }\left(\left[h\right]\right)$$

Proof. 

(i) Let $\mathfrak{P}$ be a prestack of categorical groups on $\mathrm{C}$. By Theorem 4(i), there are a presheaf of monoids $\mathcal{M}$, a $\mathrm{D}\left(\mathcal{M}\right)$-module A, a 3-cocycle $h\in Z_s^3(\mathcal{M},A)$ and an equivalence $\mathfrak{P}(\mathcal{M},A,h)={\mathfrak{P}}_h\simeq \mathfrak{P}$. Then, ${\mathfrak{P}}_h$ is a prestack of categorical groups as $\mathfrak{P}$ is; that is, ${\mathfrak{P}}_h\left(U\right)$ is a categorical group, for every object U of $\mathrm{C}$. Therefore, for any $x\in \mathcal{M}\left(U\right)=\mathrm{Ob}{\mathfrak{P}}_h\left(U\right)$ it must exist another $x^{\prime }\in \mathcal{M}\left(U\right)$ with a morphism $x\otimes x^{\prime }=x{x}^{\prime }\to \iota =e$ in ${\mathfrak{P}}_h\left(U\right)$. As the groupoid ${\mathfrak{P}}_h\left(U\right)$ is skeletal, necessarily $x{x}^{\prime }=e$ in $\mathcal{M}\left(U\right)$, which means that $x^{\prime }$ is an inverse of x in the monoid $\mathcal{M}\left(U\right)$. Therefore, every $\mathcal{M}\left(U\right)$ is a group and $\mathcal{G}=\mathcal{M}$ is actually a presheaf of groups.

Now, by Proposition 9, there is a $\mathcal{G}$-module $A^{\prime }$ with an isomorphism of $\mathrm{D}\left(\mathcal{G}\right)$-modules $F:A^{\prime }\cong A$. Then, Theorem 4$\left(ii\right)$ gives the existence of an equivalence $\mathfrak{P}(\mathcal{G},A,h)\simeq \mathfrak{P}(\mathcal{G},A^{\prime },F_{\ast }^{-1}\left(h\right))$, whence an equivalence $\mathfrak{P}(\mathcal{G},A^{\prime },F_{\ast }^{-1}\left(h\right))\simeq \mathfrak{P}$ follows.

(ii) This follows directly from Theorem 4(ii). □