Syzygies, Betti Numbers, and Regularity of Cover Ideals of Certain Multipartite Graphs
Abstract
1. Introduction
2. Preliminaries
3. Bipartite Graphs
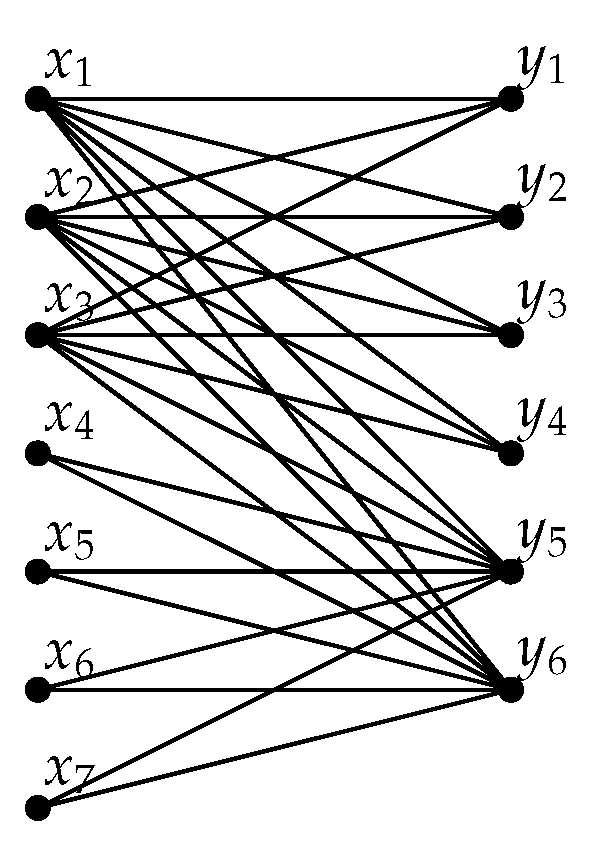
3.1. Discussion
- If , then it can be seen that for ,Since and , this expression attains maximum when i and j attain minimum, i.e., if and . Therefore, . Thus, in this case, . It can also be noted that, since , it follows from Theorem 1 that . Therefore, in this case, the stability index is also equal to 1.
- If , then for ,Therefore, , and therefore . Note that in this case, the stability index is 2.
- : Note that, in this case, . We haveSince . Since and , the above expression attains the maximum when i attains the maximum and j attains the minimum, i.e., if and . Therefore, and hence .
- : In this case, andAs in the previous case, one can conclude that the maximum is attained when and . Therefore, . Thus .
- : As done earlier, one can conclude that , and therefore .
4. Complete Multipartite Graphs
4.1. Complete Tripartite:
4.2. Complete 4-Partite Graphs
4.3. Complete m-Partite Graphs
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Peeva, I.; Stillman, M. The minimal free resolution of a Borel ideal. Expo. Math. 2008, 26, 237–247. [Google Scholar] [CrossRef][Green Version]
- Buchsbaum, D.A.; Eisenbud, D. Generic free resolutions and a family of generically perfect ideals. Adv. Math. 1975, 18, 245–301. [Google Scholar] [CrossRef]
- Guardo, E.; Van Tuyl, A. Powers of complete intersections: graded Betti numbers and applications. Ill. J. Math. 2005, 49, 265–279. [Google Scholar] [CrossRef]
- Conca, A. Hilbert function and resolution of the powers of the ideal of the rational normal curve. J. Pure Appl. Algebra 2000, 152, 65–74. [Google Scholar] [CrossRef][Green Version]
- Herzog, J.; Hibi, T.; Zheng, X. Monomial ideals whose powers have a linear resolution. Math. Scand. 2004, 95, 23–32. [Google Scholar] [CrossRef]
- Conca, A.; Herzog, J. Castelnuovo-Mumford regularity of products of ideals. Collect. Math. 2003, 54, 137–152. [Google Scholar]
- Ene, V.; Olteanu, A. Powers of lexsegment ideals with linear resolution. Ill. J. Math. 2012, 56, 533–549. [Google Scholar] [CrossRef]
- Kodiyalam, V. Asymptotic behaviour of Castelnuovo-Mumford regularity. Proc. Amer. Math. Soc. 2000, 128, 407–411. [Google Scholar] [CrossRef]
- Cutkosky, S.D.; Herzog, J.; Trung, N. Asymptotic behaviour of the Castelnuovo-Mumford regularity. Compos. Math. 1999, 118, 243–261. [Google Scholar] [CrossRef]
- Seyed Fakhari, S.A. Symbolic powers of cover ideal of very well-covered and bipartite graphs. arXiv 2016, arXiv:1604.0065. [Google Scholar] [CrossRef]
- Hang, N.T.; Trung, T.N. Regularity of powers of cover ideals of unimodular hypergraphs. J. Algebra 2018, 513, 159–176. [Google Scholar] [CrossRef]
- Mohammadi, F.; Moradi, S. Weakly polymatroidal ideals with applications to vertex cover ideals. Osaka J. Math. 2010, 47, 627–636. [Google Scholar]
- Morey, S. Depths of powers of the edge ideal of a tree. Comm. Algebra 2010, 38, 4042–4055. [Google Scholar] [CrossRef]
- Herzog, J.; Hibi, T. The depth of powers of an ideal. J. Algebra 2005, 291, 534–550. [Google Scholar] [CrossRef]
- Herzog, J.; Hibi, T. Monomial Ideals, Volume 260 of Graduate Texts in Mathematics; Springer: London, UK, 2011. [Google Scholar]
- Chen, J.; Morey, S.; Sung, A. The stable set of associated primes of the ideal of a graph. Rocky Mt. J. Math. 2002, 32, 71–89. [Google Scholar] [CrossRef]
- Grayson, D.R.; Stillman, M.E. Macaulay2, A Software System for Research in Algebraic Geometry. Available online: http://www.math.uiuc.edu/Macaulay2/ (accessed on 17 February 2018).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jayanthan, A.V.; Kumar, N. Syzygies, Betti Numbers, and Regularity of Cover Ideals of Certain Multipartite Graphs. Mathematics 2019, 7, 869. https://doi.org/10.3390/math7090869
Jayanthan AV, Kumar N. Syzygies, Betti Numbers, and Regularity of Cover Ideals of Certain Multipartite Graphs. Mathematics. 2019; 7(9):869. https://doi.org/10.3390/math7090869
Chicago/Turabian StyleJayanthan, A. V., and Neeraj Kumar. 2019. "Syzygies, Betti Numbers, and Regularity of Cover Ideals of Certain Multipartite Graphs" Mathematics 7, no. 9: 869. https://doi.org/10.3390/math7090869
APA StyleJayanthan, A. V., & Kumar, N. (2019). Syzygies, Betti Numbers, and Regularity of Cover Ideals of Certain Multipartite Graphs. Mathematics, 7(9), 869. https://doi.org/10.3390/math7090869



