1. Introduction
Detecting the existence of cycles in graphs is a fundamental problem in graph theory (cf. [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15]). Graph theoretic algorithms exist to enumerate both odd and even cycles. In [
16], the first author, together with Francisco and Van Tuyl, gave an algebraic algorithm to detect and exhibit all induced odd cycles in an undirected graph. The work in [
16] is an example of the rich interaction between commutative algebra and graph theory. In fact, using algebraic methods to study combinatorial structures and using combinatorial data to understand algebraic properties and invariants has evolved to be an active research topic in combinatorial commutative algebra in recent years (cf. [
17,
18] and references therein).
In the present paper, we continue this line of work and describe an algebraic algorithm to enumerate even circuits in an undirected graph; a
circuit is a closed walk in which the edges are all distinct and a
cycle is a closed walk in which the vertices are all distinct. We also discuss an application of our work to the problem of finding directed cycles in a directed graph (digraph). Let
be a finite simple undirected graph on the vertex set
. Let
be a field and identify the vertices in
V with the variables in
. The
edge ideal of
G is defined to be
The construction of edge ideals of graphs was first introduced by Villarreal in [
19] (see also [
20,
21] for edge ideals of simplicial complexes and hypergraphs) and has been an essential tool in various studies in this area of research. Our main result states that even circuits in
G can be detected by considering the
reduced Jacobian dual of the edge ideal
, a notion which we define in
Section 2.
An even circuit is called
indecomposable if it cannot be realized as the edge-disjoint union of two smaller even circuits. Our first theorem reads as follows, leaving unexplained terminology until
Section 2.
Theorem 1. Let G be a graph, , and ϕ the presentation matrix from the Taylor resolution of I. Then, the indecomposable even circuits of G correspond exactly to the binomial minors of the reduced Jacobian dual , which satisfy the following conditions:
- 1.
the monomials in these binomials are square-free and relatively prime; and
- 2.
the columns of the corresponding submatrices are pairwise center-distinct.
We focus on even circuits because they form a larger class than that of even cycles. With a slight modification of Condition (2), we can also obtain an algebraic characterization for cycles of even lengths in G (see Remark 5). The proof of Theorem 1 is based on an ad hoc analysis of the possible forms of minors of the reduced Jacobian dual .
Theorem 1 allows us to derive an algebraic algorithm to enumerate all indecomposable even circuits in a given graph that runs in polynomial time on the size of the edge set of the graph (see Algorithm 1). Our goal is not to compare the running time of our algorithm to that of existed ones, rather we aim to exhibit yet another interesting connection between commutative algebra and graph theory. Theorem 1 also has an algebraic consequence to finding defining equations for the Rees algebras of edge ideals of graphs (see Theorem 3).
Theorem 1 furthermore has an interesting application toward the study of directed cycles in digraphs. For a digraph
D, we construct a bipartite graph
(see Definition 7). Note that this bipartite graph has a natural perfect matching, which we denote by
. There is an established equivalence between the directed cycles in
D and the even cycles in
G with a certain property that traces its roots back to work done by Dulmage and Mendelsohn in the 1950s (see, for example, [
22,
23]), which we restate for convenience. Specifically, again leaving unexplained terminology until later, we have:
Theorem 2. The directed cycles in a digraph D correspond exactly to the even cycles in in which a collection of alternating edges forms a subset of the perfect matching .
Theorem 2, combined with Algorithm 1, gives an algebraic algorithm to enumerate all directed cycles in digraphs (see Corollary 4). As a consequence of Theorems 1 and 2, we are also able to translate the famous Caccetta–Häggkvist conjecture for directed cycles in digraphs to a statement about binomial minors of the Jacobian dual matrix (see Conjecture 5).
2. Preliminaries
In this section, we collect important notations and definitions used in the paper. For unexplained terminology in commutative algebra, we refer the reader to [
24,
25], and, in graph theory, we refer the reader to [
26].
Algebra. Throughout the paper, denotes an infinite field. Let be a polynomial ring over k and let . Let be an ideal and use to denote the minimal number of generators of I. Let be a presentation matrix of I.
Definition 1. The Rees algebra
of I is defined to be the graded ring Suppose that . Then, there exists a natural presentation of the Rees algebra of I, namely,given by for , where are indeterminates. Set . Then, , and J is referred to as the ideal of equations
or defining ideal
of . Since , we say that corresponds to the generator of I. By the definition of a presentation matrix
, the linear (in the variables
) equations of
J are generated by entries of the matrix
. When these entries are linear in
, that is, when the entries of
are linear, then
is the Jacobian matrix of these equations with respect to
. In this setting, one can also define another Jacobian matrix of the same polynomials in
but with respect to
. This new Jacobian matrix is usually denoted by
and referred to as the
Jacobian dual of
. We now give the generalized version of this notion when the entries of
are not necessarily all linear. See [Section 1.5] in [
27,
28] for further information on Jacobian duals.
Definition 2 (Jacobian dual). Let and let ϕ be a presentation matrix of I with respect to a set of r generators of I.
- 1.
A Jacobian dual
of ϕ, denoted by , is defined to be a matrix, whose entries are in and linear in the variables , that satisfies the equation - 2.
The reduced Jacobian dual of ϕ, denoted by , is defined to be .
Observe that, given a fixed
, there may be more than one choice for
, but
exists uniquely up to elementary row and column rearrangements that come from re-orderings (see, for example, [
28]). The matrix
, or
, has served as a source for the higher degree generators of
J (see, e.g., [
28,
29,
30,
31,
32]), with the emphasis being on minors of
.
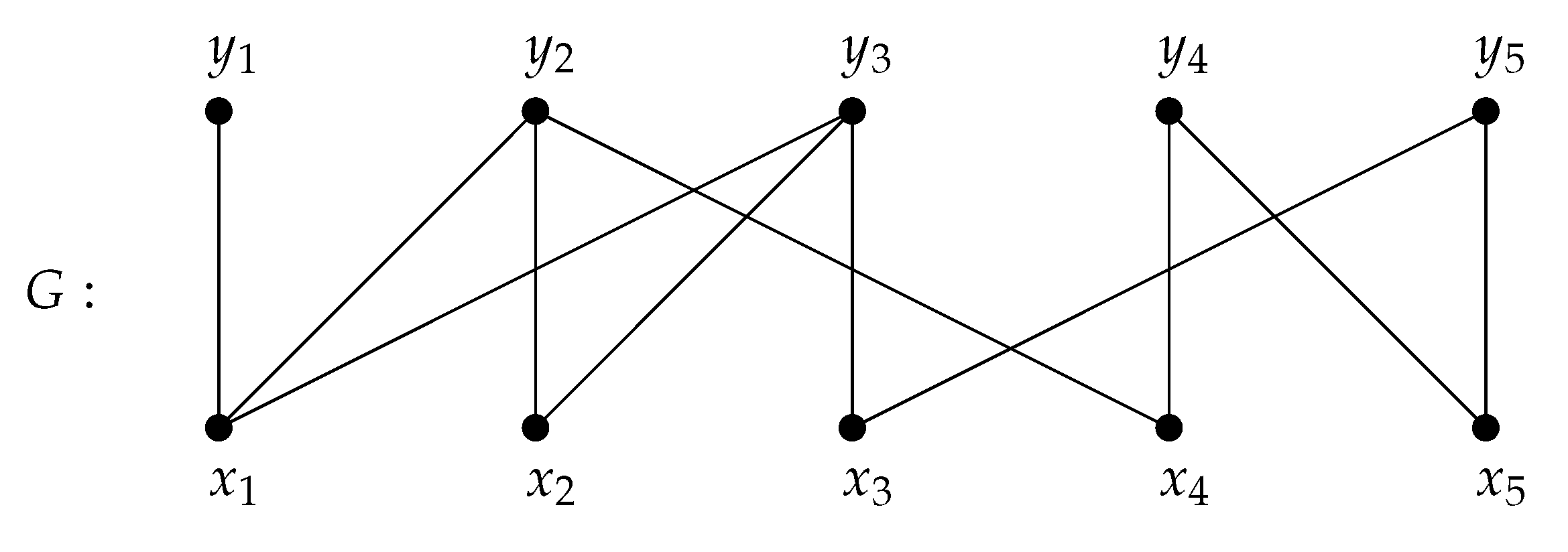
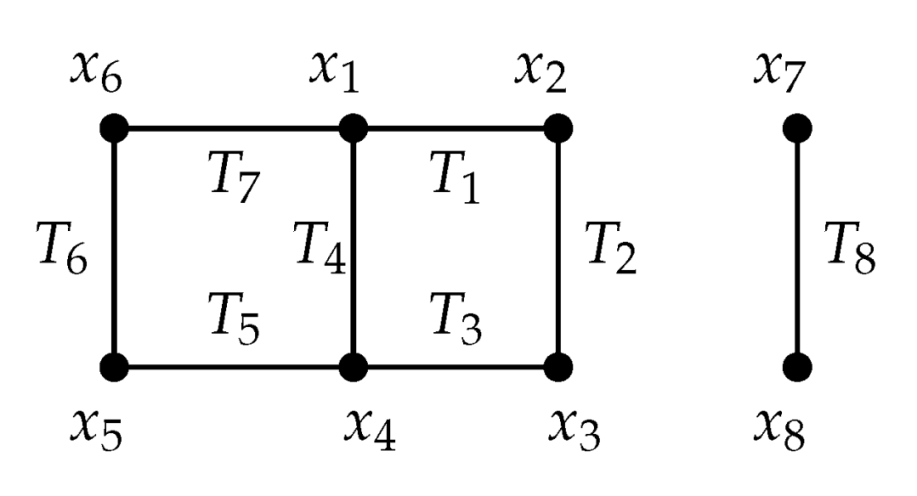
Example 1. Consider the graph![Mathematics 07 00859 i001 Mathematics 07 00859 i001]() corresponding to Then,where the remaining columns of ϕ correspond to the rest of the (quadratic) Koszul relations on disjoint pairs of edges. The Koszul relations involving have been included for illustration. Now,When using these equations to form as in Definition 2, the nonlinear terms (in the variables s) are ambiguous. For example, can be viewed as or as . Different choices of arise from different interpretations for each such nonlinear term in the s. The coefficient of of the jth equation goes in the entry of . One such choice of is
corresponding to Then,where the remaining columns of ϕ correspond to the rest of the (quadratic) Koszul relations on disjoint pairs of edges. The Koszul relations involving have been included for illustration. Now,When using these equations to form as in Definition 2, the nonlinear terms (in the variables s) are ambiguous. For example, can be viewed as or as . Different choices of arise from different interpretations for each such nonlinear term in the s. The coefficient of of the jth equation goes in the entry of . One such choice of is Tensoring with yields Note that entries of that result from interpretations of the nonlinear terms of become zero when passing to . Thus, the nonzero columns of correspond precisely to the linear columns of and the 0-rows of correspond to vertices that do not appear as endpoints of any path of length two in G. Such vertices can be isolated, part of a connected component consisting of a single edge, or the center vertex of a connected component that is a tree of diameter 2. Deleting zero-rows and zero-columns will not change the minors of a matrix. Thus, in practice, when focusing on minors, one can work with a smaller matrix defined by the linear columns of , and assume that the content ideal, , is generated by a subset of the variables, say . In this case, .
When
I is a monomial ideal, a particular presentation matrix
of
I that we make use of comes from the Taylor resolution of
I. We now recall the construction of the Taylor resolution and its presentation matrix (see [
33,
34] for more details). For a collection
of polynomials in
R and a subset
, let
denote the least common multiple of
.
Definition 3. Let be a monomial ideal with the unique set of monomial generators . The Taylor resolution
of I is the following complex:where, for , is the free R-module of rank whose basis corresponds to all subsets of p elements from , and the differential map is defined, for each basis element corresponding to a subset σ of cardinality p in , by The presentation matrix of I from its Taylor resolution is the matrix corresponding to the map ; its -entry, for , with , is equal to 0 if , equal to if and , and equal to if and .
The matrix in Example 1 is an instance of the presentation matrix that comes from the Taylor resolution of a monomial ideal. Another important notion that we use is minors and ideals of minors of a matrix.
Definition 4. Let A be an matrix whose entries are polynomials in R. For , a minor of A is the determinant of a submatrix of A. The ideal in R generated by all minors of A is often denoted by . A minor is binomial if it can be written as the sum (or difference) of two monomials in R.
Graph theory. An undirected graph consists of a set V of distinct points, called the vertices, and a collection E of unordered pairs of vertices, called the edges. We assume that all graphs in this paper are simple; that is, a graph has neither loops nor multiple edges. We write for the undirected edge between vertices x and y in a graph.
Definition 5. Let G be an undirected graph.
- 1.
A walk is an alternating sequence of vertices and edges such that for all . Such a walk is said to be closed if .
- 2.
A walk is called a trail if its edges are distinct (while its vertices may repeat). A closed trail is called a circuit.
- 3.
A walk is called a path if its edges and vertices are distinct (except possibly at ). A closed path is called a cycle.
- 4.
The length of a walk is the number of edges that the walk transverses (including multiplicities). A walk is even (or odd) if its length is an even (or odd) number.
We often list only the vertices to indicate a walk since the edges are obvious from the vertices. The main graph-theoretic structure that our work captures in this paper is indecomposable even circuits, which we define below. We also recall a similar notion of primitive even closed walks.
Definition 6. Let G be a graph.
- 1.
An even circuit is indecomposable if it cannot be realized as the edge-disjoint union of two smaller even circuits.
- 2.
An even closed walk is primitive if it does not contain an even closed subwalk.
Remark 1. There is a close connection between even closed walks in a graph G and the equations of the Rees algebra of the edge ideal of G (see [35]). In particular, suppose , where and , is an even closed walk and as in Definition 1. Then,so . An application of our work is to directed graphs, thus we also recall basic terminology for directed graphs. A digraph consists of a set Z of distinct points, called the vertices, and a collection of ordered pairs of vertices, called the directed edges. We also assume that all digraphs in this paper are simple digraphs. We write for the directed edge from x to y in a digraph.
Directed walks, paths, circuits and cycles in a digraph can be defined similarly to those in an undirected graph with only one difference, that is, if represents a directed walk from to , then is the directed edge for all .
The application of our work to directed cycles in digraphs is based on the following construction [
36].
Definition 7. Let be a digraph over the vertex set . The bipartite graph , associated to D, is constructed as follows.
- 1.
The vertices of are .
- 2.
The edges of are:
- (a)
for all ; and
- (b)
, for , if is an edge in .
It is easy to see that, for any digraph , the bipartite graph has a perfect matching . We denote this perfect matching of by .
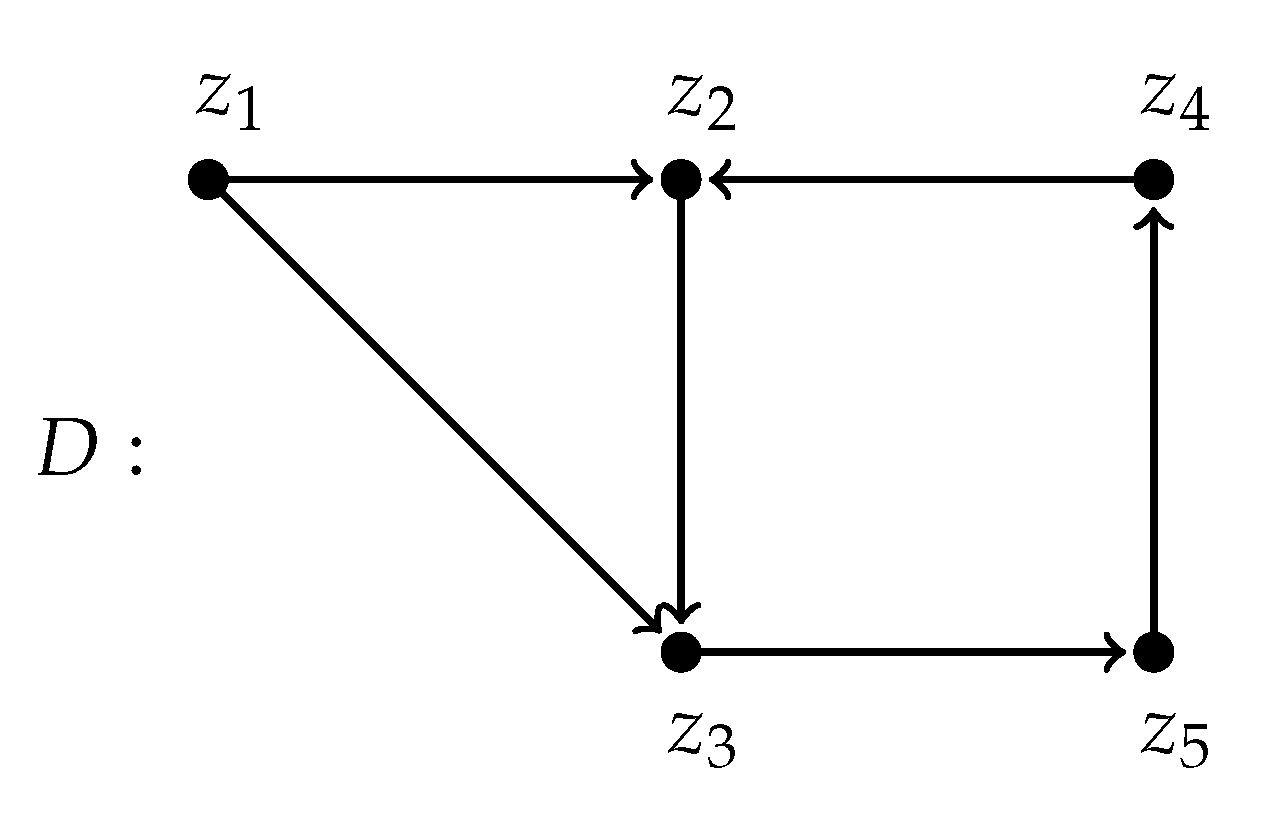
Example 2. Let D be directed graph![Mathematics 07 00859 i002 Mathematics 07 00859 i002]()
Then, the bipartite graph associated to D is![Mathematics 07 00859 i003 Mathematics 07 00859 i003]()
3. Even Circuits in Graphs
In this section, we present an algebraic algorithm to enumerate indecomposable even circuits in a graph. Recall that is a simple graph on the vertex set with . For , fix to be the presentation matrix of that results from the Taylor resolution of I, as in Definition 3. For the remainder of the paper, always refers to the Taylor presentation matrix unless otherwise noted.
We start with the following simple observation about . Example 1 already illustrates the statements below, which are generally known but written here for ease of reference.
Lemma 1. If G is a graph and , then the following statements hold.
- 1.
The entries of ϕ are monomials in .
- 2.
Every column of ϕ has precisely two nonzero entries.
- 3.
The nonzero entries in each column of ϕ are either both linear or both quadratic.
- 4.
Every linear column of ϕ corresponds to a path of length 2 in G whose end-vertices are the nonzero entries of this column.
- 5.
Every quadratic column of ϕ corresponds to a pair of disjoint edges.
Proof. The assertions are straightforward from the construction of the Taylor resolution of . Note that, in general, all relations on a set of monomials can be generated by pairwise relations (i.e., relations of two monomials). If are monomials, then a minimal relation between them has the form where and are monomials. If both have degree 2, then if have disjoint support. Otherwise, both have degree one. The results follow. □
As above, we denote by and the Jacobian dual and the reduced Jacobian dual of , respectively. We obtain an immediate corollary of Lemma 1 when is assumed to be the Taylor presentation matrix of for a graph G.
Corollary 1. The nonzero columns of are precisely the columns of that correspond to linear columns of ϕ. Particularly, each nonzero column of contains precisely two nonzero entries, each of which is a degree one monomial in .
Proof. By definition, the nonzero entries of
come from nonzero entries of
that are contained in
. Observe, by the equation
that the columns of
correspond to columns of
. Moreover, by Lemma 1, the nonzero entries in each column of
are of the same degrees (either linear or quadratic). It further follows from Equation (
1) that the degree with respect to the
s of nonzero entries of a column in
is exactly one less than that of the corresponding column of
. Hence, nonzero columns of
correspond to columns without the
s in
, which correspond to columns of linear forms (and 0) in
.
The second statement also follows from Lemma 1. □
Remark 2. Note that, since zero columns of a matrix do not play any role in what follows, we could define to exclude all its zero columns. That is, we are working just with the (uniquely defined) columns of ϕ, whose nonzero entries are linear, that result from binomial relations of edges in paths of length 2 in G. As mentioned above, zero rows of do not play a role and can be eliminated by using the content ideal of ϕ to define rather than . However, since zero rows do not affect minors, which are our main focus when using , it is a matter of convenience to allow them.
As stated in Lemma 1, the linear columns of are generated by pairs of monomials corresponding to edges that share a vertex. In other words, the linear columns of correspond to paths of length 2 in the graph. It can be desirable for computational purposes to use a minimal presentation matrix for rather than the full Taylor presentation matrix. It is easy to check that there are three paths of length two in each triangle, yielding three linear relations, any two of which generate the third. Since this is the only redundancy among the linear relations for a graph, if the graph is triangle free, the linear columns of a minimal presentation matrix will be the same as the linear columns of the Taylor presentation matrix.
Since the linear columns arise from paths of length two, as seen in Lemma 1, the endpoints of each path are the nonzero entries of that column of . These endpoints will thus be encoded in the corresponding column of as the rows in which the nonzero entries appear. It is natural to expect that the third vertex, the midpoint of the path, would play a role.
Definition 8. We call two nonzero columns of center-distinct if their corresponding paths of length 2 in G have distinct middle vertices. We also call the middle vertices of these paths of length 2 the mid-points of the corresponding columns.
Finding the mid-point of a column of can be done easily by examining the corresponding edges of G. If and are the two nonzero entries of a column of and are the corresponding edges of G (that is, , and ), then the mid-point of the column is , or equivalently .
The next lemma collects information that can be gleaned about a graph from minors of of a form that appears frequently in the remainder of the article.
Lemma 2. If has a minor of the formthen G contains an even closed walk corresponding to . Moreover, - 1.
the walk is primitive if and only if the columns of M are pairwise center-distinct; and
- 2.
the walk is a circuit if and only if the nonzero entries of M are distinct, in which case the circuit is indecomposable if and only if the columns of M are pairwise center-distinct.
Proof. Combining Equation (
1) with Lemma 1 gives that each column of
M corresponds to a path of length 2 in
G whose end-vertices are labeled by the rows of
M corresponding to the nonzero entries in that column. By re-indexing the variables, we may assume that the rows of
M correspond to the variables
. Then, the
ith column of
M, for
, corresponds to a path of length 2 from
to
, and the last column of
M corresponds to a path of length 2 from
to
. We denote those paths by
, for
, and
. Furthermore, edges on these paths correspond to the variables
. Hence, these paths glue together to form an even closed walk of length
in
G. Since
, we have that
corresponds to an even closed walk in
G, as in Remark 1. This walk is a circuit if and only if the
, and thus the corresponding edges, are distinct. Finally, the columns of
M are pairwise center-distinct if and only if the vertices
are pairwise distinct. Note that the vertices
are distinct by definition. This guarantees that the obtained closed walk or circuit of length
in
G is primitive or indecomposable, respectively, if and only if the columns of
M are pairwise center-distinct. □
We are now ready to prove the main result of the paper, Theorem 1. Note that relabeling the vertices or edges of a graph corresponds to rearranging the rows of or of . Such a rearrangement will not affect the minors of a matrix, thus, when convenient, a specific labeling of vertices can be used without loss of generality.
Theorem 1. Let G be a graph. Then, the indecomposable even circuits of G correspond exactly to the binomial minors of , which satisfy the following conditions:
Proof. Suppose that
C is an indecomposable even circuit in
G. For ease of notation, select a labeling on the vertices and edges so that the edges of
C (in order) are
, where
for
and
. Since
C is indecomposable, it is easy to see that
are pairwise distinct. Particularly, the linear relations of
include
which correspond to the following columns of
:
where, for convenience, labelings were chosen so that
corresponds to
for
.
We can reorder the columns of
so that these are the first
t columns. These columns produce
as linear equations of the Rees algebra
, which correspond to the first
t equations of
. Thus, the first
t columns of
are:
By Corollary 1, these columns of
are unchanged when passing to
. Consider the
submatrix
M of
consisting of the first
t columns and the
t identified nonzero rows:
Then, . This is a binomial whose monomials are square-free and relatively prime. Observe further that, since C is indecomposable, are pairwise distinct. Therefore, the columns of M are pairwise center-distinct.
Conversely, suppose that M is a submatrix of whose determinant is a binomial of degree t with square-free and relatively prime monomials, and whose columns are pairwise center-distinct. It follows from Lemma 1 and Corollary 1 that each column of M contains at most two nonzero entries. Since the monomials in are relatively prime, each column of M must contain exactly two nonzero entries. Particularly, M contains exactly nonzero entries. In addition, since the monomials in are relatively prime, contains exactly distinct variables. Thus, all the nonzero entries of M are distinct. Since each row also contains at least two distinct entries in order for the monomials to be relatively prime, a simple counting argument guarantees exactly two nonzero entries per row as well.
Now, by rearranging the rows and columns of
M, it is easy to put
M in a block-matrix form, where each nonzero block is of the form in Equation (
2) and lies on the diagonal. Observe further that, if
M has more than one such block, then
is not a binomial since all entries of
M are distinct. Therefore, we can assume that
M is exactly as in Equation (
2). The result now follows from Lemma 2. □
Theorem 1 gives us the following algebraic algorithm to detect the existence of and list all even circuits in a given graph G.
| Algorithm 1 To enumerate all indecomposable even circuits in a given graph G |
Form . Compute . for t from 1 to the rank of compute all minors of . Test if each minor satisfies the following conditions:
- (a)
its columns are pairwise center-distinct; and - (b)
its determinant is a binomial whose monomials are square-free and relatively prime.
If the answer is “Yes”, then return the rows and centers of the columns corresponding to the minor. These are the vertices of an indecomposable even circuit in G.
|
Remark 3. Note that only the linear columns of ϕ are necessary in this process and so in Step 1 only the linear relations need be considered. Note also that the Taylor resolution and its presentation matrix can be constructed in polynomial time on the number of generators of (i.e., the number of edges in G). Note further that the computation of the determinant of a matrix can also be done in polynomial time on the size of the matrix, and the rank of is at most the number of edges in G. Finally, testing if the columns of a minor in are center-distinct can be done in polynomial time on the size of the minor, which is bounded by the number of edges in G. Thus, Algorithm 1 runs in polynomial time on the size of the edge set of G.
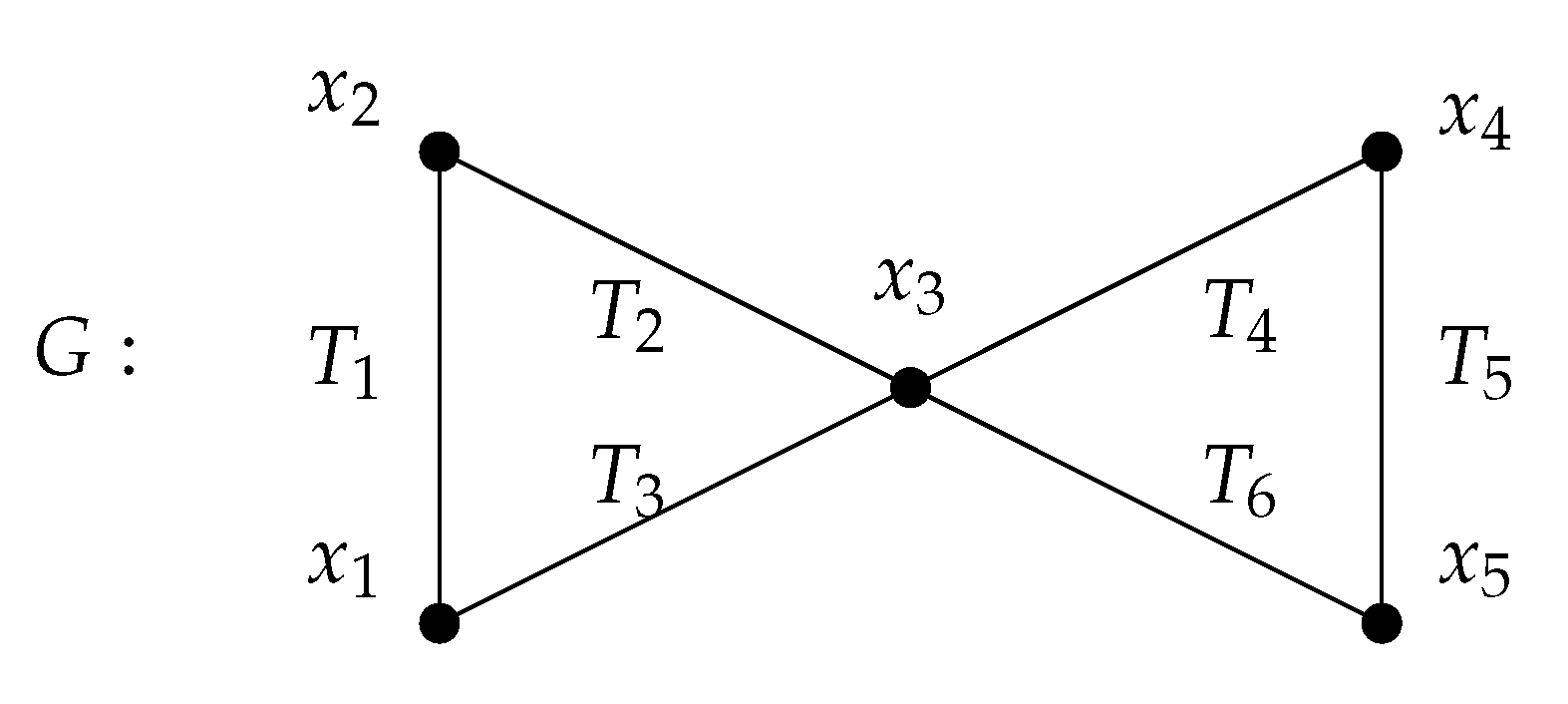
Example 3. Consider the following graph.![Mathematics 07 00859 i004 Mathematics 07 00859 i004]()
The nonzero columns of the reduced Jacobian dual of G corresponding to the Taylor presentation matrix ϕ are computed to be:where the labels indicate the variables of the corresponding rows. Furthermore, the mid-points of the columns are successively . By evaluating the minors of , the only binomial minor whose monomials are square-free and relatively prime is , which corresponds to the only indecomposable even circuit in G. This minor appears using the submatrix formed by taking Rows and Columns , for example, or the one formed by Rows and Columns . Remark 4. There can be binomial minors of whose monomials are neither square-free nor relatively prime. These minors may correspond to even closed walks which transverse an edge multiple times.
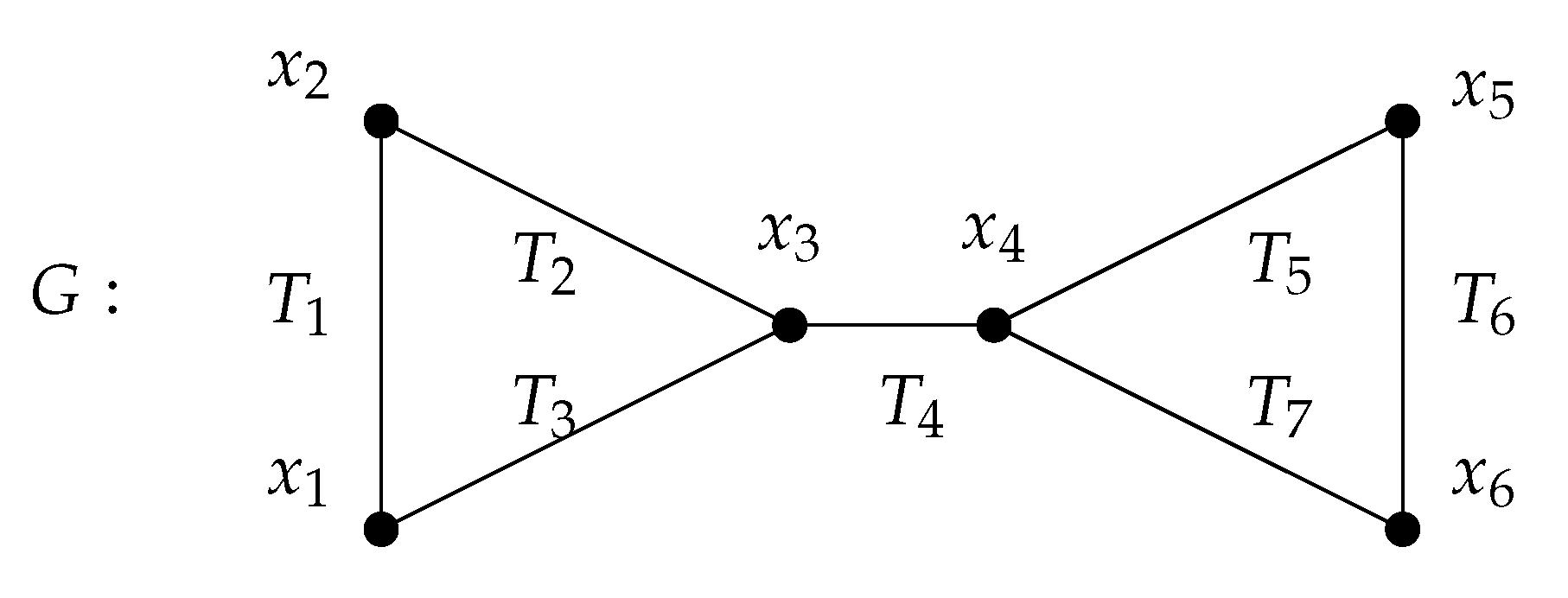
Example 4. Consider the following graph.![Mathematics 07 00859 i005 Mathematics 07 00859 i005]()
The nonzero columns of the reduced Jacobian dual of with respect to the Taylor presentation matrix ϕ are computed to be:where the labels indicate the variables of the corresponding rows. Furthermore, the mid-points of the columns are successively . The only binomial minor of is . This corresponds to submatrices formed using Rows and Columns for example, or Rows and Columns . A monomial of this minor is not square-free. This indicates that G contains an even closed walk , but this walk is not a circuit because it transverses through the edge twice. Hence, G has no indecomposable even circuits.
Remark 5. With basically the same proof as that of Theorem 1, it can be shown that the even cycles of G correspond exactly to the binomial minors of , which satisfy the following conditions:
- 1.
the monomials in these binomials are square-free and relatively prime; and
- 2.
the variables labeling the rows and the mid-points of the columns of the corresponding submatrices are pairwise distinct.
Example 5. Let G be the graph in Example 3. As shown in Example 3, the only binomial minor of whose monomials are square-free and relatively prime is . This minor is obtained by taking Rows and Columns . In this minor, the mid-points of the columns are and . On the other hand, the variables labeling the rows are and . Clearly, we have a repeated among the mid-points and the row labels. Thus, this minor corresponds to an even indecomposable circuit, which is not a cycle.
Example 6. Let G be the graph in Example 1. A binomial minor of whose monomials are square-free and relatively prime is . This minor is obtained by taking Rows and Columns . The mid-points of the columns are and , and the variables labeling the rows are and . Since these are distinct variables, this minor corresponds to an even cycle .
We continue this section by discussing an algebraic consequence of Theorem 1 in finding defining equations for the Rees algebras of edge ideals of graphs. Recall that the Rees algebra of I has a presentation , and is called the defining ideal of .
It was shown in [
35] that the nonlinear equations of
J arise from the even closed walks in the graph
G. An alternate proof of this fact appears in Chapter 10.1 of [
24]. In addition, it was proved in [Corollary 10.1.5] of [
24] that the generators correspond to primitive even closed walks and form a reduced Gröbner basis for
J. The binomials corresponding to indecomposable even circuits of
G are thus known to be elements of
J. However, there are elements of
J that do not correspond to indecomposable circuits, as seen in Example 4. It is worth noting that it was established in a more general setting that the maximal minors of
are contained in
J (see, for example, [
31]). A close examination of the proof of Theorem 1 shows that any even closed walk in
G corresponds to a binomial minor of
.
Corollary 2. Let G be a graph with edge ideal , and let J be the defining ideal of . Then, every nonlinear generator of J appears as a binomial minor of .
Proof. By the work in [
35] and (Chapter 10.1 [
24]), we have that the nonlinear generators of
J correspond to primitive even closed walks in
G. Consider any primitive even closed walk
W in
G and, after a re-labeling, suppose that the vertices on
W are
(not necessarily distinct).
Observe that, since W is primitive, if is a repeated vertex in W, then i and j are of different parity. View W as the union of t paths of length 2, namely, , for (where ). Then, the endpoints of each path are distinct vertices. Thus, corresponds to a column of with exactly two nonzero entries, appearing in the rows labeled by . Selecting these columns and the corresponding nonzero rows results in a submatrix of .
As in the proof of Theorem 1, the rows and columns of
can be rearranged so that
is a block-matrix in which each block is of the form of Equation (
2). If there are multiple blocks, then each corresponds to an even closed walk contained in
W by Lemma 2, a contradiction to the fact that
W is primitive. Therefore,
is of the form in Equation (
2), where the nonzero entries may not be distinct. Hence, the corresponding generator of
J is the same as
, which is a binomial minor of
. □
Let
. Corollary 2 gives us the containment
where
k is the rank of
. The reverse containment fails to hold. In general,
will contain monomials that are not in
J. For instance, in Example 1,
but
. Interestingly, we see that by restricting to binomial minors we in fact obtain an equality. While not all binomial minors of
are minimal generators of
J, such minors correspond to multiples of binomials which come from (not necessarily primitive) even closed walks and are elements of
J. The following lemma is used in proving the desired equality. For convenience, we consider 1 to be a trivial monomial.
Lemma 3. Suppose ψ is an matrix such that:
- 1.
is a nonzero binomial; and
- 2.
every column of ψ has at most 2 nonzero entries.
Then, after row and column rearrangements, ψ has a block decompositionwhere is a monomial, is a binomial, , and every row of Z has at least two nonzero entries and every column of Z has exactly two nonzero entries. Proof. If every row of has at least two nonzero entries and every column of has exactly two nonzero entries, set to be empty matrices and . Then, since an empty product is defined to be 1, is a (degenerate) monomial, and the result holds. In particular, the result holds when . Assume .
Assume there exist
s rows of
with a single nonzero entry. Since
, every row and column of
has at least one nonzero entry and no two rows (columns) have a single nonzero entry in the same column (row). Note also that row and column exchanges modify only the sign of the determinant and not the binomial nature. By performing row exchanges, we can rearrange all rows with a single nonzero entry to come before all rows with multiple nonzero entries. That is, we may assume that
has the form
where
is an
diagonal matrix, and
is a matrix where each column has at most one nonzero entry. Observe that
is a monomial and
, thus
is again a nonzero binomial. As before, each column of
has either one or two nonzero entries and each row has at least one nonzero entry. Since
is
with
, by induction,
where
is a monomial,
is a binomial,
, and every row of
has at least two nonzero entries and every column of
has exactly two nonzero entries. Now,
where
consist of the appropriate rows of
. Set
,
,
, and
. Note that
and the result follows.
Similarly, if any column of
has a single nonzero entry, then by performing column exchanges, we may assume
has the form
where
is a diagonal matrix. Observe that
and
is a monomial, thus
is again a nonzero binomial. As before, each column of
has either one or two nonzero entries and each row has at least one nonzero entry and the result follows by induction as in the case above. □
Note that in the above lemma, since the columns of Z have two nonzero entries each and the columns of have at most two nonzero entries, it follows that . To state our next result formally, for a matrix M, set to be the collection of minors of M that are binomials.
Theorem 3. Let G be a graph with edge ideal . Let J be the defining ideal of and let . Then, Proof. One inclusion follows directly from Corollary 2.
For the reverse inclusion, suppose that is a submatrix of with a binomial. We show that . Indeed, since , every row and column of has at least one nonzero entry and no two rows (columns) have a single nonzero entry in the same column (row). As noted before, each nonzero column of has precisely two nonzero entries. Thus, each column of has at most two nonzero entries. Applying Lemma 3, we can assume that where is a minor of in which every column has exactly two nonzero entries, every row has at least two nonzero entries, and is a nonzero binomial with . Thus, if , then .
Now, we can reorder the rows of
so that the nonzero entries of the first column appear in the first two rows. Since the second row has at least two nonzero entries, we can rearrange the remaining columns of
so that the
entry is not zero. If the second nonzero entry of Column 2 is not in Row 1, then we can rearrange the remaining rows so that the
entry of
is not zero. We can continue to rearrange the rows and columns of
in this manner (see also Equation (
2)) until for some row
i, the remaining columns with nonzero entries in row
i have the second nonzero entry in row
j for some
. At this point,
has the following form
where ∗ denotes a nonzero entry and the position of the second ∗ in the final column before
N is illustrative. Notice that
has a minor of the form of Equation (
2). In addition,
has the form
where
is lower triangular (the empty matrix if
), and
has the form of Equation (
2). Note that
By Lemma 2, , and since J is closed under multiplication, as required. □
Remark 6. It can be seen in the proof above that every row of has at least two nonzero entries and each column has either one or two nonzero entries. We can continue the process to get a block decomposition of ψ, in which the determinant is the product of the determinants of the diagonal blocks, each of which is either a monomial or a binomial coming from a block of the form of Equation (2). Hence, can be written as a product of monomials and of binomials coming from blocks of the form of Equation (2). Since minors of the form of Equation (2) correspond to (not necessarily primitive) even closed walks, these binomials are in J by [35]. Thus, not only are the binomial minors in J, if they are not irreducible, they factor as products of monomials and binomial elements of J. In the proof of Theorem 3, the fact that was a binomial came from the statement. Since the entries of are not assumed to be distinct, it is possible for the product of two binomials to be a binomial. However, much of the proof holds if instead is assumed not to be a monomial. The following result demonstrates how to use this to obtain all nonlinear generators of J from a single sized ideal of minors of .
Corollary 3. Let . Then, all nonlinear generators of J can be obtained as factors of generators of .
Proof. By Corollary 2, every nonlinear generator of
J appears as some binomial minor of
. Let
f be a nonlinear generator of
J and let
M be the corresponding submatrix of
. Since
J is generated by primitive even walks, the monomials in
f are relatively prime, thus every column of
M contains exactly two nonzero entries. By performing row and column exchanges, write
The set of columns of
used to form
M can be extended to a set of columns of full rank. That is, by selecting appropriate columns and rows from
, there is a
submatrix of
of the form
with nonzero determinant. Since
,
f is a factor of an element of
as desired. □
4. Directed Cycles in Digraphs
In this part of the paper, we discuss an interesting application of our main result, Theorem 1, to the problem of detecting the existence of directed cycles in a given directed graph.
Let be a directed graph over the vertex set . Let be the undirected bipartite graph constructed from D as in Definition 7. Recall that represents the perfect matching in .
The connection between directed cycles in a digraph
D and even cycles in
is well established (see, for example, [
22,
23]). We present the following known result in a form that is convenient for applying Theorem 1. Note that, in an even circuit, we can start at any place and collect the first, third, fifth, etc. (all the odd ordered) edges, or collect the second, fourth, etc. (all the even ordered) edges. This way we get two sets of disjoint edges, each consisting of exactly half the number of edges on the circuit. We refer to each of these two sets a
collection of alternating edges in the even circuit.
Theorem 2. The directed cycles in D correspond exactly to the even cycles in in which a collection of alternating edges forms a subset of the perfect matching in G.
Proof. We start the proof with the following observation. Consider an even circuit C in G with the property that its alternating edges form a subset of the perfect matching . It can be seen that, if one transverses around C on its edges and hits (or ) from an edge that is not in , then the next edge of C has to be . Since in a circuit the edges are distinct, this ensures that C cannot contain (or ) more than once. That is, C is a cycle (which is necessarily indecomposable). Thus, the indecomposable circuits in G with the property that a collection of their alternating edges forms a subset of the perfect matching are exactly the even cycles in G with the same property.
Suppose that is a directed cycle in D. By the construction of G, it is easy to see that is an indecomposable even circuit in G. Moreover, the collection of even edges in this circuit is , which is a subset of the perfect matching .
Conversely, suppose that G contains an indecomposable even circuit C in which a collection of alternating edges form a subset of the perfect matching . Since G is bipartite, every edge in G (and so any edge in C) connects a vertex to a vertex . Thus, without loss of generality, we may assume that the circuit C is of the form . Since C is a circuit and C contains , it follows that are distinct indices. By the construction of G again, we have a directed cycle in D. □
Example 7. Let D be the directed graph in Example 2 and let be its associated bipartite graph. It can be seen that G has only one even cycle whose alternating edges form a subset of the perfect matching , namely, . This even cycle of G corresponds to the directed cycle in D.
Note that does not form a directed cycle in D even though its undirected edges would form a triangle. This is reflected by the fact that there is no even cycle between in G. Furthermore, not all even cycles in G would correspond to directed cycles in D. For instance, consider the even cycle in G. Neither collection of alternating edges of this cycle is a subset of the perfect matching , and this even cycle does not correspond to any directed cycle in D ( does not form a directed cycle in D).
As a corollary of Theorem 2, we derive an algebraic algorithm to enumerate all directed cycles in a given digraph. Note that, by the proof of Theorem 2, indecomposable even circuits of , in which a collection of alternating edges is a subset of , are exactly the even cycles in G with the same property.
Corollary 4. Let D be a digraph and let be its corresponding bipartite graph. Let ϕ be the presentation of the edge ideal of G that results from its Taylor resolution. Let be its reduced Jacobian dual. Then, the directed cycles of length t in D correspond exactly to the binomial minors of that satisfy the following conditions:
- 1.
their columns are pairwise center-distinct;
- 2.
their monomials are square-free and relatively prime; and
- 3.
one of these monomials is the product of variables that correspond to a subset of the perfect matching .
Proof. The assertion is a direct consequence of Theorems 1 and 2. □
We recall the famous Caccetta–Häggkvist conjecture for directed cycles in digraphs [
37].
Conjecture 4 (Caccetta–Häggkvist). Let D be a digraph on n vertices. Let and suppose that the outdegree of each vertex in D is at least . Then, D contains a directed cycle of length at most ℓ.
As a consequence of Theorems 1 and 2, we are able to present a Jacobian dual matrix interpretation of the Caccetta–Häggkvist conjecture as follows. Note that every cycle is an indecomposable even circuit, and that, for a bipartite graph, the two notions coincide.
Conjecture 5. Let D be a digraph on n vertices such that the outdegree of each vertex in D is at least . Let ϕ be the Taylor presentation matrix of . Then, for some , contains a binomial with square-free, relatively prime terms, one of which is a product of elements of .
By Theorems 1 and 2, Conjectures 4 and 5 are equivalent. Conjecture 5 can also be rephrased using the language of Rees algebras by using Theorem 3.
Conjecture 6. Let D be a digraph on n vertices such that the outdegree of each vertex in D is at least . If J is the defining ideal of the Rees algebra , then, for some , J has a binomial generator of degree q that is square-free and has relatively prime terms, one of which is a product of elements of .
We conclude the paper with the observation that Conjecture 5 can be further translated into a problem in linear algebra. Notice that, if the outdegree of a vertex
is at least
r, then there are at least
r paths of length 2 using the edge
with
as the mid-point. The corresponding linear relations
give specific information about
r columns of
, each of which has an element from the perfect matching. If
D has
m vertices, this yields
columns of
, each of which contains an element from the perfect matching, which form a fertile source of potential minors using submatrices of the form of Equation (
2) that would correspond to directed cycles in
D.
 corresponding to Then,
corresponding to Then,