Global Properties of a Delay-Distributed HIV Dynamics Model Including Impairment of B-Cell Functions
Abstract
1. Introduction
2. The Mathematical Model
- (i)
- if , then the model has only one equilibrium point ; and
- (ii)
- if , then the model has two equilibria and .
Global Stability of Equilibria
3. Numerical Simulations
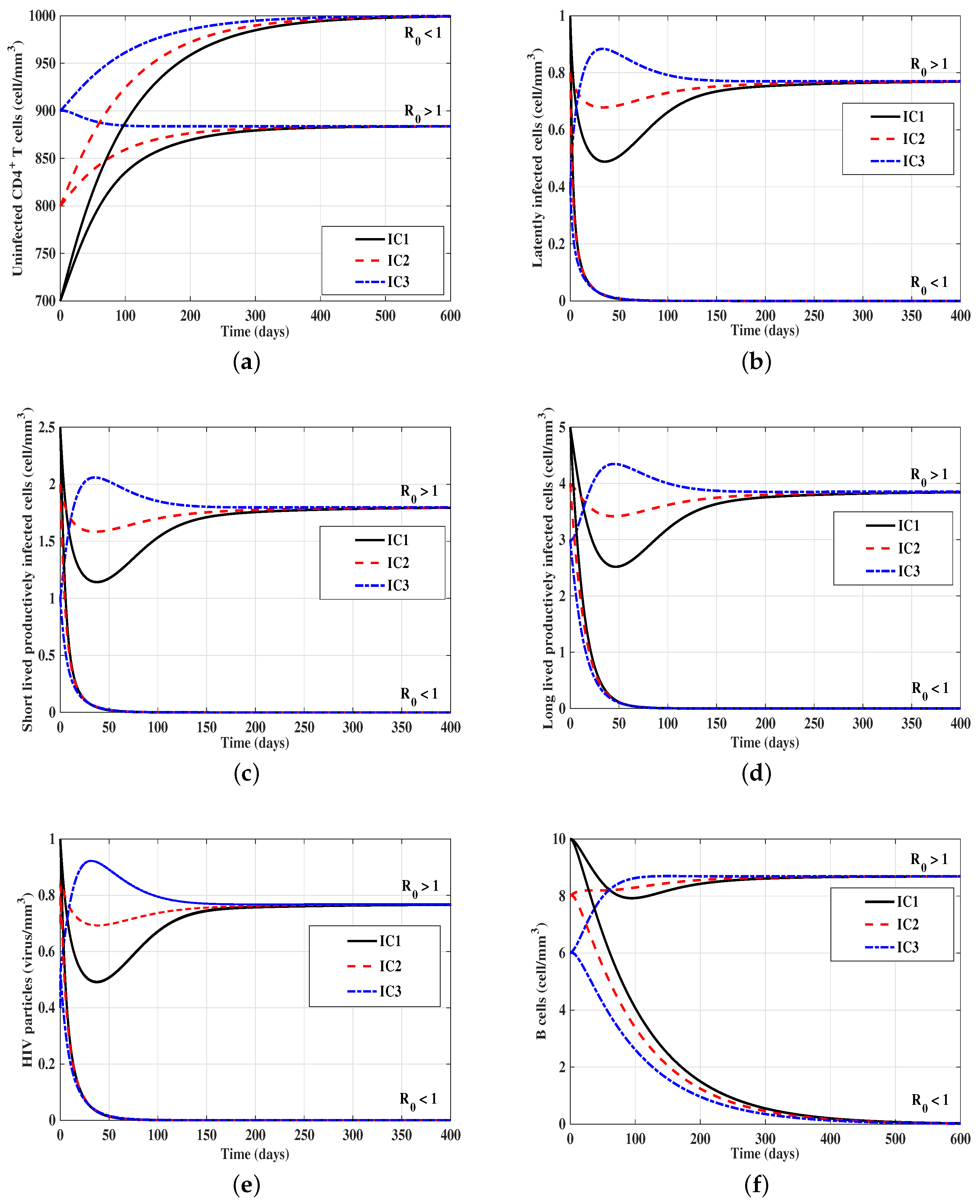
3.1. Stability of Equilibria
- IC1:
- cells mm, cells mm, cells mm, cells mm, virus mm, cells mm,
- IC2:
- , ,
- IC3:
- , , .
- (A)
- mmcells, then . Figure 1 shows that, for all IC1–IC3, the solutions of the model tend to . This means that, is G.A.S., and the HIV is predicted to be completely cleared from the body.
- (B)
- mmcells, then we compute . Figure 1 shows that the solutions of the model converge to the equilibrium for all IC1–IC3. Then, is G.A.S., and a chronic HIV infection is attained. Moreover, we have the following:
- (i)
- is G.A.S. when , and
- (ii)
- is G.A.S. when .
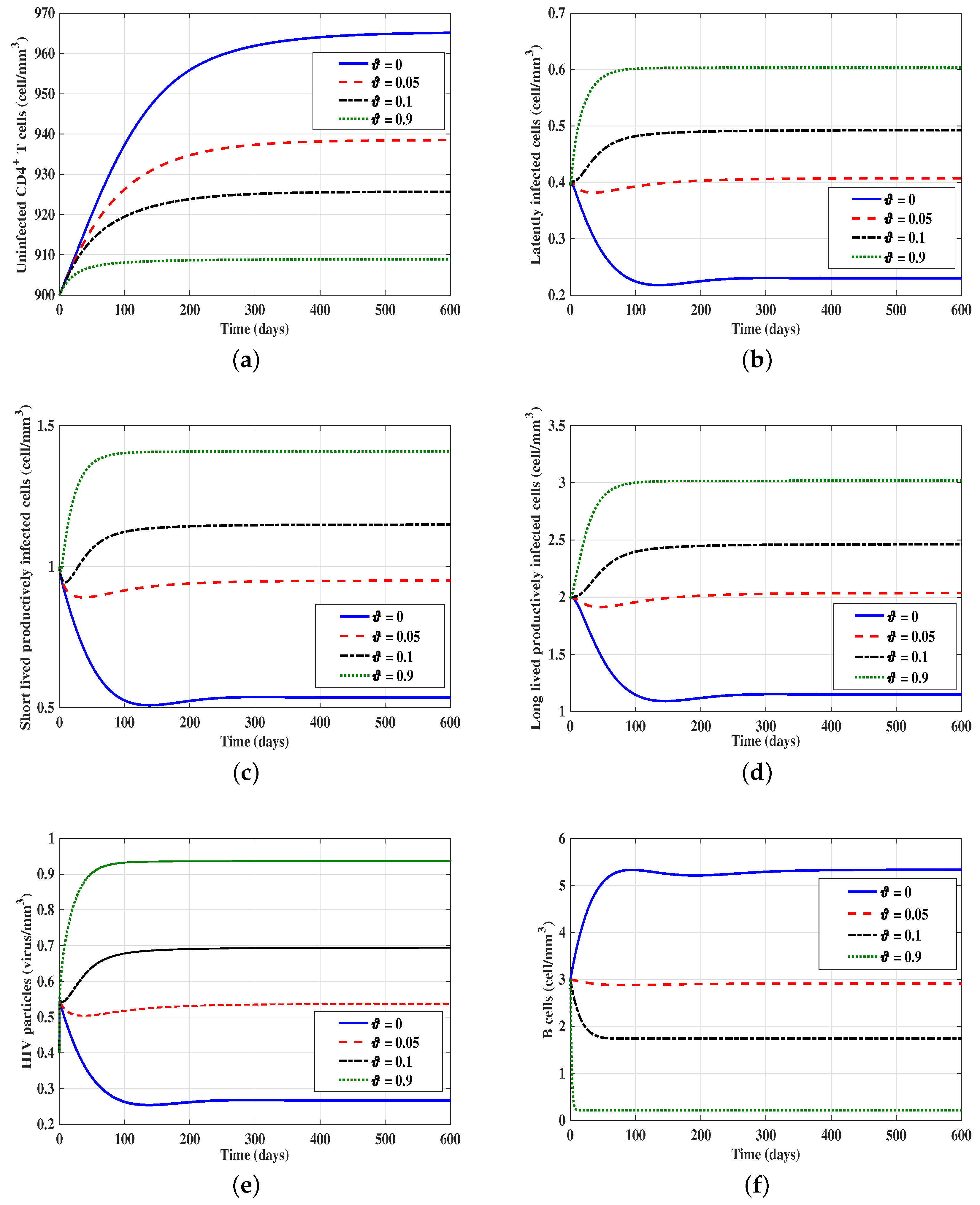
3.2. The Effect of the Time Delay on the Stability of Equilibria
- (i)
- is G.A.S. when .
- (ii)
- is G.A.S. when .
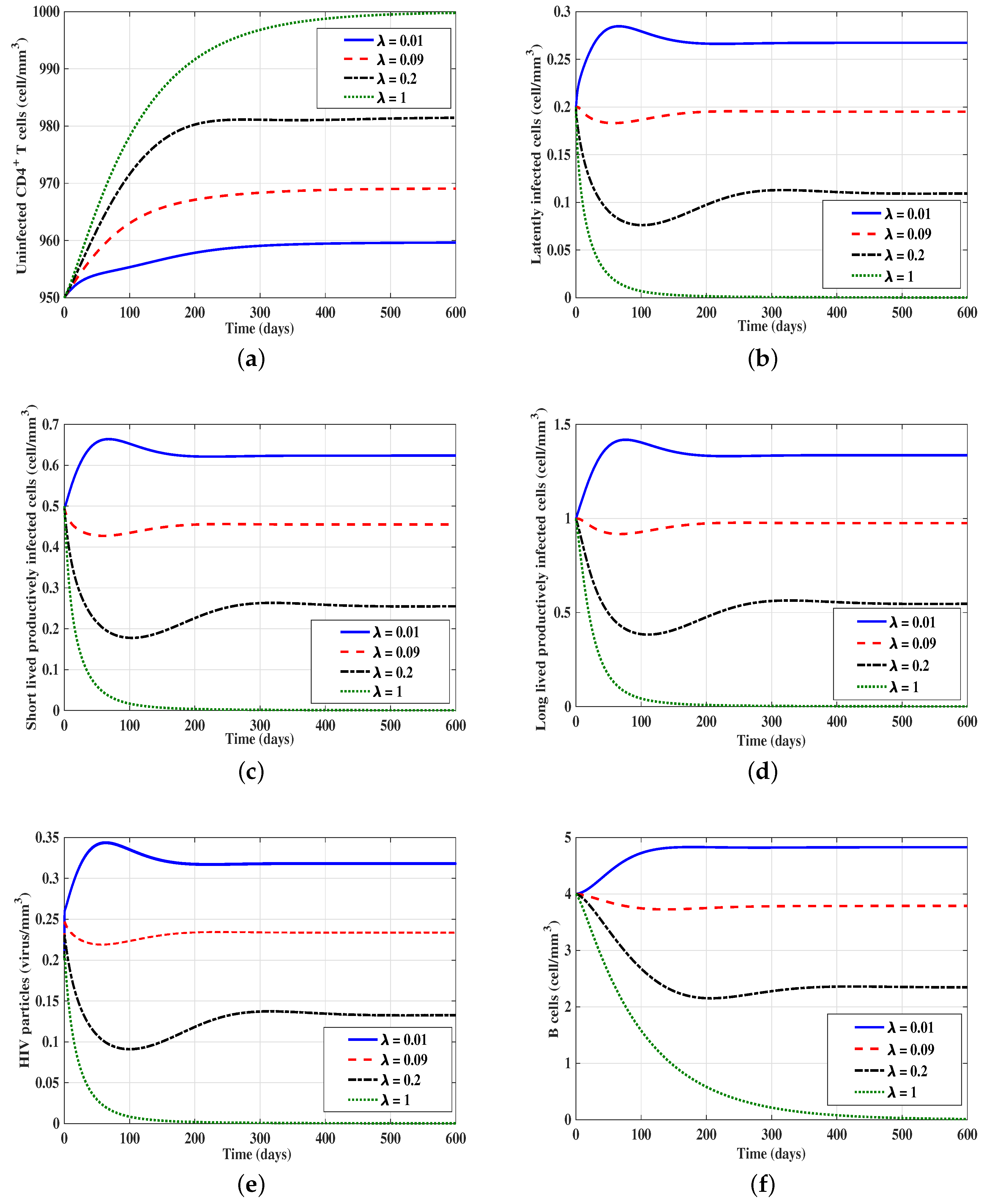
3.3. Effect of B-Cell Impairment Parameter on the HIV Dynamics
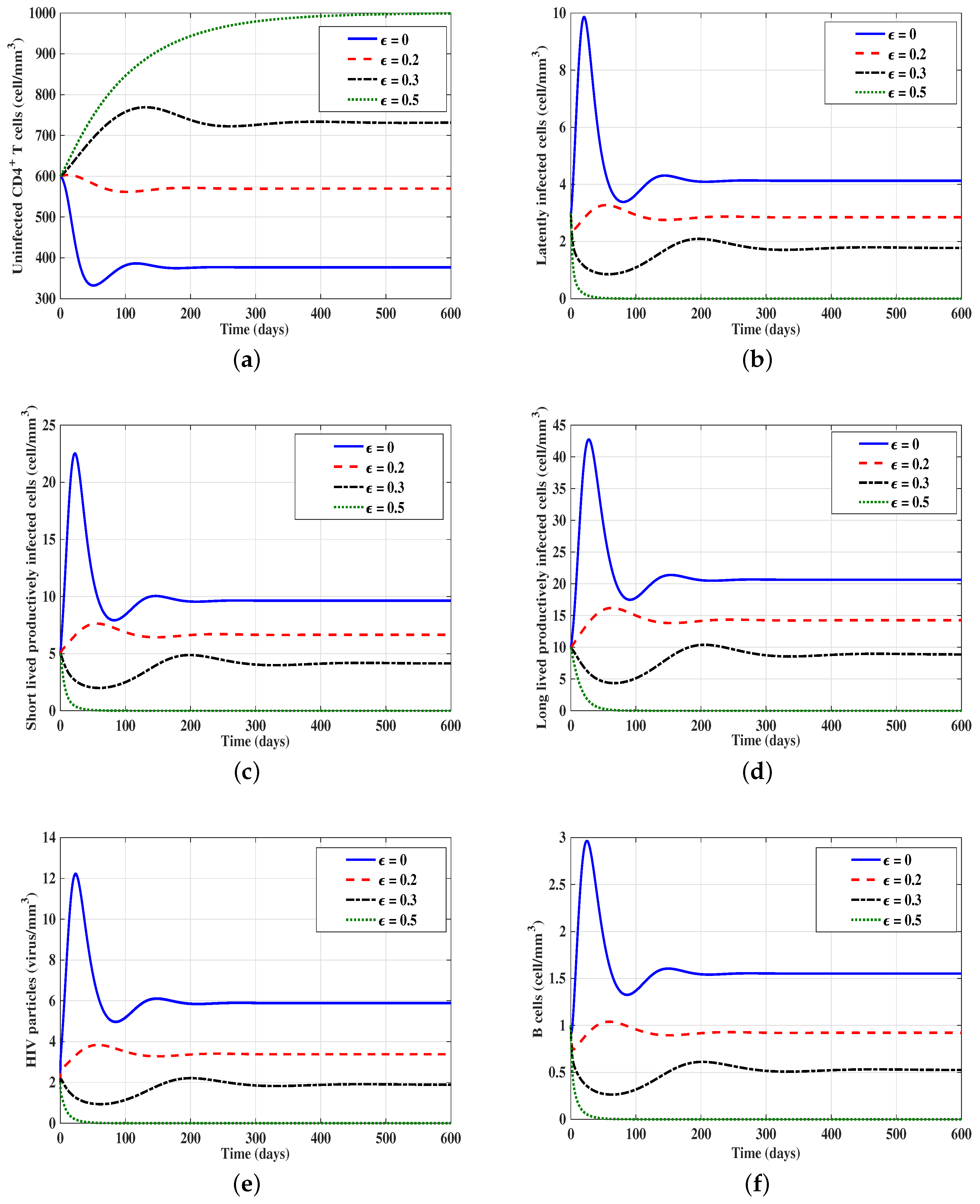
3.4. Effect of Antiviral Treatment on the HIV Dynamics
- (i)
- if , then , and is G.A.S.;
- (ii)
- if , then , and is G.A.S.
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Perelson, A.S.; Nelson, P.W. Mathematical Analysis of HIV-1 Dynamics In Vivo. SIAM Rev. 1999, 41, 3–44. [Google Scholar] [CrossRef]
- Nowak, M.A.; Bangham, C.R.M. Population dynamics of immune responses to persistent viruses. Science 1996, 272, 74–79. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S.; Essunger, P.; Cao, Y.; Vesanen, M.; Hurley, A.; Saksela, K.; Markowitz, M.; Ho, D.D. Decay characteristics of HIV-1-infected compartments during combination therapy. Nature 1997, 387, 188–191. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; May, R.M. Virus Dynamics: Mathematical Principles of Immunology and Virology; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Wodarz, D.; Nowak, M.A. Mathematical models of HIV pathogenesis and treatment. BioEssays 2002, 24, 1178–1187. [Google Scholar] [CrossRef] [PubMed]
- Graw, F.; Perelson, A.S. Modeling Viral Spread. Annu. Rev. Virol. 2016, 3, 555–572. [Google Scholar] [CrossRef] [PubMed]
- De Leenheer, P.; Smith, H.L. Virus dynamics: A global analysis. SIAM J. Appl. Math. 2003, 63, 1313–1327. [Google Scholar]
- Wong, J.K.; Hezareh, M.; Gunthard, H.F.; Havlir, D.V.; Ignacio, C.C.; Spina, C.A.; Richman, D.D. Recovery of replication-competent HIV despite prolonged suppression of plasma viremia. Science 1997, 278, 1291–1295. [Google Scholar] [CrossRef] [PubMed]
- Callaway, D.S.; Perelson, A.S. HIV-1 infection and low steady state viral loads. Bull. Math. Biol. 2002, 64, 29–64. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S.; Kirschner, D.E.; Boer, R.D. Dynamics of HIV infection of CD4+ T cells. Math. Biosci. 1993, 114, 81–125. [Google Scholar] [CrossRef]
- Korobeinikov, A. Global properties of basic virus dynamics models. Bull. Math. Biol. 2004, 66, 879–883. [Google Scholar] [CrossRef]
- Elaiw, A.M. Global properties of a class of HIV models. Nonlinear Anal. Real World Appl. 2010, 11, 2253–2263. [Google Scholar] [CrossRef]
- Elaiw, A.M. Global properties of a class of virus infection models with multitarget cells. Nonlinear Dyn. 2012, 69, 423–435. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Azoz, S.A. Global properties of a class of HIV infection models with Beddington-DeAngelis functional response. Math. Methods Appl. Sci. 2013, 36, 383–394. [Google Scholar] [CrossRef]
- Hlavacek, W.S.; Stilianakis, N.I.; Perelson, A.S. Influence of follicular dendritic cells on HIV dynamics. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2000, 355, 1051–1058. [Google Scholar] [CrossRef] [PubMed]
- Rong, L.; Perelson, A.S. Modeling HIV persistence, the latent reservoir, and viral blips. J. Theor. Biol. 2009, 260, 308–331. [Google Scholar] [CrossRef] [PubMed]
- Dixit, N.M.; Markowitz, M.; Ho, D.D.; Perelson, A.S. Estimates of intracellular delay and average drug efficacy from viral load data of HIV-infected individuals under antiretroviral therapy. Antivir. Ther. 2004, 9, 237–246. [Google Scholar]
- Sahani, S.K.; Yashi. Effects of eclipse phase and delay on the dynamics of HIV infection. J. Biol. Syst. 2018, 26, 421–454. [Google Scholar] [CrossRef]
- Herz, A.; Bonhoeffer, S.; Anderson, R.M.; May, R.M.; Nowak, M.A. Viral dynamics in vivo: Limitations on estimates of intracellular delay and virus decay. Proc. Natl. Acad. Sci. USA 1996, 93, 7247–7251. [Google Scholar] [CrossRef] [PubMed]
- Nelson, P.W.; Murray, J.D.; Perelson, A.S. A model of HIV-1 pathogenesis that includes an intracellular delay. Math. Biosci. 2000, 163, 201–215. [Google Scholar] [CrossRef]
- Xu, R. Global stability of an HIV-1 infection model with saturation infection and intracellular delay. J. Math. Anal. Appl. 2011, 375, 75–81. [Google Scholar] [CrossRef]
- Elaiw, A.M.; AlShamrani, N.H. Stability of a general adaptive immunity virus dynamics model with multi-stages of infected cells and two routes of infection. Math. Meth. Appl. Sci. 2019. [Google Scholar] [CrossRef]
- Xu, R. Global dynamics of an HIV-1 infection model with distributed intracellular delays. Comput. Math. Appl. 2011, 61, 2799–2805. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Hassanien, I.A.; Azoz, S.A. Global stability of HIV infection models with intracellular delays. J. Korean Math. Soc. 2012, 49, 779–794. [Google Scholar] [CrossRef]
- Hattaf, K.; Yousfi, N.; Tridane, A. Stability analysis of a virus dynamics model with generalincidence rate and two delays. Appl. Math. Comput. 2013, 221, 514–521. [Google Scholar]
- Elaiw, A.M.; Almuallem, N.A. Global dynamics of delay-distributed HIV infection models with differential drug efficacy in cocirculating target cells. Math. Methods Appl. Sci. 2016, 39, 4–31. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Almuallem, N.A. Global properties of delayed-HIV dynamics models with differential drug efficacy in cocirculating target cells. Appl. Math. Comput. 2015, 265, 1067–1089. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Raezah, A.A. Stability of general virus dynamics models with both cellular and viral infections and delays. Math. Methods Appl. Sci. 2017, 40, 5863–5880. [Google Scholar] [CrossRef]
- Li, B.; Chen, Y.; Lu, X.; Liu, S. A delayed HIV-1 model with virus waning term. Math. Biosci. Eng. 2016, 13, 135–157. [Google Scholar] [CrossRef]
- Elaiw, A.M. Global dynamics of an HIV infection model with two classes of target cells and distributed delays. Discret. Dyn. Nat. Soc. 2012, 2012, 253703. [Google Scholar] [CrossRef]
- Lv, Y.; Hu, Z.; Liao, F. The stability and Hopf bifurcation for an HIV model with saturated infection rate and double delays. Int. J. Biomath. 2018, 11, 1850040. [Google Scholar] [CrossRef]
- Alshorman, A.; Wang, X.; Meyer, M.J.; Rong, L. Analysis of HIV models with two time delays. J. Biol. Dyn. 2017, 2, 40–64. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Zhang, J.-F. Dynamics of two time delays differential equation model to HIV latent infection. Phys. A 2019, 514, 384–395. [Google Scholar] [CrossRef]
- Shu, H.; Wang, L.; Watmough, J. Global stability of a nonlinear viral infection model with infinitely distributed intracellular delays and CTL imune responses. SIAM J. Appl. Math. 2013, 73, 1280–1302. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Abukwaik, R.M.; Alzahrani, E.O. Global properties of a cell mediated immunity in HIV infection model with two classes of target cells and distributed delays. Int. J. Biomath. 2014, 7, 1450055. [Google Scholar] [CrossRef]
- Wang, J.; Qin, C.; Chen, Y.; Wang, X. Hopf bifurcation in a CTL-inclusive HIV-1 infection model with two time delays. Math. Biosci. Eng. 2019, 16, 2587–2612. [Google Scholar] [PubMed]
- Lydyard, P.; Whelan, A.; Fanger, M. BIOS Instant Notes in Immunology; Taylor & Francis e-Library: London, UK, 2005. [Google Scholar]
- Murase, A.; Sasaki, T.; Kajiwara, T. Stability analysis of pathogen-immune interaction dynamics. J. Math. Biol. 2005, 51, 247–267. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zou, D. Global stability of in-host viral models with humoral immunity and intracellular delays. Appl. Math. Model. 2012, 36, 1313–1322. [Google Scholar] [CrossRef]
- Wang, T.; Hu, Z.; Liao, F. Stability and Hopf bifurcation for a virus infection model with delayed humoral immunity response. J. Math. Anal. Appl. 2014, 411, 63–74. [Google Scholar] [CrossRef]
- Wang, T.; Hu, Z.; Liao, F.; Ma, W. Global stability analysis for delayed virus infection model with general incidence rate and humoral immunity. Math. Comput. Simul. 2013, 89, 13–22. [Google Scholar] [CrossRef]
- Elaiw, A.M.; AlShamrani, N.H. Stability of a general delay-distributed virus dynamics model with multi-staged infected progression and immune response. Math. Methods Appl. Sci. 2017, 40, 699–719. [Google Scholar] [CrossRef]
- Hobiny, A.D.; Elaiw, A.M.; Almatrafi, A. Stability of delayed pathogen dynamics models with latency and two routes of infection. Adv. Differ. Equ. 2018, 276. [Google Scholar] [CrossRef]
- Elaiw, A.M.; AlShamrani, N.H. Stability of an adaptive immunity pathogen dynamics model with latency and multiple delays. Math. Methods Appl. Sci. 2018, 41, 6645–6672. [Google Scholar] [CrossRef]
- Lin, J.; Xu, R.; Tian, X. Threshold dynamics of an HIV-1 virus model with both virus-to-cell and cell-to-cell transmissions, intracellular delay, and humoral immunity. Appl. Math. Comput. 2017, 315, 516–530. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Elnahary, E.K.; Raezah, A.A. Effect of cellular reservoirs and delays on the global dynamics of HIV. Adv. Differ. Equ. 2018, 2018, 85. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Elnahary, E.K. Analysis of general humoral immunity HIV dynamics model with HAART and distributed delays. Mathematics 2019, 7, 157. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Alshaikh, M.A. Stability analysis of a general discrete-time pathogen infection model with humoral immunity. J. Differ. Equ. Appl. 2019. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Almatrafi, A.; Hobiny, A.D.; Hattaf, K. Global properties of a general latent pathogen dynamics model with delayed pathogenic and cellular infections. Discret. Dyn. Nat. Soc. 2019, 2019, 9585497. [Google Scholar] [CrossRef]
- Miao, H.; Teng, Z.; Kang, C.; Muhammadhaji, A. Stability analysis of a virus infection model with humoral immunity response and two time delays. Math. Methods Appl. Sci. 2016, 39, 3434–3449. [Google Scholar] [CrossRef]
- Brrow, P.; Lewicki, H.; Wei, X.; Horwitz, M.S.; Peffer, N.; Meyers, H.; Nelson, J.A.; Gairin, J.E.; Beatrice, H.H.; Oldstone, M.B.A.; et al. Antiviral pressure exerted by HIV specific cytotoxic t lymphocytes (CTLs) during primary infection demonstrated by rapid selection of CTL escape virus. Nat. Med. 1997, 3, 205–211. [Google Scholar] [CrossRef]
- Goulder, P.J.R.; Phillips, R.E.; Colbert, R.A.; McAdam, S.; Ogg, G.; Nowak, M.A.; Giangrande, P.; Luzzi, G.; Morgan, B.; Edwards, A.; et al. Late escape from an immunodominant cytotoxic t-lymphocyte response associated with progression to AIDS. Nat. Med. 1997, 3, 212–217. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, J.; Wang, H.; Ma, W.; Liao, F. Dynamics analysis of a delayed viral infection model with logistic growth and immune impairment. Appl. Math. Model. 2014, 38, 524–534. [Google Scholar] [CrossRef]
- Regoes, R.; Wodarz, D.; Nowak, M.A. Virus dynamics: the effect to target cell limitation and immune responses on virus evolution. J. Theor. Biol. 1998, 191, 451–462. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Song, X.; Ge, Z. Dynamics analysis of a delayed viral infection model with immune impairment. Appl. Math. Model. 2011, 35, 4877–4885. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Raezah, A.A.; Azoz, S.A. Stability of delayed HIV dynamics models with two latent reservoirs and immune impairment. Adv. Differ. Equ. 2018, 2018, 414. [Google Scholar] [CrossRef]
- De Milito, A. B lymphocyte dysfunctions in HIV Infection. Curr. HIV Res. 2004, 2, 11–21. [Google Scholar] [CrossRef] [PubMed]
- Amu, S.; Ruffin, N.; Rethi, B.; Chiodi, F. Impairment of B-cell functions during HIV-1 infection. AIDS 2013, 27, 2323–2334. [Google Scholar] [CrossRef] [PubMed]
- Chiodi, F.; Scarlatti, G. HIV-Induced damage of B-cells and production of HIV neutralizing antibodies. Front. Immunol. 2018, 9, 297. [Google Scholar] [CrossRef] [PubMed]
- Miao, H.; Abdurahman, X.; Teng, Z.; Zhang, L. Dynamical analysis of a delayed reaction-diffusion virus infection model with logistic growth and humoral immune impairment. Chaos Solitons Fractals 2018, 110, 280–291. [Google Scholar] [CrossRef]
- Huang, G.; Takeuchi, Y.; Ma, W. Lyapunov functionals for delay differential equations model of viral infections. SIAM J. Appl. Math. 2010, 70, 2693–2708. [Google Scholar] [CrossRef]
- Elaiw, A.M.; AlShamrani, N.H. Global properties of nonlinear humoral immunity viral infection models. Int. J. Biomath. 2015, 8, 1550058. [Google Scholar] [CrossRef]
- Elaiw, A.M.; AlShamrani, N.H. Global stability of humoral immunity virus dynamics models with nonlinear infection rate and removal. Nonlinear Anal. Real World Appl. 2015, 26, 161–190. [Google Scholar] [CrossRef]
- Hale, J.K.; Lunel, S.V. Introduction to Functional Differential Equations; Springer: New York, NY, USA, 1993. [Google Scholar]
- Kuang, Y. Delay Differential Equations with Applications in Population Dynamics; Academic Press: San Diego, CA, USA, 1993. [Google Scholar]
- Gibelli, L.; Elaiw, A.; Alghamdi, M.A.; Althiabi, A.M. Heterogeneous population dynamics of active particles: Progression, mutations, and selection dynamics. Math. Models Methods Appl. Sci. 2017, 27, 617–640. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, Y. Stability of a CD4+ T-cell viral infection model with diffusion. Int. J. Biomath. 2018, 11, 1850071. [Google Scholar] [CrossRef]
- McCluskey, C.C.; Yang, Y. Global stability of a diffusive virus dynamics model with general incidence function and time delay. Nonlinear Anal. Real World Appl. 2015, 25, 64–78. [Google Scholar] [CrossRef]
- AlAgha, A.D.; Elaiw, M.A. Stability of a general reaction-diffusion HIV-1 dynamics model with humoral immunity. Eur. Phys. J. Plus 2019, 134, 390. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elaiw, A.M.; Alshehaiween, S.F.; Hobiny, A.D. Global Properties of a Delay-Distributed HIV Dynamics Model Including Impairment of B-Cell Functions. Mathematics 2019, 7, 837. https://doi.org/10.3390/math7090837
Elaiw AM, Alshehaiween SF, Hobiny AD. Global Properties of a Delay-Distributed HIV Dynamics Model Including Impairment of B-Cell Functions. Mathematics. 2019; 7(9):837. https://doi.org/10.3390/math7090837
Chicago/Turabian StyleElaiw, Ahmed M., Safiya F. Alshehaiween, and Aatef D. Hobiny. 2019. "Global Properties of a Delay-Distributed HIV Dynamics Model Including Impairment of B-Cell Functions" Mathematics 7, no. 9: 837. https://doi.org/10.3390/math7090837
APA StyleElaiw, A. M., Alshehaiween, S. F., & Hobiny, A. D. (2019). Global Properties of a Delay-Distributed HIV Dynamics Model Including Impairment of B-Cell Functions. Mathematics, 7(9), 837. https://doi.org/10.3390/math7090837



